Исследование функции с помощью производной
На этой странице вы узнаете- Кто всегда протянет руку помощи в определении производной?
- Что такое сложная функция и зачем тут матрешка?
- Как никогда не ошибаться при решении задач с производными?
Теория теорией, а дифференцировать хочется всегда. Эта статья посвящена практике нахождения производных.
Производные основных функцийДолжно быть, вы уже слышали о производной и даже пробовали взять её мозговым штурмом. При отрицательном ответе вам обязательно нужно прокатиться на американских горках в нашей статье «Производная». В ней рассмотрели основные понятия производной.
Главный вопрос этой статьи: как ее находить? Для этого существуют свои формулы и правила, которых необходимо придерживаться для правильного решения заданий.
Ниже приведена таблица с формулами для нахождения производных основных функций. Применяя эти формулы, можно найти производную почти любой функции. x\)
x\)
С полной уверенностью можем сказать, что вам встречались сложные функции. Даже намного сложнее, чем те, которые приведены в таблицах. Там и сумма, и произведение, и формула в формуле. Одним словом: ужас! Как брать производную, если перед функцией стоит коэффициент, или в функцию включено несколько разных выражений? На этот случай существуют правила дифференцирования.
| Кто всегда протянет руку помощи в определении производной? В сложных функциях невозможно пользоваться только формулами для нахождения производной. Если функция 5. Производная сложной функции. Сложная функция — это функция, внутри которой есть другая функция.
Чтобы найти производную сложной функции, необходимо найти производную “внутренней” функции и умножить ее на производную “внешней” функции. (f(g(x))’ = g'(x) * f'(g(x)) Найдем производную уже рассмотренной функции \(f(x) = cos(\sqrt{x})\). \(f'(x) = (cos(\sqrt{x}))’ = (\sqrt{x})’ * (cos(\sqrt{x}))’ = \frac{1}{2\sqrt{x}} * (-sin(\sqrt{x})) = -\frac{sin(\sqrt{x})}{2\sqrt{x}}\) Исследование функции с помощью производнойВ задании нам может быть дана только функция без ее графика. В этом случае мы можем проанализировать поведение функции с помощью производной. Исследуем функцию f(x) = (x — 4)2(x + 11) + 4. Cначала возьмем производную от этой функции: f'(x) = ((x — 4)2(x + 11))‘ + 4′ = ((x — 4)2(x + 11))’ = ((x — 4)2)'(x + 11) + (x — 4)2(x + 11)’ Любое исследование функции с помощью производной начинается именно с дифференцирования функции. Теперь рассмотрим алгоритм нахождения точек минимума и максимума:
Найдем точки минимума и максимума в нашей функции. Поскольку производную мы уже взяли, можно сразу перейти ко второму шагу: (x — 4)(3x + 18) = 0 Полученные значения х расставляем на числовой прямой: Теперь определим знаки на промежутках слева направо. 1. Возьмем точку -10 и подставим ее в производную функции: 2. Возьмем точку 0 и подставим ее в производную функции: 3. Возьмем точку 5 и подставим ее в производную функции: Расставим полученные знаки на прямой: Остался последний пятый шаг. В точке -6 производная меняет знак с плюса на минус, значит, это точка максимума. В точке 4 производная меняет знак с минуса на плюс, значит, это точка минимума.
Но это не все выводы, которые уже можно сделать о функции. Вспомним, что функция возрастает, когда производная положительна, а убывает, когда производная отрицательна. Однако могут встретиться задания, в которых необходимо найти наибольшее или наименьшее значение функции на определенном интервале. Для выполнения таких заданий существует следующий алгоритм нахождения наибольшего и наименьшего значения функции.
Для примера найдем наибольшее значение функции f(x) = (x — 4)2(x + 11) + 4 на отрезке [-10; 0]. Первые два шага мы уже выполнили, когда рассматривали алгоритм нахождения точек минимума и максимума. Из них отрезку [-10; 0] принадлежит х = -6 — точка максимума. Теперь определим значение функции в трех точках: f(-10) = (-10 — 4)2(-10 + 11) + 4 = 196 + 4 = 200 Наибольшее из полученных значений — это 504. Это и будет ответ.
Подведем итог.
Задание 1.
Задание 2.
Ответы: 1. — 3 2. — 1 3. — 2 4. — 2 5. — 1 Исследование функции с помощью производной: условия, график, примерыСодержание:
Содержание
Как применить производную к исследованию функцииПроизводная функции — это скорость, с которой функция изменяется в зависимости от входной переменной. Применение производнойОсновные способы использования производной при изучении функций:
Полная схема исследования функцийОбласть функции — это множество всех возможных входных значений (также называемых независимой переменной), для которых функция определена. Другими словами, это множество всех значений x, для которых функция дает допустимый результат. Область функции может быть задана явно или неявно, в зависимости от характера функции. Например, рассмотрим функцию \(f(x) = 1/x\). Знаменатель функции не может быть нулевым, поэтому областью функции являются все действительные числа, кроме x = 0, то есть D = {x ∈ R | x ≠ 0}. Другой пример — функция \(g(x) = √(x — 2)\). Радиканда (x — 2) должна быть неотрицательной, поэтому областью функции являются все действительные числа, большие или равные 2, т.е. D = {x ∈ R | x ≥ 2}. Иногда область действия функции неявно определяется контекстом, в котором она используется. Например, в задаче о расстоянии, пройденном автомобилем за время, область функции неявно определяется как множество всех неотрицательных действительных чисел (поскольку время не может быть отрицательным). Пересечения — это точки, в которых график пересекает ось x или y. Они полезны при анализе поведения функции и поиске важных особенностей ее графика.
Асимптоты — это линии, к которым приближается график функции, но никогда не касается их. Они могут быть вертикальными, горизонтальными или косыми (наклонными). Вот некоторые распространенные типы асимптот:
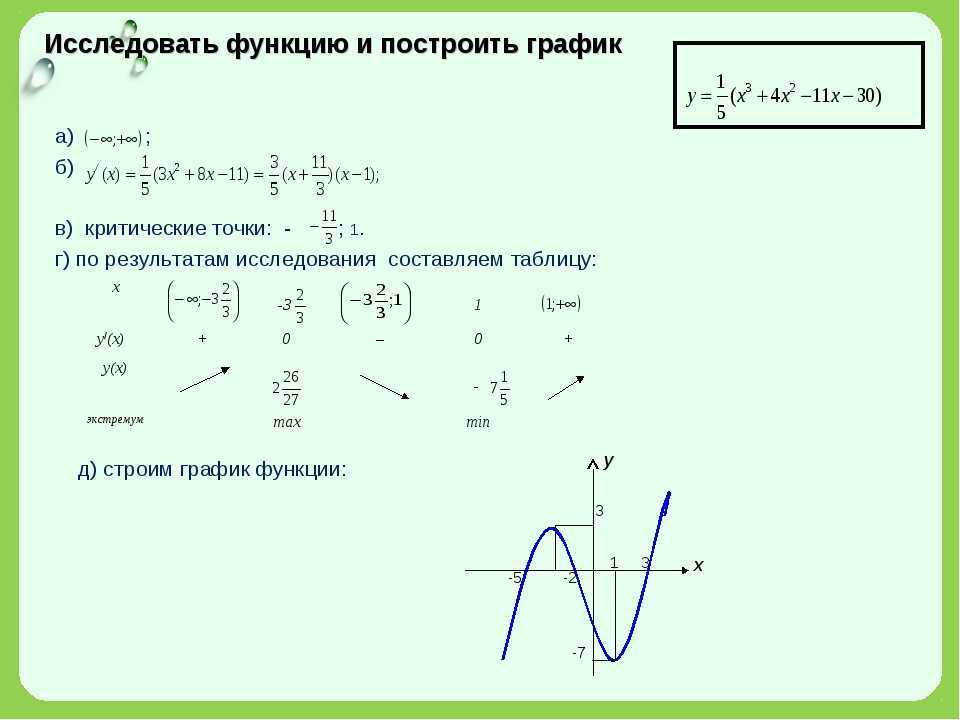
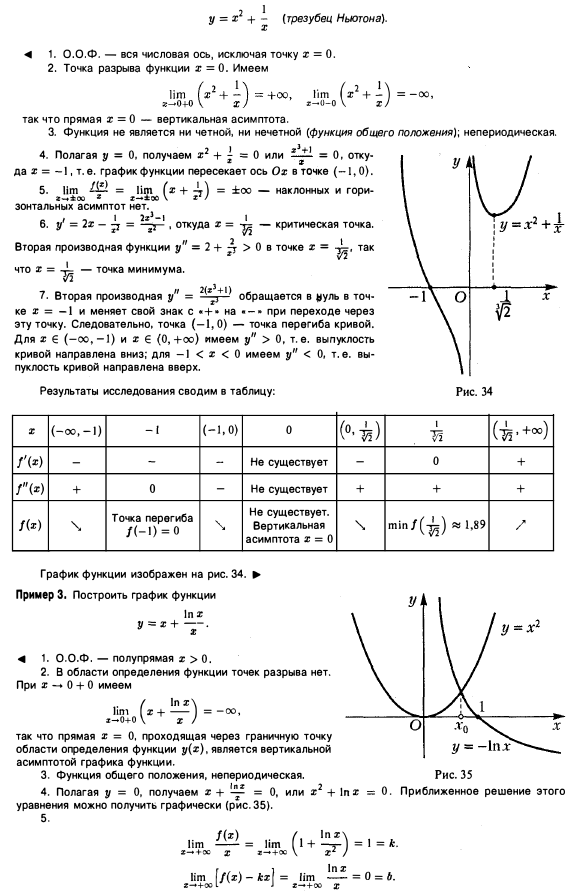
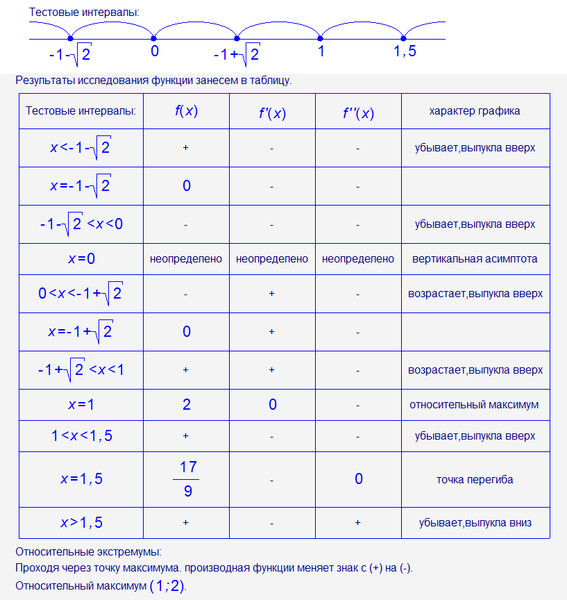
УсловияЭкстремумы и монотонностьЭкстремумы — это максимальные и минимальные значения, которых достигает функция в своей области. Они могут возникать либо в критических точках, либо в конечных точках области. 1. Проверка на первую производную предполагает нахождение критических точек функции, то есть точек, в которых производная равна нулю или не определена. Затем анализируем знак производной по обе стороны от каждой критической точки, чтобы определить, является ли она локальным максимумом, локальным минимумом или ни тем, ни другим. Если в критической точке знак производной меняется с положительного на отрицательный, то это локальный максимум. Если знак меняется с отрицательного на положительный, то это локальный минимум. Если знак не меняется, то это ни максимум, ни минимум. 2. Проверка второй производной предполагает нахождение критических точек функции, а затем анализ вогнутости функции в каждой критической точке с помощью второй производной. Монотонность относится к поведению функции в отношении ее возрастания или убывания на интервале. Считается, что функция монотонно возрастает, если ее значения увеличиваются по мере увеличения независимой переменной (обычно обозначаемой x) на этом интервале. Аналогично, функция монотонно убывает на интервале, если ее значения уменьшаются с увеличением x на этом интервале. Функция, которая не является ни возрастающей, ни убывающей на интервале, называется немонотонной на этом интервале. Монотонность функции можно определить, анализируя ее производную. Если производная функции положительна на интервале, то функция монотонно возрастает на этом интервале. Важно отметить, что монотонность функции зависит от рассматриваемого интервала. Функция может быть монотонно возрастающей на одном интервале и монотонно убывающей на другом. Выпуклость и точки перегибаВыпуклость относится к форме графика функции. Считается, что функция выпуклая, если ее график выгнут или изогнут вверх, а функция вогнутая, если ее график выгнут внутрь или изогнут вниз. Термин «выпуклость» происходит от того, что график выпуклой функции похож на выпуклую линзу. Точка перегиба — это точка на графике функции, в которой изменяется вогнутость. Это точка, в которой график меняется с вогнутого вверх (раскрывается вверх) на вогнутый вниз (раскрывается вниз), или наоборот. ГрафикПостроение графика \(f(x) = x2\) имеет производную \(f(x) = 2x\). При каждом x график f имеет наклон 1, поэтому при каждом x высота графика \(f’\) также 1. При каждом x график f имеет наклон -1/2, поэтому при каждом x высота графика \(f’ \) также -1/2. Когда кривая \(y = f» (x)\) выше x — ось, вторая производная положительна, поэтому f вогнута вверх. Аналогично, когда кривая \(y = f» (x)\) ниже x — ось, вторая производная отрицательна, поэтому f вогнута вниз. Примеры решения задачЗадача 1 Нахождение монотонности функции по графику ее производной.
Ответ: В этом вопросе нам дана кривая \(y = f’ (x)\) и попросили найти интервалы, на которых \(f (x)\) увеличивается. Обычно мы смотрим на график и ищем те части графика, где наклон положительный, чтобы увидеть, где функция возрастает, и где наклон отрицательный, чтобы увидеть, где функция убывает. Чтобы ответить на этот вопрос, нам нужно запомнить: наклон функции \(f (x)\) задается \(f’ (x)\). Это означает, что мы также можем увидеть эту информацию на графике \(y = f’ (x)\). Производная \(f’ (x)\) будет положительным, когда кривая находится выше отметки x и будет отрицательным, когда кривая находится ниже оси x. Когда x ∈] 1,5 [, что мы имеем \(f′(x) >0\),поэтому наклон \(f (x)\) положительный. Это означает, что для этих значений x наша функция f должна быть возрастающей. Аналогично, когда x ∈] 0,1 [ или x ∈] 5,6 [, мы видим, что \(f′ (x) <0\)f′, поэтому наклон \(f (x)\) отрицательный для этих значений x, что означает, что f уменьшается на этих интервалах. Таким образом, мы смогли показать, что f увеличивается на интервале ] 1,5 [ и уменьшается на интервалах ]0,1[ и ]5,6 [. Стоит отметить, что \(f′ (1) = 0 и f′ (5)=0\) . Поскольку эти значения x являются конечными точками возрастающих или убывающих интервалов, мы технически можем включить эти значения в наш ответ. На самом деле, в некоторой литературе конечные точки с нулевой производной всегда включаются в интервалы, где функция возрастает или убывает. Включать или не включать конечные точки с нулевой производной в интервалы возрастания или убывания — это личное предпочтение. Кроме того, поскольку наша функция не дифференцируема, когда \(x ≤0 и x ≥6\). Задача 2 Нахождение x-координат точек перегиба функции по графику ее второй производной. Используйте заданный график функции f′′ для нахождения x-координат точек перегиба из f. Ответ: Мы хотим найти точки перегиба функции \(f (x)\). Это точки, где \(f (x)\) непрерывна и изменяет вогнутость, либо с вогнутой вверх на вогнутую вниз, либо наоборот. Мы знаем, что все точки перегиба возникают, когда \(f′′ (x) = 0\) или когда вторая производная не существует. Итак, из нашей диаграммы видно, что это может произойти только тогда, когда x = 1, x = 4 или x = 7. Однако мы только показали, что наша кривая может иметь точки перегиба при этих значениях x. Кривая вогнута вверх, если ее вторая производная положительна, и вогнута вниз, если ее вторая производная отрицательна. Нам дан график кривой \(y = f′′ (x)\), поэтому можем определить, когда она положительна или отрицательна, посмотрев, где кривая находится выше или ниже точки оси x. Теперь видно, что когда x = 1, кривая y = f (x) изменится с вогнутой вниз на вогнутую вверх. Таким образом, существует две точки перегиба для кривой y = f (x), один, когда x = 1 и другой, когда x =7. Задача 3 Нахождение вогнутости функции по графику ее производной. График первой производной f’ функции f показан на рисунке. На каких интервалах f вогнута вверх или вогнута вниз?
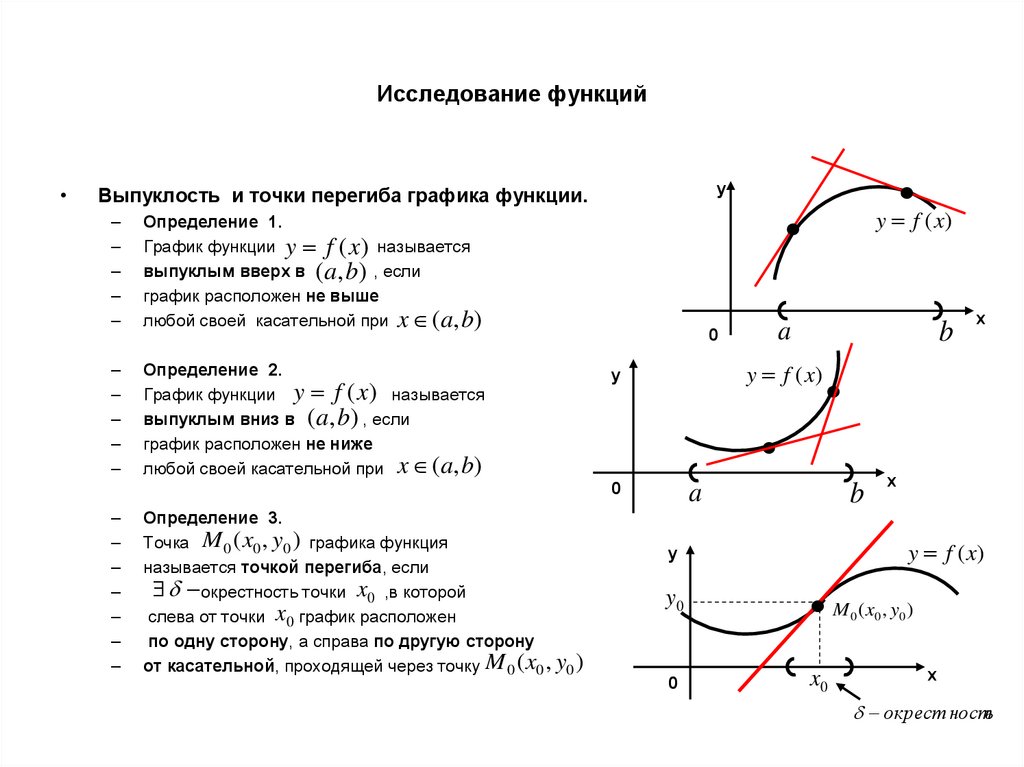
Во-первых, кривая вогнута вверх, если ее вторая производная положительна, и вогнута вниз, если ее вторая производная отрицательна. Это означает, что нужно определить знак второй производной по графику первой производной. Для этого нужно помнить, что если мы продифференцируем первую производную, то получим вторую производную — \(f» (x)\) — это наклон кривой \(y = f’ (x)\). Мы можем отметить интервалы, где наклон положительный и отрицательный, на предоставленном нам графике. Мы видим, что f вогнута вверх на ]0,1[, ]2,3[, и ]5,7[ и вогнуты вниз на ]1,2[, ]3,5[, и ] 7,9[/ Математическая сцена — Функции 2 — Урок 4Математическая сцена — Функции 2 — Урок 4 — Исследование функций с помощью производных
Урок 4 Исследование функций с помощью производных Производная функции является мерой градиент графика, поэтому мы можем сделать следующие выводы:
Это означает, что когда производная меняет знак от положительного к отрицательному или от отрицательного к положительному должен быть поворотный момент или вершина на графе. Это так называемые максимальные и минимальные точки. Они есть не обязательно наибольшие или наименьшие общие значения функции. Глядя на таблицу знаков производной показывает нам, где находятся эти стационарные точки. Помните, непрерывная функция не может изменяться между отрицательными и положительными значениями, не переходя через ноль, поэтому мы ищите стационарные точки, выясняя, когда производная равна 0, Пример 1 Найдите производную f(x) = x 2 , составьте таблицу знаков и используйте ее, чтобы нарисовать график функции f(x). Если f(x) = x 2 тогда f(x) = 2x. Стационарные точки возникают, когда f(x) = 2x = 0 , то есть когда x = 0. Ниже приведена таблица, показывающая знак f (x) .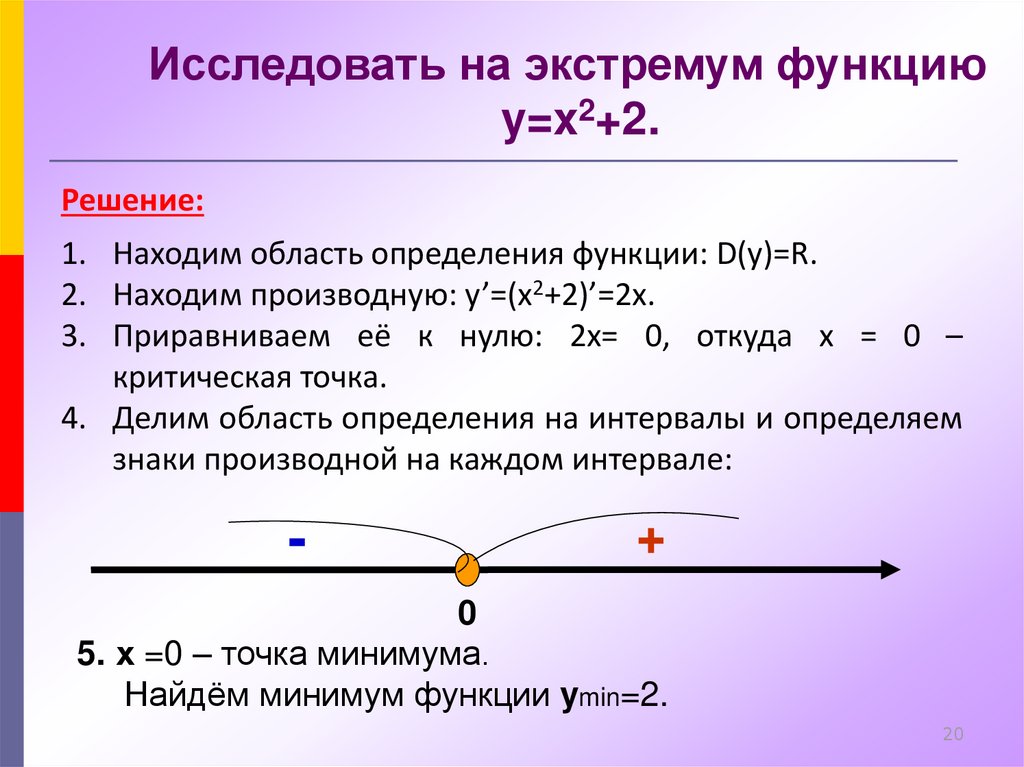
Y = х 2 Производная равна 0 когда х = 0 а градиент меняется с на +, так что это точка минимума.
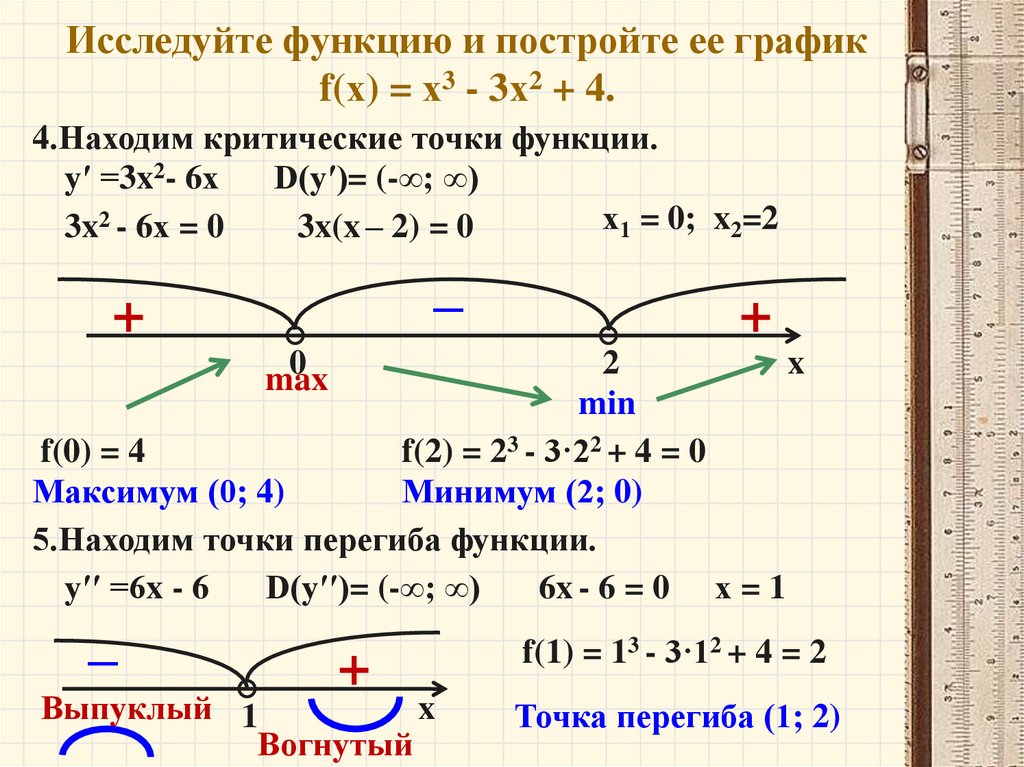
Пример 2 Найдите производную f(x) = x 3 3x 2 + 4, составьте таблицу знаков производной и используйте это, чтобы найти стационарные точки. Сравните свои результаты с графиком, показанным на ваш графический калькулятор. Если f(x) = x 3 3x 2 + 4, затем f(x) = 3x 2 6x. Найти производную 0. 3x 2 6х = 0 3x(x 2) = 0 Это уравнение имеет решения х = 0 и х = 2 и в этих точках производная меняет знак. Находим знак f(x) = 3x 2 6x. Мы могли бы составить таблицу без факторизации во-первых, просто выбирая значения x между нулями и находя знак производная. ж(1) = 3(1) 2 6(1) = 3 + 6 = 9 (+) ж(1) = 31 2 61 = 3 () ж(3) = 33 2 63 = 9 (+) Это дает более простую таблицу
выше, но показывает ту же информацию. Из таблицы мы можем сделать вывод, что у нас есть максимум, когда x = 0. Градиент равен 0, поэтому график горизонтальный, а градиент изменяется от + (подъем) до (снижение). Производная также равна нулю, когда x = 2. и градиент меняется с на +, так что здесь у нас есть минимум. Мы можем найти максимальное и минимальное значения функции, помещая эти значения x в Формула исходной функции. ж(0) = 0 3 30 2 + 4 = 4 Функция имеет максимум стоимость в точке (0, 4) . f(2) = 2 3 32 2 + 4 = 8 12 + 4 = 0 Функция имеет минимум значение в точке (2, 0). Графический калькулятор показывает следующий график.
Иногда производная от
функция равна нулю без изменения знака производной по ходу
через нулевую точку. В таких случаях нет никакой стационарной точки, но то, что
называется точкой перегиба. Пример 3 Рассмотрим функцию f(x) = x 3 . Производная f(x) = 3x 2 и равен нулю, когда x = 0, Ниже приведена таблица знаки производной. Точка (0, 0) — это точка сгибания. График возрастает до x = 0, горизонтален по x = 0 и затем продолжает увеличиваться после 0,
Расчеты с использованием производная имеет множество практических применений, в частности, для нахождения максимальных и минимальные значения. Следующие два примера демонстрируют это. Пример 4 Мы хотим сделать картон коробку из квадратного картона со стороной 1 м. Для этого сгибаем углы, как показано на схеме. Сколько нам нужно вырезать из углы в порядке чтобы коробка имела вид как можно больший объем?
Назовите это x , что означает длину
каждой стороны коробки будет в 2 раза короче карты, то есть в 1 2 раза. V = высотадлинаширина = х(1 2х)(1 2х) = x(1 4x + 4x 2 ) = x 4x 2 + 4x 3 Различие этого и нахождение, когда производная равна 0, дает нам: V = 1 8x + 12x 2 = 0 Это квадратное уравнение можно решить с помощью калькулятора или квадратной формулы. Очевидно, что мы не может быть х = , как если бы мы отрезали метр не было бы коробка осталась. Таким образом, это должно дать минимальное значение объема. Максимальный объем будет когда х = . V() = (1 2)(1 2) = м 3 Максимальный объем коробка будет м 3 когда мы режем м с каждого угла.
Пример 5 Прямоугольник рисуется как
показано на схеме. Одна сторона образована линией y = 3 и одним углом,
P, лежит на графике f(x) = x 2 . Стороны прямоугольника х и 3 года или 3 x 2 так как точка P лежит на графике f(x) = x 2 . Следовательно, площадь равна A = длина в ширину = x(3 x 2 ) = 3x 3 Различие этого и поиск, где производная равна нулю, дает: А = 3 3x 2 = 0 3 = 3x 2 х = 1 Прямоугольник находится в положительный квадрант, поэтому мы не можем иметь x = 1. Максимальная площадь достигается, когда x = 1 поэтому мы можем подставить это значение в формулу площади. А = 3x 3 = 3 1 = 2 Попрактикуйтесь в этих методах, затем попробуйте
Тест 4 по функциям 2.
Калькулятор производных — MathCracker. com comИнструкции: Используйте этот калькулятор производной, чтобы найти производную функции, которую вы предоставляете, показывая все этапы процесса. Пожалуйста, введите функцию, для которой вы хотите вычислить производную, в поле ниже. Калькулятор производных 93).Обратите внимание, что его можно назвать калькулятором первой производной, так же как и калькулятором производной. Первая производная и производные представляют одно и то же, а «первая» часть обычно опускается. Предоставленная функция может быть полностью упрощена или нет, это не имеет значения, так как калькулятор сначала упростит функцию, если
необходимо перед вычислением его производной. После того, как действительная функция была предоставлена, вам просто нужно нажать «Рассчитать», подождать несколько секунд, и вам будут представлены все этапы расчета. Дифференциация является основным инструментом, используемым в исчислении (наряду с интегрированием), и это важная операция, которая широко используется в более сложной математике. Некоторые очень распространенные приложения включают расчет касательной, максимумы и минимумы и многое другое. Как вычислить производную функции?Процесс вычисления производной функции называется дифференцированием и заключается в определении мгновенной скорости изменения точки в точке каждой точке области определения функции. Какова мгновенная скорость изменения функции? Итак, начнем с определения скорости изменения: Рассмотрим функцию \(f\), и предположим, что у нас есть две точки, \(x_0\) и \(x_1\). В точке \(x_0\) функция равна \(f(x_0)\), а в точке \(x_1\) функция принимает значение \(f(x_1)\) Тогда изменение f определяется как \(\Delta y = f(x_1) — f(x_0)\) (что также называется изменением y). Графически: Производная формулаТаким образом, если \(\Delta x\) представляет собой изменение x, а \(\Delta y\) представляет собой изменение значения функции из-за изменения в x, соответствующий скорость изменить это: \[\text{Скорость изменения} = \displaystyle \frac{\Delta y}{\Delta x} \] Тогда какой будет мгновенная скорость изменения? Это соответствует анализу того, что произойдет, если \(\Delta x\) станет очень маленьким. Можно было бы ожидать, что \(\Delta y\) тоже станет маленьким, но что произойдет со скоростью между \(\Delta y\) и \(\Delta x\)? Итак, в этом контексте мгновенная скорость изменения определяется как \[\text{Мгновенная скорость изменения} = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} \] Итак, с точки зрения непрофессионала, мы устанавливаем \(x_0\) фиксированным и вычисляем скорость изменения для значений \(x_1\), которые все ближе и ближе к \(x_0\). \[f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) — f (x_0)}{x_1 — x_0} \] Если указанный выше предел выходит за пределы, мы говорим, что функция f дифференцируема в точке \(x_0\). Также будем говорить, что функция дифференцируема на множестве A, если функция дифференцируема в каждой точке множества. Этапы использования формулы производной
Обратите внимание, что шаг 6 — это шаг 6, который некоторым нравится по умолчанию. Действительно, альтернативная производная формула, которая может показаться более простой для упрощения: \[f'(x_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0 + h) — f(x_0)}{h} \] , это формула, которую вы можете найти в своем учебнике, вместо другой. Правила производныхКазалось бы, вычисление производной по формуле — это чертовски много работы. И действительно, это мог бы быть трудоемкий процесс, если бы мы решили проработать каждый процесс дифференцирования по формуле производной. К счастью, есть ряд функций (а именно полиномы, тригонометрические функции)
для которых мы точно знаем, каковы их производные. Кроме того, у нас есть правила дифференцирования, которые позволяют нам найти производную функции, которая является составной функцией и/или комбинацией элементарных функций (для которых мы знаем их производную), в терминах элементарных производных. Каковы шаги для вычисления производной?
Часто функция, для которой вы пытаетесь найти производную, не является простой функцией, а является базовой комбинацией нескольких простых функций. \[f(x) = x + \cos(x) + \sin(x)\] сама по себе не является элементарной функцией, а является составной функцией трех элементарных функций, \(x\), \(\sin x\) и \(\cos x\). Применение производныхКто-то может подумать: «Ну, производные предполагают пределы, и это сверхтеоретически, поэтому у них не должно быть слишком много применений», но вы совершенно ошибаетесь. Магия производных в том, что они, по сути, связаны со скоростью изменения функций, которые могут представлять различные типы процессов. 92\справа)\) Таким образом, мы получаем следующий график для функции на интервале \([-5, 5]\): Пример: Калькулятор производныхНайдите производную от \( f(x) = \displaystyle \ дробь{4}{х}\). Везде ли он четко определен? График это. Решение. Функция, для которой требуется производная, имеет вид \(\displaystyle f(x)=\frac{4}{x}\). Дальнейшее упрощение не требуется, поэтому мы можем перейти непосредственно к вычислению его производной: 92}\) Графически: Подробнее о производных и функциях Этот калькулятор производных с шагами окажется для вас очень полезным, так как он проведет вычисление производной любой заданной функции, показывая все шаги
процесса, применяя соответствующие производные правила и сообщая вам, когда они применяются и почему. |

 2}\)
2}\) Что делать в таком случае, если нам нужно найти, например, отрезки возрастания, точки экстремума, наибольшее или наименьшее значение функции? Не во всех случаях получится построить график, да и это займет достаточно большое количество времени, которое и без того ограничено на экзамене.
Что делать в таком случае, если нам нужно найти, например, отрезки возрастания, точки экстремума, наибольшее или наименьшее значение функции? Не во всех случаях получится построить график, да и это займет достаточно большое количество времени, которое и без того ограничено на экзамене.  Нужно найти производную функции.
Нужно найти производную функции. Производная на этом промежутке будет положительной.
Производная на этом промежутке будет положительной.  Поскольку мы уже определили знаки производной, то смело можем сделать вывод, что на промежутках до -6 и после 4 функция будет возрастать, а на промежутке от -6 до 4 — убывать.
Поскольку мы уже определили знаки производной, то смело можем сделать вывод, что на промежутках до -6 и после 4 функция будет возрастать, а на промежутке от -6 до 4 — убывать. 
 С их помощью можно найти производную любой из основных функций.
С их помощью можно найти производную любой из основных функций. {2}(x)}\)
{2}(x)}\) 2 — 9x + 10, то f»(x) = 6x — 6\). Приравнивание \(f»(x)\) к нулю дает x=1, что является точкой перегиба кривой.
2 — 9x + 10, то f»(x) = 6x — 6\). Приравнивание \(f»(x)\) к нулю дает x=1, что является точкой перегиба кривой.
 3 и f(x) = sin(x)\) .
3 и f(x) = sin(x)\) .
 Чтобы найти y-пересечение функции, мы задаем x равным нулю и оцениваем функцию при этом значении. Полученное значение представляет собой точку пересечения графика с осью y.
Чтобы найти y-пересечение функции, мы задаем x равным нулю и оцениваем функцию при этом значении. Полученное значение представляет собой точку пересечения графика с осью y.
 Если вторая производная положительна, то критическая точка является локальным минимумом. Если вторая производная отрицательна, то критическая точка является локальным максимумом. Если вторая производная равна нулю, то тест не дает результатов, и нужно использовать другой метод, например, тест на первую производную.
Если вторая производная положительна, то критическая точка является локальным минимумом. Если вторая производная отрицательна, то критическая точка является локальным максимумом. Если вторая производная равна нулю, то тест не дает результатов, и нужно использовать другой метод, например, тест на первую производную. Если производная отрицательна на интервале, то функция монотонно убывает на этом интервале. Если производная равна нулю на интервале, то функция может иметь максимум или минимум в этой точке, но это не указывает на монотонность.
Если производная отрицательна на интервале, то функция монотонно убывает на этом интервале. Если производная равна нулю на интервале, то функция может иметь максимум или минимум в этой точке, но это не указывает на монотонность. Она является функцией общего наклона. Она дает наклон любой линии, касательной к графику f. Например, если нам нужен наклон касательной линии в точке (-2,4), мы оцениваем производную по координате x этой точки и получаем f(-2) = -4. На рисунке слева показано несколько касательных линий, каждая из которых обозначена своим наклоном.
Она является функцией общего наклона. Она дает наклон любой линии, касательной к графику f. Например, если нам нужен наклон касательной линии в точке (-2,4), мы оцениваем производную по координате x этой точки и получаем f(-2) = -4. На рисунке слева показано несколько касательных линий, каждая из которых обозначена своим наклоном. На каких интервалах f возрастает или убывает?
На каких интервалах f возрастает или убывает?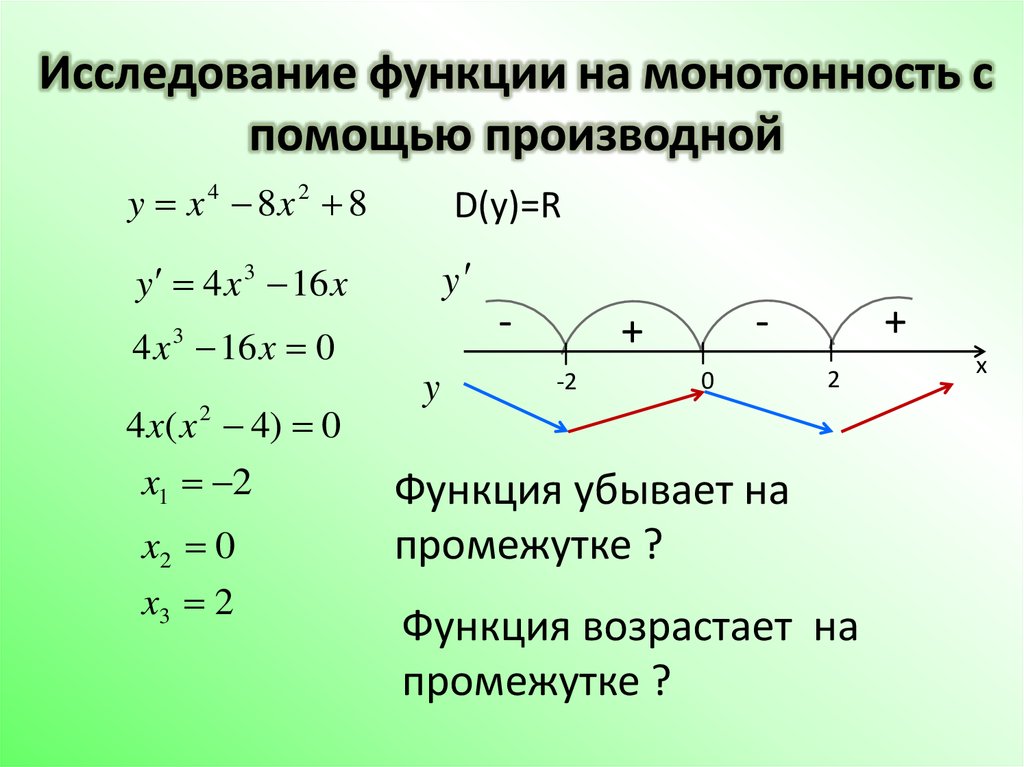
 Аналогично, когда x = 7, кривая y = f (x) изменится с вогнутой вверх на вогнутую вниз. Таким образом, обе эти точки являются точками перегиба для нашей кривой. Однако мы видим, что вогнутость не меняется с положительной на отрицательную или наоборот в точке x = 4, поэтому это не точка перегиба.
Аналогично, когда x = 7, кривая y = f (x) изменится с вогнутой вверх на вогнутую вниз. Таким образом, обе эти точки являются точками перегиба для нашей кривой. Однако мы видим, что вогнутость не меняется с положительной на отрицательную или наоборот в точке x = 4, поэтому это не точка перегиба.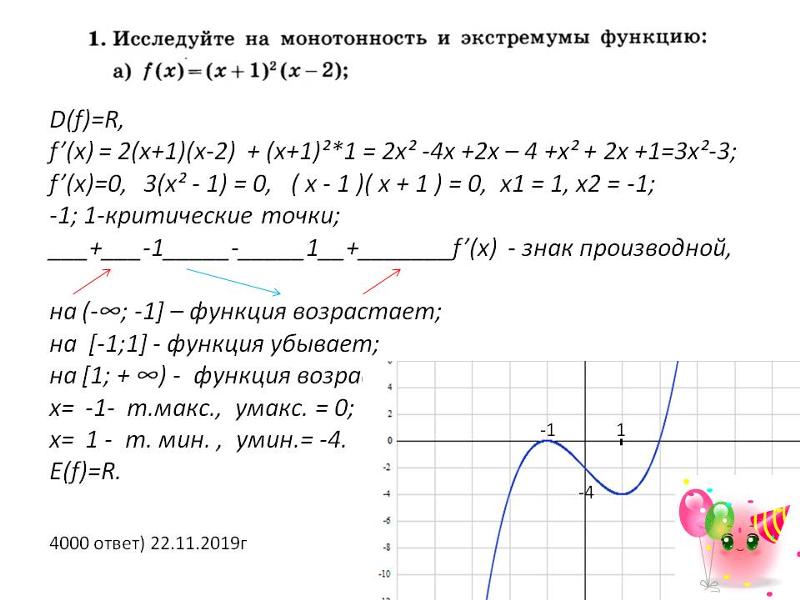

 высота ящика тоже будет х, а объем V можно записать так:
высота ящика тоже будет х, а объем V можно записать так: Найдите координаты точки P, чтобы прямоугольник имел
максимально возможная площадь.
Найдите координаты точки P, чтобы прямоугольник имел
максимально возможная площадь.
 Кроме того, изменение x определяется как
\(\Дельта х = х_1 — х_0)\). Проще говоря, \(\Delta x\) — это изменение x, тогда как \(\Delta y\) — это изменение значения функции из-за изменения x.
Кроме того, изменение x определяется как
\(\Дельта х = х_1 — х_0)\). Проще говоря, \(\Delta x\) — это изменение x, тогда как \(\Delta y\) — это изменение значения функции из-за изменения x. Используя эту идею мгновенного
скорости изменения, мы можем дать следующую формулу для производной в точке \(x_0\).
Используя эту идею мгновенного
скорости изменения, мы можем дать следующую формулу для производной в точке \(x_0\). Это,
подставьте значения x0 и x1 в f и посмотрите, как формула выглядит алгебраически
Это,
подставьте значения x0 и x1 в f и посмотрите, как формула выглядит алгебраически
 Например,
функция
Например,
функция