Инъективное отображение это: Инъективное отображение | это… Что такое Инъективное отображение?

Отображения. Инъективные и сюръективные отображения

Если указан закон, сопоставляющий каждому элементу множества А единственный элемент множества В, то говорят, что имеется однозначное отображение АВ.

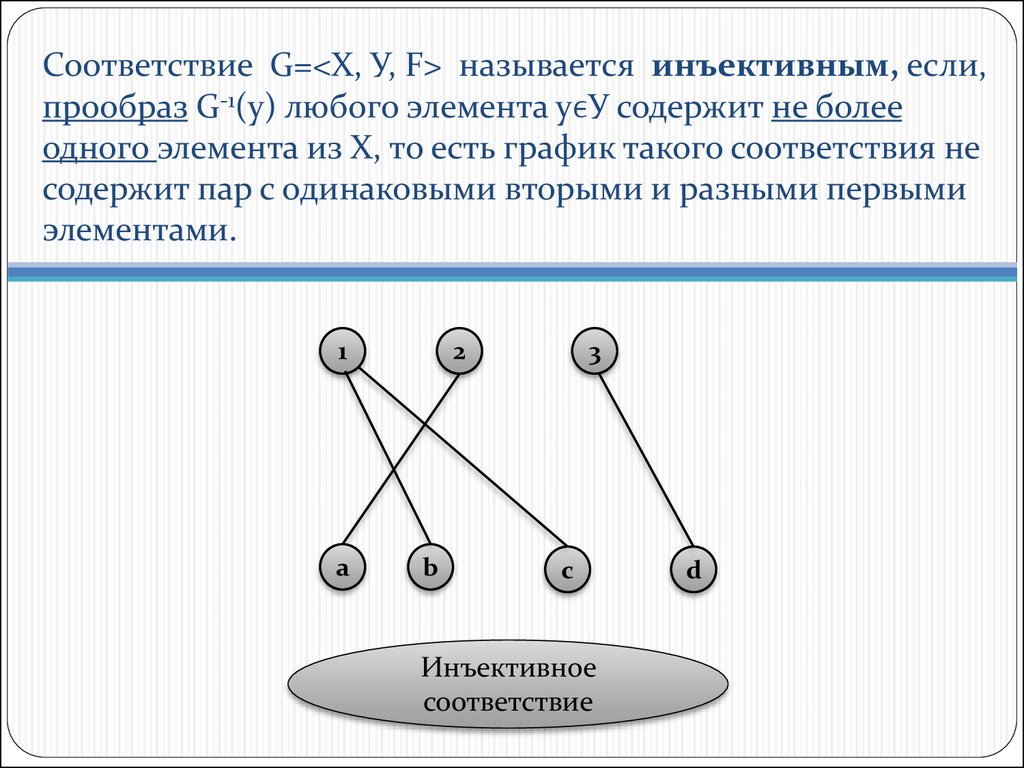
Отображение АВ называется инъективным, если разные элементы множестваA переходят в разные элементы множества B: если а в, то .

Отображение АВ называется сюръективным, если каждый элемент множества В имеет свой прообраз в множестве А.

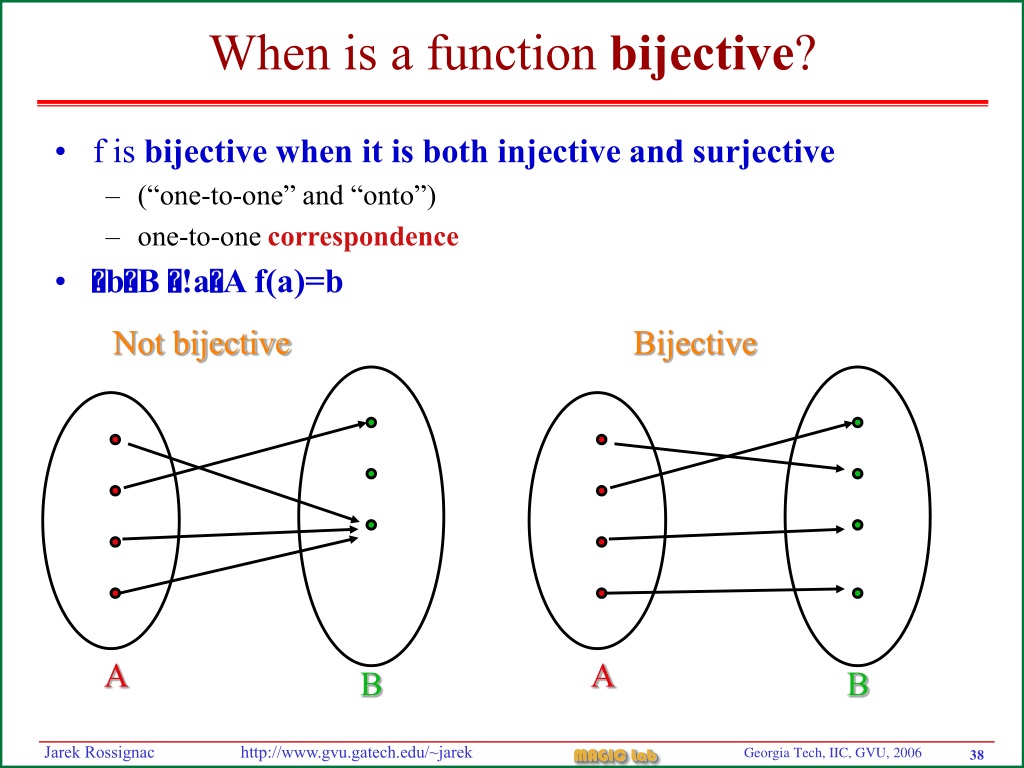
Если отображение одновременно инъективное и сюръективное, то оно называется биективным.

1. Пусть f: RR задано формулой f(x) = x²-1 (рис.3). Определить, является ли отображение f инъективным, сюръективным, биективным.

Область определения функции – R, область значений функции – [-1;+).

1. f – отображение.

   Если (х,у)  f и (х,z)  f , то y = z, так как (x,y)f, т.е. y = x²-1, (x,z)f, т.е. z = x²-1.

2. Найдутся х₁, х₂R, такие что х₁ х₂, но: f(x₁) = f(x₂), например, пусть х₁ = 1, х₂ = -1, тогда f(x₁) = 0 и f(x₂) = 0, т.е. х₁ х₂, а f(x₁) = f(x₂). Таким образом, это неинъективное отображение.

3. Так как область значений функции [1;+ ) не совпадает сR, то отображение несюръективно.

2. Пусть f: RR задано формулой f(x) = x⁴. Является ли отображение инъективным, сюръективным?

1. Поскольку х₁=2R, х₂ = -2R, f(2) = f(-2) = 16, т.е. х₁ х₂, а f(x₁

   ) = f(x₂), то отображение неинъективно.

2. Для любого xR не существует f(х), такого что f(х) = -16, так как х⁴-16, поэтому отображение несюръективно.

3. Пусть отображение f: [0;+)[0;+) задано формулойf(x)=x². Является ли оно инъективным, сюръективным?

1. Для любых х₁, х₂[0;+), х₁х₂, f(x₁)=x₁², f(x₂)=x₂², но f(x₁) f(x₂), т.е для каждого х существует единственное f(x), следовательно, f(х) — инъективное отображение.

2. Для каждого значения f(x)[0;+) найдётся х[0;+), поэтомуf(х) — сюръективное отображение.

из 1. и 2. следует, что отображение биективно.

Всякое подмножество Г декартова произведения АхА называется отношением на множестве А.

Отношение Г называют рефлексивным, если aГа для всех aA.

Отношение Г называют симметричным, если аГbbГа.

Отношение Г называют транзитивным, если аГb, bГааГс.

Если отношение рефлексивно, симметрично, транзитивно, то оно называется отношением эквивалентности.

1. Проверить, является ли D отношением эквивалентности на R, если D={(x;y)| sin x = sin y}.

1. D – рефлексивно, так как для любого R ()D, т.е. для любого xR имеем sin x = sin x.

2. D – симметрично, так как для любой пары (,)D имеем ()D, т.е. для любых R из (x,y)D следует, что sin x = sin y, тогда и sin y = sin x, следовательно, (y,x)D.

3. D – транзитивно, так как для любых а,b,cR из того что ()D и ()D следует, что ()D, т. е. если (x,y)D, то sinx=siny, если (y,z)D, то sin y = sin z, тогда sin x=sin z, следовательно, (x,z) D.

Из 1., 2., 3. следует, что D – отношение эквивалентности на R (где R – множество действительных чисел).

2. Упражнение. Выяснить, является ли отношением эквивалентности, если ху = {(x,y)| x = 3y}.

20. Отображения множеств

Пусть X и Y — два непустых множества.

Отображением f: X →Y (множества X во множество Y) называется тройка (

X, Y, F). Здесь X, Y — два непустых множества, F – правило, сопоставляющее каждому элементу Х ϵ X однозначно определенный элемент У = f(x) ϵ Y. Множество X называется Областью определения Отображения, элемент Х ϵ X – Аргументом отображения F, элемент F(x) ϵ Y –Образом элемента Х при отображении F. При этом пишут Х → f(x). Часто, в случае когда множества X, Y –числовые, отображение называют Функцией. Если только множество Y– числовое, то отображение называют Функционалом.

Если А X, то F(A) = {f(x) : x ϵ A} называется Образом подмножества А при отображении F. Прообразом подмножества В Y называется множество {xϵ X:f(x)ϵ B},которое будем обозначать

F-1B. В частности, для В = {у} любой элемент из множества F-1B({Y}) называется Прообразому.

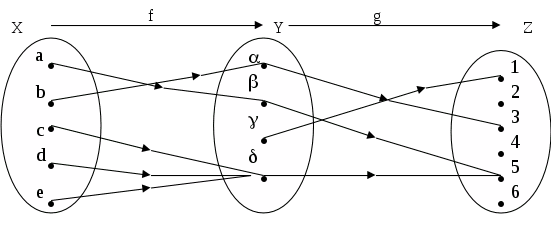
Пример. Пусть X = Y = {1,2,3}. Отображение F: X → Y задано следующим образом:

F(1)=1; F(2)=1; F(3)=2.

Тогда F(X) = {1,2}. У элемента 1 ϵ Y два прообраза — 1 и 2; у элемента 2ϵ У один прообраз — 3; у элемента 3 ϵ Y прообразов нет.

Отображение F: X → Y Называется Сюръективным (или Отображением «на»), если F(X) = Y, т. е. для каждого элемента из Y есть прообраз.

Отображение F: X→ Y Называется Инъективным (или Отображением «в»), Если из F(x) = f(x1) следует, что Х = X1, т. е. для каждого элемента Y имеется не более одного прообраза.

Отображение F: X → Y Называется Биективным (или Взаимно-однозначным), если это отображение одновременно и сюръективно, и инъективно, т. е. это отображение «на» и каждый элемент множества Y имеет ровно один прообраз. (Одно и то же правило соответствия может быть сюръективным, инъективным или биективным отображением в зависимости от исходных множеств X и У.)

Пример. Обозначим через R+ = {х ϵ R: х ≥ 0}. Рассмотрим следующие три отображения:

F: R→R+ ;g: R+ →R; h: R+ →R+ ;

Эти отображения зададим одной формулой: f(x) = x2; g(x) =x2; h(x) = x2. Они различны, так как различны исходные множества. При этом F является сюръективным, но не инъективным; G — инъективно, но не сюръективно; H — биективно.

Отображения вида F: X→X Называются Преобразованиями множества X.

Тождественным преобразованием данного множества X называется преобразование Ех

такое, что Ех (х) = х, Х ϵ X.

Пусть F: X → Y и G: Y → Z – некоторые отображения. Суперпозицией этих отображений называется отображение Gf: X → Z, определяемое следующим образом:

(gf)(x) = g(f(x)), x ϵX.

Заметим, что суперпозиция определена не для любых пар отображений. Однако суперпозиция двух преобразований одного и того же множества определена всегда.

Пусть F: X → Y и G: Y →Х

Отображение G называется Обратным к отображению F (а отображение F обратным к G), если Fg = еу;gf = ех.

Если обратное отображение существует, то оно единственно. В самом деле, пусть F: X → Y — некоторое отображение множества X во множество Y и отображения G: Y → X и H: Y → X — отображения, обратные к

F.

Тогда

(G(Fh))(Y) = (GЕу)(у) = G(у)

И ((Gf)H)(Y) = (ехH)(Y) = H(Y).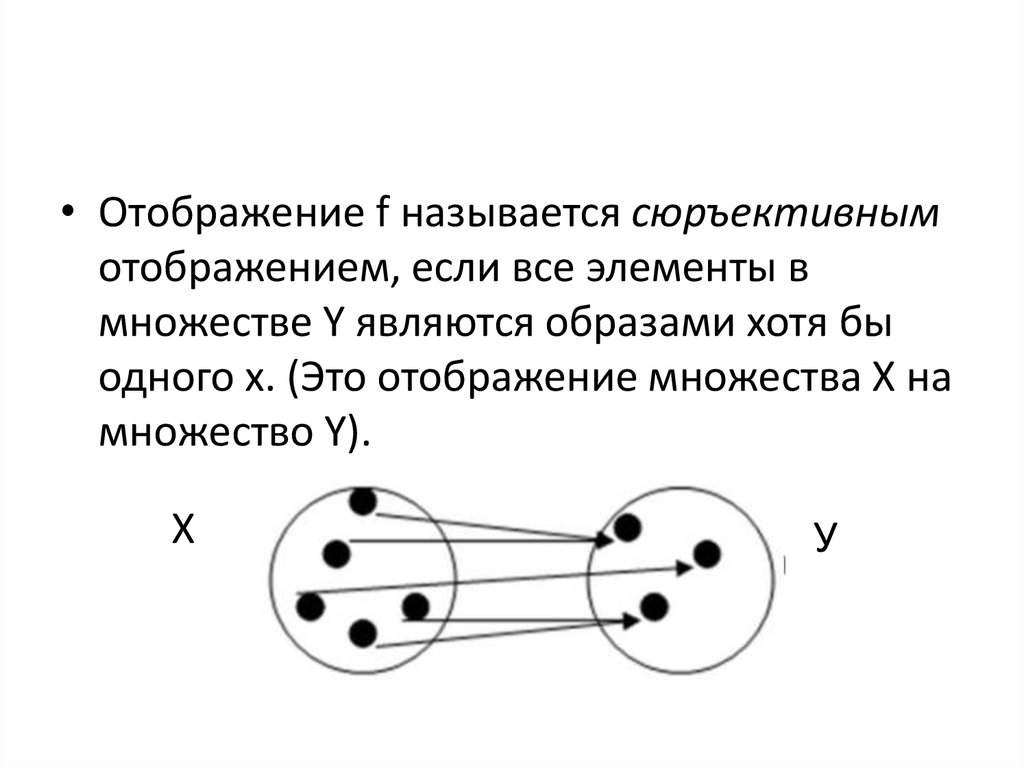

Имеем G(Fh) = (Gf)H. Отсюда получаем G(у) = H(Y),YϵY, т. е. отображения g и HСовпадают.

Обратное отображение обозначается F -1. Оно существует не всегда. Необходимое и достаточное условие существования обратного отображения дает следующая теорема.

Теорема. Отображение F имеет обратное тогда и только тогда, когда оно биективно.

Доказательство. Пусть F: X → Y.

1. Необходимость: Итак, пусть существует обратное отображение

F -1 = G: Y → X.

Рассмотрим любой У ϵ Y и Х = G(у). Тогда F(x) = f(g(y)) = у и Х – прообраз У при отображении F. Таким образом, любой У ϵ Y Имеет прообраз X, т. е. F Сюръективно.

Далее, если X, х1ϵ X, причем F(x) = F(Х1), то G(f(x)) = g(f(х1)). Следовательно, т. е.

Ех(X)=ех(х1),

Х = х1 и F инъективно. Отсюда F Биективно, и необходимость доказана.

2. Достаточность: Пусть F Биективно.

Определим отображение G: Y →Х следующим образом. Положим G(у) = х, если F(x) = у. В силу биективности F Отображение G определено на всем Y, и G = F

-1.

< Предыдущая		Следующая >

Инъективная функция — определение, формула, примеры

LearnPracticeDownload

Инъективная функция — это функция, связывающая элемент данного набора с отдельным элементом другого набора. Инъективную функцию также называют взаимно однозначной функцией. Существует множество примеров инъективных функций. Имя учащегося в классе и его порядковый номер, личность и его тень — все это примеры инъективной функции.

Давайте узнаем больше об определении, свойствах, примерах инъективных функций.

1.	Что такое инъективная функция?
2.	Свойства инъективной функции
3.	Примеры инъективной функции
4.	Практические вопросы
5.	Часто задаваемые вопросы по инъекционной функции

Что такое инъективная функция?

В инъективной функции каждый элемент данного набора связан с отдельным элементом другого набора. Функция f : X → Y называется взаимно однозначной (или инъективной), если образы различных элементов X при f различны, т. е. для любых x1, x2 ∈ X существуют различные y1, y2 ∈ Y , такие что f(x1) = y1 и f(x2) = y2.

Инъективная функция может быть представлена ​​в виде уравнения или набора элементов. Функция f(x) = x + 5 является взаимно однозначной функцией.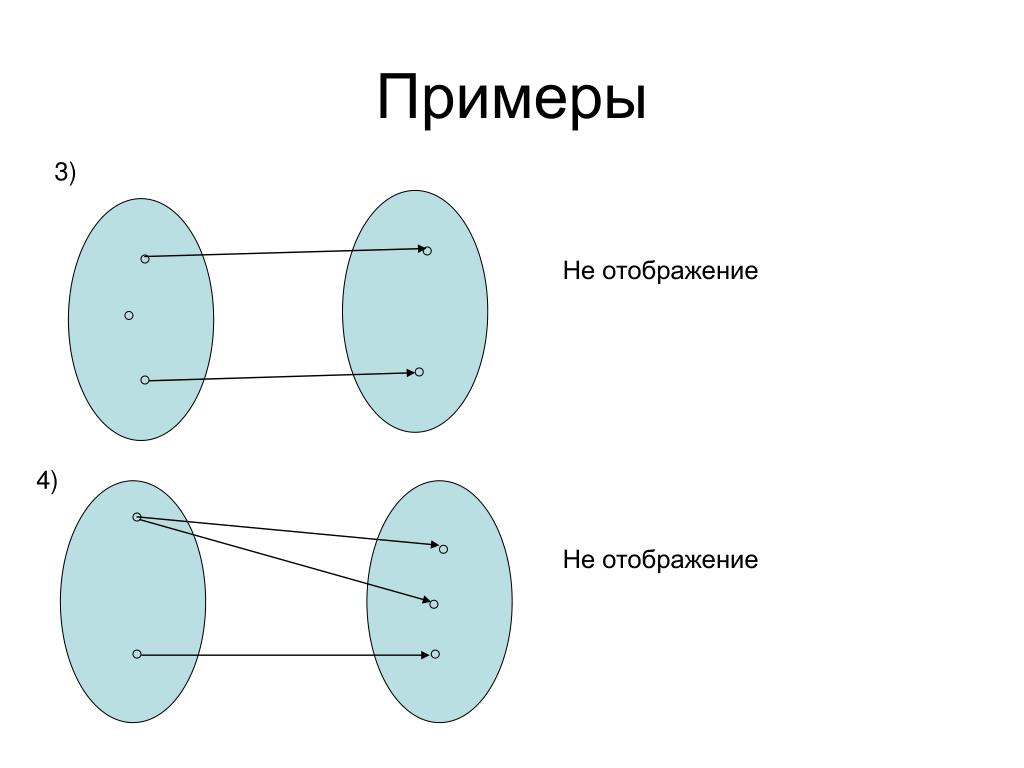 Это можно понять, взяв первые пять натуральных чисел в качестве элементов области определения функции. Функция f = {(1, 6), (2, 7), (3, 8), (4, 9), (5, 10)} — инъективная функция.

Следующие изображения в формате диаграммы Венна помогают легко найти и понять инъективную функцию. Мы можем заметить, что каждый элемент множества A отображается в уникальный элемент множества B. Далее, если какой-либо элемент множества B является образом более чем одного элемента множества A, то он не является взаимно-однозначным или инъективная функция.

Свойства инъективной функции

Ниже приведены несколько важных свойств инъективных функций.

• Область определения и область значений инъективной функции являются эквивалентными множествами.
• Множества, представляющие область определения и набор значений инъективной функции, имеют одинаковое кардинальное число.
• Инъективные функции, представленные в виде графика, всегда представляют собой прямую линию.
• Инъективная функция следует рефлексивному, симметричному и транзитивному свойству.

Связанные темы

Следующие темы помогают лучше понять инъективную функцию.

• Отношения и функции
• Функция идентификации
• Нулевая функция
• Четные и нечетные функции
• На работу
• Периодическая функция
• Сигнум Функция
• Непрерывная функция

 

Примеры инъективной функции

1. Пример 1: Покажите, что функция, связывающая имена 30 учеников класса с их соответствующими номерами в списках, является инъективной функцией.

   Решение:

   Учитывая, что домен представляет 30 учеников класса и имена этих 30 учеников. Диапазон представляет собой бросковые номера этих 30 студентов. Здесь никакие два студента не могут иметь одинаковый регистрационный номер. Следовательно, функция, связывающая имена студентов с их номерами по спискам, является взаимно однозначной или инъективной функцией.

2. Пример 2: Две функции f(x) = x + 1 и g(x) = 2x + 3 являются взаимно однозначными. Найдите gof(x), а также покажите, является ли эта функция инъективной функцией.

   Решение:

   заданными функциями являются f(x) = x + 1 и g(x) = 2x + 3. Нам нужно объединить эти две функции, чтобы найти gof(x).

   g(f(x)) = g(x + 1) = 2(x + 1) + 3 = 2x + 2 + 3 = 2x + 5

   gof(x) = 2x + 5

   Давайте теперь возьмите первые пять натуральных чисел в качестве области определения этой составной функции.

   gof(1) = 2(1) + 5 = 2 + 5 = 7

   gof(2) = 2(2) + 5 = 4 + 5 = 9

   gof(3) = 2(3) + 5 = 6 + 5 = 11

   gof(4) = 2(4) + 5 = 8 + 5 = 13

   gof(5) = 2(5) + 5 = 10 + 5 = 15

   gof(x) = {(1, 7), (2, 9), (3, 11), (4, 13) , (5, 15)}.

   Здесь отдельный элемент в области определения функции имеет отдельный образ в диапазоне.

   Следовательно, функция является инъективной.

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по инъективной функции

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы по инъекционной функции

Что такое инъективная функция?

Функция, в которой каждый элемент данного набора связан с отдельным элементом другого набора, называется инъективной функцией. Функция f : X → Y называется взаимно однозначной (или инъективной), если образы различных элементов X при f различны, т. е. для любых x1, x2 ∈ X существуют различные y1, y2 ∈ Y , такие что f(x1) = y1 и f(x2) = y2.

Как узнать, является ли функция инъективной функцией?

Функцию можно назвать инъективной, если каждый элемент множества связан с отдельным элементом другого множества. Элемент домена четко связан с различными элементами данного набора.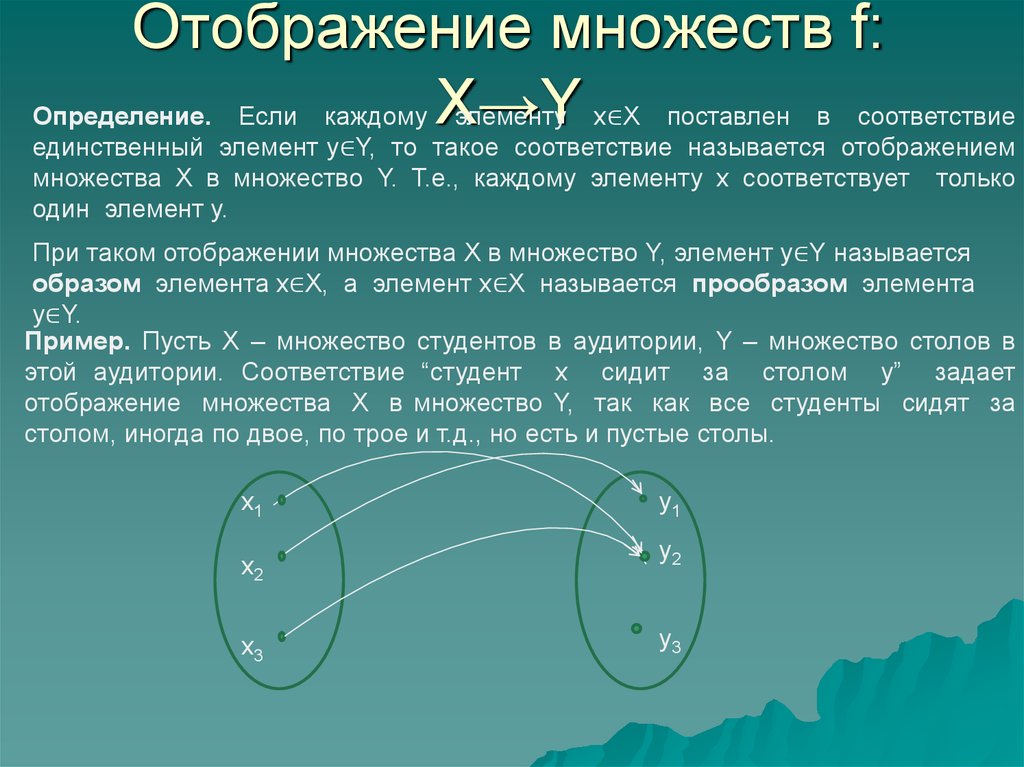 Если это невозможно, то это не инъективная функция.

В чем разница между инъективной и сюръективной функциями?

Инъективная функция связывает каждый элемент данного набора с отдельным элементом другого набора и также называется взаимно однозначной функцией. Субъективная функция связывает каждый элемент в диапазоне с отдельным элементом в домене данного набора. Субъективную функцию также называют онтофункцией. Инъективная функция и субъективная функция могут появляться вместе, и такая функция называется биективной функцией.

Приведите несколько примеров инъективной функции из реальной жизни?

Ниже приведены несколько реальных примеров инъективной функции.

• Имя учащегося класса и регистрационный номер класса.
• Лицо и тень человека, для одного источника света.
• Путешественник и его забронированный билет для поездки на поезде из одного пункта назначения в другой.

Рабочие листы по математике и визуальный учебный план

Какое точное определение инъективной функции

спросил 7 лет, 5 месяцев назад

Изменено 7 лет, 5 месяцев назад

Просмотрено 20 тысяч раз

$\begingroup$

Правильно ли я считаю, что функция инъективна, если некоторые элементы первого множества отображаются в некоторые элементы второго множества?

Возможно ли также, чтобы 4 элемента первого набора отображались на такой же элемент второго набора?

Это правильно?

Очень ценен простой ответ, уже достаточно запутанный 🙂

СПАСИБО

• функции
• определение

$\endgroup$

4

$\begingroup$

$f\colon X\to Y$ является инъективным тогда и только тогда, когда:

• $x\neq y\Rightarrow f(x)\neq f(y)$ или
  • Если $f(x)=f(y)\Стрелка вправо x=y$

Интуиция подсказывает, что вы можете иметь копию $X$ в $Y$, это означает, что для всех $x\in X$ существует $y\in Y$, для которых $f(x)=y$ и не являются другими $x’$ с тем же утверждением, $\these$ Y содержит копию множества X

Примечание

• Это работает для $X\to Y$, если мы хотим что-то похожее от $Y\to X$, это называется сюръективным.
• Возможно ли, что для некоторых $y\in Y, \не{\существует}x\in X$ таких $f(x)=y$

$\endgroup$

$\begingroup$

Инъективная функция (она же функция взаимно однозначного вывода) — это функция, для которой каждый элемент диапазона функции соответствует ровно одному элементу области определения.

Это означает, что он никогда не сопоставляет различные элементы своего домена с одним и тем же элементом своего кодового домена.

$\endgroup$

3

$\begingroup$

Функция $f:X\rightarrow Y$ является не инъективной, если существуют два различных элемента $a,b\in X$ с $f(a)=f(b)$.

Если это не так, то функция инъективна.

$\endgroup$

$\begingroup$

Инъективная функция — это отношение, удовлетворяющее условию $f(x) = f(y) \Rightarrow x=y$.