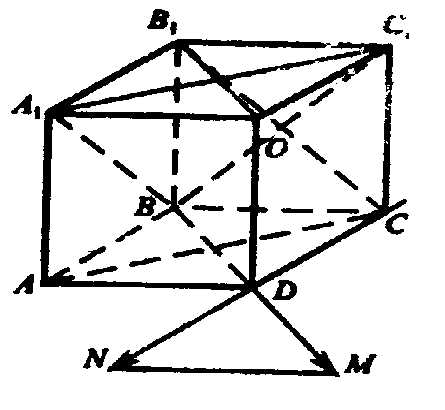
а) В1В и В1С; б) DA и B1D1; в) А1С1 и А1В; г) ВС и АС; д) ВВ1 и АС; е) В1С и AD1; ж) A1D1 и ВС; з) АА1 и С1С.
441. Дан куб ABCDA1B1C1D1. Найдите угол между векторами: а) В1В и В1С; б) DA и B1D1; в) А1С1 и А1В; г) ВС и АС; д) ВВ1 и АС; е) В1С и AD1; ж) A1D1 и ВС; з) АА1 и С1С.
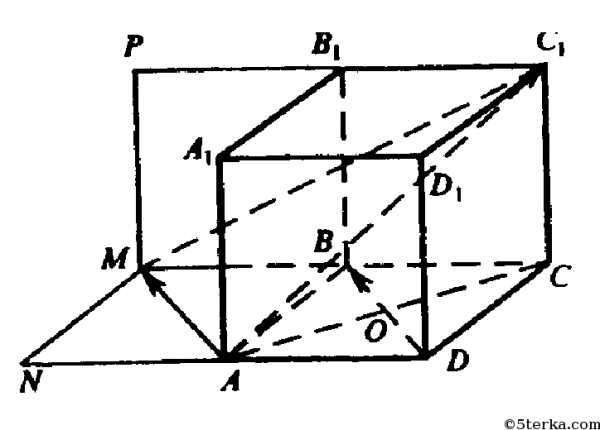
Сделаем рисунок.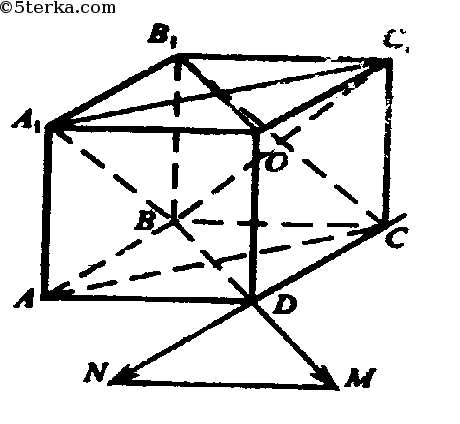
а) Векторы ВВ1 и В1С совпадают с катетом и гипотенузой прямоугольного треугольника BВ1С, следовательно, ВВ1С=45°.
б) BD = B1D1, т.к. они сонаправлены и имеют одинаковую длину. BD = B1D1 =- DB .
Угол между DB и DA — угол между стороной и диагональю квадрата, т.е. α=45°. Тогда угол между
DA и B1D1 равен 135°.
в) A1C1 и A1B совпадают со сторонами равностороннего треугольника АВС и отложены из одной точки. Следовательно, угол 60°.
г)
(угол между стороной и диагональю
квадрата).
д)
е)
Пусть О — точка пересечения диагоналей В1С и ВС1,
квадрата ВВ1С1С.
ж)
следовательно,
з)
следовательно, угол между ними равен 180°
5terka.com
сделаем рисунок. г) (угол между стороной и диагональю квадрата). д) е) пусть о — точка пересечения диагоналей в1с и вс1, квадрата вв1с1с. следовательно, ж) следовательно, з) следовательно, угол между ними равен 180° |
davay5.com
а) АА1 и AC1; б) BD1 и DB1; в) DB и АС1.
Источник: 
Решебник
по
геометрии
за 10 класс (Л.С.Атанасян, 2001 год),
задача №455
к главе «Глава V. Метод координат в пространстве. § 2. Скалярное произведение векторов
Все задачи >
Пусть сторона куба равна а, следовательно: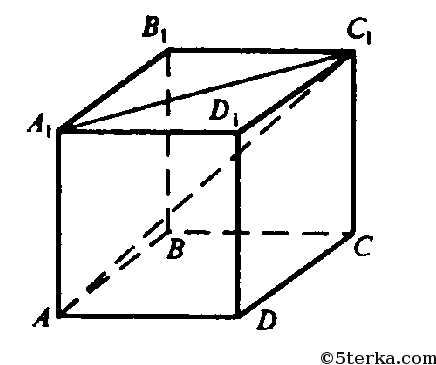
а) В прямоугольном треугольнике АА1С1 положим, АА1= =0, тогда
по теореме Пифагора.
б) Векторы
лежат в плоскости BB1D, сечение куба этой плоскостью — это прямоугольник BB1D1D со сторонами а и а
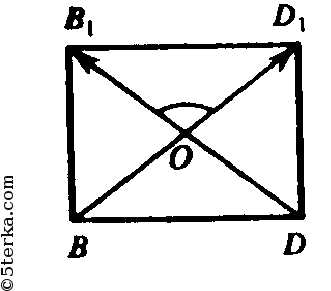
По теореме косинусов в ΔB1OD1:
следовательно
в)
(no свойству
диагонали квадрата).
Следовательно, BD перпендикулярно плоскости АС1С, тогда, BD ⊥ AC1,
← 454. Найдите углы, периметр и площадь треугольника, вершинами которого являются точки A(1; -1; 3;), В (3; -1; 1) и С(- 1; 1; 3).456. Дан прямоугольный параллелепипед ABCDA1B1C1D1, в котором АВ = 1, ВС = СС1 = 2. Вычислите угол между векторами DB1 и BC1. →- Вконтакте
5terka.com