Интеграл 1 tgx: Интеграл тангенса, tgx

Решение. Примем за , тогда  .

Найдем  , . Тогда

Задача 15. Вычислить определенный интеграл  .

Решение. Пусть , тогда , .

Если х=0, то , если х=3, то . Тогда

.

Задача 16. Исследовать несобственный интеграл  на  сходимость и найти его значение в случае сходимости.

Решение. Промежуток интегрирования не ограничен, следовательно, это несобственный интеграл первого рода.

Несобственный интеграл сходится и равен 1/8.

Задача 17. Исследовать несобственный интеграл  на сходимость и найти его значение в случае сходимости.

Решение. Функция не ограничена на промежутке интегрирования, следовательно, это несобственный интеграл второго рода.

Несобственный интеграл сходится и равен .

Задача 18. Найти площадь фигуры, ограниченной линиями  .

Решение. Построим данные параболы.

                                             Y                                                   

                                               3                              

                                               1                                                 

                                   -2  -1  0        1    2                 X               

Найдем абсциссы точек пересечения.

Получим  х₁ = -1,  х₂ =1.

Фигура ограничена графиками двух функций, следовательно, площадь ее находится по формуле

,  где  . Тогда

.

Ответ: .

Задача 19. Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, ограниченной линиями: .

Решение. Сделаем чертеж.

                                                Y                y=tgx                          

                              —p/2                                p/2          X             

                                                        p/4                                      

Так как вращение фигуры происходит вокруг оси

.

Ответ: .

найдите общий интеграл (общее решение) дифференциального уравнения y» * tgx=2y’ — вопрос №3462345 — Учеба и наука

04. 10.19 Лучший ответ по мнению автора

Другие ответы

y = 1/2 c1 (x — 1/2 sin2x) + c2 04. 10.19 Ответ не понравился автору вопроса

Посмотреть всех экспертов из раздела Учеба и наука > Математика

ВЫЧИСЛИТЕ 1,2 3 ФОТО РЕШИТЕ УРАВНЕНИЕ ПОЖАЛУЙСТА

Разложить в ряд Фурье функцию f(x), заданную в интервале (0; π), продолжив (доопределив) ее четным и нечетным образом. Построить графики для каждого продолжения.

Решено

Решить интеграл способом замены переменной

вирішити 1й варіант

Задание по физике

Пользуйтесь нашим приложением

неопределенных интегралов — $-1 = 0$ интегрированием по частям $\tan(x)$

спросил 9 лет, 9 месяцев назад

Изменено 5 лет, 10 месяцев назад

Просмотрено 7к раз

$\begingroup$

Вчера у меня был выпускной экзамен по вычислениям, и в вопросе нам нужно было найти примитив $\tan(x)$, чтобы решить дифференциальное уравнение. 92} дх \\ [0,1 дюйма] &= -1 + \int \tan(x)dx \end{align*}$$

Таким образом, мы получаем:

$$ \int \tan(x)dx = -1 + \int \tan(x)dx \implies 0 = -1$$

Что ? Рассуждение кажется мне правильным.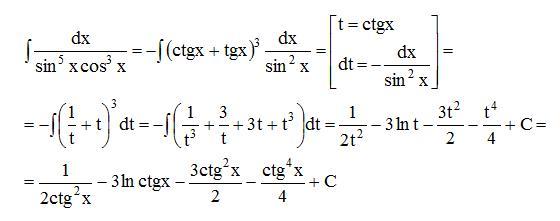 Может кто-нибудь объяснить, где что-то пошло не так?

Спасибо, Кристоф.

• интеграция
• неопределенные интегралы
• фальшивые доказательства

$\endgroup$

1

$\begingroup$

Даже не читая отвечаю: первообразные функции равны только с точностью до аддитивной константы, то есть любые две первообразные всегда будут отличаться на константу на интервале .

Редактировать: Хорошо, теперь, прочитав вопрос, я подтверждаю свое подозрение, обратите внимание, что символ $\int f(x)dx$ не является четко определенной функцией. Вы должны интерпретировать символ $\int f(x)dx$ как недоопределенную дифференцируемую функцию, которая после дифференцирования дает $f(x)$. Хотя более формально я считаю, что $\int f(x)dx$ чаще определяют как 9х\тангенс т\,дт \end{выравнивание} что, конечно, мало что говорит, не так ли? ;-)

Фиксация нижнего предела интегрирования — это выбор хорошо определенного примитива (или первообразной). Всегда делайте это в случае сомнений.

$\endgroup$

$\begingroup$

Я хотел бы сказать, что вы смогли доказать, что $-1 = 0$, но, к сожалению, вы использовали некоторые (или очень много) плохие вычисления. 🙁

При интегрировании уравнения
$$\int\tan(x)~dx$$
вы должны разделить его на две части, как вы сделали, чтобы получить $\int \frac{\sin(x)}{\cos(x)}dx$,

Затем вы должны найти $u$ и выполнить замену $u$. $u = \cos(x)$ и $du = -\sin(x) dx$

, затем замените $u$ и $du$, чтобы получить $\int \frac{du}{u}$, что дифференцируется в $\ln|u|$, где $u = \cos(x)$, поэтому ответ на самом деле $\ln|\cos(x)|$, а не что-то еще, кроме $-\ln|\cos(x )|$ или $\ln|1/\cos(x)|$ или $\ln|\sec(x)|$ с C.

Кроме того, было бы плохим исчислением подставлять оценки в уравнение до того, как на самом деле дифференцируя, так что весь $\int \tan(x)dx =$ материал совершенно неверен 92)/tg x]dx . Укажите метод.

Выберите область веб-сайта для поиска

MathAllУчебные пособияПомощь в выполнении домашних заданийПланы уроков

Искать на этом сайте

Начать бесплатную пробную версию

См. eNotes без рекламы

Начните с 48-часовой бесплатной пробной версией , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые наши эксперты ответили.

Уже зарегистрирован? Войдите здесь.

Утверждено редакцией eNotes

Задайте вопрос

Похожие вопросы

Математика

Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.

Что означают буквы R, Q, N и Z в математике?

14 ответов педагога

Математика

Последний ответ опубликован 07 октября 2013 г. в 20:13:27.

Как определить, является ли это уравнение линейной или нелинейной функцией?

84 Ответы воспитателя

Математика

Последний ответ опубликован 25 февраля 2016 г. в 18:48:45.

Сколько времени (в часах) займет ваше путешествие, если вы проедете 350 км со средней скоростью 80 км/ч? Какова формула с данными: время, расстояние, скорость или скорость?

1 Ответ воспитателя

Математика

Последний ответ опубликован 09 октября 2017 г.