6.7 Интегралы, показательные функции и логарифмы
Цели обучения
- Запишите определение натурального логарифма как интеграла.
- Распознать производную натурального логарифма.
- Интегрируйте функции, включающие натуральный логарифм.
- Определить число [latex]e[/latex] через интеграл.
- Распознать производную и интеграл экспоненциальной функции.
- Докажите свойства логарифмов и показательных функций, используя интегралы.
- Выражайте общие логарифмические и экспоненциальные функции в терминах натуральных логарифмов и экспонент.
Мы уже рассматривали экспоненциальные функции и логарифмы в предыдущих главах. Тем не менее, мы упустили некоторые ключевые детали в предыдущих обсуждениях. Например, мы не изучали, как обращаться с экспоненциальными функциями с иррациональными показателями. Определение числа [латекс]е[/латекс] — еще одна область, где предыдущая разработка была несколько неполной. Теперь у нас есть инструменты для более строгой математической обработки этих концепций, и мы делаем это в этом разделе.
Теперь у нас есть инструменты для более строгой математической обработки этих концепций, и мы делаем это в этом разделе.
Для целей этого раздела предположим, что мы еще не определили натуральный логарифм, число [latex]e[/latex] или какие-либо формулы интегрирования и дифференцирования, связанные с этими функциями. К концу раздела мы изучим эти понятия математически строгим образом (и мы увидим, что они согласуются с понятиями, которые мы изучили ранее).
Мы начнем этот раздел с определения натурального логарифма через интеграл. Это определение составляет основу раздела. Из этого определения мы выводим формулы дифференцирования, определяем число [латекс]е,[/латекс] и расширяем эти понятия до логарифмов и показательных функций по любому основанию. 9{1}\frac{1}{t}dt,[/latex], поэтому в данном случае это отрицательная площадь под кривой от [latex]x\text{ до }1[/latex] (см. фигура).
Рис. 1. (a) Когда [latex]x>1,[/latex] натуральный логарифм представляет собой площадь под кривой [latex]y=1\text{/}t[/latex] из [latex]1 \text{ в }x.
Обратите внимание, что [latex]\text{ln}1=0.[/latex] Кроме того, функция [latex]y=1\text{/}t>0[/latex] для [latex]x>0. [/latex] Следовательно, по свойствам интегралов видно, что [latex]\text{ln}x[/latex] возрастает при [latex]x>0.[/latex]
Из-за того, как мы определили натуральный логарифм, следующая формула дифференцирования сразу выпадает из основной теоремы исчисления.
Производная натурального логарифма
Для [latex]x>0,[/latex] производная натурального логарифма определяется как
[latex]\frac{d}{dx}\text{ln}x= \frac{1}{x}.[/latex]
Следствие из производной натурального логарифма
Функция [latex]\text{ln}x[/latex] дифференцируема; следовательно, он непрерывен. 9{2}[/латекс]
Показать раствор
Обратите внимание, что если мы используем функцию абсолютного значения и создаем новую функцию [latex]\text{ln}|x|,[/latex], мы можем расширить область значений натурального логарифма, включив в нее [latex]x<0.
Интеграл от (1/[latex]u[/latex])
duНатуральный логарифм является первообразной функции [latex]f(u)=1\text{/}u\text{:} [/латекс] 9{3}+6}dx.[/latex]
Показать решение
Хотя мы назвали нашу функцию «логарифмом», мы на самом деле не доказали, что для этой функции выполняются какие-либо свойства логарифмов. Мы делаем так здесь.
Свойства натурального логарифма
Если [latex]a,b>0[/latex] и [latex]r[/latex] является рациональным числом, то
- [latex]\text{ln}1= 0[/латекс]
- [латекс]\текст{лн}(аб)=\текст{лн}а+\текст{лн}б[/латекс]
- [латекс]\text{ln}(\frac{a}{b})=\text{ln}a-\text{ln}b[/latex] 9{r})=r\text{ln}x[/latex] и доказательство завершено. Обратите внимание, что мы можем распространить это свойство на иррациональные значения [latex]r[/latex] позже в этом разделе.

Часть III. следует из части II. и IV. и доказательство остается за вами.
□
Использование свойств логарифмов
Использование свойств логарифмов для упрощения следующего выражения до одного логарифма:
[латекс]\текст{лн}9-2\текст{лн}3+\текст{лн} (\frac{1}{3}).[/latex]
Показать решение
Используйте свойства логарифмов, чтобы упростить следующее выражение до единого логарифма:
[latex]\text{ln}8-\text{ln}2-\text{ln}(\frac{1}{4}) .[/latex]
Показать решение
Теперь, когда мы определили натуральный логарифм, мы можем использовать эту функцию для определения числа [latex]e.[/latex]
Определение
Число [latex]e[/latex] определяется как действительное число такое, что
[латекс]\текст{ln}e=1.[/латекс]
Другими словами, площадь под кривой [latex]y=1\text{/}t[/latex] между [latex]t=1[/latex] и [latex]t=e[/latex] равно 1 ((Рисунок)). Доказательство того, что такое число существует и уникально, остается за вами. ( Подсказка : Используйте теорему о промежуточном значении, чтобы доказать существование и тот факт, что [латекс]\текст{ln}x[/латекс] увеличивается, чтобы доказать уникальность.)
Доказательство того, что такое число существует и уникально, остается за вами. ( Подсказка : Используйте теорему о промежуточном значении, чтобы доказать существование и тот факт, что [латекс]\текст{ln}x[/латекс] увеличивается, чтобы доказать уникальность.)
Рисунок 3. Площадь под кривой от 1 до [latex]e[/latex] равно единице.
Можно показать, что число [латекс]е[/латекс] иррационально, хотя мы не будем этого делать здесь (см. Студенческий проект в сериях Тейлора и Маклорена во втором томе этого текста). Его приблизительное значение равно 9{x}.[/latex] Обратите внимание, что натуральный логарифм один к одному и, следовательно, имеет обратную функцию. На данный момент мы обозначаем эту обратную функцию как [латекс]\текст{ехр}х.[/латекс] Затем
[латекс]\текст{ехр}(\текст{ln}х)=х\текст{ для } x>0\text{ и }\text{ln}(\text{exp}x)=x\text{для всех}x.[/latex]
На следующем рисунке показаны графики [latex]\text{ exp}x[/latex] и [latex]\text{ln}x.[/latex]
Рисунок 4. Графики [latex]\text{ln}x[/latex] и [latex]\text{ exp}x.[/латекс] 9{y})\hfill \\ \hfill \text{ln}x& =\hfill & y\text{ln}a\hfill \\ \hfill y& =\hfill & \frac{\text{ln}x}{\ text{ln}a}\hfill \\ \hfill {\text{log}}_{}x& =\hfill & \frac{\text{ln}x}{\text{ln}a}.\hfill\end {array}[/latex]
Графики [latex]\text{ln}x[/latex] и [latex]\text{ exp}x.[/латекс] 9{y})\hfill \\ \hfill \text{ln}x& =\hfill & y\text{ln}a\hfill \\ \hfill y& =\hfill & \frac{\text{ln}x}{\ text{ln}a}\hfill \\ \hfill {\text{log}}_{}x& =\hfill & \frac{\text{ln}x}{\text{ln}a}.\hfill\end {array}[/latex]
Таким образом, мы видим, что все логарифмические функции постоянно кратны друг другу. Затем мы используем эту формулу, чтобы найти формулу дифференцирования для логарифма с основанием [латекс]а.[/латекс] Снова пусть [латекс]у = {\текст{лог}}_{а}х.[/латекс] Затем
[латекс]\begin{array}{cc}\hfill \frac{dy}{dx}& =\frac{d}{dx}({\text{log}}_{a}x)\ hfill \\ & =\ frac {d} {dx} (\ frac {\ text {ln} x} {\ text {ln} a}) \ hfill \\ & = (\ frac {1} {\ text {ln }a})\frac{d}{dx}(\text{ln}x)\hfill \\ & =\frac{1}{\text{ln}a}·\frac{1}{x}\hfill \\ & =\frac{1}{x\text{ln}a}.\hfill \end{массив}[/latex] 9{х})=х[/латекс] Z
Для следующих упражнений найдите производную [latex]\frac{dy}{dx}.[/latex]
1.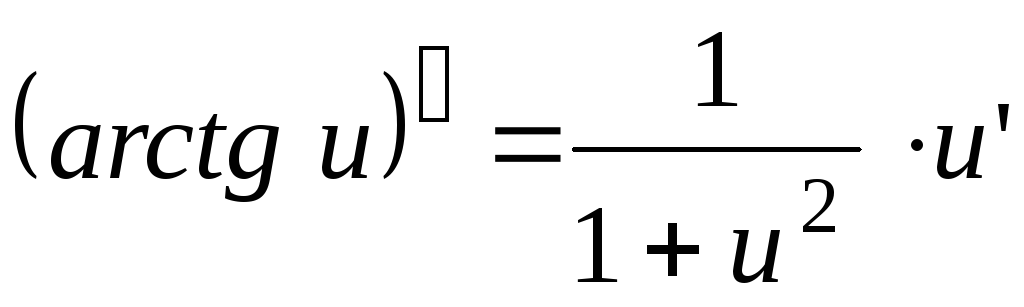 [latex]y=\text{ln}(2x)[/latex]
[latex]y=\text{ln}(2x)[/latex]
Показать решение
2. [латекс]y=\text{ln}(2x+1)[/latex]
3. [латекс]y=\frac{1}{\text{ln}x}[ /латекс]
Показать решение
Для следующих упражнений найдите неопределенный интеграл.
4. [латекс]\int \frac{dt}{3t}[/латекс]
5. [латекс]\int \frac{dx}{1+x}[/latex]
[латекс]\text{ln}(x+1)+C[/latex]
Для В следующих упражнениях найдите производную [latex]dy\text{/}dx.[/latex] (Вы можете использовать калькулятор, чтобы построить функцию и производную, чтобы убедиться, что она верна.)
6. [T] [латекс]y=\frac{\text{ln}(x)}{x}[/latex]
7. [T] [латекс]y=x\text{ln}(x)[/ латекс]
[латекс]\текст{ln}(x)+1[/латекс]
8. [T] 9{2}}\frac{dt}{t}[/latex]
Показать решение
40. [латекс]\frac{d}{dx}\text{ln}( \sec x+ \tan x)[/latex]
[латекс]\frac{d}{dx}\text{ln}( \sec x+ \tan x)[/latex]
В следующих упражнениях используйте функцию [latex]\text{ ln}x.[/latex] Если вы не можете найти точки пересечения аналитически, воспользуйтесь калькулятором.
41. Найдите площадь области, заключенной между [latex]x=1[/latex] и [latex]y=5[/latex] над [latex]y=\text{ln}x.[/ латекс]
Показать решение
42. [Т] Найдите длину дуги [латекс]\текст{ln}x[/латекс] от [латекс]х=1[/латекс] до [латекс]х=2.[/латекс]
43. Найдите область между [latex]\text{ln}x[/latex] и осью [latex]x[/latex] от [latex]x=1\text{ до }x=2.[/latex]
Показать Решение
44. Найдите объем фигуры, созданной при вращении этой кривой от [latex]x=1\text{ до }x=2[/latex] вокруг оси [latex]x[/latex], как изображено здесь.
45. [Т] Найдите площадь поверхности фигуры, созданной при повороте кривой в предыдущем упражнении от [латекс]х=1[/латекс] до [латекс]х=2[/латекс] вокруг [латекс]х[/латекс]- ось.
Показать раствор
Если вам не удается аналитически найти точки пересечения в следующих упражнениях, воспользуйтесь калькулятором.
46. Найдите площадь гиперболической четверти окружности, заключенной между [латексом]x=2\text{ и }y=2[/latex] над [латексом]y=1\text{/}x.[ /латекс]
47. [Т] 9{2}}}[/латекс]
53. [латекс]\int \frac{dx}{x\text{ln}(x)\text{ln}(\text{ln}x)}= \text{ln}(\text{ln}(\text{ln}x))+C[/latex]
Видео с вопросами: Идентификация сходящихся и расходящихся рядов натуральных логарифмов с использованием интегрального теста
Стенограмма видео
Используйте интегральный тест, чтобы определить, сходится или расходится ряд, сумма от 𝑛 равна единице до ∞ натурального логарифма 𝑛, деленного на 𝑛.
Вопрос требует, чтобы мы определили сходимость или расхождение ряда с помощью интегрального теста. Итак, давайте начнем с того, что вспомним, что говорит нам интегральный тест.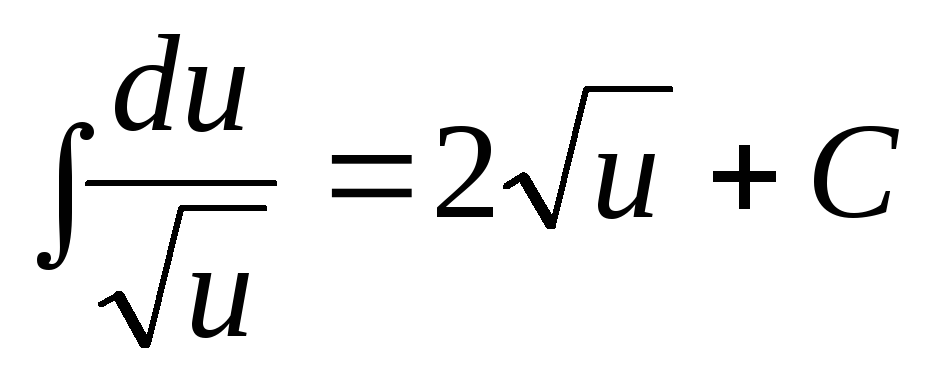
Интегральный тест дает нам способ превратить вопрос о сходимости или расходимости бесконечного ряда в вопрос о сходимости или расходимости интеграла. Поскольку вопрос требует, чтобы мы использовали интегральный критерий суммы от 𝑛, равной единице, до ∞ натурального логарифма 𝑛, деленного на 𝑛, мы установим наше значение 𝑘 равным единице. И наша функция 𝑓 от 𝑥 должна быть равна натуральному логарифму 𝑥, деленному на 𝑥. Теперь, чтобы использовать интегральный тест, нам нужно показать, что наша функция 𝑓 от 𝑥, равная натуральному логарифму 𝑥, деленному на 𝑥, является положительной, непрерывной и убывающей функцией для всех значений 𝑥, превышающих или равно единице.
Теперь, чтобы использовать интегральный тест, нам нужно показать, что наша функция 𝑓 от 𝑥, равная натуральному логарифму 𝑥, деленному на 𝑥, является положительной, непрерывной и убывающей функцией для всех значений 𝑥, превышающих или равно единице.
Если бы мы попытались показать, что наша функция 𝑓 от 𝑥 положительна на этом интервале, мы сразу же столкнулись бы с проблемой. Мы видим, что когда 𝑥 равно единице, наша функция равна натуральному логарифму единицы, деленной на единицу. Однако натуральный логарифм единицы равен нулю. Итак, мы видим, что 𝑓 единицы равно нулю. Итак, наша функция 𝑓 от 𝑥 не положительна на этом интервале. Однако мы можем легко обойти это. Мы замечаем, что это также первый термин в нашем ряду. Если первый член в нашем ряду равен нулю, то мы можем просто взять его за пределы нашего ряда. Это не изменит значения нашей бесконечной суммы.
Другими словами, сумма от 𝑛, равная единице до ∞ натурального логарифма 𝑛, деленного на 𝑛, равна сумме от 𝑛, равной двум, до ∞ натурального логарифма 𝑛, деленного на 𝑛.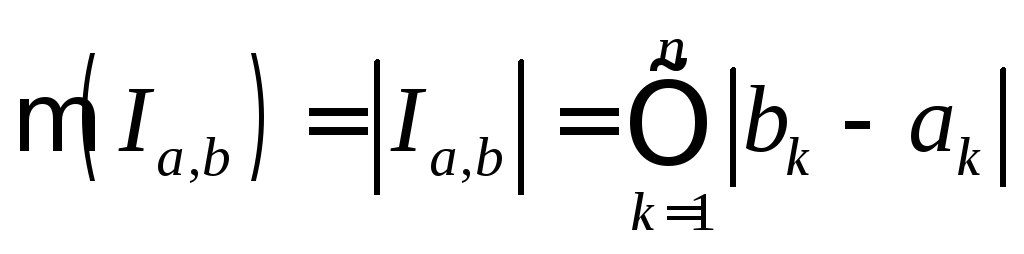 Поэтому вместо этого мы попробуем использовать интегральный тест во второй серии. Мы установим наше значение 𝑘 равным двум. И мы оставляем нашу функцию 𝑓 от 𝑥 как натуральный логарифм 𝑥, деленный на 𝑥. Итак, давайте освободим немного места и обновим наш интегральный тест, чтобы наше значение 𝑘 было равно двум. Теперь нам нужно показать, что наша функция 𝑓 от 𝑥 положительна, непрерывна и убывает для всех значений 𝑥, больших или равных двум.
Поэтому вместо этого мы попробуем использовать интегральный тест во второй серии. Мы установим наше значение 𝑘 равным двум. И мы оставляем нашу функцию 𝑓 от 𝑥 как натуральный логарифм 𝑥, деленный на 𝑥. Итак, давайте освободим немного места и обновим наш интегральный тест, чтобы наше значение 𝑘 было равно двум. Теперь нам нужно показать, что наша функция 𝑓 от 𝑥 положительна, непрерывна и убывает для всех значений 𝑥, больших или равных двум.
Итак, давайте начнем с того, что покажем, что наша функция 𝑓 от 𝑥 положительна на этом интервале. Если 𝑥 больше или равно двум, мы знаем, что натуральный логарифм 𝑥 положительный, а 𝑥 положительный. Это означает, что когда 𝑥 больше или равно двум, наша функция 𝑓 от 𝑥 является частным двух положительных чисел. Это означает, что наша функция 𝑓 от 𝑥 положительна, поскольку 𝑥 больше или равно двум. Теперь мы хотим проверить, что наша функция 𝑓 от 𝑥 непрерывна для значений 𝑥, больших или равных двум. Ну, мы знаем, что числитель, натуральный логарифм 𝑥, непрерывен, и знаменатель 𝑥 также непрерывен. Итак, 𝑓 из 𝑥 — это частное двух непрерывных функций. И мы знаем, что частное двух непрерывных функций будет непрерывным во всей области определения.
Итак, 𝑓 из 𝑥 — это частное двух непрерывных функций. И мы знаем, что частное двух непрерывных функций будет непрерывным во всей области определения.
Итак, нам нужно проверить домен нашей функции 𝑓 из 𝑥. Мы не можем делить на ноль, поэтому мы знаем, что 𝑥 не может быть равно нулю. И мы не можем взять логарифм числа меньше или равного нулю. Таким образом, область определения нашей функции 𝑓 — это все значения 𝑥 больше нуля. В частности, это означает, что 𝑓 из 𝑥 непрерывно для значений 𝑥, больших или равных двум. Все, что нам нужно сейчас показать, это то, что наша функция 𝑓 от 𝑥 убывает для всех значений 𝑥, больших или равных двум. Мы сделаем это, найдя наклон нашей функции. Для этого начнем с рассмотрения нашей функции 𝑓 от 𝑥 как произведения двух функций. Это произведение натурального логарифма 𝑥 и единицы на 𝑥.
Затем мы можем дифференцировать это, используя правило произведения. Помните, правило произведения говорит нам, что производная от 𝑢 от 𝑥, умноженная на 𝑣 от 𝑥 по отношению к 𝑥, равна 𝑢 простому числу от 𝑥, умноженному на 𝑣 от 𝑥, плюс 𝑣 простому числу от 𝑥, умноженному на 𝑢 от 𝑥. Таким образом, мы можем найти выражение для 𝑓 простого числа 𝑥. Мы знаем, что производная натурального логарифма 𝑥 по 𝑥 равна единице над 𝑥. И мы знаем, что производная обратной функции по 𝑥 отрицательна, деленная на 𝑥 в квадрате. Используя это в правиле произведения, мы получаем 𝑓 простое число 𝑥 равно единице на 𝑥, умноженной на единицу на 𝑥 плюс отрицательная единица на 𝑥 в квадрате, умноженному на натуральный логарифм 𝑥. А затем мы упростим это выражение, чтобы получить единицу минус натуральный логарифм 𝑥, деленный на 𝑥 в квадрате.
Таким образом, мы можем найти выражение для 𝑓 простого числа 𝑥. Мы знаем, что производная натурального логарифма 𝑥 по 𝑥 равна единице над 𝑥. И мы знаем, что производная обратной функции по 𝑥 отрицательна, деленная на 𝑥 в квадрате. Используя это в правиле произведения, мы получаем 𝑓 простое число 𝑥 равно единице на 𝑥, умноженной на единицу на 𝑥 плюс отрицательная единица на 𝑥 в квадрате, умноженному на натуральный логарифм 𝑥. А затем мы упростим это выражение, чтобы получить единицу минус натуральный логарифм 𝑥, деленный на 𝑥 в квадрате.
Помните, что это представляет наклон нашей функции 𝑓 из 𝑥. И мы знаем, что наша функция будет уменьшаться, когда ее наклон отрицательный. Итак, чтобы найти значения 𝑥, при которых наша функция убывает, нам просто нужно найти значения 𝑥, при которых это выражение отрицательно. Мы видим, что знаменатель нашей функции равен 𝑥 в квадрате. Поскольку нас интересует только то, что 𝑥 больше или равно двум, мы можем видеть, что это значение всегда будет положительным.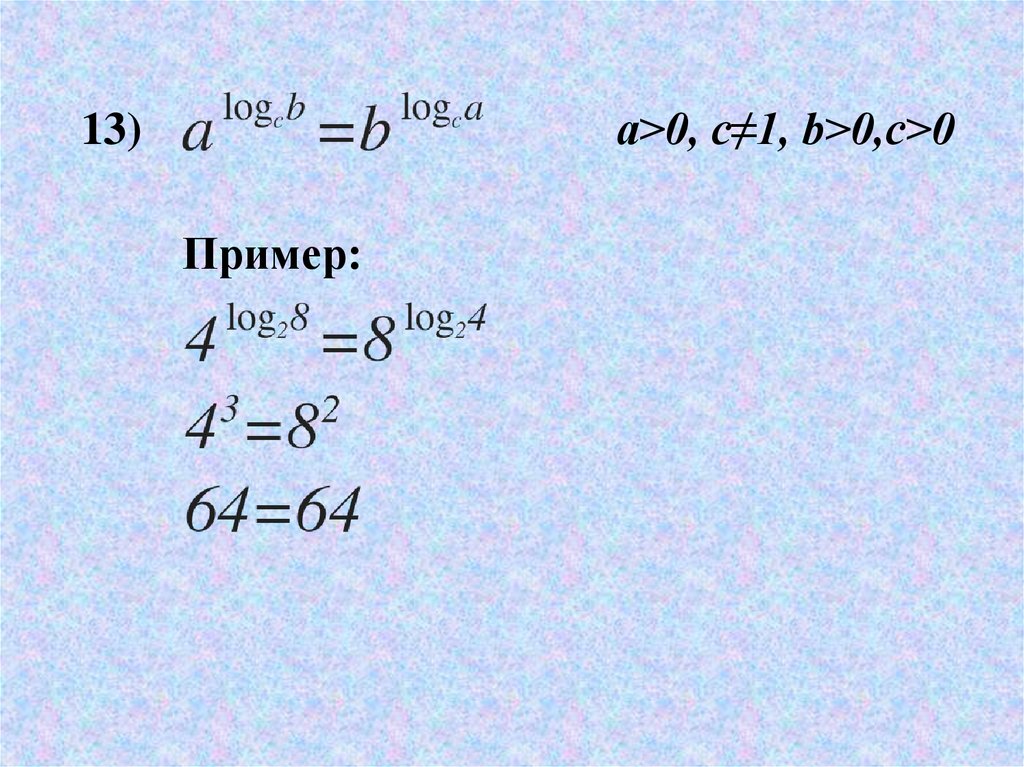 Таким образом, единственный способ сделать наш наклон отрицательным — это отрицательный числитель. Числитель отрицательный, когда единица минус натуральный логарифм 𝑥 меньше нуля или, наоборот, единица меньше натурального логарифма 𝑥.
Таким образом, единственный способ сделать наш наклон отрицательным — это отрицательный числитель. Числитель отрицательный, когда единица минус натуральный логарифм 𝑥 меньше нуля или, наоборот, единица меньше натурального логарифма 𝑥.
И мы знаем, как это решить. Мы знаем, что когда 𝑥 равно 𝑒, натуральный логарифм 𝑥 будет равен единице. Мы также знаем, что функция натурального логарифма является возрастающей функцией. Поэтому, когда 𝑥 больше 𝑒, натуральный логарифм 𝑥 будет больше единицы. Итак, что же мы показали на самом деле? Мы показали, что наклон нашей функции 𝑓 от 𝑥 отрицателен, когда 𝑥 больше 𝑒. Это означает, что наша функция 𝑓 от 𝑥 убывает для всех значений 𝑥, больших или равных 𝑒. Но этого недостаточно, чтобы использовать наш интегральный тест в его нынешнем виде. Нам нужно, чтобы наша функция убывала для всех значений 𝑥, больших или равных двум.
Однако мы знаем, что наше значение 𝑒 приблизительно равно 2,7. Таким образом, мы фактически показали, что наша функция 𝑓 от 𝑥 убывает для всех значений 𝑥, больших или равных трем. Так что на самом деле мы могли бы попробовать использовать интегральный тест с нашим значением 𝑘, равным трем. И это все равно даст нам ответ на наш первоначальный вопрос. Помните, что сумма от 𝑛, равная единице до ∞ натурального логарифма 𝑛, деленного на 𝑛, равна сумме от 𝑛, равной трем до ∞, натурального логарифма 𝑛, деленного на 𝑛. Где мы добавляем первый и второй член нашей последовательности. Таким образом, сходимость или расхождение этих двух рядов будет одинаковым.
Так что на самом деле мы могли бы попробовать использовать интегральный тест с нашим значением 𝑘, равным трем. И это все равно даст нам ответ на наш первоначальный вопрос. Помните, что сумма от 𝑛, равная единице до ∞ натурального логарифма 𝑛, деленного на 𝑛, равна сумме от 𝑛, равной трем до ∞, натурального логарифма 𝑛, деленного на 𝑛. Где мы добавляем первый и второй член нашей последовательности. Таким образом, сходимость или расхождение этих двух рядов будет одинаковым.
Итак, давайте на этот раз перепишем наш интегральный тест с 𝑘 равным трем. И мы сохраняем 𝑓 из 𝑥 как натуральный логарифм 𝑥, деленный на 𝑥. Ну, мы уже показали, что эта функция положительна для этих значений 𝑥. Мы уже показали, что она непрерывна для этих значений 𝑥. И мы уже показали, что она уменьшается для этих значений 𝑥. Итак, теперь, когда мы показали, что все наши предварительные условия для интегрального теста верны, давайте расчистим место и поработаем над применением интегрального теста.
Во-первых, нас может обеспокоить заключительная формулировка интегрального теста. Теперь у нас есть вывод о сходимости или расходимости суммы от 𝑛 равно трем к ∞ нашей последовательности 𝑎 𝑛. Что ж, в нашем случае наша последовательность 𝑎 𝑛 — это натуральный логарифм 𝑛, деленный на 𝑛. И мы знаем, что сумма от 𝑛 равна единице до ∞ натурального логарифма 𝑛, деленного на 𝑛, равна первому члену плюс второму члену плюс сумма от 𝑛 равна трем до ∞ натурального логарифма 𝑛, деленного на 𝑛. И натуральный логарифм от единицы, деленной на единицу, и натуральный логарифм от двух, деленной на два, являются константами. Итак, эти два ряда отличаются некоторой константой. На самом деле мы знаем, что они различаются на натуральный логарифм двух, деленный на два. Таким образом, это говорит нам о том, что сходимость или расхождение обоих этих двух рядов одинаковы.
Теперь у нас есть вывод о сходимости или расходимости суммы от 𝑛 равно трем к ∞ нашей последовательности 𝑎 𝑛. Что ж, в нашем случае наша последовательность 𝑎 𝑛 — это натуральный логарифм 𝑛, деленный на 𝑛. И мы знаем, что сумма от 𝑛 равна единице до ∞ натурального логарифма 𝑛, деленного на 𝑛, равна первому члену плюс второму члену плюс сумма от 𝑛 равна трем до ∞ натурального логарифма 𝑛, деленного на 𝑛. И натуральный логарифм от единицы, деленной на единицу, и натуральный логарифм от двух, деленной на два, являются константами. Итак, эти два ряда отличаются некоторой константой. На самом деле мы знаем, что они различаются на натуральный логарифм двух, деленный на два. Таким образом, это говорит нам о том, что сходимость или расхождение обоих этих двух рядов одинаковы.
Таким образом, это оправдывает использование нами интегрального критерия для определения сходимости или расхождения ряда, данного нам в вопросе. Теперь, чтобы использовать интегральный тест, нам нужно определить сходимость или расхождение интеграла от трех до ∞ натурального логарифма 𝑥, деленного на 𝑥 по отношению к 𝑥. Во-первых, мы уже показали, что наша подынтегральная функция, натуральный логарифм 𝑥, деленный на 𝑥, непрерывна на нашем интервале интегрирования. Он непрерывен для всех значений 𝑥, больших или равных трем.
Во-первых, мы уже показали, что наша подынтегральная функция, натуральный логарифм 𝑥, деленный на 𝑥, непрерывна на нашем интервале интегрирования. Он непрерывен для всех значений 𝑥, больших или равных трем.
Таким образом, единственная неправильная вещь в этом интеграле — это его верхний предел, равный ∞. Таким образом, используя наши правила для несобственных интегралов, мы можем записать этот интеграл как предел, когда 𝑡 приближается к ∞ интеграла от трех до 𝑡 натурального логарифма 𝑥, деленного на 𝑥 относительно 𝑥. И если этот предел сходится, мы говорим, что наш интеграл сходится. Однако если этот предел расходится, то мы говорим, что наш интеграл расходится. И стоит отметить, что теперь верхний предел нашего интеграла — это некоторое конечное положительное число 𝑡. Значит, наша подынтегральная функция непрерывна на всем интервале интегрирования. Таким образом, мы можем использовать любой из наших инструментов для вычисления этого интеграла.
Есть несколько способов вычислить этот интеграл. Проще всего заметить, что натуральный логарифм 𝑥 появляется в нашем подынтегральном выражении. И если мы продифференцируем это, мы получим единицу больше 𝑥. Таким образом, наше подынтегральное выражение представляет собой функцию, умноженную на ее производную. Это означает, что мы можем оценить это с помощью подстановки. Мы будем использовать замену 𝑢 равно натуральному логарифму 𝑥. Дифференцируя обе части по 𝑥, мы получаем d𝑢 на d𝑥 равно единице над 𝑥. И мы знаем, что d𝑢 на d𝑥 — это не дробь. Однако при интегрировании путем подстановки мы можем обращаться с ним как с дробью. Это дает нам эквивалентное утверждение d𝑢 равно единице над 𝑥 d𝑥.
Проще всего заметить, что натуральный логарифм 𝑥 появляется в нашем подынтегральном выражении. И если мы продифференцируем это, мы получим единицу больше 𝑥. Таким образом, наше подынтегральное выражение представляет собой функцию, умноженную на ее производную. Это означает, что мы можем оценить это с помощью подстановки. Мы будем использовать замену 𝑢 равно натуральному логарифму 𝑥. Дифференцируя обе части по 𝑥, мы получаем d𝑢 на d𝑥 равно единице над 𝑥. И мы знаем, что d𝑢 на d𝑥 — это не дробь. Однако при интегрировании путем подстановки мы можем обращаться с ним как с дробью. Это дает нам эквивалентное утверждение d𝑢 равно единице над 𝑥 d𝑥.
Мы почти готовы применить нашу замену. Но помните, это определенный интеграл. Итак, нам нужно рассчитать новые пределы нашей интеграции. Начнем с нового нижнего предела нашего интеграла. Наш старый нижний предел был, когда 𝑥 равно трем. Итак, мы подставляем это в наше выражение для 𝑢, и мы получаем, что 𝑢 равно натуральному логарифму трех. И мы сделаем то же самое, чтобы найти новый верхний предел нашего интеграла. Получаем натуральный логарифм 𝑡. Итак, теперь мы готовы вычислить этот интеграл с помощью подстановки. Мы начнем с того, что перепишем пределы нашей интеграции. Мы получаем нижний предел — натуральный логарифм трех, а верхний предел — натуральный логарифм 𝑡.
Получаем натуральный логарифм 𝑡. Итак, теперь мы готовы вычислить этот интеграл с помощью подстановки. Мы начнем с того, что перепишем пределы нашей интеграции. Мы получаем нижний предел — натуральный логарифм трех, а верхний предел — натуральный логарифм 𝑡.
Далее, помните, натуральный логарифм 𝑥 равен 𝑢. И мы знаем, что единица более 𝑥, умноженная на d𝑥, равна d𝑢. Таким образом, мы упростили это выражение, чтобы оно было пределом, когда 𝑡 приближается к ∞ интеграла от натурального логарифма трех до натурального логарифма 𝑡 от 𝑢 относительно 𝑢. И тогда мы можем просто вычислить этот интеграл, используя степенное правило для интегрирования. Когда 𝑡 приближается к ∞, мы получаем предел половины 𝑢 в квадрате, оцененный в пределах интегрирования, натурального логарифма трех и натурального логарифма 𝑡. И мы немного упростим это выражение. Мы возьмем постоянный множитель половины за пределы нашего предела.
Теперь мы просто оцениваем это в пределах интегрирования. Мы получаем половинный предел, когда 𝑡 приближается к ∞ натурального логарифма 𝑡 в квадрате минус натуральный логарифм трех в квадрате. И теперь мы можем просто оценить этот предел как есть. Мы видим, что 𝑡 приближается к ∞. Мы знаем, что натуральный логарифм трех в квадрате является константой. Оно не изменится при изменении значения 𝑡. Однако по мере того, как 𝑡 приближается к ∞, натуральный логарифм 𝑡 в квадрате неограниченно растет. И это на самом деле говорит нам, что весь наш предел неограниченно растет. Таким образом, наш предел дает нам ∞.
И теперь мы можем просто оценить этот предел как есть. Мы видим, что 𝑡 приближается к ∞. Мы знаем, что натуральный логарифм трех в квадрате является константой. Оно не изменится при изменении значения 𝑡. Однако по мере того, как 𝑡 приближается к ∞, натуральный логарифм 𝑡 в квадрате неограниченно растет. И это на самом деле говорит нам, что весь наш предел неограниченно растет. Таким образом, наш предел дает нам ∞.
Итак, этот предел расходится. И помните, расхождение этого предела означает, что наш интеграл от трех до ∞ от натурального логарифма 𝑥, деленного на 𝑥 относительно 𝑥, также расходится. Итак, мы находимся во второй части нашего интегрального теста. Это означает, что мы знаем, что сумма от 𝑛 равно трем до ∞ числа 𝑎 𝑛 также расходится. И мы уже объяснили, что это эквивалентно утверждению, что ряд, данный нам в вопросе, расходится. Следовательно, с помощью интегрального теста мы смогли показать, что сумма от 𝑛, равной единице, до ∞ натурального логарифма 𝑛, деленного на 𝑛, расходится.

