Интеграл тангенса и котангенса
Среди простых формул интегрирования отсутствуют готовые зависимости, позволяющих найти интеграл от тангенса (tg (x)) и котангенса (ctg (x)). Но такие примеры в задачах встречаются и нужно знать: «Как вычислить интеграл от тангенса и котангенса?«.
Начнем с тангенса, распишем его в виде частки синуса на косинус
tg(x)=sin(x)/cos(x)
и подставим в интеграл.
Сейчас Вам понятно. Далее нужно внести синус под дифференциал, чтобы свести интеграции в логарифма
В результате получимТаким образом вывели простую и нужную на практике формулу — интеграл от тангенса равен логарифму косинуса со знаком минус.
Int(tan(x),x)=-log(cos(x)).
По приведенной схеме выведем формулу для интеграла от котангенса. Записываем частку косинуса на синус в интеграл и после внесения косинуса под дифференциал сводим интеграл к логарифму
Интеграл от котангенса равный логарифму от синуса.
Int(cot(x),x)=log(sin(x)).
Простые на вид формулы интегралов от тангенса и котангенса позволяют решить немало сложных примеров, например интегрирования тангенса двойного угла или котангенса половины угла.
Пример 1. Найти интеграл от тангенса tan(4*x).
Вычисления: Применяем приведенную выше методику для интегрирования тангенса
Здесь в скобках мы сначала вычисляем дифференциал от косинуса, а дальше выделяем значение, которое нам нужно достать. Далее интегрирования сводим к логарифму.
Таким образом можем записать обобщенную формулу для интегралаtan(k*x)
Int(tan(k*x),x)=-1/k*(log(cos(x)).
По этой формуле интеграл от тангенса двойного угла равен логарифму косинуса двойного угла умноженному на -0,5.
Для тангенса половины угла tan (phi / 2) интеграл равен -2 умножить на логарифм косинуса половины угла
По индукции получим формулу интеграла для тангенса одной третьей угла tan(phi/3)
Пример 2. Проинтегрировать котангенс двойного угла
Вычисления: По аналогии с формулами для тангенса мы могли бы выписать готовую формулу, но лучше выполнить промежуточные переходы чтобы Вы лучше поняли и заучили методику внесения под дифференциал
Таким образом, если имеем котангенс тройного угла то перед интегралом получим множителем 1/3
Интегралы от котангенса половины и трети угла будут иметь множителями перед логарифмом соответственно двойку и тройку
При нахождении первоначальной от тангенса и котангенса следует справа добавить постоянную
Зная данную методику, Вы знаете как найти интеграл от тангенса, аргумент которого содержит множителем произвольное число. 2
2
Интегральный тангенс(х)
Интегральный тангенс(х)| Дом | Учитель | Родители | Глоссарий | О нас | |||||
|
|
1. Доказательство
u = СО x. то находим du = — sin x dx заменить du=-sin x, u=COs x
= — пер |у| + С заменить обратно u=COs x = — ln |СО x| + C 2. Альтернативная форма результата | |||||||||||||||||||||||||
© 2000-2005 Math.com. Все права защищены. Юридический Уведомления. Пожалуйста, ознакомьтесь с нашей Конфиденциальностью Политика. |
Интегрирование тангенса x
Стандартный результат интегрирования тангенса x: ln|sec x| + C. Тригонометрическая функция tan x интегрируема, и этот стандартный результат интегрирования tan x запоминается как формула. Давайте узнаем, как решить интеграцию tan x в следующем разделе.
| 1. | Что такое интеграция Tan X? |
2.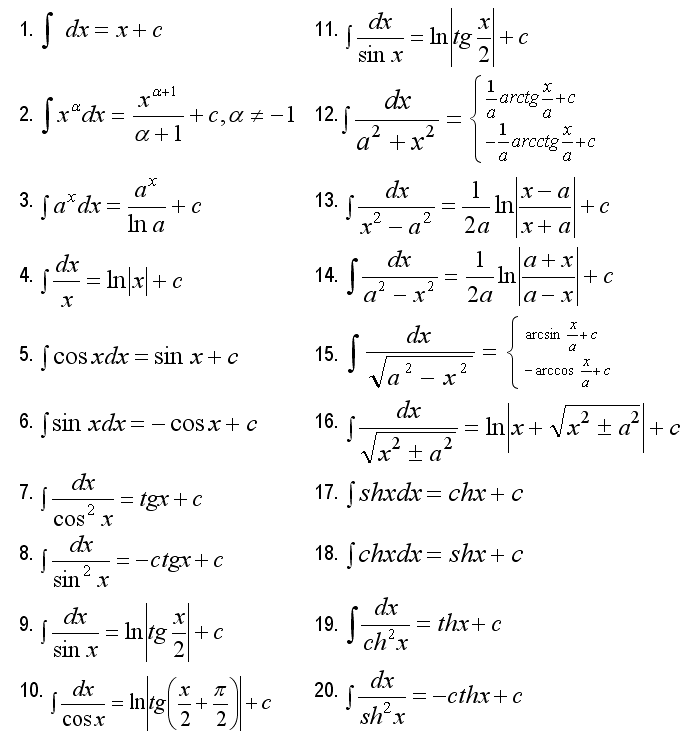 | Как решить интеграцию Tan X? |
| 3. | Определенная интеграция Tan X |
| 4. | График интеграции Tan X |
| 5. | Часто задаваемые вопросы по интеграции Tan X |
Что такое интеграция Tan X?
Интегрирование tan x равно -ln|cos x| + C (или) ln|sec x| + C. Функция f(x) = tan x непрерывна во всех действительных числах, кроме x = (2n + 1)π/2. Область определения функции = область значений функции tan(x), за исключением нечетных кратных π/2. Следовательно, tan x интегрируем, за исключением этого интервала по x. Мы делаем интегрирование тангенса x интегрированием подстановкой.
Как решить проблему интеграции Tan X?
Чтобы найти интегрирование тангенса х по х, мы выражаем тангенс х через синус и косинус так, чтобы он стал интегрируемой функцией. В соответствии с определением тангенса x мы имеем тангенс x = sin x / cos x
∫ tan x =∫ (sin x /cos x) . dx
dx
Это можно переписать как \(\int \dfrac{1} {\ соз х} \). грех х. dx
Найдем неопределенный интеграл от tan x, используя метод подстановки интегрирования.
∫ f(g(x)) g'(x) dx = ∫ f(u) du = F(u) + C
Пусть u = cos x. Тогда du = — sin x . dx
⇒ dx = — du/ sin x
∫(sin x /cos x). dx = — ∫ du/ u
По стандартной формуле интегрирования мы знаем, что ∫ dx/x = ln x+ C
Таким образом, ∫ (sin x /cos x) .dx = — ∫ du/ u = — ln|u | + c
= -ln |(cos x)+C
= ln |(cos x) -1 +C
= ln (sec x) + C
∫ (sin x /cos x) . dx = ln (сек x) + C
∫ tan x = ln (сек x) + C 9{\pi/2}_0\)
= ln|sec π/2| — ln|сек 0|
=ln(∞)- ln(1)
= ∞
Таким образом, график интеграла от tan x расходится к бесконечности в интервале [0,π/2].
☛ Также проверьте
- Формулы интегрирования
- Производное tan x
Часто задаваемые вопросы по интеграции Tan X
Что такое интеграция Tan X?
Интегрирование tan x равно ln|sec x| + C (или) -ln|cos x| + С.

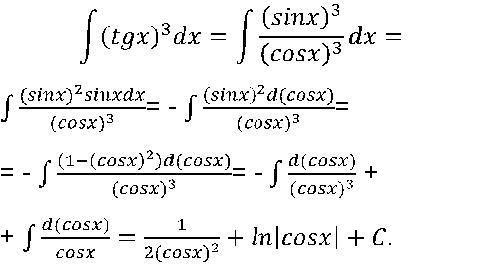
 E.D.
E.D.