Основы вычислительной математики — тест 9
Главная / Алгоритмы и дискретные структуры / Основы вычислительной математики / Тест 9
Упражнение 1:
Номер 1
В каком случае матрица считается невырожденной?
Ответ:
 (1) когда ее определитель неравен 0 
 (2) когда на большой диагонали отсутствуют нули 
 (3) когда малая диагональ не содержит нулей 
Номер 2
Какая матрица называется невырожденной?
Ответ:
 (1) определитель которой отличен от нуля 
 (2) определитель которой больше нуля 
 (3) определитель которой меньше нуля 
Номер 3
Если определитель матрицы неравен нулю, то такую матрицу называют
Ответ:
 (1) положительной 
 (2) стандартной 
 (3) невырожденной 
Упражнение 2:
Номер 1
Пустьu- вектор-столбец решения,f- вектор-столбец свободных членов,A- матрица системы.Сколько решений имеет система
Au= f, если матрица системы является невырожденной?
Ответ:
 (1) ни одного 
 (2) одно 
 (3) множество 
Номер 2
Получение точного решения задачи за конечное число арифметических действий возможно с помощью
Ответ:
 (1) прямых численных методов 
 (2) структурных численных методов 
 (3) рекурсивных численных методов 
Номер 3
Вычисление последовательности, сходящейся к решению задач при бесконечном числе элементов, реализуется с помощью
Ответ:
 (1) прямых численных методов 
 (2) итерационных численных методов 
 (3) интерпретационных численных методов 
Упражнение 3:
В векторном n-мерном линейном нормированном пространстве нормой вектора можно назвать
Ответ:
 (1) кубическую норму 
 (2) квадратную норму 
 (3) рекурсивную норму 
Номер 2
В векторном n-мерном линейном нормированном пространстве к понятию нормы вектора следует отнести
Ответ:
 (1) октаэдрическую норму 
 (2) структурную норму 
 (3) стандартную норму 
Номер 3
Какое из нижеприведенных понятий следует считать нормой вектора в векторном n-мерном линейном нормированном пространстве?Ответ:
 (1) евклидову норму 
 (2) норму Коши 
 (3) норму Лагранжа 
Упражнение 4:
Номер 1
В векторном n-мерном линейном нормированном пространстве нормы вектора могут быть
Ответ:
 (1) кубическими 
 (2) октаэдрическими 
 (3) евклидовыми 
Номер 2
Евклидова норма вектора, в комплексном случае, носит название
Ответ:
 (1) биквадратной нормы 
 (2) эрмитовой нормы 
 (3)
Номер 3
Эрмитова норма вектора представляет собой
Ответ:
 (1) евклидову норму в комплексном пространстве 
 (2) октаэдрическую норму в комплексном пространстве 
 (3) структурную норму в полярных координатах 
Упражнение 5:
Номер 1
Когда норма матрицы равняется нулю?
Ответ:
 (1) когда матрица нулевая 
 (2) когда матрица содержит нули на главной диагонали 
 (3) когда матрица содержит нули на побочной диагонали 
Номер 2
Если определитель матрицы равен нулю, то норма матрицы будет
Ответ:
 (1) равна единице 
 (2) равна нулю 
 (3) бесконечной 
Номер 3
Норма матрицы представляет собой
Ответ:
 (1) комплексное число 
 (2) действительное число 
 (3) число 1 
Упражнение 6:
Номер 1
Может ли норма матрицы быть подчиненной норме вектора?
Ответ:
 (1) нет, не может 
 (2) да, может 
 
Номер 2
Может ли норма матрицы быть согласованной с нормой вектора?
Ответ:
 (1) да, может 
 (2) нет, не может 
 (3) это неизвестно, так как не имеет смысла 
Номер 3
Подчиненная норма согласована
Ответ:
 (1) с соответствующей метрикой векторного пространства 
 (2) с детерминированным представлением матрицы 
 (3) с интегрированным представлением контекста определителя матрицы 
Упражнение 7:
Номер 1
Норма суммы матриц равна
Ответ:
 (1) сумме норм этих матриц 
 (2) разности норм этих матриц 
 (3) произведению норм этих матриц 
Номер 2
Норма произведения матриц
Ответ:
 (1) меньше произведения норм этих матриц 
 (2) больше произведения норм этих матриц 
 (3) меньше или равна произведению норм этих матриц 
Номер 3
Погрешности, возникающие при численном решении СЛАУ, могут оцениваться с помощью
Ответ:
 (1) согласованных норм матриц и векторов 
 (2) рекурсивных интегралов 
 (3) дифференциалов Виета 
Упражнение 8:
Номер 1
Произведение нормы матрицы на норму обратной ей матрицы носит название
Ответ:
 (1) число обусловленности матрицы 
 (2) степень обусловленности матрицы 
 (3) уровень обусловленности матрицы 
Номер 2
Число обусловленности матрицы определяется
Ответ:
 (1) произведением нормы матрицы на норму обратной ей матрицы 
 (2) суммой нормы матрицы и нормы обратной ей матрицы 
 (3) разностью нормы матрицы и нормы обратной ей матрицы 
Номер 3
Возможно ли определение числа обусловленности матрицы без определения нормы этой матрицы?
Ответ:
 (1) нет, невозможно 
 (2) да, возможно 
 (3) возможно только в случае с комплексными матрицами 
Упражнение 9:
Номер 1
Для чего применяют число обусловленности матрицы?
Ответ:
 (1) для определения того, насколько погрешность входных данных может повлиять на решение системы  
 (2) для определения корней системы 
 
Номер 2
Каким по своему значению может быть число обусловленности матрицы?
Ответ:
 (1) меньше нуля 
 (2) меньше единицы 
 (3) не меньше единицы 
Номер 3
Может ли число обусловленности матрицы быть равным -1?
Ответ:
 (1) да, но только в одном случае — в случае с нулевой матрицей 
 (2) только в случае с единичной матрицей 
 (3) нет, не может 
Упражнение 10:
Номер 1
Система считается хорошо обусловленной, когда число обусловленности матрицы
Ответ:
 (1) не больше 10 
 (2) лежит в пределах от 100 до 1000 
 (3) больше 106 
Номер 2
Ошибки входных данных слабо сказываются на решении, когда число обусловленности матрицы
Ответ:
 (1) не превышает значение 10 
 (2) больше 1000 
 (3) лежит в пределах от 1000 до 106 
Номер 3
Если число обусловленности матрицы больше 103, тоОтвет:
 (1) система является хорошо обусловленной 
 (2) система является плохо обусловленной 
 (3) система является неопределенной 
Упражнение 11:
Номер 1
Пусть система уравнений имеет матрицу общего вида.В чем заключается прямой ход стандартной схемы решения такой системы?
Ответ:
 (1) в обнулении коэффициентов при неизвестных членах 
 (2) в приведении матрицы к треугольному виду 
 (3) в последовательном умножении элементов матрицы коэффициентов на элементы столбца свободных членов 
Номер 2
Пусть теперь система уравнений имеет матрицу общего вида. В чем заключается обратный ход стандартной схемы решения такой системы?
Ответ:
 (1) в последовательном умножении элементов матрицы коэффициентов на элементы столбца свободных членов 
 (2) в приведении матрицы к треугольному виду 
 (3) в вычислении решения системы 
Номер 3
Количество арифметических действий прямого хода метода Гаусса при n-мерной системе равно
Ответ:
 (1) 2/3(n2) 
 (2) n2 
 (3) 1/3(n2-1) 
Упражнение 12:
Номер 1
Количество арифметических действий обратного хода метода Гаусса при n-мерной системе равно
Ответ:
 (1) n2 
 (2) 2/3(n2) 
 (3) 1/3(n2-1) 
Номер 2
Для решения систем с трехдиагональными матрицами применяется метод, называемый
Ответ:
 (1) алгоритм Томаса 
 (2) алгоритм Коши 
 (3) алгоритм Тейлора 
Номер 3
ПустьA- вещественная, симметричная, положительно определенная матрица.В этом случае итерационный метод Зейделя
Ответ:
 (1) не определен 
 (2) сходится 
 (3) расходится 
Главная / Алгоритмы и дискретные структуры / Основы вычислительной математики / Тест 9
что это такое, как обозначается, элементы главной и побочной диагонали
Матрица — это прямоугольная таблица чисел, состоящая из определенного количества строк и столбцов. Существует множество матричных видов, и один из них — диагональный. Разберемся, что он из себя представляет.
Что такое диагональная матрица
У диагональной матрицы элементы, расположенные вне главной диагонали, равны нулю.
Напомним, что матрица считается квадратной, если количество строк равно количеству столбцов (m = n).
Особенности и свойства
Для начала нужно понять, что такое матричный определитель.
Определитель (детерминант) — это некоторая величина, с которой можно сопоставить любую квадратную матрицу.
Определитель А = (2×2), к примеру, вычисляется по формуле:
Из этого следует свойство №1: определитель диагональной матрицы равен произведению ее диагональных элементов.
Свойство №2: обратная матрица для диагональной равна:
Свойство №3: ранг равен количеству ненулевых диагональных элементов.
Главная и побочная диагонали
Главную диагональ образуют элементы, расположенные на местах \(а_{11}\), \(а_{22}\), \(а_{33}\)…\(а_{NN}\). Их соответственно называют диагональными.
Побочной диагональю называют диагональ элементов от правого верхнего угла до нижнего левого. Эти диагонали параллельны друг другу.
Эти диагонали параллельны друг другу.
Частные случаи диагональных матриц
Существуют три основных подвида: единичная, нулевая, скалярная.
Единичная матрица
У единичной матрицы все диагональные элементы равны единице.
В формулах ее обозначают буквой Е.
Нулевая матрица
В нулевой матрице все элементы, в том числе диагональные, равны нулю.
В формулах ее обозначают цифрой 0.
Скалярная матрица
В скалярной матрице все элементы на главной диагонали равны друг другу.
В некоторых случаях говорят, что скалярная матрица — это произведение скаляра на единичную матрицу Е. В ней диагональные элементы могут быть как положительными, так и отрицательными.
Примеры решения диагональных матриц
Иногда недиагональная матрица может быть приведена к диагональному виду.
Условие: дана матрица А
Задача: привести к диагональному виду.
Решение: характеристическое уравнение равно
а его корни: \(λ_1 = 5\), \(λ_2 = (-2)\)
Если \(λ_1 = 5\), то
Пусть \(х_2 = с\), тогда вектор равен:
Если \(x = λ_2 = (-2)\), то
Пусть \(х_2 = с\), тогда вектор равен:
Таким образом, диагональная матрица имеет вид:
Изучение данных математических объектов имеет свои подводные камни. Если у вас нет времени на учебу, Феникс.Хелп может помочь вам с решением контрольных, самостоятельных и иных проверочных работ.
{-1} \neq I$, но я застрял.- линейная алгебра
- матрицы
$\endgroup$
$\begingroup$
Win Vineeth предоставил самый быстрый способ увидеть это. Конечно, вы также можете увидеть это, используя основные свойства матричного умножения. {-1} =$$adj(A)\over det(A)$ не определено.
{-1} =$$adj(A)\over det(A)$ не определено.
$\endgroup$
$\begingroup$
Если строка $i$ матрицы $A$ равна нулю, то для любой матрицы $B$ строка $i$ произведения $AB$ (если она вообще определена) также будет нулевой, откуда $AB\neq I$ . Аналогично, если столбец $j$ матрицы $A$ равен нулю, то для любой матрицы $B$ столбец $j$ произведения $BA$ также будет равен нулю, поэтому $BA\neq I$. Таким образом, при любом условии $A$ необратима.
(Обратите внимание, что для того, чтобы $B$ была обратной $A$, матрицы $AB$ и $BA$ должны быть единичными). 9n$, где $t \in \mathbb{R}$ — $i$-й элемент вектора $v(t)$, а — все остальные элемента равны (например, все $1$). Затем, поскольку $i$-й столбец $A$ равен нулю, все эти векторы сопоставляются с теми же векторами под $A$. Итак, $A$ не инъективен, в частности, необратим (не биективен).
Аналогично рассматривается случай, когда $i$-я строка равна нулю.
$\endgroup$
$\begingroup$
Еще один взгляд на это:
Система однородных уравнений
AX = 0имеет только тривиальное решениеX = 0тогда и только тогда, когдаAобратимо.
Теперь, если есть строка/столбец со всеми нулями, то хотя бы одна из переменных в указанной системе однородных уравнений будет свободна, что приведет к нетривиальному решению. Таким образом, A необратимы.
$\endgroup$
линейная алгебра — Что такое матрица $0\times0$ или $0\times3$? 9{m\times n}$ как пространство функций $$ M: \{1,\ldots,m\} \times \{1,\ldots,n\} \longrightarrow \mathbb R \тег 1 $$ которые присваивают действительные числа (соответственно числа из вашего любимого поля) парам чисел $(i,j)$ не больше, чем $m$ и $n$. Обычно мы обозначаем $M(i,j)$ как $M_{ij}$, но это всего лишь обозначения.
 (Для векторов просто примите $m$ или $n$ равным $1$.)
(Для векторов просто примите $m$ или $n$ равным $1$.)Если $n$ равно нулю, то целочисленный интервал $\{1,\ldots,n\}$ пуст, и, следовательно, то же самое и с декартовым произведением, что означает, что матрицы и векторы нуль на ноль, $n$ на ноль и ноль на $n$ должны пониматься как функции $$ M:\varnothing\longrightarrow\mathbb R \тег 2 $$ из пустого набора в поле.
А это, в свою очередь, означает, что этот вопрос является просто версией гораздо более «ванильного» примера вопроса, который ставит людей в тупик:
есть функция из пустого набора в реалы?
Ответ на этот вопрос — да, и он известен как «пустая функция», которая объясняется в Википедии здесь и в хороших темах на этом сайте, начиная здесь и здесь, а также в других связанных темах.
Короче говоря, пустая функция в $\mathbb R$ — это функция, которая ставит в соответствие вещественное число каждому элементу $i\in\varnothing$ $-$, что легко, поскольку таких $i$ не существует и, следовательно, нет необходимости делать какие-либо фактические назначения действительных чисел.
Или, другими словами, вектор $n$ на ноль — это массив из $n$ строк, где в каждой строке есть одно действительное число для каждого столбца, но нет столбцов и, следовательно, нет чисел. А нулевая матрица — это массив чисел в столбцах и строках с одним действительным числом на каждом пересечении строк и столбцов, но столбцов и строк нет, поэтому нет чисел.
Тем не менее, все становится интереснее, когда вы хотите рассматривать матрицы как нечто большее, чем просто массивы чисел, и вы также хотите понимать их как конкретные представления линейной карты между векторными пространствами. 9m A_{ij} w_i. \тег 3 $$
Что происходит, когда $n$ (соответственно $m$) равно нулю? В этом случае само векторное пространство $V$ имеет нулевую размерность, а это означает, что $V=\{\vec 0\}$. Это означает, что $V$ — векторное пространство, состоящее только из нулевого вектора, натянутого на пустой базис $\beta = \varnothing$.
Итак, имея это в виду:
- Если $n=0$, то уравнение $(3)$ тривиально верно для всех $v_j\in \beta$, так как нет таких $v_j$, о которых нужно беспокоиться.


 Сколько решений имеет система
Сколько решений имеет система 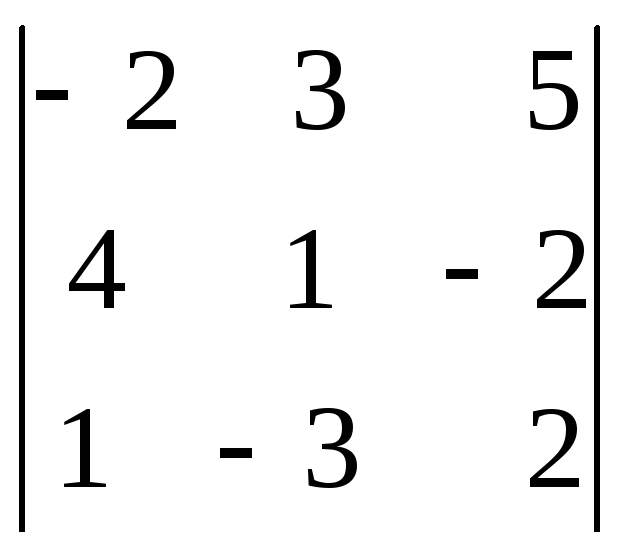 В чем заключается прямой ход стандартной схемы решения такой системы?
В чем заключается прямой ход стандартной схемы решения такой системы? В этом случае итерационный метод Зейделя
В этом случае итерационный метод Зейделя