Лучший ответ по мнению автора
| |||||||||||||||||
04.17
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
задача для 5 класса.
После строительства дома осталось некоторое количество плиток. Их можно использовать для выкладывания прямоугольной площадки на
Решено
В прямоугольном треугольнике АВС угол С равен 90 градусов, AB = 4, tg А=0.75 . Найдите АС.
Решено
в зоопарке живут крокодилы и страусы. В сумме у них 40 голов и 94 ноги. Сколько там крокодилов и страусов?
Решено
основание прямой призмы ромб с острым углом 60градусов.боковое ребро призмы 10см а площадь боковой поверхности 240см в квадрате найдите площадь…
Задача: На прошлой неделе Саша прочитал3/7 всей книги, а на этой неделе- половину оставшихся страниц, да еще 20 и дочитал книгу до конца. Сколько
Пользуйтесь нашим приложением
Интеграл от xcosx – формула, доказательство, примеры
LearnPracticeDownload
Интеграл от xcosx равен xsinx + cosx + C, где C – постоянная интегрирования.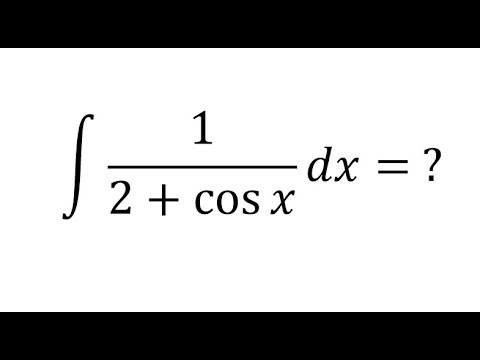
Мы можем оценить интеграцию xcosx, используя метод интегрирования по частям. Интеграл функции есть не что иное, как ее первообразная, поскольку интегрирование есть процесс, обратный дифференцированию. Следовательно, интеграл xcosx равен первообразной xcosx, которая математически записывается как ∫xcosx dx = xsinx + cosx + C.
В этой статье вычислим интеграл от xcosx и выведем его формулу методом интегрирования по частям. Мы также оценим определенное интегрирование xcosx с пределами от 0 до pi/2 и решим несколько примеров, используя интеграл xcosx для лучшего понимания концепции.
| 1. | Что такое интеграл от xcosx? |
| 2. | Интеграл xcosx Formula |
| 3. | Интеграл xcosx Доказательство |
| 4. | Определенная интеграция xcosx |
| 5. | Часто задаваемые вопросы по интегралу xcosx |
Что такое интеграл от xcosx?
Интеграл от xcosx дает площадь под кривой функции f(x) = xcosx и дает различные эквивалентные ответы при использовании различных методов интегрирования.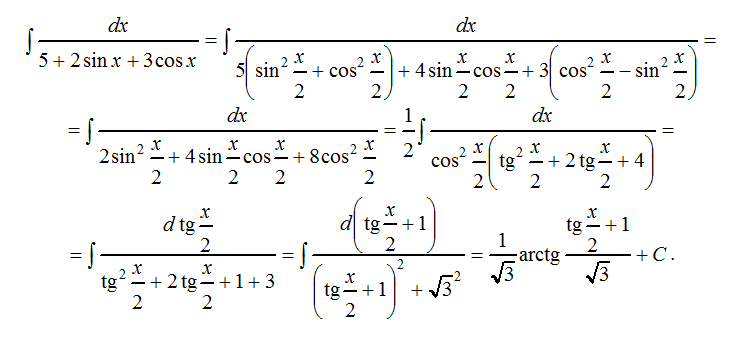
Интеграция xcosx задается формулой ∫xcosx dx = xsinx + cosx + C, где C — постоянная интегрирования, ∫ — символ интегрирования, а dx показывает, что интегрирование xcosx происходит по отношению к x. В следующем разделе рассмотрим формулу интеграла от xcosx.
Интеграл xcosx Formula
Формула для интеграла от xcosx имеет следующий вид: ∫xcosx dx = xsinx + cosx + C, где C — постоянная интегрирования. Мы можем определить этот интеграл от xcosx, используя метод интегрирования по частям. Формула интеграла xcosx показана на изображении ниже:
Интеграл xcosx Доказательство
Теперь, когда мы знаем, что интергал xcosx равен xsinx + cosx + C, мы докажем это, используя метод взаимодействия интегрирования по частям. Формула интегрирования по частям имеет вид ∫udv = uv — ∫vdu. Для интергала xcosx, то есть ∫xcosx dx, предположим, что u = x и dv = cosx dx, тогда v = sinx и du = dx, поскольку производная sinx равна cosx. Следовательно, используя данную формулу, имеем
∫xcosx dx = ∫udv
= uv — ∫v du
= xsinx — ∫sinx dx
= xsinx — (-cosx) + C —- [Поскольку интеграл от sinx равен -cosx + C]
= xsinx + cosx + C, где C — постоянная интегрирования.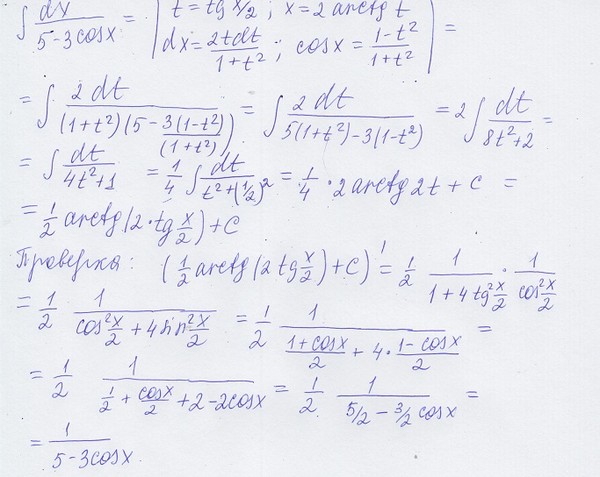
Таким образом, мы доказали, что интеграл от xcosx равен xsinx + cosx + C.
Определенная интеграция xcosx
В этом разделе мы будем использовать формулу интегрирования xcosx, которая задается как ∫xcosx dx = xsinx + cosx + C, чтобы определить определенный интеграл xcosx в пределах от 0 до π/2. По формуле имеем 9{\ frac {\ pi} {2}} \\ & = (\ frac {\ pi} {2} \ sin (\ frac {\ pi} {2}) + \ cos \ frac {\ pi} {2} +C)-(0\sin 0+\cos 0+C)\\&=\frac{\pi}{2}\sin (\frac{\pi}{2})+\cos \frac{\pi {2}+C-0\sin 0-\cos 0-C\\&=\frac{\pi}{2}+0-0-1\\&=\frac{\pi}{2}- 1\end{align}\)
Следовательно, значение определенного интеграла от xcosx в пределах от 0 до pi/2 равно π/2 — 1.
Важные замечания по поводу интеграла от xcosx Интеграл от xcosx равен xsinx + cosx + C. ☛ Связанные темы: Пример 1: 9{\ frac {\ pi} {2}} \\ & = (\ frac {\ pi} {2} \ sin (\ frac {\ pi} {2}) + \ cos \ frac {\ pi} {2} +C)-((-\frac{\pi}{2})\sin (-\frac{\pi}{2})+\cos (-\frac{\pi}{2})+C)\ \&=\frac{\pi}{2}\sin (\frac{\pi}{2})+\cos \frac{\pi}{2}+C-\frac{\pi}{2}\ sin (\ frac {\ pi} {2}) — \ cos (- \ frac {\ pi} {2}) — C \\ & = \ frac {\ pi} {2} + 0- \ frac {\ pi {2}-0\\&=0\end{align}\) Ответ: Интеграл xcosx от -π/2 до π/2 равен 0. Пример 2: Вычислить интеграл от xsinx. Решение: Мы вычислим интеграл от xsinx таким же образом, как мы определили интеграл от xcosx. Воспользуемся методом интегрирования по частям. Формула интегрирования по частям имеет вид ∫udv = uv — ∫vdu.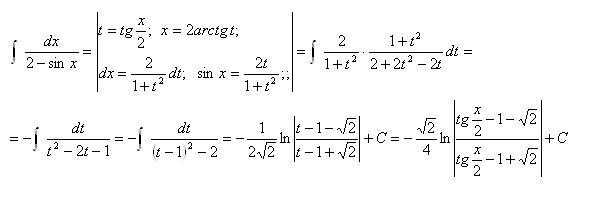
Интеграл xcosx Примеры
∫xsinx dx = ∫udv
= uv — ∫v du
= -xcosx + ∫cosx dx
= -xcosx + sinx + C —- [Поскольку интеграл от cosx равен sinx + C ]
= -xcosx + sinx + C, где C — постоянная интегрирования.
Ответ: ∫xsinx dx = -xcosx + sinx + C
перейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Запись на бесплатный пробный урок
Интеграл вопросов xcosx
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по интегралу xcosx
Что такое интеграл xcosx в исчислении?
Интеграл от xcosx равен xsinx + cosx + C, где C — постоянная интегрирования.
Интегрирование xcosx дает площадь под кривой функции f(x) = xcosx, потому что интеграл функции дает площадь под кривой функции.
Как найти интеграцию xcosx?
Мы можем найти интеграл от xcosx, используя правило интегрирования произведения, то есть метод интегрирования по частям. Мы можем использовать формулу ∫udv = uv — ∫vdu, чтобы найти интеграл и принять u = x и dv = sinx dx и решить соответственно.
Какова формула интеграла от xcosx?
Формула для интеграла от xcosx имеет следующий вид: ∫xcosx dx = xsinx + cosx + C, где C — постоянная интегрирования. Мы можем найти эту формулу интеграла, используя интегрирование методом интегрирования по частям.
Какой определенный интеграл от xcosx от 0 до Pi/2?
Значение определенного интеграла от xcosx в пределах от 0 до pi/2 равно π/2 — 1. Это можно вычислить по формуле интеграла от xcosx.
Является ли интеграл xcosx таким же, как первообразная xcosx?
Антидифференцировка есть не что иное, как обратный процесс дифференциации, который также является интеграцией.