Определение сходимости интеграла онлайн. Несобственные интегралы
Определенные интегралы онлайн на сайт для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов.
Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно. Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой — и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса. Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B.
Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов.
которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам. Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница.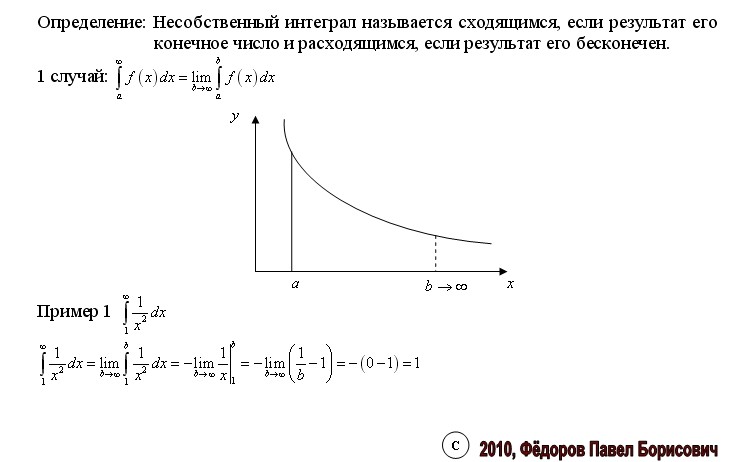
Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение».
Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн.
Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.
Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….
Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.
Что значит вычислить несобственный интеграл?
Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).
Несобственные интегралы бывают двух видов.
Несобственный интеграл с бесконечным пределом (ами) интегрированияИногда такой несобственный интеграл называют несобственным интегралом первого рода . В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: . В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .
Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: , и их мы рассмотрим позже – когда войдёте во вкус:)
Ну а сейчас разберём самый популярный случай . В подавляющем большинстве примеров подынтегральная функция непрерывна на промежутке , и этот важный факт следует проверять в первую очередь! Ибо если есть разрывы, то есть дополнительные нюансы.
Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл численно равен её площади . При этом возможны следующие варианты:
1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то », иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что несобственный интеграл расходится .
2) Но . Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится .
3) О третьем варианте чуть позже.
В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.
А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл (расходится) либо равен конечному отрицательному числу.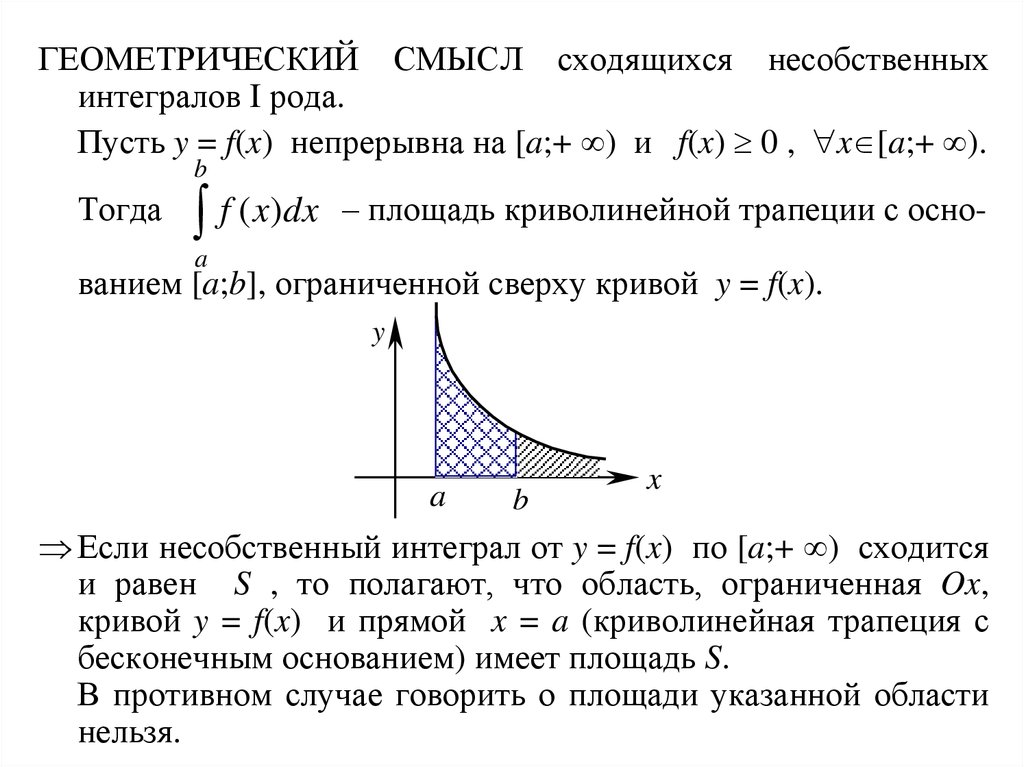
Таким образом, несобственный интеграл может быть отрицательным .
Важно! Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно . Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.
Коль скоро, несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: . На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: . Наверное, многие догадались, что это уже попахивает применением теории пределов, и формула запишется так: .
В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела.
У кого с ними плохо, изучите урок Пределы функций. Примеры решений , ибо лучше поздно, чем в армии.
Рассмотрим два классических примера:
Пример 1
Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно .
Подынтегральная функция непрерывна на полуинтервале , значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.
Применение нашей формулы и решение задачи выглядит так:
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому что любая буква ничем не хуже стандартного «икса».
Если Вам не понятно почему при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций .
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Чистовое оформление задания должно выглядеть примерно так:
“
! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией – непрерывна она на промежутке интегрирования или нет . Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
Пример 2
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд. Решаем с помощью формулы :
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах).
Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Чистовое оформление примера должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на
“
Что делать, если вам встретится интеграл наподобие – с точкой разрыва на интервале интегрирования? Это говорит о том, что в примере опечатка (вероятнее всего) , либо о продвинутом уровне обучения. В последнем случае, в силу свойства аддитивности , следует рассмотреть два несобственных интеграла на промежутках и и затем разобраться с суммой.
Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать , так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.
Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: . Несмотря на определённость и непрерывность косинуса, такого несобственного интеграла не существует! Почему? Всё очень просто, потому что:
– не существует соответствующего предела .
И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».
Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:
Пример 3
Вычислить несобственный интеграл или установить его расходимость.
Сначала попытаемся найти первообразную функцию (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.
Проведем замену:
Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.
На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему при ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.
(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на .
“
Пример 4
Вычислить несобственный интеграл или установить его расходимость.
! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей .
Пример 5
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. У кого какая математическая подготовка.
Полные решения и ответы в конце урока.
Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов . Там же разобран случай, когда оба предела интегрирования бесконечны.
Несобственные интегралы от неограниченных функцийИли несобственные интегралами второго рода
Сразу пример, чтобы было понятно: . Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования .
В этой связи проверим и верхний предел: . Здесь всё хорошо.
Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
* по умолчанию привычно полагаем, что несобственный интеграл существует
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению справа. Легко проследить по чертежу: по оси мы должны бесконечно близко приблизиться к точке разрыва справа .
Посмотрим, как это реализуется на практике.
Пример 6
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)
Сначала вычислим неопределенный интеграл:
Замена:
У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле .
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом . В данном случае у нас правосторонний предел .
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с при . Как определить, куда стремится выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.
В данном случае несобственный интеграл равен отрицательному числу.
3+1}.
\]
Несобственные интегралы первого рода: распространение понятия определённого интеграла на случаи интегралов с бесконечным верхним или нижними пределами интегрирования, или оба предела интегрирования бесконечны.
Несобственные интегралы второго рода: распространение понятия определённого интеграла на случаи интегралов от неограниченных функций, подынтегральная функция в конечном числе точек конечного отрезка интегрирования не существует, обращаясь в бесконечность.
Для сравнения. При введении понятия определённого интеграла предполагалось, что функция f (x ) непрерывна на отрезке [a , b ], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений. Так появляются несобственные интегралы.
Геометрический смысл несобственного интеграла выясняется довольно просто.
В случае, когда график функции y = f (x )
находится выше оси Ox , определённый интеграл
выражает площадь криволинейной трапеции, ограниченной кривой y = f (x )
,
осью абсцисс и ординатами x = a , x = b .
В свою очередь несобственный интеграл
выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями y = f (x )
(на рисунке ниже — красного цвета), x = a и осью абсцисс.
Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:
Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный интеграл называется расходящимся.
Использование предела интеграла вместо самого несобственного
интеграла. Для того, чтобы вычислить несобственный интеграл, нужно использовать предел
определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то
несобственный интеграл называется сходящимся, а в противном случае — расходящимся. К чему стремится
переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода
или второго рода.
Узнаем об этом сейчас же.
Несобственные интегралы первого рода — с бесконечными пределами и их сходимость
Несобственные интегралы с бесконечным верхним пределом
Итак, запись несобственного интеграла как отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.
Определение. Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции f (x ) на промежутке от a до ∞ называется предел интеграла этой функции с верхним пределом интегрирования b и нижним пределом интегрирования a при условии, что верхний предел интегрирования неограниченно растёт , т.е.
.
Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся , а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся и ему не приписывается никакого значения.
Пример 1. Вычислить несобственный интеграл (если он сходится).
Решение. На основании определения несобственного интеграла находим
Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.
В следующем примере подынтегральная функция почти как в примере 1, только степень икса — не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость. То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится, а при каких расходится?
Пример 2. Исследовать на сходимость несобственный интеграл (нижний предел интегрирования больше нуля).
Решение. Предположим сначала, что , тогда
В полученном выражении перейдём к пределу при :
Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .
В первом случае, то есть при
имеет место .
Если , то
и
не существует.
Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .
Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница , можно вывести следующую очень похожую на неё формулу:
.
Это обобщённая формула Ньютона-Лейбница.
Пример 3. Вычислить несобственный интеграл (если он сходится).
Предел этого интеграла существует:
Второй интеграл, составляющий сумму, выражающую исходный интеграл:
Предел этого интеграла также существует:
.
Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:
Несобственные интегралы второго рода — от неограниченных функций и их сходимость
Пусть функция f (x ) задана на
отрезке от a до b и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b ,
в то время как во всех остальных точках отрезка она непрерывна.
Определение. Несобственным интегралом функции f (x ) на отрезке от a до b называется предел интеграла этой функции с верхним пределом интегрирования c , если при стремлении c к b функция неограниченно возрастает, а в точке x = b функция не определена , т.е.
.
Если этот предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае — расходящимся.
Используя формулу Ньютона-Лейбница, выводим.
Несобственные интегралы — презентация онлайн
Математический анализ
Раздел: Определенный интеграл
Тема: Несобственные интегралы
2. §4. Несобственные интегралы
bДля существования
f ( x)dx
необходимы условия:
1) [a;b] – конечен, a
2) f(x) – ограничена (необходимое условие существования
определенного интеграла).
Несобственные интегралы – обобщение понятия определенного
интеграла на случай когда одно из этих условий не
выполнено.
3. 1. Несобственные интегралы I рода (по бесконечному промежутку)
Пусть y = f(x) непрерывна на [a;+ ).y = f(x) непрерывна на [a;b], где b a .
b
существует
a
b
Имеем:
f ( x)dx.
f ( x)dx I (b) ,
D(I) = [a;+ ) .
a
ОПРЕДЕЛЕНИЕ. Несобственным интегралом I рода от
функции f(x) по промежутку [a;+ ) называется предел функции I(b) при b + .
Обозначают:
f ( x)dx
a
Таким образом, по определению
b
f ( x)dx lim I (b) lim
b
a
b
f ( x)dx
(1)
a
При этом, если предел в правой части формулы (1) существует
и конечен, то несобственный интеграл называют
сходящимся.
В противном случае (т.е. если предел не существует или равен
бесконечности)
несобственный
интеграл
называют
расходящимся.
Если y = f(x) непрерывна на (– ;b] , то аналогично определяется и обозначается несобственный интеграл I рода для
функции f(x) по промежутку (– ;b]:
b
b
a
f ( x)dx .
f ( x)dx alim
Если y = f(x) непрерывна на ℝ , то несобственным интегралом
I рода для функции f(x) по промежутку (– ;+ ) называют
c
f ( x)dx
f ( x)dx
f ( x)dx ,
(2)
c
где c – любое число.
Несобственный интеграл от f(x) по промежутку (– ;+ )
называется сходящимся, если ОБА интеграла в правой части
формулы (2) сходятся.
В противном случае, несобственный интеграл по промежутку
(– ;+ ) называется расходящимся.
Будем рассматривать несобственные интегралы I рода по
промежутку [a;+ ). Для интегралов по промежутку (– ;b] и
(– ;+ ) все полученные результаты останутся справедливы.
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ сходящихся несобственных
интегралов I рода.
Пусть y = f(x) непрерывна на [a;+ ) и f(x) 0 , x [a;+ ).
b
Тогда
f ( x)dx
– площадь криволинейной трапеции с осно-
a
ванием [a;b], ограниченной сверху кривой y = f(x).
y
a
b
x
Если несобственный интеграл от y = f(x) по [a;+ ) сходится
и равен S , то полагают, что область, ограниченная Ox,
кривой y = f(x) и прямой x = a (криволинейная трапеция с
бесконечным основанием) имеет площадь S.
В противном случае говорить о площади указанной области
нельзя.
На сходящиеся несобственные интегралы I рода переносятся
некоторые свойства определенных интегралов
(свойства 4, 5, 6, 7, 8).
Кроме того, для несобственных интегралов существует
обобщение формулы Ньютона – Лейбница.
Пусть F(x) – первообразная для f(x) на [a;+ ).
Тогда b [a;+ ) имеем
b
f ( x)dx
b
F ( x) a
F ( b) F ( a )
a
b
f ( x)dx lim F (b) F (a)
b
b
lim
a
a
f ( x)dx lim F (b) F (a)
b
(3)
lim F (b) F (a)
Обозначим
b
F ( x) a .
Тогда (3) примет вид:
f ( x)dx F ( x) a lim F ( x) F (a) .
x
a
(4)
Формулу (4) называют обобщением формулы Ньютона –
Лейбница для несобственных интегралов по промежутку
[a;+ ).
Аналогично для несобственных интегралов по промежутку
(– ;b] доказывается справедливость формулы
b
f ( x)dx
b
F ( x)
F (b) lim F ( x) .
x
ПРИМЕРЫ.
Вычислить несобственныеустановить их расходимость:
1)
cos xdx ;
0
dx
2) n dx ;
x
a
( a 0)
0
dx
4)
;
2
4 x
xdx
7)
.
2
1 x
3)
x
e
dx ;
x
e
dx ;
0
0
5)
интегралы
6)
x
e
dx .
или
10. 2. Признаки сходимости несобственных интегралов I рода
ТЕОРЕМА 1 (первый признак сравнения).Пусть f(x) и (x) непрерывны на [a;+ ) и
0 f(x) (x) , x [c; + ) (где c a).
Тогда:
1) если
( x)dx – сходится, то f ( x)dx тоже сходится,
a
причем
a
c
c
a
f ( x)dx ( x)dx ;
2) если
f ( x )dx – расходится, то
ходится.
( x)dx
a
тоже рас-
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ теоремы 1:
Пусть (σ1) и (σ2) – области в xOy , ограниченные осью Ox,
прямой x = c и кривыми y = (x) и y = f(x) соответственно.
Неравенство 0 f(x) (x) (где x [c;+ )) означает, что
область (σ2) является частью области (σ1).
y
( 2 )
( 1)
c
x
1) если область (σ1) имеет площадь, то ее часть (σ2) тоже
имеет площадь;
2) если говорить о площади области (σ2) нельзя, то и для
содержащей ее области (σ1) тоже нельзя говорить о
площади.
ТЕОРЕМА 2 (второй признак сравнения)
Пусть f(x) и (x) непрерывны и неотрицательны на [a;+ ).
f ( x)
Если lim
h , где h – действительное число, отличное
x ( x)
от нуля, то интегралы
f ( x)dx
a
и
( x)dx
a
ведут себя одинаково относительно сходимости.
ДОКАЗАТЕЛЬСТВО – самостоятельно
Замечания.
1) Теорема 2 остается справедливой и в том случае, если f(x) и
(x) непрерывны и СОХРАНЯЮТ ЗНАК на [a;+ ).
2) При использовании теорем 1 и 2 в качестве «эталонных»
интегралов обычно используют следующие несобственные
интегралы:
сходится, при n 1,
dx
dx
n
x
расходится при n 1.
a
( a 0)
e
0
x
сходится, при 0 ,
dx
расходится при 0.
Пусть f(x) непрерывна на [a;+ ).
Тогда определены несобственные интегралы
f ( x)dx
è
a
f ( x) dx .
a
ТЕОРЕМА 3 (признак абсолютной сходимости).
Если сходится интеграл
тоже будет сходиться.
a
a
f ( x) dx , то и интеграл f ( x)dx
При этом интеграл
сходящимся.
f ( x )dx
называется абсолютно
a
ДОКАЗАТЕЛЬСТВО
y f (x)
y f (x)
y f (x)
Если
f ( x) dx
расходится, то об интеграле
f ( x)dx
ничего
a
a
сказать нельзя. Он может расходиться, а может и сходиться.
Если
f ( x) dx
a
интеграл
расходится, а
f ( x)dx
a
f ( x)dx
– сходится, то
a
называют условно сходящимся.
17. 3. Несобственные интегралы II рода (от неограниченных функций)
Пусть y = f(x) непрерывна на [a;b) и limx b 0
f ( x ) ( )
y = f(x) непрерывна на [a;b1], где a b1 < b .
b1
существует
a
b1
Имеем:
f ( x)dx
f ( x)dx I (b1) ,
D(I) = [a;b) .
a
ОПРЕДЕЛЕНИЕ. Несобственным интегралом II рода по
промежутку [a;b] от функции f(x), неограниченной в точке b,
называется предел функции I(b1) при b1 b – 0 .
b
Обозначают:
f ( x)dx.
a
Таким образом, по определению
b1
b
f ( x)dx lim I (b1 ) lim
b1 b 0
a
b1 b 0
f ( x)dx
(5)
a
При этом, если предел в правой части формулы (5) существует
и конечен, то несобственный интеграл называют
сходящимся.
В противном случае (т.е. если предел не существует или равен
бесконечности)
несобственный
интеграл
называют
расходящимся.
Если y = f(x) непрерывна на (a;b] и
lim
x a 0
f ( x ) ( ) ,
то аналогично определяется и обозначается несобственный
интеграл II рода по промежутку [a;b] от функции f(x),
неограниченной в точке a :
b
b
f ( x)dx a lima 0 f ( x)dx.
a
1
a1
Если y = f(x) непрерывна на [a;b]\{c} и x = c – точка бесконечного разрыва функции, то несобственным интегралом
II рода от функции f(x) по промежутку [a;b] называют
b
a
c
b
f ( x)dx f ( x)dx f ( x)dx.
a
(6)
c
Несобственный интеграл по промежутку [a;b] от функции f(x),
неограниченной внутри этого отрезка, называется сходящимся, если ОБА интеграла в правой части формулы (6)
сходятся.
В противном случае, несобственный интеграл по промежутку
[a;b] называется расходящимся.
Будем рассматривать несобственные интегралы II рода по
промежутку [a;b] от функции, неограниченной в точке b .
Длядругих несобственных интегралов II рода все полученные
результаты останутся справедливы.
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ сходящихся несобственных
интегралов II рода.
Пусть y = f(x) непрерывна на [a;b) и f(x) 0 , x [a;b) .
b1
Тогда
f ( x)dx – площадь криволинейной трапеции с осно-
a
ванием [a;b1], ограниченной сверху кривой y = f(x).
y
b1 b x
a
Если несобственный интеграл от y = f(x) по [a;b] сходится и
равен S , то полагают, что область, ограниченная Ox, кривой
y = f(x) и прямыми x = a, x = b (неограниченная
криволинейная трапеция) имеет площадь S.
В противном случае говорить о площади указанной области
нельзя.
На сходящиеся несобственные интегралы II рода переносятся те
же свойства определенных интегралов, что и для сходящихся
интегралов I рода (свойства 4, 5, 6, 7, 8).
Кроме того, для несобственных интегралов II рода также
существует обобщение формулы Ньютона – Лейбница.
Пусть F(x) – первообразная для f(x) на [a;b) .
Тогда b1 [a;b) имеем
b1
f ( x)dx
a
b1
F ( x) a
F (b1 ) F (a)
b1
f ( x)dx lim F (b1 ) F (a)
b b 0
b b 0
lim
1
1
a
b
f ( x)dx b limb 0 F (b1) F (a)
a
1
(7)
Ранее вводили обозначение: F (b 0) lim
b1 b 0
F (b1 )
b 0
lim F (b1) F (a) F (b 0) F (a) F ( x) a
b1 b 0
.
Тогда (7) примет вид:
b
f ( x)dx
b 0
F ( x) a
lim F ( x) F (a) .
a
x b 0
(8)
Формулу (8) называют обобщением формулы Ньютона –
Лейбница
для несобственных интегралов II рода от
функций, неограниченных в точке b.
Аналогично для несобственных интегралов II рода от функций,
неограниченных в точке a, доказывается справедливость
формулы
b
f ( x)dx
a
b
F ( x) a 0
F (b) lim F ( x) .
x a 0
ПРИМЕРЫ. Вычислить несобственные
установить их расходимость:
b
dx
1)
dx ;
n
( x a)
a
b
dx
2)
dx ;
n
(b x)
a
интегралы
или
1
dx
3) 2 .
x
1
Сформулированные в п.2 признаки сходимости несобственных
интегралов (теоремы 1, 2 и 3) останутся справедливы и для
несобственных интегралов II рода.
При использовании теорем 1 и 2 в роли «эталонных»
интегралов используют интегралы
b
сходится, при n 1,
расходится при n 1.
b
сходится, при n 1,
расходится при n 1.
dx
(b x)n dx
a
dx
( x a)n dx
a
Замечание.
Некоторым расходящимся несобственным интегралам можно
приписать определенное числовое значение. А именно:
1) Если
f ( x)dx
N
– расходится, но lim
N
f ( x)dx A ,
N
то число A называют главным значением этого несобb
ственного интеграла.
2) Главным значением расходящегося интеграла f ( x )dx
a
от функции, имеющей бесконечный разрыв в точке c [a;b]
называют число A, равное
b
c
lim f ( x)dx f ( x)dx A.
0
c
a
Обозначают соответствено: v. p.
f ( x)dx ,
b
v. p.
f ( x)dx.a
Несобственный интеграл 1-го и 2-го рода. Сходимость несобственного интеграла. Решение задач и контрольных работ по высшей математике онлайн
Краткая теория
Понятие несобственного интеграла является обобщением понятия определенного интеграла на случай, когда либо промежуток интегрирования бесконечен (интеграл имеет бесконечные пределы интегрирования), либо подынтегральная функция в некоторых точках обращается в бесконечность.
Несобственные интегралы 1-го рода
Рассмотрим несобственные интегралы первого рода.
Если функция определена на промежутке и при любом существует определенный интеграл
то можно рассматривать
этот предел и называют несобственным интегралом от функции на промежутке . Его обозначают
примем, если предел
конечен, то говорят, что несобственный интеграл сходится, а функция
интегрируема
на промежутке
; если же предел бесконечен или вовсе не
существует, то говорят, что несобственный интеграл расходится, а функция
не интегрируема
на
.
Таким образом, по определению, если существует
то
Подобным образом определяются несобственные интегралы и для других бесконечных промежутков:
Так как несобственные интегралы с бесконечными пределами получаются предельным переходом из соответствующих определенных (собственных) интегралов, то на первые переносятся все те свойства последних, которые сохраняются при этом предельном переходе.
Несобственные интегралы 2-го рода
Перейдем теперь к рассмотрению несобственного интеграла от неограниченной функции (несобственного интеграла второго рода). Пусть функция определена на отрезке , за исключением точки , в окрестности которой она не ограничена. Если существует определенный интеграл
при любом , то можно рассматривать
Этот предел называется несобственным интегралом второго рода на от неограниченной на нем функции и обозначается
При этом, если
предел
существует и конечен, то несобственный интеграл называется сходящимся, а
неограниченная функция
– интегрируемой
на
.
Если же
предел
бесконечен или вовсе не
существует, то несобственный интеграл называется расходящимся, а функция
– не
интегрируемой на
.
Аналогично определяется несобственный интеграл для случая, когда функция определена на отрезке , за исключением точки , в окрестности которой она не ограничена.
В случае, если точка разрыва функции – точка – лежит между точками и и несобственные интегралы на отрезках и существуют, то считают, то
Примеры решения задач
Задача 1
Вычислить несобственный интеграл или доказать его расходимость.
Решение
В этом примере для вычисления неопределенного интеграла используется
интегрирование путем подведения под знак дифференциала.
Несобственный интеграл сходится.
Ответ:
Задача 2
Вычислить несобственный интеграл или доказать его расходимость.
Решение
Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:
ВКонтакте
WhatsApp
Telegram
Я буду работать с вами, над вашей проблемой, пока она не решится.
В этом примере для вычисления неопределенного интеграла применяется метод интегрирования по частям.
Несобственный интеграл сходится.
Ответ:
Задача 3
Вычислить несобственные интегралы или доказать их расходимость.
Решение
В этом примере для вычисления неопределенного интеграла используется интегрирование путем подведения под знак дифференциала.
Несобственный интеграл
сходится.
Ответ:
Задача 4
Вычислить несобственные интегралы или доказать их расходимость.
Решение
В этом примере для вычисления неопределенного интеграла используется интегрирование путем подведения под знак дифференциала.
Ответ: несобственный интеграл расходится.
Калькулятор несобственных интегралов — вычисление неправильных интегралов
Введение в калькулятор несобственных интегралов
Калькулятор несобственных интегралов помогает математикам и студентам измерять несобственные интегралы. Этот калькулятор неправильных интегралов с шагами легко находит неправильный интеграл, используя методы интегрирования в секундах. Вам просто нужно составить уравнение и поставить нижнюю границу, чтобы получить ответ. Вам нужно будет выбрать одну нижнюю границу, так как другая будет бесконечностью.
Калькулятор сходимости несобственного интеграла помогает определить, является ли вставленная функция расходящейся или сходящейся.
Если вы изучаете исчисление или математик, то этот калькулятор неправильной интегральной сходимости станет для вас идеальным помощником.
Потому что это будет удобно при выполнении заданий и если вы структурированы в своем вопросе. Это инструмент ежедневного использования для вычисления неправильных интегралов.
Для решения повседневных задач мы также рекомендуем использовать другие наши инструменты, такие как многократный интегральный калькулятор с шагами, интегральный тройной калькулятор и многие другие, которые предоставляет этот интегральный калькулятор.
Что такое неправильный калькулятор интегралов?
Это инструмент, используемый для оценки неверных интегралов Калькулятор, который работает для получения интегрированного значения для несобственного интеграла. Калькулятор несобственного определенного интеграла хорошо разработан, чтобы помочь пользователям вычислять сложные интегральные функции в мгновение ока. Результаты будут точными благодаря потрясающему алгоритму, работающему в его бэкэнде.
Как и при изучении исчисления, тип интегрирования, который дает площадь между кривой, является несобственным интегралом. Необходимо определить верхний и нижний пределы таких интегралов. Мы можем классифицировать несобственные интегралы как определенные интегралы.
Связанный: Чтобы вычислить определенные интегралы и неопределенные интегралы, используйте онлайн-калькулятор определенных интегралов и калькулятор интегральных неопределенностей бесплатно бесплатно.
Однако расчет неправильных интегралов сложен, и мы предлагаем более простой метод для выполнения такого расчета. Если вы хотите узнать этот метод, придерживайтесь приведенного ниже описания для полной процедуры.
Калькулятор неподходящих интегралов не предоставляет подстановочных методов интегрирования. Таким образом, для этой цели вам нужно использовать калькулятор подстановки u или калькулятор тригонометрического интеграла подстановки. 9∞f(x)dx$$
Для понимания этой формулы необходимо знать, что один из пределов должен быть бесконечен.
Как будто любой предел, который может быть a или b, бесконечен, это будет называться неправильным интегрированием.
Этот неправильный интегральный калькулятор с шагами решает весь процесс в своем алгоритме, чтобы дать ответ в секундах с шагами, используя эту формулу.
Как пользоваться калькулятором неподходящих интегралов
Многие из вас могут захотеть понять, как начать работу с этим калькулятором неподходящих интегралов. Вот несколько простых шагов, которые вам нужно выполнить, чтобы получить наилучшие результаты в кратчайшие сроки. тем не менее, при использовании нашего онлайн-калькулятора неподходящих интегралов необходимо помнить о некоторых важных моментах.
Шаг 1: введите функцию в поле «введите функцию». Вы также можете загрузить примеры, чтобы попробовать калькулятор. Этот удивительный калькулятор содержит множество различных типов примеров.
Шаг 2: Выберите нужные переменные из списка, содержащего переменные X, Y и Z.
Шаг 3: ограничения очень важны для четкого определения функции.
Вы должны добавить нижнюю и верхнюю границы перед расчетом.
Шаг 4: На последнем этапе вам просто нужно нажать кнопку «Рассчитать», чтобы получить быстрые результаты. Этот инструмент также определяет, сходится функция или нет. 92?
Интеграл будет $$-x\frac13+c$$ Так как вам нужно будет добавить коэффициент для решения, иначе интеграл не будет сходиться как калькулятор преобразования Лапласа и калькулятор преобразования синуса Фурье
Как найти неправильные интегралы онлайн?
Если вы ищете быстрый и простой способ найти неправильный интеграл, вам просто нужно найти наш калькулятор несобственного интеграла. Это дает вам наилучшие результаты с надежностью. Вы также можете выполнить вышеупомянутые шаги для вычисления неправильных интегралов.
Однако вы должны иметь четкое представление об этой концепции, чтобы избежать любых неправильных представлений. Необходимо определить точные пределы нахождения несобственных интегралов в режиме онлайн.
Надеемся, вам понравился наш инструмент.
Также попробуйте другие наши инструменты, чтобы упростить вашу работу, так как интегральный калькулятор предоставляет множество онлайн-инструментов для облегчения вашей работы. Вы можете попробовать наши некоторые из известных калькуляторов, такие как калькулятор объема цилиндрических оболочек и калькулятор интегрирования с помощью частичной дроби.
Таким образом, очевидно, что гамма-функция является несобственным интегралом.
Несобственные интегралы — исчисление 2
Все ресурсы исчисления 2
9 Диагностические тесты 308 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
Исчисление 2 Помощь » Интегралы » Нахождение интегралов » Несобственные интегралы
Оценка:
Возможные ответы:
Правильный ответ:
Объяснение:
Напишите правило формулы для случая:
Примените это правило к следующему вопросу.
Сообщить об ошибке
Оценить .
Возможные ответы:
Правильный ответ:
Объяснение:
По правилу формулы мы это знаем . Поэтому мы это знаем.
Продолжаем вычисление:
По степенному правилу для интегралов, для всех с произвольной константой интегрирования. Следовательно:
.
Так,
Как,
Сообщить об ошибке
Оценить.
Возможные ответы:
Правильный ответ:
Объяснение:
По правилу формулы мы это знаем . Поэтому мы это знаем.
Продолжаем вычисление:
По степенному правилу для интегралов, для всех с произвольной константой интегрирования.
Следовательно:
.
Итак,
.
Сообщить об ошибке
Оценить .
Возможные ответы:
Правильный ответ:
Объяснение:
По правилу формулы мы это знаем . Поэтому мы это знаем.
Продолжаем вычисление:
По степенному правилу для интегралов, для всех с произвольной константой интегрирования. Следовательно:
.
Итак,
.
Report an Error
Evaluate:
Possible Answers:
Diverge
Correct answer:
Diverge
Объяснение:
Чтобы оценить , обратите внимание, что знаменатель не существует в .
Интеграл нужно переписать так, чтобы он был предельным. Это несобственный интеграл.
Вычислите интегралы.
Вычисляя члены и подставляя пределы, мы заметим, что интеграл в результате расходится, так как члены не могут быть сокращены в результате.
Правильный ответ: Расхождение
Сообщить об ошибке
Вычислить следующий интеграл:
Возможные ответы:
Правильный ответ:
04
Пояснение:
Интеграл, который мы дали в условии задачи, является неправильным, потому что верхний предел интегрирования дает 0 в знаменателе дроби.
Чтобы исправить это, мы используем следующую технику:
Обратите внимание, что мы переместили тройку за пределы интеграла, а затем и вовсе за предел. Это можно сделать с помощью коэффициентов, что значительно упрощает рассмотрение!
Далее, сохраняя коэффициент и предел, интегрируем:
Интегрирование было выполнено по следующему правилу:
Далее, решите результат:
Мы выбрали 1 слева в нашем пределе, потому что 1 является верхним пределом интегрирования.
Отчет о ошибке
Оцените неправильный интеграл
Возможные ответы:
Интеграл не существует.
Правильный ответ:
Объяснение:
Сначала перепишите функцию, используя отрицательную экспоненту.
.
Затем сделайте замену u=1+x. Тогда du=dx. Мы также можем переписать пределы интегрирования через u. Когда x приближается к бесконечности, u приближается к бесконечности. Когда .
Переписав и вычислив интеграл с помощью степенного правила, , мы получим:
Сообщить об ошибке
Вычислить следующий интеграл:
Возможные ответы:
Правильный ответ:
Объяснение:
Интеграл неправильный из-за верхнего предела интегрирования (бесконечность).
Чтобы вычислить интеграл, мы должны сделать следующее:
Теперь проинтегрируем и оценим интеграл от t до 1:
Интегрирование было выполнено по следующему правилу:
но поскольку это было определенное интегрирование, мы подставляем верхний предел и вычитаем из того, что мы получаем от подстановки нижнего предела.
При вычислении предела член, содержащий t, представляет собой дробь с бесконечностью в знаменателе, которая равна нулю.
Сообщить об ошибке
Вычислить следующий интеграл:
Возможные ответы:
Правильный ответ:
Объяснение:
Интеграл неправильный из-за нижнего предела интегрирования (составляет равное бесконечности).
Следовательно, мы должны сделать следующее:
Мы оцениваем предел справа, потому что 1 — это нижний предел интегрирования.
Затем мы перемещаем константу 2 перед пределом и сохраняя предел , интегрируем:
При интегрировании использовалось следующее правило:
в верхнем и нижнем пределах в функцию, которую мы получаем путем интегрирования и вычитания двух (как показано выше).
Наконец, оцените предел:
Доминирующий член в пределе — это когда натуральный логарифм приближается к нулю, т. е. к отрицательной бесконечности. Перед этим термином стоит знак минус, поэтому он превращается в положительную бесконечность.
Отчет о ошибке
Оцените неправильный интеграл
Возможные ответы:
Интегральные дивергии
Правильный ответ:
Правильный ответ:
Правильный ответ:
Правильный ответ:
. Объяснение: Замена упрощает вычисление этой первообразной. Пусть и . Нам также нужно переписать пределы интегрирования с точки зрения . Когда и когда. После этих подстановок интеграл становится равным Затем для нахождения первообразной требуется правило степени. Общий случай степенного правила: . Следовательно, интеграл равен Поскольку интеграл не стремится к конечному значению, он расходится. Сообщить об ошибке ← Назад 1 2 3 4 Далее → Уведомление об авторских правах 9 Диагностические тесты
308 практических тестов
Вопрос дня
Карточки
Learn by Concept Содержание Калькулятор несобственных интегралов бесплатно отображает интегрированное значение несобственного интеграла онлайн. Чтобы использовать неправильный интегральный калькулятор, выполните следующие действия:
0005 Все ресурсы исчисления 2
Калькулятор неправильных интегралов
Онлайн-калькулятор неправильных интегралов STUDYQUERIES ускоряет вычисления и отображает значение за доли секунды. Неправильный калькулятор интегралов }\) на \([−1,1]\).
Заштрихованная область безгранично растет, как показано на рисунке ниже.
Пример несобственного интеграла Формализация этого примера приводит к понятию несобственного интеграла. Есть два способа расширить основную теорему исчисления. Один из них — использовать бесконечный интервал, т.
е. \([a,\infty),(−\infty,b]\) или \((−\infty,\infty)\).
Второй — позволить интервалу \([a,b]\) содержать бесконечный разрыв \(f(x)\). В любом случае интеграл называется несобственным интегралом. Распределения вероятностей являются одним из наиболее важных применений этой концепции, поскольку для определения таких величин, как кумулятивное распределение или ожидаемое значение, обычно требуются интегралы на бесконечных интервалах. 9{b}f(x)dx$$
Поскольку мы имеем дело с пределами, нас интересует сходимость и расходимость несобственного интеграла. Когда предел существует и является конечным числом, мы говорим, что несобственный интеграл сходится. В качестве альтернативы мы говорим, что несобственный интеграл расходится, как это отражено в следующем определении.
Конвергенция и дивергенция Если предел существует и является конечным числом, мы говорим, что несобственный интеграл сходится. Если предел равен \(\pm{\infty}\) или не существует, мы говорим, что несобственный интеграл расходится.
{b}f(x)dx\) сходятся, то \(f\) над \( [а,б]\) равно 9{b}f(x)dx$$
Что такое несобственный интеграл на примере?
Несобственный интеграл — это интеграл, который имеет один или оба бесконечных предела или подынтегральную функцию, стремящуюся к бесконечности в одной или нескольких точках диапазона интегрирования. Интегралы Римана нельзя использовать для вычисления несобственных интегралов.
Что делает интеграл неправильным?
Интегрирование является неправильным, если либо нижний предел интегрирования бесконечен, либо верхний предел интегрирования бесконечен, либо верхний и нижний пределы интегрирования бесконечны.
Что такое собственный и несобственный интеграл?
Интеграл без бесконечного предела и подынтегральной функции, стремящийся к бесконечности в любой точке своего диапазона.
Какие существуют два типа несобственных интегралов?
Несобственные интегралы бывают двух типов: Тип 1 — когда пределы интегрирования бесконечны, и Тип 2 — когда пределы интегрирования конечны.