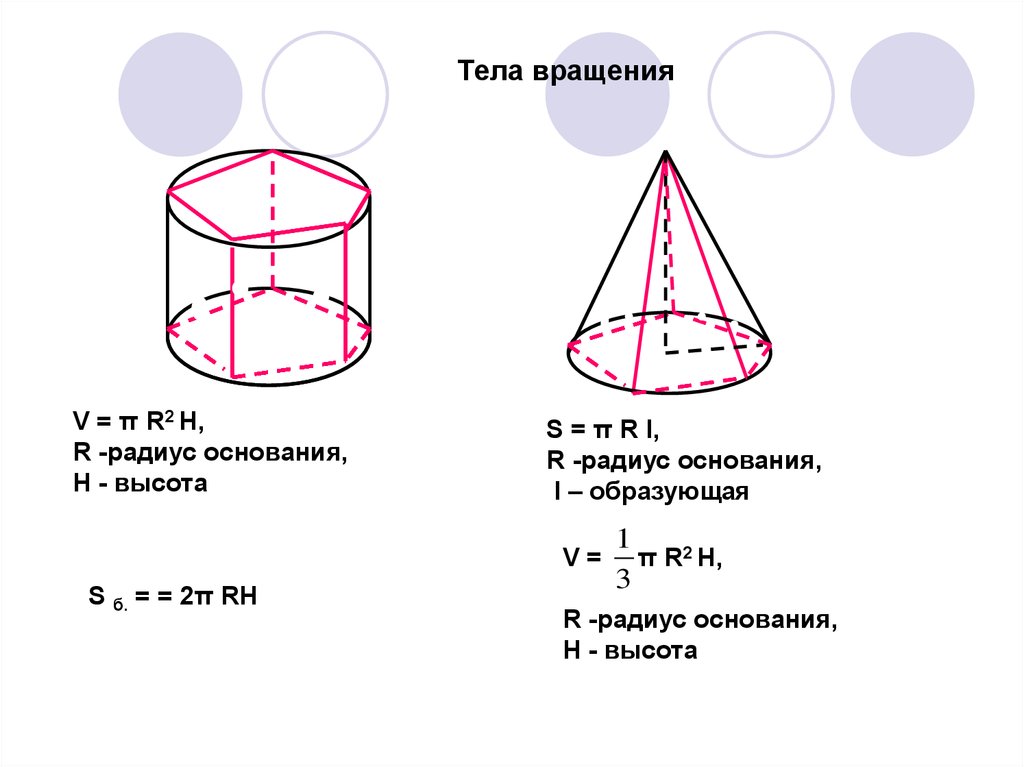
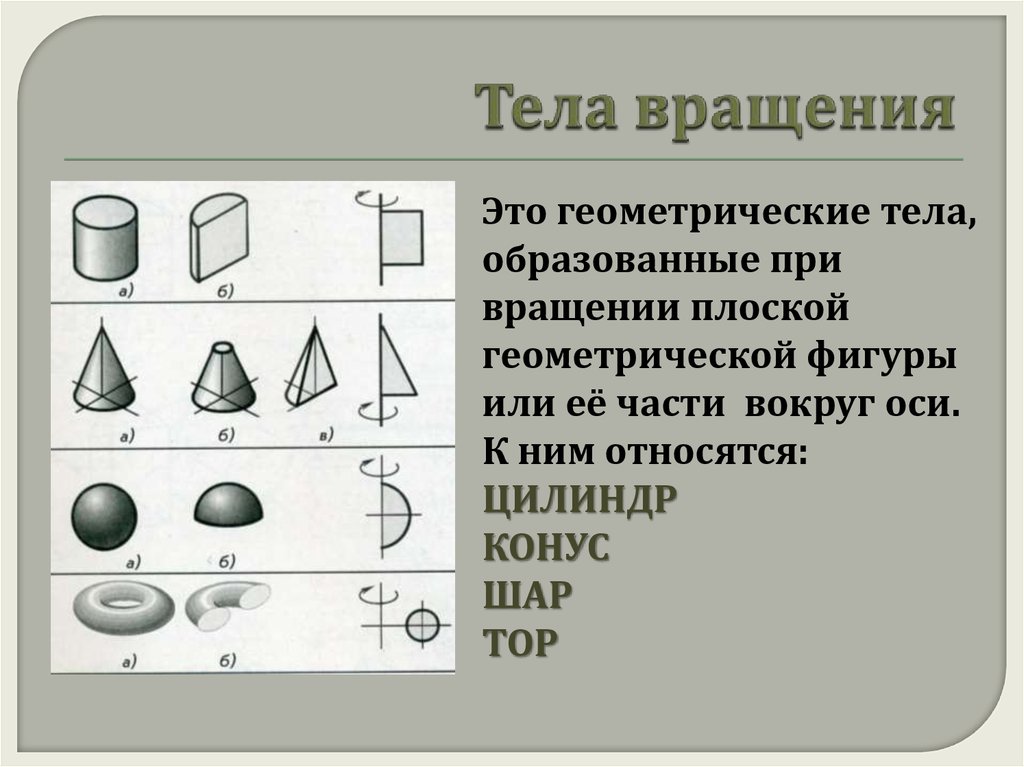
Тела вращения
Тела вращения – это объемные тела, которые возникают при вращении некой плоской фигуры, которая, в свою очередь, ограничена кривой и крутится вокруг оси, лежащей в той же плоскости.
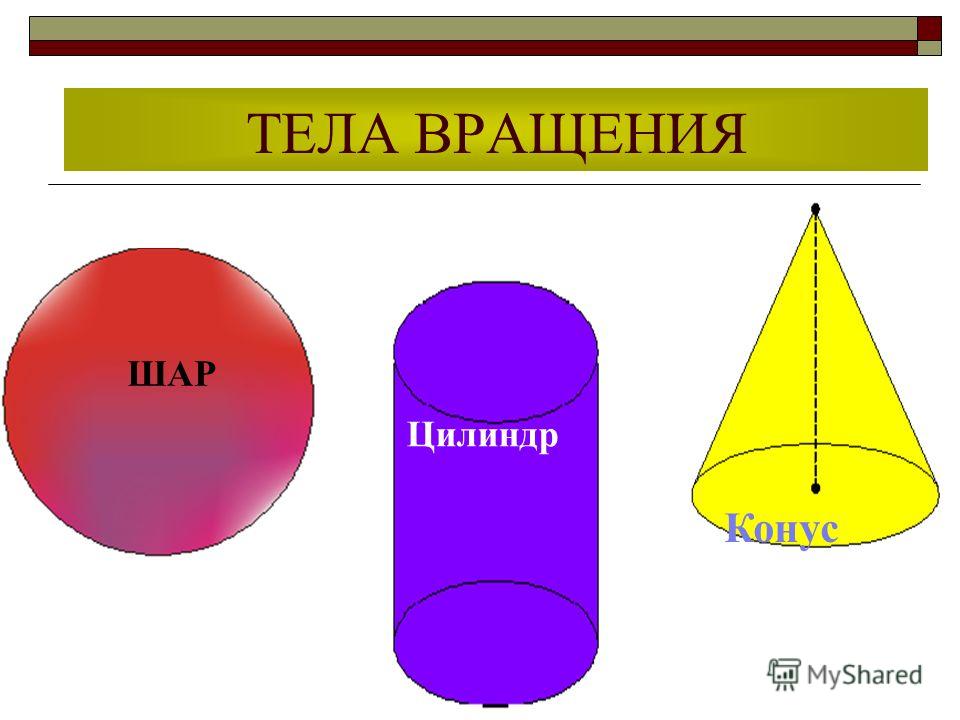
Какие же основные тела вращения существуют?
- Шар. Это геометрическая фигура, которая образована в результате вращения полукруга вокруг диаметра разреза.
- Цилиндр. Это геометрическая фигура, которая образована в результате вращения прямоугольника вокруг одной из его сторон.
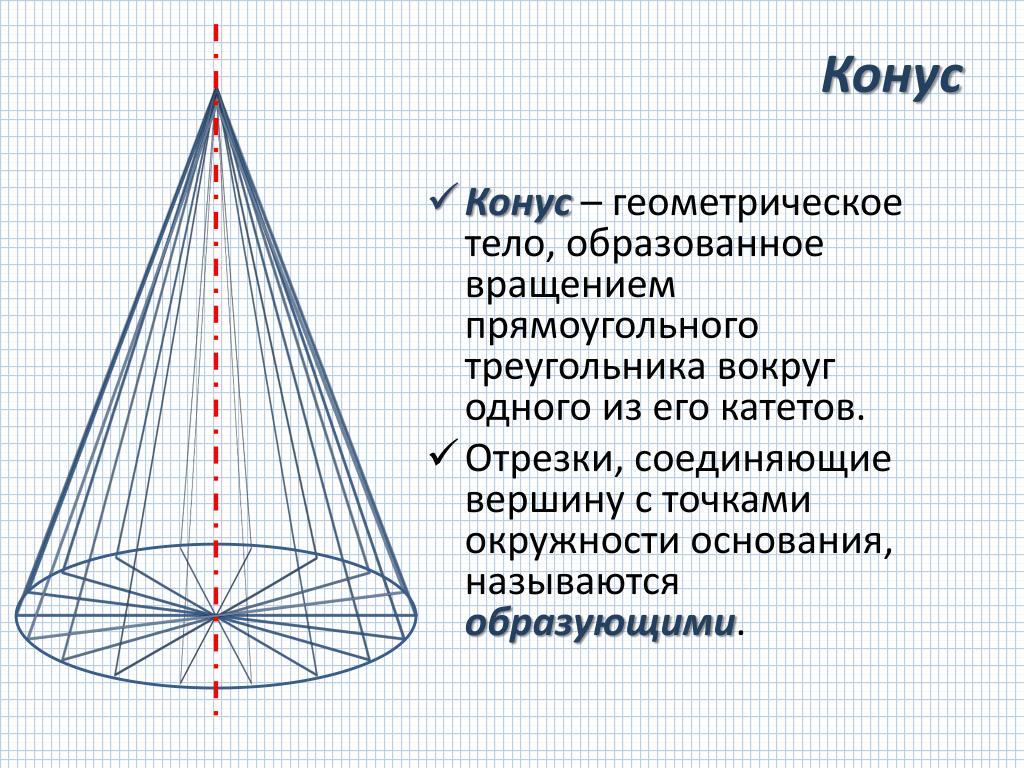
- Конус. Это геометрическая фигура, которая образована в результате вращения прямоугольного треугольника вокруг одного из своих катетов.
- Тор. Это геометрическая фигура, которая образована в результате вращения окружности вокруг прямой, при этом окружность прямую не пересекает.
Стоит отметить такой интересный факт, что если вращаются контуры фигур, то у нас возникает поверхность вращения. Пример – сфера, которая образовывается в результате вращения окружности.
Тела вращения, разумеется, имеют свой объем и свою площадь. И то и другое, можно узнать с помощью теорем Гульдина-Паппа.
Первая теорема гласит о том, что площадь поверхности линии, которая образуется при вращении и лежит целиком в плоскости по одну сторону от оси вращения, равняется произведению длины линии на длину окружности, пробегаемой центром масс этой линии.
Вторая теорема говорит о том, что объем тела, который образуется при вращении фигуры и лежит целиком в плоскости по одну сторону от оси вращения, равняется произведению площади фигуры на длину окружности, пробегаемой центром масс этой фигуры.
Цилиндр | |||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||
Конус | |||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||
Усеченный конус | |||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||
Шар | |||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||
Шаровой сектор | |||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||
Шаровой сегмент | |||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||
Шаровой пояс(слой) | |||||||||||||||||||||||||||||
|
Тела и поверхности вращения.
 Шар. Цилиндр. Конус
Шар. Цилиндр. КонусТела и поверхности вращения.
Шар. Цилиндр. Конус. Площади поверхности и объемы этих фигур.
Подробная теория с наглядными иллюстрациями и основные формулы.
Читай эту статью, здесь все это есть.
Всего за 15 минут ты полностью во всём разберешься!
А теперь гораздо хитрее. Бывает так, что ось вращения находится далеко от фигуры, которая вращается.
Например, так:
Вращаем:
Что получится? Бублик. А по-научному – ТОР.
Ну и так вот можно любую фигуру вертеть вокруг любой оси, и будут получаться разные более или менее сложные тела вращения.
Ну, а поверхность вращения – это просто граница тела вращения. Ведь поверхность это всегда граница тела.
Здесь мы рассмотрим подробно несколько тел вращения. Те, которые встречаются в школьных задачах. Это шар, цилиндр и конус.
Вообще-то есть и другое определение шара – через ГМТ (геометрическое место точек)
Шар – геометрическое место точек, удаленных от одной фиксированной точки на расстояние, не более заданного.
{2}}\)
\( R\) – радиус
Откуда взялось? Умные математики придумали – это не так уж просто – придется просто запомнить.
Это еще одна хитрая формула, которую придется запомнить, не понимая, откуда она взялась.
Если ты знаком с производной, то можешь заметить это:
\( {{V’}_{шара}}={{S}_{поверхности}}\)И это не случайно! Но почему это так вышло, мы тоже здесь обсуждать не будем. Можешь попробовать доказать это сам!
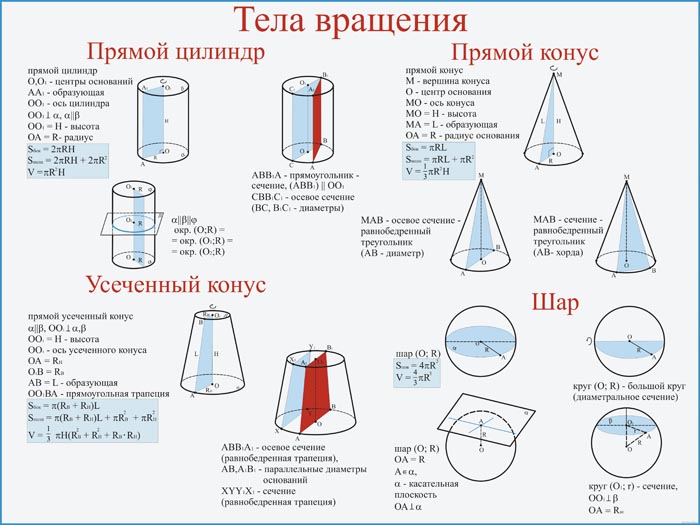
Цилиндр
Цилиндр – тело, образованное вращением прямоугольника вокруг одной из сторон.
Вообще-то, полное имя этого тела – «прямой круговой цилиндр», но составители задач и мы вместе с ними по дружбе называем его просто цилиндром. Названия, относящиеся к цилиндру, такие:
Основания у цилиндра – это круги
Еще у цилиндра есть так называемая развертка.
Представь, что у нас от цилиндра осталась только боковая поверхность, и мы ее разрезали вдоль образующей и развернули.
{2}}}_{два\ круга}\)
И опять же, полное название этого тела: «прямой круговой конус», но во всех задачах у нас говорится просто «конус».
Названия, относящиеся к конусу:
Что тут нужно твердо помнить?
- Основание корпуса – круг
- Все образующие конуса – равны.
Ясно ли это? Вроде должно быть ясно, ведь образующая – это гипотенуза (одна и та же!) Треугольника, который вращаем, а радиус основания – катет.
У конуса тоже есть развертка.
Снова представим, что основания нет, разрежем боковую поверхность вдоль образующей и развернём кулек. Что получится?
Представь себе сектор круга. Пусть длина образующей равна \( l\).
Развертка конуса – сектор круга радиуса \( l\)
Площадь поверхности конуса
Как найти площадь боковой поверхности корпуса? Вспомним о развертке, ведь для цилиндра все было просто именно с помощью развертки.
{2}}\)
Можно вынести \( \pi R\):
\( {{S}_{полн. }}=\pi R\left( l+R \right)\)
Но, как и для цилиндра, не надо запоминать вторую формулу, гораздо проще всегда пользоваться первой.
Это так же, как у пирамиды
\( V=\frac{1}{3}{{S}_{осн.}}\cdot H\), только
\( {{S}_{осн. }}\) — это не площадь многоугольника, а площадь круга.
А вот откуда взялась \( \frac{1}{3}\)?, по-прежнему остается загадкой, потому что эта \( \frac{1}{3}\) получена в результате довольно хитрых рассуждений умных математиков.
А тебе нужно очень твердо запомнить, что в формулах объёма «треугольных» фигур: конуса и пирамиды эта \( \frac{1}{3}\) и есть, а в формулах параллелепипеда, призмы и цилиндра ее нет!
Бонус: Вебинары по стереометрии из нашего курса подготовки к ЕГЭ по математике
ЕГЭ 14 Стереометрия.
Расстояние между точками и от точки до прямой
В этом видео мы научимся «видеть» 3-мерное пространство и изображать 3-мерные объекты на бумаге (то есть на плоской поверхности).
Затем мы научимся двум основным вещам — находить расстояние между точками на таких рисунках, а также расстояние от точки до прямой.
На этих умениях строится всё дальнейшее изучение стереометрии. В общем это очень важное, базовое видео, с которого нужно начинать изучение стереометрии.
Не перескакивайте, не пропускайте его! Даже если вы знаете стереометрию, вы найдете для себя очень много полезного и нового в этом видео.
ЕГЭ 14. Стереометрия. Пирамида. Разбор варианта профильного ЕГЭ 2020
В этом видео:
- Как нарисовать шестиугольную пирамиду.
- Как подписать вершины пирамиды чтобы потом легче было решать задачу.
- Как исправить рисунок, если грани пирамиды сливаются.
- Доказательство пунктов А и Б, а также их правильная запись, которую примет любой проверяющий на ЕГЭ.
- Нахождение площади основания и объема пирамиды.
- Самое главное, на что нужно обратить внимание.
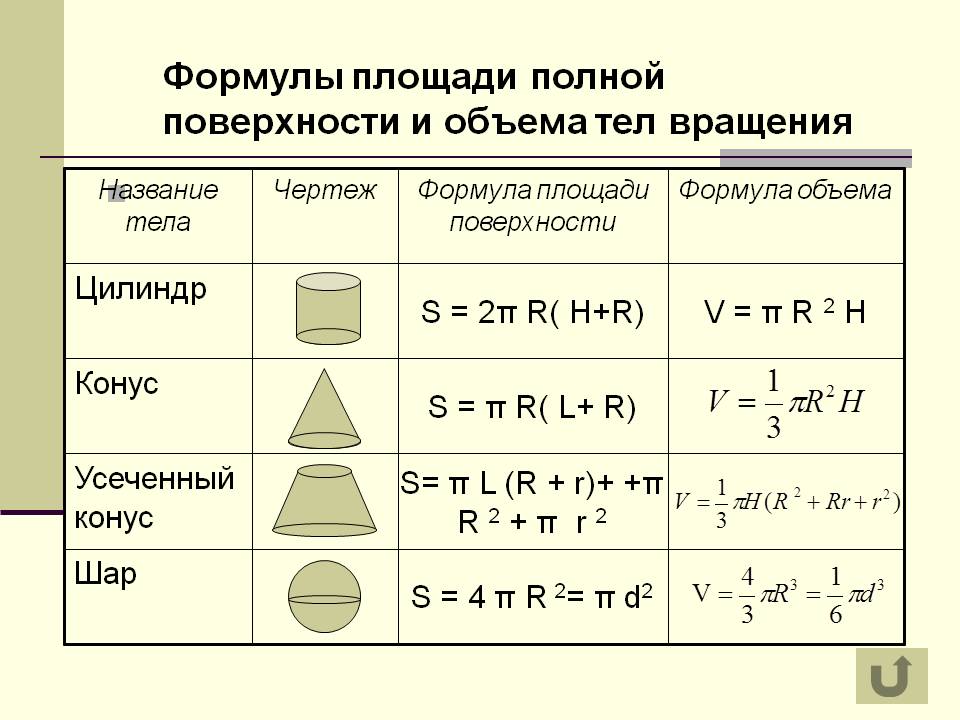
ТЕЛА ВРАЩЕНИЯ (объемные геометрические фигуры): определения, формулы
Тела вращения (объемные геометрические фигуры) : определения, формулы периметра поверхности и площади. Виды: цилиндр, конус, шар, шаровой сектор, шаровой сегмент.
Цилиндр
- Цилиндр — тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями.
- Цилиндрическая поверхность — поверхность, образуемая однопараметрическим семейством параллельных прямых (образующих) и проходящими через точки некоторой кривой (направляющей).
- Основания цилиндра — плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями, ограничивающими цилиндр.
- Высота цилиндра — расстояние между основаниями цилиндра.
Виды цилиндров
- Прямой — цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), прямая между которыми перпендикулярна плоскостям этих оснований. Данная прямая называется осью цилиндра.
- Косой — цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), отрезок между которыми не перпендикулярен плоскостям этих оснований.
- Круговой — цилиндр с окружностью в роли направляющей.
- Цилиндр вращения (или прямой круговой) — цилиндр, который можно получить вращением (то есть тело вращения) прямоугольника вокруг одной из его сторон, содержащая которую прямая в таком случае будет осью этого цилиндра и его осью симметрии.
- Эллиптический, параболический и гиперболический – цилиндр, основания которого являются эллипсами, параболами или гиперболами.
Последние два имеют бесконечный объём.
- Равносторонний — цилиндр вращения, диаметр основания которого равен его высоте.
Формулы для цилиндра:
Объем цилиндра: V=π∙R2∙h или V=So∙h
Поверхность цилиндра: S= 2∙So + Sбок или S= 2∙π∙R2 + 2∙π∙R∙h
Площадь основания: So= 2∙π∙R2
Площадь боковой поверхности: Sбок=2∙π∙R∙h
Где: V — объем цилиндра, R — радиус цилиндра, h — высота цилиндра, So — площадь основания цилиндра, π = 3.141592.Формулы для полого цилиндра:
Объем цилиндра: V = π ∙ h ∙ (r22 — r12) где r2 > r1
Конус
Площадь боковой поверхности: Sбок = 2 ∙ π ∙ h ∙ (r1 + r2)
Где: V — объем цилиндра, R — радиус цилиндра, h — высота цилиндра, So — площадь основания цилиндра, π = 3.141592.
- Конус – поверхность, образованная в пространстве множеством лучей (образующих конуса), соединяющих все точки некоторой плоской кривой (направляющей конуса) с данной точкой пространства (вершиной конуса).
- Боковая поверхность конуса — объединение образующих конуса; образующая поверхность конуса является конической поверхностью.
- Высота конуса — отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка).
- Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
- Конусность — соотношение высоты и диаметра основания конуса.
Типы конусов
- Прямой — конус, основание которого имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром.
Прямая, соединяющая вершину и центр основания, называется осью конуса.
- Косой (или наклонный) — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
- Круговой — конус, основание которого является кругом.
- Конус вращения или прямой круговой конус (часто под конусом подразумевают именно его) — конус, который можно получить вращением (то есть тело вращения) прямоугольного треугольника вокруг прямой, содержащей катет треугольника (эта прямая является осью конуса).
- Эллиптический, параболический и гиперболический — конус, опирающийся на эллипс, параболу или гиперболу. Последние два имеют бесконечный объем.
- Усечённый или конический слой — часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием.
- Равносторонний — конус вращения, образующая которого равна диаметру основания.
Формулы для конуса:
Объем конуса: V = 1/3·π·R2·h или V=1/3·So·h
Поверхность конуса: S=So+Sбок или S=π∙R2+π∙R∙h
Площадь основания: So=π∙R2
Площадь боковой поверхности: Sбок=π∙R∙l
Образующая: l=√(R2+h2)
Где: V — объем конуса, So — площадь основания, R — радиус основания, h — высота конуса, l — образующая, π=3.141592.Формулы для усеченного конуса:
Объем конуса: V=1/3·π·(r12+r22+r1·r2)·h
Шар
Площадь боковой поверхности: Sбок=π∙(r1+r2)∙l
Где: r1 — радиус нижнего основания усеченного конуса; r2 — радиус верхнего основания усеченного конуса; l — образующая усеченного конуса, π=3.141592.
Формулы для шара:
Объем шара: V = 4/3 ·π· R3 или V=1/6 ·π · D3
Площадь поверхности сферы: S= 4 ·π· R2 или S=π · D2
Площадь основания: So=π∙R2
Где: R — радиус шара, π = 3.141592.Формулы для шарового сектора:
Высота конуса: hконуса=R2−r2
Высота сегмента: hсегмента= R−R2−r2
Площадь поверхности шарового сектора: Sсектора= Sсегмента+ Sконуса
или Sсектора= 2∙π∙R∙hсегмента + π∙R∙rили Sсектора=2∙π∙ R ∙(R−R2−r2) + π∙R∙r
Объем шарового сектора: V = 2/3∙(π∙R2∙h) или V = 1/3∙( R∙S)
Где: R — радиус шара, r — радиус сегмента, π = 3.141592.
Формулы для шарового сегмента:
Площадь поверхности шарового сегмента : S = 2∙π∙R∙h
Объем шарового сегмента : V = (π ·H2 (R -1/3 ·h)
Где: R — радиус шара, r — радиус сегмента, h= высота шарового сегмента, π = 3.141592.
Maths — Вращение вокруг точки
Для двумерных вращений вокруг x,y мы можем представить это с помощью следующей матрицы 3×3:
r 00 р 01 х-р 00 *х-р 01 *у р 10 р 11 у-р 10 *х-р 11 *у 0 0 1 Это то же самое, что и вращение вокруг начала координат, но со смещением на:
(- r 00 *x — r 01 *y, — r 10 *x — r 11 *y).
Для трехмерных вращений вокруг x,y мы можем представить это с помощью следующей матрицы 4×4:
r 00 р 01 р 02 x — r 00 *x — r 01 *y — r 02 *z р 10 р 11 р 12 у — г 10 *х — г 11 *у — г 12 *г р 20 р 21 р 22 z — r 20 *x — r 21 *y — r 22 *z 0 0 0 1 То же, что и вращение вокруг начала координат, но со смещением на: 11 *y — r 12 *z,- r 20 *x — r 21 *y — r 22 *z).
Затем мы покажем, что в двух измерениях верно и обратное. То есть любая комбинация переноса и вращения может быть представлена одним вращением при условии, что мы выбираем правильную точку для вращения.
Комбинированное вращение и перемещение
Чтобы вычислить вращение вокруг произвольной точки, нам нужно вычислить его новое вращение и перевод. Другими словами, вращение вокруг точки есть «правильное» преобразование изометрии, что означает, что оно имеет линейную и вращательную составляющую.
Предположим, у нас есть матрица [R0], которая определяет поворот вокруг начала координат:
Теперь мы хотим применить тот же поворот, но относительно произвольной точки P:
Как мы видим, его ориентация такая же, как если бы он вращался вокруг начала, но она была перемещена в другую точку пространства в результате вращения.
Чтобы доказать это и рассчитать количество линейного перевода, мы нужно заменить:
- перевести про произвольную точку P (Px,Py,Pz).
Со следующими тремя более простыми преобразованиями, которые при выполнении по порядку эквивалентны:
- перевести произвольную точку в начало координат (вычесть P, который переводит по -Px,-Py,-Pz)
- повернуть вокруг начала координат (можно использовать матрицу 3×3 R0)
- затем переведите обратно. (добавьте P, который переводится как +Px,+Py,+Pz)
Итак, если мы используем глобальную систему отсчета (как описано здесь) затем
[результирующее преобразование] = [третье преобразование] * [второе преобразование] * [первое преобразование]
[результирующее преобразование] = [+Px,+Py,+Pz] * [поворот] * [-Px,-Py,-Pz]
Примечание для матричной алгебры, порядок операций важен, поэтому эти переводы не отменять.
Итак, матрица, представляющая вращение вокруг заданной точки:
[R] = [T] -1 * [R0] * [T]
где:
[T] -1 = обратное преобразование = перевод точки в исходную точку
1 0 0 х 0 1 0 г 0 0 1 г 0 0 0 1 [R0] = вращение вокруг начала координат (если это неясно, см.
это обсуждение)
r 00 р 01 р 02 0 р 10 р 11 р 12 0 р 20 р 21 р 22 0 0 0 0 1 [T] = перевод источника в точку
1 0 0 -х 0 1 0 -у 0 0 1 -з 0 0 0 1 Перемножение этих матриц даст следующий результат для вращение вокруг x,y,z:
(чтобы увидеть все шаги, см.
эту страницу)
r 00 р 01 р 02 x — r 00 *x — r 01 *y — r 02 *z р 10 р 11 р 12 у — г 10 *х — г 11 *у — г 12 *г р 20 р 21 р 22 z — r 20 *x — r 21 *y — r 22 *z 0 0 0 1 Таким образом, компоненты вращения те же, но вращение перемещает положение центра.
Изометрия в двух измерениях SE(2)
Теперь мы хотим проверить обратное, то есть любую комбинацию переноса и вращения можно представить одним вращением при условии, что мы выберем правильную точку для ее вращения.
Представьте, что мы хотим преобразовать твердое тело в точке «А» в твердое тело в точке «В».
Затем мы можем определить точку на А (например, центр B. Затем мы можем объединить два преобразования:
- Выполните линейное перемещение таким образом, чтобы точка на «А» трансформировалась в точку на «В».
- Выполните вращение вокруг точки, чтобы правильно преобразовать твердое тело.
Тем не менее, есть второй вариант, мы можем сделать перевод всего за один оборот:
Итак, при условии, что мы можем найти подходящую точку для вращения (в приведенном выше примере показана зеленой точкой), мы можем сделать перемещение и вращение за одну операцию. Точка, вокруг которой мы вращаемся, должна быть равноудалена от выбранной точки на каждом теле, поэтому она должна лежать на линии, перпендикулярной линии, соединяющей две точки. Так всегда ли мы можем найти точку, которая будет выполнять любую комбинацию переноса и поворота? Чтобы выяснить это, мы можем принять две крайности:
- Если точка вращения находится точно посередине двух объектов, то объект будет повернут на 180 градусов.
- Если точка вращения находится в бесконечности вдоль биссектрисы, то объект только перемещается, и вращение будет равно нулю.
Поместив точку на некотором расстоянии между ними, мы можем получить любой поворот от 0 до 180 градусов. Мы можем получить отрицательные углы, двигаясь в противоположном направлении вдоль линии.
Поэтому мы можем сделать любой поворот, комбинацию перемещений за один оборот.
Выполнение поворота-перемещения за одну операцию может упростить некоторые вычисления, и нам не нужно думать, делаем ли мы сначала вращение вокруг исходного положения, а затем перемещение, или сначала выполняем перемещение, а затем вращение вокруг его конечное положение, или сначала выполните перенос в среднюю точку, затем вращение вокруг среднего положения и затем заключительный полуперевод.
Вычисление точки вращения
Учитывая смещение (заданное двумерным вектором) и вращение (заданное скалярным углом в радианах), как мы вычисляем точку вращения P?
Мы знаем точки А и В и угол при Р, который равен тета.
sin(θ/2) = v/(2*r)
r = v/(2*sin(θ/2))
где:
- r = скалярное расстояние P от A и B
- v = скалярное расстояние B от A
- θ = угол поворота
Мы также знаем по Пифагору:
(Px — Ax) 2 + (Py — Ay) 2 = r 2
(Px-Bx) 2 + (Py — By) 2 = r 2Это становится немного грязно! Можем ли мы найти P в векторных координатах?
Думаю, мне придется отказаться от этого подхода и вместо этого инвертировать матричные уравнения, с которых мы начали:
Из матрицы, полученной выше:
r 00 р 01 х-р 00 *х-р 01 *у р 10 р 11 у-р 10 *х-р 11 *у 0 0 1 Мы получаем уравнения для смещения:
OffSetx = x — r 00 *x — r 01 *y
OffSety = y — r 10 *X — R 11 *y
Где :
- Смещение = линейное расстояние, на которое переместилась точка на объекте.
- x, y = координаты точки, вокруг которой мы вращаемся (относительно начального положения объекта).
Мы хотим найти x и y, поэтому возьмем обратное значение:
Offsetx Офсет =
1-р 00 -р 01 -р 10 1-р 11 передать:
=
__1__
(1-р 00 )(1-р 11 ) — р 01 р 10
1-р 11 р 01 р 10 1-р 00
Смещениеx Офсет В этом случае матрица вращения:
cos(θ) — грех(θ) sin(θ) соз(θ) , где
θ = угол поворота
, что дает:
=
__1__
(1-cos(θ))(1-cos(θ)) + sin(θ)sin(θ)
1-cos(θ) — грех(θ) sin(θ) 1-косин(θ)
Смещениеx Офсет расширение определителя (и использование sin 2 (θ)+cos 2 (θ)=1) дает:
=
__1__ 2-2cos(θ)
1-cos(θ) — грех(θ) sin(θ) 1-косин(θ)
Смещениеx Офсет Проверить
Мы можем проверить некоторые особые случаи, чтобы увидеть, получаем ли мы разумные результаты:
если θ = 0, то:
= ∞
0 0 0 0
Смещениеx Офсет Если тета = 0, то точка вращения находится в бесконечности.
если θ = 90°, то:
=
__1__ 2
1 -1 1 1
Смещениеx Офсет , поэтому, если смещение равно (1,0), то точка вращения находится в (0,5,0,5)
, если θ = 180°, тогда:
= 1/4
2 0 0 2
Смещениеx Смещение Итак, мы вращаемся вокруг точки на полпути к B.
Комбинирование вращений вокруг разных точек
Как применить два таких вращения одно за другим, чтобы получить третий эквивалентный поворот?
Итак, представьте, что мы применяем ротацию:
ra 00 ра 01 ра 10 ра 11 С центром: (налог,тай,таз) с последующим чередованием:
руб. 00 руб 01 руб 10 руб 11 С центром в: (tbx,tby,tbz)
Общее вращение является произведением двух матриц вращения:
ra 00 *rb 00 + ра 01 *рб 10 ra 00 *rb 01 + ra 01 *rb 11 ра 10 *rb 00 + ra 11 *rb 10 ra 10 *rb 01 + ra 11 *rb 11 =
ра 00 ра 01 ра 10 ра 11
руб 00 руб 01 руб 10 руб 11 Смещение будет:
налог — ra 00 *налог — ra 01 *tay + tbx — rb 00 *tbx — rb 01 *tby tay — ra 10 *tay — ra 11 *tay + tbx — rb 00 *tbx — rb 01 *tby Таким образом, общий центр будет:
В трех измерениях мы также можем представить изометрию как вращение и перемещение.
Можем ли мы представить любую изометрию как одно вращение, как в двумерном случае, как описано выше?
В трех измерениях есть три степени свободы вращения, но когда мы ищем точки, которые равноудалены от центров объектов до и после преобразования положения. Равноудаленные точки лежат на плоскости, которая имеет только две степени свободы, но есть также возможность вращаться вокруг линии из точки. Поэтому имеется достаточно степеней свободы для представления всех возможных изометрий.
Итак, представьте, что мы хотим перевести из точки A (0,0) в точку B (0,1), мы можем сделать это, вращаясь вокруг любой точки плоскости x=0,5.
Если, например, мы хотим объединить его с поворотом на 90° вокруг оси Z, мы можем сделать это, повернув вокруг (0.5,0.5,0):
Если, например, мы хотим объединить его с поворот на 90° вокруг оси y, мы можем сделать это, повернув вокруг (0.5,0,0.5):
Если, например, мы хотим объединить его с поворотом на 90° вокруг оси x, у нас есть проблема !
Нам нужно повернуть его вокруг оси x, чтобы получить желаемое вращение, и нам нужно повернуть вокруг оси y или z, чтобы получить желаемое перемещение, и эти два варианта не кажутся совместимыми?
Таким образом, когда есть компонент оси вращения в том же направлении, что и вектор перемещения, они не кажутся совместимыми.
Чтобы представить все возможные перемещения и повороты в одной операции, мы должны разрешить вращение вокруг точки вместе с перемещением вдоль вектора, параллельного оси вращения. Операция представлена линией вокруг внешней стороны цилиндра. Это известно как винт (см. эту страницу, чтобы продолжить эту тему).
На следующих страницах есть код для расчета аффинного перевода при вращении о точке:
Вас могут заинтересовать другие способы представления ориентации и вращения такие величины, как:
Или вас может заинтересовать, как эти величины используются для имитации физических объекты:
4.2: Вращение твердого тела — Математика LibreTexts
В уравнениях 4.1.62–4.1.65 мы формально ввели понятие времени как параметра для определения некоторых простых типов движения, которые имеют стационарный характер.
Теперь мы исследуем полезность этих результатов, рассматривая инерционные движения твердого тела, закрепленного в одной из своих точек, так называемого гироскопа.
Мы можем обобщить соответствующие экспериментальные факты следующим образом: существуют объекты достаточно высокой симметрии (сферический волчок), которые действительно демонстрируют стационарное инерционное вращение вокруг любой из своих осей. В общем случае (асимметричный волчок) такое стационарное вращение возможно только вокруг трех основных направлений, выделенных в триаде тел.
Наибольший интерес для нас, однако, представляет тот факт, что существуют также виды движения, которые можно считать стационарными в более слабом смысле этого слова.
Имеется в виду так называемая прецессия. Мы будем рассматривать здесь только правильную прецессию симметричного волчка, или гироскопа, которую можно представить в терминах хорошо известной геометрической конструкции, разработанной Пуансо в 1853 г. \(\sum_{c}\) прокатиться по круговому конусу, закрепленному в пространственной триаде \(\sum_{s}\) (см. рис. 4.2)
Примечательно, что биаксиальная природа спиноров делает их хорошо подходящими для создания алгебраического аналога этой геометрической картины.
Чтобы доказать это, мы должны использовать теорему о том, что угловые скорости вокруг различных осей могут быть сложены по правилам векторного сложения. Эта теорема является простым следствием нашего формализма.
Рассмотрим композицию бесконечно малых вращений с \(\delta \phi = \omega \delta t << 1\):
\[\begin{array}{c} {U_{2}(\hat{u}_{2}, \frac{\omega_{2} \delta t}{2}) \приблизительно (1-\frac {\omega_{2} \delta t}{2} \hat{u}_{2} \cdot \vec{\sigma})(1-\frac{\omega_{1} \delta t}{2} \ hat{u}_{1} \cdot \vec{\sigma})} \end{массив} \label{EQ4.2.1}\]
\[\begin{array}{c} {1-\frac{\delta t}{2}(\omega_{2} \hat{u}_{2}+ \omega_{1}\hat{u} _{1}) \cdot \vec{\sigma}} \end{массив}\]
Определим векторы угловой скорости
\[\begin{array}{c} {\vec{\omega} = \omega \hat{u}} \end{array}\] 9{2}+2\dot{\alpha}\dot{\gamma} \cos\beta}\end{массив}\]
\[\ begin{array}{c} {\beta = \hat{x}_{3} \cdot \hat{e}{3}} \end{array}\]
Мы можем описать прецессию в спинориальных терминах следующим образом.
{i \dot{\gamma} t/2}} \end{pmatrix}} \end{массив} \label {EQ4.2.8}\]
Так
\[\ begin {массив} {cc} {\ alpha = \ alpha (0) + \ dot {\ alpha} t} & {\ gamma = \ gamma (0) + \ dot {\ gamma} t} \ end {массив}\]
Это соотношение графически отображает двухосный характер V-матрицы. Таким образом, предварительное умножение соответствует вращению в \(\sum_{s}\), а постумножение — в \(\sum_{c}\).
Обратите внимание, что ситуации, представленные на рис. 4.2 (а) и (б), называются соответственно прогрессивной и ретроградной прецессией.
Ось вращения \(\vec{\omega}\) мгновенно находится в состоянии покоя в обеих системах отсчета. Компоненты вектора можно выразить следующим образом:
\[\begin{array}{ccc} {}&{\mathcal{S} \sum_{s}}&{ \mathcal{S} \sum_{c}}\\ {(a)}&{\omega_ {1} = \dot{\gamma} \sin \beta \cos\alpha}&{\omega_{1} = \dot{\alpha} \sin \beta \cos\gamma}\\ {(b)}& {\omega_{2} = \dot{\gamma} \sin\beta\sin\alpha}&{\omega_{2} = \dot{\alpha}\sin\beta\sin\gamma}\\ {(c )}&{\omega_{3} = \dot{\gamma} \sin \beta+\dot{\alpha}} &{\omega_{3} = \dot{\alpha} \sin \beta+\dot{\gamma }} \end{массив} \label{EQ4.
2.10}\]
Эти выражения могут быть формально получены из уравнения \ref{EQ4.2.8}. Левая колонка уравнения \ref{EQ4.2.10} следует из применения левого оператора к кет-спинору, а правая колонка уравнения \ref{EQ4.2.10} — из правой операции к барному спинору.
Другой способ получения этих результатов заключается в следующем: выражения в левом столбце уравнения \ref{EQ4.2.10} очевидны из правила сложения векторов, приведенного в \ref{EQ4.2.4}. Выражения в правой колонке уравнения \ref{EQ4.2.10} не следуют так просто из геометрической интуиции. Однако мы можем обратиться к кинематической относительности между двумя триадами. Вращение \(\sum_{c}\) относительно \(\sum_{s}\) также можно рассматривать как обратное вращение \(\sum_{s}\) в \(\sum_{c }\). Таким образом, \(V_{c}\) эквивалентно 9{\dagger} = V(-\alpha, -\beta, -\gamma)} \end{массив}\]
, и мы получаем столбцы слева направо в уравнении \ref{EQ4.2.10} с помощью следующей замены:
\[\begin{array}{c} {\alpha \rightarrow -\gamma} \end{array}\]
\[\begin{array}{c} {\beta \rightarrow -\beta} \end{array}\]
\[\begin{array}{c} {\gamma \rightarrow -\alpha} \end{array}\]
\[\begin{array}{c} {t \rightarrow -t} \end{array}\]
До сих пор обсуждение было только описательным, кинематическим.
Мы должны обратиться к динамике, чтобы ответить на более глубокие вопросы относительно факторов, определяющих природу прецессии в каждом конкретном случае.
Мы вызываем кинематическую связь Уравнение 4.1.62:
\[\ begin {массив} {c} {\ exp (-i \ frac {\ omega t} {2} \ hat {k} \ cdot \ vec {\ sigma} | \ hat {k}, \ frac { \gamma}{2} = \exp (-i \frac{\omega t}{2} | \hat{k}, \frac{\gamma}{2}} \end{array}\]
Это выражение предлагает способ обобщения динамики. Если это соотношение действительно описывает стационарный процесс, то образующие \(\frac{i}{2} \sigma_{j}\) унитарного оператора являются константами этого движения. Позже мы будем развивать эту идею, чтобы установить понятие углового момента и его квантование. Однако на этом предварительном этапе мы просто ищем элементарную иллюстрацию формализма и опираемся на стандартные результаты динамики твердого тела.
Динамический закон состоит из трех положений. Во-первых, у нас есть в \(\sum_{s}\)
\[\ begin {массив} {c} {\ frac {d \ vec {L} _ {s}} {dt} = \ vec {N}} \ end {массив} \]
, где N — внешний крутящий момент.
В \(\sum_{c}\) мы имеем определяющее соотношение , соединяющее угловую скорость и угловой момент. предполагаем, что триада объектов расположена вдоль главных осей инерции:
\[\begin{array}{c} {L_{c1} = I_{1} \omega_{1}} \end{array}\]
\[\begin{массив}{c} {L_{c2} = I_{2} \omega_{2}} \end{массив}\]
\[\begin{массив}{c} {L_{c3} = I_{3} \omega_{3}} \end{массив}\]
Наконец, компоненты углового момента в \(\sum_{s}\) и \(\sum_{c}\) связаны соотношением
\[\ begin {массив} {c} {\ frac {d \ vec {L} _ {s}} {dt} = \ frac {d \ vec {L} _ {c}} {dt} + \ vec {\omega} \times \vec{L}_{c}} \end{массив}\]
Уравнения 4.2.18–4.2.20 подразумевают уравнения Эйлера. Динамически прецессия может происходить либо из-за внешнего крутящего момента, либо из-за анизотропии момента инерции (или из-за того и другого).
Предположим, что \(\vec{N} = 0\) и \(I_{1} = I_{2} \ne I_{3}\). Соответственно упрощенные уравнения Эйлера дают для прецессии, как показано в \(\sum_{c}\):
\[\ begin{array}{c} {\dot{\omega}_{c1}+i \dot{\omega}_{c2} = -i(\omega_{c1}+i \omega_{c2} ) \omega_{3} \delta}\\ {I_{3} \dot{\omega}_{3} = 0} \end{массив} \label{EQ4.
2.21}\]
с
\[\begin{array}{c} {\delta = 1-\frac{I_{3}}{I_{1}}} \end{array} \label{EQ4.2.22}\]
Из уравнения \ref{EQ4.2.10}, правый столбец, строки (a) и (b), мы получаем
\[\begin{array}{c} {\dot{\omega}_{1}+i \dot{\omega}_{2} = -i \dot{\gamma} (\omega_{c1}+ я \omega_{c2})} \end{массив}\]
и по сравнению с \ref{EQ4.2.21} имеем
\[\ begin{array}{c} {\dot{\gamma} = \omega_{3} \delta = \omega_{3}(1-\frac{I_{3}}{I_{1}}) } \end{массив} \label{EQ4.2.24}\]
Из \ref{EQ4.2.24}, \ref{EQ4.2.22} и \ref{EQ4.2.10} (правый столбец, строка c) получаем:
\[\begin{array}{c} {I_{3} \omega_{3} = I_{1} \dot{\alpha} \cos \beta} \end{array} \label{EQ4.2.25}\ ]
и
\[\ begin {массив} {c} {\ frac {\ dot {\ gamma}} {\ dot {\ alpha} \ cos \ beta} = \ frac {I_ {1}} {I_ {3}} — 1} \конец{массив}\]
Таким образом, природа инерционной прецессии определяется инерционной анизотропией \ref{EQ4.2.22}. В частности,
пусть \(\cos\beta > 0\), затем
\[\begin{array}{cc} {I_{1} > I_{3} \rightarrow \frac{\dot{\gamma}}{\dot{\alpha}} > 0}&{ см.
рис. 4.2- а} \конец{массив}\]
\[\begin{array}{cc} {I_{1} < I_{3} \rightarrow \frac{\dot{\gamma}}{\dot{\alpha}} < 0}&{ см. рис. 4.2- б} \конец{массив}\] 9{2}} \end{массив}\]
Обратите внимание, что \(L_{c3} = I_{1} \dot{\alpha} \cos \beta\) является проекцией полного углового момента на ось фигуры. Прецессия \(\gamma\) в \(\sum_{c}\) возникает, если \(I_{3} \ne I_{1}\). Для получения дополнительной информации см. [KS65].
Отметим также, что теория Эйлера была переведена на современный язык групп Ли В. Арнольдом ([Arn66], стр. 319-361). Однако в этой работе требуется, чтобы стационарные движения имели фиксированные оси вращения.
Рисунок 4.2: Прогрессивная (а) и ретроградная (б) прецессия.
Эта страница под названием 4.2: Rigid Body Rotation распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Ласло Тисой (MIT OpenCourseWare) посредством исходного контента, отредактированного в соответствии со стилем и стандартами.
платформы LibreTexts; подробная история редактирования доступна по запросу.
геометрия — Трансформация осей вращением
Спросил
Изменено 2 года, 6 месяцев назад
Просмотрено 3к раз
$\begingroup$
Как я могу интуитивно понять формулу для получения новой координаты точки P после поворота осей, которые были P(x,y) относительно старых осей?
- геометрия
$\endgroup$
2
$\begingroup$
Сначала рассмотрим, что векторы записаны в канонической базе, поэтому вращение этого вектора эквивалентно вращению канонической базы, а затем просмотру координат этого вектора в этой новой базе, глядя на фигуру, которая вращает базу векторов канонической базы в тета-угле, мы можем видеть, что
$$e’_1=\left(\cos\left(θ\right),\sin\left(θ\right)\right)$$ и $$ e’_2=\left(-\sin\left(θ\right),\cos \left(θ\right)\right)$$
то преобразование есть матрица
$$ М= \влево[ \begin{массив}{cc} \cos(\тета) и \sin(\тета)\\ -\sin(\theta) & \cos(\theta)\\ \конец{массив} \right]$$
поэтому после поворота вектора $$\left(x,y\right)$$ мы получим
$$\left(x\cos \left(θ\right)+y\sin\ влево(θ\вправо),-x\sin\влево(θ\вправо)+y\cos\влево(θ\вправо)\вправо)$$
$\endgroup$
$\begingroup$
Рассмотрим следующий рисунок
Здесь красная система координат повернута на $\alpha$.
Имеем для черных координат $$x=R\cos(\beta),y=R\sin(\beta)$$,
Также для красных координат имеем
$$x’=R \cos(\gamma), y’=R\sin(\gamma).$$
Обратите внимание на то, что $\gamma=\beta-\alpha$ и используйте соответствующую формулу триггера:
$$x’=R\ cos(\beta-\alpha)=R(\cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta))=x\cos(\alpha)+y\sin( \альфа)$$
и …
$\endgroup$
$\begingroup$
Пусть старая точка будет в $1$, а новая точка будет в $2$ в первом квадранте. Пусть угол поворота равен маленьких $\theta$ против часовой стрелки.
$$x_{новый} =x_{старый} \, cos \,\theta -y_{старый} \,sin \,\theta \tag1 $$
$$y_{новый} = x_{старый} \ ,\sin\theta + y _{old}\cos\theta \tag2 $$
Замечено, что
относительно нового $x$ справа стоит знак минус и его координата x получил сокращение.
что касается нового $y$, то справа стоит плюсик и его координата y увеличилась.
$\endgroup$
$\begingroup$
Трудно понять, что вы подразумеваете под интуитивным пониманием, когда говорите о системе уравнений. Но вот некоторый контекст, который может помочь больше.
Как вы должны знать формулы
$$\begin{array} &x=x’\cos\phi& -&y’\sin\phi&\\ y=x’\sin\phi &+&y’\cos\phi& \end{array}$$
дают нам способ преобразовать уравнение $F(x,y)=0$ в $G(x’,y’)=0.$ Это дает карту (вращение по мере того, как вы уже известно) из системы координат $(x,y)$ в $(x’,y’).$ Явное решение относительно $x’,y’$ в системе уравнений дает 92.$ Чтобы увидеть, что это поворот, вычислите определитель, чтобы убедиться, что он равен $1.$ Таким образом, квадраты в прямоугольной системе $(x,y)$ сохраняют свою ортогональность, так что их соответствующая площадь в системе преобразования $(x’,y’)$ остается прежним.
$\endgroup$
$\begingroup$
Предположим, что луч в точку (x,y) из начала координат составляет угол $\alpha$ против часовой стрелки с +ve оси x.

 {2}}\)
{2}}\) {2}}}_{два\ круга}\)
{2}}}_{два\ круга}\) {2}}\)
{2}}\) Расстояние между точками и от точки до прямой
Расстояние между точками и от точки до прямой 

 Последние два имеют бесконечный объём.
Последние два имеют бесконечный объём. 141592.
141592. Прямая, соединяющая вершину и центр основания, называется осью конуса.
Прямая, соединяющая вершину и центр основания, называется осью конуса.
 141592.
141592.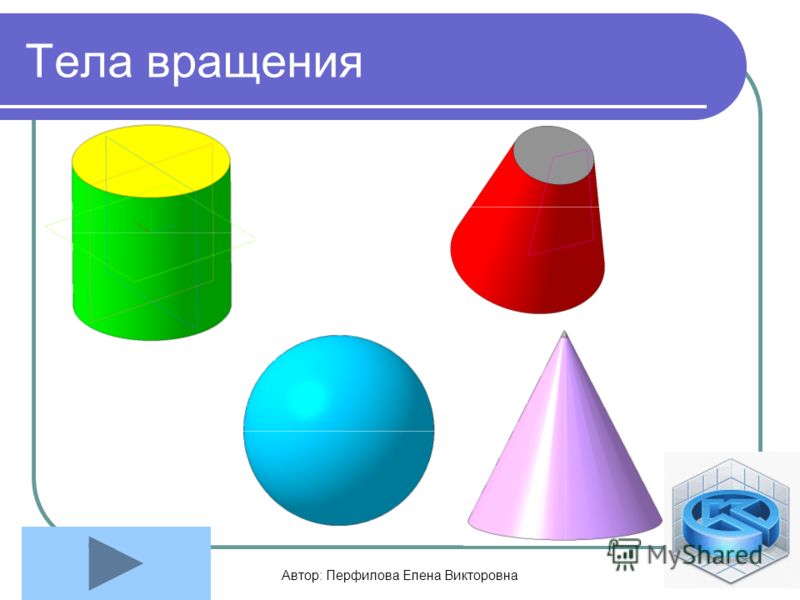 141592.
141592.


 это обсуждение)
это обсуждение) эту страницу)
эту страницу)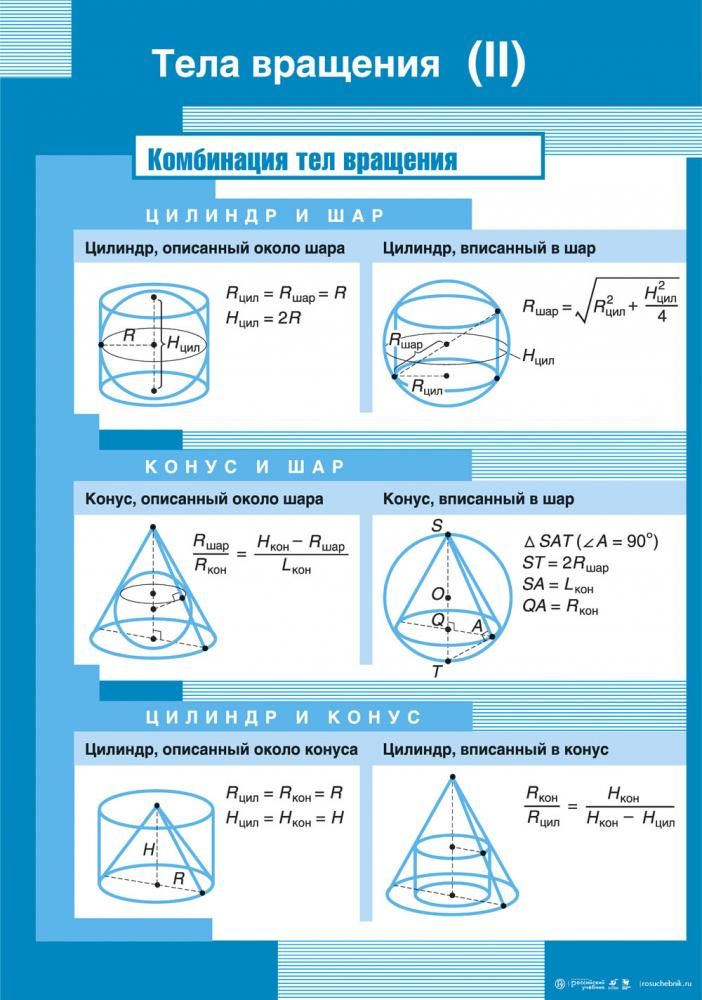




 Можем ли мы представить любую изометрию как одно вращение, как в двумерном случае, как описано выше?
Можем ли мы представить любую изометрию как одно вращение, как в двумерном случае, как описано выше?
 {i \dot{\gamma} t/2}} \end{pmatrix}} \end{массив} \label {EQ4.2.8}\]
{i \dot{\gamma} t/2}} \end{pmatrix}} \end{массив} \label {EQ4.2.8}\]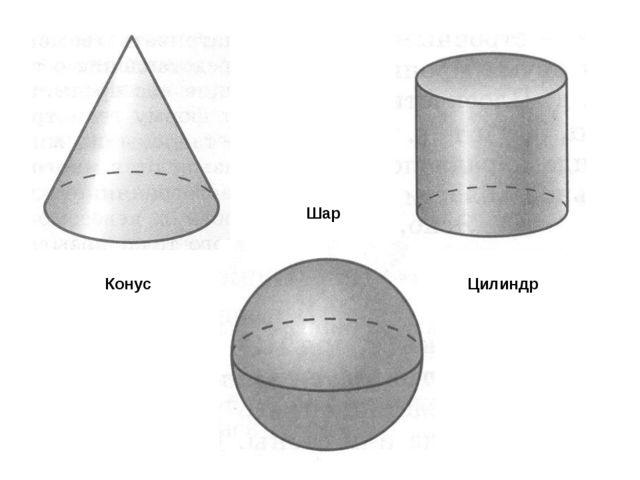 2.10}\]
2.10}\]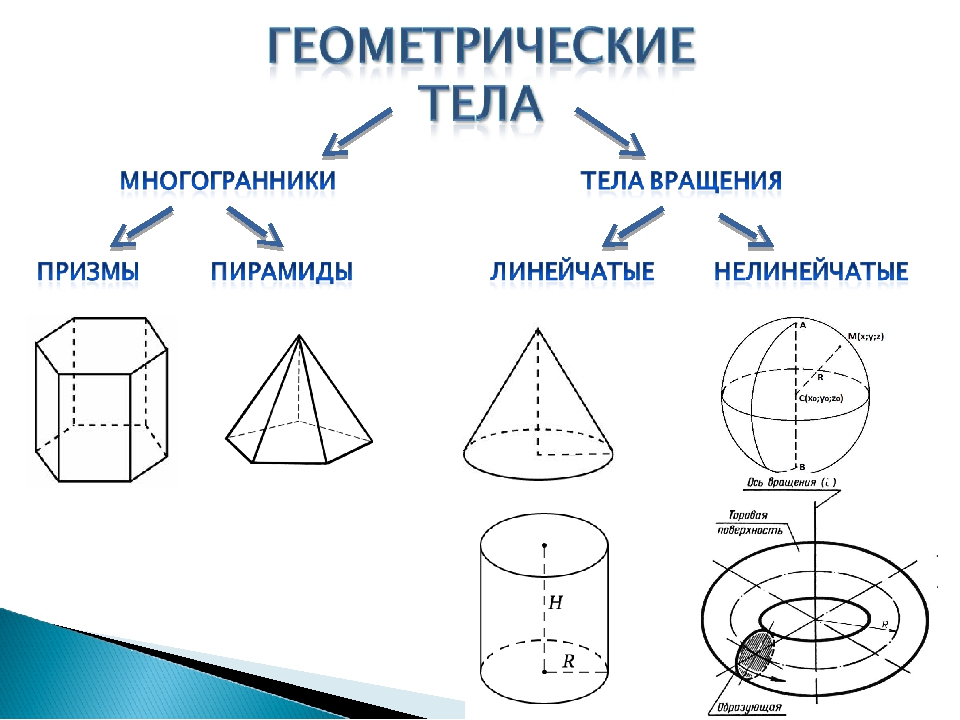 Мы должны обратиться к динамике, чтобы ответить на более глубокие вопросы относительно факторов, определяющих природу прецессии в каждом конкретном случае.
Мы должны обратиться к динамике, чтобы ответить на более глубокие вопросы относительно факторов, определяющих природу прецессии в каждом конкретном случае.
 2.21}\]
2.21}\] рис. 4.2- а} \конец{массив}\]
рис. 4.2- а} \конец{массив}\] платформы LibreTexts; подробная история редактирования доступна по запросу.
платформы LibreTexts; подробная история редактирования доступна по запросу.