Методические указания к выполнению лабораторной работы № 5
Методические указания
к выполнению лабораторной работы №5
«Численные методы интегрирования»
Цель работы: Изучение методов численного интегрирования, оценки погрешности по правилу Рунге, оценки порядка аппроксимации, уточнения значений по Ричардсону.
Задание: Разработать программы, реализующие численное интегрирование заданной пользователем функции различными методами (по вариантам). Оценить порядок аппроксимации метода по нескольким интегрируемым функциям и сравнить его с теоретическим. Оценить погрешность по правилу Рунге. Уточнить значения интеграла по Ричардсону и сравнить с точным значением. Изучить влияние сгущения сетки в местах осцилляции функции. При разработке тестов использовать функции, интеграл от которых вычисляется аналитически.
Требования
к реализации: Функцию задавать в виде подпрограммы, все остальные входные
данные (сетку, отрезок и т.
Всего в вариантах заданий рассмотрено шесть методов численного интегрирования:
· Метод прямоугольников
· Метод трапеций
· Метод Симпсона
· Метод Гаусса-2
· Метод Гаусса-3
· Метод Гаусса-4
Содержание
Основные определения. 3
Каноническая формула прямоугольников. 4
Усложненная квадратурная формула прямоугольников. 4
Каноническая квадратурная формула трапеций. 5
Усложненная квадратурная формула трапеций. 6
Каноническая формула Симпсона. 6
Усложненная квадратурная формула Симпсона. 7
Многочлены Лежандра. 7
Интерполяционный многочлен Лагранжа. 8
Каноническая квадратурная формула Гаусса. 9
Усложненная квадратурная формула Гаусса. 10
Правило Рунге практической оценки погрешности. 11
Уточнение приближенного решения по Ричардсону.
11
Особенности вычисления интегралов с помощью компьютера. 12
Порядок выполнения задания по лабораторной работе. 13
Основные определения
Общий принцип численного интегрирования истекает из определения интеграла: интеграл – предел последовательности частичных сумм функции, а также из геометрического значения: интеграл численно равен площади области, заключенной между осью Ох, пределами интегрирования и графиком функции.
Все методы численного интегрирования основаны на следующей теореме.
Обобщенная теорема о среднем
Пусть , причем . Тогда существует такая точка , что
Теперь введем понятие квадратурной формулы. Пусть дан определенный интеграл
от непрерывной на [a;b] функции f. Приближенное равенство
где –
некоторые числа, – некоторые точки отрезка [a;b], называется квадратурной
формулой, определяемой весами и узлами .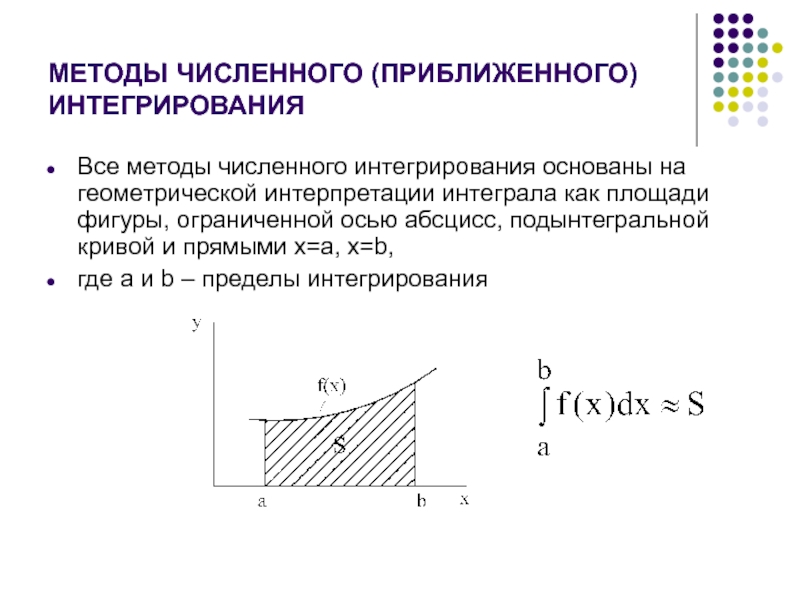
Говорят, что квадратурная формула точна для многочленов степени m, если при замене f на произвольный алгебраический многочлен степени m приближенное равенство становится точным. Отсюда вытекает следующее определение.
Порядок точности – | максимальная степень многочлена, при которой аналитическая погрешность метода равна нулю. |
Порядок аппроксимации – | Величина, характеризующая во сколько раз уменьшается погрешность метода при уменьшении шага. , где – точное значение интеграла – значение интеграла, вычисленное с шагом h |
Каноническая формула прямоугольников
Допустим, что , . Положим приближенно
где , то есть площадь
криволинейной трапеции, ограниченной сверху графиком функции аппроксимируется
площадью заштрихованного прямоугольника (см.
рис. 1), высота которого равна
значению f в средней точке
основания трапеции.
Найдем теперь остаточный член, то есть погрешность формулы .
|
. Т.к. , то согласно формуле Тейлора с остаточным членом в форме Лагранжа имеем:
Где . Функция является первообразной , поэтому для интеграла, стоящего в левой части приближенного равенства из формулы Ньютона-Лейбница с учетом вытекает:
.
Отсюда вытекает выражения для формулы с остаточным членом.
Формула называется квадратурной формулой прямоугольников с остаточным членом.
Лекция 6. Методы численного интегрирования
Похожие презентации:
Численное интегрирование и его погрешности. Методы прямоугольников и трапеций. Метод Симпсона. Правило Рунге. (Лекция 5)
Численное интегрирование
Методы численного интегрирования (нахождение определенных интегралов)
Лекция 6. Численное интегрирование функций
Приближенные методы решения определенных интегралов
Численные методы решения инженерных задач
Численные методы
Численное интегрирование
Геометрическая интерпретация метода простых итераций
Численное интегрирование. Лекция №6
1. Тема 2. Численное интегрирование Лекция 6. Методы численного интегрирования.
1.Обзор методов численного интегрирования.2. Метод прямоугольников.
3. Метод трапеций.
4. Численное интегрирование методом
Симпсона.
Литература: [1] с.123-134.
2. 1. Обзор методов численного нтегрирования
Задача численного интегрированияbвычислить интеграл
f ( x)dx используя
a
ряд значений подинтегральной
функции
y=f(x), которые известны заранее.
Методы численного интегрирования:
•Методы Ньютона-Котеса – основаны на
аппроксимации подинтегральной функции
полиномами степени n при равноотстоящих
друг от друга узлах;
•Методы сплайн – интегрирования основаны
на аппроксимации подинтегральной функции
сплайнами – функциями, форма которых
близка к интегрируемой функции;
•Метод Гаусса использует специально
выбираемые неравноотстоящие узлы, что
обеспечивает высокую точность вычислений;
•Метод Монте-Карло используется для
вычисления кратных интегралов на случайно
выбираемых узлах; результат является
случайной величиной и определяется с
заданной вероятностью.
Методы Ньютона-Котеса предусматривают
разбиение интервала интегрирования [a,b] на
n равных частей с шагом:
h=xi+1- xi=(b-a)/n, i=1,n
(4)
При этом известны в узлах разбиения
значения подинтегральной функции известны:
yi=f(xi)
(5)
2. Метод прямоугольников
Интерполяционный многочлен 1-го порядка,
т.
е. линейная интерполяция.y
y=f(x)
a
xi
xi+1 b
x
b
a
n
f ( x)dx h f ( kh)
(6)
k 1
1. Если узел α=а- левому краю отрезка
интегрирования, то (6) – формула «левых»
прямоугольников;
2. Если узел α=xi+1 –правому краю отрезка, то
(6) – формула «правых» прямоугольников;
3. Если узел α=(xi+1+xi)/2 – середине отрезка
то
(6)
–
формула
«средних»
прямоугольников;
Погрешности:
(b a )
Rn ( f , a )
max{ f ( x)};
2n
2
(b a )
Rn ( f , a h)
max{ f ( x)};
2n
3
(b a )
Rn ( f , a h / 2)
max{
f
( x)};
2
24n
2
(7)
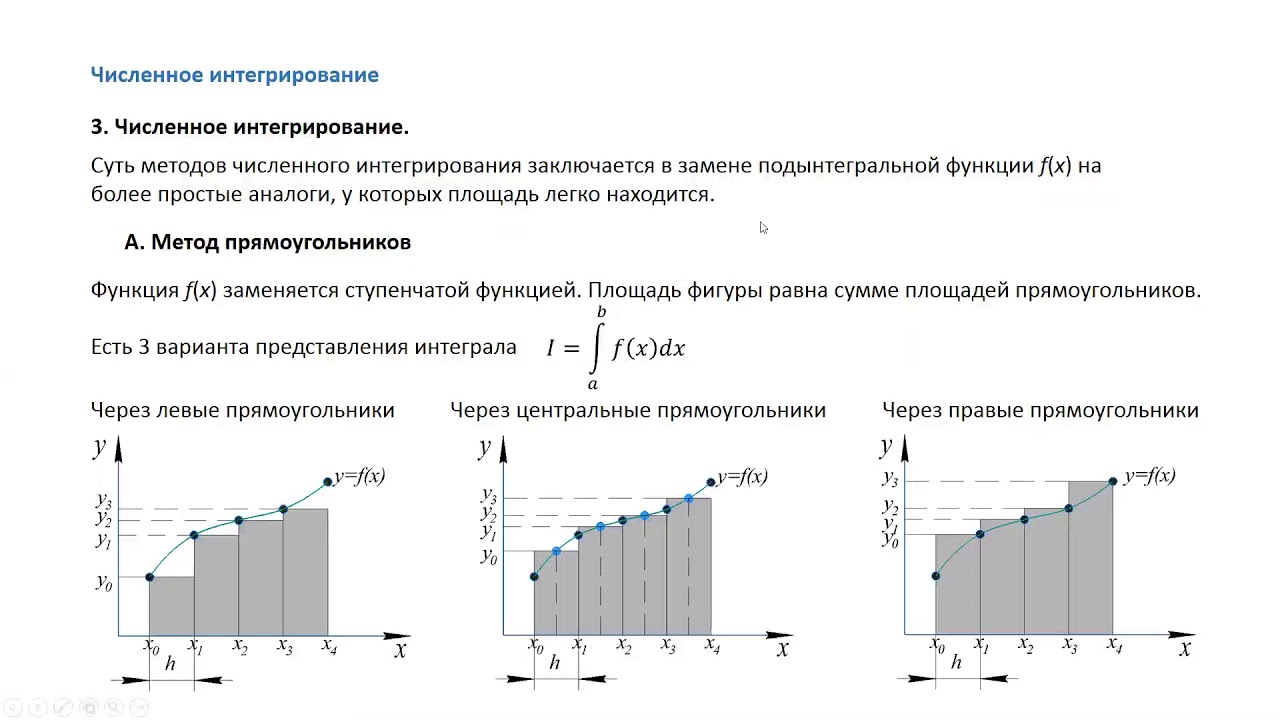
3. Метод трапеций
Интерполяционный многочлен 1-го порядка,
т.е. линейная интерполяция.
y
yi
yi+1
y=f(x)
a
xi
xi+1 b
x
b
a
f ( x)dx h / 2[ y0 2( y1 y2 … yn 1 ) yn ]
(8)
Погрешность:
(b a)
Rn
max{
f
( x)}
2
24n
3
(9)
10.
4. Метод Симпсона. Описание метода. ba
h
f ( x)dx [ y0 y2 n 4( y1 y3 … y2 n 1 )
3
(1)
2( y2 y4 … y2 n 2 )]
b-a
где шаг определяется : h
2n
(2)
При этом, необходимым условием является то,
что количество интервалов разбиения отрезка
интегрирования должно быть четным.
yi+2
y
y=f(x)
yi
yi+1
xi
xi+1
xi+2
x
Погрешность метода Симпсона:
(b a)
( IV )
R
max{
f
(
x
*)}
4
180(2n)
5
где:
x [a; b]
*
(3)
Начало
S=S+Cf(x)
C=6-C
x=x+H
f(x)
Ввод A,B,N,H
S=SH/3
S=f(A)+f(B)
Вывод S
C=4
x=A
Конец
i=1,2N-1
English Русский Правила
2.5: Численное интегрирование — средняя точка, трапеция, правило Симпсона
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 10269
Эта страница является черновиком и находится в активной разработке.
Первообразные многих функций либо не могут быть выражены, либо не могут быть легко выражены в замкнутой форме (то есть через известные функции). Следовательно, вместо непосредственного вычисления определенных интегралов этих функций мы прибегаем к различным методам численного интегрирования для аппроксимации их значений. В этом разделе мы рассмотрим некоторые из этих методов. Кроме того, мы исследуем процесс оценки ошибки при использовании этих методов.
n_{i=1}f(m_i)Δx\) соответствует сумме площадей прямоугольников, аппроксимирующих площадь между графиком \(f(x)\) и осью \(x\) над \([ а, б]\). На графике показаны прямоугольники, соответствующие \(M_4\) для неотрицательной функции на замкнутом интервале \([a,b].\)
Рисунок \(\PageIndex{1}\): Правило середины аппроксимирует площадь между график \(f(x)\) и оси \(x\) путем суммирования площадей прямоугольников со средними точками, являющимися точками на \(f(x)\). Пример \(\PageIndex{1}\): использование правила средней точки с \(M_4\) 92\,dx\) с использованием четырех подынтервалов.
Решение: Каждый подинтервал имеет длину \( Δx=\dfrac{1−0}{4}=\dfrac{1}{4}.\) Следовательно, подынтервалы состоят из
\[\left[0,\ tfrac{1}{4}\right],\,\left[\tfrac{1}{4},\tfrac{1}{2}\right],\,\left[\tfrac{1}{2} ,\tfrac{3}{4}\right],\, \text{and}\, \left[\tfrac{3}{4},1\right].\nonumber\]
Середины этих подинтервалов являются \(\left\{\frac{1}{8},\,\frac{3}{8},\,\frac{5}{8},\, \frac{7}{8}\right \}.\) Таким образом, 92_1\frac{1}{x}\,dx.\)
- Подсказка
\( Δx=\frac{1}{2}, \quad m_1=\frac{5}{4},\quad \text{and} \quad m_2=\frac{7}{4}.\)
- Ответить
\(\dfrac{24}{35}\)
Правило трапеций
Мы также можем аппроксимировать значение определенного интеграла, используя трапеции, а не прямоугольники. На рисунке \(\PageIndex{2}\) область под кривой аппроксимирована трапециями, а не прямоугольниками.
Правило трапеций для оценки определенных интегралов использует трапеции, а не прямоугольники для аппроксимации площади под кривой. Чтобы получить представление об окончательной форме правила, рассмотрите трапеции, показанные на рисунке \(\PageIndex{2}\). Мы предполагаем, что длина каждого подынтервала равна \(Δx\). Во-первых, напомним, что площадь трапеции с высотой \(h\) и длинами оснований \(b_1\) и \(b_2\) определяется выражением \(\text{Area}=\frac{1}{ 2}h(b_1+b_2)\). Мы видим, что первая трапеция имеет высоту \(Δx\) и параллельные основания длины \(f(x_0)\) и \(f(x_1)\). Таким образом, площадь первой трапеции на рисунке \(\PageIndex{2}\) равна 9b_af(x)\,dx≈\frac{Δx}{2}\big(f(x_0)+2\,f(x_1)+2\,f(x_2)+2\,f(x_3)+f( x_4)\big).\nonumber\]
Обобщая, сформулируем формально следующее правило.
Правило трапеций
Предположим, что \(f(x)\) непрерывно над \([a,b]\).
Пусть \(n\) — натуральное число и \(Δx=\dfrac{b−a}{n}\). Пусть \([a,b]\) разбит на \(n\) подынтервалов, каждый длиной \(Δx\), с концами в \( P=\{x_0,x_1,x_2…,x_n\}.\ )
Набор
\[T_n=\frac{Δx}{2}\big(f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+2\, f(x_ {n−1})+f(x_n)\big).\] 9nf(x_i)Δx.\)
То есть \(L_n\) и \(R_n\) аппроксимируют интеграл, используя левую и правую конечные точки каждого подинтервала соответственно. Кроме того, внимательное изучение рисунка \(\PageIndex{3}\) позволяет нам сделать следующие замечания об использовании правил трапеций и правил середины для оценки определенного интеграла неотрицательной функции. Правило трапеций имеет тенденцию систематически завышать значение определенного интеграла на интервалах, где функция вогнута вверх, и систематически занижать значение определенного интеграла на интервалах, где функция вогнута вниз. С другой стороны, правило средней точки имеет тенденцию несколько усреднять эти ошибки, частично переоценивая и частично занижая значение определенного интеграла на тех же самых типах интервалов.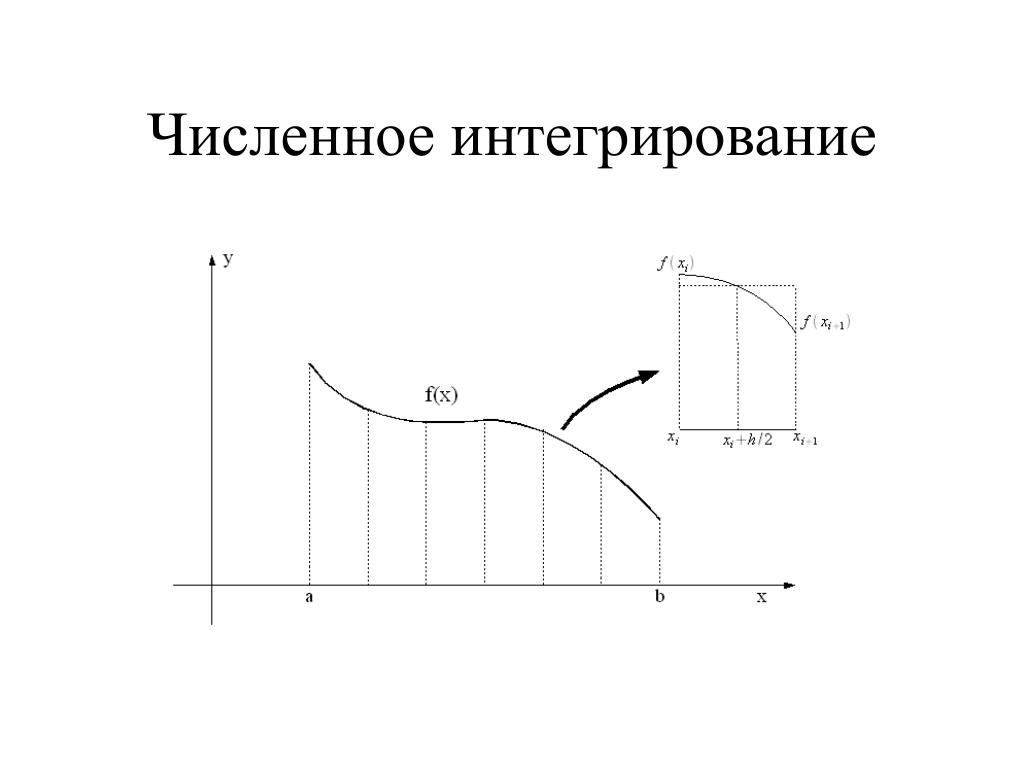
- Подсказка
Множество \(Δx=\dfrac{1}{2}.\) Концы подинтервалов являются элементами множества \(P=\left\{1,\frac{3}{2},2\right \}.\)
- Ответить
\(\dfrac{17}{24}\)
Абсолютная и относительная погрешность
Важным аспектом использования этих правил численной аппроксимации является вычисление погрешности их использования для оценки значения определенного интеграла. Сначала нам нужно определить абсолютную ошибку и относительную ошибку.
Определение: абсолютная и относительная ошибка
Если \(B\) является нашей оценкой некоторой величины, имеющей фактическое значение \(A\), то абсолютная ошибка определяется выражением \(|A−B|\ ).
Относительная ошибка представляет собой ошибку в процентах от фактического значения и определяется как \[\left\lvert\frac{A−B}{A}\right\rvert⋅100\%.
2\,dx\), используя правило средней точки, найденное в Пример \(\PageIndex{1}\). 92_1\frac{1}{x}\,dx\) в \(\frac{24}{35}\) с использованием \(T_2\). Фактическое значение этого интеграла равно \(\ln 2\). Используя \(\frac{24}{35}≈0,6857\) и \(\ln 2≈0,6931,\), вычислите абсолютную ошибку и относительную ошибку.
- Подсказка
Используйте предыдущие примеры в качестве руководства.
- Ответить
абсолютная ошибка \(\приблизительно 0,0074,\) и относительная ошибка \(\приблизительно 1,1\%\)
Границы погрешности для средней точки и правил трапеций
В двух предыдущих примерах мы смогли сравнить нашу оценку интеграла с фактическим значением интеграла; однако у нас обычно нет такой роскоши. В общем, если мы аппроксимируем интеграл, мы делаем это потому, что не можем легко вычислить точное значение самого интеграла. Поэтому часто полезно иметь возможность определить верхнюю границу ошибки приближения интеграла.
2\,dx.\)
- Подсказка
\(f»(x)=2,\) поэтому \(M=2.\)
- Ответить
\(\dfrac{1}{192}\)
Правило Симпсона
С помощью правила средней точки мы оценили площади областей под кривыми с помощью прямоугольников. В некотором смысле мы аппроксимировали кривую кусочно-постоянными функциями. С помощью правила трапеций мы аппроксимировали кривую, используя кусочно-линейные функции. Что, если бы мы вместо этого аппроксимировали кривую с помощью кусочно-квадратичных функций? С 9{x_4}_{x_2}f(x)\,dx\) с интегралом от другой квадратичной функции, проходящей через \( (x_2,f(x_2)), \,(x_3,f(x_3)),\) и \((x_4,f(x_4)).\) Этот процесс продолжается с каждой последующей парой подынтервалов.
Рисунок \(\PageIndex{4}\): С помощью правила Симпсона мы аппроксимируем определенный интеграл, интегрируя кусочно-квадратичную функцию. Чтобы понять формулу, которую мы получаем для правила Симпсона, мы начнем с вывода формулы для этой аппроксимации для первых двух подынтервалов.
Проходя через вывод, мы должны помнить о следующих соотношениях: 9{x_4}_{x_0}f(x)\,dx=\frac{Δx}{3}(f(x_0)+4\,f(x_1)+2\,f(x_2)+4\,f( x_3)+f(x_4)).\nonumber\]
Шаблон продолжается, когда мы добавляем пары подынтервалов к нашему приближению. Общее правило можно сформулировать следующим образом.
Правило Симпсона
Предположим, что \(f(x)\) непрерывно над \([a,b]\). Пусть \(n\) — четное положительное число и \(Δx=\dfrac{b−a}{n}\). Пусть \([a,b]\) разбит на \(n\) подынтервалов, каждый длиной \(Δx\), с концами в \(P=\{x_0,x_1,x_2,…,x_n\}. \) Набор 9b_af(x)\,dx.\nonumber\]
Точно так же, как правило трапеций является средним значением правил левой и правой руки для оценки определенных интегралов, правило Симпсона может быть получено из правил средней точки и правил трапеций с помощью взвешенное среднее. Можно показать, что \(S_{2n}=(\dfrac{2}{3})M_n+(\dfrac{1}{3})T_n\).
Также можно ограничить ошибку при использовании правила Симпсона для аппроксимации определенного интеграла.
Граница ошибки задается следующим правилом: 92_1\frac{1}{x}\,dx.\)
- Подсказка
\[S_2=(\frac{1}{3}Δx(f(x_0)+4f(x_1)+f(x_2))\]
- Ответить
\(\ гидроразрыва{25}{36}\)
Ключевые понятия
- Мы можем использовать численное интегрирование для оценки значений определенных интегралов, когда сложно найти замкнутую форму интеграла или когда требуется приблизительное значение только определенного интеграла.
- Наиболее часто используемыми методами численного интегрирования являются правило средней точки, правило трапеций и правило Симпсона.
- Правило средней точки аппроксимирует определенный интеграл, используя прямоугольные области, тогда как правило трапеций аппроксимирует определенный интеграл, используя трапециевидные приближения.
- Правило Симпсона аппроксимирует определенный интеграл, сначала аппроксимируя исходную функцию с помощью кусочно-квадратичных функций.
- числовое интегрирование
- множество численных методов, используемых для оценки значения определенного интеграла, включая правило средней точки, правило трапеций и правило Симпсона
- относительная ошибка Ошибка
- в процентах от фактического значения, определяемая как \[\text{относительная ошибка}=∣\frac{A−B}{A}∣⋅100\%\nonumber\]
- Правило Симпсона 9b_af(x)\,dx\) задается как \[T_n=\frac{Δx}{2}\big(f(x_0)+2\, f(x_1)+2\, f(x_2)+⋯+ 2\, f(x_{n−1})+f(x_n)\big).\nonnumber\]
Авторы
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Лицензия
- CC BY-NC-SA
- Показать страницу TOC
- да
- Стадия
- Проект
- Теги
- расчетный график:да
- юпитер: питон
- правило средней точки
- Сумма Римана
- Правило Симпсона
Краткий обзор численного интегрирования | Исчисление II
Краткое изложение численного интегрирования
Основные понятия
- Мы можем использовать численное интегрирование для оценки значений определенных интегралов, когда сложно найти замкнутую форму интеграла или когда требуется приблизительное значение только определенного интеграла .
- Наиболее часто используемыми методами численного интегрирования являются правило средней точки, правило трапеций и правило Симпсона. 9{n}f\left({m}_{i}\right)\Delta x[/latex]
- Правило трапеций
[латекс]{T}_{n}=\frac{1}{2}\Delta x\left(f\left({x}_{0}\right)+2f\left( {x}_{1}\right)+2f\left({x}_{2}\right)+\cdots +2f\left({x}_{n — 1}\right)+f\left( {x}_{n}\справа)\справа)[/латекс] - Правило Симпсона
[латекс] {S}_{n}=\frac{\Delta x}{3}\left(f\left({x}_{0}\right)+4f\left({ x}_{1}\справа)+2f\влево({x}_{2}\справа)+4f\влево({x}_{3}\справа)+2f\влево({x}_{4 }\right)+4f\left({x}_{5}\right)+\cdots +2f\left({x}_{n — 2}\right)+4f\left({x}_{n — 1}\вправо)+f\влево({x}_{n}\вправо)\вправо)[/латекс] 9{b}f\left(x\right)dx[/латекс]- числовое интегрирование
- разнообразие численных методов, используемых для оценки значения определенного интеграла, включая правило средней точки, правило трапеций и правило Симпсона
- относительная ошибка Ошибка
- в процентах от абсолютного значения, заданного как [латекс]|\frac{A-B}{A}|=|\frac{A-B}{A}|\cdot 100\text{%}[/latex]
- Правило Симпсона
- правило, которое аппроксимирует [латекс] {\ displaystyle \ int} _ {a} ^ {b} f \ left (x \ right) dx [/latex] с использованием интегралов кусочно-квадратичной функции.
