Алгебра свободных и скользящих векторов
Алгебра свободных и скользящих векторов
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА 2. Определение вектора. 3. Классификация векторов. 4. Равенство векторов. 5. Перенос вектора. 6. Нуль-вектор. 7. Компланарность и коллинеарность векторов. 8. Прямопротивоположные векторы. § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ 2. Сумма векторов. 3. Свойства суммы векторов. 4. Правила параллелограмма и параллелепипеда. 5. Разность двух векторов. 6. Свойства модуля суммы векторов. § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО 2. Свойства произведения. 3. Деление вектора на число. 4. Единичные векторы. 5. Орт оси. 6. Коллинеарность двух векторов. § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ 3. Разложение вектора по трем другим векторам.  4. Разложение вектора по ортам базиса. § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ 2. Условие коллинеарности двух векторов. 3. Условие компланарности трех векторов. 4. Линейная зависимость четырех векторов. § 6. ПРОЕКЦИИ ВЕКТОРА 2. Свойства составляющих вектора. 3. Проекция вектора на ось. 4. Свойства проекций. 5. Угол между векторами. 6. Вычисление проекций вектора. 7. Теорема о проекции сумммы векторов. 8. Псевдоскаляры. § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА 2. Естественный способ задания свободного вектора. 3. Задание свободного вектора с помощью его проекций (координатный метод). 4. Связь между естественным и координатным способами задания вектора. 5. Задание несвободного вектора. 6. Задание скользящего вектора. 7. Некоторые приложения. § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ 3. Выражение скалярного произведения через проекции векторов. 4. Векторные уравнения геометрических мест.  5. Уравнение плоскости. 7. Изменение проекций вектора при преобразовании координат. 8. Другое определение вектора. § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ 2. Примеры из физики. 3. Способ Н. Е. Жуковского построения векторного произведения. 4. Свойства векторного произведения. 5. Разложение вектора-произведения по координатным ортам. 6. Условие коллинеарности двух векторов. 7. Тождество Лагранжа. 8. Полярные и аксиальные векторы. § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 2. Двойное векторное произведение. 3. Разложение вектора по трем другим векторам. 4. Скалярное произведение двух векторных произведений. 5. Векторное произведение двух векторных произведений. 6. Произведение двух смешанных произведений. 7. Взаимные реперы. § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ 2. Уравнение прямой, проходящей через две заданные точки. 3. Плюкерово уравнение прямой в пространстве. 4. Прямая как пересечение двух плоскостей. § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ ГЛАВА II.  АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ§ 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА 2. Момент вектора относительно точки. 3. Проекции момента. 4. Момент вектора относительно оси. 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей. § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ 2. Главный вектор системы векторов. 3. Главный момент системы векторов. 4. Система двух равнопротивоположных векторов. 5. Первая теорема Вариньона. 7. Инварианты системы векторов. 8. Минимальный момент и центральная ось системы. 9. Распределение главных моментов в пространстве. 10. Понятие о винте. 11. Винт системы векторов. § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ 2. Основные определения и аксиомы. § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение).  § 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Условия эквивалентности двух систем скользящих векторов. 3. Преобразование эквивалентных систем. § 19. ТЕОРИЯ ПАР 1. Пара векторов и ее момент. 2. Свойства пар. 3. Винт § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение). 3. Приведение системы скользящих векторов к вектору и паре. 4. Пример из кинематики. 5. Приведение системы скользящих векторов к винту. 6. Примеры. 7. Уравнения равновесия векторов. 8. Вторая теорема Вариньона. § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ 2. Плоская система скользящих векторов. 3. Система параллельных скользящих векторов. 4. Центр системы параллельных векторов. |
определение, формула для нахождения, аналитический метод и графическое построение
В математике и физике студентам и школьникам зачастую попадаются задачи на векторные величины и на выполнение различных операций над ними.
В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.
[block id=»32″]
…
Оглавление:
- Определения векторной математики
- Аналитический метод
- Вычисление разности графически
- Решение задач
[block id=»33″]
Максимально наглядно применение векторных величин объясняется в физике. Самыми простыми примерами являются силы (сила трения, сила упругости, вес), скорость и ускорение, поскольку помимо численных значений они также обладают направлением действия. Для сравнения приведём пример скалярных величин: это может быть расстояние между двумя точками или масса тела. Для чего же необходимо выполнять действия над векторными величинами такие как сложение или вычитание? Это нужно, чтобы было возможно определить результат действия системы векторов, состоящей из 2 или более элементов.
Определения векторной математики
Введём главные определения, используемые при выполнении линейных операций.
- Вектором называют направленный (имеющий точку начала и точку конца) отрезок.
- Длина (модуль) — это длина направленного отрезка.
- Коллинеарными называют такие два вектора, которые либо параллельны одной и той же прямой, либо одновременно лежат на ней.
- Противоположно направленными векторами называют коллинеарные и при этом направленные в разные стороны. Если же их направление совпадает, то они являются сонаправленными.
- Вектора являются равными, когда они сонаправлены и одинаковы по модулю.
- Суммой двух векторов a и b является такой вектор c, начало которого совпадает с началом первого, а конец — с концом второго при условии, что b начинается в той же точке, в которой заканчивается a.
- Разностью векторов a и b называют сумму a и (— b), где (— b) — противоположно направленный к вектору b.
Также определение разности двух векторов может быть дано следующее: разностью c пары векторов a и b называют такой c, который при сложении с вычитаемым b образует уменьшаемое a.
Также определение разности двух векторов может быть дано следующее: разностью c пары векторов a и b называют такой c, который при сложении с вычитаемым b образует уменьшаемое a.Аналитический метод
Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.
Для двухмерного пространства и векторных величин a {a₁; a₂} и b {b₁; b₂} расчёты будут иметь следующий вид: c {c₁; c₂} = {a₁ — b₁; a₂ — b₂}.
В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a {a₁; a₂; a₃} и b {b₁; b₂; b₃} координаты разности будут также получены попарным вычитанием: c {c₁; c₂; c₃} = {a₁ — b₁; a₂ — b₂; a₃ — b₃}.
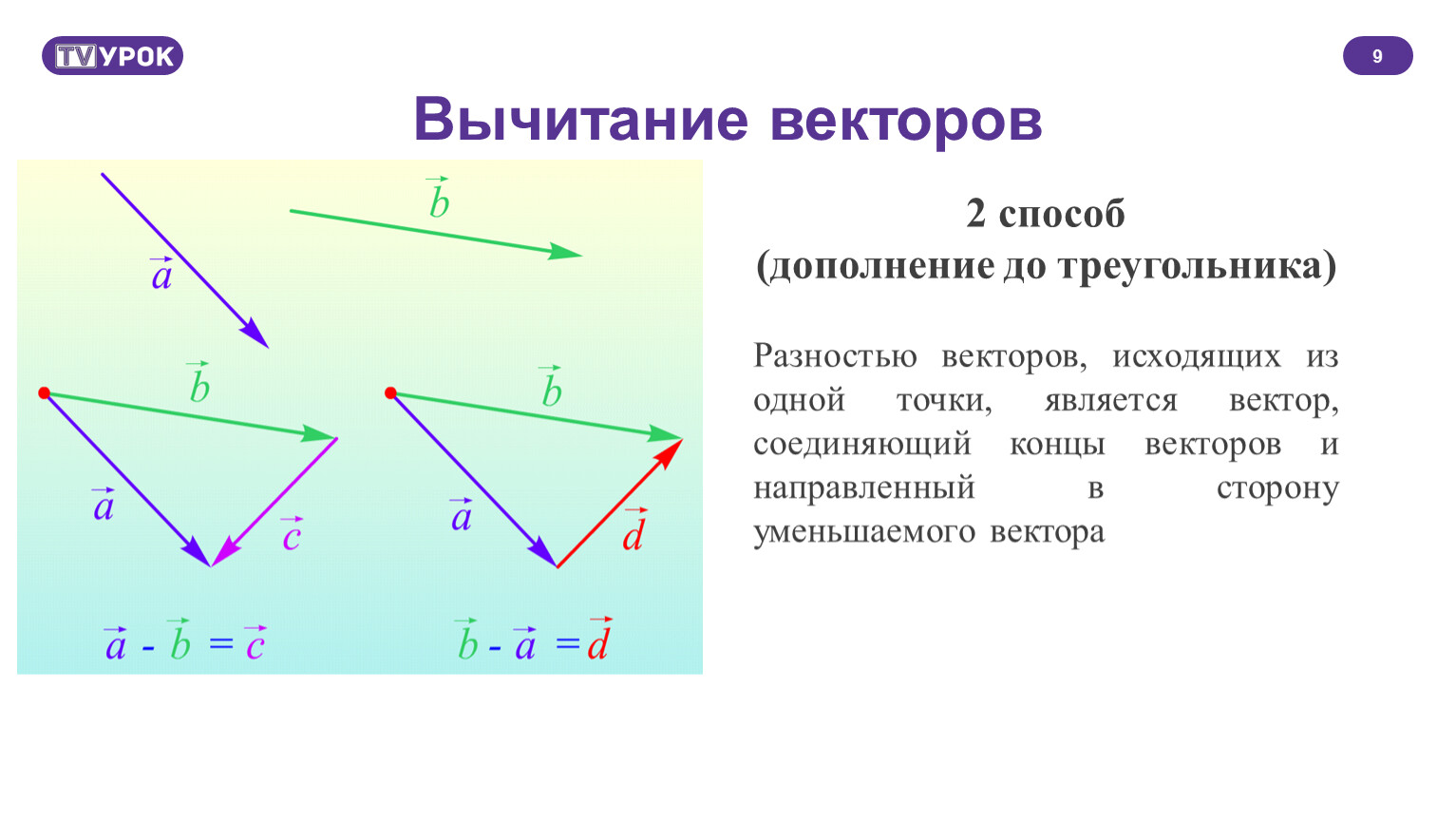
Вычисление разности графически
Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:
- По заданным координатам построить векторы, для которых нужно найти разность.
- Совместить их концы (т. е. построить два направленных отрезка, равных заданным, которые будут оканчиваться в одной и той же точке).
- Соединить начала обоих направленных отрезков и указать направление; результирующий будет начинаться в той же точке, где начинался вектор, являющийся уменьшаемым, и заканчиваться в точке начала вычитаемого.
[block id=»4″]
Результат операции вычитания показан на рисунке ниже.
Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму.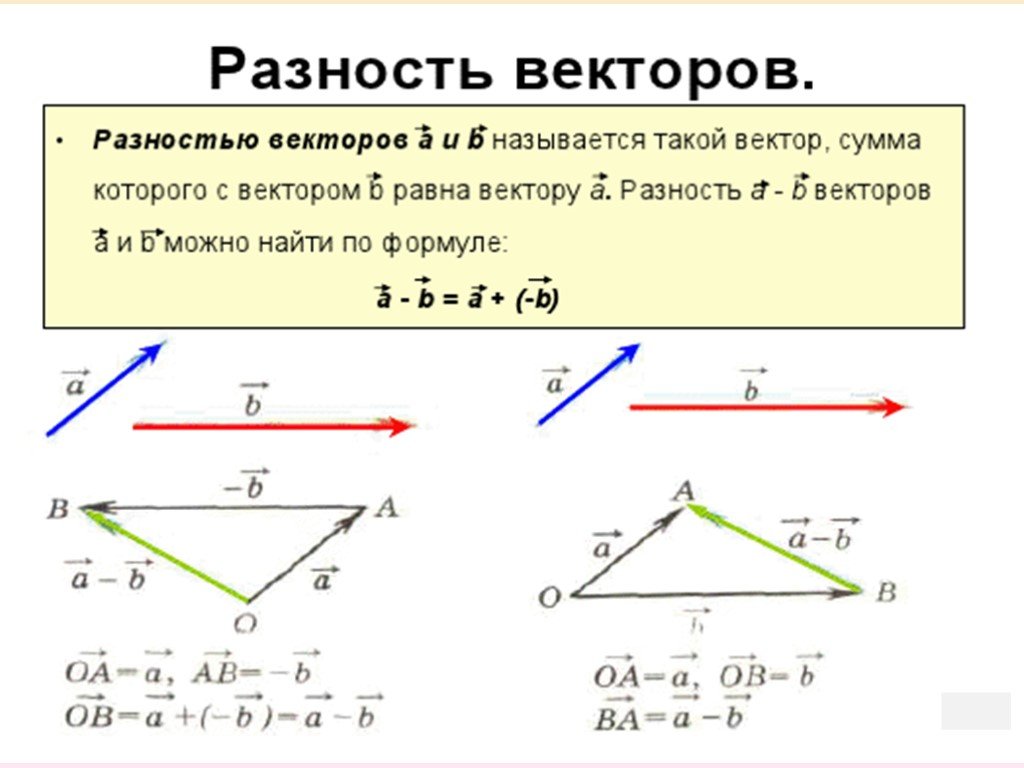
Алгоритм построения будет иметь следующий вид:
- Построить исходные направленные отрезки.
- Тот, что является вычитаемым, необходимо отразить, т. е. построить противоположно направленный и равный ему отрезок; затем совместить его начало с уменьшаемым.
- Построить сумму: соединить начало первого отрезка с концом второго.
Результат такого решения изображён на рисунке:
Решение задач
Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.
Задача 1. На плоскости заданы 4 точки: A (1; —3), B (0; 4), C (5; 8), D (—3; 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.
Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1; —3), а концом — B (0; 4).
Рассчитаем координаты направленного отрезка:
AB {0 — 1; 4 — (— 3)} = {— 1; 7}
Аналогичный расчёт выполняется для CD:
CD {— 3 — 5; 2 — 8} = {— 8; — 6}
Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид {c₁; c₂} = {a₁ — b₁; a₂ — b₂}. Для конкретного случая можно записать:
q = {— 1 — 8; 7 — ( — 6)} = { — 9; — 1}
Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.
[block id=»5″]
Задача 2. На рисунке изображены векторы m, n и p.
Необходимо построить для них разности: p — n; m — n; m — n — p. Выяснить, какая из них обладает наименьшим модулем.
Решение. В задаче требуется выполнить три построения.
Рассмотрим каждую часть задания более подробно.
Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.
Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:
[block id=»6″]
Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:
- m — (n + p): в этом случае вначале строится сумма n + p, которая затем вычитается из m;
- (m — n) — p: здесь сначала нужно найти m — n, а затем отнять от этой разности p;
- (m — p) — n: первым действием определяется m — p, после чего из полученного результата нужно вычесть n.
Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).
Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.
[block id=»2″]
[block id=»10″]
Вычисление разности двух векторов
Разность векторов, расчет онлайн
Сводка:
Функция vector_difference используется для вычисления разницы двух векторов в режиме онлайн.
vector_difference онлайн
Описание:
векторный калькулятор позволяет определить разность двух векторов плоскости или пространства.
- Вычислить разность двух векторов плана
- Вычислить разность двух векторов в пространстве
- Вычислить разность двух векторов в пространстве любой размерности Векторный калькулятор используется по тому же принципу для любой размерности пространств.
Пусть (O,`vec(i)`,`vec(j)`) — каркас плана, `vec(u)` и `vec(v)` — два вектора, имеющие соответствующие координаты (`x_u`,`y_(u)`) и (`x_(v)`,`y_(v)`) в кадре (O,`vec(i)`,`vec(j)`) .
Вектор `vec(u)-vec(v)` имеет координаты (`x_(u)`-`x_(v)`,`y_(u)`-`y_(v)`) в системе (` vec(i)`,`vec(j)`).
Векторный калькулятор может вычитать векторы, имеющие числовые или буквенные координаты.
Пусть `vec(u)`(1;2) `vec(v)`(3;5) для вычисления разницы `vec(u)`-`vec(v)`, введите vector_difference(`[1;2];[3;5]`) , после вычисления возвращается вектор [-2;-3].
Пусть `vec(u)`(a;b) `vec(v)`(2*a;`b`) для вычисления разницы `vec(u)`-`vec(v)`, введите vector_difference(`[a;b];[2*a;b]`)
Пусть (O,`vec(i)`,`vec(j)`,`vec(k)`) пространственная система отсчета, `vec(u)` и `vec(v)` два вектора, которые имеют соответствующие координаты
(`x_u`,`y_(u)`,`z_(u)`) и (`x_(v)`,`y_(v)`,`z_(v)`) в кадре (O,`vec (i)`,`vec(j)`,`vec(k)`) .
Вектор `vec(u)-vec(v)` имеет координаты (`x_(u)`-`x_(v)`,`y_(u)`-`y_(v)`,`z_(u) `-`z_(v)`) в системе (`vec(i)`,`vec(j)`,`vec(k)`).
Векторный калькулятор может вычитать векторы, имеющие числовые или буквенные координаты.
Пусть `vec(u)`(1;2;1) `vec(v)`(3;5;2) для вычисления разницы `vec(u)`-`vec(v)`, введите vector_difference(`[3;5;2];[1;2;1]`) после вычисления возвращается результат [2;3;1].
Пусть `vec(u)`(a;b,c) `vec(v)`(2*a;2-b,c+1) для вычисления разницы `vec(u)`-`vec(v) `, введите vector_difference(`[a;b;c];[3*a;2;2*c+1]`) , после расчета возвращается результат.
Синтаксис:
vector_difference(vector;vector)
Примеры:
vector_difference(`[1;1;1];[5;5;6]`) возвращает [-4;-4;-5]
Расчет онлайн с помощью vector_difference (вычисление разности двух векторов)
См.
также
Список связанных калькуляторов:
- Векторный калькулятор : vector_calculator.
- Вычисление координат вектора по двум точкам. : вектор_координаты. Векторный калькулятор позволяет рассчитать координаты вектора по координатам двух точек в режиме онлайн.
- Калькулятор определителя: определитель. Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.
- Вычисление разности двух векторов: vector_difference. Функция vector_difference используется для вычисления разницы двух векторов в режиме онлайн.
- Вычисление нормы вектора: vector_norm. Векторный калькулятор позволяет рассчитать норму вектора онлайн.
- Исчисление скалярного тройного произведения: scalar_triple_product. Калькулятор скалярного тройного произведения позволяет онлайн рассчитать скалярное тройное произведение.
- Калькулятор скалярного произведения: dot_product. Калькулятор скалярного произведения позволяет вычислить скалярное произведение двух векторов онлайн по их координатам.
- Произведение вектора на число: product_vector_number. Векторный калькулятор позволяет вычислить произведение вектора на число онлайн.
- Калькулятор перекрестного произведения: перекрестное_произведение. Векторный калькулятор позволяет вычислить векторное произведение двух векторов онлайн по их координатам.
- Вычисление суммы двух векторов: vector_sum. Векторный калькулятор позволяет вычислить сумму двух векторов онлайн.
Прочие ресурсы
- Исправленные упражнения на векторах
- Игры векторного расчета
- Научитесь считать с векторами
Разница между двумя векторами в R
В этой статье мы увидим, как найти разницу между двумя векторами в языке программирования R.
Разница (A-B) между двумя векторами в R Programming эквивалентна элементам, присутствующим в A, но отсутствующим в B. Результирующие элементы всегда являются подмножеством A. В случае, если оба множества не пересекаются, возвращается весь набор A.
Метод 1: использование setdiff() методМетод setdiff() в R используется для извлечения элементов вектора X, которые не содержатся в Y. Этот метод может применяться, когда два векторы также могут принадлежать к разным типам данных, где элементы первого вектора-аргумента возвращаются без изменений. В случае, если входные векторы эквивалентны, то есть содержат одни и те же элементы, результирующий вектор будет иметь нулевые записи и ссылаться на выходные данные типа данных (0). Также разные типы результатов получаются при изменении порядка векторов во время вызова функции.
Синтаксис:
setdiff( X, Y)
Пример:
R
9013 7 print |
) 90 138Выход
[1] "Исходный вектор1" [1] 1 2 3 4 5 [1] "Исходный вектор2" [1] 4 5 6 7 8 [1] «Век1-Век2» [1] 1 2 3
Этот метод работает и для строковых векторов.
Пример:
R
901 37 печать |
) |
) Выход
[1] "Исходный вектор1" [1] «Geeksforgeeks» «Интервью» «Наука» [1] "Исходный вектор2" [1] 1 2 3 5 5 [1] "Век2 - Век1" [1] 1 2 3 5Способ 2: использование оператора %in%
Оператор %in% можно использовать для проверки наличия элемента в списке. Этот подход сначала проверяет, какие индексы вектора1 не находятся в векторе2, а затем возвращаются соответствующие элементы вектора1. Затем следует применение метода unique(), который возвращает только уникальные элементы результирующего вектора.
Синтаксис:
vec1[! vec1 %in% vec2]
Пример:
R
|
) Вывод
[1] «Исходный вектор1»
[1] «Компьютерщики» «Интервью» «Наука»
[1] «Исходный вектор2»
[1] «Алгоритмы» «Наука» «размещение «структуры данных»
[1] «Vec1 – Vec2»
[1] «Geeksforgeeks» «Интервью»
Этот подход также совместим с векторами, принадлежащими к разным типам данных. В этом случае возвращаются элементы vec1.
Пример:
R
|
