Интегрирование функций с разрывами и несобственные интегралы
До сих пор мы интересовались в первую очередь интегралами непрерывных функций. Именно для такого случая мы доказали формулу Ньютона — Лейбница: непрерывность подынтегральной функции является важным её условием. Что бывает, когда подынтегральная функция терпит разрывы? Мы не сможем дать полный ответ на этот вопрос, но обсудим некоторые важные частные случаи.27.1Интегрирование функций с конечным числом скачков
27.1.1Скачки интегралу не помеха
Пусть функция f имеет на отрезке [a,b] конечное число (m штук) разрывов в точках z1,…,zm, во всех остальных точках отрезка она непрерывна, и все разрывы являются скачками, то есть в них определены пределы справа и слева. Можно ли посчитать интеграл по [a,b] от такой функции? Если воспринимать задачу интегрирования геометрически, это не выглядит проблемой.
Интеграл — это площадь, а площадь обладает свойством аддитивности — если
разрезать фигуру, площадь от которой мы находим, на несколько непересекающихся
кусочков, площадь всей фигуры должна равняться сумме площадей этих кусочков.
Возьмём произвольное размеченное разбиение P, у которого границами
отрезков разбиения являются точки (x0,…,xn) и отмечены точки
(x∗1,…,x∗n). Поскольку функции f и g различаются лишь в конечном
числе точек, эти точки могут попасть лишь в конечное число отрезков
разбиения. (В худшем случае точка может оказаться общим концом двух отрезков
разбиения, значит, число затронутых отрезков не более чем в два раза больше
числа точек различия.
∣∣ ∣∣M∑i=1f(x∗ki)−g(x∗ki)Δxki∣∣ ∣∣≤M∑i=1|f(x∗ki)−g(x∗ki)|⋅|Δxki|.
Модуль разности между значениями функций f и g не превосходит 2C, поскольку сами значения ограничены по модулю числом C. (Мы используем неравенство |a−b|≤|a|+|b|.) Длина отрезка разбиения |Δxki| не превосходит диаметра разбиения d(P). Всего слагаемых M штук, где M≤2m. Значит разница между двумя интегральными суммами не превосходит (2m)⋅(2C)⋅d(P)=4mC⋅d(P) и стремится к нулю при d(P) стремящемся к нулю. Значит, пределы интегральных сумм совпадают.∎Теорема 1. Пусть функция f имеет конечное число точек разрывов z1<z2<…<zm на отрезке [a,b] и все разрывы являются скачками, то есть в каждой точке разрыва есть конечные односторонние пределы функции справа и слева. В остальных точках функция непрерывна. Тогда она интегрируема на отрезке [a,b].
 5), разобьем
интеграл в сумму интегралов:
5), разобьем
интеграл в сумму интегралов:∫baf(x)dx=∫z1af(x)dx+∫z2z1f(x)dx+…+∫zmzm−1f(x)dx+∫bzmf(x)dx.(27.1)
Рассмотрим любой из получившихся отрезков интегрирования, обозначим его концы через α и β. Функция f непрерывна на [α,β], за исключением, быть может, концов отрезка. Но в концах существуют односторонние пределы (поскольку все точки разрывов — скачки), и следовательно для вычисления интеграла по [α,β] функцию можно переопределить в α и β, таким образом, чтобы сделать её непрерывной на всём отрезке (как обычно, в концах требуется односторонняя непрерывность). По лемме, значение интегралов от этого не поменяется, равно как и факт интегрируемости. Но функция, непрерывная на отрезке, интегрируема на этом отрезке, и значит все интегралы в правой части равенства (27.1) существует и функция интегрируема на всём отрезке [a,b].∎ Пример 1. Пусть sign(x)=⎧⎨⎩1,x>00,x=0−1,x<0НайдёмF(t):=∫t−2sign(x)dx.
Возможно три варианта: t<0, t=0 или t>0. В первом случае наш интеграл — это площадь прямоугольника высотой 1 и шириной (t−(−2)), взятая со знаком «минус» (потому что значение функции отрицательно), то есть −2−t (см. анимацию на рис. 27.1). При t=0 можно
переопределить функцию таким образом, чтобы в точке x=0 она принимала
значение (−1) и тем самым сделать её непрерывной на всём отрезке
интегрирования. Если же t>0, наш интеграл разбивается в сумму двух
интегралов: по отрезку [−2,0] и по отрезку [0,t]. Первый равен −2,
второй является площадью прямоугольника с шириной t и высотой 1, то есть
t.
анимацию на рис. 27.1). При t=0 можно
переопределить функцию таким образом, чтобы в точке x=0 она принимала
значение (−1) и тем самым сделать её непрерывной на всём отрезке
интегрирования. Если же t>0, наш интеграл разбивается в сумму двух
интегралов: по отрезку [−2,0] и по отрезку [0,t]. Первый равен −2,
второй является площадью прямоугольника с шириной t и высотой 1, то есть
t.Рис. 27.1: Интеграл от sign(x) как функция верхнего предела. Сверху: подынтегральная функция и площадь; снизу: значение интеграла.import matplotlib.pyplot as plt import numpy as np import qqmbr.odebook as ob # see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py def nansign(x): sign = np.sign(x) return np.where(sign != 0, sign, np.nan) fig, (ax1, ax2) = plt.subplots(2, 1, sharex=True) camera = Camera(fig) x = np.linspace(-3, 3, 201) for t in np.linspace(-2, 3, 11): ax1.plot(x, nansign(x), label=r'$y=\mathrm{sign}(x)$', color='gray') ax1.plot([0], [0], 'o', color='gray') ax1.plot([0, 0], [1, -1], 'o', color='gray', markerfacecolor='white') t_span_neg = np.linspace(-2, min(t, 0), 200) ax1.fill_between(t_span_neg, -np.ones_like(t_span_neg), color='red', alpha=0.5) if (t > 0): t_span_pos = np.linspace(0, t, 200) ax1.fill_between(t_span_pos, np.ones_like(t_span_pos), color='green', alpha=0.5) ax1.annotate('$t$', (t, 0), xytext=(t, 0.1)) ob.center_spines(grid=False, minor_ticks=False, ax=ax1) ob.settle_axes(xmin=-3, xmax=3, ymin=-1.3, ymax=1.3, xlabel="x", ylabel="y", ax=ax1) ax1.set_xticks([-2, -1, 0, 1, 2]) ax1.set_yticks([-1, 1]) t_span = np.linspace(-2, t) ax2.plot(t_span, -2+np.abs(t_span), color='C0') ob.center_spines(grid=False, minor_ticks=False, ax=ax2) ob.settle_axes(xmin=-3, xmax=3, ymin=-3.2, ymax=3.2, xlabel="t", ylabel="y", ax=ax2) camera.snap() animation = camera.animate()
 Итак,
Итак,F(t)=⎧⎨⎩−2−t,t<0;−2,t=0;−2+t,t>0.
Это выражение можно записать короче: F(t)=−2+|t|.F′(t)=sign(t).
Это неудивительно: первая часть формулы Ньютона — Лейбница выполняется для всех точек, в которых подынтегральная функция непрерывна, а разрыв у нас только в нуле. В нуле же функция F не является дифференцируемой, но является непрерывной. Оказывается, так будет всегда.27.1.2Интеграл с переменным верхним пределом непрерывен
Утверждение 1. Пусть функция f интегрируема на отрезке [a,b]. Тогда функцияF(t)=∫taf(x)dx
непрерывна на отрезке [a,b]. Доказательство. Действительно, для любых точек t,t0∈[a,b]F(t)−F(t0)=∫taf(x)dx−∫t0af(x)dx=∫tt0f(x)dx.
Иными словами, разность значений F в точках t и t0 равна интегралу от f по отрезку [t0,t]. Поскольку функция под интегралом интегрируема, она ограничена, и значит интеграл по маленькому отрезку от неё будет маленьким. Следовательно, значения функции F в близких точках близки. Аккуратное доказательство выглядит так. Поскольку функция f ограничена,
найдётся такое C, что для всех x∈[a,b]
Следовательно, значения функции F в близких точках близки. Аккуратное доказательство выглядит так. Поскольку функция f ограничена,
найдётся такое C, что для всех x∈[a,b]−C≤f(x)≤C.
Интегрируя эти неравенства по отрезку [t0,t] (будем считать, что t>t0, противоположный случай разбирается аналогично), имеем:∫tt0(−C)dx≤∫tt0f(x)dx≤∫tt0Cdx.
Считая интегралы в левой и правой части, получаем:−C(t−t0)dx≤∫tt0f(x)dx≤C(t−t0).
В пределе при t→t0, левая и правая части стремятся к нулю, значит и интеграл посередине стремится к нулю. Но этот интеграл равен разности F(t)−F(t0), следовательно эта разность стремится к нулю, и значитlimt→t0F(t)=F(t0),
то есть F непрерывна в точке t0.∎ Теперь мы можем заключить, что интеграл от кусочно-непрерывной функции f с
конечным числом скачков, если рассматривать его как функцию от верхнего предела,
является непрерывной функцией, дифференцируемой во всех точках, кроме точек
разрывов f; в точках разрывов f у интеграла точки излома и производная не
существует (если только эти разрывы не являются устранимыми, устранимые разрывы
интеграл «не замечает» в силу леммы).
27.2Несобственные интегралы
До сих пор мы рассматривали интегралы, которые отвечали площадям ограниченнух фигур — то есть таких фигур, которые можно поместить в достаточно большой прямоугольник. Действительно, в горизонтальном направлении мы были ограничены отрезком интегрирования, а в вертикальном — ограниченностью подынтегральной функции — мы всегда говорили, что раз функция не является ограниченной, она и не интегрируемая, и даже однажды это доказали.Однако, можно представить себе фигуру, которая не будет помещаться ни в какой прямоугольник, но тем не менее будет иметь конечную площадь. Как бы нам её найти?
27.2.1Несобственные интегралы с бесконечными пределами интегрирования
Начнём с примера.Пример 2. Пусть мы хотим найти такой интеграл:∫+∞11x2dx.(27.2)
Область интегрирования теперь — не отрезок, а бесконечный луч, см. рис. 27.2. import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook. py
fig, ax1 = plt.subplots()
x = np.linspace(-1.2, 3, 201)
ax1.plot(x, 1 / x ** 2)
x_clip = np.linspace(1, 3, 201)
ax1.fill_between(x_clip, 1 / x_clip ** 2, alpha=0.5)
ob.center_spines(grid=False, minor_ticks=False, ax=ax1)
ob.settle_axes(xmin=-1.2, xmax=3, ymin=-0.7, ymax=3,
xlabel="x", ylabel="y", ax=ax1)
ax1.set_xticks([1, 2])
ax1.set_yticks([])
py
fig, ax1 = plt.subplots()
x = np.linspace(-1.2, 3, 201)
ax1.plot(x, 1 / x ** 2)
x_clip = np.linspace(1, 3, 201)
ax1.fill_between(x_clip, 1 / x_clip ** 2, alpha=0.5)
ob.center_spines(grid=False, minor_ticks=False, ax=ax1)
ob.settle_axes(xmin=-1.2, xmax=3, ymin=-0.7, ymax=3,
xlabel="x", ylabel="y", ax=ax1)
ax1.set_xticks([1, 2])
ax1.set_yticks([])Использовать обычное определение нельзя — луч нельзя разбить в конечное
число отрезков. Теоретически, можно было бы расширить понятие разбиения,
разрешив разбиения на бесконечное число отрезков, но тогда в интегральных
суммах было бы бесконечное число слагаемых, и надо было думать, как эти
суммы определять…В общем, мы сделаем иначе. Положим по определению, что интеграл (27.2) равен такому пределу:
∫+∞11x2dx:=limt→+∞∫t11x2dx.
То есть мы считаем интеграл до какой-то конечной границы t, для разных t получаем разные значения интеграла, и дальше устремляем t к бесконечности, см. анимацию на рис. 27.3.
27.3.Это выглядит логичным: если мы будем всё сильнее увеличивать верхний предел интегрирования t, мы будем захватывать всё большую и большую часть нашей неограниченной фигуры, так что в пределе ничего не останется не захваченным, и значит площадь захваченного куска должна стремиться к площади всей фигуры.
import matplotlib.pyplot as plt
import numpy as np
import qqmbr.odebook as ob
# see https://github.com/ischurov/qqmbr/blob/master/qqmbr/odebook.py
fig, ax1 = plt.subplots()
camera = Camera(fig)
x = np.linspace(-1.2, 3, 201)
for t in np.linspace(1, 3, 11):
ax1.plot(x, 1 / x ** 2, color='C0')
x_clip = np.linspace(1, 3, 201)
ax1.fill_between(x_clip, 1 / x_clip ** 2, alpha=0.5, color='C0')
x_clip_t = np.linspace(1, t, 201)
ax1.fill_between(x_clip_t, 1 / x_clip_t ** 2, alpha=0.5,
color='C1')
ob.center_spines(grid=False, minor_ticks=False, ax=ax1)
ob.settle_axes(xmin=-1.2, xmax=3, ymin=-0.7, ymax=3,
xlabel="x", ylabel=None, ax=ax1)
ax1. annotate('$y$', (0.03, 3 - 0.15))
ax1.annotate('$t$', (t, 0), xytext=(t + 0.03, -0.25))
ax1.set_xticks([1, 2])
ax1.set_yticks([])
camera.snap()
animation = camera.animate()
annotate('$y$', (0.03, 3 - 0.15))
ax1.annotate('$t$', (t, 0), xytext=(t + 0.03, -0.25))
ax1.set_xticks([1, 2])
ax1.set_yticks([])
camera.snap()
animation = camera.animate()limt→+∞∫t11x2dx=limt→+∞(−1x)∣∣∣t1=limt→+∞(−1t−(−11))=1.
Получилось! Искомая площадь равна 1. Определение 1. Пусть функция f интегрируема на любом отрезке [a,t], t>a. Интеграл∫+∞af(x)dx
называется несобственным интеграл по бесконечному промежутку. По определению он равен∫+∞af(x)dx:=limt→+∞∫taf(x)dx.
Всегда ли предел будет существовать? Конечно, нет — легко придумать пример, когда не будет. Скажем,
∫+∞12dx=limt→+∞2(t−1)=+∞.
Но тут история понятная — подынтегральная функция является константой, наша фигура — «бесконечный прямоугольник», неудивительно, что у него бесконечная площадь. Но что если подынтегральная функция стремится к нулю. Может ли быть
так, чтобы интеграл по лучу не существовал? Давайте рассмотрим ещё один пример.
Пример 3. Найдём
Но что если подынтегральная функция стремится к нулю. Может ли быть
так, чтобы интеграл по лучу не существовал? Давайте рассмотрим ещё один пример.
Пример 3. Найдём∫+∞11xdx.
Действуя так же, как и раньше, запишем этот интеграл в виде предела. Напомним, что первообразная 1/x при положительных x — это lnx. Имеем:∫+∞11xdx:=limt→+∞∫t11xdx=limt→+∞lnx|t1=limt→+∞(lnt−ln1)=+∞.
Определение 2. Если предел в определении несобственного интеграла существует, говорят, что интеграл сходится, в противном случае он расходится.
Итак, интеграл по одному и тому же лучу [1,+∞) от функции 1/x2 сходится, а от функции 1/x расходится. Почему так? Казалось бы, они обе стремятся к нулю при x→+∞, и на глаз их графики очень похожи. Однако, мало стремиться к нулю, нужно делать это ещё достаточно быстро. Функция 1/x стремится к нулю медленнее, чем 1/x2, и этого стремления не хватает, чтобы площадь оказалась конечной.
Является ли требование стремления к нулю необходимым для сходимости интеграла?
Оказывается, нет.
Упражнение 1. Придумайте пример функции, которая не стремится к нулю при x→+∞, но интеграл от которой по лучу [0,+∞) сходится.
Определение 3. Легко определить интеграл по лучу (−∞,a]:∫a−∞f(x)dx=limt→−∞∫atf(x)dx.
Интеграл по всей прямой (−∞,∞) определяется так:∫∞−∞f(x)dx=∫a−∞f(x)dx+∫+∞af(x)dx,
где промежуточную точку a можно выбирать произвольным образом, значение интеграла от этого не изменится (почему?).27.2.2Признак сравнения
Часто бывает важно даже не найти значение несобственного интеграла, а просто показать, что он сходится. В этом случае полезной оказывается следующая теорема. Теорема 2. Пусть функции f и g интегрируемы на любом отрезке [a,t], t>a. Пусть также для всякого x≥a0≤f(x)≤g(x)(27.3)
и интеграл∫+∞ag(x)dx(27.4)
сходится. Тогда∫+∞af(x)dx(27.5)
тоже сходится. Доказательство. Утверждение выглядит естественным. Фигура, соответствующая интегралу (27.5), содержится внутри фигуры, соответствующей интегралу (27.4). Логично предположить, что если площадь первой конечна, то и второй тоже.
Формальное доказательство выглядит так. Введём обозначения:
G(t):=∫tag(x)dx,F(t):=∫taf(x)dx.
Заметим, что обе функции F и G неубывают на [a,+∞): это следует из того факта, что их производные, равные подынтегральным функциям, неотрицательны. Также интегрируя неравенства (27.3) по отрезку [a,t], имеем:F(t)=∫taf(t)dt≤∫tag(t)dt=G(t).
По предположению, G(t) имеет предел при t→+∞. Обозначим его через L. Все значения неубывающей функции не превосходят предела: действительно, если для какого-то t0, G(t0)>L, то найдётся такое c>0, что G(t0)>L+c (можно в качестве c взять половину разности G(t0)−L, тогда L+c — середина отрезка [L,G(t0)]), и значит для всех t>t0 выполняется такое же неравенство (в силу неубывания G), а значит предел не меньше L+c, то есть строго больше L — противоречие. Значит для всех t≥a:F(t)≤G(t)≤L.
Итак, функция F неубывает и ограничена. Можно легко адаптировать теорему Вейерштрасса для функций (сделайте это!) и получить, что существует пределlimt→+∞F(t),
то есть интеграл (27. 5) сходится.∎
Пример 4. Докажем, что
5) сходится.∎
Пример 4. Докажем, что∫+∞0e−x2dx
сходится.Действительно, разобьём этот интеграл в сумму двух:
∫+∞0e−x2dx=∫10e−x2dx+∫+∞1e−x2dx.
С первым слагаемым никаких проблем нет: это обычный (собственный) интеграл Римана, подынтегральная функция непрерывна, значит, интеграл существует. Рассмотрим второе слагаемое. Заметим, что при x≥1, x2≥x и0≤e−x2≤e−x.
Таким образом, если интеграл∫+∞1e−xdx
сходится, то и наш интеграл сходится. Но e−x легко проинтегрировать явно: первообразная равна (−e−x). Таким образом,∫+∞1e−xdx=limt→+∞∫t1e−xdx=limt→+∞(−e−x)|t1=limt→+∞(−e−t−(−e−1))=1e.
Мы нашли этот интеграл явно, значит, он сходится, и значит наш исходный интеграл тоже сходится.В том виде, в котором мы его сформулировали, признак сравнения работает только с неотрицательными подынтегральными функциями.
Вопрос 1. Покажите, что условие неотрицательности здесь существенно. Приведите пример
функций f и g, для которых условие f(x)≤g(x) выполняется для всех
x, ∫+∞0g(x)dx сходится, а интеграл ∫+∞0f(x)dx расходится.
Следующее утверждение позволяет расширить признак сравнения на случай знакопеременных подынтегральных выражений:
Утверждение 2. Если сходится интеграл∫+∞a|f(x)|dx,
то сходится и интеграл∫+∞af(x)dx.
Мы не будем сейчас доказывать это утверждение. Однако, из него мгновенно следует, что если существует такая функция g(x), что для всех x, |f(x)|≤g(x) и ∫+∞ag(x)dx сходится, то и ∫+∞af(x)dx тоже сходится.
27.2.3Несобственные интегралы и вертикальные асимптоты
Итак, нам удалось расширить понятие интеграла на случай бесконечных промежутков интегрирования. Может быть, и с неограниченными функциями удастся что-то сделать? До сих пор мы много раз повторяли мантру «раз функция неограничена, значит, она
и не интегрируема» — и даже доказали утверждение
на эту тему. Однако, значит ли это, что соответствующие площади на самом деле
не определены? Нам уже удалось найти площади некоторых неограниченных фигур, как
в примере 2 выше. Может быть, и с площадями под графиками
неограниченных функций ситуация может быть аналогичной — и наш реузльтат о
неинтегрируемости вызван просто неудачным определением интеграла? Можно ли
модифицировать это определение каким-то образом, чтобы хотя бы некоторые
неограниченные функции стали интегрируемыми? Давайте попробуем.
∫101√xdx.
Подынтегральная функция стремится к бесконечности при x→0+, и значит не является ограниченной — стало быть интеграл в обычном смысле не определён. Однако, давайте воспользуемся тем же приёмом, которым мы воспользовались для нахождения интеграла по бесконечному промежутку. Положим по определению∫101√xdx:=limt→0+∫1t1√xdx.
Для всякого t>0 интеграл под знаком предела определён. Более того: его можно найти явно — подынтегральная функция 1/√x может быть записана в виде x−1/2, а все степенные функции мы имеем интегрировать. Первообразная имеет вид 2×1/2=2√x (проверьте дифференцированием!) и значит∫101√xdx:=limt→0+∫1t1√xdx=limt→0+2√x|1t=limt→0+(2√1−2√t)=2.
Интеграл сошёлся, ура! Определение 4. Пусть функция f имеет вертикальную асимптоту в точке a и для всякого t∈(a,b) функция f интегрируема по Риману на отрезке [t,b]. Несобственный интеграл∫baf(x)dx
определяется следующим образом:∫baf(x)dx:=limt→a+∫btf(x)dx.
Как обычно, предел может существовать (в этом случае говорят, что интеграл сходится), или не существовать (значит, интеграл расходится).
Пример 6. Сходится ли интеграл∫101x2dx?
Мы уже считали интеграл от этой функции, но по другой области — по бесконечному промежутку [1,+∞) — и он сошёлся. Может быть, и в этот раз нам повезёт?∫101x2dx=limt→0+∫1t1x2dx=limt→0+(−1x)∣∣∣1t=limt→0+(−11+1t)=+∞.
Увы, этот интеграл расходится.Почему такая разница с функцией 1/√x? Дело в том, что √x стремится к нулю гораздо медленнее, чем x2, и значит 1/√x стремится к бесконечности гораздо медленнее, чем 1/x2. Поэтому площадь под графиком 1/√x оказывается конечной, а под графиком 1/x2 — бесконечной.
В определении 4 вертикальная асимптота находится на левой границе отрезка интегрирования. Конечно, можно с тем же успехом определить несобственный интеграл для функции с вертикальной асимптотой на правой границе области отрезка интегрирования.
Определение 5. Пусть функция f имеет вертикальную асимптоту в точке b и для всякого t∈(a,b) функция f интегрируема по Риману на отрезке [a,t]. Несобственный интеграл
Несобственный интеграл∫baf(x)dx
определяется следующим образом:∫baf(x)dx:=limt→b−∫taf(x)dx.
А что если точка бесконечного разрыва попала куда-то внутрь нашего отрезка? Ничего страшного — просто разобьем интеграл на два.
Определение 6. Пусть функция f имеет вертикальную асимптоту в точке c∈(a,b) и интегрируема на любой отрезке [a,t], t<c и на любом отрезке [t,b], t>c. Тогда∫baf(x)dx:=∫caf(x)dx+∫bcf(x)dx,
где интегралы в правой части — несобственные. Если хотя бы один из этих двух интегралов расходится, интеграл в левой части тоже считается расходящимся. Пример 7. Что вы можете сказать про интеграл∫1−11xdx?
Очень хочется сказать, что он равен нулю: ведь это интеграл от нечётной функции по симметричному отрезку, и значит положительная и отрицательные площади должны взаимно уничтожиться. Однако, это не так: по определению,∫1−11xdx:=∫0−11xdx+∫101xdx,
и оба интеграла в правой части расходятся, значит и исходный интеграл расходится. (Подробнее о том, почему это правильный подход, будет обсуждаться на семинаре. )
)27.2.4Несобственные интегралы с несколькими особенностями
Каждое из определений несобственных интегралов, которые мы обсуждали, рассматривает только одну «особенность» — бесконечный разрыв или бесконечную границу интегрирования. Если у интересующего нас интеграла несколько особенностей, его следует разбить в сумму интегралов, у каждого из которых лишь одна особенность, и воспользоваться нашими определениями.Пример 8. Пусть у функции f бесконечные разрывы в точках 2, 5 и 7, и мы хотим
посчитать от неё интеграл по всей числовой прямой. Его следует представить в
таком виде:
∫∞−∞f(x)dx=∫1−∞f(x)dx+∫21f(x)dx+∫42f(x)dx+∫54f(x)dx++∫65f(x)dx+∫76f(x)dx+∫107f(x)dx+∫+∞10f(x)dx.
Каждый из получившихся интегралов — один из несобственных интегралов,
которые мы обсуждали. Промежуточные точки 1, 4, 6, 10 выбраны
произвольным образом — можно выбрать какие-то другие точки, лежаще на тех же
промежутках, от этого ничего не изменилось бы. Если хотя бы один из
интегралов в правой части расходится, значит, весь исходный интеграл тоже
расходится.
27.3Заключение
Мы вышли за пределы уютного и безопасного мира, в котором все подыинтегральные функции непрерывны. И тут много всего интересного! Во-первых, если функция имеет разрывы типа «скачок», и их конечное число, никаких проблем для интегрирования это не представляет. Правда, интеграл, если думать о нём как о функции от его верхнего предела, будет иметь изломы в точках разрывов подынтегральной функции — но по крайней мере сам останется непрерывным. Случай бесконечных разрывов подынтегральной функции представляет большую опасность: несобственные интегралы, которые мы придумали специально для этого случая, существуют не всегда, иногда они сходится, а иногда расходится. Но тут уж ничего не поделать — площадь под графиком неограниченной функции может быть бесконечной. Мы также обсудили интегралы по бесконечным промежуткам — особенно важный для нас случай, поскольку такие интегралы сплошь и рядом встречаются в теории вероятностей, которую вы будете проходить совсем скоро.
На этом наш краткий экскурс в теорию интегрирования заканчивается. Конечно, мы успели обсудить не всё, но фундамент заложен. Время идти дальше!
← Предыдущая глава Следующая глава →
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Интегрирование функций. Понятие и основное свойство первообразной. Неопределенный интеграл. Правила интегрирования. Определенный интеграл. Формула Ньютона-Лейбница. Свойства геометрический и физический смысл определенного интеграла Понятие и основное свойство первообразной. Неопределенный интеграл. Правила интегрирования. Определенный интеграл. Формула Ньютона-Лейбница. Свойства геометрический и физический смысл определенного интегралаПоделиться:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. {-1/2}}{-1/2}+C=-\frac{2}{\sqrt{tg x}}+C=-2\sqrt{ctg x}+C.$$ {-1/2}}{-1/2}+C=-\frac{2}{\sqrt{tg x}}+C=-2\sqrt{ctg x}+C.$$Ответ: $-{2}{\sqrt{ctg x}}+C.$ {jumi[*4]} 6.214. $\int\cos\frac{x}{2}\cos\frac{x}{3}.$ Решение. $$\int\cos\frac{x}{2}\cos\frac{x}{3}=\int\frac{1}{2}\left(\cos\left(\frac{1}{2}-\frac{1}{3}\right)x+\cos\left(\frac{1}{2}+\frac{1}{3}\right)x\right)\,dx=$$ $$=\frac{1}{2}\int\left(\cos\frac{1}{6}x+\cos\frac{5}{6}x\right)\,dx=\frac{6}{2}\sin\frac{1}{6}x+\frac{6}{10}\sin\frac{5}{6}x+C=$$ $$=3\sin\frac{x}{6}+0,6\sin\frac{5x}{6}+C.$$ Ответ: $3\sin\frac{x}{6}+0,6\sin\frac{5x}{6}+C.$
6.215. $\int\sin \frac{x}{3}\cos\frac{2x}{3}\,dx.$ Решение. $$\int\sin\frac{x}{3}\cos\frac{2x}{3}=\int\frac{1}{2}\left(\sin\left(\frac{1}{3}-\frac{2}{3}\right)x+\sin\left(\frac{1}{3}+\frac{2}{3}\right)x\right)\,dx=$$ $$=\frac{1}{2}\int\left(\sin\frac{-x}{3}+\sin x\right)\,dx=\frac{3}{2}\cos\frac{1}{3}x-\frac{1}{2}\cos x+C.
ФОШ (функция ФОШ) — Служба поддержки OfficeВ этой статье описаны синтаксис формулы и использование функции ФОШ в Microsoft Excel. ОписаниеВозвращает функцию ошибки, проинтегрированную от значения аргумента «нижний_предел» до значения аргумента «верхний_предел». СинтаксисФОШ(нижний_предел;[верхний_предел]) Аргументы функции ФОШ описаны ниже.
Замечания
ПримерСкопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Интегрирование по частям, формулы и примеры решенийСодержание: Рассмотрим функции $u=u(x)$ и $v=v(x)$, которые имеют непрерывные производные. Согласно свойствам дифференциалов, имеет место следующее равенство: $d(u v)=u d v+v d u$ Проинтегрировав левую и правую части последнего равенства, получим: $\int d(u v)=\int(u d v+v d u) \Rightarrow u v=\int u d v+\int v d u$ Полученное равенство перепишем в виде: $\int u d v=u v-\int v d u$ Эта формула называется формулой интегрирования по частям. С ее помощью интеграл $\int u d v$ можно свести к нахождению интеграла $\int v d u$, который может быть более простым. Замечание В некоторых случаях формулу интегрирования частями нужно применять неоднократно. Формулу интегрирования по частям целесообразно применять к интегралам следующего вида: 1) $\int P_{n}(x) e^{k x} d x$ ; $\int P_{n}(x) \sin (k x) d x$ ; $\int P_{n}(x) \cos (k x) d x$ Здесь $P_{n}(x)$ — многочлен степени
$n$,
$k$ — некоторая константа. 2)$\int P_{n}(x) \arcsin x d x$ ; $\int P_{n}(x) \arccos x d x$ ; $\int P_{n}(x) \ln x d x$ Здесь принимают, что $d v=P_{n}(x) d x$, а в качестве $u$ оставшиеся сомножители. Пример Задание. Найти интеграл $\int \ln x d x$ Решение. В исходном интеграле выделим функции $u$ и $v$, затем выполним интегрирование по частям. $$\int \ln x d x\left\|\begin{array}{l} u=\ln x \quad d v=d x \\ d u=\frac{d x}{x} \quad v=x \end{array} \quad\right\|=x \ln x-\int x \cdot \frac{d x}{x}=$$$=x \ln x-\int d x=x \ln x-x+C=x(\ln x-1)+C$ Ответ. $\int \ln x d x=x(\ln x-1)+C$ Больше примеров решений Решение интегралов онлайнПример Задание. Найти интеграл $\int \arcsin x d x$ Решение. В исходном интеграле выделим функции
$u$ и
$v$, затем выполним интегрирование по частям. Читать дальше: простейшие дроби. Страница не найдена — ПриМат© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Юлия Стерлянко (8), Денис Стехун (8), Елизавета Савицкая (8), Игорь Любинский (8), Олег Шпинарев (7), Александр Базан (7), Валентин Малявко (7), Анна Чалапчий (7), Константин Берков (7), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Кирилл Волков (6), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Обзор методов вычисления интегралов по времени и пространствуИнтегрирование — один из важнейших математических инструментов, особенно в численном моделировании. Важность интеграловВ COMSOL используется метод конечных элементов, который преобразует описывающее некоторый процесс уравнение в частных производных в интегральное уравнение — другими словами, в слабую форму (weak form). При детальном и глубоком изучении формулировок, используемых в интерфейсах COMSOL, вы обнаружите, что множество граничных условий реализованы через интегралы. В качестве наиболее характерных примеров можно привести условия Total heat flux (Общий тепловой поток) или Floating potential (Плавающий потенциал). Вычисление интегралов также играет ключевую роль в процессе постобработки результатов, поскольку COMSOL рассчитывает большое количество вспомогательных величин через интегралы, например энергию электрического поля, скорость потока или общий тепловой поток. где [t_0,t_1] — это временной интервал, \Omega — это пространственная область, а F(u) — это произвольное выражение, включающее зависимую переменную u и произвольные функции от нее, в том числе производные по пространству, времени, а также любой другой величине. Наиболее удобный способ вычисления интегралов — использование узла Derived Values (Расчет выражений) в разделе Results (Результаты) ленты Ribbon или дерева модели (Лента Ribbon отсутствует в том случае, если ваш компьютер работает не под управлением ОС Windows®). Вы можете обратиться к любому доступному решению, выбрав соответствующий набор данных (data set). В поле Expression (Выражение) вводится подынтегральная функция, включающая зависимые или производные переменные. Для данных расчета во временной области пространственный интеграл вычисляется на каждом временном шаге. Оператор Average (Усреднение) — еще одна операция в разделе Derived Values, связанная с вычислением интегралов. Оператор вычисляет интеграл и делит его на объем, площадь или длину выбранной области. Операция Averageв узле Data Series Operations аналогично вводит деление на продолжительность временного диапазона. Операторы узла Derived Values — важный инструмент, однако их можно использовать только во время постобработки, а значит с их помощью можно рассчитать далеко не любой интеграл. Именно поэтому в COMSOL представлены другие более мощные и гибкие инструменты для вычисления интегралов. Стационарное решение, нажмите на изображение для увеличения. Нестационарное решение (для момента времени 100 секунд), нажмите на изображение для увеличения. Вычисление пространственного интеграла с использованием операторов узла Component CouplingОператоры узла Component Coupling (Сопряжение компонентов) используются в тех случаях, когда, например, в одном выражении объединяются несколько интегралов, или интегралы требуются в процессе вычислений, или требуется множество контурных интегралов. Операторы данного узла определяются в разделе Definitions (Определения). На этом этапе режультат использования оператора не просчитывается, а указываются только их название и выборки областей.
В нашем примере мы для начала хотим вычислить пространственный интеграл для стационарного распределения температуры, равный \int_{\Omega}T(x,y)\ \mathrm{d}x\mathrm{d}y = 301. В пакете COMSOL оператор вычисления интеграла по умолчанию получает имя intop1. Окно настроек оператора интегрирования. Расчет результата интегрирования через оператор. Теперь давайте рассмотрим, как оператор интегрирования может использоваться непосредственно в процессе расчета модели. С его помощью мы могли бы, например, выяснить, какая нагревательная мощность потребуется для получения средней температуры 303.15 К, то есть температуры, на 10 К превышающей температуру окружающей среды. Прежде всего нам необходимо вычислить разницу между требуемым и действительным средними значениями. Среднее значение вычисляется путем деления интеграла от T на интеграл от постоянной функции 1, который равен площади области. Нетрудно догадаться, что вычисление подобного вида легко выполнить с помощью представленного в COMSOL оператора Average (Усреднение), см. комментарии выше. По умолчанию данный оператор получает название aveop1. Вычисление неопределенного интеграла посредством оператора интегрированияВ своих обращениях в службу поддержки пользователи часто задают один и тот же вопрос: как рассчитать неопределенный пространственный интеграл? Для этой цели нам также пригодится оператор интегрирования, задаваемый через Component Couplings. Нахождение неопределенного интеграла — операция, обратная дифференцированию. Неопределенный интеграл позволяет вычислять площади произвольных областей, ограниченных графиками функций. Одна из самых важных прикладных задач — вычисление вероятностей в статистическом анализе. Для того чтобы это продемонстрировать, мы зафиксируем y=0 и обозначим неопределенный интеграл от T(x,0) как u(x). Это значит, что \frac{\partial u}{\partial x}=T(x,0). Тогда неопределенный интеграл имеет вид u(\bar x) = \int_0^{\bar x}T(x,0)\mathrm{d} x Здесь мы используем \bar x, чтобы отличать переменную интегрирования от внешней переменной. Во-вторых, нам понадобится оператор вычисления интеграла, который будет действовать на нижней границе области из примера. Давайте обозначим его как intop2. В-третьих, мы должны отличать переменную интегрирования от внешней переменной. Принятые обозначения для такого случая: x называется источником (source), а \bar x — точкой назначения (destination). При использовании операторов интегрирования доступен встроенный оператор dest, который позволяет явно оглашать, что соответствующее выражение не относится к переменным интегрирования. Точнее, это значит, что в COMSOL \bar x=dest(x). Объединив логическое выражение с оператором dest, мы получим выражение вида T*(x<=dest(x)), которое является именно тем входным выражением, которое требуется для intop2. Объединив все вместе, мы можем вычислить неопределенный интеграл, воспользовавшись выражением intop2(T*(x<=dest(x))).
В пакете COMSOL дополнительно доступны еще два оператора вычисления интеграла, а именно общая проекция (general projection) и линейная проекция (linear projection). Эти операторы можно использовать для получения множества контурных интегралов в любом направлении в области. Другими словами, вычисление интеграла производится только вдоль одного измерения. В результате мы получаем функцию размерности на единицу меньше, чем размерность области. Для двухмерного примера результатом будет одномерная функция, которая может быть рассчитана на любой границе. Более подробная информация об использовании данных операторов будет представлена в одной из следующих публикаций в нашем компоративном блоге. Вычисление пространственного интеграла посредством дополнительного физического интерфейсаНаиболее гибким способом вычисления пространственных интегралов является техника с добавлением дополнительного PDE-интерфейса. \frac{\partial u}{\partial x}=T(x,y) с граничным условием типа Дирихле u=0 на левой границе. Расчет такого уравнения проще всего реализовать в физическом (математическом) интерфейсе Coefficient Form PDE (Дифференциальное уравнение в частных производных, коэффициентная форма записи), который потребует следующих настроек:
Зависимая переменная u представляет собой неопределенный интеграл по x и доступна в процессе расчета модели и в постобработке. Помимо гибкости, дополнительным преимуществом данного подхода является точность, так как интеграл рассчитывается не вспомогательными инструментами на основе уже определенного распределения переменной, а непосредственно в процессе расчета с учетом алгоритмов оценки погрешностей и т. На поверхностном графике ниже представлен результирующий интеграл, являющийся функцией пространственных переменных (x,y):
Схожие операторы существуют для вычисления интегралов на сферических зонах, а именно ballint, circint, diskint и sphint. Вычисление временного интеграла посредством дополнительного физического интерфейсаВ случае если временные интегралы нужно использовать непосредственно в модели в процессе расчета, вам будет необходимо задать их как дополнительные зависимые переменные. Аналогично представленному выше примеру с интерфейсом Coefficient Form PDE, это можно сделать, добавив ODE-интерфейс из раздела Mathematics. Предположим, например, что на каждом временном шаге требуется вычислять интеграл от величины общего теплового потока на промежутке от старта до текущего момента, который показывает накопленную энергию.
В чем польза подобной техники? Полученный интеграл можно повторно использовать в других физических интерфейсах, поля в которых могут зависеть от накопленной в системе энергии. Более того, полученный резултат будет мгноменно доступен для всех видов постобработки, что удобнее и быстрее, чем использование встроенных операторов. Рекомендуем ознакомится с моделью Carbon Deposition in Hetereogeneous Catalysis (Образование сажевых отложений при гетерогенном катализе), в которой ОДЕ в области используется для вычисления пористости катализатора при наличии химических реакций в виде нестационарной полевой переменной. Вычисление интеграла от аналитических функций и выраженийДо сих пор мы демонстрировали, каким образом вычислять интеграл от искомых переменных в процессе расчета или при постобработке. Но не касались случая взятия интегралов от аналитических функций или выражений. Для этой операции в среде COMSOL доступен встроенный оператор integrate(expression, integration variable, lower bound, upper bound). Выражение может представлять собой любую одномерную функцию, например sin(x). При этом допускается включение дополнительных переменных, например sin(x*y). Второй параметр определяет, по какой переменной вычисляется интеграл. Например, integrate(sin(x*y),y,0,1) выдает функцию переменной x, потому что интегрирование выполняется только по переменной y. Обратите внимание, что данный оператор также может использоваться для работы с аналитическими функциями, заданными в узле Definitions (Определения) текущего компонента. Добавление аналитической функции. Вычисление интеграла от аналитической функции. Материалы для дальнейшего изученияПравила интеграцииИнтеграцияIntegration можно использовать для поиска областей, объемов, центральных точек и многих полезных вещей. Он часто используется для поиска области под графиком функции и осью x . Первое правило, которое необходимо знать, — интегралы и производные противоположны! Правила интеграцииВот наиболее полезные правила с примерами ниже:
ПримерыПример: какой интеграл от sin (x)?Из приведенной выше таблицы это указано как −cos (x) + C Записывается как: ∫sin (x) dx = −cos (x) + C Пример: каков интеграл от 1 / x?Из приведенной выше таблицы это указано как ln | x | + C Записывается как: ∫ (1 / x) dx = ln | x | + C Вертикальные стержни || по обе стороны от x означает абсолютное значение, потому что мы не хотим давать отрицательные значения функции натурального логарифма ln . Правило мощностиПример: Что такое ∫x3 dx?Возникает вопрос: «Что такое интеграл x 3 ?» Мы можем использовать правило мощности, где n = 3: ∫x n dx = x n + 1 n + 1 + C ∫x 3 dx = x 4 4 + C Пример: Что такое ∫√x dx? √x также равно x 0. Мы можем использовать правило мощности, где n = 0,5: ∫x n dx = x n + 1 n + 1 + C ∫x 0,5 dx = x 1,5 1,5 + C Умножение на константуПример: Что такое ∫6x2 dx?Мы можем переместить 6 за пределы интеграла: ∫6x 2 dx = 6∫x 2 dx А теперь используйте правило мощности на x 2 : = 6 x 3 3 + C Упростить: = 2x 3 + C Правило суммыПример: Что такое ∫ (cos x + x) dx?Используйте правило суммы: ∫ (cos x + x) dx = cos x dx + ∫x dx Определите интеграл каждого (используя таблицу выше): = грех х + х 2 /2 + С Правило разницыПример: Что такое ∫ (ew — 3) dw?Используйте правило разницы: ∫ (e w -3) dw = ∫e w dw — ∫3 dw Затем вычислите интеграл каждого (используя таблицу выше): = e Вт — 3 Вт + C Правила суммы, разности, постоянного умножения и мощностиПример: Что такое ∫ (8z + 4z3 — 6z 2 ) dz?Используйте правило суммы и разности: ∫ (8z + 4z 3 — 6z 2 ) dz = ∫8z dz + ∫4z 3 dz — ∫6z 2 dz Постоянное умножение: = 8∫z dz + 4∫z 3 dz — 6∫z 2 dz Правило мощности: = 8z 2 /2 + 4z 4 /4 — 6z 3 /3 + C Упростить: = 4z 2 + z 4 — 2z 3 + C Интеграция по частям См. Правило замещенияСм. Интеграцию заменой Заключительный совет
6834, 6835, 6836, 6837, 6838, 6839, 6840, 6841, 6842, 6843 Calculus II — Интеграция по частямПоказать уведомление для мобильных устройств Показать все заметки Скрыть все заметки Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, разговариваете по мобильному телефону). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы сможете прокручивать их, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана. Левая часть достаточно проста для интегрирования (мы знаем, что интегрирование производной просто «отменяет» производную), и мы разделим правую часть интеграла. \ [fg = \ int {{f ‘\, g \, dx}} + \ int {{f \, g’ \, dx}} \]Обратите внимание, что технически у нас должна была отображаться константа интегрирования слева после выполнения интегрирования. Мы можем отбросить его на этом этапе, поскольку другие константы интеграции будут отображаться в будущем, и они просто поглотят эту. Наконец, перепишите формулу следующим образом, и мы придем к формуле интегрирования по частям. \ [\ int {{f \, g ‘\, dx}} = fg — \ int {{f’ \, g \, dx}} \] Однако это не самая простая формула. Итак, сделаем пару замен. \ [\ begin {align *} u = f \ left (x \ right) \ hspace {0. 5in} v = g \ left (x \ right) \\ & du = f ‘\ left (x \ right) \, dx \ hspace {0,5 дюйма} dv = g ‘\ left (x \ right) \, dx \ end {align *} \] 5in} v = g \ left (x \ right) \\ & du = f ‘\ left (x \ right) \, dx \ hspace {0,5 дюйма} dv = g ‘\ left (x \ right) \, dx \ end {align *} \]Обе из них — стандартные замены Calculus I, к которым, надеюсь, вы уже привыкли.Не радуйтесь тому факту, что мы используем здесь две замены. Они будут работать так же. Использование этих замен дает нам формулу, которую большинство людей считают формулой интегрирования по частям. Интеграция по частям\ [\ int {{u \, dv}} = uv — \ int {{v \, du}} \] Чтобы использовать эту формулу, нам нужно будет идентифицировать \ (u \) и \ (dv \), вычислить \ (du \) и \ (v \), а затем использовать формулу. Также обратите внимание, что вычислить \ (v \) очень просто.Все, что нам нужно сделать, это интегрировать \ (dv \). \ [v = \ int {{dv}} \] Одна из самых сложных вещей при использовании этой формулы — это то, что вам необходимо правильно идентифицировать как \ (u \), так и \ (dv \). Это приводит к очевидному вопросу: как узнать, правильно ли мы сделали выбор для \ (u \) и \ (dv \)? Ответ на самом деле довольно прост.{6x}} \, dx}} \] Показать решение Итак, на некотором уровне проблема здесь в \ (x \), стоящем перед экспонентой. Если бы этого не было, мы могли бы выполнить интеграл. Также обратите внимание, что при выполнении интеграции по частям все, что мы выбираем для \ (u \), будет дифференцироваться. Таким образом, кажется, что выбор \ (u = x \) будет хорошим выбором, поскольку при дифференцировании \ (x \) выпадет. Теперь, когда мы выбрали \ (u \), мы знаем, что \ (dv \) будет всем остальным, что останется.{6x}} + c \ end {align *} \] После того, как мы выполнили последний интеграл в задаче, мы добавим константу интегрирования, чтобы получить окончательный ответ. Также обратите внимание, что, как отмечалось выше, мы знаем, что сделали правильный выбор для \ (u \) и \ (dv \), когда получили новый интеграл, который мы фактически вычисляем после применения формулы интегрирования по частям. Теперь давайте посмотрим на интегрирование по частям для определенных интегралов.b \) в первом члене — это просто стандартное обозначение интегральной оценки, с которым вы должны быть знакомы на этом этапе. Все, что мы делаем, это оцениваем член, в данном случае uv , в \ (b \), а затем вычитаем оценку члена в \ (a \). На каком-то уровне нам здесь действительно не нужна формула, потому что мы знаем, что при вычислении определенных интегралов все, что нам нужно сделать, это вычислить неопределенный интеграл, а затем выполнить вычисление. На самом деле, это, вероятно, будет немного проще, поскольку нам не нужно отслеживать таким образом оценку каждого термина.{- 6}} \ end {align *} \] Любой из методов вычисления определенных интегралов с интегрированием по частям довольно прост, так что какой вариант вы решите использовать, в значительной степени зависит от вас. Так как нам нужно иметь возможность вычислить неопределенный интеграл, чтобы вычислить определенный интеграл, а выполнение определенного интеграла сводится к не более чем вычислению неопределенного интеграла в паре точек, мы сконцентрируемся на вычислении неопределенных интегралов в остальной части этого раздел.Фактически, на протяжении большей части этой главы так и будет. Мы будем делать гораздо больше неопределенных интегралов, чем определенных интегралов. Давайте взглянем еще на несколько примеров. Пример 3 Вычислите следующий интеграл. \ [\ int {{\ left ({3t + 5} \ right) \ cos \ left ({\ frac {t} {4}} \ right) \, dt}} \] Показать решениеЕсть два способа продолжить этот пример. Для многих первое, что они пробуют, — это умножить косинус на скобки, разделить интеграл и затем выполнить интегрирование по частям для первого интеграла. Хотя это вполне приемлемый способ решения проблемы, это больше работы, чем нам действительно нужно. Тогда интеграл равен . \ [\ begin {align *} \ int {{\ left ({3t + 5} \ right) \ cos \ left ({\ frac {t} {4}} \ right) \, dt}} & = 4 \ left ({3t + 5} \ right) \ sin \ left ({\ frac {t} {4}} \ right) — 12 \ int {{\ sin \ left ({\ frac {t} {4}} \ right) \, dt}} \\ & = 4 \ left ({3t + 5} \ right) \ sin \ left ({\ frac {t} {4}} \ right) + 48 \ cos \ left ({\ frac {t} {4}} \ right) + c \ end {align *} \]Обратите внимание, что мы вытащили все константы из интеграла, когда использовали формулу интегрирования по частям.2}}} {{10}} \ cos \ left ({10w} \ right) + \ frac {1} {5} \ int {{w \ cos \ left ({10w} \ right) \, dw}} \] В этом примере, в отличие от предыдущих примеров, новый интеграл также потребует интегрирования по частям. Будьте осторожны с коэффициентом интеграла для второго применения интегрирования по частям.Поскольку интеграл умножается на \ (\ frac {1} {5} \), нам нужно убедиться, что результаты фактического выполнения интеграла также умножаются на \ (\ frac {1} {5} \). Забыть об этом — одна из наиболее распространенных ошибок при интеграции по частям. Как показал этот последний пример, иногда нам потребуется несколько приложений интегрирования по частям, чтобы полностью оценить интеграл. Это то, что произойдет, поэтому не волнуйтесь, когда это произойдет. В следующем примере нам нужно признать важный момент, касающийся методов интеграции. Некоторые интегралы могут быть получены с использованием нескольких различных методов. Так обстоит дело с интегралом в следующем примере.
Сначала обратите внимание, что в этом интеграле нет триггерных функций или экспонент. Хотя довольно много интегралов по частям будет включать триггерные функции и / или экспоненты, не все из них будут слишком зациклены на идее ожидания их появления. В этом случае мы будем использовать следующие варианты для \ (u \) и \ (dv \). \ [\ begin {align *} u & = x & \ hspace {0,5 дюйма} dv & = \ sqrt {x + 1} \, dx \\ du & = dx & \ hspace {0.{\ frac {5} {2}}} + c \ end {align *} \]b Используя стандартную замену Calculus I. Показать решение Теперь займемся интегралом с заменой. Итак, в этом примере мы использовали два разных метода интеграции и получили два разных ответа.Тогда возникает очевидный вопрос: мы сделали что-то не так? На самом деле, мы не сделали ничего плохого. Нам необходимо помнить следующий факт из исчисления I. \ [{\ rm {If}} \, \, f ‘\ left (x \ right) = g’ \ left (x \ right) \, \, \, {\ rm {then}} \, \, \ , е \ влево (х \ вправо) = г \ влево (х \ вправо) + с \]Другими словами, если две функции имеют одинаковую производную, то они будут отличаться не более чем на константу. Итак, как это применимо к указанной выше проблеме? Сначала определите следующее: \ [f ‘\ left (x \ right) = g’ \ left (x \ right) = x \ sqrt {x + 1} \]Затем мы можем вычислить \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) путем интегрирования следующим образом: \ [е \ left (x \ right) = \ int {{f ‘\ left (x \ right) \, dx}} \ hspace {0. 5in} g \ left (x \ right) = \ int {{g ‘\ left (x \ right) \, dx}} \] 5in} g \ left (x \ right) = \ int {{g ‘\ left (x \ right) \, dx}} \]Мы будем использовать интегрирование по частям для первого интеграла и замену для второго интеграла. Тогда согласно тому, что \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) должны отличаться не более чем на константу. Давайте проверим это и посмотрим, так ли это. Мы можем убедиться, что они различаются не более чем на константу, если мы посмотрим на разницу между ними и сделаем небольшие алгебраические манипуляции и упрощения.{\ frac {3} {2}}} \ left (0 \ right) \\ \ hspace {2.0in} = 0 \ end {array} \] Итак, в этом случае оказывается, что две функции — это одна и та же функция, поскольку разница равна нулю. Учтите, что это происходит не всегда. Иногда разница дает ненулевую константу. Пример этого можно найти в разделе «Константа интеграции» в примечаниях к исчислению I. Итак, что мы узнали? Во-первых, иногда будет несколько методов вычисления интеграла.Во-вторых, мы увидели, что разные методы часто приводят к разным ответам. Когда мы сталкиваемся с интегралом, первое, что нам нужно решить, — это то, есть ли более одного способа сделать интеграл. Если существует несколько способов, нам нужно будет определить, какой из них следует использовать. Общее практическое правило, которое я использую в своих классах, заключается в том, что вы должны использовать метод, который вы считаете наиболее простым.Возможно, это не самый простой способ, но это не значит, что это неправильный метод. Одна из наиболее распространенных ошибок интеграции по частям — это слишком сильная привязанность людей к воспринимаемым шаблонам. Например, во всех предыдущих примерах использовался базовый шаблон, согласно которому \ (u \) был полиномом, стоящим перед другой функцией, а затем позволял \ (dv \) быть другой функцией. Это не всегда будет происходить, поэтому нам нужно быть осторожными и не связываться с какими-либо шаблонами, которые, как нам кажется, мы видим. Давайте взглянем на некоторые интегралы, которые не вписываются в приведенный выше шаблон. Пример 6 Вычислите следующий интеграл. \ [\ int {{\ ln x \, dx}} \] Показать решениеИтак, в отличие от любого другого интеграла, который мы сделали до этого момента, в интеграле есть только одна функция и нет полинома перед логарифмом. Первый выбор многих здесь — попытаться вписать это в шаблон сверху и сделать следующие выборы для \ (u \) и \ (dv \). \ [u = 1 \ hspace {0,5 дюйма} dv = \ ln x \, dx \]Однако это приводит к реальной проблеме, поскольку это означает, что \ (v \) должно быть, \ [v = \ int {{\ ln x \, dx}} \]Другими словами, нам нужно знать ответ заранее, чтобы решить проблему. Так что этот выбор просто не сработает. Следовательно, если логарифм не принадлежит \ (dv \), он должен принадлежать \ (u \). Тогда интеграл равен . \ [\ begin {align *} \ int {{\ ln x \, dx}} & = x \ ln x — \ int {{\ frac {1} {x} \, x \, dx}} \\ & = x \ ln x — \ int {{dx}} \\ & = x \ ln x — x + c \ end {align *} \] Пример 7 Вычислите следующий интеграл.{\ frac {5} {2}}} + c \ end {align *} \]Итак, в двух предыдущих примерах мы видели случаи, которые не совсем вписывались в какой-либо воспринимаемый шаблон, который мы могли бы получить из первых двух примеров. Это всегда то, к чему мы должны обращать внимание при интеграции по частям. Давайте взглянем на другой пример, который также иллюстрирует другой метод интеграции, который иногда возникает из-за проблем интеграции по частям. Хорошо, до сих пор мы всегда выбирали \ (u \) таким образом, чтобы при дифференцировании эта часть уходила или, по крайней мере, превращалась в интеграл в форму, которая упростила бы работу с . В этом случае, какую бы часть мы ни делали \ (u \), она никогда не уйдет в процессе дифференцирования. Не имеет большого значения, какой мы выбираем \ (u \), поэтому мы выберем следующий способ.\ theta} \ sin \ theta} \ right) + c \] Обратите внимание, что после деления на два мы добавляем постоянную интегрирования в этой точке. Эту идею интегрирования до тех пор, пока вы не получите одинаковый интеграл по обе стороны от знака равенства, а затем простое решение для интеграла, неплохо запомнить. Это не так уж и часто, но когда это происходит, это может быть единственный способ на самом деле выполнить интеграл. Также обратите внимание, что это на самом деле просто алгебра, по общему признанию, сделанная таким образом, что вы, возможно, не привыкли к этому, но на самом деле это просто алгебра. На данном этапе вашей математической карьеры каждый может решить, \ [x = 3 — x \ hspace {0,5 дюйма} \ to \ hspace {0,5 дюйма} x = \ frac {3} {2} \]Мы все еще решаем «уравнение». Единственное отличие состоит в том, что вместо решения для \ (x \) в мы решаем для интеграла, и вместо хорошей константы «3» в приведенной выше задаче алгебры мы получили функцию «беспорядка». У нас есть еще один пример. Как мы увидим, некоторые проблемы могут потребовать от нас выполнять интеграцию по частям много раз, и существует короткий метод, который позволит нам быстро и легко выполнять несколько приложений интеграции по частям.{\ frac {x} {2}}} \, dx}} \] Показать решение Мы начинаем с выбора \ (u \) и \ (dv \), как всегда. Мы получили интеграл. Это намного проще, чем записывать все различные \ (u \) и \ (dv \), которые нам пришлось бы делать в противном случае. Итак, в этом разделе мы увидели, как выполнять интеграцию по частям. На более поздних уроках математики это, вероятно, будет одним из наиболее частых методов интеграции, с которыми вы столкнетесь. Важно не зацикливаться на шаблонах, которые, как вам кажется, вы уже видели.В большинстве случаев любой шаблон, который, как вы думаете, вы видели, может (и будет) нарушен в какой-то момент времени. Интегрируйте функцию с программой «Пошаговое решение математических задач» Первообразные Три примера проблем, возникающих в различных контекстах:
следующее: найти функцию затрат C (x), если известны предельные затраты C ‘(x); найти
популяция P (t) биологической колонии, если скорость P ‘(r), с которой
популяция меняется, как известно; найти смещение s (t) объекта при
время t, если известна скорость v (t) = s ‘(r). и фактически для любого числа a, Определение В нашем вводном примере каждая из функций затрат x 2 , x 2 + 1, а x 2 + 10 является первообразной f (x) = 2x; кроме того, C (x) = x 2 + a является первообразной f (x) = 2x для любого выбора a. В В общем, если g (x) является первообразной f (x), то же самое и g (x) + a для любого номер а, начиная с Можно доказать следующий, даже более сильный результат: Если g является любой первообразной от f, то каждая другая первообразная должна иметь
форма g (x) + a для некоторого числа a. Немецкий математик Готфрид Вильгельм Лейбниц (1646-1716) ввел обозначение (читается как «первообразная от f» или «неопределенный интеграл от f»)
представляют собой наиболее общую первообразную f. Таким образом, если g — любая первообразная
f, то для любого числа a. Вкратце: Пример 1
Пример 2 Пример 3 Число a, возникающее при антидифференцировании, часто называют «произвольным».
постоянный «. (По причинам, которые станут очевидными позже, его также называют
«константа интегрирования»). В наших примерах мы использовали букву a для
обозначают эту константу, но на практике обычно используется c.(Мы использовали букву a вместо c для нашей первоначальной иллюстрации, включающей стоимость, поскольку c
использовался для обозначения стоимости. Пример 4 Предположим, что на начальных этапах производства предельные затраты до произвести товар стоит C ‘(x) = 2x доллара за единицу. На этот раз предположим, что производитель также знает, что фиксированная стоимость производства C (0) составляет 500 долларов.Находить соответствующая функция стоимости C (x). Мы уже видели, что любая функция затрат для этих предельных затрат должна иметь форма C (x) = x 2 + a для некоторой постоянной a. С С (0) = 500 = 0 2 + а = а, мы имеем a = 500. Таким образом, функция стоимости определяется как C (x) = x 2 + 500 Из этого примера мы видим, что произвольная константа c является фиксированной стоимостью
производство. Зная только предельную стоимость, мы не можем сказать, что это за фиксированная стоимость.
является; фиксированная стоимость — дополнительная информация. C (x) = x 2 + (фиксированная стоимость). Следующие два результата очень полезны при оценке первообразных. Здесь n обозначает действительное число, а c — постоянная интегрирования. Обратите внимание, что Правило (2) выполняется для n! = — 1, а Правило (3) распространяется на случай, когда n = -1. Для проверки правила (2) воспользуемся определением (1) следующим образом: Чтобы проверить Правило (3), вспомните, что Пример 5 Используйте правило (2) для оценки каждого первообразного: методов интеграции | Безграничное исчислениеОсновные принципы интеграцииИнтегрирование — это процесс поиска области, ограниченной функцией; этот процесс использует несколько важных свойств. Цели обученияПрименение основных принципов интеграции к интегральным задачам Основные выводыКлючевые моменты
Тригонометрическая заменаТригонометрические функции могут быть заменены другими выражениями, чтобы изменить форму подынтегральных выражений и упростить интегрирование. Цели обученияИспользуйте тригонометрическую замену для решения интеграла Основные выводыКлючевые моменты
Ключевые термины
Тригонометрические функции могут быть заменены другими выражениями, чтобы изменить форму подынтегральных выражений. Можно использовать тригонометрические тождества для упрощения некоторых интегралов, содержащих радикальные выражения (или выражения, содержащие корни [latex] n [/ latex] th).2 (\ theta)}} \\ & = \ int \ frac {d \ theta} {a} \\ & = \ frac {\ theta} {a} + C \\ & = \ frac {1} {a} \ arctan \ left (\ frac {x} {a} \ right) + C \ end {align} [/ latex] Метод частичных дробейРазложение на частичные дроби обеспечивает подход к интеграции общей рациональной функции. Цели обученияИспользовать частичное дробное разложение для интегрирования рациональных функций Основные выводыКлючевые моменты
Разложение на частичные дроби обеспечивает подход к интеграции общей рациональной функции. Любую рациональную функцию действительной переменной можно записать как сумму многочлена и конечного числа рациональных дробей, знаменателем которых является степень неприводимого многочлена, а числитель имеет степень ниже, чем степень этого неприводимого многочлена. Вот несколько общих примеров. Многочлен 1-й степени в знаменателеЗамена [latex] u = ax + b [/ latex], [latex] du = a \, dx [/ latex] уменьшает интеграл [latex] \ int {1 \ over ax + b} \, dx [/ латекс] к: [латекс] \ begin {align} \ int {1 \ over u} \, {du \ over a} & = {1 \ over a} \ int {du \ over u} \\ & = {1 \ over a } \ ln \ left | u \ right | + C \\ & = {1 \ over a} \ ln \ left | ax + b \ right | + C \ end {align} [/ latex] Повторяющийся многочлен 1-й степени в знаменателеТа же самая замена уменьшает такие интегралы, как [latex] \ int {1 \ over (ax + b) ^ 8} \, dx [/ latex], до [латекс] \ begin {align} \ int {1 \ over u ^ 8} \, {du \ over a} & = {1 \ over a} \ int u ^ {- 8} \, du \\ & = {1 \ over a} \ cdot {u ^ {- 7} \ over (-7)} + C \\ & = {-1 \ over 7au ^ 7} + C \\ & = {-1 \ over 7a ( ах + b) ^ 7} + C \ end {align} [/ latex] Неприводимый многочлен 2-й степени в знаменателеДалее мы рассматриваем такие интегралы, как [латекс] \ displaystyle {\ int {x + 6 \ over x ^ 2-8x + 25} \, dx} [/ latex] Самый быстрый способ увидеть, что знаменатель, [латекс] x ^ 2 — 8x + 25 [/ latex], несократим, — это заметить, что его дискриминант отрицательный. Интеграция с использованием таблиц и компьютеровДля интегрирования обычно используются таблицы известных интегралов или компьютерных программ. Цели обученияОпределить, какие интегралы следует решать с помощью таблиц или компьютеров в силу их сложности Основные выводыКлючевые моменты
Ключевые термины
Интегрирование — основная операция в интегральном исчислении. Интеграция с использованием таблицСборник списка интегралов и методов интегрального исчисления был опубликован немецким математиком Мейером Хиршем еще в 1810 году. Более обширные таблицы были составлены в 1858 году голландским математиком Давидом де Биренс де Хааном.Новое издание вышло в 1862 году. Эти таблицы, содержащие в основном интегралы от элементарных функций, использовались до середины 20 века. Затем их заменили гораздо более обширные таблицы Градштейна и Рыжика. Вот несколько примеров интегралов в этих таблицах для логарифмических функций: [латекс] \ int \ ln ax \; dx = x \ ln ax — x [/ латекс] [латекс] \ displaystyle {\ int \ ln (ax + b) \; dx = \ frac {(ax + b) \ ln (ax + b) — ax} {a}} [/ латекс] [латекс] \ int (\ ln x) ^ 2 \; dx = x (\ ln x) ^ 2 — 2x \ ln x + 2x [/ латекс] [латекс] \ Displaystyle {\ int (\ пер х) ^ п \; dx = x \ sum ^ {n} _ {k = 0} (- 1) ^ {n-k} \ frac {n!} {k! } (\ ln x) ^ k} [/ латекс] [латекс] \ Displaystyle {\ int \ frac {dx} {\ ln x} = \ ln \ left | \ ln x \ right | + \ ln x + \ sum ^ \ infty_ {k = 2} \ frac {(\ ln x) ^ k} {k \ cdot k! }} [/ latex] [латекс] \ Displaystyle {\ int \ frac {dx} {(\ ln x) ^ n} = — \ frac {x} {(n-1) (\ ln x) ^ {n-1}} + \ frac {1} {n-1} \ int \ frac {dx} {(\ ln x) ^ {n-1}} \ qquad \ mbox {(для} n \ neq 1 \ mbox {)}} [/ латекс ] Вы, конечно, видите, что эти интегралы сложно сделать просто «вручную». Интеграция с использованием компьютеровКомпьютеры могут использоваться для интеграции двумя основными способами. Во-первых, численные методы с использованием компьютеров могут быть полезны при вычислении определенного интеграла. Есть много методов и алгоритмов. Мы вкратце узнаем о численном интегрировании в другом атоме. Во-вторых, существует несколько коммерческих программ, таких как Mathematica или Matlab, которые могут выполнять символьную интеграцию. Интеграция : Численное интегрирование заключается в нахождении численных приближений для значения [латекс] S [/ латекс].{b} f (x) \, dx = \ frac {ba} {2N} (f (x_1) + 2f (x_2) + 2f (x_3) + \ ldots + 2f (x_N) + f (x_ {N + 1) }))[/латекс]. Ключевые термины
Численное интегрирование, в некоторых случаях также известное как числовая квадратура, требует значения определенного интеграла. Правило трапеции имеет тенденцию становиться чрезвычайно точным, когда периодические функции интегрированы по их периодам. Аппроксимация линейными функциями : Функция [латекс] f (x) [/ latex] (синим цветом) аппроксимируется линейной функцией (красным цветом). Числовая реализация правила трапецииДля домена, дискретизированного на [латекс] N [/ латекс] равномерно разнесенные панели или [латекс] N + 1 [/ латекс] точки сетки [латекс] (1, 2, \ cdots, N + 1) [/ latex] , где шаг сетки равен [latex] h = \ frac {(ba)} {N} [/ latex], аппроксимация интеграла принимает следующий вид: [латекс] \ begin {align} \ int_ {a} ^ {b} f (x) \, dx & \ приблизительно \ frac {h} {2} \ sum_ {k = 1} ^ {N} \ left ( f (x_ {k + 1}) + f (x_ {k}) \ right) {} \\ & = \ frac {ba} {2N} (f (x_1) + 2f (x_2) + \ cdots + 2f ( x_N) + f (x_ {N + 1})) \ end {align} [/ latex] Хотя в этом методе также может использоваться неоднородная сетка, в этом примере для аппроксимации использовалась равномерная сетка. Ключевые термины
Несоответствующий интеграл — это предел определенного интеграла, когда конечная точка интервала (ов) интегрирования приближается либо к заданному действительному числу, либо к [latex] \ infty [/ latex] или [latex] — \ infty [/ latex] или , в некоторых случаях, когда обе конечные точки приближаются к пределам. , в котором устанавливается ограничение на одной или другой конечной точке (а иногда и на обеих). Несобственный интеграл второго рода : Несобственный интеграл Римана второго рода. Интеграл может не существовать из-за вертикальной асимптоты функции. Интегралы также являются неправильными, если подынтегральное выражение не определено во внутренней точке области интегрирования или в нескольких таких точках. Часто необходимо использовать несобственные интегралы, чтобы вычислить значение интегралов, которые могут не существовать в обычном смысле (например, интеграл Римана) из-за сингулярности функции или бесконечной конечной точки области интегрирования. .2} \, \ mathrm {d} x \\ & = \ lim_ {b \ to \ infty} \ left (- \ frac {1} {b} + \ frac {1} {1} \ right) \\ & = 1 \ end {align} [/ latex] Пример 2 Узкое определение интеграла Римана также не распространяется на функцию [latex] \ frac {1} {\ sqrt {x}} [/ latex] на интервале [latex] [0, 1] [/ latex]. Численное интегрированиеЧисленное интегрирование представляет собой широкое семейство алгоритмов для вычисления числового значения определенного интеграла.б \! f (x) \, dx [/ латекс]. Ключевые термины
Численное интегрирование представляет собой широкое семейство алгоритмов для вычисления числового значения определенного интеграла, и, в более широком смысле, этот термин также иногда используется для описания численного решения дифференциальных уравнений. Методы одномерных интеграловБольшой класс квадратурных правил может быть получен путем построения интерполирующих функций, которые легко интегрировать.б е (х) \, дх \ приблизительно (б-а) \, е \ влево (\ гидроразрыв {а + б} {2} \ вправо)} [/ латекс] Правило прямоугольника : Иллюстрация правила прямоугольника. Интерполирующая функция может быть аффинной функцией (полиномом степени 1), проходящей через точки [latex] (a, f (a)) [/ latex] и [latex] (b, f (b)) [/ латекс]. Это называется правилом трапеции. Линия трапеции : Иллюстрация линейки трапеции. Для любого из этих правил мы можем сделать более точное приближение, разбив интервал [latex] [a, b] [/ latex] на некоторое количество [latex] n [/ latex] подинтервалов, вычислив приближение для каждый подынтервал, затем складываются все результаты.{n-1} \ left (f \ left (a + k \ frac {b-a} {n} \ right) \ right) + {f (b) \ over 2} \ right)} [/ латекс] , где подынтервалы имеют вид [latex] [kh, (k + 1) h] [/ latex], где [latex] h = \ frac {(ba)} {n} [/ latex] и [latex] k = 0, 1, 2, \ cdots, n − 1 [/ latex]. Функция интеграции с Excel Мы демонстрируем, как интегрировать определяемую пользователем функцию VBA с ∫12log (x + p) ⋅dx, где p — постоянный параметр. VBA поддерживается только в ExceLab 7.0. ExceLab 365, основанный на кроссплатформенной технологии Office JS, несовместим с VBA .Решение
⇒ . Имя вашей функции VBA должно иметь префикс «vb», чтобы его можно было использовать с решателями ExceLab. X1 — это просто фиктивная переменная для подынтегральной функции. Его значение игнорируется. Калькулятор интегралов: интеграция с Wolfram | AlphaЧто такое интегралы?Интеграция — важный инструмент в исчислении, который может дать первообразную или представить площадь под кривой.Неопределенный интеграл от, обозначенный, определяется как первообразная от. Другими словами, производная от is. Поскольку производная константы равна 0, неопределенные интегралы определяются только с точностью до произвольной константы.Например, так как производная от. Определенный интеграл от до, обозначенный, определяется как область со знаком между и осью, от до. Оба типа интегралов связаны основной теоремой исчисления. Это означает, что если непрерывен на и является его непрерывным неопределенным интегралом, то. Как Wolfram | Alpha вычисляет интегралы Wolfram | Alpha вычисляет интегралы иначе, чем люди. Он вызывает функцию Integrate системы Mathematica, которая представляет собой огромное количество математических и вычислительных исследований. Integrate не выполняет интегралы, как это делают люди. Вместо этого он использует мощные общие алгоритмы, которые часто включают очень сложную математику. Есть несколько подходов, которые используются чаще всего. Один из них включает разработку общей формы интеграла, затем дифференцирование этой формы и решение уравнений для сопоставления неопределенных символьных параметров.Даже для довольно простых подынтегральных выражений уравнения, сгенерированные таким образом, могут быть очень сложными, и для их решения требуются сильные алгебраические вычислительные возможности Mathematica. Хотя эти мощные алгоритмы дают Wolfram | Alpha возможность очень быстро вычислять интегралы и обрабатывать широкий спектр специальных функций, понимание того, как будет интегрироваться человек, также важно.В результате в Wolfram | Alpha также есть алгоритмы для пошаговой интеграции. В них используются совершенно разные методы интеграции, имитирующие подход человека к интегралу. Это включает интегрирование путем подстановки, интегрирование по частям, тригонометрическую замену и интегрирование по частичным дробям. Интеграция(scipy.integrate) — Справочное руководство SciPy v1.6.3 Интеграция набора обыкновенных дифференциальных уравнений (ОДУ), заданного
начальные условия — еще один полезный пример.{2}} \ Gamma \ left (\ frac {2} {3} \ right)} \) и \ (\ left. Сначала преобразуйте это ОДУ в стандартную форму, задав \ (\ mathbf {y} = \ left [\ frac {dw} {dz}, w \ right] \) и \ (t = z \). Таким образом, дифференциальное уравнение принимает вид \ [\ begin {split} \ frac {d \ mathbf {y}} {dt} = \ left [\ begin {array} {c} ty_ {1} \\ y_ {0} \ end {array} \ right] = \ left [\ begin {array} {cc} 0 & t \\ 1 & 0 \ end {array} \ right] \ left [\ begin {array} {c} y_ {0} \\ y_ {1} \ конец {массив} \ right] = \ left [\ begin {array} {cc} 0 & t \\ 1 & 0 \ end {array} \ right] \ mathbf {y}.{t} \ mathbf {A} \ left (\ tau \ right) d \ tau \ right) \ mathbf {y} \ left (0 \ right), \] Однако в этом случае \ (\ mathbf { A} \ left (t \ right) \) и его интеграл не коммутируют. Это дифференциальное уравнение можно решить с помощью функции Как видно, Решение Чтобы указать определенные пользователем моменты времени для решения Если матрица якобиана функции известна, ее можно передать в Решение системы с ленточной матрицей Якоби где \ (D_u \) и \ (D_v \) — коэффициенты диффузии
компоненты \ (u \) и \ (v \), соответственно, и \ (f \) и \ (k \)
являются константами. Предположим, что граничные условия Неймана (т. Е. «Отсутствие потока»): \ [\ frac {\ partial u} {\ partial x} (0, t) = 0, \ quad \ frac {\ partial v} {\ partial x} (0, t) = 0, \ quad \ frac {\ partial u} {\ partial x} (L, t) = 0, \ quad \ frac {\ partial v} {\ partial x} (L, t) = 0 \] Чтобы применить метод линий, мы дискретизируем переменную \ (x \), определяя равномерно распределенная сетка \ (N \) точек \ (\ left \ {x_0, x_1, \ ldots, x_ {N-1} \ right \} \), с \ (x_0 = 0 \) и \ (x_ {N-1} = L \).2 — (f + k) v_ {N-1} \ end {split} \ end {split} \] Наша полная система обыкновенных дифференциальных уравнений \ (2N \) имеет вид (1) для \ (k = 1, 2, \ ldots, N-2 \) вместе с (2) и (3). Теперь мы можем приступить к реализации этой системы в коде. Мы должны объединить
\ (\ {u_k \} \) и \ (\ {v_k \} \) в один вектор длины \ (2N \).
Два очевидных варианта:
\ (\ {u_0, u_1, \ ldots, u_ {N-1}, v_0, v_1, \ ldots, v_ {N-1} \} \)
а также
\ (\ {u_0, v_0, u_1, v_1, \ ldots, u_ {N-1}, v_ {N-1} \} \). Когда переменные заказаны как \ (\ {u_0, u_1, \ ldots, u_ {N-1}, v_0, v_1, \ ldots, v_ {N-1} \} \), образец ненулевых элементов матрицы Якоби \ [\ begin {split} \ begin {smallmatrix} * & * & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 & 0 & 0 \\ * & * & * & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 & 0 \\ 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 \\ 0 & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 \\ 0 & 0 & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 \\ 0 & 0 & 0 & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & * & 0 \\ 0 & 0 & 0 & 0 & 0 & * & * & 0 & 0 & 0 & 0 & 0 & 0 & * \\ * & 0 & 0 & 0 & 0 & 0 & 0 & * & * & 0 & 0 & 0 & 0 & 0 \\ 0 & * & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & 0 & 0 & 0 \\ 0 & 0 & * & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & 0 & 0 \\ 0 & 0 & 0 & * & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & 0 \\ 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 \\ 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 & 0 & * & * & * \\ 0 & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 &) & * & * \\ \ end {smallmatrix} \ end {split} \] Якобианский паттерн с перемежающимися переменными поскольку \ (\ {u_0, v_0, u_1, v_1, \ ldots, u_ {N-1}, v_ {N-1} \} \) равно \ [\ begin {split} \ begin {smallmatrix} * & * & * & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ * & * & 0 & * & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ * & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & * & * & * & 0 & * & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & * & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & * & * & * & 0 & * & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & * & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & * & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & * & 0 & * & * & * & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & * & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & * & 0 & * & * & * & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & * \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & * & 0 & * & * \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & * & * & * \\ \ end {smallmatrix} \ end {split} \] В обоих случаях нетривиальных диагоналей всего пять, но
когда переменные чередуются, пропускная способность намного
меньше. Приняв это решение, мы можем написать функцию, которая реализует систему дифференциальных уравнений. Сначала мы определяем функции для источника и реакции условия системы: def G (u, v, f, k):
вернуть f * (1 - u) - u * v ** 2
def H (u, v, f, k):
возврат - (f + k) * v + u * v ** 2
Затем мы определяем функцию, которая вычисляет правую часть системы дифференциальных уравнений: def grayscott1d (y, t, f, k, Du, Dv, dx):
"" "
Дифференциальные уравнения для одномерных уравнений Грея-Скотта. Мы не будем реализовывать функцию для вычисления якобиана, но расскажем Сначала мы определяем необходимые входы: В [31]: y0 = np.random.randn (5000) В [32]: t = np.linspace (0, 50, 11) В [33]: f = 0,024 В [34]: k = 0,055 В [35]: Du = 0,01 В [36]: Dv = 0,005 В [37]: dx = 0,025 Время вычисления без использования полосовой структуры матрицы Якоби: В [38]:% timeit sola = odeint (grayscott1d, y0, t, args = (f, k, Du, Dv, dx)) 1 петля, лучше 3:25.2 с на петлю Теперь установите В [39]:% timeit solb = odeint (grayscott1d, y0, t, args = (f, k, Du, Dv, dx), ml = 2, mu = 2) 10 циклов, лучшее из 3: 191 мс на цикл Это намного быстрее! Давайте удостоверимся, что они вычислили один и тот же результат: В [41]: np. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 fill_between(t_span_neg, -np.ones_like(t_span_neg), color='red',
alpha=0.5)
if (t > 0):
t_span_pos = np.linspace(0, t, 200)
ax1.fill_between(t_span_pos, np.ones_like(t_span_pos), color='green',
alpha=0.5)
ax1.annotate('$t$', (t, 0), xytext=(t, 0.1))
ob.center_spines(grid=False, minor_ticks=False, ax=ax1)
ob.settle_axes(xmin=-3, xmax=3, ymin=-1.3, ymax=1.3,
xlabel="x", ylabel="y", ax=ax1)
ax1.set_xticks([-2, -1, 0, 1, 2])
ax1.set_yticks([-1, 1])
t_span = np.linspace(-2, t)
ax2.plot(t_span, -2+np.abs(t_span), color='C0')
ob.center_spines(grid=False, minor_ticks=False, ax=ax2)
ob.settle_axes(xmin=-3, xmax=3, ymin=-3.2, ymax=3.2,
xlabel="t", ylabel="y", ax=ax2)
camera.snap()
animation = camera.animate()
fill_between(t_span_neg, -np.ones_like(t_span_neg), color='red',
alpha=0.5)
if (t > 0):
t_span_pos = np.linspace(0, t, 200)
ax1.fill_between(t_span_pos, np.ones_like(t_span_pos), color='green',
alpha=0.5)
ax1.annotate('$t$', (t, 0), xytext=(t, 0.1))
ob.center_spines(grid=False, minor_ticks=False, ax=ax1)
ob.settle_axes(xmin=-3, xmax=3, ymin=-1.3, ymax=1.3,
xlabel="x", ylabel="y", ax=ax1)
ax1.set_xticks([-2, -1, 0, 1, 2])
ax1.set_yticks([-1, 1])
t_span = np.linspace(-2, t)
ax2.plot(t_span, -2+np.abs(t_span), color='C0')
ob.center_spines(grid=False, minor_ticks=False, ax=ax2)
ob.settle_axes(xmin=-3, xmax=3, ymin=-3.2, ymax=3.2,
xlabel="t", ylabel="y", ax=ax2)
camera.snap()
animation = camera.animate() py
fig, ax1 = plt.subplots()
x = np.linspace(-1.2, 3, 201)
ax1.plot(x, 1 / x ** 2)
x_clip = np.linspace(1, 3, 201)
ax1.fill_between(x_clip, 1 / x_clip ** 2, alpha=0.5)
ob.center_spines(grid=False, minor_ticks=False, ax=ax1)
ob.settle_axes(xmin=-1.2, xmax=3, ymin=-0.7, ymax=3,
xlabel="x", ylabel="y", ax=ax1)
ax1.set_xticks([1, 2])
ax1.set_yticks([])
py
fig, ax1 = plt.subplots()
x = np.linspace(-1.2, 3, 201)
ax1.plot(x, 1 / x ** 2)
x_clip = np.linspace(1, 3, 201)
ax1.fill_between(x_clip, 1 / x_clip ** 2, alpha=0.5)
ob.center_spines(grid=False, minor_ticks=False, ax=ax1)
ob.settle_axes(xmin=-1.2, xmax=3, ymin=-0.7, ymax=3,
xlabel="x", ylabel="y", ax=ax1)
ax1.set_xticks([1, 2])
ax1.set_yticks([]) annotate('$y$', (0.03, 3 - 0.15))
ax1.annotate('$t$', (t, 0), xytext=(t + 0.03, -0.25))
ax1.set_xticks([1, 2])
ax1.set_yticks([])
camera.snap()
animation = camera.animate()
annotate('$y$', (0.03, 3 - 0.15))
ax1.annotate('$t$', (t, 0), xytext=(t + 0.03, -0.25))
ax1.set_xticks([1, 2])
ax1.set_yticks([])
camera.snap()
animation = camera.animate() 3 x\,dx.$
3 x\,dx.$


 {2}-1\right) \sin x+2 x \cos x+C$
{2}-1\right) \sin x+2 x \cos x+C$ {2 x+1} \sin x}{5}+C$
{2 x+1} \sin x}{5}+C$ Например, дифференциальные уравнения в частных производных обычно выводятся из интегральных уравнений сохранения. Когда возникает необходимость численного решения уравнения в частных производных, интегрирование также играет важную роль. В этой статье приведен обзор методов и подходов интегрирования, доступных в COMSOL Multiphysics, а также конкретные примеры их использования.
Например, дифференциальные уравнения в частных производных обычно выводятся из интегральных уравнений сохранения. Когда возникает необходимость численного решения уравнения в частных производных, интегрирование также играет важную роль. В этой статье приведен обзор методов и подходов интегрирования, доступных в COMSOL Multiphysics, а также конкретные примеры их использования. {t_1}\int_{\Omega}F(u)\ \mathrm{d A} \mathrm{d} t
{t_1}\int_{\Omega}F(u)\ \mathrm{d A} \mathrm{d} t В качестве альтернативы, в окне Settings (Настройки) узла Data Series Operations (Операции с массивами данных) можно выбрать опцию Integral (Интегрирование), что позволит вычислить общий пространственно-временной интеграл.
В качестве альтернативы, в окне Settings (Настройки) узла Data Series Operations (Операции с массивами данных) можно выбрать опцию Integral (Интегрирование), что позволит вычислить общий пространственно-временной интеграл. 2. Стационарное и нестационарное решение (в момент времени 100 секунд) представлены на иллюстрациях ниже.
2. Стационарное и нестационарное решение (в момент времени 100 секунд) представлены на иллюстрациях ниже. 65
65 2. Т.е. полученное значение можно задать в качестве граничного условия для общего входящего теплового потока, чтобы средняя температура в рассматриваемой области стала равна 303.15 К.
2. Т.е. полученное значение можно задать в качестве граничного условия для общего входящего теплового потока, чтобы средняя температура в рассматриваемой области стала равна 303.15 К. 1T(x,0)\cdot(x\leq\bar x)\ \mathrm{d} x
1T(x,0)\cdot(x\leq\bar x)\ \mathrm{d} x Результат данной операции можно проиллюстрировать следующим графиком:
Результат данной операции можно проиллюстрировать следующим графиком: Давайте вспомним пример выше с неопределенным интегралом и предположим, что мы хотим вычислить неопределенный интеграл не только для y=0. Данная задача может быть сформулирована в виде дифференциального уравнения в частных производных
Давайте вспомним пример выше с неопределенным интегралом и предположим, что мы хотим вычислить неопределенный интеграл не только для y=0. Данная задача может быть сформулирована в виде дифференциального уравнения в частных производных {100}T(x,y,t)\ \mathrm{d} t
{100}T(x,y,t)\ \mathrm{d} t Переменная для общего теплового потока рассчитывается в COMSOL автоматически и называется ht.tfluxMag. Интеграл может быть вычислен как дополнительная зависимая переменная с помощью узла Distributed ODE (Распределенное обыкновенное дифференциальное уравнение) интерфейса Domain ODEs and DAEs. Правой частью (источниковым членом) для доменного ОДЕ должна выступать подынтегральная функция, что и показано на иллюстрации ниже.
Переменная для общего теплового потока рассчитывается в COMSOL автоматически и называется ht.tfluxMag. Интеграл может быть вычислен как дополнительная зависимая переменная с помощью узла Distributed ODE (Распределенное обыкновенное дифференциальное уравнение) интерфейса Domain ODEs and DAEs. Правой частью (источниковым членом) для доменного ОДЕ должна выступать подынтегральная функция, что и показано на иллюстрации ниже.

 Интеграцию по частям
Интеграцию по частям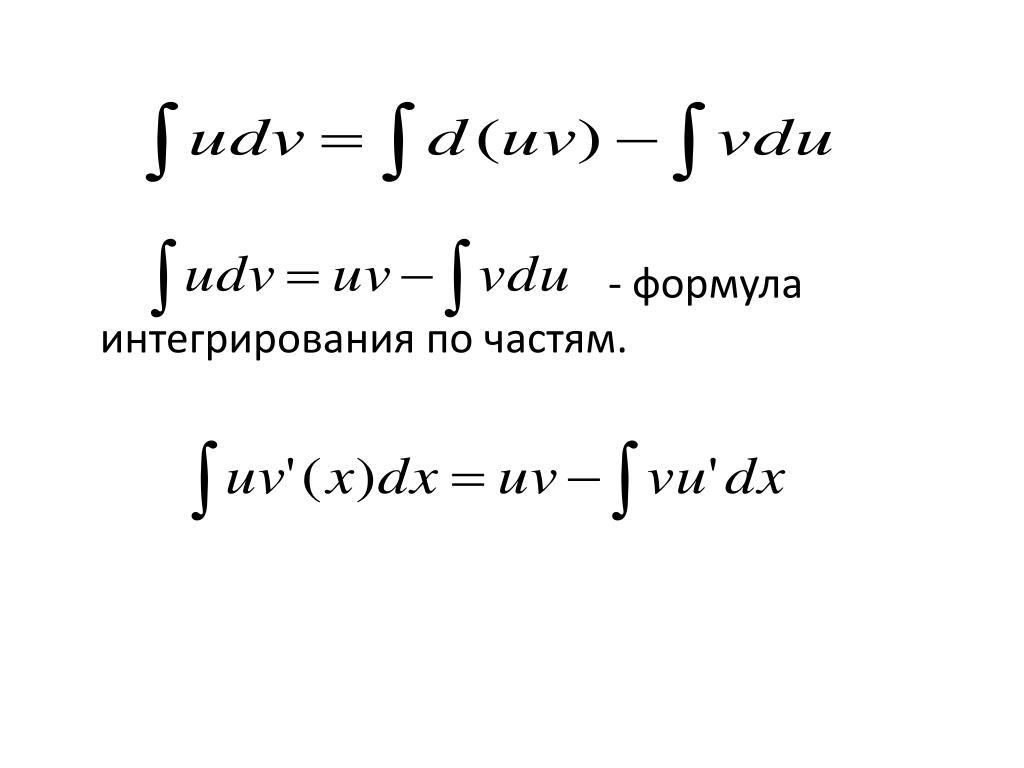 5
5  Интеграцию по частям
Интеграцию по частям {6x}} \) сама по себе, мы могли бы сделать интеграл достаточно легко.\ prime} \, dx}} = \ int {{f ‘\, g + f \, g’ \, dx}} \]
{6x}} \) сама по себе, мы могли бы сделать интеграл достаточно легко.\ prime} \, dx}} = \ int {{f ‘\, g + f \, g’ \, dx}} \] Не всегда будет ясно, каков правильный выбор, и иногда мы делаем неправильный выбор. Это не повод для беспокойства. Если мы сделаем неправильный выбор, мы всегда можем вернуться и попробовать другой набор вариантов.
Не всегда будет ясно, каков правильный выбор, и иногда мы делаем неправильный выбор. Это не повод для беспокойства. Если мы сделаем неправильный выбор, мы всегда можем вернуться и попробовать другой набор вариантов.

 Вместо того, чтобы разделять интеграл, давайте вместо этого воспользуемся следующими вариантами для \ (u \) и \ (dv \).
Вместо того, чтобы разделять интеграл, давайте вместо этого воспользуемся следующими вариантами для \ (u \) и \ (dv \). 2}}} {{10}} \ cos \ left ({10w} \ right) + \ frac {w} {{50}} \ sin \ left ({10w} \ right) + \ frac {1} {{500}} \ cos \ left ({10w} \ вправо) + c \ end {align *} \]
2}}} {{10}} \ cos \ left ({10w} \ right) + \ frac {w} {{50}} \ sin \ left ({10w} \ right) + \ frac {1} {{500}} \ cos \ left ({10w} \ вправо) + c \ end {align *} \]
 {\ frac {3} {2}}} + c \ end {align *} \]
{\ frac {3} {2}}} + c \ end {align *} \] Наконец, хотя ответы разные, иногда с большим трудом можно показать, что они отличаются не более чем на константу.
Наконец, хотя ответы разные, иногда с большим трудом можно показать, что они отличаются не более чем на константу.
 Итак, давайте использовать следующие варианты вместо
Итак, давайте использовать следующие варианты вместо

 Однако вместо того, чтобы вычислять \ (du \) и \ (v \), мы помещаем их в следующую таблицу. Затем мы дифференцируем столбец, соответствующий \ (u \), пока не дойдем до нуля. В столбце, соответствующем \ (dv \), мы интегрируем один раз для каждой записи в первом столбце. Существует также третий столбец, который мы немного объясним, и он всегда начинается со знака «+», а затем чередуются знаки, как показано.{\ frac {x} {2}}} + c \ end {align *} \]
Однако вместо того, чтобы вычислять \ (du \) и \ (v \), мы помещаем их в следующую таблицу. Затем мы дифференцируем столбец, соответствующий \ (u \), пока не дойдем до нуля. В столбце, соответствующем \ (dv \), мы интегрируем один раз для каждой записи в первом столбце. Существует также третий столбец, который мы немного объясним, и он всегда начинается со знака «+», а затем чередуются знаки, как показано.{\ frac {x} {2}}} + c \ end {align *} \] Будь осторожен!
Будь осторожен!
 В общих условиях это может быть
формулируется следующим образом:
В общих условиях это может быть
формулируется следующим образом: Следовательно, самая общая первообразная от f — не отдельная функция, а
скорее класс функций g (x) + a, которые зависят от a.
Следовательно, самая общая первообразная от f — не отдельная функция, а
скорее класс функций g (x) + a, которые зависят от a. ) Следующий пример дает нам представление о
значение этой произвольной константы.
) Следующий пример дает нам представление о
значение этой произвольной константы. Каждая из функций стоимости
что соответствует предельным затратам C ‘(x) = 2x, будет иметь вид
Каждая из функций стоимости
что соответствует предельным затратам C ‘(x) = 2x, будет иметь вид b \! f (x) \, dx [/ latex] неофициально определяется как область области на плоскости [latex] xy [/ latex], ограниченная графиком [latex] f [/ latex], [latex] ] x [/ latex] -ось, а вертикальные линии [latex] x = a [/ latex] и [latex] x = b [/ latex], так что область над [latex] x [/ latex] -осью прибавляет к общей сумме, а то, что ниже оси [latex] x [/ latex], вычитает из общей суммы.Термин интеграл может также относиться к понятию антипроизводной, функции [латекс] F [/ латекс], производной которой является заданная функция [латекс] f [/ латекс].
b \! f (x) \, dx [/ latex] неофициально определяется как область области на плоскости [latex] xy [/ latex], ограниченная графиком [latex] f [/ latex], [latex] ] x [/ latex] -ось, а вертикальные линии [latex] x = a [/ latex] и [latex] x = b [/ latex], так что область над [latex] x [/ latex] -осью прибавляет к общей сумме, а то, что ниже оси [latex] x [/ latex], вычитает из общей суммы.Термин интеграл может также относиться к понятию антипроизводной, функции [латекс] F [/ латекс], производной которой является заданная функция [латекс] f [/ латекс]. a f (x) \, dx} [/ latex]
a f (x) \, dx} [/ latex]
 Правило можно вывести в одну строку, просто интегрировав правило дифференциации продукта.
Правило можно вывести в одну строку, просто интегрировав правило дифференциации продукта.

 Ниже приводится список интегралов от тригонометрических функций. Некоторые из них были вычислены с использованием свойств тригонометрических функций, в то время как другие использовали такие методы, как интегрирование по частям.
Ниже приводится список интегралов от тригонометрических функций. Некоторые из них были вычислены с использованием свойств тригонометрических функций, в то время как другие использовали такие методы, как интегрирование по частям. 2 [/ latex], пусть [latex] x = a \ sec (\ theta) [/ latex].
2 [/ latex], пусть [latex] x = a \ sec (\ theta) [/ latex]. 2 + 1 [/ латекс]
2 + 1 [/ латекс] 2-8x + 25) + {10 \ over 3} \ arctan \ left ({x-4 \ over 3} \ right) + C} [/ latex]
2-8x + 25) + {10 \ over 3} \ arctan \ left ({x-4 \ over 3} \ right) + C} [/ latex] В то время как дифференцирование имеет простые правила, по которым производная сложной функции может быть найдена путем дифференцирования ее более простых компонентных функций, интегрирование этого не делает, поэтому часто полезны таблицы известных интегралов. Нам также, возможно, придется прибегнуть к компьютерам для выполнения интеграла.
В то время как дифференцирование имеет простые правила, по которым производная сложной функции может быть найдена путем дифференцирования ее более простых компонентных функций, интегрирование этого не делает, поэтому часто полезны таблицы известных интегралов. Нам также, возможно, придется прибегнуть к компьютерам для выполнения интеграла. ”
” Популярные методы используют одну из формул Ньютона – Котеса (например, правило средней точки или правило Симпсона) или квадратуру Гаусса. Эти методы основаны на стратегии «разделяй и властвуй», при которой интеграл относительно большого множества разбивается на интегралы меньшего множества. В более высоких измерениях, где эти методы становятся непомерно дорогими с точки зрения вычислительных затрат, можно использовать другие методы, такие как метод Монте-Карло. Здесь мы изучим очень простой метод аппроксимации, называемый правилом трапеции.{b} f (x) \, dx \ приблизительно (b-a) \ frac {f (a) + f (b)} {2}} [/ latex]
Популярные методы используют одну из формул Ньютона – Котеса (например, правило средней точки или правило Симпсона) или квадратуру Гаусса. Эти методы основаны на стратегии «разделяй и властвуй», при которой интеграл относительно большого множества разбивается на интегралы меньшего множества. В более высоких измерениях, где эти методы становятся непомерно дорогими с точки зрения вычислительных затрат, можно использовать другие методы, такие как метод Монте-Карло. Здесь мы изучим очень простой метод аппроксимации, называемый правилом трапеции.{b} f (x) \, dx \ приблизительно (b-a) \ frac {f (a) + f (b)} {2}} [/ latex] bf (x) \, \ mathrm {d} x [/ latex].bf (x) \, \ mathrm {d} x [/ latex], в котором берется ограничение в одной или другой (а иногда и в обеих) конечных точках.
bf (x) \, \ mathrm {d} x [/ latex].bf (x) \, \ mathrm {d} x [/ latex], в котором берется ограничение в одной или другой (а иногда и в обеих) конечных точках. bf (x) \, \ mathrm {d} x [/ latex]
bf (x) \, \ mathrm {d} x [/ latex] +} (2 \ sqrt {1} -2 \ sqrt {a}) \\ & = 2 \ end {align} [/ latex]
+} (2 \ sqrt {1} -2 \ sqrt {a}) \\ & = 2 \ end {align} [/ latex] 2) [/ latex], первообразная которого (функция ошибки, умноженная на константу) не может быть записана в элементарной форме.
2) [/ latex], первообразная которого (функция ошибки, умноженная на константу) не может быть записана в элементарной форме.

 Это означает . Иногда требуется приближение к определенному интегралу. Обычный способ сделать это — разместить под кривой тонкие прямоугольники и сложить области со знаком.Wolfram | Alpha может решать широкий спектр интегралов.
Это означает . Иногда требуется приближение к определенному интегралу. Обычный способ сделать это — разместить под кривой тонкие прямоугольники и сложить области со знаком.Wolfram | Alpha может решать широкий спектр интегралов. Другой подход, который Mathematica использует при вычислении интегралов, состоит в том, чтобы преобразовать их в обобщенные гипергеометрические функции, а затем использовать наборы соотношений об этих очень общих математических функциях.
Другой подход, который Mathematica использует при вычислении интегралов, состоит в том, чтобы преобразовать их в обобщенные гипергеометрические функции, а затем использовать наборы соотношений об этих очень общих математических функциях. \ Frac {dw} {dz} \ right | _ {z = 0} = — \ frac {1} {\ sqrt [3] {3} \ Gamma \ left (\ frac {1} {3} \ right)}. \) Известно, что решение этого дифференциального уравнения с этими
граничными условиями является функция Эйри
\ Frac {dw} {dz} \ right | _ {z = 0} = — \ frac {1} {\ sqrt [3] {3} \ Gamma \ left (\ frac {1} {3} \ right)}. \) Известно, что решение этого дифференциального уравнения с этими
граничными условиями является функция Эйри Требуется производная, fprime , временной интервал [t_start, t_end] и вектор начальных условий, y0 , в качестве входных аргументов и возвращает
объект, чье поле y представляет собой массив с последовательными значениями решения как
столбцы.Поэтому начальные условия приведены в первом выходном столбце.
Требуется производная, fprime , временной интервал [t_start, t_end] и вектор начальных условий, y0 , в качестве входных аргументов и возвращает
объект, чье поле y представляет собой массив с последовательными значениями решения как
столбцы.Поэтому начальные условия приведены в первом выходном столбце. Проходя t_eval опция вызова функции
Проходя t_eval опция вызова функции  (Для получения дополнительной информации о системе см.
http://groups.csail.mit.edu/mac/projects/amorphous/GrayScott/)
(Для получения дополнительной информации о системе см.
http://groups.csail.mit.edu/mac/projects/amorphous/GrayScott/) Математически это не имеет значения, но выбор влияет на то, как
эффективно
Математически это не имеет значения, но выбор влияет на то, как
эффективно  То есть главная диагональ и сразу две диагонали
вверху и два сразу под главной диагональю
— ненулевые диагонали.
Это важно, т.к. входы
То есть главная диагональ и сразу две диагонали
вверху и два сразу под главной диагональю
— ненулевые диагонали.
Это важно, т.к. входы  ОДУ выводятся методом линий."" "
# Векторы u и v чередуются по y. Мы определяем
# видов u и v при разрезании y.
u = y [:: 2]
v = y [1 :: 2]
# dydt - возвращаемое значение этой функции.
dydt = np.empty_like (y)
# Так же, как u и v - это виды чередующихся векторов
# в y, dudt и dvdt - это представления чередующегося вывода
# векторов в dydt.
dudt = dydt [:: 2]
dvdt = dydt [1 :: 2]
# Вычислить du / dt и dv / dt. Конечные и внутренние точки
# обрабатываются отдельно.dudt [0] = G (u [0], v [0], f, k) + Du * (-2,0 * u [0] + 2,0 * u [1]) / dx ** 2
dudt [1: -1] = G (u [1: -1], v [1: -1], f, k) + Du * np.diff (u, 2) / dx ** 2
dudt [-1] = G (u [-1], v [-1], f, k) + Du * (- 2,0 * u [-1] + 2,0 * u [-2]) / dx ** 2
dvdt [0] = H (u [0], v [0], f, k) + Dv * (-2,0 * v [0] + 2,0 * v [1]) / dx ** 2
dvdt [1: -1] = H (u [1: -1], v [1: -1], f, k) + Dv * np.diff (v, 2) / dx ** 2
dvdt [-1] = H (u [-1], v [-1], f, k) + Dv * (-2,0 * v [-1] + 2,0 * v [-2]) / dx ** 2
вернуть дыдт
ОДУ выводятся методом линий."" "
# Векторы u и v чередуются по y. Мы определяем
# видов u и v при разрезании y.
u = y [:: 2]
v = y [1 :: 2]
# dydt - возвращаемое значение этой функции.
dydt = np.empty_like (y)
# Так же, как u и v - это виды чередующихся векторов
# в y, dudt и dvdt - это представления чередующегося вывода
# векторов в dydt.
dudt = dydt [:: 2]
dvdt = dydt [1 :: 2]
# Вычислить du / dt и dv / dt. Конечные и внутренние точки
# обрабатываются отдельно.dudt [0] = G (u [0], v [0], f, k) + Du * (-2,0 * u [0] + 2,0 * u [1]) / dx ** 2
dudt [1: -1] = G (u [1: -1], v [1: -1], f, k) + Du * np.diff (u, 2) / dx ** 2
dudt [-1] = G (u [-1], v [-1], f, k) + Du * (- 2,0 * u [-1] + 2,0 * u [-2]) / dx ** 2
dvdt [0] = H (u [0], v [0], f, k) + Dv * (-2,0 * v [0] + 2,0 * v [1]) / dx ** 2
dvdt [1: -1] = H (u [1: -1], v [1: -1], f, k) + Dv * np.diff (v, 2) / dx ** 2
dvdt [-1] = H (u [-1], v [-1], f, k) + Dv * (-2,0 * v [-1] + 2,0 * v [-2]) / dx ** 2
вернуть дыдт
 Это позволяет основному
решатель (LSODA), чтобы избежать вычисления значений, которые, как ему известно, равны нулю. Для большого
системы, это значительно улучшает производительность, как показано на
после сеанса ipython.
Это позволяет основному
решатель (LSODA), чтобы избежать вычисления значений, которые, как ему известно, равны нулю. Для большого
системы, это значительно улучшает производительность, как показано на
после сеанса ipython.