5 секретов решения всех математических задач
 1. Перед началом решения новых типов задач повторите основы.
1. Перед началом решения новых типов задач повторите основы.
Задачи будут решаться легко, если вы будете стараться понять, как к ним применить основы математики. Большинство студентов не умеют решать задачи по одной причине: они не владеют основными понятиями. Как говорилось ранее, эта проблема решается через повторение программы прошлых лет. Но не думайте, что это займет много времени. Ведь вам нужно прочитать только старые уроки, связанные с новыми математическими задачами. На это уйдет всего несколько минут.
Избегая этой простой работы — заглядывать в старые учебники, — плохие студенты накапливают непонятные моменты, и предмет становится для них сложнее с каждым днем.
Нет необходимости страдать из-за этой проблемы. Поступайте разумно и выясняйте все непонятное, обратившись к старым конспектам, друзьям и преподавателям за помощью. Если знание основ математики у вас крепкое, вы справитесь с любой задачей. Поэтому не допускайте слабости со своей стороны.
2. Стремитесь не запомнить, а понять ход решения задачи.
Большое преимущество математики в том, что не нужно ничего запоминать, кроме формул и единиц измерения. Но стать специалистом можно только одним путем: через постоянную практику.
Чем больше вы решаете задач определенного типа, тем лучше вы понимаете их логику, тем опытнее вы становитесь. Когда вы тренируетесь:
— мозг автоматически записывает решение и предпринимаемые шаги;
— увеличивается скорость решения задач;
— повышается уверенность в себе, которая помогает решать задачи на экзамене спокойно и правильно.
Практикуйтесь в решении задач как можно чаще. Лучше всего для этого перерешать все задачи из учебника. Также решите все задачи, предложенные преподавателем. Выполнив и это, найдите задачи прошлогодних экзаменов и решите их тоже.
3. Подробно записывайте в тетрадь решение задач за преподавателем на уроке.
В математических задачах логика решения так же важна, как и правильный ответ. Поэтому, когда преподаватель объясняет решение задачи, будьте внимательны. Обязательно запишите его в тетрадь в точной последовательности, чтобы потом не забыть все этапы. Усвоив логику решения задач разного типа, вы не растеряетесь на экзамене.
4. Выполняйте домашние задания по математике как можно раньше, пока вы хорошо помните объяснения.
Выполнение домашнего задания в тот же день очень полезно, потому что все еще свежо в памяти. Можно легко вспомнить все рекомендации и сделать задание за более короткое время.
Хотя этот совет касается всех предметов, он особенно важен для математики. Если вы отложите выполнение задания по математике, то можете забыть этапы решения задач. Это важно, если математика сложна для вас. Зная о простом секрете (выполнять домашние задания по математике как можно раньше), вы сделаете этот предмет более легким для себя.
5. Разбирайте все непонятное немедленно.
В отличие от изучения языков, математика является таким предметом, по которому можно набрать 100 %-ное количество баллов! Поэтому добросовестно учите ее, не накапливайте непонятных моментов. Обращайтесь за помощью к преподавателям, друзьям и репетиторам и выясняйте все мелочи.
Решайте много задач, тогда математика вам будет нравиться и ваши баллы станут выше.
blog.zao4nik.ru
цены на услуги от фирмы Решатель
Учеба в средних и высших образовательных учреждениях сопровождается постоянными контрольными, модулями и лабораторными. А в период сессии объем заданий по всем предметам возрастает в несколько раз, что часто становится для студентов непосильным к выполнению даже в чисто физическом плане. Знакомы такие проблемы? Не стоит изводить себя бессонными ночами и постоянными волнениями. Образование – это, безусловно, важно, но есть способы облегчить его получение. Например, за счет профессиональной помощи для студентов.
Наша компания оказывает такие услуги и позволяет ученикам быстрее, проще и спокойнее проходить некоторые этапы сессии или текущего учебного процесса. В этом разделе нашего сайта можно получить помощь в решении математических задач. Опытные исполнители по этому направлению предоставят вам точные и правильные результаты в грамотном оформлении. В штате фирмы трудятся преподаватели и квалифицированные эксперты в области математики, поэтому мы гарантируем качество их работы.
Заинтересовались возможностью заказать помощь по математике? Хорошая идея! Изучайте детали
Мы имеем большую и ценную практику в написании студенческих работ, поэтому вы оцените то, как легко и выгодно с нами сотрудничать. Для начала нужно заполнить форму на сайте – далее вы попадете в Личный Кабинет, где вам будет удобно получить результат и уточнять текущие детали. У нас налажены схемы взаимодействия с клиентами, поэтому все происходит четко и без задержек.
Предлагаем еще несколько плюсов решения задач по математике у нас:
- работа без посредников – все задания выполняются только нашими авторами;
- не продаем готовых проектов – только персональный подход к каждому заказу;
- бессрочная гарантия;
- обоснованная стоимость;
- бесплатные доработки;
- строгое соблюдение сроков.
Принимая заявку на заказ, мы сразу же обсуждаем с клиентом даты сдачи готового проекта и четко их придерживаемся, а по возможности даже раньше предоставляем результат. С нами вы гарантированно вовремя закроете все «хвосты» в университете и сможете спокойно заниматься личными делами.
Хотите узнать цены от компании «Решатель»?
Мы не будем вводить вас в заблуждение, что у нас все услуги максимально дешево стоят. У нас лояльная ценовая политика, а все тарифы – не выше средних на рынке и полностью оправданны качеством выполнения работы. Вам нужно успешно сдать задание и получить хорошую отметку? Тогда не рискуйте и воспользуйтесь нашей недорогой, но полезной и надежной помощью. Ждем вас!
reshatel.org
Как решать задачи по математике?
Как научить ребенка решать задачи по математике?
Решая задачу о блинчиках мы увидим, что:
• сложными могут оказаться и простые с виду задачи.
Статья будет длинная и нудная. Она
может быть интересна исключительно родителям, желающим научить собственного ребенка понимать математику. Научить думать.
Простоe и сложное
Чем проще принцип, тем сложнее его доказательство и длиннее объяснение
собственные наблюдения
К примеру, большая теорема Ферма.
Теорема простая, понять ее способен даже ученик начальной школы. А вот доказать её удалось лишь спустя три столетия, в 1994 г. Говорят и сейчас не более двухсот математиков в мире понимают это доказательство. Я в их число не вхожу
Как(не)научить понимать: «Принцип короткого замыкания»
Главный принцип (не)успешного обучения, который я обнаружил — «принцип короткого замыкания»: Понимание не возникает из простоты, оно возникает из сложности. Простота и понимание возникают в процессе и являются результатом обучения . И категорически запрещено укорачивать этот путь!Именно на этом пункте и спотыкается традиционная школа.
«Игровой подход», как ласково они это называют, цветные картинки, два притопа – три прихлопа … Это НЕ обучение, а его имитация. (Я уже писал о «самолетопоклонниках» Ричарда Фейнмана в книге «Школа понимания».)
«Ах, как все просто и понятно!»
«Ах, как понятно объясняет учительница! Дети все схватывают с первого раза!» Только вот беда: со второго раза, когда встречается чуть видоизмененная задача, путаются и заявляют, что «Они этого не проходили!». Что является абсолютной правдой. И «заслуженному учителю» вновь приходится «в игровой форме» исполнять танец с бубном около «интерактивной доски».
Но и танцевать большинство школьных учителей мастера не великие. Им бы лучше в хор: орать на детей они умеют громко, эмоционально, с душой …
Да, ирония злая. Но большинством школьных функционеров, маскирующихся под Учителей, вполне заслуженная.
На выходе «игрового подхода» к 9-11 классам мы имеем ужасающую статистику непонимания математики, равно, как и других предметов.
Если уже известный ответ задачи, готовое «решение» препарировать, разложить на составляющие, «понятно объяснить», то, естественно, ребенок запомнит «решения» десятка задач. И, также естественно, не научится их решать.
Объяснить готовый ответ и решить задачу – две гигантские разницы!
«Главное — возбудить аппетит и чувства: иначе воспитаете осла, нагруженного книгами …»
Монтень
Кто должен учить?
Основам науки должен учить тот, кто сам эти основы понимает.
Научить думать сможет только тот, кто умеет думать сам.
В начальной же школе работают … ну, вы сами это знаете.
Почему-то считается, что основам математики может научить кто угодно, даже педагог, который сам не умеет решать простейших задач. Но почему-то потом, в старших классах дети массово отказываются понимать математику и что-либо вообще.Итак,
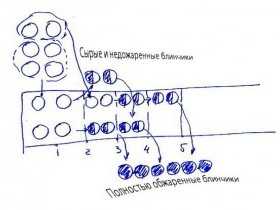
Задача о блинчиках
«Мама жарит блинчики с творогом. Каждый блинчик она обжаривает с двух сторон: 2 минуты с одной и 1 минуту с другой. На сковороду одновременно умещаются 4 блинчика. Вопрос: за какое минимальное время мама обжарит 7 блинчиков?»
…Поместите эту задачу в раздел самых сложных задач профильного ЕГЭ и процентов 80 выпускников с ней не справятся и/или потеряют неоправданно много времени. Ожидание «подвоха» не позволит выпускникам, чьё математическое мышление за 11 лет так и не было развито, найти верное решение. Смутное чувство интуиции заставит их сомневаться, перебирать варианты в поисках «красивого» ответа…
Решение задачи
Задачи в начальной школе простые, даже примитивные. Ответ получается методом перебора плюс немного здравого смысла и чуть-чуть воображения…
…Сначала мама обжаривает 4 блинчика за 3 минуты ( 2+1=3).
Затем оставшиеся 3 блинчика (7 — 4 = 3), тоже за 3 минуты.
Итого 6 минут. Вроде все верно?
Но:
• Как доказать, что решение верное? Не может же ответ быть настолько простым! Прямо как теорема Ферма …
• И как решить эту же задачу, если мама – директор «блинной фабрики» и за день обжаривает N блинчиков?
Оставим в покое маму – фабриканта и вернемся к условию.
Анализ решения задачи
Сразу бросается в глаза неэффективность использования сковороды. Как-то некрасиво, не по-школьному получается. Незрелый ум школьника замечает: КПД сковороды слишком низкий, одно место при второй обжарке пустует. Сковорода греет воздух, а масло горит …. Можно ли как-нибудь использовать одно свободное место во втором цикле обжарки?
Разумный вопрос: его следует задать и поискать ответ.
Метод перебора
Перебор вариантов это метод. Но не столько метод решения, сколько метод оценки данных, используя который иногда можно нащупать решение.
Но нащупать — не значит доказать, что оно верное.И сомневающийся школьник продолжает в поисках правильного ответа перебирать варианты … То есть действует методически неверно.
«Предположим, что …» — метод
Предположим, что для обжарки требовалось бы три «неделимых» минуты — блинчики обжаривались бы за один раз с одной стороны. Решение оказалось бы настолько тривиальным, что и решать тогда было бы нечего!
Но в условии сказано: блины переворачивают!
Поэтому количество вариантов возрастает и школьник судорожно ищет «что в какую формулу вставить, и что на что разделить»
(по ироничному наблюдению за отличниками академика В.И.Арнольда, одного из крупнейших математиков ХХ века). Смутное чувство интуиции шепчет: здесь что-то не так, не все так просто. Человек бессистемно перебирает варианты, пока не доходит до «перестановок из N по M». Но и комбинаторика в младшешкольной задаче выигрыша во времени не дает …
Человеку кажется: он что-то упустил и судорожные эксперименты с перекладыванием блинов, попытки вспомнить «похожие» задачи и «волшебные» формулы продолжаются. Пока уставший от непродуктивной механической деятельности ум не ошибется и не «нащупает красивый ответ»: 5 минут.
Именно такое «решение» получила учительница начальных классов в школе, которую посещал мой сын. Он тогда поспорил с учительницей, но она настаивала: «Все-таки здесь получается скомбинировать! Сейчас не помню как именно, но точно – получается!». Задачу она дала на уроке «Умники и умницы», поэтому нашлась еще пара «Умников», поддержавших «красивое» решение.
Это вообще не шутка.
«Ум человеческий склонен верить непонятному»
Тацит
Математическая логика и интуиция
Неразвитое мышление активизирует «интуицию». Но ум человеческий не приспособлен адекватно воспринимать мир цифр. Это, кстати, научно подтвержденный факт.
Например: как вы думаете, сколькими способами можно разложить колоду всего лишь из 52 карт? Правильный ответ шокирует: неужели мы способны НАСТОЛЬКО ошибаться?!
Чтобы шок состоялся, прикиньте ответ, а потом посчитайте на калькуляторе факториал 52. Пожалуй, это больше, чем количество атомов в известной Вселенной …
… Без специальной подготовки ум человеческий воспринимает мир цифровой СЛИШКОМ уж несовершенно. Поэтому и возникает «смутное чувство интуиции».
Решение задачи о 6 блинчиках
Предположим, что теперь мама обжаривает только 6 блинчиков. Можно ли теперь уложиться в 5 минут?
Решение.
Итого: 2 + 1 +1 + 1 = 5 минут.
Минуту удалось-таки сэкономить!
Хотя и тут разбазаривание ресурсов налицо: последнюю минуту на сковороде было только 2 блина … . Как говорится, абсолюты в реальном мире недостижимы, считай – не считай …
Арифметика или геометрия? Визуализация VS абстрагирования
Сложно было следить за текстовым изложением решения, не правда ли? А теперь представьте, каково это детям!..Не проще ли изобразить процесс решения графически? Попросту – нарисовать?!

… Детям исключительно полезно решать задачи подобным образом.
С помощью рисунков они приучаются думать (а не запоминать типовые «решения»). Оперирование образами формирует связное, логическое мышление, они узнают, что такое понимание.
Но вряд ли хотя бы 0,1% учителей математики представляет, как работает ум и что в нем происходит во время решения математической задачи! В МПГУ этому не учат.
Родителю – на заметку: всемирно известный академик В.И Арнольд славился доходчивым стилем преподавания и геометрическим подходом к традиционным разделам математики. А также жесткой критикой попыток американцев и, особенно, французов излагать математику на излишне высоком уровне абстракции. «Это великий-то математик?,- удивитесь вы,- «Представитель самой абстрактной из всех наук?!»
Вот именно.
Доказательство очевидного: «правильный ответ» задачи
Как узнать, верен ли полученный ответ? Проверка решения это составная часть решения, не менее важная, чем само решение.
Как доказать, что за 5 минут 7 блинчиков обжарить нельзя, а 6 — можно?..
Дроби появляются незаметно …
Как максимальная скорость автомобиля: не обязательно «выживмать» все, можно двигаться и медленнее. Но быстрее — невозможно.
Хотя для такой оценки и требуется понимание дробей, но не очень глубокое.
Дроби, кстати — раздел арифметики, в котором массово «плавает» большинство школьников на ЕГЭ (???). Поэтому, насколько это задача для 3 класса … зависит от способа ее подачи и квалификации «подающего» блинчики к столу решающих задачу
Итак:
при полной загрузке сковороды для обжарки 7 блинчиков требуется больше 5 минут. Не надо больше мучиться и «комбинировать».
А вот для 6 блинчиков можно варианты и поискать.
Задача о блинной фабрике
А что насчет мамы – блинного капиталиста? Если ребенок уяснил метод решения, то теперь ему не составит труда масштабировать решение на любые количества. Но скажите: разве это было очевидно до того, как мы прошли весь этот довольно сложный путь?!
Единственный способ научить ребенка решать задачи это научиться решать их самому. Не так уж и сложно взрослому и заинтересованному человеку научиться решать задачи младшей школы, не так ли? Было бы желание. А если желание отсутствует у наиболее заинтересованных в ребенке людей … тогда дело швах. Сегодня рассчитывать на школу, также, как на репетиторов — абсолютно дохлое дело.
Вернитесь к началу статьи и представьте, что все это происходило в классе. Получилось? А потом представьте, то же самое в присутствии репетитора и ответьте себе на два вопроса:
«Соображайте, мужчина!», — как четверть века назад строго заметила мне смотрительница около турникета метро на «Комсомольской», когда я по ошибке сунулся не в те ворота.
butorov.ru
О решении текстовых задач по математике
Разделы: Математика
О решении текстовых задач по математике
Одним из вопросов методики преподавания математики является вопрос формирования у учащихся умений и навыков решения текстовых задач.
Задачи являются материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, полученные при изучении математики, при решении вопросов, которые возникают в жизни человека. Этапы решения задач являются формами развития мыслительной деятельности.
Для решения текстовых задач применяются три основных метода: арифметический, алгебраический и комбинированный. Рассмотрим каждый из этих методов.
I. Арифметический метод.
Первым этапом решения задач арифметическим методом является разбор условия задачи и составление плана её решения. Этот этап решения задачи сопровождается максимальной мыслительной деятельностью.
Вторым этапом является решение задачи по составленному плану. Этот этап решения проводится учащимися без особых затруднений и в большинстве случаев носит тренировочный характер.
Третьим важным этапом решения задачи является проверка решения задачи. Она проводится по условию задачи. Пренебрежение проверкой при решении задачи, замена её проверкой ответов снижает роль решения задачи в процессе развития логического мышления учащихся.
При решении текстовых задач арифметическим методом у учащихся вырабатываются определённые умения и навыки, которые в процессе дальнейшего обучения должны совершенствоваться и закрепляться.
При арифметическом методе решения задач формируются 56 основных умений и навыков. Из них 38 умений и навыков приобретаются при решении задач как арифметическим, так и алгебраическим методами.
К ним относятся следующие умения и навыки:
- Краткая запись условия задачи.
- Изображение условия задачи с помощью рисунка.
- Логические приёмы мышления: наблюдение и сравнение, анализ и синтез, абстрагирование и конкретизация, обобщение и ограничение, умозаключения индуктивного и дедуктивного характера и умозаключения по аналогии.
- Выполнение арифметических действий над величинами (числами).
- Изменение (увеличение или уменьшение) величины (числа) в несколько раз.
- Нахождение разностного сравнения величин (чисел).
- Нахождение кратного сравнения величин (чисел).
- Использование свойств изменения результатов действий в зависимости от изменения компонентов.
- Изменение (увеличение или уменьшение) величины (числа) на несколько единиц величины (числа).
- Нахождение дроби от величины (числа).
- Нахождение величины (числа) по данной её (его) дроби.
- Нахождение процентов данной величины (данного числа).
- Нахождение величины (числа) по её (его) проценту.
- Нахождение процентного отношения двух величин (чисел).
- Составление пропорций.
- Понятие прямой и обратной пропорциональной зависимости величин (чисел).
- Понятие производительности труда.
- Определение производительности труда при совместной работе.
- Определение части работы, выполненной в течение некоторого промежутка времени.
- Определение скорости движения.
- Определение пути, пройденного телом.
- Определение времени движения тела.
- Понятие о собственной скорости (скорости в стоячей воде) движения тела по воде.
- Нахождение пути, пройденного двумя телами при встречном движении.
- Нахождение скорости движения тела по течению и против течения реки.
- Нахождение времени прохождения телом единицы пути при заданной скорости движения.
- Нахождение скорости сближения тел, движущихся в одном направлении, и скорости удаления.
- Нахождение скорости сближения или скорости удаления тел, движущихся в противоположных направлениях или при встречном движении.
- Нахождение части пути, пройденного телом за определённое время, когда известно время прохождения всего пути.
- Нахождение количества вещества, содержащегося в растворе, смеси, сплаве.
- Нахождение концентрации, процентного содержания.
- Нахождение стоимости товара, акции.
- Нахождение цены товара, акции.
- Нахождение прибыли.
- Нахождение количества вредных веществ в воде, воздухе.
- Нахождение себестоимости продукции.
- Расчёт начислений банка на вклады.
- Проверка решения задачи по условию.
Умения и навыки, которые формируются в процессе решения задач только арифметическим методом, можно разбить на две группы. К первой группе относятся умения и навыки, которые необходимы для дальнейшего изучения математики.
К первой группе относятся следующие умения и навыки:
- Перевод календарного времени в арифметическое число.
- Перевод арифметического числа в календарное время.
- Нахождение времени предыдущего события.
- Нахождение времени последующего события.
- Нахождение промежутка времени между двумя событиями.
Все умения и навыки этой группы формируются в процессе решения задач на вычисление времени, т.е. тех задач, которые нет смысла решать алгебраически.
Вторая группа – это те умения и навыки, без знания которых можно решить все текстовые задачи алгебраическим методом, и в дальнейшем их незнание не будет пробелом в математическом образовании учащихся.
Ко второй группе относятся следующие умения и навыки:
- Введение понятия «часть».
- Выполнение действий сложения и вычитания частей.
- Выполнение умножения и деления части на число.
- Приём уравнивания большего числа с меньшим и меньшего с большим.
- Приём уравнивания прибавлением к меньшему числу и вычитанием из большего числа их полуразности.
- Определение числа частей, составляющих данное число.
- Введение понятий условной единицы.
- Нахождение дроби условной единицы и её частей.
- Сравнение частей величин.
- Сложение и вычитание частей единицы.
- Метод исключения неизвестного посредством замены одной величины другой.
- Решение задач методом предположения.
- Составление плана решения задачи.
Эти умения и навыки, несомненно, представляют интерес. Но почти все из них можно отнести к числу умений и навыков, формирующихся у учащихся при решении нестандартных задач. Решение таких задач следует проводить систематически наряду с решением стандартных текстовых задач.
II. Алгебраический метод.
Под алгебраическим методом решения задач понимается такой метод решения, когда неизвестные величины находятся в результате решения уравнения или системы уравнений, решения неравенства или системы неравенств, составленных по условию задачи. Иногда алгебраическое решение задачи бывает очень сложным.
При решении задач алгебраическим методом основная мыслительная деятельность сосредотачивается на первом этапе решения задачи: на разборе условия задачи и составлении уравнений или неравенств по условию задачи.
Вторым этапом является решение составленного уравнения или системы уравнений, неравенства или системы неравенств.
Третьим важным этапом решения задач является проверка решения задачи, которая проводится по условию задачи.
При алгебраическом методе решения формируются 55 основных умений и навыков.
Отличными от тех, которые формируются при арифметическом их решении, являются следующие:
- Введение неизвестного.
- Введение двух неизвестных.
- Введение трёх и более неизвестных.
- Выполнение действий сложения и вычитания неизвестных.
- Выполнение действий умножения и деления неизвестных.
- Запись зависимости между величинами с помощью букв и чисел.
- Решение линейных уравнений.
- Решение линейных неравенств.
- Решение квадратных уравнений и неравенств.
- Решение дробно-рациональных уравнений и неравенств.
- Решение систем уравнений и систем неравенств.
- Составление одного уравнения (неравенства) с двумя неизвестными.
- Решение уравнения (неравенства) с двумя неизвестными.
- Выбор значений неизвестных по условию задачи.
- Составление уравнений с параметром по условию текстовой задачи.
- Решение уравнений с параметром.
- Исследовательская работа.
В связи с внедрением в школьную программу элементов высшей математики, с ускоренным развитием и внедрением во все сферы вычислительной математики большое значение имеет формирование у учащихся не отдельных специфических навыков, а тех умений и навыков, которые имеют дальнейшее приложение. К числу этих умений и навыков относятся умения и навыки, которые формируются в процессе решения задач алгебраическим методом.
III. Комбинированный метод.
Этот метод получается в результате включения в алгебраический метод решения задач решение, в котором часть неизвестных величин определяется с помощью решения уравнения или системы уравнений, неравенств или систем неравенств, а другая часть – арифметическим методом. В этом случае решение текстовых задач значительно упрощается.
При решении текстовых задач учащимся могут помочь несколько простых и общих советов, а также приведённые ниже примеры решения задач.
Совет 1. Не просто прочитайте, а тщательно изучите условие задачи. Попытайтесь полученную информацию представить в другом виде – это может быть рисунок, таблица или просто краткая запись условия задачи.
Совет 2. Выбор неизвестных.
В задачах «на движение» – это обычно скорость, время, путь. В задачах “на работу” - производительность и т.д.
Не надо бояться большого количества неизвестных или уравнений. Главное, чтобы они соответствовали условию задачи и можно было составить соответствующую “математическую модель” (уравнение, неравенство, система уравнений или неравенств).
Совет 3. Составление и решение “математической модели”.
При составлении “математической модели” (уравнения, неравенства, системы уравнений или неравенств) ещё раз внимательно прочитайте условие задачи. Проследите за тем, что соответствует каждой фразе текста задачи в полученной математической записи и чему в тексте задачи соответствует каждый “знак” полученной записи (сами неизвестные, действия над ними, полученные уравнения, неравенства или их системы).
Очень важно не только составить уравнение, неравенство, систему уравнений или неравенств, но и решить составленное.
Если решение задачи не получается, то нужно ещё раз прочитать и проанализировать задачу (заданный текст и полученную запись).
Иногда по условию задачи достаточно отыскать не сами неизвестные, а их комбинации. Например, не x и y, а x+y, x/y, 1/x и т.п.
Если кажется, что получилось правильное, но очень сложное выражение, то попробуйте ввести другие неизвестные, может быть, изменив их количество, чтобы получилась более простая модель.
Иногда неизвестные в задачах выражаются только целыми числами, тогда при решении задач нужно использовать свойства целых чисел.
Совет 4. Решение сложной текстовой задачи – процесс творческий. Иной раз требуется вернуться к самому началу задачи, учитывая и анализируя уже полученные результаты.
При решении задач короткую запись задачи можно сделать с помощью рисунка или таблицы.
Таблица является универсальным средством и позволяет решать большое количество идейно близких задач.
Можно выделить семь вопросов, которые дают верное направление решению задач разных типов.
Вопросы к задаче с комментариями к ним:
- О каком процессе идёт речь? Какими величинами характеризуется этот процесс? (Количество величин соответствует числу столбцов таблицы).
- Сколько процессов в задаче? (Количество процессов соответствует числу строк в таблице).
- Какие величины известны? Что надо найти? (Таблица заполняется данными задачи; ставится знак вопроса).
- Как связаны величины в задаче? (Вписать основные формулы, выяснить связи и соотношения величин в таблице).
- Какую величину (величины) удобно выбрать в качестве неизвестной или неизвестных? (Клетки в таблице заполняются в соответствии с выбранными неизвестными).
- Какие условия используются для составления “модели”? (Выписать полученную “модель”)
- Легко ли решить полученное? (Если решить сложно, ввести новые переменные, использовать другие соотношения).
Пример решения задачи.
Задача. Расстояние между двумя городами скорый поезд проходит на 4 часа быстрее товарного и на 1 час быстрее пассажирского. Найти скорости товарного и скорого поездов, если известно, что скорость товарного поезда составляет 5/8 от скорости пассажирского и на 50 км/ч меньше скорости скорого.
Решение (черновик).
Отвечаем на вопросы, поэтапно составляя таблицу.
1. Речь идёт о процессе движения, которое характеризуется тремя величинами: расстояние, скорость, время (3 столбца таблицы).
2. В задаче 3 процесса: движение скорого, пассажирского и товарного поездов (3 строчки таблицы).
Можно составить “скелет” таблицы.
Величины Процессы |
Расстояние (км) | Скорость (км/ч) |
Время (ч) |
|---|---|---|---|
| Скорый поезд | с | с | с |
| Пассажирский поезд | с | с | с |
| Товарный поезд | с | с | с |
3. Заполняем таблицу в соответствии с условиями задачи
4. Вводим неизвестные величины: x, км/ч – скорость товарного поезда, y, ч – время движения скорого поезда.
5. Составим “модель”.
(x+50)y = 8/5 x(y+1)
8/5 x(y+1) = x(y+4)
6. Решаем эту систему. Из первого уравнения находим у. Из второго уравнения находим х.
Решение задачи (чистовик).
Пусть х, км/ч – скорость товарного поезда (х>0), у, ч – время движения скорого поезда (у>0).
Составляем таблицу.
Величины Процессы |
Расстояние (км) | Скорость (км/ч) | Время (ч) |
|---|---|---|---|
| Скорый поезд | (х+50)у | х+50 ? | у |
| Пассажирский поезд | 8/5 х(у+1) | 8/5 х | у+1 |
| Товарный поезд | х(у+4) | х ? | у+4 |
По условию задачи поезда прошли одно и то же расстояние. Получаем систему уравнений
8/5 х(у+1) = х(у+4)
(х+50)у = х(у+4).
По условию задачи х>0, тогда
8(у+1) = 5(у+4)
(х+50)у = х(у+4),
3у = 12
(х+50)у = х(у+4),
у = 4
х+50 = 2х,
у = 4
х = 50.
Полученные значения неизвестных удовлетворяют условию х>0, у>0, значит удовлетворяют условию задачи.
50 км/ч – скорость товарного поезда.
50+50 = 100 (км/ч) – скорость скорого поезда.
Проверка по условию задачи.
50 км/ч – скорость товарного поезда,
4+4 = 8 (ч) – время движения товарного поезда.
50*8 = 400 (км) – расстояние, которое прошёл товарный поезд.
50*8/5 = 80 (км/ч) – скорость пассажирского поезда.
4+1 = 5 (ч) – время движения пассажирского поезда.
80*5 = 400 (км) – расстояние, которое прошёл пассажирский поезд.
4 ч – время движения скорого поезда.
50+50 = 100 (км/ч) – скорость скорого поезда.
100*4 = 400 (км) – расстояние, которое прошёл скорый поезд.
Каждый поезд прошёл одно и то же расстояние.
Задача решена верно.
Ответ: 50 км/ч, 100 км/ч.
Анал
xn--i1abbnckbmcl9fb.xn--p1ai
