Интегрирование методом замены переменной
С помощью замены переменной можно вычислить простые интегралы и, в некоторых случаях, упростить вычисление более сложных.
Метод замены переменной заключается в том, что мы от исходной переменной интегрирования, пусть это будет x, переходим к другой переменной, которую обозначим как t. При этом мы считаем, что переменные x и t связаны некоторым соотношением x = x(t), или t = t(x). Например, x = ln t, x = sin t, t = 2x + 1, и т.п. Нашей задачей является подобрать такую зависимость между x и t, чтобы исходный интеграл либо свелся к табличному, либо стал более простым.
Основная формула замены переменной
Рассмотрим выражение, которое стоит под знаком интеграла. Оно состоит из произведения подынтегральной функции, которую мы обозначим как f(x) и дифференциала dx: . Пусть мы переходим к новой переменной t, выбрав некоторое соотношение x = x(t). Тогда мы должны выразить функцию f(x) и дифференциал dx через переменную t.
Чтобы выразить подынтегральную функцию f(x) через переменную t, нужно просто подставить вместо переменной x выбранное соотношение x = x(t).
Преобразование дифференциала выполняется так:
.
То есть дифференциал dx равен произведению производной x по t на дифференциал dt.
Тогда
.
На практике, чаще всего встречается случай, в котором мы выполняем замену, выбирая новую переменную как функцию от старой: t = t(x). Если мы догадались, что подынтегральную функцию можно представить в виде
,
где t′(x) – это производная t по x, то
.
Итак, основную формулу замены переменной можно представить в двух видах.
(1) ,
где x – это функция от t.
(2) ,
где t – это функция от x.
Важное замечание
В таблицах интегралов переменная интегрирования, чаще всего, обозначается как x. Однако стоит учесть, что переменная интегрирования может обозначаться любой буквой. И более того, в качестве переменной интегрирования может быть какое-либо выражение.
В качестве примера рассмотрим табличный интеграл
.
Здесь x можно заменить любой другой переменной или функцией от переменной. Вот примеры возможных вариантов:
;
;
.
В последнем примере нужно учитывать, что при переходе к переменной интегрирования x, дифференциал преобразуется следующим образом:
.
Тогда
.
В этом примере заключена суть интегрирования подстановкой. То есть мы должны догадаться, что
.
После чего интеграл сводится к табличному.
.
Можно вычислить этот интеграл с помощью замены переменной, применяя формулу (2). Положим t = x2 + x. Тогда
;
;
.
Примеры интегрирования заменой переменной
1) Вычислим интеграл
.
Замечаем, что (sin x)′ = cos x. Тогда
.
Здесь мы применили подстановку t = sin x.
2) Вычислим интеграл
.
Замечаем, что . Тогда
.
Здесь мы выполнили интегрирование заменой переменной t = arctg x.
3) Проинтегрируем
.
Замечаем, что . Тогда
. Здесь, при интегрировании, произведена замена переменной t = x2 + 1.
Линейные подстановки
Пожалуй, самыми распространенными являются линейные подстановки. Это замена переменной вида
t = ax + b,
где a и b – постоянные. При такой замене дифференциалы связаны соотношением
.
Примеры интегрирования линейными подстановками
A) Вычислить интеграл
.
Решение.
.
B) Найти интеграл
.
Решение.
Воспользуемся свойствами показательной функции.
.
ln 2 – это постоянная. Вычисляем интеграл.
.
C) Вычислить интеграл
.
Решение.
Приведем квадратный многочлен в знаменателе дроби к сумме квадратов.
.
Вычисляем интеграл.
.
D) Найти интеграл
.
Решение.
Преобразуем многочлен под корнем.
.
Интегрируем, применяя метод замены переменной .
.
Ранее мы получили формулу
.
Отсюда
.
Подставив это выражение, получим окончательный ответ.
E) Вычислить интеграл
.
Решение.
Применим формулу произведения синуса и косинуса.
;
.
Интегрируем и делаем подстановки.
.
Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.
16. Метод замены переменной, интегрирование по частям
Во многих случаях удается введением вместо X новой переМенной Z, связанной с Х некоторым соотношением, свести интеграЛ к новому интегралу, который содержится в таблице ИЛи легко находится другим методом. Этот метод интегрирования получил название Метода замены переменной или метода интегрироВАния ПодстаноВКой.
Введем вместо Х новую переменную Z, связанную с Х соотНОшенИЕм , где — непрерывная, строго монотонная функция, имеющая непрерывную производную . Покажем, что тогда имеет место равенство
(1)
Формула (1) называется формулой замены переменного.
Для доказательства соотношения (1) достаточно убедиться, что дифференциалы обеих его частей равны.
Дифференцируя левую часть соотношения (1), имеем:
Но так как то Это дает
(2)
С другой стороны, дифференцируя правую часть соотношения (1), имеем:
(3)
Соотношения (2) и (3) показывают, что
Откуда следует равенство интегралов:
Таким образом, формула (1) доказана.
Допустим, что функция такова, что интеграл, стоящий в правой части соотношения (1), легко находится. Пусть
Тогда для нахождения интеграла достаточно разрешить уравнение относительнО Z, т. Е. найти обратную функцию и подставить ее в Ф(Z):
Замечание. Формулу (1) легко запомнить. Ее правая часть получается, если в интеграле формально заменИТь Х На , a Dx на .
Рассмотрим несколько примеров.
Пример 1.
Положив , находим Dx = Adz. ПримЕНяя, формулу (1), получаем
Но интеграл согласно формуле VIII.
Поэтому
Возвращаясь снова к переменной Х, получим
Пример 2.
Полагая , и применяя формулу (1), имеем:
Если под интегралом стоит суперпозиция двух функций, умноженная на производную от внутренней функции, то вычисления обычно упрощаются, если заменить внутреннюю функцию новой переменной. Действительно, применяя тогда формулу замены переменной, получим
Где . Заметим, что эта формула отличается от формулы (1) только обозначением независимых переменных.
Пример 3.
Замечая, что полагаем
ЭТО дает: Dz = CosXdx и
УдачноЙ заменой переменного мы свели наш интеграл к интегралу от степенной функции.
Так как
То
Пример 4.
Замечая, что положим Это дает и, следовательно,
Таким образом,
(XI)
Пример 5.
Полагая имеем:
Итак,
(XII)
Пример 6.
Этот интеграл, конечно, можно было бы вычислить методом разложения, если разложить по формуле бинома Ньютона.
Возвращаясь к переменной Х, окончательно получим
Пример 7.
Заметим, что диффЕРенциал знаменателя отличается от числителя на постоянный множитель — 5; поэтому напрашивается следующая замена переменной: , откуда и, СлеДовательно,
Из таблицы находим: Поэтому
Пример 8. Интегралы в примерах 4, 5, 7 являются частными СЛучаями интеграла более общего вида:
Т. Е. интеграла от дроби, числитель которой является дифференциалом знаменателя.
Полагая , имеем ,
Так, например,
Так как
С приобретением навыка в интегрировании, можно не производить в простейших интегралах подробно всех выкладок, связанных с заменой переменной. Покажем это на примерАХ.
Пример 9.
Замечая, что и вводя поправку , имеем:
Пример 10.
Замечая, что , имеем согласНО формуле X:
Пример 11.
Часто применяют одновременно метод интегрирования разложением и метод замены переменной.
Пример 12.
Так как а
То
Метод интегрирования по частям состоит в следующем. Пусть и — Две функции от Х, имеющие непрерывные производные. Известно, что
(4)
Интегрируя обе части равенства (4), имеем:
или
Откуда
(5)
Произвольной постоянной, получившейся при интегрировании выражения D(Uv), мы не пишем, включая ее мысленно в оставшийся в правой части интеграл .
Формула (5) называется Формулой интЕГрирования по частям, Она дает возможность свести вычисление интеграла к вычислению интеграла .
Для успешного применения этого метода целесообразно пользоваться следующими общими указаниями:
1.
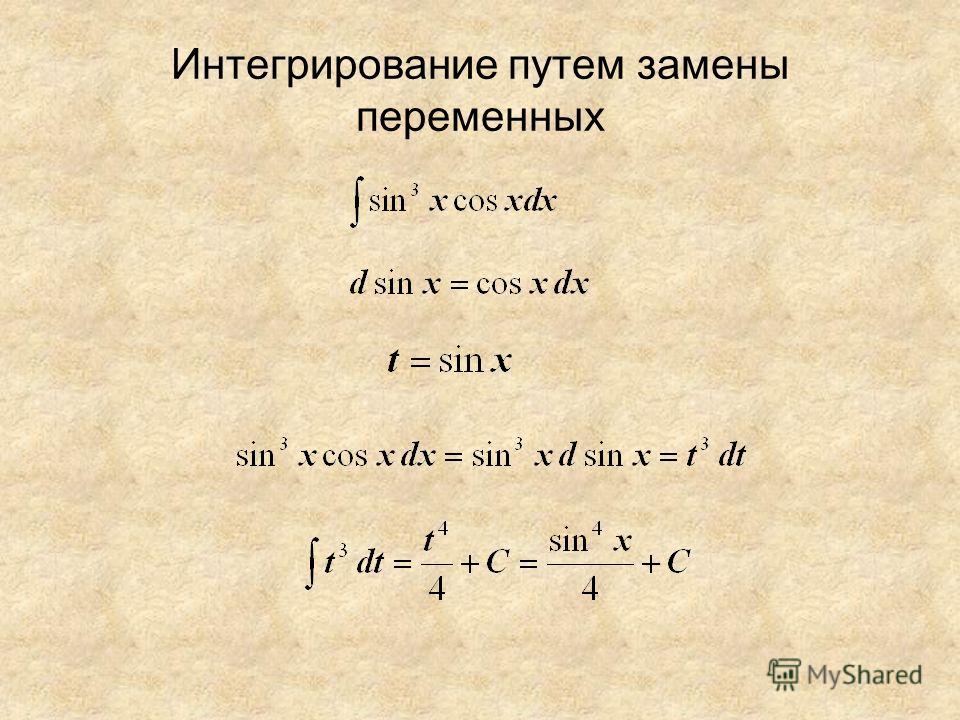Подынтегральное выражение разбивают на 2 множителя: И и DN (множиТЕль DN обязательно содержит Dx).
2. Множитель Dv выбирается так, чтобы по нему можно было бы найти первообразную V.
3. Интеграл должен получиться, вообще говоря, проще, чем данный интеграл.
ПояСНим применение этого метода примерами.
ПРимер 1.
Имеется несколько возможностей. Например, Можно положить , a , можно положить , a
Полагая найдем
Применяя формулу (5), получаем
Это разбиение на множители следует признать неудачНЫм, так как оно приводит к более сложному интегралу.
Положим теперь
отсюда найдем
Применяя формулу (5), имеем:
Но Поэтому окончательно получаем
Следовательно, это разбиение Подынтегрального выражения на множители следует признать удачным.
Пример 2.
Положим
; это дает
Применяя формулу (5), получим
Таким образом,
Иногда для получения окончательного результата ЦелесообРазно интегрирование по частям применять послеДОвательно несколько раз.
Укажем на некоторые, часто встречающиеся интегралы, которые вычисляются методом интегрирования по частям.
I. Интегралы вида: ГДе Р(Х) — Многочлен, а — Постоянное число, легко берутся методом интегрирования по частям, если положить Р(Х)=И.
Применяя этот метод, например, к интегралу Получим
Следовательно,
Второй интеграл является интегралом того ЖЕ типа, что и первый, но степень многочлена Р’(Х) на единицу ниже степени многочлена Р(Х). Применяя к нему снова интегрирование по частям и повторяя его столько раз, какова степень многочлена сведем, в коНЦе концов, наш ИНтеграл к интегралу .
Таким же путем вычисляются и интегралы
Пример. Вычислить интеграл
Положим
Применяя формулу интегрирования по частям, получим
К последнему интегралу снова применяем метод интегрирования по частям:
Следовательно,
Изложенный метод интегрирования показывает, что интегралы вида Где Р(Х) — многочлен, всегда берутся в элементарных функциях.
В отличие от них, интегралы где R(X) — Рациональная дробь, не всегда интегрируются в элементарных функциях. Так, например, интегралы Не выражаются в элЕмЕнтарных функциях.
II. Интегралы ВИда: Где Р(Х) — Многочлен, всегда берутся методом интегрирования по частям, если за И принять трансцендентную функцию, являющуюся множителем при Р(Х). Рассмотрим примеры.
Пример 1.
Полагаем
Формула (5) дает:
Пример 2.
Полагаем
Следовательно,
III. Вычисление интегралов вида:
Укажем, наконец, еще на один случай, когда интегрироВАние по частям приводит к цели. Пусть нам надо вычислить иНТеграл
Допустим, что после однократного или двукратного интегрирования по частям оказалось возможным представить этот интеграл в виде суМмЫ некоторой известной функции и интеграла от F(X), причем перед интеграЛОм стоит коэффициент K
Тогда, перенося второе слагаемое в левую часть, получим
Откуда где одна из первообразных от ВыражеНия .
Чтобы НАйти семейство всех первообразных (т. Е. неопределенный интеграл) остается к правой части добавить произвольное постоянное С:
Интегралы вида берутся с помощью только что указанного приема. Рассмотрим конкретный пример:
Пример.
Положим
Тогда
К последнему интегралу снова применим интегрирование по частям, положив
Тогда
Следовательно:
Определяем отсюда
Мы разобрали основные методы интегрирования. Перейдем тЕПерь к систематическому изучению того, как применяются эти методы к интегрированию конкретных классов элементарных функций. Для дальнейшего изложения нам понадобятся некоторые сведения о многочленах, которые мы приводим в слеДующем Пункте.
| < Предыдущая | Следующая > |
|---|
u-подстановка Как заменить переменные в интегралах
u-подстановка Как заменить переменные в интегралах Copyright 20022022 Стэн Браун, BrownMath.
com
Резюме: Подстановка — чрезвычайно мощный метод интеграции. Хотя шаги аналогичны для определенного и неопределенного интегралов, есть два различия, и многие студенты, кажется, не могут их удержать прямой. Эта страница сортирует их в удобной таблице, затем следует параллельный пример.
Процедура
Просто для простоты предположим, что исходная переменная х . Естественно, те же шаги будут работать для любой переменной интегрирования.
| Неопределенные интегралы | Определенные интегралы | |
|---|---|---|
| 1 | Определите u для изменения переменных. (Обычно u будет внутренней функцией в составной функции.) | |
| 2 | Дифференцируйте и , чтобы найти du , и найдите dx . | |
| 3 | Подставить под интеграл и упростить. | |
| 4 | (нечего делать) | Используйте подстановку, чтобы изменить пределы интегрирования. Будьте осторожны, чтобы не изменить порядок. Пример: если u = 3− x тогда
становится . |
| 5 | Если x все еще встречается в любом месте подынтегральной функции, возьмите ваше определение u из шага 1, решите x через u , подставьте под интеграл и упростите. | |
| 6 | Интегрировать. | |
| 7 | Замените на , так что ваш ответ будет равен x . | Оцените с помощью u верхний и нижний новых пределов и вычтите. Нет необходимости конвертировать из u обратно в x . |
Пример
Вот полный пример с неопределенными и определенными интегралами показаны параллельно.
| Неопределенный интеграл | Определенный интеграл | |
|---|---|---|
| 1 | u = x −5 (внутренний функция) | |
| 2 | дю = 3 х дх дх = дю / (3 х ) | |
| 3 | После подстановки u является переменной интегрирования, а не x .  Но границы в терминах и еще не установлены, и это существенно. | |
| 4 | (нечего делать) | u = x -5 x = -1 дает u = -6; x = 1 дает u = −4 |
| 5 | Подынтегральная функция по-прежнему содержит x (в форме x ). Используйте уравнение из шага 1, u = x −5, и найдите x = u +5. | |
| 6 | U 6 + 6 U 5 + C = ( U +6) U 5 + C | (Факторинг, хотя и не является строго обязательным, упрощает следующий шаг.) |
| 7 | ( х -5+6)( х -5) 5 + С = ( х +1)( х -5) 5 + 2 2 | (−4+6)(−4) 5 − (−6+6)(−6) 5 = 2(−1024) − 0 = −2048 (ответ) |
Поскольку эта статья поможет вам,
, пожалуйста, нажмите, чтобы сделать пожертвование!Поскольку эта статья поможет вам,
, пожалуйста, сделайте пожертвование на
BrownMath.
com/donate.
Обновления и новая информация: https://BrownMath.com/calc/
Карта сайта | Поиски | Главная страница | Контакт
2.13 Замена переменных Формула
Наиболее простой арифметической операцией является сложение. Интегральное исчисление обобщает эту операцию определенным интегралом, представляющим собой обобщенную сумму. Определенные интегралы будут играть важную роль в наших обсуждениях стоимости, подверженной риску (VaR). Действительно, задача расчета стоимости портфеля, подверженного риску, в значительной степени состоит в оценке определенного интеграла.
Определенные интегралы часто можно упростить путем разумной замены переменных. Если интеграл должен быть оценен с использованием численных методов, замена переменных может быть существенной, чтобы избежать сингулярности или преобразовать неограниченную область интегрирования в ограниченную. Идея замены переменных так же стара, как и само сложение. Легче считать яйца десятками, чем по отдельности.
Для одномерного интеграла по интервалу [a, b] обратимая непрерывно дифференцируемая замена переменных x = G ( U ) Выход
[2,166]
Например,
[2,167]
Обобщение до нескольких измерений, рассмотрите интегрируемую функцию F : N , , и в : 7, рассмотрите интегрируемую функцию F : N . 1, и в интегрируемой функции F : n . . . . . непрерывно дифференцируемая замена переменных g : n → n . Тогда
[2.168]
где Ω n , и | джг ( у )| является определителем якобиана g . Рассмотрим интеграл:
[2.169]
, где область Ω указана на рис. 2.21.
Приложение 2.21: область ω ограничена четырьмя линиями x 1 = 0, x 2 = 0, x 2 = 1 — x 7 , 2 = 1 — x 7 , и , 1 — x , 2 = 1 — x = 1 — x .
х 2 = 2 – х 1 .
Интеграл [2.169] трудно решить напрямую, но рассмотрим замену переменных x = G ( U ) Определено
[2,170]
Якобианский детерминант G —
[2,171]
, так, на 2,166 88].
[2.172]
Регион г -1 (Ом) указан в Приложении 2.22. Его площадь в два раза больше исходной области, поэтому неудивительно, что определитель Якоби вводит в интеграл компенсирующий масштабный коэффициент 1/2 [2.172].
Приложение 2.22: область G –1 (ω) ограничена четырьмя линиями U 2 = 1, U 2 = 2, U 2 48 = 2, U 2 48 = 2, U 7 2 48 = 2, U 2 = 2. 1 и u 2 = – u 1 .
Область г -1 (Ω) имеет удобную форму, позволяющую представить интеграл в виде
[2,173]
Это легко оценить как 0,8146.