Иррациональные числа какой буквой обозначается: Иррациональные числа: определение и примеры. Также примеры рациональных чисел

Содержание

Рациональное иррациональное число — Большая Энциклопедия Нефти и Газа, статья, страница 3

Cтраница 3

Множество ( совокупность) всех рациональных и иррациональных чисел называется множеством действительных чисел. [31]

Множество действительных чисел R имеет подмножества натуральных, целых, рациональных и иррациональных чисел. Поэтому рассмотрим случаи, когда показатель г есть натуральное, целое, рациональное и иррациональное числа. [32]

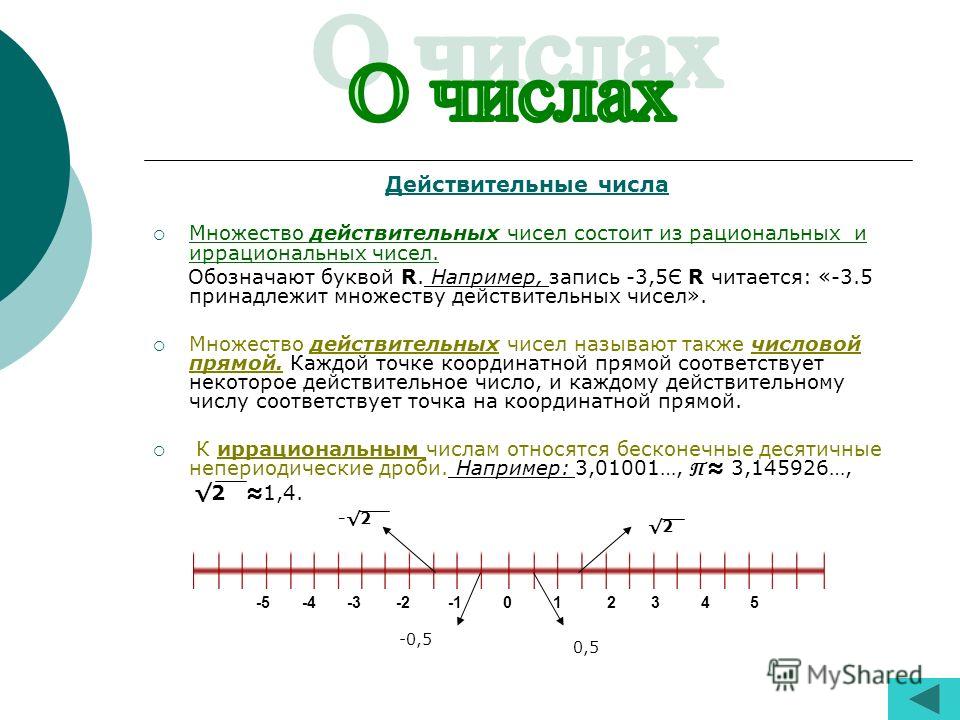
Действительными ( или вещественными) числами называются рациональные и иррациональные числа. Множество всех действительных чисел обозначается буквой R. Каждое действительное число может быть изображено точкой на числовой прямой. [33]

Очевидно, для системы рациональных чисел все рациональные и иррациональные числа являются точками сгущения; она представляет собой простой пример числовой последовательности с бесконечно большим, числом точек сгущения. [34]

Действительными ( или вещественными) числами называются

рациональные и иррациональные числа. Множество всех действительных чисел обозначается буквой R. Каждое действительное число может быть изображено точкой на числовой прямой. [35]

Действительными ( или вещеспиенными) числами называются рациональные и иррациональные числа. Множество всех действительных чисел обозначается буквой R. Каждое действительное число может быть изображено точкой на числовой прямой. [36]

Возможны только два типа движений: с рациональным и иррациональным числом вращения. [37]

Таким образом, множество действительных чисел состоит из рациональных и иррациональных чисел. [38]

В чем состоит различие бесконечных десятичных дробей, представляющих рациональные и иррациональные числа. [39]

При практических вычислениях с ограниченной точностью различие между рациональными и иррациональными числами

не проявляется.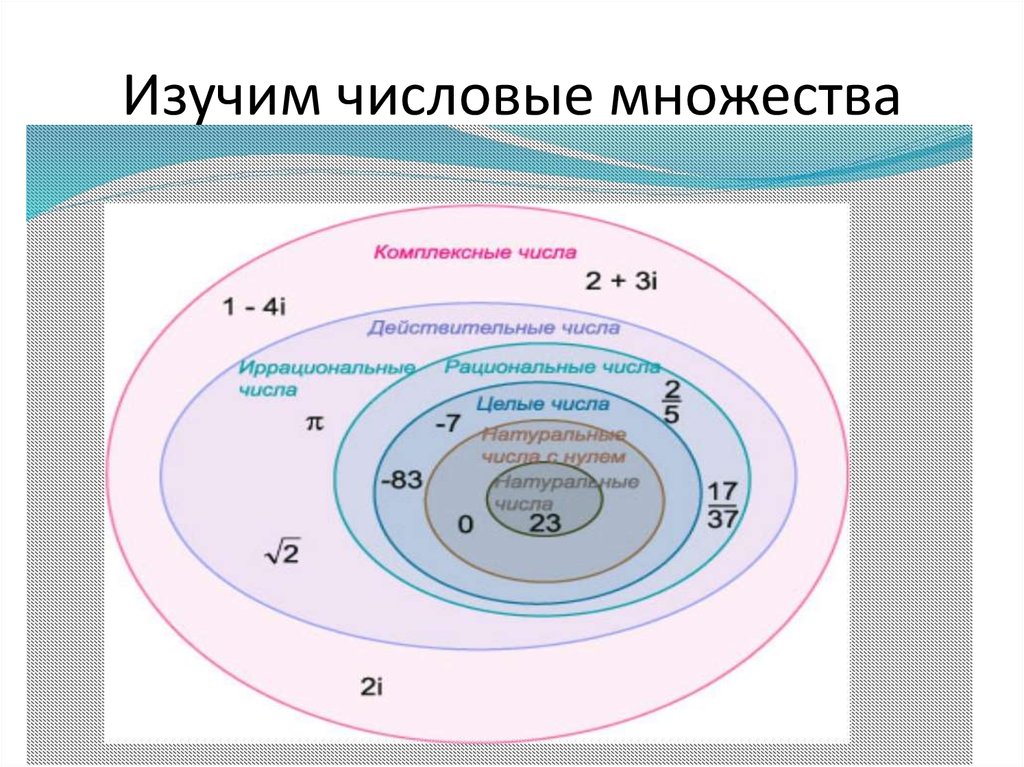

[40]

Через Q и Р обозначим подпространства пространства R, состоящие из рациональных и иррациональных чисел соответственно. [41]

Множество всех рациональных чисел принято обозначать символом Q; множество всех рациональных и иррациональных чисел обозначается символом R и называется множеством действительных чисел. [42]

Напомним, что множество вещественных чисел разбивается на два множества — рациональных и иррациональных чисел. [43]

Действительные числа ( примеры их были продемонстрированы на рис. 6, б, в и г) соответствуют рациональным и иррациональным числам в обычном понимании. Значение действительного числа задается или непосредственным написанием, или вводится, или является результатом вычисления, но во всех случаях — с некоторой конечной погрешностью, которая определяется ограниченной разрядной сеткой машины. Для определенности будем предполагать, что действительные числа могут быть представлены девятью цифровыми разрядами.

[44]

Все эти трудности исчезают при простом признании иррациональных чисел и знакомстве с некоторыми свойствами совокупности вещественных чисел, то есть объединения рациональных и иррациональных чисел. [45]

Страницы: 1 2 3

Иррациональные числа — презентация онлайн

Подготовил:
Лычагин Андрей 34 группа.
Проверила:
Индюкова Наталья Федоровна.

2. Определение

Иррациона́льное число́ — это
вещественное число, которое
не является рациональным, то
есть которое не может быть
представленным в виде
дроби m/n , где m — целое
число, n — натуральное
число.
Множество иррациональных
чисел(I) обычно обозначается
таким образом: I=R/Q —
множество иррациональных
чисел есть разность множеств
вещественных и
рациональных чисел.

3. История

Иррациональные числа были неявным образом
восприняты индийскими математиками в VII
веке до нашей эры, когда Манава (ок.

2 четное, тогда и b четно.
Однако было доказано, что b нечетное. Противоречие.
Открытие Гиппаса поставило перед пифагорейской математикой
серьезную проблему, разрушив предположение, что числа и
геометрические объекты едины и неразделимы, лежавшее в основе
всей теории.
Феодор Киренский доказал иррациональность
корней натуральных чисел до 17 (исключая,
естественно, точные квадраты — 1, 4, 9 и 16), но
остановился на этом, так как имевшаяся в его
инструментарии алгебра не позволяла доказать
иррациональность квадратного корня из 17.
Позже Евдокс Книдский (410 или 408 г. до н. э. — 355
или 347 г. до н. э.) развил теорию пропорций, которая
принимала во внимание как рациональные, так и
иррациональные отношения. Это послужило
основанием для понимания фундаментальной сути
иррациональных чисел. Величина стала считаться не
числом, но обозначением сущностей, таких как
отрезки прямых, углы, площади, объемы, промежутки
времени — сущностей, которые могут меняться
непрерывно (в современном понимании этого
слова).

6. Свойства

Всякое вещественное число может быть записано бесконечной
десятичной дробью, при этом иррациональные числа и только
они записываются непериодическими бесконечными
десятичными дробями.
Иррациональные числа определяют Дедекиндовы сечения в
множестве рациональных чисел, у которых в нижнем классе нет
наибольшего, а в верхнем нет наименьшего числа.
Каждое трансцендентное число является иррациональным.
Каждое иррациональное число является либо алгебраическим,
либо трансцендентным.
Множество иррациональных чисел всюду плотно на числовой
прямой: между любыми двумя числами имеется
иррациональное число.
Множество иррациональных чисел несчётно, является
множеством второй категории

7. Число «пи»

-это
одно из множества
представителей иррациональных чисел
«пи» — математическая константа,
выражающая отношение длины
окружности к длине её диаметра.
Обозначается буквой греческого
алфавита «пи».

8. Трансцендентность

π — трансцендентное число, это означает, что оно не
может быть корнем какого-либо многочлена с
целыми коэффициентами. Транцендентность числа
π была доказана в 1882 году профессором
Кенигсбергского, а позже Мюнхенского университета
Линдеманом. Доказательство упростил Феликс Клейн
в 1894 году.
Поскольку в евклидовой геометрии площадь круга и
длина окружности являются функциями числа π, то
доказательство трансцендентности π положило конец
спору о квадратуре круга, длившемуся более 2,5
тысяч лет.

9. Соотношения

Известно много
формул числа π:
Франсуа Виет, 1593:
Формула
Ряд
Валлиса:
Лейбница:
Тождество Эйлера:
Т. н. «интеграл Пуассона» или
«интеграл Гаусса»
Интегральный синус:

11. История

Впервые обозначением этого числа
греческой буквой воспользовался
британский математик Джонс в
1706 году, а общепринятым оно
стало после работ Леонарда
Эйлера в 1737 году.

Это обозначение
происходит от начальной буквы
греческих слов περιφέρεια —
окружность, периферия и
περίμετρος — периметр.История
числа π шла параллельно с
развитием всей математики.
Некоторые авторы разделяют весь
процесс на 3 периода: древний
период, в течение которого π
изучалось с позиции геометрии,
классическая эра, последовавшая
за развитием математического
анализа в Европе в XVII веке, и эра
цифровых компьютеров.
Архимед, возможно,
первым предложил
математический способ
вычисления π. Для этого он
вписывал в окружность и
описывал около неё
правильные
многоугольники. Принимая
диаметр окружности за
единицу, Архимед
рассматривал периметр
вписанного
многоугольника как
нижнюю оценку длины
окружности, а периметр
описанного
многоугольника как
верхнюю оценку.
Рассматривая правильный
96-угольник, Архимед
получил оценку .
Около 265 года н. э.
математик Лю Хуэй из
царства Вэй
предоставил простой и
точный итеративный
алгоритм (англ.

) с
любой степенью
точности. Он
самостоятельно провёл
вычисление для 3072угольника и получил
приближённое значение
для π по следующему
принципу:
Позднее Лю Хуэй
придумал быстрый
метод вычисления π и
получил приближённое
значение 3,1416 только
лишь с 96-угольником,
используя
преимущества того
факта, что разница в
площади следующих
друг за другом
многоугольников
формирует
геометрическую
прогрессию со
знаменателем 4.

15. Нерешённые проблемы

Неизвестно,
являются ли числа π и e
алгебраически независимыми.
Неизвестно, являются ли числа π + e, π −
e, πe, π / e, πe, ππ трансцендентными.
До сих пор ничего не известно о
нормальности числа π; неизвестно
даже, какие из цифр 0—9 встречаются
в десятичном представлении числа π
бесконечное количество раз.

16. История вычисления

В
1997 году Дэйвид Бэйли, Питер
Боруэйн и Саймон Плуфф открыли
способ (англ.

) быстрого вычисления
произвольной двоичной цифры числа π
без вычисления предыдущих цифр,
основанный на формуле

17. Мнемонические правила

Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Надо только постараться
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Три, четырнадцать, пятнадцать,
Девять, два, шесть, пять, три, пять.
Чтоб наукой заниматься,
Это каждый должен знать.
Можно просто постараться
И почаще повторять:
«Три, четырнадцать, пятнадцать,
Девять, двадцать шесть и пять».
Подсчитайте количество букв в каждом слове
в нижеприведенных фразах (без учёта знаков
препинания) и запишите эти цифры
подряд — не забывая про десятичную запятую
после первой цифры «3», разумеется.
Получится приближенное число Пи:
Это я знаю и помню прекрасно: Пи многие
знаки мне лишни, напрасны.
Кто и шутя, и скоро пожелаетъ Пи узнать
число — ужъ знаетъ!
Вот и Миша и Анюта прибежали Пи узнать
число они желали.

Если
соблюдать стихотворный размер, можно
довольно быстро запомнить:
Три, четырнадцать, пятнадцать, девять два, шесть
пять, три пять
Восемь девять, семь и девять, три два, три
восемь, сорок шесть
Два шесть четыре, три три восемь, три два семь
девять, пять ноль два
Восемь восемь и четыре, девятнадцать, семь,
один

19. Дополнительные факты

Неофициальный праздник
«День числа пи» отмечается
14 марта, которое в
американском формате дат
(месяц/день) записывается
как 3.14, что соответствует
приближённому значению
числа π. Считается, что
праздник придумал в 1987
году физик из СанФранциско Ларри Шоу,
обративший внимание на то,
что 14 марта ровно в 01:59
дата и время совпадают с
первыми разрядами числа Пи
= 3,14159.
Памятник числу
«пи» на ступенях
перед зданием
Музея искусств в
Сиэтле
Ещё одной датой,
связанной с числом π,
является 22 июля,
которое называется
«Днём приближённого
числа Пи» (англ.

Pi
Approximation Day), так
как в европейском
формате дат этот день
записывается как 22/7, а
значение этой дроби
является приближённым
значением числа π.

21. А вам слабо?

17 июня 2009 года украинский нейрохирург, доктор
медицинских наук, профессор Андрей Слюсарчук установил
мировой рекорд, запомнив 30 миллионов знаков числа Пи,
которые были напечатаны в 20 томах текста. С установлением
нового рекорда Андрея Слюсарчука официально поздравил
президент Украины Виктор Андреевич Ющенко. Поскольку
устное перечисление 30 млн цифр π со скоростью одна
цифра в секунду заняло бы почти год (347 дней) при
непрерывном перечислении 24 часа в сутки, 7 дней в неделю, то
был применён следующий подход для проверки рекорда: во
время демонстраций Слюсарчука просят назвать произвольно
выбранные проверяющими последовательности цифр числа
Пи, расположенные на произвольно выбранных местах
произвольных страниц 20-томной распечатки, группированной в
упорядоченные таблицы.

Он многократно успешно проходит
этот тест.
ЧИСЛО
«Е»

23. Число «е»

-это еще одно число из
множества представителей
иррациональных чисел
e — математическая
константа, основание
натурального логарифма,
трансцендентное число.
Иногда число e называют
числом Эйлера или числом
Непера. Обозначается
строчной латинской буквой
«e». Численное значениe
е= 2,718 281 828 459 045 235
360 287 471 352 662 497 757…

24. Способы определения

Число e может быть определено несколькими
способами.
Через предел:
Как
сумма ряда:
Как
единственное число a, для которого
выполняется
Как
единственное положительное число a, для
которого верно

25. Свойства

Данное свойство
играет важную роль в
решении
дифференциальных
уравнений. Так,
например,
единственным
решением
дифференциального
уравнения
является функция
,
где c — произвольная
константа.

Число
e трансцендентно. Это первое число,
которое не было выведено как трансцендентное
специально, его трансцендентность была
доказана только в 1873 году Шарлем Эрмитом.
Предполагается, что e — нормальное число, то
есть вероятность появления разных цифр в его
записи одинакова.
Число
дробь
e разлагается в бесконечную цепную
следующим образом:
то есть
Представление
Каталана:

29. История

Данное число иногда называют неперовым
в честь шотландского учёного Непера,
автора работы «Описание удивительной
таблицы логарифмов» (1614 год). Однако
это название не совсем корректно, так как
у него логарифм числа x был равен
Константу впервые вычислил швейцарский
математик Бернулли при анализе
следующего предела:

30. Мнемоника

Мнемо́ника (греч. τα μνημονιχα — искусство запоминания),
мнемоте́хника — совокупность специальных приёмов и способов,
облегчающих запоминание нужной информации и увеличивающих
объём памяти путём образования ассоциаций (связей).

Замена
абстрактных объектов и фактов на понятия и представления,
имеющие визуальное, аудиальное или кинестетическое
представление, связывание объектов с уже имеющейся
информацией в памяти различных типов для упрощения
запоминания.
Приблизительное значение зашифровано в: «Мы порхали и
блистали, но застряли в перевале; не признали наши крали
авторалли» (нужно выписать подряд цифры, выражающие число
букв в словах следующего стишка, и поставить запятую после
первого знака)
Два и семь, восемнадцать,
Двадцать восемь, восемнадцать,
Двадцать восемь, сорок пять,
Девяносто, сорок пять.
Мнемоническое
правило: два и семь, далее два
раза год рождения Льва Толстого (1828), затем
углы равнобедренного прямоугольного
треугольника (45, 90 и 45 градусов). Стихотворная
мнемофраза, иллюстрирующая часть этого
правила: «Экспоненту помнить способ есть
простой: две и семь десятых, дважды Лев
Толстой»
Числа 45, 90 и 45 можно запоминать как «год
победы над фашистской Германией, затем
дважды этот год и снова он»

32.

Интересные фактыВ
IPO компании Google в 2004 году было
объявлено о намерении компании
увеличить свою прибыль на 2 718 281 828
долларов. Заявленное число
представляет собой первые 10 цифр
известной математической константы.

Почему иррациональные числа обозначаются буквой p?

Почему иррациональные числа обозначаются буквой p? Символ. Обычно для обозначения иррационального символа используется символ «P». Поскольку иррациональные числа определяются отрицательно, множество действительных чисел (R), которые не являются рациональным числом (Q), называется иррациональным числом. Символ P часто используется как из-за связи с действительным и рациональным числом.

Чем обозначается иррациональное число?

Обычно иррациональные числа обозначаются цифрой Р – Q .

Почему иррациональные числа обозначаются буквой Q?

На самом деле все квадратные корни натуральных чисел, кроме полных квадратов , иррациональны. Как и все действительные числа, иррациональные числа могут быть выражены в позиционной записи, в частности, в виде десятичного числа. В случае иррациональных чисел десятичное расширение не заканчивается и не заканчивается повторяющейся последовательностью.

Является ли Пи рациональным числом?

Пи — это иррациональное число — вы не можете записать это как не бесконечное десятичное число.

Какое число не записывается в форме P через Q?

Иррациональные числа — это числа, которые нельзя записать в виде p/q, где p и q — целые числа, а q≠0.

Как обозначаются рациональные числа?

Рациональные числа часто обозначаются как Q . Эти числа являются подмножеством действительных чисел, которые составляют полную числовую строку и часто обозначаются R. Действительные числа, которые не могут быть выражены как отношение двух целых чисел, называются иррациональными числами. … Таким образом, это рациональное число.

Почему целые числа обозначаются буквой Z?

Обозначение Z для набора целых чисел происходит от немецкого слова Zahlen, что означает «числа» . Целые числа, строго большие нуля, являются положительными целыми числами, а целые числа, строго меньшие нуля, являются отрицательными целыми числами.

Что означает r q в математике?

Именно из этого я бы все же предположил разность множеств — RQ это множество иррациональных чисел . Это отличается от R / Q, который был бы частной группой. 4.

Почему иррациональные числа нельзя представить в виде дробей?

Иррациональное число не может быть выражено как отношение между двумя числами и не может быть записано в виде простой дроби , потому что не существует конечного числа чисел при записи в виде десятичной дроби . Вместо этого числа в десятичной дроби будут продолжаться вечно, не повторяясь.

Что из следующего Не может быть выражено в форме PQ, где p и Q — целые числа, а Q ≠ 0?

Согласно определению иррациональные числа : Число называется иррациональным, если оно не может быть записано в виде pq, где p и q — целые числа, а q≠0.

Почему 3,14 называется пи?

Только в 18 веке — примерно через два тысячелетия после того, как Архимед впервые вычислил значение числа 3,14 — для обозначения числа впервые было использовано имя «пи». … «Он использовал число , потому что греческая буква Пи соответствует букве «П» … и число Пи равно периметру круга».

Кто открыл число Пи?

пи, в математике отношение длины окружности к её диаметру. Символ π был изобретен британским математиком Уильямом Джонсом в 1706 году для обозначения отношения, а позже популяризирован швейцарским математиком Леонардом Эйлером.

Пи иррационально или трансцендентно?

Значение числа пи приблизительно равно 3,14 или 22/7. До 39 знаков после запятой число пи равно 3,141592653589793238462643383279502884197. Пи равно иррациональное число , что означает, что оно не равно отношению любых двух целых чисел. Его цифры не повторяются.

Является ли ноль рациональным числом, можем ли мы записать его в виде P через q?

Да, нуль является рациональным числом . … Это в форме p/q, где p и q — целые числа, а q ≠ 0.

Почему мы настаиваем на том, что q не равно нулю?

Определено, что q не должно быть равно нулю потому что, если это не так, мы можем иметь дробь конечной формы, деленную на 0 , что не будет ничего, кроме отказа. Следовательно, это условие наложено, чтобы учитывать только определенные дроби.

Можем ли мы записать 0 в форме P через q объяснить на примере?

Каждая дробь является рациональным числом, в котором числитель и знаменатель являются целыми числами, а знаменатель не равен нулю. Поскольку деление 0 на любое число дает нам результат 0, мы можем записать 0 в форме p/q, например, 0/1, 0/2, 0/3 и т. д.

Какой буквой обозначается рациональное число?

Набор рациональных чисел обозначается буквой « Q» .

Что обозначает буква Q в математике?

В математике рациональное число — это число, которое может быть выражено как частное или дробь pq двух целых чисел, числителя p и ненулевого знаменателя q. Например, −37 — рациональное число, как и любое целое число (например, 5 = 51).

Что такое R в системе счисления?

Набор действительных чисел обозначается символом R или. и иногда его называют «настоящим». Вещественные числа можно рассматривать как точки на бесконечно длинной линии, называемой числовой линией или действительной линией, где точки, соответствующие целым числам, расположены на одинаковом расстоянии друг от друга.

Кто изобрел ноль?

Первый современный эквивалент числа ноль происходит от индийского астронома и математика Брахмагупты в 628 году. Его символом для обозначения числа была точка под числом.

Почему мы обозначаем целые числа через Z Правда или ложь?

ответ верно .

Является ли ноль действительным числом?

На самом деле действительные числа — это практически любые числа, которые только можно придумать. … Действительные числа могут быть положительными или отрицательными, и включают число ноль . Их называют действительными числами, потому что они не мнимые, а это другая система чисел.

Что означает P в математике?

В статистике буква P часто используется для обозначения вероятность . Заглавная буква P также используется в математике для обозначения периметра. Итак, как видите, P может использоваться для представления нескольких …

Что такое P union Q?

Объединение двух множеств P и Q представлено как P ∪ Q . Это набор всех различных элементов, которые включены в P или Q. Символ, используемый для обозначения объединения множества, — это ∪. … Мы можем сказать, что пересечение двух заданных множеств, т. е. P и Q, — это множество, которое включает в себя все элементы, общие как для P, так и для Q.

Что такое домен Z?

Набор из целых чисел часто обозначается жирным шрифтом (Z) или жирным шрифтом на доске. буква «Z» — первоначально обозначала немецкое слово Zahlen («числа»). является подмножеством множества всех рациональных чисел, которое, в свою очередь, является подмножеством действительных чисел.

Почему 2 √ иррациональное число?

В частности, греки обнаружили, что диагональ квадрата, длина стороны которого равна 1 единице, имеет диагональ, длина которой не может быть рациональной. По теореме Пифагора, длина диагонали равна квадратному корню из 2 . Так что квадратный корень из 2 иррационален!

Mathscene — Наборы 1 — Урок 3

2007 Расмус Эф ог Джанн Сак

Наборы я

Печать

Урок 3

Реальные числа

Мы можем думать о числовая линия (ось x) как непрерывный ряд точек. Каждая точка на линии обозначает расстояние этой точки от начала координат. Мы используем отрицательный знак (-), если точка находится слева от начала координат и положительный знак (+), если точка справа от начала.

Набор чисел N и Z не единственный числа на линии. Они просто обозначьте несколько точек.

Набор рациональные числа Q также могут быть найдены на прямой, но опять же есть еще другие числа. Между теми, которые у нас уже есть, бесконечно много чисел. упомянуто, что они не могут быть записаны в виде дробей и поэтому не входят в наборы мы имели дело с.

Пропущенные числа называются иррациональными числа. Это числа, которые имеют бесконечное количество цифр после десятичная точка, но цифры не повторяются ни в каком образце и поэтому не являются периодическими. Вот несколько примеров:

0,90

9

0,123456789101112

2 = 1,41421356237

3 = 1,73205080756

р = 3,141592653589

Иррациональные числа вместе с Q (который содержит множества Z и N) образуют непрерывную линию чисел, известную нам как прямую числовую линию ( ось х). Вместе эти наборы образуют набор действительных чисел, обозначенный символом буква Р.

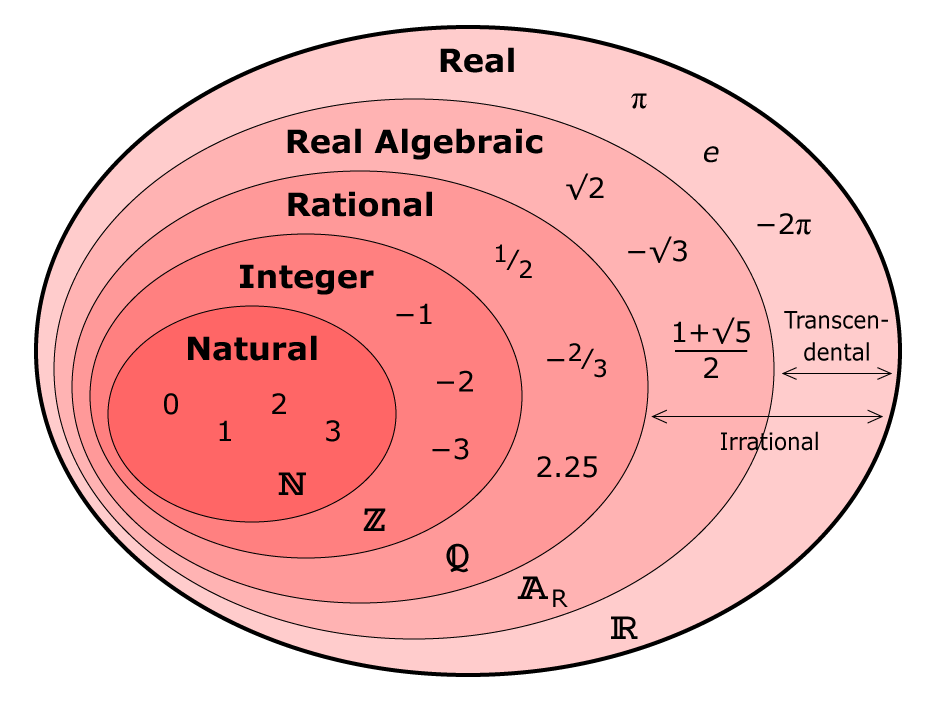
На следующей диаграмме показано соотношение между множества R, Q, Z и N. Множество R содержит другие множества и может быть разделено на рациональные числа и иррациональные числа. Часть схемы, которая не отмеченные линиями, содержат иррациональные числа. Часть, отмеченная горизонтальные линии показывают рациональные числа. (множество Q). Множество Q делится на целые числа (множество Z) и дроби, не являющиеся целыми числами. Наконец Z делится на целые положительные числа (множество N ) и отрицательные числа с нулем.

Мы можем описать интервалы на прямой с действительными числами различными способами. Например, интервал между 1 и 5, включая оба эти цифры можно записать так:

Используя неравенство: 1 х 5

Использование нотации Set: { xR | 1 х 5}

С диаграммой:

Другой способ — ввести новый набор символы, называемые интервальными скобками. Приведенный выше пример можно записать:

[1; 5] или [1, 5] (это варьируется в зависимости от используемых учебников)

Интервал, такой как [1; 5] где включены обе конечные точки, называется закрытым интервалом.

Если мы хотим написать выражение для интервала между двумя числами, то есть не включая конечные точки, мы используем немного разные обозначения.

Например, числа меньше 5, но больше 1,

Используя неравенство: 1 < х < 5

Использование обозначения Set: { xR | 1 < х < 5}