Исследовательский проект по математике на тему: Линейная функция. Модуль. Графики
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа №3»
Исследовательский проект по математике
на тему:
Линейная функция.
Модуль. Графики
Выполнили учащиеся 7А класса
Фролов Григорий
Гузь Егор
Руководитель: учитель математики Митрофанова Е.А.
г. Сасово
2018-2019
Оглавление
1.ВВЕДЕНИЕ 3 2.ОСНОВНАЯ ЧАСТЬ 5
2.1. Теоретическая часть 5
2.2. Практическая часть 5
2.2.1. Задание функции несколькими формулами. 5
2.2.2. Построение графиков по формулам с модулем. 6
3.ЗАКЛЮЧЕНИЕ 9 Список использованной литературы: 10 Приложение 1 11
1. ВВЕДЕНИЕ
ВВЕДЕНИЕ
Актуальность
В 7-м классе мы изучили тему «Функции», на которой получили представление о функции и основных понятиях, связанных с ней. Первое подробное знакомство было с линейной функцией. На уроках рассмотрели основные способы построения графика такой функции. На занятиях внеурочной деятельности, мы столкнулись с трудностями при построении графиков более сложных функций. Проблемы вызвали задания, содержащие функции, заданные с помощью нескольких формул и с модулем. Исходя из всего вышесказанного, мы решили рассмотреть приемы и методы построения графиков, заданных более сложными формулами.
Цель:
Получить навыки построения сложных графиков.
Объекты исследования:
Графики функций и уравнений, заданных «сложными» формулами.
Задачи:
Вспомнить необходимый теоретический материал и систематизировать его.
Разработать план построения графика функции, заданной несколькими формулами.
Выявить закономерности изменения графика линейной функции при наличии знака модуля.
Получить представление о графике уравнения, учиться его строить.
Гипотеза:
Предположим, что появление модуля в формуле линейной функции «ломает» прямую, при этом имеет большое значение, где поставлен знак модуля в формуле.
Методы исследования.
Проанализировать и обобщить теоретический материал.
Опытным путём (по точкам) построить графики уравнений, содержащих модуль.
Проанализировав полученные результаты, составить план построения графиков.
Практическая значимость исследования
Более глубокое рассмотрение темы даст возможность не только получить навыки построения графиков таких функций, но и получить хорошую базу для дальнейшего изучения математики.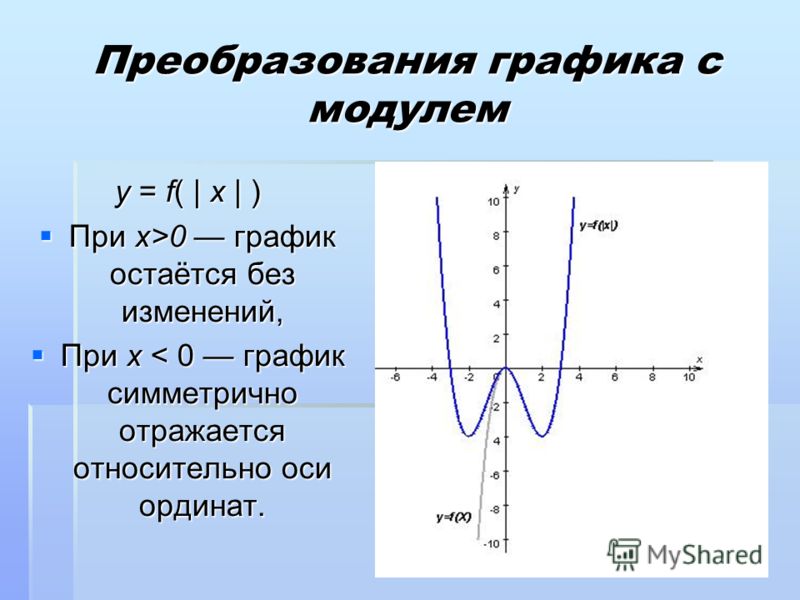
2.ОСНОВНАЯ ЧАСТЬ
2.1. Теоретическая часть
Для работы по данной теме вспомним о линейной функции и ее графике; о модуле числа.
Определение
Линейной функцией называется функция, которую можно задать формулой вида у = kx + b, где х – независимая переменная, k и b – некоторые числа.
Графиком линейной функции является прямая. Для построения графика нужно:
Составить таблицу для двух точек.
Отметить их в системе координат.
Провести через эти точки прямую.
Расположение прямой зависит от значений коэффициентов k и b. Систематизировали все случаи и результаты оформили в таблице. (Приложение1).
Если область определения линейной функции состоит не из всех чисел, то ее график представляет собой соответствующую часть прямой. Например, это может быть полупрямая или отрезок.
Определение модуля
Модулем числа х, называется: само это число, если х – положительное число; нуль, если число х – нуль, число противоположное числу х, если х – отрицательное число. Это определение можно записать в виде:
2.2. Практическая часть
2.2.1. Задание функции несколькими формулами.
На уроке алгебры мы строили график движения туристов по следующим данным: Группа туристов отправилась со станции на турбазу. Первые 2 ч они шли со скоростью 4.5 км/ч. Затем сделали привал на 1ч. На оставшуюся часть пути они затратили полтора часа, проходя ее со скоростью 6 км/ч.(№334).
График получился составленным из трех отрезков, каждый из которых можно задать формулой линейной функции (рис.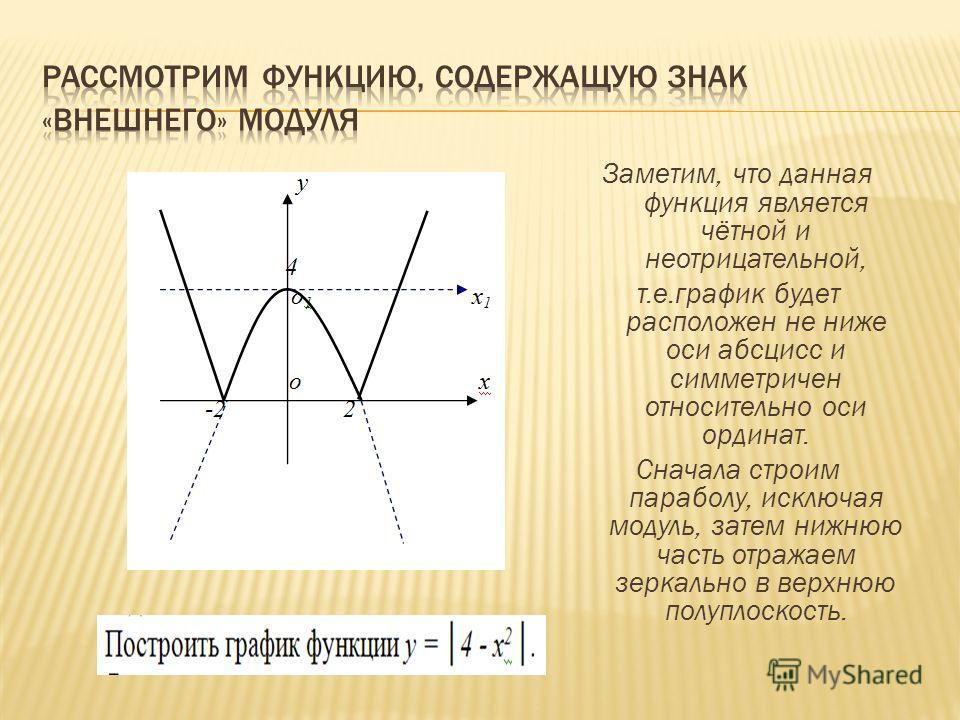 1).
1).
Рис.1
Существуют функции, заданные несколькими формулами. Мы рассмотрели несколько таких функций. Построили их графики.
(рис.2) 2. (рис.3)
Рис.2 Рис.3
Итак, как построить графики таких функций? Очень просто. Нужно каждый кусочек функции построить на выделенном участке, не залезая на соседние.
2.2.2. Построение графиков по формулам с модулем.
Свою работу с модулем мы начали с построения графика функции у =│х│. Используя определение модуля, получили кусочную функцию. (Рис.4)
Рис.4
Сделали вывод, что для построения графиков с модулем надо его раскрыть.
Примеры:
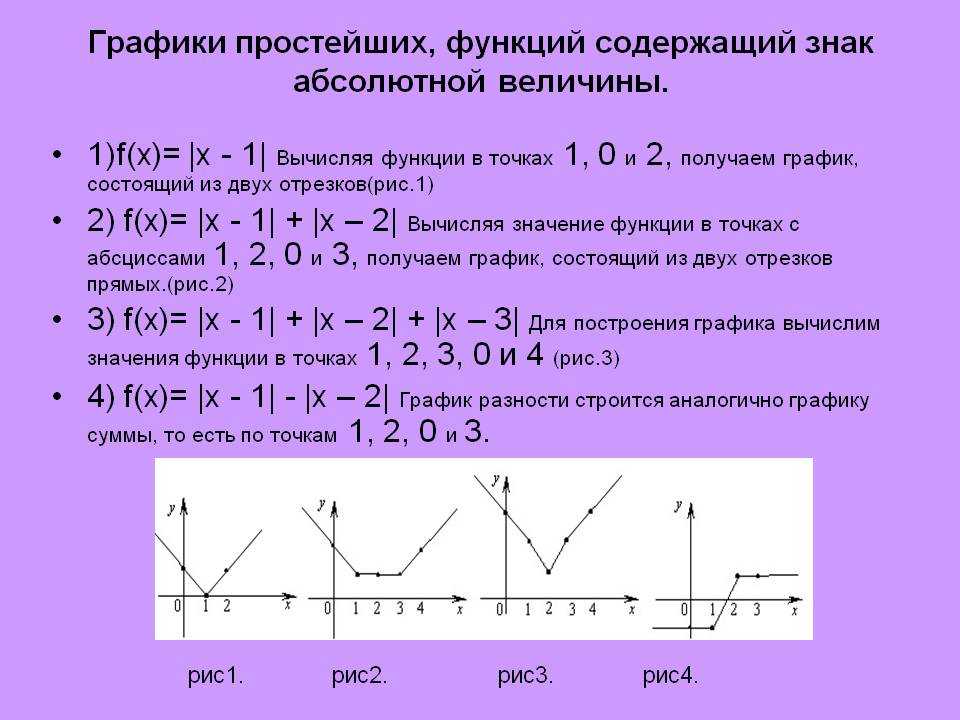
1) у =│х│- 2. (Рис.5)
2) у = 3х — │х│+1.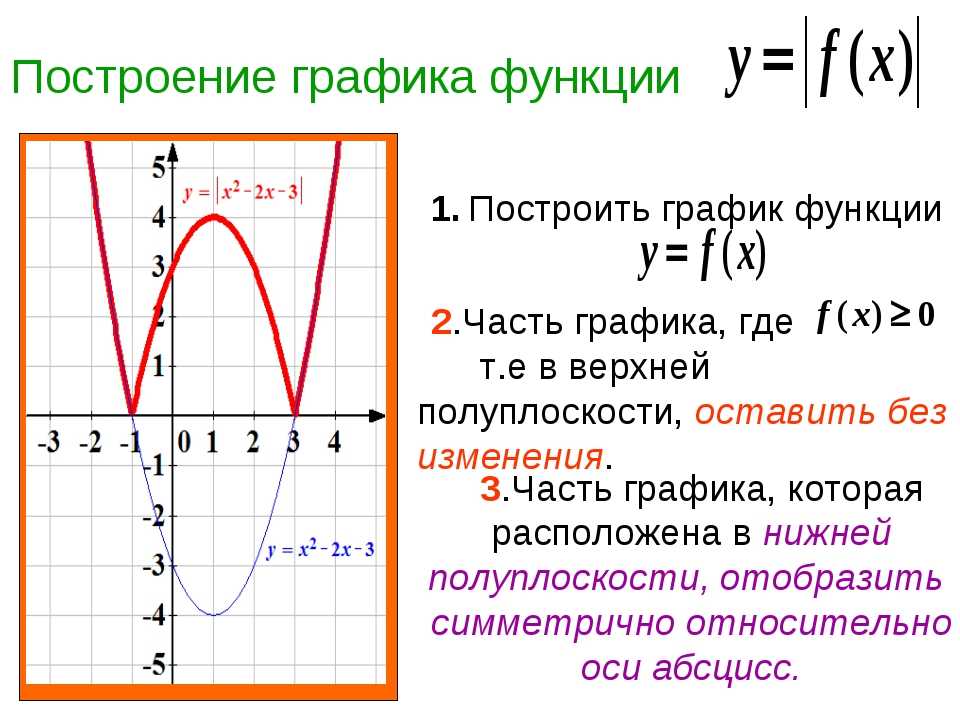 (Рис.6)
(Рис.6)
Рис.5 Рис.6
Итак, для построения графиков подобных функций надо:
1)Раскрыть модуль по определению.
2)Получить функцию, заданную несколькими формулами.
3)Построить график функции, состоящей из нескольких формул.
А как поведет себя график, если модуль в формуле поставить в другом месте? Для этой работы взяли линейную функцию у = х – 2.
Далее, для подтверждения нашей гипотезы о том, что прямая при этом будет «ломаться», были исследованы несколько случаев.
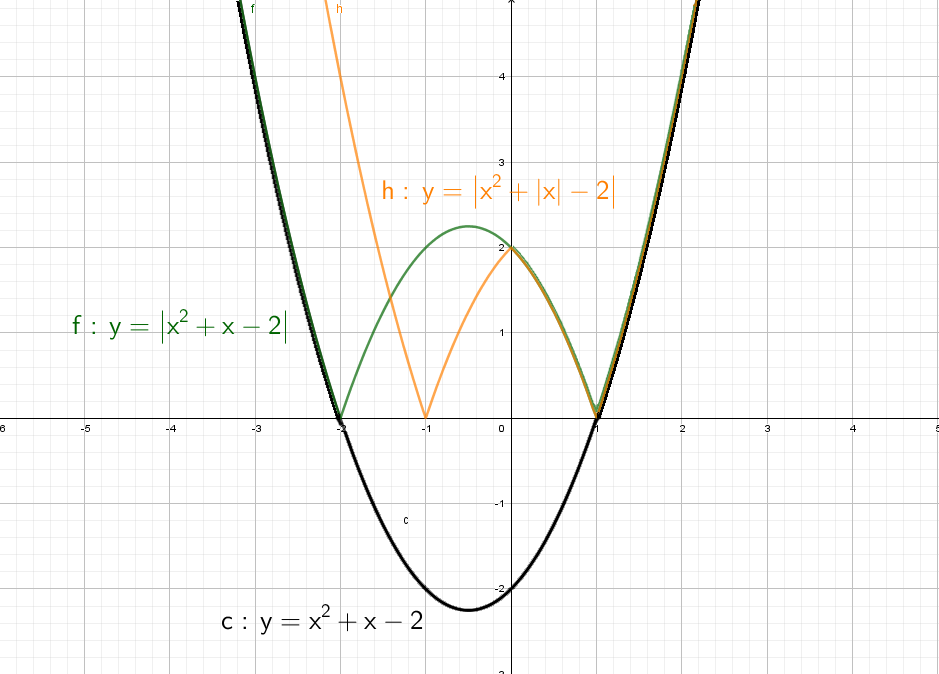
а) у =│х│- 2 ; б) у =│х — 2│; в) │у│= х – 2; г) │у│=│х — 2│.
а) График у =│х│- 2 был построен ранее (рис.5). График симметричен относительно оси Оу.
б) у =│х — 2│
Весь график расположен выше оси Ох (рис. 7).
7).
в) │у│= х – 2.
Так как │у│≥ 0, то х – 2 ≥ 0. Поэтому у = х – 2 выполняется при у ≥ 0. Строим часть прямой, расположенную выше оси Ох. Если х =5, то х – 2 = 3. │у│= 3, а это выполняется при у = 3 и у = — 3. Аналогично для других точек, для которых х–2≥0. График симметричен относительно оси Ох (рис.8).
г) │у│=│х — 2│
Модули равных и противоположных выражений равны, значит, у = х – 2 или у = — х + 2. Графиком в последнем случае является пара прямых (рис.9).
Важно отметить, что в последних двух случаях мы имеем дело не с функциями, так как каждому значению х соответствует не единственное значение у.
Рис.7 Рис.8
Рис. 9
9
В результате проведенных исследований при построении графиков функций и уравнений, содержащих модули, можно сделать следующие выводы:
если независимая переменная стоит под знаком модуля у = k│x│ + b, то от прямой у = kx + b оставляют только часть, где х ≥ 0, а затем отображают ее симметрично относительно оси Оу.
если имеем у = │kx + b│, то от прямой у = kx + b оставляют часть, где у ≥ 0, а часть графика, где у симметрично отображают относительно оси Ох.
если имеем │у │= kx + b, то от прямой у = kx + b оставляют часть, где у ≥ 0 а за-тем отображают ее симметрично относительно оси Ох.
если имеем │у│ = │kx + b│, то строим две прямые у = kx + b и у = — kx – b.
в других случаях, где встречается модуль, необходимо
1) Раскрыть модуль по определению.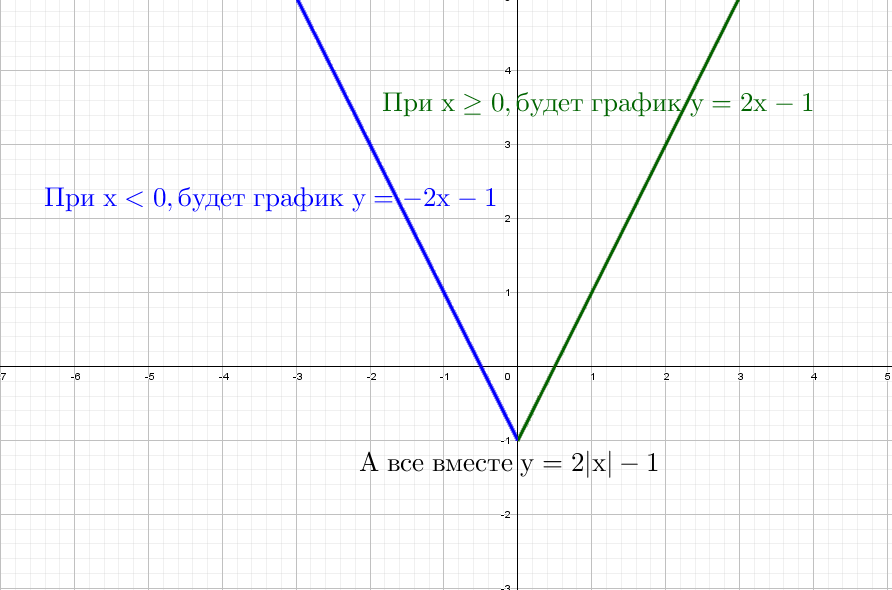
2) Получить функцию, заданную несколькими формулами.
3) Построить график функции, состоящей из нескольких формул.
3.ЗАКЛЮЧЕНИЕ
Выводы:
На основе графика линейной функции с применением некоторых математических знаний мы рассмотрели построение «необычных» графиков не только функций, но и уравнений.
Рассмотрев графики, мы поняли, что их достаточно много и они разнообразны.
Свои знания мы можем использовать при изучении новых функций. Такие функции встречаются в заданиях ГИА.
Список использованной литературы:
Алгебра. 7 класс: учеб. для общеобразоват. учреждений / [Ю.Н.Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б.Суворова]; под ред.С.А. Теляковского. – М.: Просвещение, 2017. – 240 с. : ил.
Математика. 6 класс: учеб. для общеобразоват. учреждений / [Н.Я. Виленкин и др.].– М.: Мнемозина, 2015. – 288 с. : ил.
для общеобразоват. учреждений / [Н.Я. Виленкин и др.].– М.: Мнемозина, 2015. – 288 с. : ил.
Математика : Наглядная геометрия. 5-6 кл. : учебник / И.Ф.Шарыгин, Л.Н. Ерганжиева. – М. : Дрофа, 2014. – 189, [3] с. : ил.
ОГЭ. Математика : типовые экзаменационные варианты : 36 вариантов / под. Ред. И.В. Ященко. – М. : Издательство «Национальное образование», 2019. –240 с. — (ОГЭ.ФКР – школе).
Приложение 1
12
Модуль Microsoft.Graph.Users.Functions | Microsoft Узнайте
Твиттер LinkedIn Фейсбук Электронное письмо
- Артикул
Командлеты Microsoft Graph PowerShell
| Get — Мгаллусерчатмессаже | Вызвать функцию getAllMessages |
| Get-MgUserCalendarEventDelta | Получить набор ресурсов событий, которые были добавлены, удалены или обновлены в calendarView (диапазон событий, определяемых датами начала и окончания) основного календаря пользователя. |
| Get-MgUserChatMessageDelta | Вызов функции дельта |
| Get-MgUserChatMessageReplyDelta | Вызов функции дельта |
| Get-MgUserContactDelta | Получить набор контактов, которые были добавлены, удалены или обновлены в указанной папке.
Вызов функции дельта для контактов в папке похож на запрос GET, за исключением того, что путем соответствующего \nприменения токенов состояния в одном или нескольких из этих вызовов \nвы можете запрашивать добавочные изменения в контактах в\nэтой папке. |
| Get-MgUserContactFolderChildFolderContactDelta | Получить набор контактов, которые были добавлены, удалены или обновлены в указанной папке. Вызов функции дельта для контактов в папке похож на запрос GET, за исключением того, что путем соответствующего \nприменения токенов состояния в одном или нескольких из этих вызовов \nвы можете запрашивать добавочные изменения в контактах в\nэтой папке. Это позволяет поддерживать и синхронизировать локальное хранилище контактов пользователя без необходимости каждый раз получать весь набор контактов с сервера. |
| Get-MgUserContactFolderChildFolderDelta | Получить набор папок контактов, которые были добавлены, удалены или удалены из почтового ящика пользователя.
Вызов функции delta для папок контактов в почтовом ящике подобен запросу GET, за исключением того, что, \nприменив соответствующие маркеры состояния в одном или нескольких из этих вызовов,\nвы можете запрашивать добавочные изменения в папках контактов. |
| Get-MgUserContactFolderContactDelta | Получить набор контактов, которые были добавлены, удалены или обновлены в указанной папке. Вызов функции дельта для контактов в папке похож на запрос GET, за исключением того, что путем соответствующего \nприменения токенов состояния в одном или нескольких из этих вызовов \nвы можете запрашивать добавочные изменения в контактах в\nэтой папке. Это позволяет поддерживать и синхронизировать локальное хранилище контактов пользователя без необходимости каждый раз получать весь набор контактов с сервера. |
| Get-MgUserContactFolderDelta | Получить набор папок контактов, которые были добавлены, удалены или удалены из почтового ящика пользователя.
Вызов функции delta для папок контактов в почтовом ящике подобен запросу GET, за исключением того, что, \nприменив соответствующие маркеры состояния в одном или нескольких из этих вызовов,\nвы можете запрашивать добавочные изменения в папках контактов. |
| Get-MgUserDelta | Вызов функции дельта |
| Get-MgUserDriveItemActivityByInterval | Вызов функции getActivitiesByInterval |
| Get-MgUserDriveItemDelta | Вызов функции дельта |
| Get-MgUserDriveItemListItemActivityByInterval | Вызвать функцию getActivitiesByInterval |
| Get-MgUserDriveListContentTypeCompatibleHubContentType | Вызов функции getCompatibleHubContentTypes |
| Get-MgUserDriveListItemActivityByInterval | Вызов функции getActivitiesByInterval |
| Get-MgUserDriveRootActivityByInterval | Вызов функции getActivitiesByInterval |
| Get-MgUserDriveRootDelta | Вызов функции дельта |
| Get-MgUserDriveRootListItemActivityByInterval | Вызов функции getActivitiesByInterval |
| Get-MgUserEventDelta | Получить набор ресурсов событий, которые были добавлены, удалены или обновлены в calendarView (диапазон событий, определяемых датами начала и окончания) основного календаря пользователя. |
| Get-MgUserEventInstanceDelta | Получить набор ресурсов событий, которые были добавлены, удалены или обновлены в calendarView 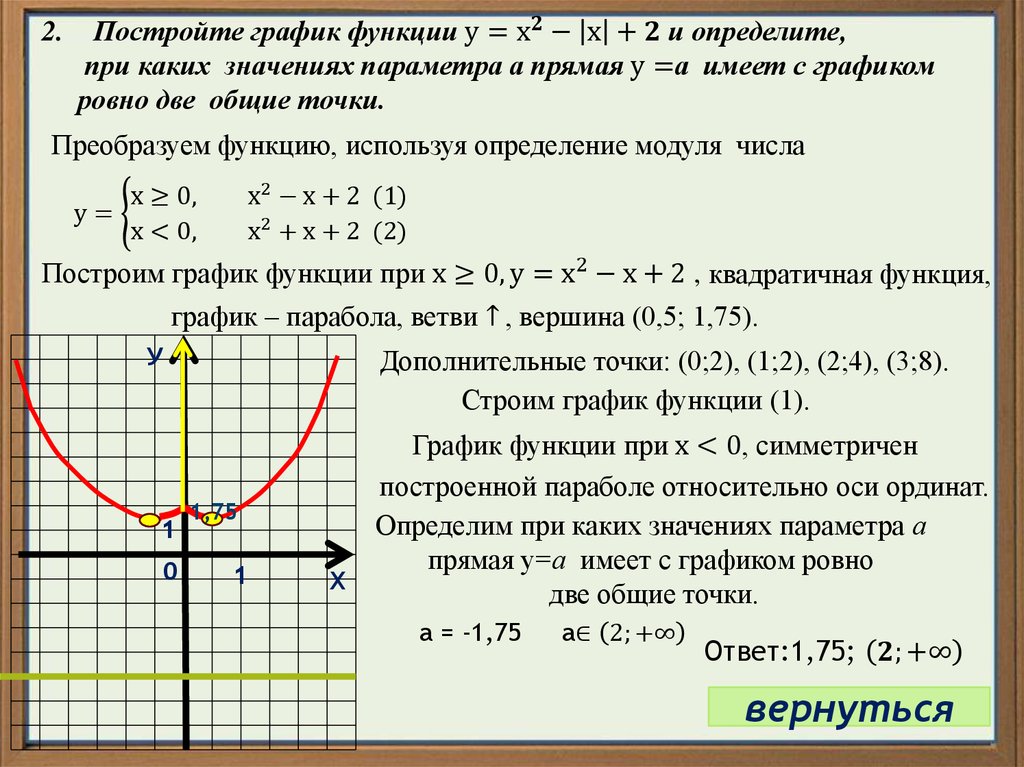 Первоначальный вызов представляет собой полную синхронизацию, и каждый последующий вызов дельта в том же цикле получает добавочные изменения (добавления, удаления или обновления).
Это позволяет поддерживать и синхронизировать локальное хранилище событий в указанных calendarView , без необходимости каждый раз получать все события этого календаря с сервера. Первоначальный вызов представляет собой полную синхронизацию, и каждый последующий вызов дельта в том же цикле получает добавочные изменения (добавления, удаления или обновления).
Это позволяет поддерживать и синхронизировать локальное хранилище событий в указанных calendarView , без необходимости каждый раз получать все события этого календаря с сервера. |
| Get-MgUserMailFolderChildFolderDelta | Получить набор почтовых папок, которые были добавлены, удалены или удалены из почтового ящика пользователя.
Вызов функции delta для почтовых папок в почтовом ящике похож на запрос GET, за исключением того, что, \nприменяя соответствующим образом токены состояния в одном или нескольких из этих вызовов, \nвы можете запросить добавочные изменения в почтовых папках.
Это позволяет вам поддерживать и синхронизировать \nлокальное хранилище почтовых папок пользователя без необходимости каждый раз получать все почтовые папки этого почтового ящика с сервера. |
| Get-MgUserMailFolderChildFolderMessageDelta | Получить набор сообщений, которые были добавлены, удалены или обновлены в указанной папке. Вызов функции delta для сообщений в папке похож на запрос GET, за исключением того, что, \nприменив соответствующие маркеры состояния в одном или нескольких из этих вызовов, вы можете запросить добавочные изменения в сообщениях в\nэтой папке. Это позволяет поддерживать и синхронизировать локальное хранилище сообщений пользователя без необходимости каждый раз получать весь набор сообщений с сервера. |
| Get-MgUserMailFolderDelta | Получить набор почтовых папок, которые были добавлены, удалены или удалены из почтового ящика пользователя.
Вызов функции delta для почтовых папок в почтовом ящике похож на запрос GET, за исключением того, что, \nприменяя соответствующим образом токены состояния в одном или нескольких из этих вызовов, \nвы можете запросить добавочные изменения в почтовых папках. |
| Get-MgUserMailFolderMessageDelta | Получить набор сообщений, которые были добавлены, удалены или обновлены в указанной папке. Вызов функции delta для сообщений в папке похож на запрос GET, за исключением того, что, \nприменив соответствующие маркеры состояния в одном или нескольких из этих вызовов, вы можете запросить добавочные изменения в сообщениях в\nэтой папке. Это позволяет поддерживать и синхронизировать локальное хранилище сообщений пользователя без необходимости каждый раз получать весь набор сообщений с сервера. |
| Get-MgUserManagedAppDiagnosticStatuses | Получает статус проверки диагностики для данного пользователя. |
| Get-MgUserManagedAppPolicy | Получает ограничения приложения для данного пользователя. |
| Get-MgUserMessageDelta | Получить набор сообщений, которые были добавлены, удалены или обновлены в указанной папке.
Вызов функции |
| Get-MgUserOnenoteRecentNotebook | Вызов функции getRecentNotebooks |
| Get-MgUserTodoListDelta | Вызов функции дельта |
| Get-MgUserTodoListTaskDelta | Вызов функции дельта |
| Invoke-MgCalendarUserCalendarAllowedCalendarSharingRoles | Вызов функции разрешеноCalendarSharingRoles |
| Invoke-MgGraphUserDrive | Вызов функции sharedWithMe |
| Invoke-MgPreviewUserOnenotePage | Вызов функции предварительного просмотра |
| Invoke-MgRecentUserActivity | Получить последние действия для данного пользователя. |
| Invoke-MgRecentUserDrive | Недавняя функция вызова |
| Invoke-MgSupportedUserOutlookLanguage | Получите список локалей и языков, поддерживаемых пользователем, в соответствии с настройками на сервере почтовых ящиков пользователя. |
| Invoke-MgTimeUserOutlook | Функция вызова поддерживается TimeZones |
| Invoke-MgViewUserReminder | Вызов функции напоминания View |
| Поиск-MgUserDrive | Вызов функции поиска |
| Search-MgUserDriveItem | Вызов функции поиска |
| Поиск-MgUserDriveRoot | Вызов функции поиска |
| Test-MgUserDriveListContentTypePublished | Вызов функции isPublished |
3.2 Функция пересылки модуля DGL NN — документация DGL 0.9.1post1
В модуле NN функция forward() выполняет фактическую
вычисление. По сравнению с модулем PyTorch NN, который обычно занимает
тензоры в качестве параметров, модуль DGL NN принимает дополнительный параметр дгл. .
рабочую нагрузку для функции 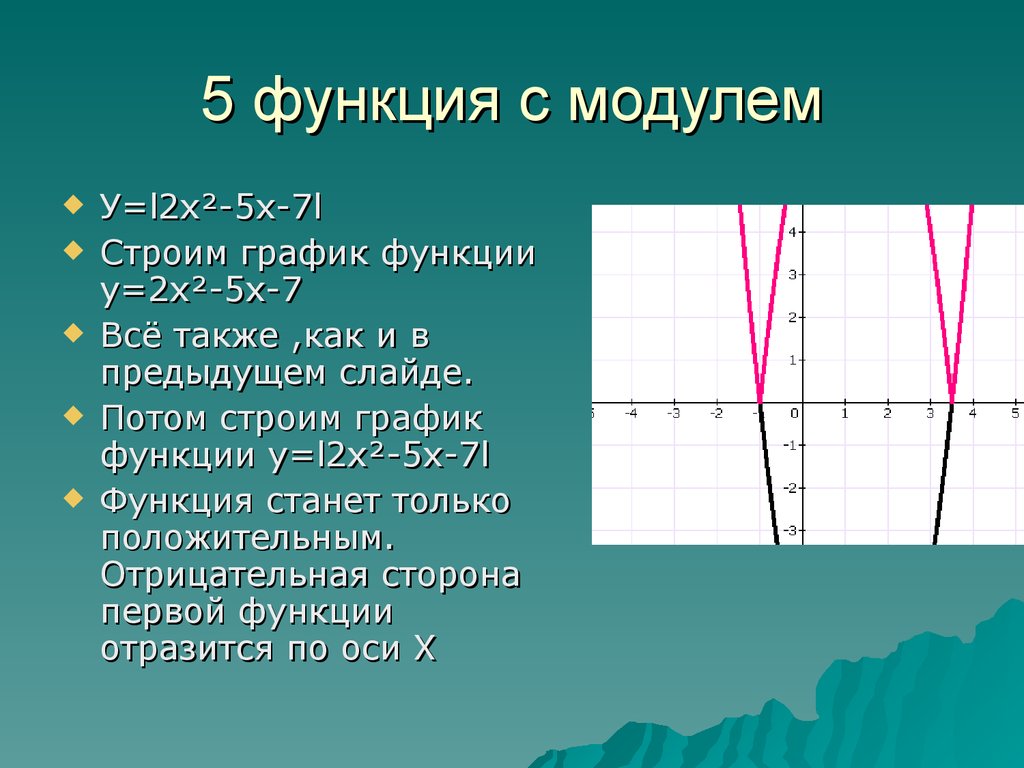 DGLГрафик
DGLГрафик forward() можно разделить на три части:
В оставшейся части раздела подробно рассматривается функция forward() в примере SAGEConv.
Проверка графика и спецификация типа графика
def forward(self, graph, feat):
с graph.local_scope():
# Укажите тип графика, затем разверните входную функцию в соответствии с типом графика
feat_src, feat_dst = expand_as_pair(feat, graph)
forward() необходимо обрабатывать множество угловых случаев на входе, которые могут
привести к недопустимым значениям при вычислении и передаче сообщений. Одна типичная проверка в конв модулях
как GraphConv , чтобы проверить, что входной граф не имеет узлов 0 в степени.
Когда узел имеет степень вхождения 0, почтовый ящик будет пуст, и функция сокращения выдаст
нулевые значения. Это может вызвать тихую регрессию в производительности модели. Однако в Модуль SAGEConv , агрегированное представление будет объединено
с исходной функцией узла, выход 9{l+1})\]
Необходимо указать функцию исходного узла feat_src и пункт назначения
функция узла feat_dst в соответствии с типом графика.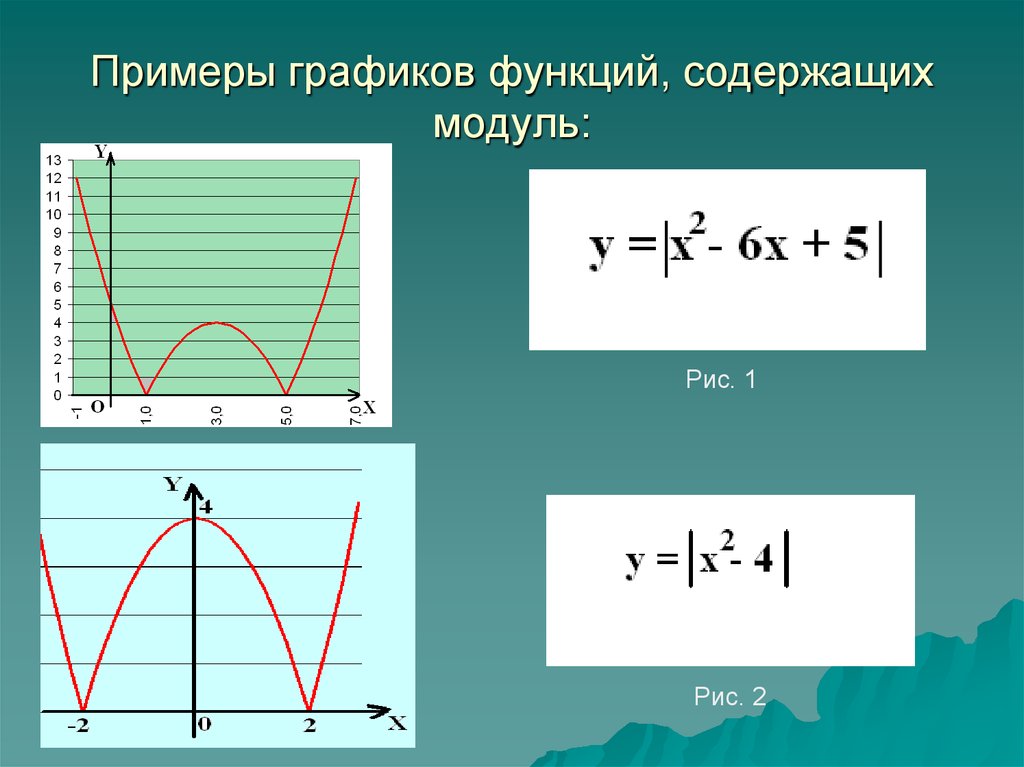
expand_as_pair() — это функция, определяющая график
введите и разверните feat в feat_src и feat_dst .
Детали этой функции показаны ниже.
по определению expand_as_pair (input_, g = нет):
если isinstance (input_, кортеж):
# Случай двудольного графа
возврат input_
elif g не None и g.is_block:
# Случай блока подграфа
если isinstance (input_, Mapping):
input_dst = {
k: F.narrow_row(v, 0, g.number_of_dst_nodes(k))
для k, v в input_.items()}
еще:
input_dst = F.narrow_row(input_, 0, g.number_of_dst_nodes())
вернуть input_, input_dst
еще:
# Однородный граф
вернуть ввод_, ввод_
Для однородного обучения всему графу, исходным узлам и узлам назначения подобные. Все они являются узлами графа.
В гетерогенном случае граф можно разбить на несколько двудольных
графики, по одному для каждого отношения. Отношения представляются как
Отношения представляются как (src_type, edge_type, dst_dtype) . Когда он определяет, что входная функция feat — это кортеж, он будет рассматривать граф как двудольный. Первое
элементом в кортеже будет функция исходного узла, а второй
элемент будет конечным элементом узла.
В мини-пакетном обучении вычисление применяется к выбранному подграфу
на основе группы узлов назначения. Подграф называется блок в DGL. На этапе создания блока dst-узлы находятся в начале списка узлов. Можно найти feat_dst по индексу [0:g.number_of_dst_nodes()] .
После определения feat_src и feat_dst вычисление для
вышеуказанные три типа графиков одинаковы.
Передача и сокращение сообщений
импортировать dgl.function как fn
импортировать torch.nn.functional как F
из dgl.utils импортировать check_eq_shape
если self._aggre_type == 'значит':
graph.srcdata['h'] = feat_src
graph. update_all(fn.copy_u('ч', 'м'), fn.mean('м', 'ржать'))
h_neigh = graph.dstdata['ржет']
elif self._aggre_type == 'gcn':
check_eq_shape (подвиг)
graph.srcdata['h'] = feat_src
graph.dstdata['h'] = feat_dst
graph.update_all(fn.copy_u('ч', 'м'), fn.sum('м', 'ржать'))
# делим in_степени
градусы = график.в_градусах().до(feat_dst)
h_neigh = (graph.dstdata['neigh'] + graph.dstdata['h']) / (degs.unsqueeze(-1) + 1)
elif self._aggre_type == 'пул':
graph.srcdata['h'] = F.relu(self.fc_pool(feat_src))
graph.update_all(fn.copy_u('ч', 'м'), fn.max('м', 'ржать'))
h_neigh = graph.dstdata['ржет']
еще:
поднять KeyError('Тип агрегатора {} не распознан.'.format(self._aggre_type))
# GraphSAGE GCN не требует fc_self.
если self._aggre_type == 'gcn':
рст = self.fc_neigh(h_neigh)
еще:
рст = self.fc_self(h_self) + self.fc_neigh(h_neigh)
update_all(fn.copy_u('ч', 'м'), fn.mean('м', 'ржать'))
h_neigh = graph.dstdata['ржет']
elif self._aggre_type == 'gcn':
check_eq_shape (подвиг)
graph.srcdata['h'] = feat_src
graph.dstdata['h'] = feat_dst
graph.update_all(fn.copy_u('ч', 'м'), fn.sum('м', 'ржать'))
# делим in_степени
градусы = график.в_градусах().до(feat_dst)
h_neigh = (graph.dstdata['neigh'] + graph.dstdata['h']) / (degs.unsqueeze(-1) + 1)
elif self._aggre_type == 'пул':
graph.srcdata['h'] = F.relu(self.fc_pool(feat_src))
graph.update_all(fn.copy_u('ч', 'м'), fn.max('м', 'ржать'))
h_neigh = graph.dstdata['ржет']
еще:
поднять KeyError('Тип агрегатора {} не распознан.'.format(self._aggre_type))
# GraphSAGE GCN не требует fc_self.
если self._aggre_type == 'gcn':
рст = self.fc_neigh(h_neigh)
еще:
рст = self.fc_self(h_self) + self.fc_neigh(h_neigh)
Код фактически выполняет передачу сообщений и сокращение вычислений. Эта часть
кода варьируется от модуля к модулю.

 Как правило, синхронизация событий в calendarView в локальном хранилище влечет за собой цикл нескольких вызовов функций delta .
Первоначальный вызов представляет собой полную синхронизацию, и каждый последующий вызов дельта в том же цикле получает добавочные изменения (добавления, удаления или обновления).
Это позволяет поддерживать и синхронизировать локальное хранилище событий в указанном
Как правило, синхронизация событий в calendarView в локальном хранилище влечет за собой цикл нескольких вызовов функций delta .
Первоначальный вызов представляет собой полную синхронизацию, и каждый последующий вызов дельта в том же цикле получает добавочные изменения (добавления, удаления или обновления).
Это позволяет поддерживать и синхронизировать локальное хранилище событий в указанном  Это позволяет поддерживать и синхронизировать локальное хранилище контактов пользователя без необходимости каждый раз получать весь набор контактов с сервера.
Это позволяет поддерживать и синхронизировать локальное хранилище контактов пользователя без необходимости каждый раз получать весь набор контактов с сервера.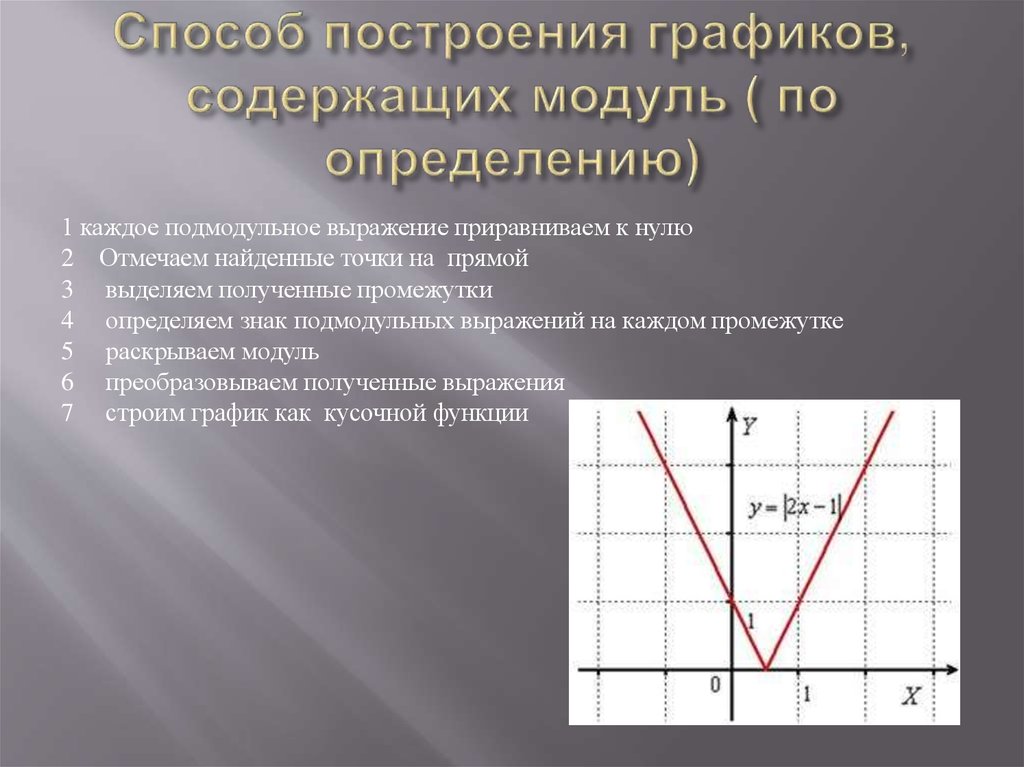
 Это позволяет вам поддерживать и синхронизировать \nлокальное хранилище папок контактов пользователя без необходимости каждый раз получать все папки контактов этого почтового ящика с сервера.
Это позволяет вам поддерживать и синхронизировать \nлокальное хранилище папок контактов пользователя без необходимости каждый раз получать все папки контактов этого почтового ящика с сервера.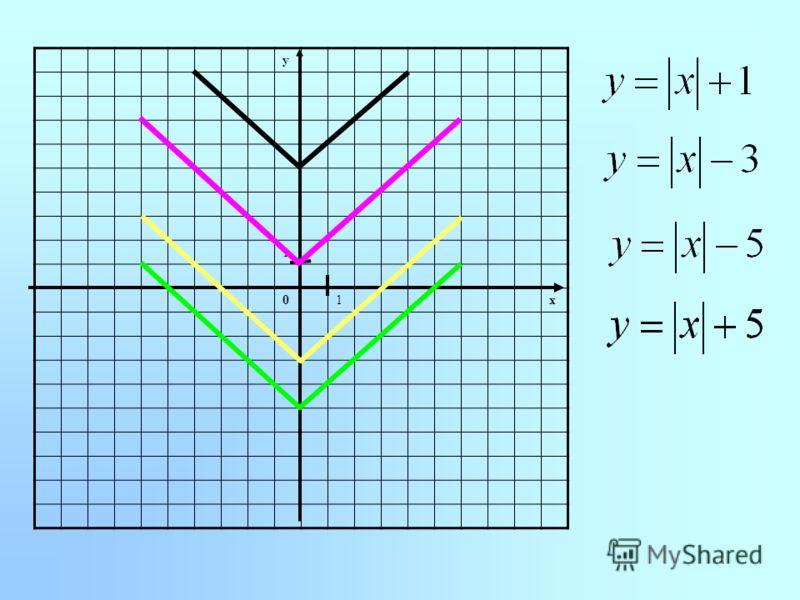 Как правило, синхронизация событий в calendarView в локальном хранилище влечет за собой цикл нескольких вызовов функций delta .
Первоначальный вызов представляет собой полную синхронизацию, и каждый последующий вызов дельта в том же цикле получает добавочные изменения (добавления, удаления или обновления).
Это позволяет поддерживать и синхронизировать локальное хранилище событий в указанном calendarView без необходимости каждый раз получать все события этого календаря с сервера.
Как правило, синхронизация событий в calendarView в локальном хранилище влечет за собой цикл нескольких вызовов функций delta .
Первоначальный вызов представляет собой полную синхронизацию, и каждый последующий вызов дельта в том же цикле получает добавочные изменения (добавления, удаления или обновления).
Это позволяет поддерживать и синхронизировать локальное хранилище событий в указанном calendarView без необходимости каждый раз получать все события этого календаря с сервера.
 Это позволяет вам поддерживать и синхронизировать \nлокальное хранилище почтовых папок пользователя без необходимости каждый раз получать все почтовые папки этого почтового ящика с сервера.
Это позволяет вам поддерживать и синхронизировать \nлокальное хранилище почтовых папок пользователя без необходимости каждый раз получать все почтовые папки этого почтового ящика с сервера.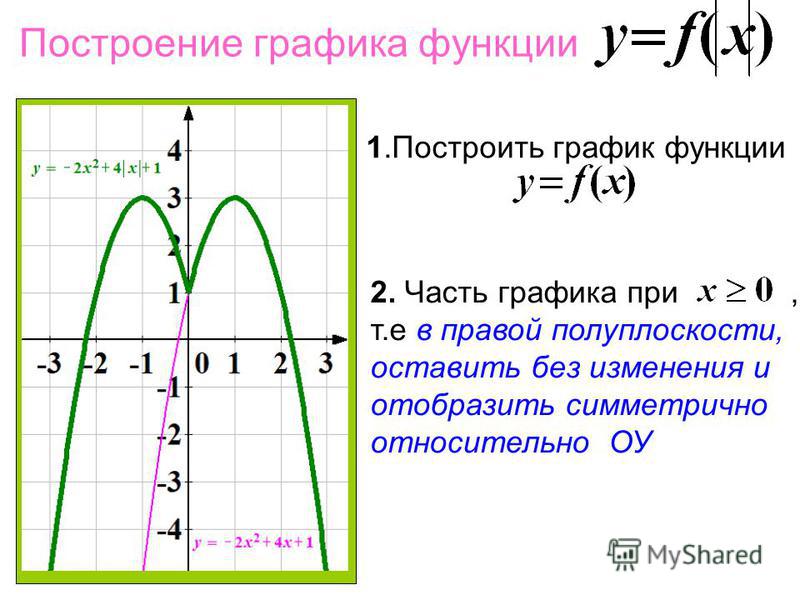
 В эту функцию OData включены некоторые варианты поведения по умолчанию, чтобы она работала как «последний использованный» API.
Служба запросит самые последние элементы истории, а затем извлечет соответствующие действия.
Мероприятия будут отсортированы в соответствии с последними lastModified on the historyItem .
Это означает, что действия без historyItems не будут включены в ответ.
Разрешение UserActivity.ReadWrite.CreatedByApp также будет применять дополнительную фильтрацию к ответу, чтобы возвращались только действия, созданные вашим приложением.
Эта фильтрация на стороне сервера может привести к пустым страницам, если пользователь особенно активен, а другие приложения создали более свежие действия.
Чтобы получить действия вашего приложения, используйте свойство nextLink для разбиения на страницы.
В эту функцию OData включены некоторые варианты поведения по умолчанию, чтобы она работала как «последний использованный» API.
Служба запросит самые последние элементы истории, а затем извлечет соответствующие действия.
Мероприятия будут отсортированы в соответствии с последними lastModified on the historyItem .
Это означает, что действия без historyItems не будут включены в ответ.
Разрешение UserActivity.ReadWrite.CreatedByApp также будет применять дополнительную фильтрацию к ответу, чтобы возвращались только действия, созданные вашим приложением.
Эта фильтрация на стороне сервера может привести к пустым страницам, если пользователь особенно активен, а другие приложения создали более свежие действия.
Чтобы получить действия вашего приложения, используйте свойство nextLink для разбиения на страницы.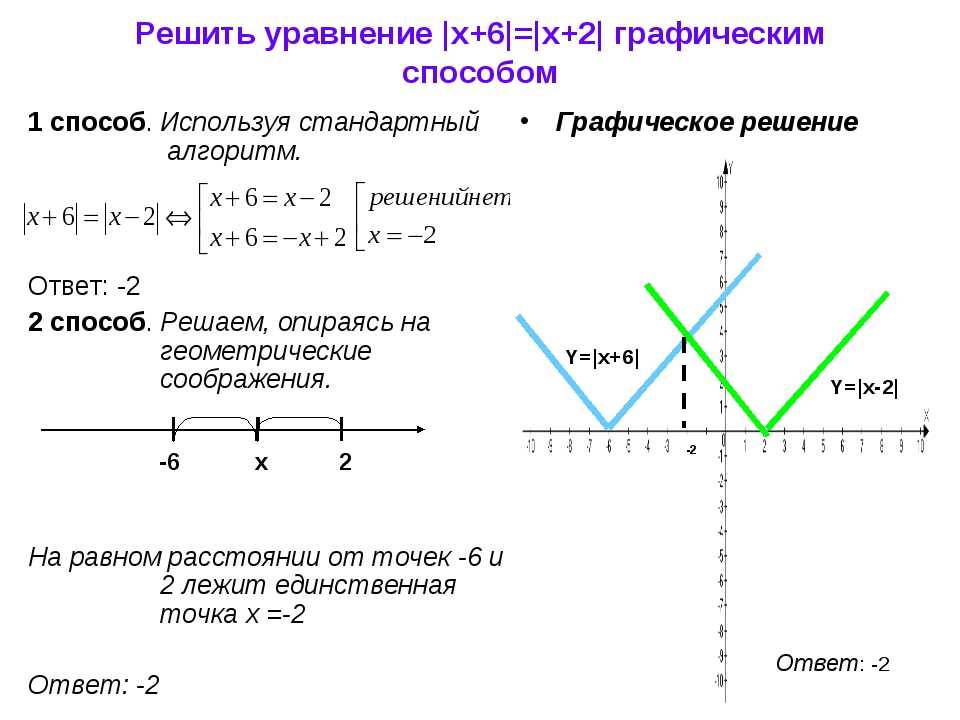 При настройке клиента Outlook пользователь выбирает предпочитаемый язык из этого поддерживаемого списка.
Впоследствии вы можете получить предпочитаемый язык, задав настройки почтового ящика пользователя.
При настройке клиента Outlook пользователь выбирает предпочитаемый язык из этого поддерживаемого списка.
Впоследствии вы можете получить предпочитаемый язык, задав настройки почтового ящика пользователя.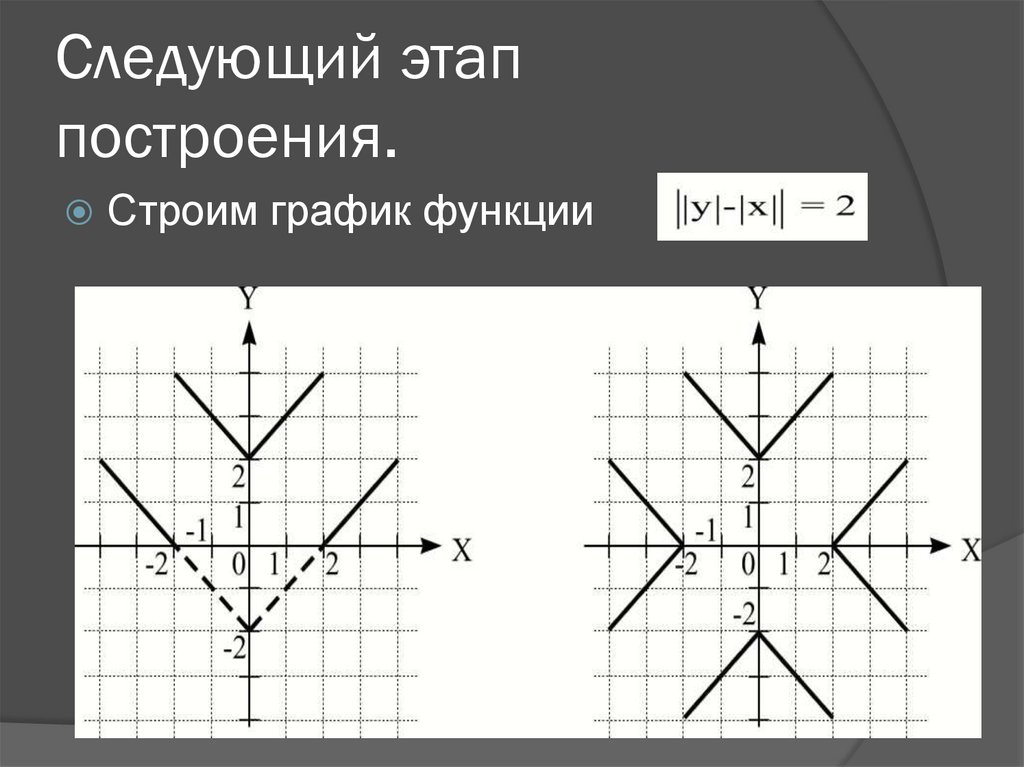 update_all(fn.copy_u('ч', 'м'), fn.mean('м', 'ржать'))
h_neigh = graph.dstdata['ржет']
elif self._aggre_type == 'gcn':
check_eq_shape (подвиг)
graph.srcdata['h'] = feat_src
graph.dstdata['h'] = feat_dst
graph.update_all(fn.copy_u('ч', 'м'), fn.sum('м', 'ржать'))
# делим in_степени
градусы = график.в_градусах().до(feat_dst)
h_neigh = (graph.dstdata['neigh'] + graph.dstdata['h']) / (degs.unsqueeze(-1) + 1)
elif self._aggre_type == 'пул':
graph.srcdata['h'] = F.relu(self.fc_pool(feat_src))
graph.update_all(fn.copy_u('ч', 'м'), fn.max('м', 'ржать'))
h_neigh = graph.dstdata['ржет']
еще:
поднять KeyError('Тип агрегатора {} не распознан.'.format(self._aggre_type))
# GraphSAGE GCN не требует fc_self.
если self._aggre_type == 'gcn':
рст = self.fc_neigh(h_neigh)
еще:
рст = self.fc_self(h_self) + self.fc_neigh(h_neigh)
update_all(fn.copy_u('ч', 'м'), fn.mean('м', 'ржать'))
h_neigh = graph.dstdata['ржет']
elif self._aggre_type == 'gcn':
check_eq_shape (подвиг)
graph.srcdata['h'] = feat_src
graph.dstdata['h'] = feat_dst
graph.update_all(fn.copy_u('ч', 'м'), fn.sum('м', 'ржать'))
# делим in_степени
градусы = график.в_градусах().до(feat_dst)
h_neigh = (graph.dstdata['neigh'] + graph.dstdata['h']) / (degs.unsqueeze(-1) + 1)
elif self._aggre_type == 'пул':
graph.srcdata['h'] = F.relu(self.fc_pool(feat_src))
graph.update_all(fn.copy_u('ч', 'м'), fn.max('м', 'ржать'))
h_neigh = graph.dstdata['ржет']
еще:
поднять KeyError('Тип агрегатора {} не распознан.'.format(self._aggre_type))
# GraphSAGE GCN не требует fc_self.
если self._aggre_type == 'gcn':
рст = self.fc_neigh(h_neigh)
еще:
рст = self.fc_self(h_self) + self.fc_neigh(h_neigh)