Какая классификация настоящих чисел? | Ресурсы самопомощи
вещественные числа является набор рациональных и иррациональных чисел чем существующие, из которых также можно найти различные типы. Они возникли в связи с необходимостью, обнаруженной между XV и XVII веками, когда расчет невозможно было описать логически и точно, поскольку часто использовались ненадежные термины или выражения, такие как «малый» или «предел».
Хотя египтяне уже использовали дроби, это было до тех пор, пока математика греков не изучала «число» более философски, когда последователи Пифагора пришли к выводу, что все вокруг них является числами; и поэтому они применялись в различных областях.
Индекс
- 1 Классификация действительных чисел по их типу
- 1.1 1. Рациональные числа
- 1.1.1 а) Целые числа
- 1.1.2 б) Дробное
- 1.2 2. Иррациональные числа
- 1.1 1. Рациональные числа
Эти числа можно разделить на два типа, о которых мы упоминали ранее, то есть рациональные числа (положительные, отрицательные и нулевые) и иррациональные (алгебраические и трансцендентные).
Это имя, данное числам, которые могут быть представлены как деление целых чисел или, что то же самое, обыкновенная и текущая дробь, в которой числитель и знаменатель не равны нулю и не меньше его.
Они, в свою очередь, также делятся на несколько типов: целые (натуральные, нулевые и отрицательные целые числа) и дробные (правильные и неправильные дроби).
а) Целые числаЦелые числа представляют собой набор натуральных чисел, отрицательных целых чисел и нуля, которые обозначаются буквой «Z». Целые числа также обычно представлены в числовой строке, где положительные или натуральные числа находятся справа, ноль — в середине, а отрицательные — слева.
- Считается «натуральные числа”Для тех, кто привык считать предметы или выполнять некоторые из наиболее распространенных и простых расчетных операций.
- El Cero Это нулевое значение, то есть в нем отсутствует значащая цифра, когда оно не сопровождается.
Однако его положение в числе может полностью изменить значение, поскольку, когда оно находится справа от него, значение умножается на десять; а с другой стороны модификации нет. - отрицательные целые числа они используются противоположно положительным или естественным, то есть вместо того, чтобы считать, их использование состоит в том, чтобы вычитать, иметь, тратить или быть ниже. Чтобы их упомянуть, необходимо перед числом указать термин «минус», например «минус четыре».
Однако его положение в числе может полностью изменить значение, поскольку, когда оно находится справа от него, значение умножается на десять; а с другой стороны модификации нет.Также среди вещественных чисел можно найти этот тип в рациональных числах, которые возникли с целью решать задачи относительно деления натуральных чисел. Дробное число — это просто выражение, которое указывает деление одной величины на другую.
Дроби характеризуются числителем и знаменателем, которые отделены друг от друга диагональной или горизонтальной чертой. Однако, несмотря на то, что в целых числах мы также можем найти «простую дробь», в этом разделе типы дробей, которые мы находим, правильные и неправильные.
- Правильные состоят из тех, у которых числитель меньше знаменателя.
- Неподходящие будут наоборот, то есть знаменатель больше знаменателя.
Иррациональные числа — это числа, которые нельзя записать в виде дроби, поскольку их десятичные дроби продолжают повторяться бесконечно. Например, невозможно записать дробь, включающую число Пи, е, соотношение золота и корней квадратные, кубические и другие.
Иррациональные числа возникли благодаря потребности ученика Пифагора записать корень в виде дроби; понимая, что это невозможно и что сегодня мы знаем это число под термином «иррациональное». Однако Пифагор не согласился с его открытием, хотя оно приписывается ему не меньше, чем его школе.
Кроме того, их можно разделить на два типа: алгебраические и трансцендентные.
- алгебраический те, которые позволяют решить алгебраическое уравнение.
- трансцендентный Это те, которые не могут быть представлены конечным числом корней (в отличие от алгебраических) и которые не следуют шаблону в своих десятичных дробях. Среди них находим число Пи.
Среди них находим число Пи.
Пока что мы подошли к классификации действительных чисел, которую, как мы надеемся, было легко читать и понимать; поскольку многие люди не любят математику, и мы сделали все возможное, чтобы дать подробное и простое объяснение.
Содержание статьи соответствует нашим принципам редакционная этика. Чтобы сообщить об ошибке, нажмите здесь.
Вы можете быть заинтересованы
Множества натуральных чисел — презентация онлайн
Похожие презентации:
Теория комплексных чисел. (Тема 2)
Числовые множества. Комплексные числа
Множество комплексных чисел
Комплексные числа
Комплексные числа
Комплексные числа
Комплексные числа
Комплексные числа
Комплексные числа и последовательности комплексных чисел. Лекция № 1
Комплексные числа. Основные понятия. Формы записи
1. Сегодня мы с вами повторим множества
натуральных чиселцелых чисел
рациональных чисел
действительных чисел
1) Что такое число?
Число — абстракция, используемая для
количественной характеристики объектов.
2) Когда возникли числа?
Числа возникли еще в первобытном обществе в связи
с потребностью людей считать предметы. С течением
времени по мере развития науки число превратилось в
важнейшее математическое понятие.
3) Какие виды чисел вам известны?
Натуральные, целые, рациональные, действительные
А) Как появились натуральные числа?
Их появление связано с необходимостью ведения
счета предметов.
Множество натуральных чисел обозначается
латинской буквой N ={1,2,3,….}
Б) Как появились целые числа?
Чтобы любое уравнение х+а=в имело корни,
положительных чисел недостаточно и поэтому
возникает потребность ввести отрицательные
числа и нуль.
Человек пришел к выводу, что
необходимо
расширение понятия числа.
Множество целых чисел состоит из трех частей –
натуральные числа, отрицательные целые числа
(противоположные натуральным числам) и число
0.
Целые числа обозначаются латинской буквой
Z={…-3,-2,-1,0,1,2,3,.
В) Как появились рациональные числа?
Одна из причин введения рациональных чисел
обусловлена требованием, чтобы всякое
линейное уравнение ax = b было разрешимо
т.к. в области целых чисел линейное уравнение
разрешимо лишь в том случае, когда b делится
нацело на a.
Рациональные
числа
–
это
числа,
представимые в виде дроби , где m — целое
число, а n — натуральное число. Для
обозначения рациональных чисел используется
латинская буква Q. Все натуральные и целые
числа – рациональные.
.
Г) Как появились действительные числа?
Одна
из
причин
расширения
множества
рациональных чисел
до множества действительных чисел была связана с
тем, чтобы выразить длину диагонали квадрата со
стороной 1. Известно, что она равна
Действительные (вещественные) числа – это числа,
которое применяются для измерения непрерывных величин.
Множество действительных чисел обозначается латинской
буквой R.
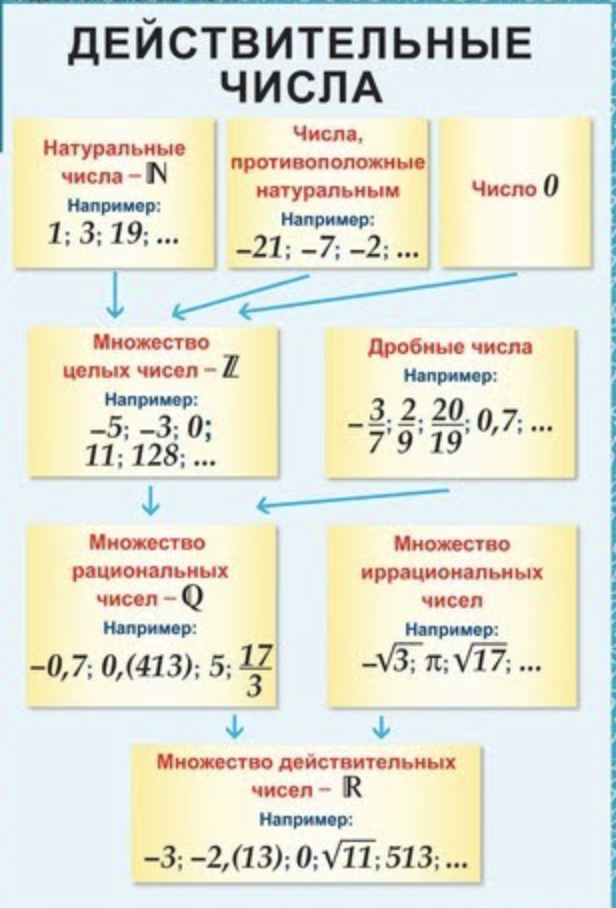Действительные числа включают в себя рациональныечисла и иррациональные числа. Иррациональные числа – это
числа, которые получаются в результате выполнения различных
операций с рациональными числами (например, извлечение
корня, вычисление логарифмов), но при этом не являются
рациональными.
Вывод: Для перечисленных выше множеств чисел
справедливо следующее высказывание:
Его можно проиллюстрировать с помощью кругов
Эйлера.
Первичное усвоение
знаний
(Исторические сведения
развития понятия числа)
Кроме привычных
действительных (буквально –
«реально существующих») чисел
еще числа вида – положительное
действительное.
Что это за числа, как их «потрогать руками» –
все это вопросы, не имеющие ответа. Мы просто
договорились считать, что они есть. И вполне
естественно, что такие числа были названы в
1637 г. французским математиком Декартом
мнимыми, т.е. «нереальными».
Число , играющее роль
«строительного блока» в мире
мнимых чисел, называют мнимой
единицей.
В 1777 г. Л.
Эйлер, предложил
использовать
первую букву
французского
слова (imaginare) –
мнимый для обозначения числа
(мнимой единицы).
Эйлер
Этот символ вошел во
всеобщее употребление
благодаря К.Гауссу.
Термин «комплексные
числа» также был введен
Гауссом в 1831 году.
Слово комплекс (от
латинского complexus)
означает связь, сочетание,
совокупность понятий,
предметов, явлений и т.д.,
образующих единое целое.
К.Гаусс
Изложение нового
материала
Комплексным числом
z
называется число
вида z
= a+bi,
где a и b – действительные числа,
i –мнимая единица;
число
a
называется действительной частью
(Re z) комплексного числа z,
число b называется мнимой
частью
(Im z)
комплексного числа z.
z = a+bi
сложение
– это ЕДИНОЕ
ЧИСЛО, а не
Определение: Два комплексных числа
равны тогда и только тогда, когда равны их
действительные части и коэффициенты при
мнимой единице.
z1 = a1+b1i и
z1 = z2
z2 = a2+b2i
a1+b1i = a2+b2i ,
если a1= a2, b1= b2
Равенство комплексного числа нулю:
z = a+bi=0, если a=0, b=0
Определение: Два комплексных числа
называются сопряженными, если они
отличаются
только
знаками
коэффициента при мнимой единице.
z = a — bi
Определение: Два комплексных числа
называется противоположными, если
они в сумме дают нуль.
Действия над комплексными числами в
алгебраической форме
Сложение комплексных чисел
Для того чтобы сложить два комплексных числа
нужно сложить их действительные и мнимые
части
z1+ z2 = (a1+b1i)+ (a2+b2i)=( a1+ a2) +(b1+ b2)* i
Вычитание комплексных чисел
Для того чтобы вычесть из одного комплексного
числа другое, нужно вычесть действительные и
мнимые части соответственно
z1 — z2 = (a1+b1i) — (a2+b2i)=( a1+ a2) — (b1+ b2)* i
Умножение комплексных чисел
Комплексные числа перемножаются как двучлены,
при этом учитывается, что
i2 = -1.
z1* z2 = (a1+b1i) * (a2+b2i)
Деление комплексных чисел
Деление
чисел
осуществляется
методом
умножения знаменателя и числителя на
сопряженное знаменателю выражение
z1 / z2= z1* z2 / z2* z2=
(a1+b1i) * (a2-b2i) / (a2+b2i) * (a2-b2i)
Рассмотрим примеры
Пример 1
Сложить два комплексных числа
z1= 2+5i, z2= 4-3i,
z = 6+2i
Пример 2
Найти разности комплексных чисел, если
z1=10-25i, z2=1-3i
Действие аналогично сложению,
единственная особенность состоит в том,
что вычитаемое нужно взять в скобки,
а затем – стандартно раскрыть эти скобки со сменой знака:
z =10-25i — (1-3i) = 9-22i
Пример 3
Найти произведение комплексных чисел z1=1- i
z2=3+6i
Ответ: z=9+3i
Пример 4
Найти отношение z1=3+ i и z2=4+i
Умножаем числитель и знаменатель на (4 — i)
Решение квадратных уравнений в поле
комплексных чисел
ax2 + bx + c = 0
1 cлучай: D>0, 2 корня, х1,2=
2 случай D=0, 1 коре нь, х =
3 cлучай: D<0, 2 корня, х1,2 =
1.
Решите уравнение x2 – 4x + 5 = 0.Решение. D = – 4 < 0,
уравнение имеет мнимые корни: 2+i, 2-i
2. Решите уравнение x2 – x + 10 = 0.
Решение. D = – 39 < 0,
,
уравнение имеет мнимые корни:
Решить самостоятельно
Пример 1
Сложить два комплексных числа:
z1=-4+10i z2=5+3i
Пример 2
Найти разности комплексных чисел:
z1=-5+10i z2=1+3i
Пример 3
Найти произведение комплексных чисел:
z1=5-2i z2=1-4i
Решите уравнения:
1.Решите уравнение x2 – 4x + 13 = 0
2. Решите уравнение x2 – 2x + 15 = 0.
Домашнее задание
1. Даны два комплексных числа z1= (4 + 2i ) и z2=(1 – 3i ).
Найти их сумму, разность, произведение и частное.
2. Даны два комплексных числа z1= (5 + 2i ) и z2=(2 – 5i ).
Найти их сумму, разность, произведение и частное.
3. Решить уравнения:
1. х2 + (5 – 2i) x + 5(1– i) = 0;
2. х2 + (1 – 2i) х – 2i = 0;
Рефлексия
1.Как вы оцениваете свою работу на занятии?
• Мне больше всего удалось…
• Для меня было открытием то, что …
• За что ты можешь себя похвалить?
• Что на ваш взгляд не удалось? Почему? Что
учесть на будущее?
• Мои достижения на уроке
2.
Подберите выражение (их может быть несколько),которое характеризует вашу работу на занятии
НА УРОКЕ Я:
• ВКЛАДЫВАЛ ДУШУ
• ПРОСИЖИВАЛ ШТАНЫ
• ХЛОПАЛ УШАМИ
• РАБОТАЛ НЕ ПОКЛАДАЯ РУК
• ШЕВЕЛИЛ МОЗГАМИ
• РАБОТАЛ ТЯП-ЛЯП
• СЧИТАЛ ВОРОН
• РАБОТАЛ В ПОТЕ ЛИЦА
• СЛЫШАЛ КРАЕМ УХА
• СТАРАЛСЯ ИЗО ВСЕХ СИЛ
• БИЛСЯ КАК РЫБА ОБ ЛЁД
English Русский Правила
Обозначение— Что такое символ для мнимых чисел?
спросил
Изменено 4 года, 9 месяцев назад
Просмотрено 27 тысяч раз
$\begingroup$
$\mathbb Q$ используется для представления рациональных чисел. $\mathbb R$ используется для представления действительных чисел.
Есть ли общепринятый символ для мнимых чисел?
- обозначения
- иррациональные числа
$\endgroup$
16
$\begingroup$
Воображаемые числа сами по себе скучны. Я буду обозначать мнимые числа через $\mathbb{I}$. Давайте посмотрим, как он устроен.
Во-первых, мы определенно можем их сложить и вычесть, и вы получите мнимое число. Но можем ли мы их умножить? Если вы умножите два ненулевых мнимых числа, вы получите ненулевое действительное число, поэтому оно больше не находится в $\mathbb{I}$.
Как насчет других свойств? Ну, вы можете определить общий порядок в $\mathbb{I}$, используя порядок в $\mathbb{R}$. Вы также можете показать, что он завершен. Но $\mathbb{R}$ — единственное полностью упорядоченное поле, и было показано, что $\mathbb{I}$ «уступает» $\mathbb{R}$ в том, что оно не замкнуто относительно умножения.
Это показывает, что «множество мнимых чисел» не является полезной концепцией. Вот почему вы, вероятно, никогда не видели этикетку для набора. Однако, если бы я выбрал один символ, это был бы $i\mathbb{R}$.
tl;dr $i\mathbb{R}$, но это бессмысленная концепция.
$\endgroup$
0
$\begingroup$
Существует принятый символ для комплексных чисел $\textbf{C}$. Другие, кажется, предположили, что вы уже знаете этот символ, но из вашего вопроса не совсем понятно, знаете вы его или нет.
Если вы имеете в виду чисто мнимые числа, числа $z$ такие, что $\Re(z) = 0$, то ответ отрицательный, для мнимых чисел не существует принятого символа.
Все согласны с тем, что если вам действительно нужен символ, вы можете использовать $\textbf{I}$, но гораздо лучше использовать $i \textbf{R}$.
И да, легко сделать вывод, что чисто мнимые числа «скучны».
Ведь они замкнуты при сложении, но не при умножении, а чисто действительные числа закрыты. Это верно и для действительных рациональных чисел.
Но мы также должны учитывать контекст, в котором вам нужен символ для чисто мнимых чисел. Вы хотите сказать, что конкретное число $bi$ чисто мнимое? Вы можете написать $bi \in i \textbf{R}$. Но тогда было бы намного проще написать $b \in \textbf{R}$, и тогда ясно, что $\Re(bi) = 0$.
Кажется немного странным, что $0$ является одновременно чисто реальным и чисто воображаемым. Если вам нужно сказать, что $bi$ — ненулевое чисто действительное мнимое число, вы можете написать, что $\Re(bi) = 0$, но $\Im(bi) \neq 0$.
$\endgroup$
$\begingroup$
Важно понимать, что хотя существует чисто мнимых чисел вида $ai$ (где $a \in \mathbb R$), эти числа являются лишь подмножеством сложных номера.
Символы для Комплекс Числа вида $a + bi$, где $a, b \in \mathbb R$ символ равен $\mathbb C$.
Не существует универсального символа для чисто мнимых чисел. Многие сочтут $\mathbb I$ или $i\mathbb R$ приемлемыми. Я бы.
Примечание:
$\mathbb R = \{a + 0*i\} \subsetneq \mathbb C$. (Действительные числа являются правильным подмножеством комплексных чисел.)
$i\mathbb R=\{0 + b*i\} \subsetneq\mathbb C$. (Чисто мнимые числа являются собственным подмножеством комплексных чисел.)
$\mathbb C = \{a+b*i\} \subseteq \mathbb C$.
[Забавный факт: $0$ — мнимое число. $0$ — действительное число. $0$ — единственное реальное число, которое является мнимым, и единственное мнимое число, которое является реальным.]
Также обратите внимание: несмотря на всю шумиху вокруг того, что мнимые числа существуют, на самом деле они ничуть не интересны и не важны. Мы используем их для определения Комплексных Чисел, которые важны (и интересны), но набор чисто мнимых чисел на самом деле лишь шаг на пути к результату.
$\endgroup$
$\begingroup$
Нет, и проблема в том, что самый «естественный» выбор, $\mathbb I$, уже перегружен.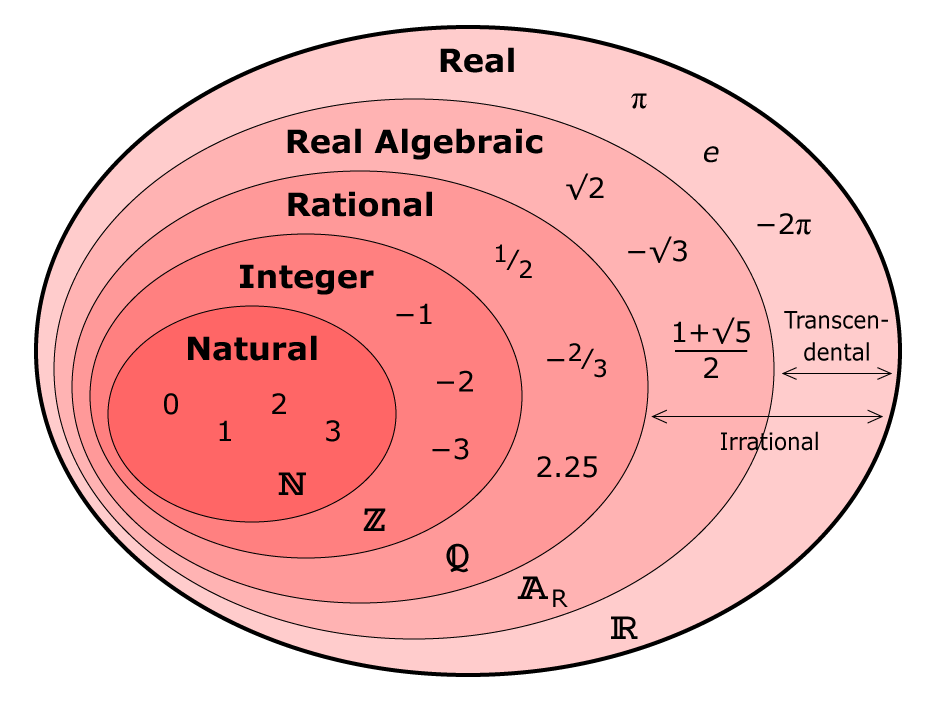
Страница Mathworld, посвященная символам с двойным ударом, дает только одно значение для $\mathbb I$: целые числа. Страница OEIS Wiki на латинском алфавите дает мнимые числа в качестве основного значения $\mathbb I$ без цитирования, затем дает «целые числа, чаще $\mathbb Z$» в качестве второго значения и дает страницу Mathworld в качестве цитирования. для этого.
Таким образом, остается $i \mathbb R$, второй вариант, предлагаемый большинством людей, как более жизнеспособная альтернатива. Этот символ должен быть знаком и удобен любому, кто хотя бы бегло изучил основные идеалы. В конце концов, что такое чисто мнимое число, как не действительное число, умноженное на $i$? Даже само $i$ можно рассматривать как $1 \times i$.
Поскольку мы имеем дело с коммутативной алгеброй (верно?), $\mathbb R i$ является приемлемым вариантом, различием без разницы.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
типов чисел, целые числа, натуральные, рациональные, иррациональные, действительные
Числа играют жизненно важную роль в нашей жизни, например, для подсчета вещей, времени, денег, возраста и многого другого. Десять математических цифр (от 0 до 9) используются для представления всех этих величин. В этой статье мы обсудим различные типы чисел в математике с примерами.
Различные типы чисел
Ниже приведены основные типы чисел, используемые в школьной математике.
Натуральные числа
Числа начинаются с 1 и выше. НЕТ нуля, НЕТ чисел с десятичными знаками и НЕТ отрицательных чисел в этой группе.
Натуральные числа также называются счетными числами или целыми положительными числами , поскольку эти числа используются для счета и упорядочивания.
Набор натуральных чисел обозначается буквой «N».
N = {1, 2, 3, 4, 5, ….}
Примеры: 45, 109, 59, 12 и т.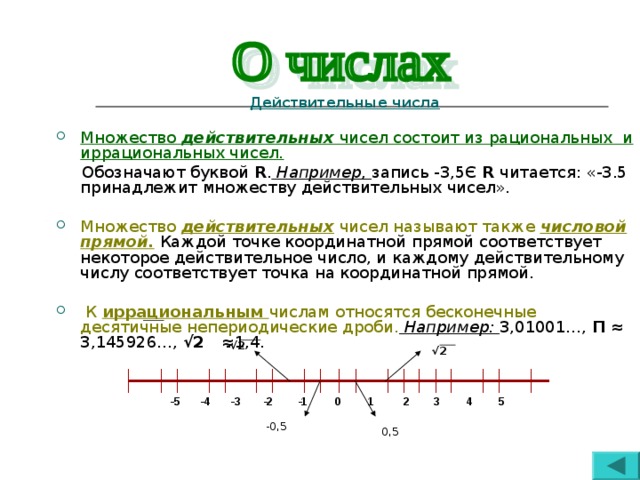
д.
Целые числа
ноль (т. е. натуральные числа + 0).
НЕТ чисел с десятичными знаками и НЕТ отрицательных чисел в этой группе.
Множество целых чисел обозначается W.
W = {0, 1, 2, 3, 4, 5, ….}
Примеры: 45, 0, 59, 11, 110 и т. д.
Целые числа
Целые числа — это все целые числа и их отрицательные значения. Набор целых чисел обозначается Z.
Z = {-4, -3, -2, -1, 0, 1, 2, 3, 4}
Примеры: -45, 0, 59, -11 , 110 и т. д.
Рациональные числа
Любое число, записанное в виде дроби или отношения, т. е. a/b, где a и b — целые числа. [Совет: корневое слово ratio nal — это «ratio»] .
Буква Q обозначает рациональное число.
[ Примечание : Знаменатель не может быть равен 0, но числитель может быть].
Примеры: 1/4, 2/5, 7/2, ⁻4/3, 0/1 и т.д. или соотношение.
Иррациональные числа могут быть бесконечными (никогда не заканчивающимися) неповторяющимися десятичными знаками.
Буква «P обозначает иррациональное число».
Примеры: 𝜋=3,14159…, √3=1,73205, постоянная Эйлера и т. д.
Вещественные числа
линия. Это могут быть натуральные числа, целые числа, целые числа, рациональные числа и иррациональные числа.
Иррациональные числа являются действительными числами, но не все действительные числа являются иррациональными числами. Вещественное число обозначается буквой «R».
Примеры: 7, ¾, 0,333, √2, 0, -19, 20, 𝜋 и т. д.
>> Простые и составные числа
ПОПРОБУЙТЕ СЕЙЧАС!
Классифицируйте каждое число по как можно большему количеству категорий.
(1) -25
(2) 0
(3) 1/5
(4) 1
(5) √2
(6) -16/4
(280005 ) ….
Ответить
1 .