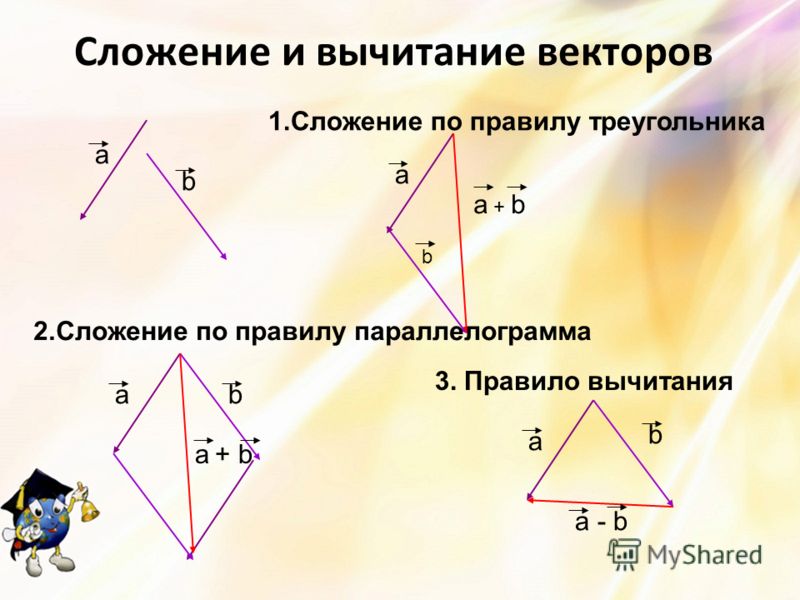
Вычитание векторов – примеры по правилу треугольника
4.6
Средняя оценка: 4.6
Всего получено оценок: 176.
4.6
Средняя оценка: 4.6
Всего получено оценок: 176.
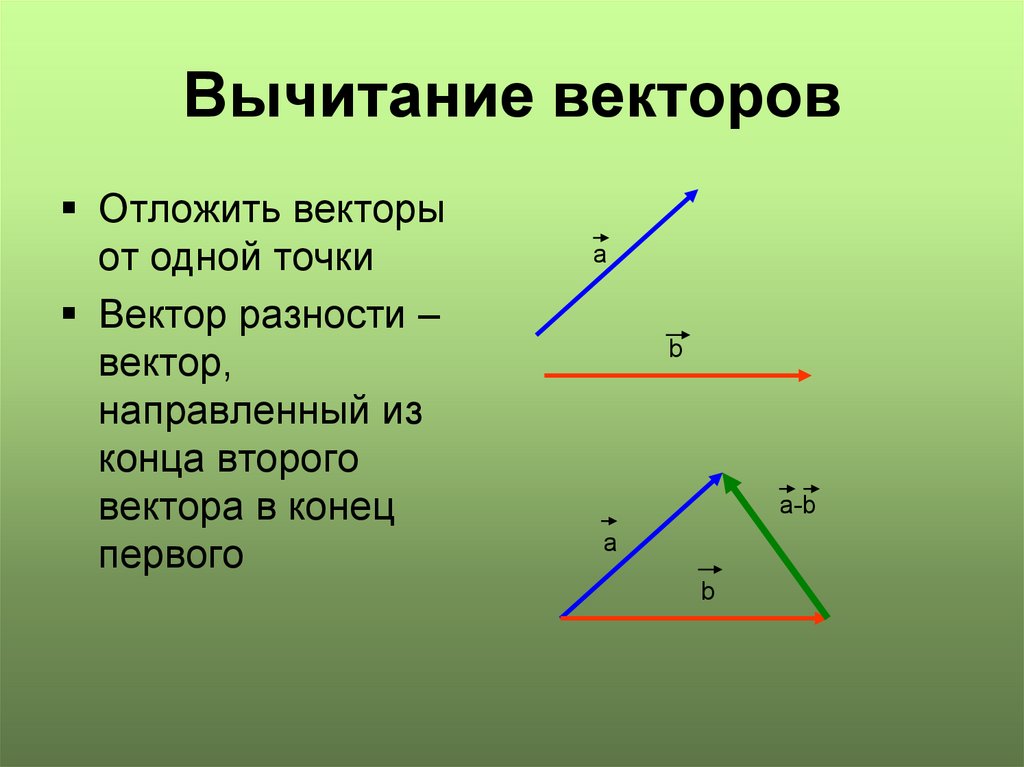
Вычитание векторов часто вызывает проблемы у учеников. Это связано с тем, что вычитание в геометрии нужно выполнять очень осторожно, чтобы не получалось отрицательных чисел. А вектор может быть отрицательным, положительным, нулевым – это вызывает много ошибок, которых можно избежать просто один раз разобравшись в вопросе.
Вектор
Вектор – одно из самых интересных явлений в математике. Это первая величина во всем школьном курсе, которая имеет две характеристики: направление и размер. Вектором называют направленный отрезок, то есть отрезок, у которого стрелкой указали направление движения.
Представьте, вы прошли километр от дома до парка. Если поставить точку в начальном положении и стрелку в конечном, то результат движениям будет являться вектором. Ведь он имеет направление: от дом до парка.
Ученики часто пугаются отрицательных векторов, но в этом нет ничего страшного. Вектор это направление некого движения, а любое движение относительно, то есть зависит от системы отсчета.
В любую систему отчета входит точка отчета, система координат и прибор для измерения времени.
Если вектор поместить в любую систему координат, даже если это будет простой координатный луч, то вектор может быть направлен в одну сторону с системой координат, но может и в разные. Если вектор и система координат направлены в разные стороны, то вектор будет отрицательным.
Рис. 1. Вектор в системе координат.При этом противоположным направлением считается любое в половине плоскости, в другую сторону которой направлен вектор.
Особые случаи векторов
Первый вопрос, который возникает у множества учеников, это возможность существования нуля в системе векторов. Ноль у векторов есть, только это не число, а точка.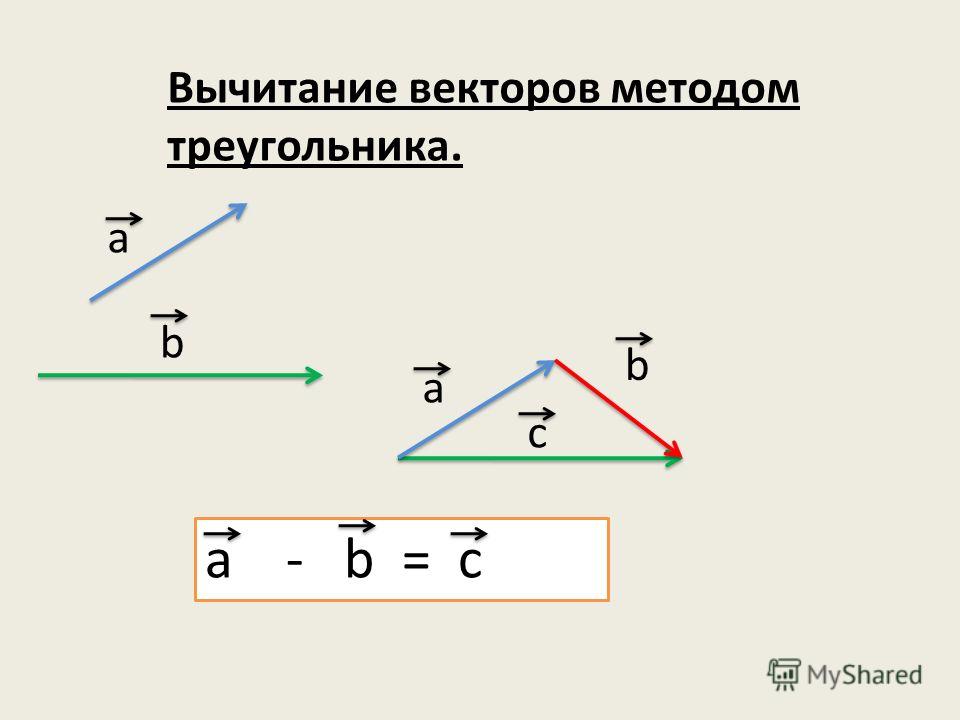
Коллинеарными называют вектора, которые лежат на одной прямой. Эти векторы могут быть сонаправлены или противоположно направлены. При этом векторы, которые лежат на одной прямой так же считаются коллинеарными, так как любая прямая параллельна самой себе. Это не трудно понять, но запомнить название лучше наизусть, так как в тематике векторов, это определение встречается довольно часто.
Результат сложения или вычитания коллинеарных векторов будет коллинеарным для каждого из начальных построений. Поэтому найти результат такой операции можно арифметически, да и построить треугольник или параллелограмм из коллинеарных векторов не получится.
Вычитание векторов
Результатом вычитания векторов может быть:
- Вектор. Если вычитание производилось в системе координат, то результат может быть положительным или отрицательным
- Нулевой вектор или точка
- Никаких других результатов быть не может
 3. Вычитание векторов.
3. Вычитание векторов.Для того, чтобы вычесть один вектор из другого, любой из векторов заменяется на противоположный и выполняется сложение по правилу треугольника или параллелограмма. Таким образом, меняется знак вектора.
В математической записи это выглядит так:
АВ-МР=АВ+РМ – в математической записи первая буква означает начало вектора, вторая – конец. Так можно без чертежа обозначить направление.
Что мы узнали?
Мы поговорили о векторах и их частных случаях. Обсудили, как правильно вычитать вектора и что может получиться в результате такого вычитания. Привели пример правильной записи вычитания 2 векторов.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Руслан Галандских
10/10
Нина Трофимова
5/10
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 176.
А какая ваша оценка?
Вычитание векторов и правила вычитания
Оглавление
Время чтения: 4 минуты
1 042
Для того, чтобы уяснить, что собой представляет разность векторов, введём понятие откладывания вектора от определённой точки и понятие суммы векторов.
Определение
Если некоторая точка A является началом вектора a, то говорят, что он является отложенным от точки A.
Теорема. От каждой точки можно отложить только один вектор, имеющий заданный модуль и направление. Докажем эту теорему.
Доказательство:
В случае, когда вектор нулевой, то теорема очевидна. Нулевые вектора в одной и той же точки совпадают между собой, т. е. являются одним и тем же вектором.
Сделаем построение. Точкой A обозначим начало вектора a, а точкой B его конец. Пусть у нас имеется некоторая точка K. Проведём через неё прямую b, которая параллельна вектору a.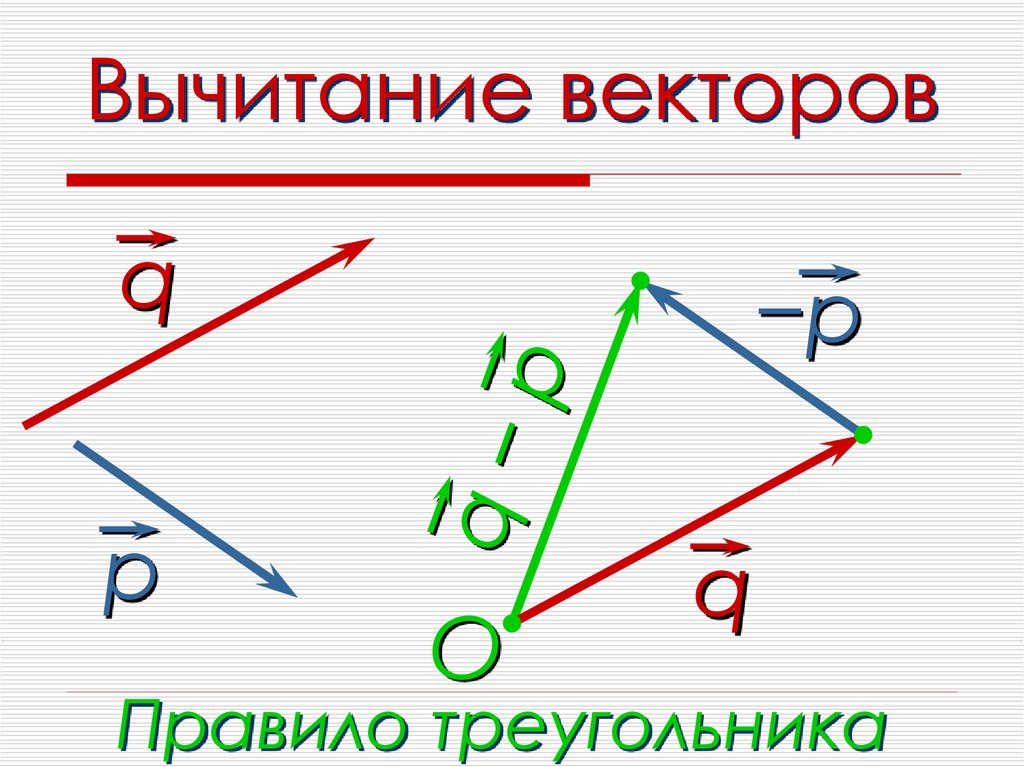 Отложим на данной прямой равные по своей абсолютной величине вектору a отрезки KL и KM. Из векторов, образованных этими отрезками искомым можно назвать только сонаправленный с a.
Отложим на данной прямой равные по своей абсолютной величине вектору a отрезки KL и KM. Из векторов, образованных этими отрезками искомым можно назвать только сонаправленный с a.
Единственность нашего вектора следует из того, что мы построили и видим.
Теорема доказана.
Определение
Суммой векторов a и b называется вектор с тем же началом, что вектор a и концом, как у вектора b. При этом вектор b должен начинаться в той же самой точке, в которой заканчивается вектор a.
Равные векторы, начинающиеся в разных точках, нередко обозначают одной и той же буквой. Иногда про подобные векторы говорят, как об одном и том же векторе, отложенном из разных мест.
Разность векторов
Определение
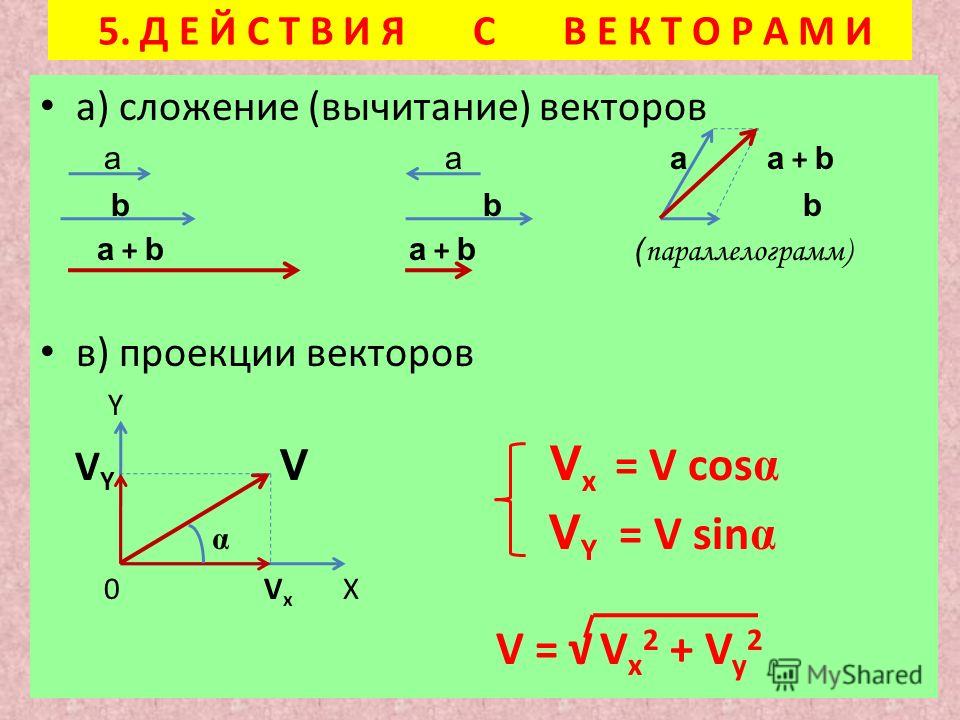
Разностью векторов a и b называется сумма вектора a c вектором, который противоположно направлен к вектору b.
По-другому это определение можно сформулировать следующим образом: разностью двух векторов a и b называется вектор c, который при сложении с вычитаемым b образует уменьшаемое, т. е. вектор a.
Формулами это записывается так:
b + c = a
a – b = c
Как найти разность векторов аналитическим способом
В двухмерном пространстве векторов a {x1, y1} и b {x2, y₂} разность векторов можно вычислить, как показано ниже:
c {x3, y3} = {x₁ — x2, y1 — y₂}.
Вычитание векторов в 3-мерном пространстве выглядит следующим образом:
c {x3; y3; z₃} = {x₁ — x2, y₂ — y₂, z1 — z2}.
Как найти разность векторов графическим способом
Нужно воспользоваться правилом треугольника. Последовательность действий следующая:
- Постройте по координатам векторы, для которых требуется найти разность;
- Совместите концы построенных векторов. Для этого нужно построить два равных заданным направленных отрезка, концы у которых будут в одной и той же точке;
- Соедините начала построенных отрезков и укажите их направление. Вектор c, называемый разностью векторов, будет иметь своё начало в той же точке, где начинается вектор, именуемый уменьшаемым и заканчивается в точке начала вычитаемого. Смотрите рисунок ниже.
Есть ещё один способ графического нахождения разности векторов. Он предусматривает следующий порядок действий:
- Постройте исходные направленные отрезки;
- Отразите вычитаемый отрезок.
 Для этого постройте противоположно направленный и равный ему отрезок и затем совместите начало этого отрезка с уменьшаемым;
Для этого постройте противоположно направленный и равный ему отрезок и затем совместите начало этого отрезка с уменьшаемым; - Постройте сумму, т. е. соедините начало первого отрезка и конец второго.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Примеры вычисления разности векторов
Примеры
Вычислить вектор c, который представляет собой разность вектора a ={1;
2} и вектора b = {4; 8}.
Решение:
Действуем по выше указанному правилу
a — b = {1 — 4; 2 — 8} = {-3; -6}
Ответ: с{-3; -6}.
Вычислить вектор c, который является разностью векторов a = {1; 2; 5} и
b = {4; 8; 1}.
Решение:
Почти всё делается, как в уже рассмотренном примере, только добавляется третья координата.
a — b = {1 — 4; 2 — 8; 5 — 1} = {-3; -6; 4}
Ответ: c {-3; -6; 4}.
На рисунке векторы
Требуется построить разности: p — n, m —
n,m — n — p и найти ту из них, которая
имеет наименьший модуль.
Решение:
Для изображения p — n проще всего воспользоваться правилом треугольника. Параллельным переносом
отрезки
следует соединить таким образом, чтобы совпали их конечные точки. Далее нужно соединить начальные точки и
определить направление. В нашем случае вектор разности берёт своё начало там же, где и вычитаемый n.
Для изображения m — n правильнее будет воспользоваться вторым графическим способом нахождения разности
векторов. Сначала построим вектор противоположный n и найдём его суммы с вектором m.
Для нахождения разности m — n — p разобьём это выражение на два действия. Возможны следующие варианты:
- m — (n + p). Сначала нужно построить сумму,
затем уже вычесть её из m; - (m — n) — p. Сначала находим m — n,
осле этого от полученной разности отнимаем p; - (m— p) — n. Сначала определяем m — p, затем от
полученного результата отнимаем n.
Из вычислений выше нам известна разность m — n. Для получения решения нам нужно вычесть из неё
p.
Используя определение 3 построим разность векторов на рисунке. На нём изображён окончательный результат
и промежуточный.
Теперь нужно определить наименьший модуль. В нашем случае для этого можно лишь визуально оценить длины p — n,
m — n и m — n — p.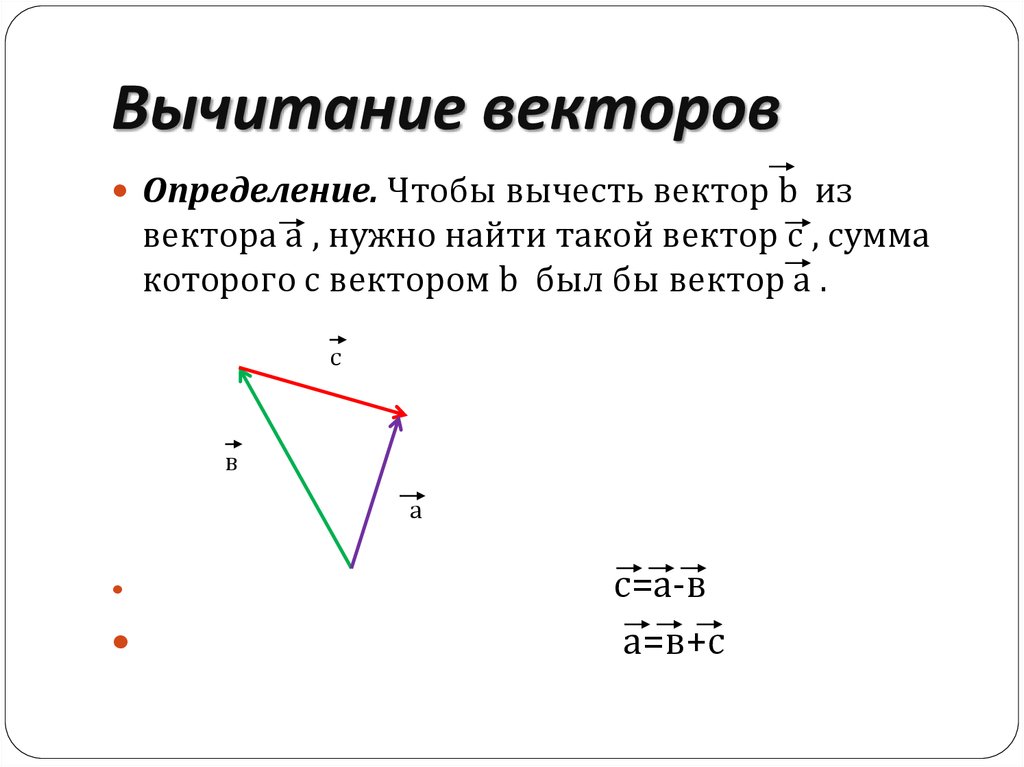 Из построения сразу видно, что наименьшим модулем обладает вектор разности m — n —
Из построения сразу видно, что наименьшим модулем обладает вектор разности m — n —
p.
Оценить статью (34 оценки):
Поделиться
Вычитание векторов — GCSE Math
Введение
Что такое векторное вычитание?
Как вычесть векторы
Рабочие листы векторного вычитания
Распространенные заблуждения
Практические вопросы по вычитанию векторов
Вычитание векторов Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Что такое векторное вычитание?
Как вычесть векторы
Рабочие листы векторного вычитания
Распространенные заблуждения
Практика вычитания векторов вопросы
Вычитание векторов Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы узнаем о вычитании векторов.
Существуют также векторные рабочие листы на основе экзаменационных вопросов Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое вычитание векторов?
Вычитание вектора вычитание одного вектора из другого вектора.
Для этого мы вычитаем горизонтальные компоненты (верхние числа) вектора-столбца и вычитаем вертикальные компоненты (нижние числа) вектора-столбца.
Давайте посмотрим на вектор a и вектор b .
\[\textbf{а}= \left(\begin{массив}{1} 5\\ 4\\ \конец{массив}\справа) \четверка \textbf{b}= \left(\begin{массив}{1} 3\\ 1\\ \end{массив}\right)\]
\[\textbf{a}-\textbf{b}= \left(\begin{массив}{1} 5\\ 4\\ \конец{массив}\справа) – \left(\begin{массив}{1} 3\\ 1\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 2\\ 3\\ \конец{массив}\справа)\]
Вычитание векторов основано на сложении векторов.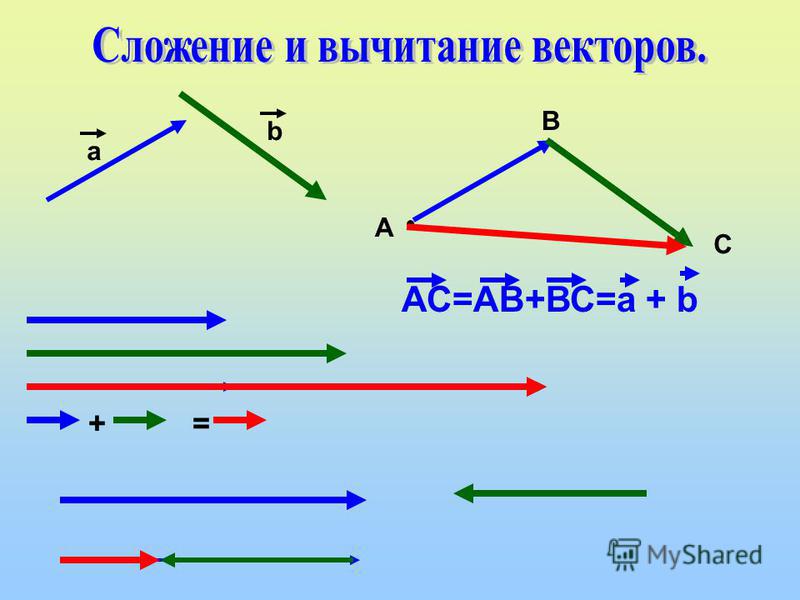 Первый вектор остается прежним, но второй вектор меняет направление на противоположное, становясь отрицательным вектором.
Первый вектор остается прежним, но второй вектор меняет направление на противоположное, становясь отрицательным вектором.
\mathbf{a}-\mathbf{b}=\mathbf{a}+-\mathbf{b}
Используя вектор a и вектор b , посмотрим, что получится.
\[\textbf{а}= \left(\begin{массив}{1} 5\\ 4\\ \конец{массив}\справа)\]
\[\textbf{b}= \left(\begin{массив}{1} 3\\ 1\\ \конец{массив}\справа)\]
Нам нужен вектор — b . Направление вектора – b противоположно направлению исходного вектора b (но имеет ту же величину).
\[-\textbf{b}= \left(\begin{массив}{1} -3\\ -1\\ \end{массив}\right)\]
Итак,
\textbf{a} — \textbf{b}= \textbf{a}+ — \textbf{b}
Из сложения векторов мы знаем, что при сложении двух векторов второй добавляется к концу первого, как показано здесь:
Окончательный ответ известен как результирующий вектор.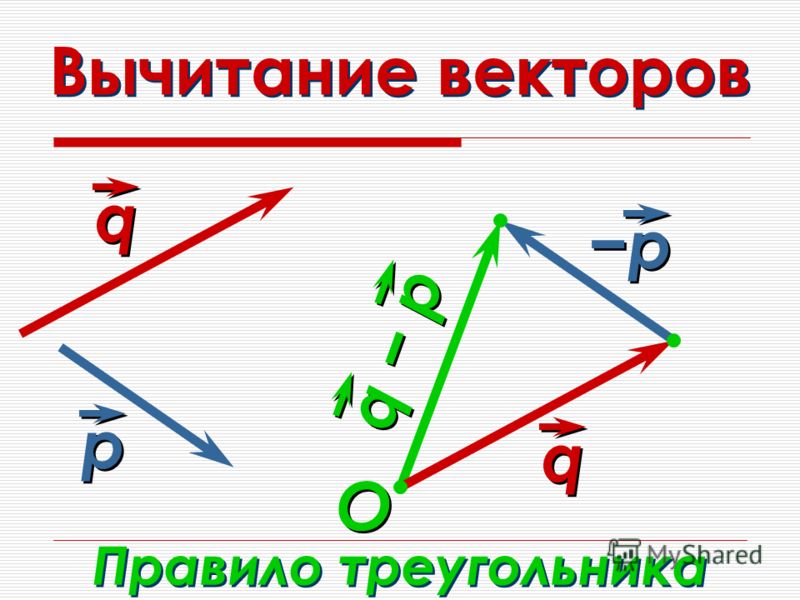
\[\textbf{a}-\textbf{b}=\textbf{a}+ -\textbf{b}= \left(\begin{массив}{1} 5\\ 4\\ \конец{массив}\справа) +\ \left(\begin{массив}{1} -3\\ -1\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 2\\ 3\\ \end{массив}\right)\]
Поэтому
\[\textbf{a} – \textbf{b}= \left(\begin{массив}{1} 5\\ 4\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 3\\ 1\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 2\\ 3\\ \end{массив}\right)\]
Что такое вычитание векторов?
Как вычесть вектор
Чтобы вычесть вектор из исходного вектора:
- Вычтите компоненты размером x .
- Вычесть компоненты и .
- Запишите результирующий вектор.
Как вычитать векторы
Лист векторов (включая вычитание векторов)
Получите бесплатный лист вычитания векторов из 20+ вопросов и ответов по векторам. Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.
СКОРО
ИксЛист векторов (включает вычитание векторов)
Получите бесплатный лист вычитания векторов из 20+ вопросов и ответов по векторам. Включает рассуждения и прикладные вопросы.
Связанные уроки по векторам
Вычитание векторов является частью нашей серии уроков для поддержки пересмотра векторов . Возможно, вам будет полезно начать с урока по основным векторам, чтобы получить общее представление о том, чего ожидать, или воспользоваться пошаговыми руководствами, приведенными ниже, для получения более подробной информации по отдельным темам. Другие уроки в этой серии включают в себя:
- Векторы
- Величина вектора
- Вектор-столбец
- Векторное обозначение
- Умножение на вектор
- Добавление вектора
- Векторные проблемы
Примеры вычитания векторов
Пример 1: вычитание векторов
Вычисление:
\[\left(\begin{array}{1} 6\\ 4\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 4\\ 3\\ \end{массив}\right)\]
- Вычесть 9Компоненты 0056 x .

Вычесть второе верхнее число из первого верхнего числа
6-4=2
2 Вычесть компоненты и .
Вычесть второе нижнее число из первого нижнего числа
4-3=1
3 Запишите результирующий вектор.
\[\left(\begin{массив}{1} 6\\ 4\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 4\\ 3\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 2\\ 1\\ \конец{массив}\справа)\]
Пример 2: вычитание векторов
Вычисление:
\[\left(\begin{array}{1} 3\\ 2\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 5\\ 1\\ \end{массив}\right)\]
Вычесть компоненты размером x .
Вычесть второе верхнее число из первого верхнего числа
3-5=-2
Вычесть компоненты и .
Вычесть второе нижнее число из первого нижнего числа
2-1=1
Запишите результирующий вектор.
Запишите два ответа в виде вектор-столбца
\[\left(\begin{array}{1} 3\\ 2\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 5\\ 1\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} -2\\ 1\\ \end{array}\right)\]
Пример 3: вычитание векторов
Вычисление:
\[\left(\begin{array}{1} 2\\ 4\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 2\\ 6\\ \end{массив}\right)\]
Вычесть 9Компоненты 0056 x .
Вычесть второе верхнее число из первого верхнего числа
2-2=0
Вычесть компоненты и .
Вычесть второе нижнее число из первого нижнего числа
4-6=-2
Запишите результирующий вектор.
Запишите два ответа в виде вектор-столбца
\[\left(\begin{array}{1} 2\\ 4\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 2\\ 6\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 0\\ -2\\ \конец{массив}\справа)\]
Пример 4: вычитание векторов
Вычисление:
\[\left(\begin{array}{1} -4\\ 3\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 2\\ 1\\ \end{массив}\right)\]
Вычесть компоненты размером x .
Вычесть второе верхнее число из первого верхнего числа
-4-2=-6
Вычесть компоненты и .
Вычесть второе нижнее число из первого нижнего числа
3-1=2
Запишите результирующий вектор.
Запишите два ответа в виде вектор-столбца
\[\left(\begin{array}{1} -4\\ 3\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 2\\ 1\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} -6\\ 2\\ \end{array}\right)\]
Пример 5: вычитание векторов
Вычисление:
\[\left(\begin{array}{1} -5\\ 2\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} -3\\ -2\\ \end{массив}\right)\]
Вычесть 9Компоненты 0056 x .
Вычесть второе верхнее число из первого верхнего числа
-5-(-3)=-2
Вычесть компоненты и .
Вычесть второе нижнее число из первого нижнего числа
2-(-2)=4
Запишите результирующий вектор.
Запишите два ответа в виде вектор-столбца
\[\left(\begin{array}{1} -5\\ 2\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} -3\\ -2\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} -2\\ 4\\ \конец{массив}\справа)\]
Пример 6: вычитание векторов
Вычисление:
\[\left(\begin{array}{1} 2\\ -1\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} -4\\ -3\\ \end{массив}\right)\]
Вычесть компоненты размером x .
Вычесть второе верхнее число из первого верхнего числа
2-(-4)=6
Вычесть компоненты и .
Вычесть второе нижнее число из первого нижнего числа
-1-(-3)=2
Запишите результирующий вектор.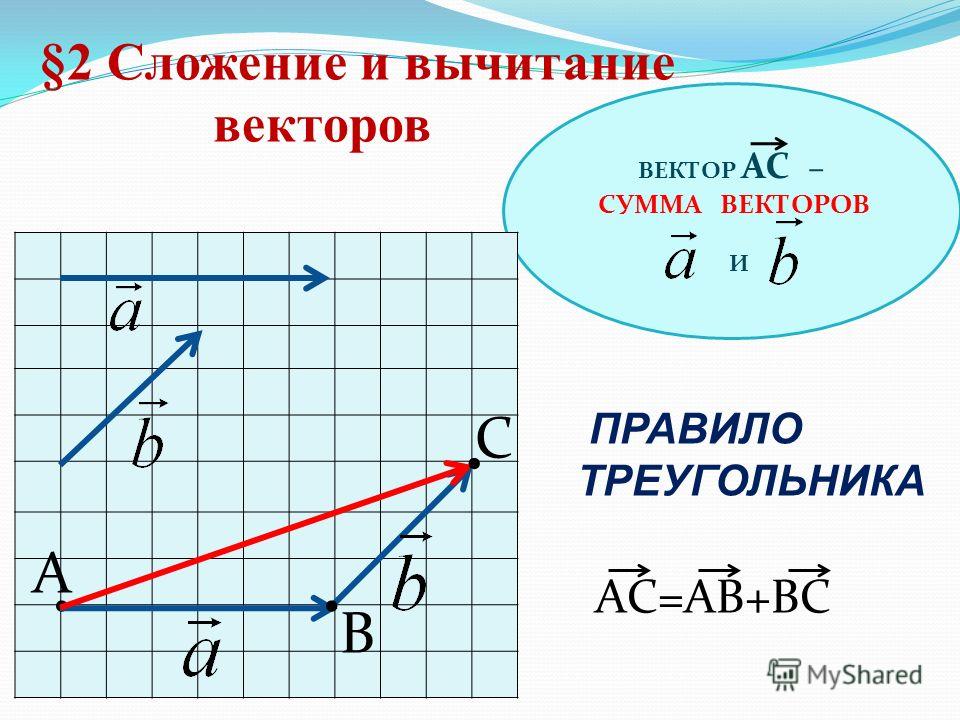
Запишите два ответа в виде вектор-столбца
\[\left(\begin{array}{1} 2\\ -1\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} -4\\ -3\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 6\\ 2\\ \end{array}\right)\]
Распространенные заблуждения
- Вычитание отрицательных целых чисел
При вычитании отрицательных целых чисел легко допустить ошибку.
Убедитесь, что навыки работы с отрицательными числами хорошо отработаны.
3-(-4)=3+4=7
- Порядок вычитания
Порядок вычитания очень важен. Вычитание векторов НЕ является коммутативным и должно выполняться в указанном порядке.
и т. д.
а — б ≠ б — а
- Обозначение векторов столбцов
Векторы-столбцы имеют только 2 числа в квадратных скобках, у них есть верхний номер и нижний номер.
Нет необходимости в каких-либо других знаках препинания, таких как запятые или точки с запятой, и нет необходимости в строке для разделения чисел.
- Окончательный ответ 0
Компонент x или компонент y может быть равен 0 . Если обе компоненты вектора равны 0, то конечным результирующим вектором будет вектор 0 . Это известно как нулевой вектор или нулевой вектор.
\[\left(\begin{массив}{1} 3\\ 7\\ \конец{массив}\справа) -\ \left(\begin{массив}{1} 3\\ 7\\ \конец{массив}\справа) знак равно \left(\begin{массив}{1} 0\\ 0\\ \конец{массив}\справа)\]
Практические вопросы по вычитанию векторов
\begin{pmatrix} \; 3 \;\\ \; 2\; \end{pmatrix}
\begin{pmatrix} \; -3 \;\\ \; 2\; \end{pmatrix}
\begin{pmatrix} \; -3 \;\\ \; -2\; \end{pmatrix}
\begin{pmatrix} \; 3 \;\\ \; -2\; \end{pmatrix}
\textbf{v}-\textbf{w}= \begin{pmatrix} \; 7 \;\\\; 3 \; \end{pmatrix} – \begin{pmatrix} \; 4 \;\\\; 1 \; \end{pmatrix} = \begin{pmatrix} \; 3 \;\\ \; 2\; \end{pmatrix}
\begin{pmatrix} \; -3 \;\\ \; 5 \; \end{pматрица}
\begin{pmatrix} \; -3 \;\\ \; -5 \; \end{pmatrix}
\begin{pmatrix} \; 3 \;\\ \; -5 \; \end{pmatrix}
\begin{pmatrix} \; 3 \;\\ \; 5 \; \end{pmatrix}
\textbf{c}-\textbf{d}= \begin{pmatrix} \; 6 \;\\\; 2\; \end{pmatrix} – \begin{pmatrix} \; 3 \;\\ \; 7\; \end{pmatrix} = \begin{pmatrix} \; 3 \;\\ \; -5 \; \end{pmatrix}
\begin{pmatrix} \; 6 \;\\ \; 2\; \end{pmatrix}
\begin{pmatrix} \; -6 \;\\ \; -2\; \end{pmatrix}
\begin{pmatrix} \; -6 \;\\ \; 2\; \end{pmatrix}
\begin{pmatrix} \; 6 \;\\ \; -2\; \end{pmatrix}
\textbf{b}-\textbf{a}= \begin{pmatrix} \; 5 \;\\\; 4\; \end{pmatrix} – \begin{pmatrix} \; -1 \;\\\; 6\; \end{pmatrix} = \begin{pmatrix} \; 6 \;\\\; -2\; \end{pmatrix}
\begin{pmatrix} \; -1 \;\\ \; -2\; \end{pmatrix}
\begin{pmatrix} \; -1 \;\\ \; 2\; \end{pmatrix}
\begin{pmatrix} \; 1 \;\\ \; -2\; \end{pmatrix}
\begin{pmatrix} \; 1 \;\\ \; 2\; \end{pmatrix}
\textbf{p}-\textbf{q}= \begin{pmatrix} \; -3 \;\\\; 6\; \end{pmatrix} – \begin{pmatrix} \; -2 \;\\\; 4\; \end{pmatrix} = \begin{pmatrix} \; -1 \;\\\; 2\; \end{pmatrix}
\begin{pmatrix} \; -5 \;\\ \; 6\; \end{pmatrix}
\begin{pmatrix} \; -5 \;\\ \; -6 \; \end{pmatrix}
\begin{pmatrix} \; 5 \;\\ \; 6\; \end{pmatrix}
\begin{pmatrix} \; 5 \;\\ \; -6 \; \end{pmatrix}
\textbf{s}-\textbf{r}= \begin{pmatrix} \; -2 \;\\\; -1\; \end{pmatrix} – \begin{pmatrix} \; 3 \;\\ \; 5 \; \end{pmatrix} = \begin{pmatrix} \; -5 \;\\\; -6 \; \end{pматрица}
\begin{pmatrix} \; 2 \;\\ \; -3\; \end{pmatrix}
\begin{pmatrix} \; 2 \;\\ \; 3 \; \end{pmatrix}
\begin{pmatrix} \; -2 \;\\ \; 3 \; \end{pmatrix}
\begin{pmatrix} \; -2 \;\\ \; -3\; \end{pmatrix}
\textbf{e}-\textbf{d}= \begin{pmatrix} \; -4\;\\\; 3 \; \end{pmatrix} – \begin{pmatrix} \; -2 \;\\\; 6\; \end{pmatrix} = \begin{pmatrix} \; -2 \;\\\; -3\; \end{pmatrix}
Вычитание векторов Вопросы GCSE
1. Вектор \textbf{v} равен \begin{pmatrix}
\; 3 \;\\
\; 1 \;
\end{pматрица}
Вектор \textbf{v} равен \begin{pmatrix}
\; 3 \;\\
\; 1 \;
\end{pматрица}
Вектор \textbf{w} равен \begin{pmatrix} \; 2 \;\\ \; 4\; \end{pматрица}
Какой из следующих векторов является ответом на \textbf{w}-\textbf{v} ?
| А | \четверка \четверка | Б | \четверка \четверка | С | \четверка \четверка | Д |
| \begin{pmatrix} \; -1 \;\\ \; 3 \; \end{pmatrix} | \четверка \четверка | \begin{pmatrix} \; 1 \;\\ \; 3 \; \end{pматрица} | \четверка \четверка | \begin{pmatrix} \; 1 \;\\ \; -3\; \end{pmatrix} | \четверка \четверка | \begin{pmatrix} \; -1 \;\\ \; -3\; \end{pmatrix} |
(1 балл)
Показать ответ
2. Вот два вектора.
\textbf{m}= \begin{pmatrix} \; 2 \;\\ \; -4\; \end{pmatrix} \; и \; \textbf{n}= \begin{pmatrix} \; 3 \;\\ \; -6 \; \end{pматрица}
Разминка \; \textbf{n}-\textbf{m}
(2 балла)
Показать ответ
\textbf{n}-\textbf{m}= \begin{pmatrix} \; 3 \;\\ \; -6 \; \end{pmatrix} – \begin{pmatrix} \; 2 \;\\\; -4\; \end{pmatrix} = \begin{pmatrix} \; 1 \;\\ \; -2\; \end{pматрица}
Для компонента x (верхнее число)
(1)
Для компонента y (нижнее число)
(1)
3. Здесь 9 — вектор вычитания.0003
Здесь 9 — вектор вычитания.0003
\begin{pmatrix} \; \текст{а} \;\\ \; -1\; \end{pматрица} – \begin{pmatrix} \; 2 \;\\ \; \текст{б} \; \end{pматрица} знак равно \begin{pmatrix} \; 4 \;\\ \; 2\; \end{pматрица}
(a) Найдите значение a .
(b) Найдите значение b .
(2 балла)
Показать ответ
(a)
а=6
(1)
(б)
б=-3
(1)
Контрольный список для обучения
Теперь вы научились:
- Вычитать векторы
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.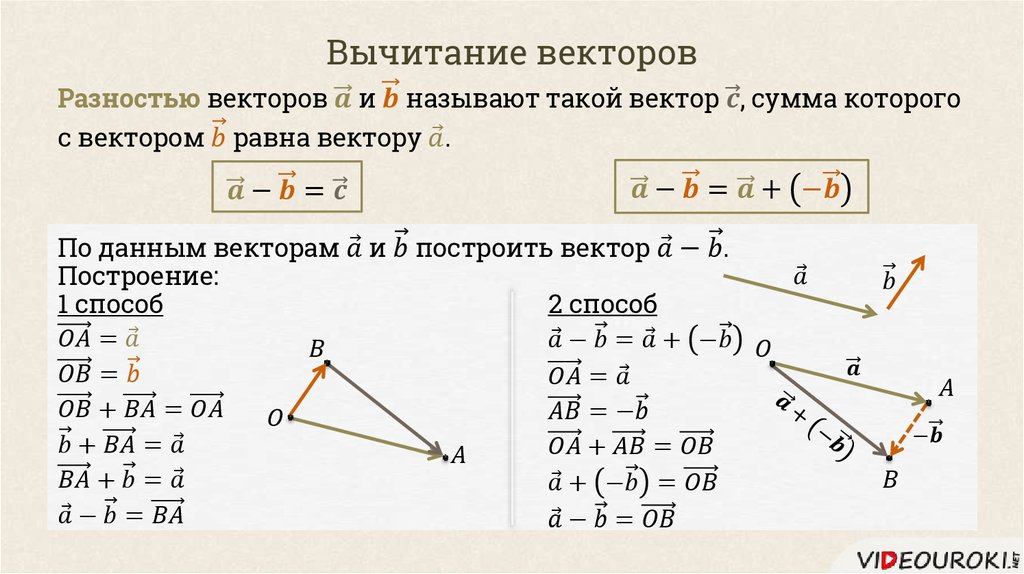
Узнайте больше о нашей программе повторения GCSE по математике.
Вычитание векторов — концепции, варианты использования, проблемы
Последнее обновление: 16 апреля 2021 г., 10:04
Поскольку мы обсудили Вектор в физике и подробно изучили сложение векторов, теперь настала очередь обсудить другую тему векторной физики, а именно Вычитание векторов .
Вычитание векторов помогает нам вычитать один вектор из другого вектора. Теперь, как это сделать?
Чтобы вычесть один вектор из другого, например, чтобы получить A – B , просто сформируйте вектор – B , который представляет собой скалярное множественное (–1) B , и добавьте его к A , т. Е.
A — B = A + ( — B )
- Вектор – вычитание с примерами
- Вычитание вектора – один вариант использования
- Численные задачи – вычитание вектора
- Относительная скорость дождя относительно движущегося наблюдателя
Вектор – вычитание с примерами
Пример: Для двух векторов A и B на диаграмме 1 найдите вектор A – B .
Решение. Переверните B вокруг, т.е. измените направление B (тем самым сформировав – B) и добавьте этот вектор к A , используя треугольный закон сложения векторов.
Диаграмма 2Вот еще один пример. На диаграмме 3 ниже показаны 2 вектора A и B, а также то, как они получены из AB.
Диаграмма 3Вычитание векторов – один вариант использования
Теперь давайте обсудим один вариант использования вычитания векторов, когда нам нужно вычесть вектор из другого вектора. Если вы знакомы с термином «относительная скорость», возможно, вы уже поняли намек.
Когда мы обсуждаем движение различных объектов, расположенных вблизи земной поверхности, мы принимаем земную поверхность за «статическую» систему отсчета. Говорят, что объект находится в движении относительно зрителя в этой статической системе отсчета.
Это круто.
Но если нам нужно рассмотреть движение объекта относительно «движущейся системы отсчета», то как поступить в этой ситуации?
Например, пассажиру движущегося поезда все близлежащие дома, деревья и другие неподвижные объекты кажутся движущимися. Это означает, что по отношению к этому пассажиру в движущемся поезде эти объекты имеют «относительную скорость», хотя на самом деле они неподвижны или статичны.
Это означает, что по отношению к этому пассажиру в движущемся поезде эти объекты имеют «относительную скорость», хотя на самом деле они неподвижны или статичны.
Вычисление относительной скорости. Когда нам нужно рассчитать относительную скорость объекта относительно движущегося наблюдателя, мы должны вычесть фактическую скорость наблюдателя из фактической скорости объекта.
Допустим, фактическая скорость объекта равна V1, а фактическая скорость наблюдателя равна V2.
Тогда относительная скорость объекта относительно движущегося зрителя = Vr = V1 – V2
Теперь при вычислении разницы между V1 и V2 мы будем использовать процесс сложения векторов, но с небольшими изменениями.
Это здесь: V1-V2 = V1 + (-V2)
Итак, мы должны рассмотреть отрицательное значение вектора V2, что означает вектор с той же величиной, что и V2, но с обратным направлением.
Затем выполните известный процесс сложения векторов между V1 и (-V2) и получите вектор V1-V2.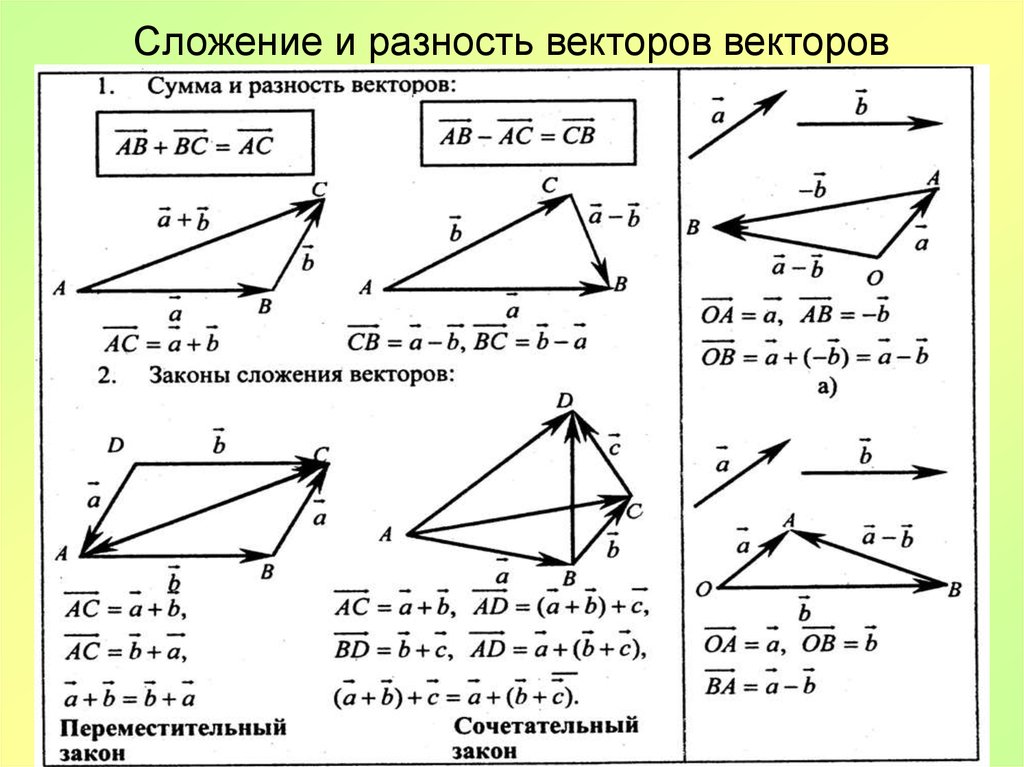
Численные задачи – вычитание векторов
1)
Автомобиль движется со скоростью 80 км/ч на север. Автобус движется со скоростью 80√2 км/ч в направлении на северо-запад. Какова относительная скорость автобуса относительно автомобиля?
2)
Один корабль движется на восток со скоростью 10 км/ч. Лодка движется на северо-восток, образуя с севером угол 30 градусов. Если наблюдателю на корабле кажется, что лодка движется на север, то какова скорость (величина) лодки?
Относительная скорость дождя относительно движущегося наблюдателя
С помощью механизма вычитания вектора , который мы только что обсуждали, мы можем легко определить относительную скорость дождя относительно движущегося наблюдателя.
Если нет сильного ветра, то капли дождя падают вертикально.
Теперь человек в состоянии покоя может держать зонт вертикально над головой и спасаться от капель дождя.
Но если человек сам находится в движении, то он должен держать зонт в наклонном положении, направленным в переднюю сторону, чтобы спастись от дождя.
Чтобы обсудить это, мы можем воспользоваться векторной диаграммой и процедурой вычитания векторов.
Допустим, скорость капель дождя вертикально вниз равна V, а человек движется на восток со скоростью U.
Теперь скажем, относительно движущегося наблюдателя (человека) относительная скорость капель дождя равна R.
Таким образом, мы получим R, вычитая скорость наблюдателя из скорости дождя.
R = V – U = V + (-U)
На диаграмме обратный вектор U рисуется путем переворачивания U и обозначается как –U.
Помните, что этот перевернутый вектор имеет ту же величину, что и исходный U, но знак – показывает только обратное направление.
В следующих вычислениях мы будем использовать только его величину, так как мы можем взять его как новый вектор.
Теперь, если мы сложим эти 2 вектора V и –U, используя векторное сложение (здесь теорема Пифагора является лучшим вариантом для этого сложения, так как 2 вектора V и –U находятся под прямым углом), мы получим R, относительную скорость дождь.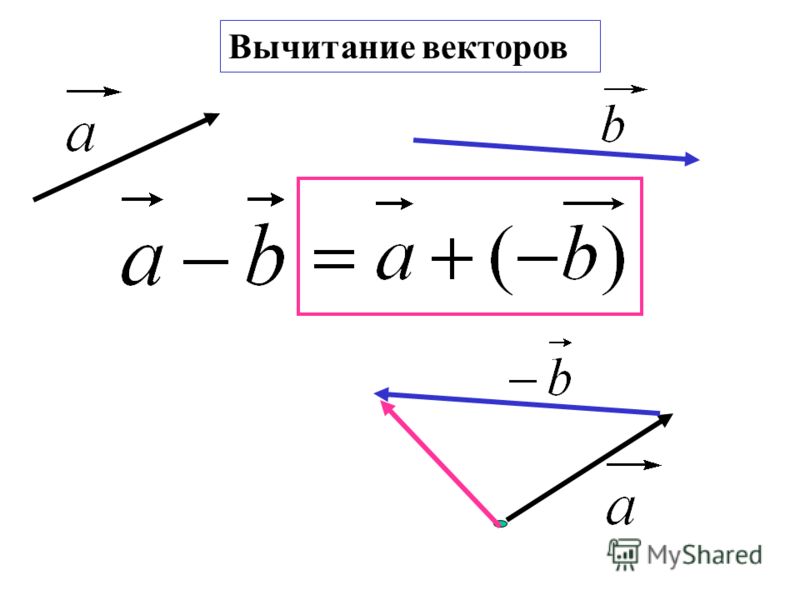

 Для этого постройте противоположно направленный и равный ему отрезок и затем совместите начало этого отрезка с уменьшаемым;
Для этого постройте противоположно направленный и равный ему отрезок и затем совместите начало этого отрезка с уменьшаемым;