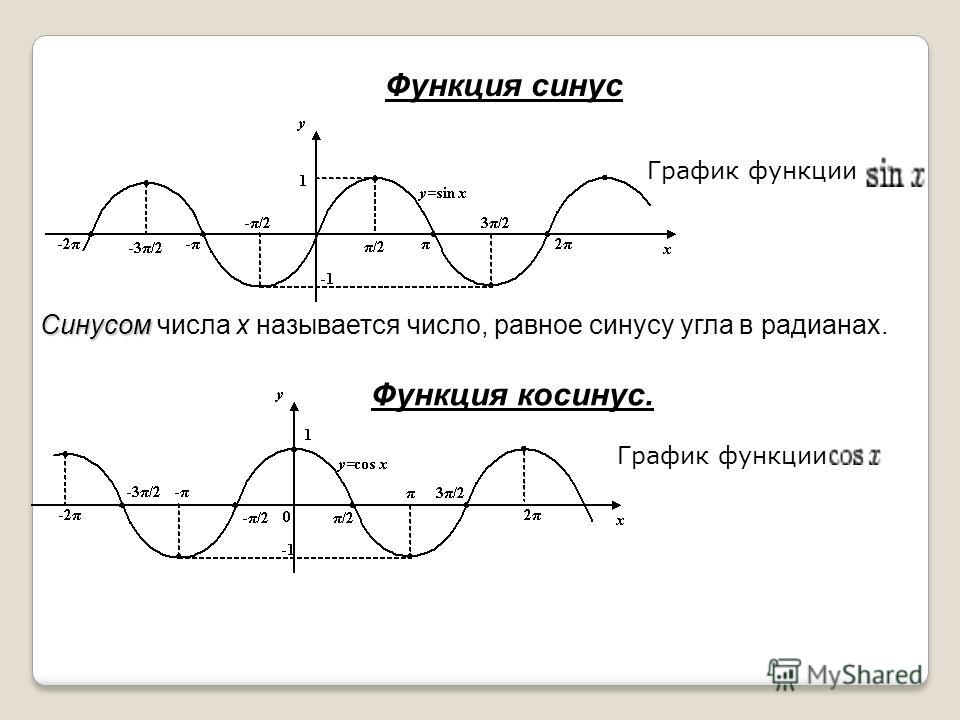
Исчисление
Вопрос задан 20.11.21Я знаю, что ответ равен 8, но как найти нули второй производной?
Подписаться І 3
Подробнее
Отчет
3 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Пол М. ответил 23.11.21
Репетитор
5 (22)
Узнайте, «как» делать математику и почему «как» работает!
Об этом репетиторе ›
Об этом репетиторе ›
Положительные x координаты точек перегиба равны (приблизительно) ,808, 1,814, 2,522 и 3,079; они были получены путем решения f «(x) = 0 с использованием деления интервала пополам в электронной таблице.
Я не согласен с замечанием Стэнтона Д. о том, что значения можно получить из точек перегиба sin x. Во-первых, x=0 не является точкой перегиба f(x), а во-вторых, полученные мной точки не равны квадратному корню из значений, предложенных Стэнтоном Д.. Я не могу объяснить, почему комментарий Стэнтона Д. не работает, но, похоже, это не так.
Голосовать за 0 голос против
Подробнее
90,5 . Действительно, вытащить цепную линейку и начать проворачивать — это перебор!— Ура, —г-н. д.
Голосовать за 0 голос против
Подробнее
Отчет
Джош Ф. ответил 21.11.21
Репетитор
5,0 (170)
Джош Ф.
: опытный репетитор по математике, английскому языку и подготовке к экзаменам
Об этом репетиторе ›
Об этом репетиторе ›
Y ‘ = 2x · Cos (x 2 )
Y « = 2COS (x 2 ) — 4x 2 грех (x 2 ) = 0
Cos (x 2 2 ) = 0 0003
Cos (x 2 2 ) = 0 0003
Cos (x 2 (x 2 ) = 0 0003 Cos (x 2 (x 2 ) = 0 0003 Cos (x 2 (x 2 ). ) — 2x 2 sin(x 2 ) = 0 Но решить это аналитически я не уверен Это четная функция, поэтому 4 положительных корня между 0 и π повторяются в отрицательном интервале Трудно представить простое алгебраическое решение, учитывая, что у нас есть степени x и тригонометрические функции x в одном и том же уравнении.0003 Голосовать за 0 голос против Подробнее Отчет Задайте вопрос бесплатно Получите бесплатный ответ на быстрый вопрос. Найдите онлайн-репетитора сейчас Выберите эксперта и встретьтесь онлайн.
Никаких пакетов или подписок, платите только за то время, которое вам нужно. 1. Почему функции синуса и косинуса называются периодическими функциями? 2. Как график [latex]y=\sin x[/latex] соотносится с графиком [latex]y=\cos x[/latex]? Объясните, как можно горизонтально перевести график [latex]y=\sin x[/latex], чтобы получить [latex]y=\cos x[/latex]. 3. Для уравнения [латекс]A\cos(Bx+C)+D[/латекс] какие константы влияют на диапазон функции и как они влияют на диапазон? 4. 5. Как можно использовать единичный круг для построения графика [латекс]f(t)=\sin t[/латекс]? 6. [латекс]f(x)=2\sin x[/латекс] 7. [латекс]f(x)=\frac{2}{3}\cos x[/латекс] 8 . [латекс]f(x)=−3\sin x[/латекс] 9. [латекс]f(x)=4\sin x[/латекс] 10. [латекс]f(x)= 2\cos x[/латекс] 11. [латекс]f(x)=\cos(2x)[/латекс] 12. [латекс]f(x)=2\sin\left(\frac{ 1}{2}x\right)[/latex] 13. [latex]f(x)=4\cos(\pi x)[/latex] 14. [latex]f(x)=3 \cos\left(\frac{6}{5}x\right)[/latex] 15. [латекс]y=3\sin(8(x+4))+5[/латекс] 16. [латекс]y=2\sin(3x−21)+4[/латекс] 17. [latex]y=5\sin(5x+20)−2[/latex] Для следующих упражнений нарисуйте один полный период каждой функции, начиная с [latex]x=0[/latex]. Для каждой функции укажите амплитуду, период и среднюю линию. Укажите максимальное и минимальное значения y и соответствующие им значения x за один период для [latex]x>0[/latex]. Все еще ищете помощи? Получите правильный ответ, быстро.
Ответы на большинство вопросов в течение 4 часов. ИЛИ
Набор задач 48: Графики функций синуса и косинуса
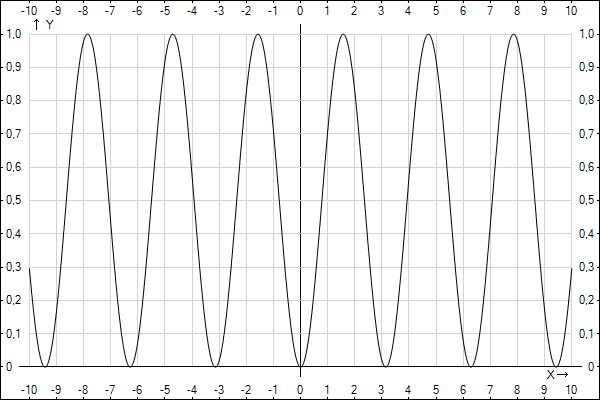Как диапазон преобразованной синусоидальной функции связан с уравнением [латекс]у=А\sin(Вх+С)+D[/латекс]?
18. [латекс]f(t)=2\sin\left(t−\frac{5\pi}{6}\right)[/латекс]
19. [латекс]f(t)=- \cos\left(t+\frac{\pi}{3}\right)+1[/latex]
20. [latex]f(t)=4\cos\left(2\left(t+\frac{ \pi}{4}\right)\right)−3[/latex]
21. [latex]f(t)=−\sin\left(12t+\frac{5\pi}{3}\right) [/latex]
22. [latex]f(x)=4\sin\left(\frac{\pi}{2}(x−3)\right)+7[/latex]
23. Определить амплитуда, средняя линия, период и уравнение, включающее синусоидальную функцию, для графика, показанного на рис. 26.
Рисунок 26
24. Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на рисунке 27. уравнение с косинусом для графика, показанного на рис. 28.
0212 Рисунок 29
27. Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на рисунке 30.
Рисунок 31
29. Определите амплитуду, период, среднюю линию и уравнение с косинусом для графика, показанного на рисунке 32.
Рисунок 32
30. Определите амплитуду, период, среднюю линию и формулу, содержащую синус, для графика, показанного на рис. 33.
рис. х[/латекс].
31. На [0,2π) решить [латекс]f(x)=\frac{1}{2}[/латекс].
32. Вычислите [латекс]f\left(\frac{\pi}{2}\right)[/latex].
33. На [0,2π], [латекс]f(x)=\frac{\sqrt{2}}{2}[/латекс]. Найдите все значения х.
34. На [0,2π) максимальное значение(я) функции происходит(ются) при каком(их) значении(ях) x?
35. На [0,2π) минимальное значение(я) функции встречается(ются) при каком(их) значении(ях) x?
36. Показать, что [latex]f(−x)=−f(x)[/latex]. Это означает, что [latex]f(x)=\sin x[/latex] является нечетной функцией и обладает симметрией в отношении ________________.
Для следующих упражнений пусть [latex]f(x)=\cos x[/latex].
37. На [0,2π) решить уравнение [латекс]f(x)=\cos x=0[/латекс].
38. На [0,2π) решить [латекс]f(x)=\frac{1}{2}[/latex].
39. На [0,2π) найти x — перехваты [латекс]f(x)=\cos x[/латекс].
40. На [0,2π) найти x -значений, при которых функция имеет максимальное или минимальное значение.
41. На [0,2π) решите уравнение [латекс]f(x)=\frac{\sqrt{3}}{2}[/latex].
42. График [латекс]h(x)=x+\sin x \text{ on}[0,2\pi][/latex]. Объясните, почему график выглядит именно так.
43. Постройте график [латекс]h(x)=x+\sin x[/латекс] на [−100,100]. Получился ли график таким, как предсказано в предыдущем упражнении?
44. Постройте график [латекс]f(x)=x\sin x[/латекс] на [0,2π] и опишите, как этот график отличается от графика [латекс]f(x)=\sin x[/латекс ].
45. Постройте график [латекс]f(x)=x\sin x[/латекс] в окне [−10,10] и объясните, что показывает график.
46. Постройте график [latex]f(x)=\frac{\sin x}{x}[/latex] в окне [−5π,5π] и объясните, что показывает график.