Вариант 1
Используя характеристическое свойство, запишите: а) множество A всех натуральных чисел, кратных 8; б) множество B всех натуральных чисел, которые при делении на 8 дают в остатке 1.
Найдите значение выражения при.
При каких значениях переменной выражение имеет смысл?
При каком значении переменной выражение не имеет смысла?
Составьте выражение для решения задачи. Моторный катер, собственная скорость которого 10 км/ч, прошел по реке расстояние, равное 25 км, вниз по течению и такое же расстояние вверх по течению. Найдите скорость течения реки, если время, затраченное на весь путь равно 5 ч.
Для ряда данных 4; 4; 4; 5; 5 найдите: а) размах; б) объем; в) среднее арифметическое; г) моду; д) медиану.
Заполните таблицу значений выражения с шагом 1 для всех целых значений переменной, удовлетворяющих условию.
Известно, что . Чему равно значение выражения: а); б); в)?
Вариант 2
Используя характеристическое свойство, запишите: а) множество A всех натуральных чисел, кратных 13; б) множество B всех натуральных чисел, которые при делении на 13 дают в остатке 12.
Найдите значение выражения при.
При каких значениях переменной выражение имеет смысл?
При каком значении переменной выражение не имеет смысла?
Составьте выражение для решения задачи. Моторная лодка, собственная скорость которой 12 км/ч, прошла по реке расстояние, равное 30 км, вниз по течению и такое же расстояние вверх по течению. Найдите скорость течения реки, если время, затраченное на весь путь равно 6 ч.
Для ряда данных 3; 4; 5; 5; 5 найдите: а) размах; б) объем; в) среднее арифметическое; г) моду; д) медиану.
Заполните таблицу значений выражения с шагом 1 для всех целых значений переменной, удовлетворяющих условию.
Известно, что . Чему равно значение выражения: а); б); в)?
Вариант 3
Используя характеристическое свойство, запишите: а) множество A всех натуральных чисел, кратных 17; б) множество B всех натуральных чисел, которые при делении на 17 дают в остатке 1.
Найдите значение выражения при.
При каких значениях переменной выражение имеет смысл?
При каких значениях переменной выражение не имеет смысла?
Составьте уравнение для решения задачи. 17 туристов во время ночевки расположились в двухместных и трехместных палатках. Всего было 7 палаток. Сколько из них было двухместных?
Для ряда данных 3; 4; 4; 5; 5 найдите: а) размах; б) объем; в) среднее арифметическое; г) моду; д) медиану
Заполните таблицу значений выражения с шагом 1 для всех целых значений переменной, удовлетворяющих условию.
Известно, что . Чему равно значение выражения: а); б); в)?
Самостоятельная работа № 4
§ 3. Степень с натуральным показателем Основные сведения
Степенью числа с натуральным показателем , большим 1, называют выражение, равное произведениюмножителей, каждый из которых равен. Степенью числас показателем 1 называют выражение, равное. Степенью числас нулевым показателем называется выражение, равное 1. Выражение не имеет смысла!
В выражении числоназываютоснованием степени, число –показателем степени. Вторую степень числа иногда называют квадратом, третью степень – кубом числа. Нахождение -ой степени числаназываютвозведением в -ю степень.
Свойства степени с натуральным показателем
Очевидно, при .
Если ,или, то.
Если
и,
гдеили,
то.
Если и, гдеили, то.
Если – произвольное число,– натуральные числа, то.
Если – произвольное число,– натуральные числа, причем, то.
|
Упражнения: В — множество четных чисел. Зная это, запишите с помощью символов следующие предложения: 1) число 20 четное: 2) число 17 не является четным. Прочитайте следующие высказывания и укажите среди них истинные: 1) 100 N; 2) -8 Z; 3) ~8 N; 4) 5,36 Q; 5) 102 R; 6) —Q, 7) -7 R 8) ; 9) 0 Z. 5. P — множество натуральных чисел, больших 7 и меньших 14.  Выясните, принадлежат или не принадлежат этому множеству числа 13, 10, 5, 7, 14. Ответ запишите, используя знаки и .
6. D — множество целых отрицательных чисел. Назовите пять чисел, принадлежащих этому множеству. Верно ли, что -1 D; 0 D; -3,2 D? 7. Даны числа: 325; 0; — 17; -3,8; 7. Установите, какие из них принадлежат множеству: 1) натуральных чисел, 2) целых чисел; 3) рациональных чисел; 4) действительных чисел. 8. Запищите множество отрезков, которым принадлежит точка С B D C A 9. Запишите с помощью знака равенства и фигурных скобок предложения:
12. Изобразите на координатной прямой множество решений неравенства: 1)x>5,3; 2) x -3,8; 3) -4,5 x13. Объясните, почему множество X = {2, 4, 6} является подмножеством множества У={0, 2, 4, 6,8,10} . а множество Z = {4, б, 12} нет. 14. Дано множество A={5, 10, 15, 25}. Запишите два множества, равные множеству А. 15. Установите, в каком отношении находятся множества решений неравенств и сами неравенства: 1)х 2) хх> 15; 3) х 12 и x> 10; 4) х 12 и -3x> -36. 16. Изобразим при помощи кругов Эйлера отношения между множествами А и В, если: I) А — множество четных чисел, В — множество чисел, кратных 3; 2) А — множество квадратов, В — множество прямоугольников; 3) А— множество квадратов, В — множество прямоугольных треугольников; 4) А — множество квадратов, В множество прямоугольников с равными сторонами. 
17. Найдите объединение множеств А и В. если: 1)А ={a, b, с, d, е,f}; B= {b, е, f,k, l}; 2)А ={26, 39, 5, 58, 17, 81}; B = { 17, 26, 58}, 3) A ={26, 39, 5, 58, 17, 81}; В = {2. 6, 3, 9, 1. 7}. Из каких элементов состоит объединение множества букв d слове «математика» и множества буки в слове «геометрия»? М — множество однозначных натуральных чисел, Р — множество нечетных натуральных чисел. Какие числа войдут в объединение. множеств М и Р? Окажутся ли в нем числа 4, 14. 17? Какую фигуру будет представлять объединение двух треугольников, если их пересечением является: 1) треугольник; 2) шестиугольник; 3) отрезок? Назовите все множества, о которых идет речь в задаче: У школы посадили 4 липы и 3 березы. Сколько всего деревьев посадили у школы? Пионеры помогали колхозу в уборке моркови.  Один отряд собрал 40 корзин моркови, а другой — на 10 корзин больше. Сколько корзин моркови собрали оба отряда?
Установите, какое множество является объединением двух других рассматриваемых в задаче: I) У Коли было 6 книг. В день рождения ему подарили еще 4 книги. Сколько книг стало у Коли? Найдите пересечение множеств А и В. если: А ={a, b, с, d, е,f}; B= {b, е, f,k, l}; 2)А ={26, 39, 5, 58, 17, 81}; B = { 17, 26, 58}; 3)A ={26, 39, 5, 58, 17, 81}; В = {2. 6, 3, 9, 1. 7}. Из каких элементов состоит пересечение множества букв в слове «математика» и множества букв в слове «геометрия»? М — множество однозначных натуральных чисел, Р — множество нечетных натуральных чисел. Какие числа войдут в пересечение данных множеств М и Р? Содержатся ли в нем числа 1,5 и 17? Найдите пересечение множеств решении неравенств, в которых переменная—действительное число: 1) х>-2 и х>0; 2} х> —3.  7 и х 4, 3) х>5 и x
Начертите два треугольника так. чтобы их пересечением: I) был треугольник; 2) был отрезок; 3) была точка; 4) был многоугольник. Какая фигура может получиться в пересечении треугольника и четырехугольника? Рассмотрите несколько случаев. Скачать 73,5 Kb. Поделитесь с Вашими друзьями: |
Укажите характеристическое свойство элементов множества:
теория категорий — Интуиция характеристического свойства свободной группы
Задать вопрос
спросил
Изменено 2 года, 4 месяца назад
Просмотрено 193 раза
$\begingroup$
Вот теорема о характеристическом свойстве свободной группы:
Теорема (Ли ТМ).
Пусть $S$ — множество. За
любой группы $H$ и любого отображения $f:S\to H$ существует единственный гомоморфизм
$g:F(S)\to H$, продолжающий $f$.Здесь $F(S)$ — свободная группа на $S$.
Я знаю, что там написано, но не знаю, почему это должно быть полезно. т. е. какова стратегия таких теорем? Как это может помочь понять $F(S)$?
Кто-нибудь может просветить на простом примере?
- теория групп
- теория категорий
- свободные группы
- свободный продукт
$\endgroup$
19
$\begingroup$
Может оказаться полезной аналогия с векторными пространствами. Если $V$ — векторное пространство с базой $B$, то любая функция множества на $B$ в другое векторное пространство $W$ может быть продолжена до линейного отображения $V \to W$. Итак, $V$ — свободное векторное пространство на базисе $B$.
В случае векторных пространств это свойство не характеризует $V$, поскольку каждое векторное пространство имеет базис. Это неверно в случае групп, даже если они абелевы. Свободные группы отличаются тем, что они допускают «базисные» расширения, а групповые гомоморфизмы из свободной группы полностью определяются их действием на «базисные элементы». Точно так же, как векторное пространство определяется (с точностью до линейного изоморфизма) своей размерностью векторного пространства, которая является мощностью любого базиса для этого пространства, свободная группа определяется (с точностью до изоморфизма группы) мощностью своего набора образующих, называется его ранг.
$\endgroup$
$\begingroup$
Эта характеристика подчеркивает, что свободные группы связаны с гомоморфизмами. Вот простое доказательство, использующее эту характеристику:
Теорема. Если $|X|\geq2$, то $F(X)$ неразрешима.
Доказательство. Симметрическая группа $S_5$ может быть порождена двумя элементами. Следовательно, по этой характеристике свободных групп $F(X)$ подчиняется $S_5$ для всех множеств $X$, содержащих не менее двух элементов. Так как $S_5$ неразрешим, так как разрешимость сохраняется при гомоморфных образах, отсюда следует результат.
(Ранее в этом ответе использовалось $S_3$ вместо $S_5$, чтобы доказать, что свободные группы ненильпотентны. Теперь ответ стал более сильным, так как неразрешимость подразумевает ненильпотентность.)
$\endgroup$
Характеристические свойства веществ: TEAS
Штатные авторы RegisteredNursing.org | Обновлено/проверено: 25 августа 2022 г.
Глоссарий терминов и терминов свойств веществ
- Изменение состояний материи: физическое свойство веществ, позволяющее твердым телам, жидкостям и газам изменять свое состояние при определенных условиях.
- Масса: Физическое свойство веществ, которое представляет собой сопротивление объекта движению при приложении силы и выражается в килограммах (кг).
- Плотность: Физическое свойство веществ, которое представляет собой измерение массы по отношению к объему и по отношению к нему.
- Объем: Физическое свойство веществ, которое является измерением количества или количества материи в трехмерном пространстве.
- Температура кипения: Физическое свойство веществ, при котором жидкость превращается в пар.
- Температура плавления: Физическое свойство веществ, представляющее собой температуру, при которой твердое тело превращается в жидкость.
- Проводимость: Физическое свойство веществ, которое является мерой способности вещества или отсутствия способности проводить электричество.
- Теплоемкость: Физическое свойство веществ, которое представляет собой количество теплоты, которое необходимо добавить или отвести от вещества для достижения определенной температуры.
- Ковкость: Физическое свойство веществ, которое представляет собой степень способности твердого тела изменять свою форму и вид под воздействием напряжения.
- Напряжение растяжения: Напряжение, прикладываемое к твердому телу в связи с его пластичностью.
Свойства веществ
Уникальные и отличительные свойства веществ отличают их от других веществ с их собственными уникальными и отличительными свойствами.
Некоторые из уникальных и отличительных свойств веществ являются физическими, а другие — химическими.
Некоторые из физических свойств веществ включают их:
- Изменение состояний без изменения или изменения свойств вещества
- Масса
- Плотность
- Том
- Температура кипения
- Температура плавления
- Проводимость
- Теплоемкость
- Пластичность
Многие физические свойства веществ зависят от количества вещества, а другие физические свойства веществ не зависят от количества вещества.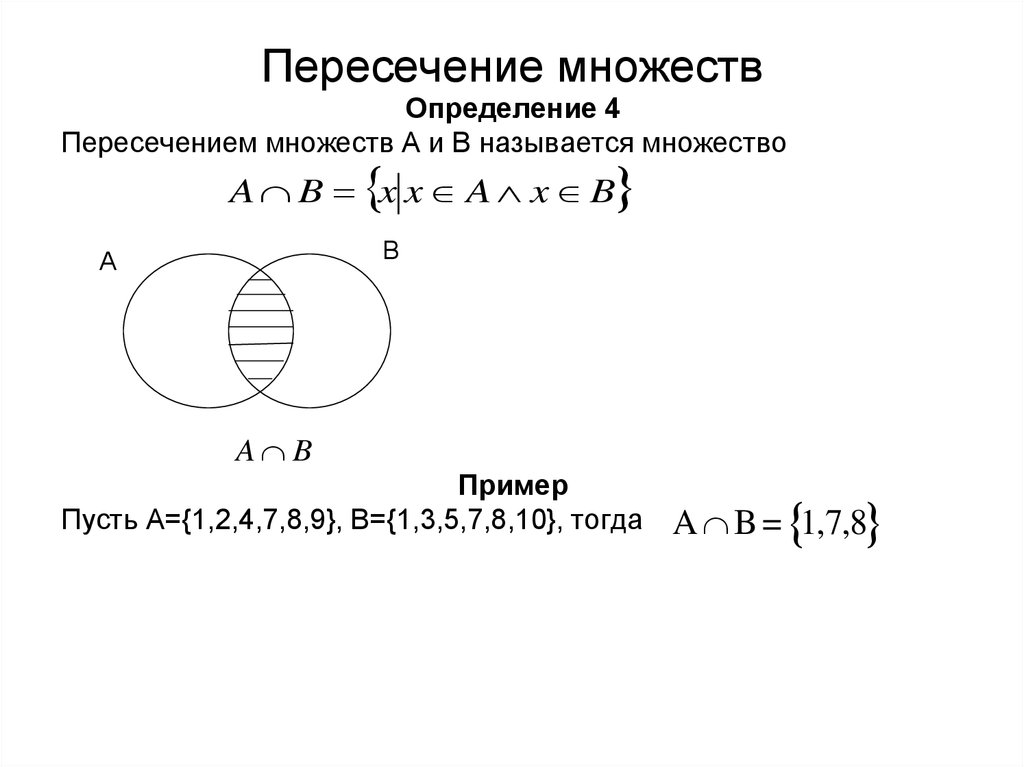
Например, масса и объем не зависят от количества вещества; но температура кипения, точка плавления, ковкость, проводимость и теплоемкость зависят от количества вещества.
Свойства веществ можно разделить на следующие категории:
- Экстенсивные свойства веществ
- Интенсивные свойства веществ
Экстенсивные свойства веществ — это такие свойства, как масса и объем, — это свойства веществ, которые изменяются в зависимости от размера вещества; а интенсивные свойства веществ, такие как температура кипения, температура плавления, ковкость, проводимость и теплоемкость, — это те свойства веществ, которые НЕ изменяются в зависимости от размера вещества.
Свойства веществ также можно разделить на следующие категории:
- Физические свойства веществ
- Химические свойства веществ
Физические свойства веществ — это те свойства, которые можно увидеть и наблюдать, а химические свойства веществ — это те свойства, которые возникают в результате химической реакции и изменения компонента вещества.
Изменение состояния
Вещество, включая твердые тела, жидкости и газы, может изменять свое состояние при определенных условиях. Например, вода может превратиться в газообразный водяной пар при испарении и в условиях повышения температуры, а лед превратится из твердого состояния в жидкое, когда температура станет достаточной для его плавления.
Масса
Проще говоря, масса — это количество материи, содержащейся в веществе. Это не вес вещества. Технически масса — это сопротивление объекта движению при приложении силы. Масса выражается в килограммах (кг).
Массу можно рассчитать математически по следующей формуле:
Масса = приложенная сила в ньютонах силы/ускорения или
M = f/a
Плотность
Плотность – это измерение массы по отношению к объему и по отношению к нему. Плотность не равна весу. Математическая формула для расчета плотности:
Плотность = масса, деленная на объем
Плотность может варьироваться в зависимости от температуры и давления, которым подвергается вещество.
Это изменение более выражено для газов, чем для твердых тел и жидкостей.
Повышение температуры уменьшает его плотность, поскольку его объем увеличивается с повышением температуры; и приложение увеличивающегося давления увеличивает плотность, потому что объем уменьшается с увеличением давления.
Объем
Мерный стакан можно использовать для измерения объема жидкостей. Эта чашка измеряет объем в чашках, жидких унциях и миллилитрах.
Объем – это измерение количества или количества материи в трехмерном пространстве. Твердые тела, жидкости, газы и плазма имеют объемы с положительной корреляцией с количеством вещества и размером сосуда. Чем больше количество материи и чем больше контейнер, тем больше объем.
Температура кипения
Температура кипения — это точка, при которой жидкость превращается в пар. Температура кипения выражается в градусах Фаренгейта или по Цельсию. Температура кипения будет варьироваться в зависимости от давления, которое окружает его в контейнере.
Температура по Фаренгейту и по Цельсию может быть преобразована в температуру по Цельсию и по Фаренгейту следующим образом:
Температура по Фаренгейту = C + 32 x 9/5
Чем выше давление окружающей среды, тем выше температура кипения этой жидкости; и чем ниже окружающее давление, тем ниже температура кипения жидкости. Например, в городе Денвер высотой в милю атмосферное давление низкое и значительно ниже, чем атмосферное давление на приморском острове, таком как Хилтон-Хед. Таким образом, когда вы кипятите воду в Денвере, она будет кипеть при более низкой температуре и быстрее, чем при кипячении воды в Хилтон-Хед, потому что точка кипения воды в Денвере ниже из-за низкого атмосферного давления и температура кипения воды на Хилтон-Хед выше, потому что атмосферное давление на уровне моря выше, чем в горах. В Денвере ваша паста приготовится быстрее, чем в Хилтон-Хед.
Различные жидкости различаются по температуре кипения. Например, точка кипения воды на уровне моря составляет 212 градусов по Фаренгейту и 100 градусов по Цельсию, но другие жидкости могут кипеть только при более высокой температуре.
Точка плавления
Проще говоря, точка плавления — это температура, при которой твердое тело превращается в жидкость. На температуру плавления также влияет температура воздуха.
Понятие, противоположное точке плавления, — это точка замерзания жидкости, при которой она превращается в твердое тело. Если рассматривать воду, лед растает и превратится в воду при определенной температуре, а вода превратится в твердый лед при определенной температуре.
Проводимость
Проводимость – это мера способности вещества или отсутствия способности проводить электричество. Некоторые вещества имеют высокий уровень проводимости, а другие вещества имеют высокий уровень сопротивления проводимости электричества.
Теплоемкость
Проще говоря, теплоемкость – это количество тепла, которое необходимо добавить или отвести от вещества для достижения определенной температуры. Теплоемкость также называется теплоемкостью, а количество добавляемого или отводимого тепла измеряется в джоулях на кельвин.
Ковкость
Опять же, просто говоря, податливость определяется как степень способности твердого тела изменять свою форму и форму под нагрузкой. Это напряжение, приложенное к твердому телу, называется напряжением растяжения.
Например, такие металлы, как олово, могут быть откованы и легко изменены с точки зрения их формы и формы при воздействии этого растягивающего напряжения молотка; в то время как другие материалы, такие как сталь, обладают высокой устойчивостью к растягивающим напряжениям.
СВЯЗАННЫЕ ЧАИ ЖИЗНЬ И ФИЗИЧЕСКИЕ НАУКИ СОДЕРЖАНИЕ:
- Основные макромолекулы в биологической системе
- Хромосомы, гены и ДНК
- Законы наследственности Менделя
- Основная атомная структура
- Характеристические свойства веществ (в настоящее время здесь)
- Изменение состояний материи
- Химические реакции
- Автор
- Последние сообщения
Ален Берк, RN, MSN
Ален Берк, RN, MSN является общепризнанным преподавателем медсестер.
Она начала свою трудовую деятельность учителем начальной школы в Нью-Йорке, а затем поступила в муниципальный колледж Квинсборо, чтобы получить степень младшего специалиста по сестринскому делу. Она работала дипломированной медсестрой в отделении интенсивной терапии местной больницы, и в это время она решила стать преподавателем медсестер. Она получила степень бакалавра наук в области сестринского дела в колледже Эксельсиор, входящем в состав Университета штата Нью-Йорк, и сразу после окончания учебы поступила в аспирантуру Университета Адельфи на Лонг-Айленде, штат Нью-Йорк. Она получила диплом с отличием в Адельфи, получив двойную степень магистра в области сестринского образования и управления сестринским делом, и сразу же начала работу над докторской диссертацией по сестринскому делу в том же университете. Она является автором сотен курсов для медицинских работников, включая медсестер, она работает консультантом по медсестрам в медицинских учреждениях и частных корпорациях, она также является утвержденным поставщиком непрерывного образования для медсестер и других дисциплин, а также является членом Американской ассоциации медсестер.