Исследование матрицы на совместность: Исследование систем линейных уравнений онлайн

Содержание

Исследовать систему уравнений на совместимость.

Пример 1:

Исследуйте совместность системы линейных уравнений и в случае совместности найдите все её решения методом Гаусса.

Решение от преподавателя:

Исследуем эту систему по теореме Кронекера-Капелли.
Выпишем расширенную и основную матрицы:

2	1	-1	2
1	-1	2	1
3	0	1	3
x1	x2	x3

Здесь матрица А выделена жирным шрифтом.
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Умножим 1-ую строку на (-1). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой:

0	-3	5	0
1	-1	2	1
3	0	1	3

Умножим 2-ую строку на (-3).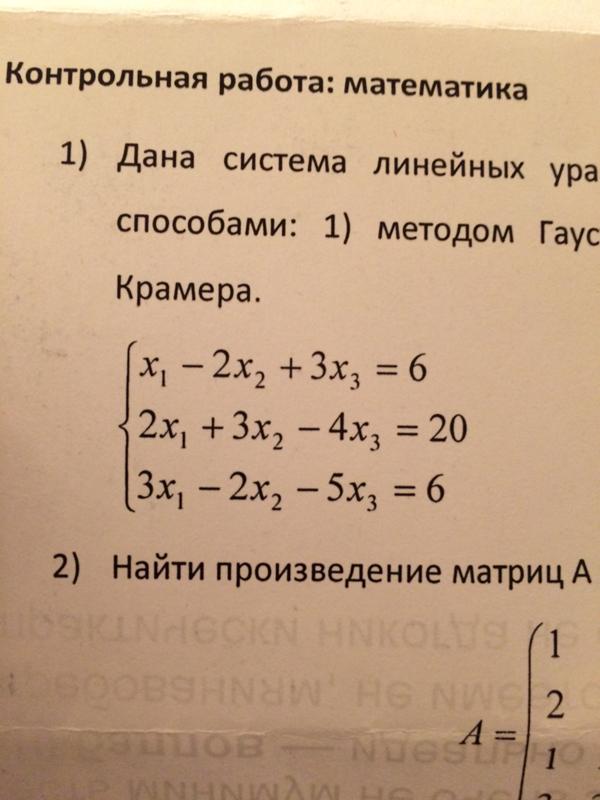 Добавим 3-ую строку к 2-ой:

0	-3	5	0
0	3	-5	0
3	0	1	3

Для удобства вычислений поменяем строки местами:

0	-3	5	0
0	3	-5	0
3	0	1	3

В матрице B 1-ая и 2-ая строки пропорциональны, следовательно, одну из них, например 1-ю, можно вычеркнуть. Это равносильно вычеркиванию 1-го уравнения системы, так как оно является следствием 2-го.

0	3	-5	0
3	0	1	3

Для удобства вычислений поменяем строки местами:

0	3	-5	0
3	0	1	3

Определим ранг системы.

0	3	-5	3
0	1

Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), причем этот минор принадлежит как основной матрице, так и расширенной, следовательно, rang(A) = rang(B) = 2. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x1,x2, значит, неизвестные x1,x2 – зависимые (базисные), а x3 – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.

0	3	0	5
3	0	3	-1

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
3×2 = 5×3
3×1 = 3 — x3
Методом исключения неизвестных находим:
Получили соотношения, выражающие зависимые переменные x1,x2 через свободные x3, то есть нашли общее решение:
x2 = 5/3×3
x1 = 1 — 1/3×3
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной, т.к. имеет более одного решения.

Пример 2:

Исследовать систему уравнений на совместность. В случае совместности найти общее решение методом Гаусса.

Решение от преподавателя:

Исследуем эту систему по теореме Кронекера-Капелли.
Выпишем расширенную и основную матрицы:

6	-2	-1	0	4
0	2	2	1	0
6	0	1	1	4
6	-4	-3	-1	4
x₁	x₂	x₃	x₄

Здесь матрица А выделена жирным шрифтом.
Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
Для удобства вычислений поменяем строки местами:

0	2	2	1	0
6	-2	-1	0	4
6	0	1	1	4
6	-4	-3	-1	4

Умножим 2-ую строку на (-1). Добавим 3-ую строку к 2-ой:

0	2	2	1	0
0	2	2	1	0
6	0	1	1	4
6	-4	-3	-1	4

В матрице B 1-ая и 2-ая строки пропорциональны, следовательно, одну из них, например, 1-ю, можно вычеркнуть. Это равносильно вычеркиванию 1-го уравнения системы, так как оно является следствием 2-го.

0	2	2	1	0
6	0	1	1	4
6	-4	-3	-1	4

Умножим 2-ую строку на (-1). Добавим 3-ую строку к 2-ой:

0	2	2	1	0
0	-4	-4	-2	0
6	-4	-3	-1	4

0	-4	-4	-2	0
6	-4	-3	-1	4

Определим ранг основной системы.

0	-4	-4	-2
6	-4	-3	-1

Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля. Ранг этой системы равен rangA=2.
Определим ранг расширенной системы.

0	-4	-4	-2	0
6	-4	-3	-1	4

Ранг этой системы равен rangB=2.
rang(A) = rang(B) = 2. Поскольку ранг основной матрицы равен рангу расширенной, то система является совместной.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x₁,x₂, значит, неизвестные x₁,x₂ – зависимые (базисные), а x₃,x₄ – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.

0	-4	0	4	2
6	-4	4	3	1

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
— 4x₂ = 4x₃ + 2x₄
6x₁ — 4x₂ = 4 + 3x₃ + x₄
получили соотношения, выражающие зависимые переменные x₁,x₂ через свободные x₃,x₄, то есть нашли общее решение:
x₂ = — x₃ — ¹/₂x₄
x₁ = ²/₃ — ¹/₆x₃ — ¹/₆x₄
Придавая свободным неизвестным любые значения, получим сколько угодно частных решений. Система является неопределенной, т.к. имеет более одного решения.

8. Исследование систем линейных уравнений. Метод Гаусса

Рассмотрим линейную систему общего вида:

Теорема Кронекера-Капелли.

Для совместности системы линейных уравнений необходимо и достаточно, чтобы ранг ее основной матрицы () был равен рангу расширенной матрицы ().

Пусть ==. Тогда верны следующие утверждения.

Следствие 1. Если ранг матрицыравен числу неизвестных, то система имеет единственное решение.

Следствие 2. Если ранг матрицыменьше числа неизвестных, то система имеет бесконечное множество решений. При этомнеизвестных, которые называются свободными, принимают произвольные значения. Говорят, что система имеетстепеней свободы.

Метод Гаусса(исключение неизвестных) состоит в том, что с помощью умножения уравнений на ненулевые числа и сложения в первом уравнении оставляем все неизвестные, во втором на одно меньше, в третьем на два меньше и т.

д. Эту операцию (назовем ее процедурой Гаусса) удобно проводить, используя матрицы.

Составим расширенную матрицу системы и отделим для удобства свободные члены вертикальной линией. С помощью элементарных преобразований приводим матрицу к треугольному виду. Элементарные преобразования матрицы проводим только для строк.

Умножая первую строку на соответствующие коэффициенты и прибавляя к лежащим ниже строкам, получим нули в первом столбце. Затем проделываем такую же процедуру со второй строкой, третьей и т.д., до предпоследней строки. В результате преобразований получаем матрицу, по которой можно записать систему, равносильную исходной.

Рассмотрим три ситуации, возникающие при исследовании линейных систем.

1) .

Система несовместна.

►Пример 10.

Решить систему уравнений методом Гаусса:

Решение.

Составим расширенную матрицу и преобразуем ее:

Как и в примере 2 над стрелочкой указаны выполняемые операции.

Для удобства вычислений переставим четвертую строку на место второй и за счет второй строки получим нули во втором столбце во всех строках ниже второй, а затем за счет третьей строки — в третьем столбце:

В четвертой строке легко было получить нули, умножив третью строку на минус единицу и прибавив ее к четвертой. Мы не упрощали вычислений, чтобы сохранить алгоритм получения нулей в нижележащих строках за один шаг.

По преобразованной матрице определяем ранги: ,, следовательно, данная система уравнений несовместна.

Ответ:система не имеет решений. ◄

2) . Система совместна и имеет единственное решение. В результате преобразований приходим к ступенчатой системе, решение которой легко находится.

►Пример 11. Решить систему уравнений методом Гаусса

Решение.

Составим расширенную матрицу и преобразуем ее:

Ранг основной матрицы равен рангу расширенной матрицы и равен числу неизвестных. Следовательно, система совместна и имеет единственное решение. По преобразованной матрице составляем систему, равносильную исходной

Полученная система имеет ступенчатый вид и легко решается.

Ответ: .◄

3) .Система совместна, но имеет бесконечное множество решений. Это множество решений находим, перенося члены со свободными неизвестными в правую часть уравнений.

►Пример 12. Решить систему уравнений

Решение.

Преобразуем расширенную матрицу системы

Ранг основной матрицы равен рангу расширенной матрицы , число неизвестных равно пяти. Следовательно, система совместна, но имеет бесконечное множество решений. Число степеней свободы равно двум. Выберем свободными неизвестнымии выразимчерез них:

отсюда получаем

Ответ запишем в виде вектора-столбца.

Ответ:. ◄

Упражнения.

Исследовать и решить системы уравнений:

1. Ответ: .

2. Ответ: .

3. Ответ: .

4. Ответ: .

Первый пациент, получивший дозу в исследовании совместимости с матрицей пищевых продуктов, которое должно стать частью регистрационного пакета фазы III в США для ведущего продукта Infacort® | Связи с инвесторами и СМИ | Дневной

❮

Первый пациент, получивший дозу в исследовании совместимости с матрицей пищевых продуктов, которое должно стать частью регистрационного пакета фазы III в США для свинцового продукта, Infacort®

Первый пациент, получивший дозу в исследовании совместимости с матрицей пищевых продуктов, которое должно стать частью регистрации фазы III в США упаковка для свинцового продукта, Infacort®

Diurnal Group plc (AIM: DNL), специализированная фармацевтическая компания, ориентированная на потребности пациентов с хроническими эндокринными (гормональными) заболеваниями, объявляет об успешном введении дозы Infacort® первому пациенту в исследовании совместимости с матрицей пищевых продуктов у здоровых добровольцев. Это исследование поддерживает запланированную регистрацию в США препарата Инфакорт® для лечения надпочечниковой недостаточности (АН) у детей. Как было объявлено ранее, Diurnal начнет базовое клиническое исследование фазы III в целевой педиатрической популяции (возраст 0–16 лет) после окончательного подтверждения дизайна исследования Управлением по санитарному надзору за качеством пищевых продуктов и медикаментов США (FDA).

Исследование совместимости пищевых матриц представляет собой одноцентровое открытое рандомизированное перекрестное исследование однократной дозы с участием 18 здоровых взрослых субъектов (номер EudraCT: 2016-001388-36). Основной целью исследования является оценка биодоступности многокомпонентных гранул Infacort®, вводимых в виде капель с мягкой пищей или йогуртом, по сравнению с прямым введением в заднюю часть рта. Второй целью является оценка безопасности и переносимости Инфакорта® на протяжении всего исследования.

AI — это состояние, характеризующееся дефицитом кортизола, основного гормона, регулирующего обмен веществ и реакцию на стресс. AI был идентифицирован как орфанное заболевание в США, где, по оценкам, насчитывается около 4500 больных в возрасте до 16 лет. Без лечения это заболевание связано со значительной заболеваемостью и повышенной смертностью. В настоящее время в США нет доступных препаратов гидрокортизона (синтетическая версия кортизола), специально разработанных для лечения этих молодых пациентов. Infacort® потенциально может стать первой фармацевтически определенной дозой и последовательной формой гидрокортизона, разработанной специально для детей.

В США Diurnal имеет статус орфанного препарата для Infacort® в педиатрической практике ИИ, что дает семь лет исключительности на рынке после утверждения заявки на новое лекарство. Надежный портфель патентов обеспечивает защиту Infacort® до 2034 года, что значительно укрепляет эксклюзивное положение компании.

Мартин Уитакер, генеральный директор Diurnal, прокомментировал:

«Мы очень рады, что ввели дозу первому пациенту в этом исследовании совместимости пищевых матриц. Это важная предпосылка для запланированного базового клинического исследования фазы III препарата Инфакорт® в США для лечения надпочечниковой недостаточности у детей, в отношении которого мы ожидаем окончательного подтверждения дизайна исследования в FDA перед его началом. Мы считаем, что США станут важным рынком для Infacort®, где он может удовлетворить значительную неудовлетворенную потребность детей с надпочечниковой недостаточностью, которые не получают удовлетворительного лечения».

В Европе Infacort® в настоящее время находится на рассмотрении в Европейском агентстве по лекарственным средствам (EMA) для лечения ИИ у детей, после того как в июле 2016 года было объявлено об успешном завершении европейского базового исследования, одобрение которого ожидается в конце 2017 года.

Для получения дополнительной информации посетите веб-сайт www.diurnal.co.uk или свяжитесь по телефону:

Diurnal Group plc +44 (0)20 3727 1000