Свойства числовых функций
Вопросы занятия:
· повторить свойства числовых функций;
· повторить геометрический смысл свойств числовых функций;
· определить в каком порядке следует перечислять эти свойства при чтении графика функции.
Материал урока
Определение.
Функцию y=f(x) называют возрастающей на множестве XD(f), если для любых точек х1 и х2 множества Х таких, что х1 < x2, выполняется неравенство f(x1) < f(x2).
Другими
словами, функция возрастает, если большему значению
аргумента соответствует большее значение функции.
Определение.
Функцию y=f(x) называют убывающей на множестве XD(f), если для любых точек х1 и х2 множества Х таких, что х1<x2, выполняется неравенство f(x1) > f(x2).
Другими словами, функция убывает, если большему значению аргумента соответствует меньшее значение функции.
Определение.
Термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание или убывание называют исследованием функции на монотонность.
Если
функция возрастает (или убывает) на своей области определения, то
говорят, что функция возрастающая (убывающая).
Рассмотрим несколько примеров.
Пример.
Пример.
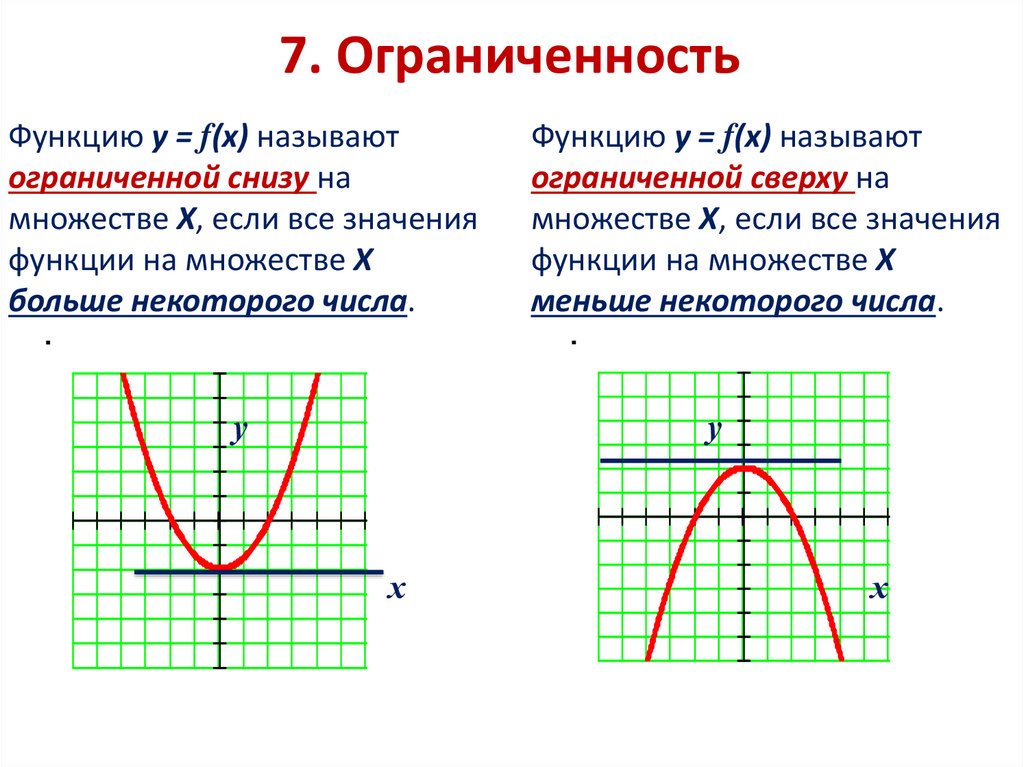
Определение.
Функцию y=f(x) называют ограниченной снизу на множестве XD(f), если все значения этой функции на множестве Х больше некоторого числа, то есть если существует число m такое, что для любого значения хϵХ выполняется неравенство f(x) > m.
Определение.
Функцию y=f(x) называют ограниченной сверху на множестве XD(f), если все значения этой функции на множестве Х меньше некоторого числа, то есть если существует число
Определение.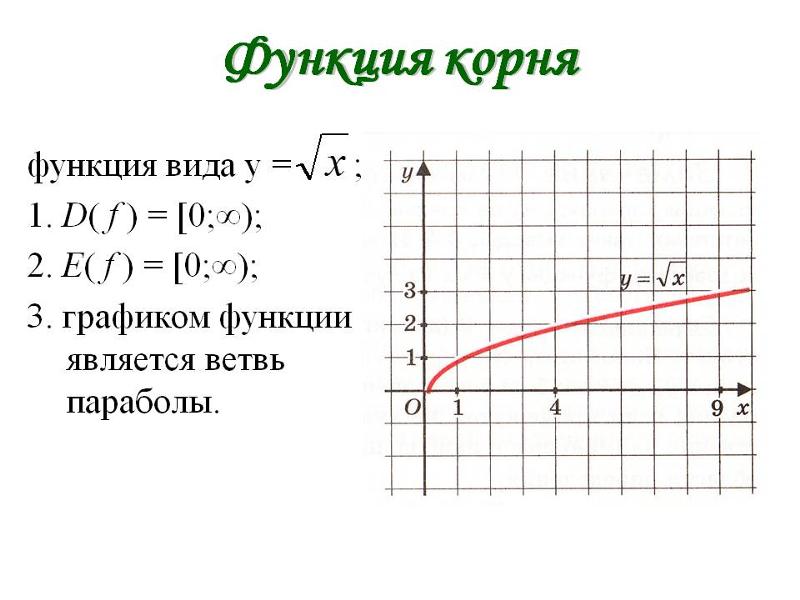
Если множество Х не указано, то подразумевается, что речь идёт об ограниченности функции сверху или снизу на всей области её определения.
Если функция ограничена и сверху и снизу на всей области определения, то её называют ограниченной.
Рассмотрим пример.
Пример.
Определение.
Число m называют наименьшим значением функции f(x) на множестве XD(f), если:
1) существует точка х0 ϵХ такая, что f(x0)=m;
2) для любого значения хϵХ выполняется неравенство f(x) ≥ f(x0).
Наименьшее
значение функции обозначают символом yнаим.
Определение.
Число М называют наибольшим значением функции f(x) на множестве XD(f), если:
1) существует точка х0ϵХ такая, что f(x0)=М;
2) для любого значения хϵХ выполняется неравенство f(x) ≤
Наибольшее значение функции обозначают символом yнаиб.
Если множество Х не указано, то подразумевается, что речь идёт об поиске наименьшего или наибольшего значения функции на всей области её определения.
Сформулируем несколько утверждений:
1)
Если у функции существует yнаим,
то она ограничена снизу.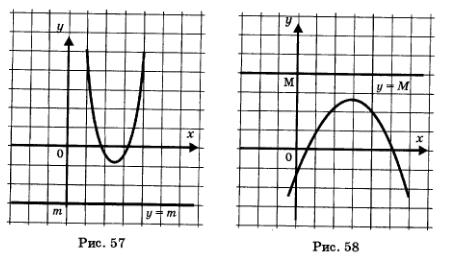
2) Если у функции существует yнаиб, то она ограничена сверху.
3) Если функция не ограничена снизу, то у неё не существует унаим.
4) Если функция не ограничена сверху, то у неё не существует унаиб.
Определение.
Функция выпукла вниз на промежутке XD(f), если, соединив любые две точки её графика с абсциссами из Х отрезком, мы обнаружим, что соответствующая часть графика лежит ниже проведённого отрезка.
Определение.
Функция выпукла вверх на промежутке XD(f), если, соединив любые две точки её графика с абсциссами из Х отрезком, мы обнаружим, что соответствующая часть графика лежит выше проведённого отрезка.
Определение.
Если график функции f(x)
на промежутке Х не имеет точек разрыва (то есть представляет собой
сплошную линию), то это значит, что функция f(x) непрерывна
на промежутке Х.
Замечание.
Обсуждая последние два свойства, мы будем пока по-прежнему опираться на наглядно-интуитивные представления. Доказательство этих свойств будет рассмотрено нами позже.
Определение.
Функцию f(x), xϵX называют чётной, если для любого значения х из множества Х выполняется равенство: f(-x) = f(x)
Функцию f(x), xϵX называют нечётной, если для любого значения х из множества Х выполняется равенство: f(-x) = —f(x)
В определениях идёт речь о значениях
функции в точках -х и х. Тем самым предполагается, что функция
определена и в точке х и в точке -х.
Например: отрезок [-5, 5] ̶ симметричное множество, а отрезок [-4, 5] ̶ не симметричное множество (в него входит число 5, но не входит противоположное ему -5).
Если функция у=f(x), хϵХ чётная или нечётная, то ее область определения Х – симметричное множество.
Если же Х – несимметричное множество, то функция у=f(x), хϵХ не может быть ни чётной ни нечётной.
Теперь давайте рассмотрим общий алгоритм исследования функции на чётность.
Рассмотрим несколько примеров.
Пример.
Пример.
Пример.
Вспомним геометрический смысл свойства чётности и свойства нечётности функции.
Прочитать функцию – это значит перечислить свойства функции. Для это надо:
1. Найти область определения функции D(f).
2. Найти область значения функции E(f).
3. Исследовать функцию на монотонность.
4. Исследовать функцию на ограниченность.
5. Найти наибольшее и наименьшее значение функции, если это возможно.
6. Исследовать функцию на чётность.
Исследование функции
Исследование функции🏠 |Education | Mathematics |
| 6 класс | 7 класс |
| 8 класс | 9 класс |
| 10 класс | 11 класс |
| ЕГЭ | ГИА |
| 1.1 Решение квадратных неравенств | Графическое решение неравенств |
| Графическое решение квадратного уравнения | 1. 2 Решение неравенств методом интервалов 2 Решение неравенств методом интервалов |
| Решение различных задач с помощью метода интервалов | 1.3 Вещественные числа |
| Числовые неравенства | Средние n чисел |
| Сравнение различных средних n чисел | Представление рациональных чисел в виде периодической десятичной дроби |
| Сравнение чисел | 1.4 Модуль |
| Два модуля | |
| Построение графиков от функций, в которых присутствует модуль | 2.3 Исследование функций. Образы и прообразы |
| 2.4 Композиции («сложные» функции) | 2.5 Понятие обратной функции и её график |
| 2.6 Отображения и их виды | 3.1 Множества, заданные уравнения и неравенствами |
| 4.1 Тригонометрия | 4.2 Определение тригонометрических функций и их основные свойства |
| Основные свойства функций y = cos(x), y = sin(x) | 4. 3 Основные формулы тригонометрии 3 Основные формулы тригонометрии |
| Тригонометрические функции двойных, тройных и половинных углов | 4.4 Формулы приведения |
| 4.5 Графики тригонометрических функций, свойства тригонометрических функций | 4.6 Преобразование выражения a·sin(α) + b·cos(α) путём введения вспомогательного аргумента |
| 4.7 Формулы преобразования произведений в суммы и наоборот | Тригонометрический «круг» |
| 4.8 Формулы универсальной подстановки. 5.9 Решение простейших уравнений и неравенств | Метод интервалов (тригонометрия) |
| 4.10 Обратные тригонометрические функции, определения, свойства, графики | 4.11 Решение тригонометрических уравнений и неравенств вида: cos(x) = a, cos(x) ≥ a, cos(x) ≤ a |
| 4.12 Решение различных тригонометрических задач | 5.1 Последовательности и пределы. Примеры задания последовательностей |
| 5.2 Ограниченные последовательности. Монотонные последовательности | 5. (1/3) (1/3)🔝 Составить уравнения множества точек равноудаленных от точки F (7;3) и прямой x — 2y = 11🔝 Ограниченность и теорема об экстремальном значении Теорема об экстремальных значениях по сути является расширением теоремы об ограниченности , которая утверждает, что непрерывная функция, определенная на замкнутом интервале, ограничена на этом интервале. Теорема была впервые доказана в 1830-х годах чешским математиком Бернаром Больцано (1781-1848). Но что именно говорит эта теорема? Хорошо, помните, что если функция непрерывна , в нем нет пробелов и разрывов. Другими словами, вы можете нарисовать график функции от руки, не отрывая карандаша от бумаги. Помните также, что закрытый интервал — это интервал между двумя точками на оси x , который включает конечных точек. Замкнутый интервал между точками a и b на оси x , например, будет включать точки a и b и будет обозначаться как [ a , б ]. Функция называется ограниченной , если существуют как верхний, так и нижний пределы значений, которые она может принимать. Другими словами, функция имеет как максимальное, так и минимальное значение, которого она может достичь. На самом деле, это немного сложнее, чем это. Чтобы понять почему, нам нужно изучить концепцию верхней и нижней границ . Верхняя граница может быть любым числом, равным или превышающим максимальное значение, которое может принимать функция. Точно так же нижняя граница может быть любым числом, которое меньше или равно наименьшему значению, которое может принимать функция. Если значения, возвращаемые некоторой непрерывной функцией, могут варьироваться, например, от один до два , то числа один , ноль и минус один являются нижними границами функции, а числа два , три и пять все верхние границы функции. Однако здесь нас особенно интересует идея функции, имеющей наименьшую верхнюю границу и наибольшую нижнюю границу . наименьшая верхняя граница функции — это верхняя граница, которая либо равна , либо меньше каждой верхней границы функции. Следовательно, по определению это также будет максимальное значение , которое может получить функция. Точно так же наибольшая нижняя граница функции — это нижняя граница, которая либо равна , либо больше каждой нижней границы функции. Таким образом, это число будет минимальным значением , которое может получить функция. Мы можем выразить это немного более формально в терминах самой функции. Предположим, у нас есть функция ƒ( x ), которая непрерывна для всех x на отрезке [9].0003 A , B ], где A ≤ x ≤ B , затем ƒ ( x ) ограничено [ A , B ] по верхней границе Y UB. 4 ,4 , ]. Также должно существовать по крайней мере одно значение x = d , где d находится на [ a , b ], такое, что ƒ( d ) = 0 lb 6 909 y 9000 Рассмотрим следующую иллюстрацию. Также должно существовать по крайней мере одно значение x = d , где d находится на [ a , b ], такое, что ƒ( d ) = 0 lb 6 909 y 9000 Рассмотрим следующую иллюстрацию. Если бы это было так, то, очевидно, не было бы ни верхних, ни нижних границ, ни абсолютных экстремумов. Если бы это было так, то, очевидно, не было бы ни верхних, ни нижних границ, ни абсолютных экстремумов. Поскольку он определен на замкнутом интервале, он соответствует критериям теоремы об экстремальных значениях и будет иметь как абсолютное максимальное значение, так и абсолютное минимальное значение. Мы также знаем, что все экстремумы должны происходить в критических точках. Таким образом, каждый экстремум функции должен приходиться либо на стационарная точка (то есть поворотная точка ) или в одной из конечных точек интервала. Глядя на приведенную выше иллюстрацию, мы уже можем видеть, что экстремумы будут возникать в конечных точках интервала, но помимо этого график не дает нам большого представления о том, какими будут их значения. Поскольку он определен на замкнутом интервале, он соответствует критериям теоремы об экстремальных значениях и будет иметь как абсолютное максимальное значение, так и абсолютное минимальное значение. Мы также знаем, что все экстремумы должны происходить в критических точках. Таким образом, каждый экстремум функции должен приходиться либо на стационарная точка (то есть поворотная точка ) или в одной из конечных точек интервала. Глядя на приведенную выше иллюстрацию, мы уже можем видеть, что экстремумы будут возникать в конечных точках интервала, но помимо этого график не дает нам большого представления о том, какими будут их значения. Хотя мы видим, что две стационарные точки функции в данном случае не будут абсолютными экстремумами (хотя они и будет конечно будет локальные экстремумы ), продемонстрируем процедуру полностью. Чтобы найти стационарные критические точки функции (то есть точки поворота), мы должны сначала найти производную от ƒ( x ) = 3 x 3 — 5 x + 1, применяя соответствующие правила дифференцирования: Хотя мы видим, что две стационарные точки функции в данном случае не будут абсолютными экстремумами (хотя они и будет конечно будет локальные экстремумы ), продемонстрируем процедуру полностью. Чтобы найти стационарные критические точки функции (то есть точки поворота), мы должны сначала найти производную от ƒ( x ) = 3 x 3 — 5 x + 1, применяя соответствующие правила дифференцирования: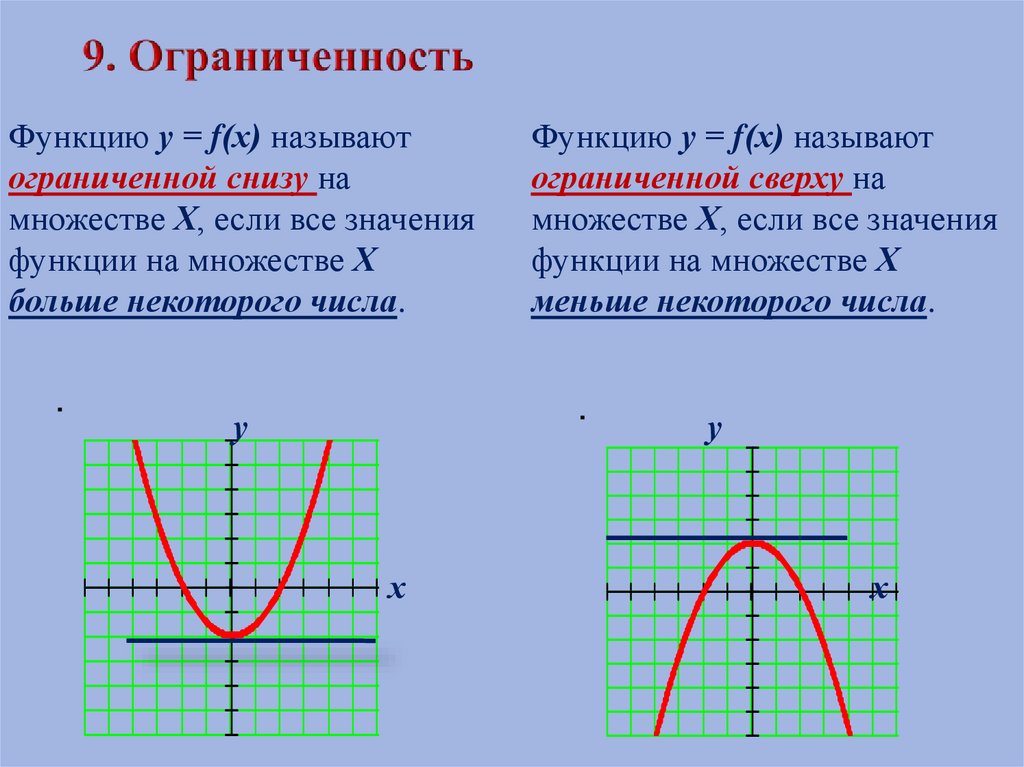 -пять (-65) и абсолютный максимум при x = 3 из шестьдесят семь (67). Вот еще раз график функции, на этот раз с осью y , уменьшенной по отношению к оси х , чтобы мы могли видеть, где кривая пересекает границы интервала. Хотя мы не можем сказать, просто взглянув на график, какие именно y координаты точек абсолютного максимума и минимума, график действительно соответствует рассчитанным нами значениям. -пять (-65) и абсолютный максимум при x = 3 из шестьдесят семь (67). Вот еще раз график функции, на этот раз с осью y , уменьшенной по отношению к оси х , чтобы мы могли видеть, где кривая пересекает границы интервала. Хотя мы не можем сказать, просто взглянув на график, какие именно y координаты точек абсолютного максимума и минимума, график действительно соответствует рассчитанным нами значениям. Однако мы будем оценивать ƒ( x ) для другой определенной критической точки ( x = 0) и для двух конечных точек интервала: Однако мы будем оценивать ƒ( x ) для другой определенной критической точки ( x = 0) и для двух конечных точек интервала:  Этот
может
помогите нам сузить возможности рациональных нулей. Другой
Концепция на этой странице — Теорема о промежуточном значении. Это может
помочь сузить возможности реальных нулей, особенно тех, которые
земли между целыми значениями. Мы также будем работать с ненастоящими
сложный
числа. Знаете ли вы, что если недействительное комплексное число равно нулю
полиномиальной функции, что ее сопряженная тоже? Мы
воля
Проследите это, используя Фундаментальную теорему алгебры и
Линейный
Теорема о факторизации для нахождения полиномиальных функций с заданными нулями.
Ух ты,
похоже, у нас есть наша работа вырезали для нас. Я думаю, тебе лучше
начать. Этот
может
помогите нам сузить возможности рациональных нулей. Другой
Концепция на этой странице — Теорема о промежуточном значении. Это может
помочь сузить возможности реальных нулей, особенно тех, которые
земли между целыми значениями. Мы также будем работать с ненастоящими
сложный
числа. Знаете ли вы, что если недействительное комплексное число равно нулю
полиномиальной функции, что ее сопряженная тоже? Мы
воля
Проследите это, используя Фундаментальную теорему алгебры и
Линейный
Теорема о факторизации для нахождения полиномиальных функций с заданными нулями.
Ух ты,
похоже, у нас есть наша работа вырезали для нас. Я думаю, тебе лучше
начать.Если вы делите полиномиальную функцию f ( x ) по ( х — с ), где c > 0, используя синтетическое деление, и это дает все положительные числа, тогда c является верхней границей действительных корней уравнения f ( x ) = 0,  быть верхней границей. Один c > 0
или положительный.
Во-вторых, все коэффициенты частного, а также
остаток
являются положительными. быть верхней границей. Один c > 0
или положительный.
Во-вторых, все коэффициенты частного, а также
остаток
являются положительными.Если вы делите полиномиальную функцию f ( x ) по ( x — c ), где c < 0, с использованием синтетического деления, что приводит к чередованию знаков, тогда c является нижней границей действительных корней уравнения f ( x ) = 0. Обратите внимание, что нули могут быть как положительными, так и отрицательный.  Давайте применим синтетическое деление с — 4 и посмотрим, получим ли мы чередующиеся знаки:  Давайте применим синтетическое деление на 4 и посмотрим, получим ли мы все положительные значения: между a и b так, что f ( c ) = 0,   Если бы мне нужно было больше, например, знаки частного, например
выше,
тогда я бы использовал синтетическое деление. Если бы мне нужно было больше, например, знаки частного, например
выше,
тогда я бы использовал синтетическое деление. 4): 4): 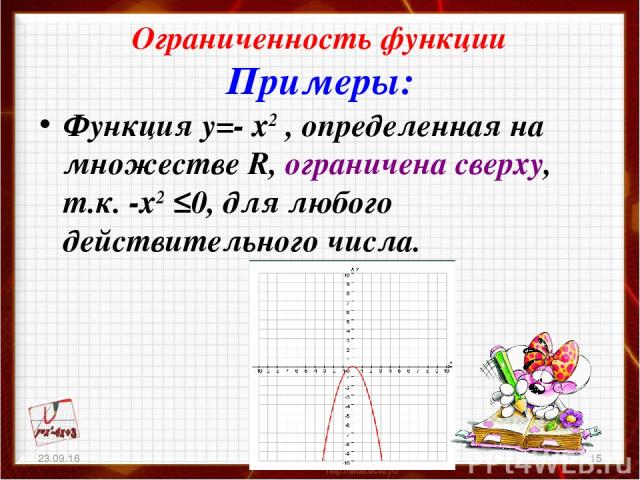 Это означает, что мы немного сузили его
лучше.
Между 2,44 и 2,45 есть ноль. Это означает, что мы немного сузили его
лучше.
Между 2,44 и 2,45 есть ноль. (возможно реальный и не обязательно отдельно)   Это поможет нам разбить функцию, чтобы найти
любые другие корни. Это поможет нам разбить функцию, чтобы найти
любые другие корни. Отсюда мы можем
переписать оригинал
проблема с использованием корней, которые у нас есть выше, и частного, которое мы
закончился
с этим последним синтетическим подразделением. Отсюда мы можем
переписать оригинал
проблема с использованием корней, которые у нас есть выше, и частного, которое мы
закончился
с этим последним синтетическим подразделением.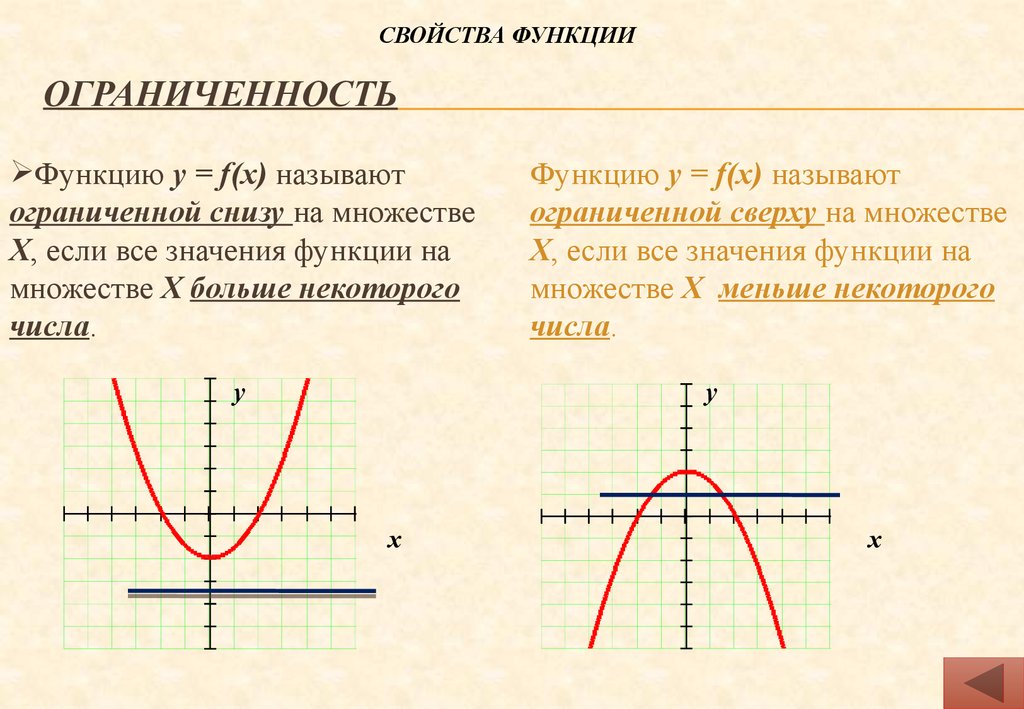    *Упростить ( i в квадрате = -1) *Умножить оставшиеся множители   На самом деле практики много не бывает. На самом деле практики много не бывает.(ответ/обсуждение к 1а)  ;
между -1 и -2. ;
между -1 и -2. (ответ/обсуждение к 2а) (ответ/обсуждение к 3а) (ответ/обсуждение к 4а)  |

 Пока все хорошо, но что мы подразумеваем под , ограниченным ?
Пока все хорошо, но что мы подразумеваем под , ограниченным ?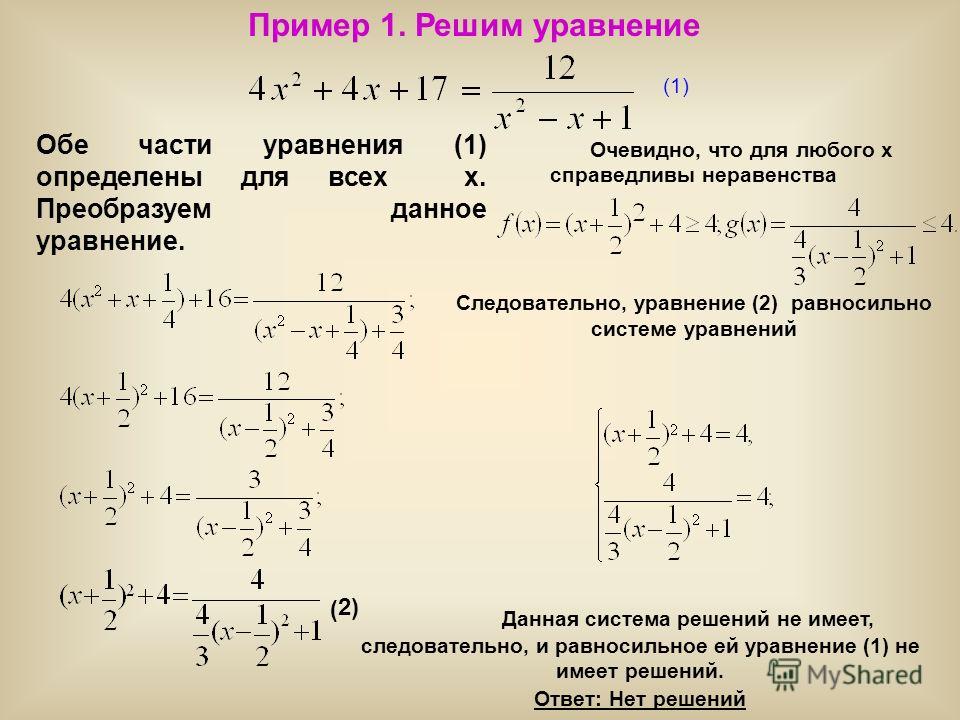
 , что ƒ( x ) никогда не превышает, и по нижнему пределу значения y фунтов что ƒ( x ) никогда не меньше, чем для всех x на [ a ,
, что ƒ( x ) никогда не превышает, и по нижнему пределу значения y фунтов что ƒ( x ) никогда не меньше, чем для всех x на [ a , Помните, что критические точки, выходящие за пределы интервала, нас не интересуют.
Помните, что критические точки, выходящие за пределы интервала, нас не интересуют.