Вычислите определитель четвертого порядка: Найти определитель матрицы четвертого порядка

alexxlab / / Разное

Вычисление определителей 2-го и 3-го порядков.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

 

Квадратная таблица $$A=\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}$$ составленная из четырех действительных или комплексных чисел называется квадратной матрицей 2-го порядка. Определителем 2-го порядка, соответствующим матрице $A$ (или просто определителем матрицы $A$) называется число $$\det A=\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}.$$

Аналогично если $$A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}$$

— квадратная матрица 3-го порядка, то соответсвующим ей определителем 3-го порядка называется число

$$\det A=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}=$$ $$a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{23}a_{32}a_{11}. 2+5x+4=0:$

$D=25-16=9$

$x_1=\frac{-5-3}{2}=-4;\qquad x_2=\frac{-5+3}{2}=-1.$

Ответ: $x_1=-4;\,\,\, x_2=-1.$

 {jumi[*4]}

 

3.13. $\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}.$

Решение.

$\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}=3\cdot 7\cdot8+(-5)\cdot 8\cdot(-1)+4\cdot(-2)\cdot2-(-5)\cdot7\cdot2-$

$-4\cdot8\cdot8-3\cdot(-2)\cdot(-1)=168+40-16+70-256-6=0.$

Ответ: $0.$

 

3.16. $\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}.$

 Решение.

 $\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}=\sin\alpha\cos\beta+\sin\beta\cos\gamma+\cos\alpha\sin\gamma-$

$-\cos\beta\sin\gamma-\sin\alpha\cos\gamma-\cos\alpha\sin\beta=$

$=\sin(\alpha-\beta)+\sin(\beta-\gamma)+\sin(\gamma-\alpha). T=\det A.$

2) Если все элементы строки (столбца) умножить на одно и тоже число, то определитель умножится на это число.

3) Если поменять местами две строки (столбца), то определитель поменяет знак. В частности, если две строки (столбца) равны, то определитель равен нулю.

4) Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором — вторые слагаемые.

5) Если одна строка (столбец) является линейной комбинацией других строк (столбцов), то определитель равен нулю.

6) Определитель не меняется если к одной из его строк (столбцов) добавить линейную комбинацию его других строк (столбцов).

 

Примеры:

3.24. Используя свойства определителя доказать следующее тождество: $\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}. $

Доказательство.

$\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$

 $\begin{vmatrix}a_1&a_1-b_1x&c_1\\a_2&a_2-b_2x&c_2\\a_3&a_3-b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1-b_1x&c_1\\b_2x&a_2-b_2x&c_2\\b_3x&a_3-b_3x&c_3\end{vmatrix}=$ 

 

$=\begin{vmatrix}a_1&a_1&c_1\\a_2&a_2&c_2\\a_3&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}b_1x&b_1x&c_1\\b_2x&b_2x&c_2\\b_3x&b_3x&c_3\end{vmatrix}=$ 

$-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}=$ $-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$ 

$-2\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}. {3+4}\begin{vmatrix}2&-3&4\\4&-2&3\\3&-1&4\end{vmatrix}=$

$=a(-27-8-8+3+24+24)-b(18+16+24-9-16-48)+$

$+c(-12-4-18+6+4+36)-d(-16-16-27+24+6+48)=$

$=8a+15b+12c-19d.$

Ответ: $8a+15b+12c-19d.$

   {jumi[*4]}

3.61. Вычислить определитель: $\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}.$

Решение.

 Вычислим этот определитель с помощью приведения определителя к треугольному виду:

$\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}=$ от каждой из первых четырех строк отнимем пятую $=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\1&1&1&1&6\end{vmatrix}=$ от пятой строки отнимем первую, затем пятую строку умножим на два 

$=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&1&1&1&11\end{vmatrix}=$ $\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&2&2&2&22\end{vmatrix}=$ Далее от пятой строки отнимем вторую, после чего пятую строку умножим на $\frac{3}{2}:$ $=\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&2&2&27\end{vmatrix}=$ $\frac{1}{2}\frac{2}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&3&3&40,5\end{vmatrix}=$ Теперь от пятой строки отнимем третью, после чего пятую строку умножим на $\frac{4}{3}:$ $=\frac{1}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&3&45,5\end{vmatrix}=$ $\frac{1}{3}\frac{3}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&4&\frac{182}{3}\end{vmatrix}=$ Отнимем от пятой строки четвертую и перемножив диагональные элементы получаем ответ: $=\frac{1}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&0&\frac{197}{3}\end{vmatrix}=$ $=\frac{1}{4}\cdot2\cdot3\cdot4\cdot\frac{197}{3}=394. 2.$

 

Вычислить определители, используя подходящее разложение по строке или столбцу.

 

3.51. $\begin{vmatrix}-1&5&2\\0&7&0\\1&2&0\end{vmatrix}.$

Ответ: $-14.$

 

3.52. $\begin{vmatrix}2&1&0\\1&2&1\\0&1&2\end{vmatrix}.$

Ответ: $4.$

 

3.54. (б) $\begin{vmatrix}5&a&2&-1\\4&b&4&-3\\2&c&3&-2\\4&d&5&-4\end{vmatrix}.$

Ответ: $2a-8b+c+5d.$

 

3.62. Вычислить определитель: $\begin{vmatrix}5&6&0&0&0\\1&5&6&0&0\\0&1&5&6&0\\0&0&1&5&6\\0&0&0&1&5\end{vmatrix}.$

Ответ: $665.$

  {jumi[*4]}

4.1.2 Вычисление определителя — го порядка

Определение. Если в определителе -го порядка вычеркнуть строку и столбец, то оставшийся определитель -го порядка называется минором данного элемента и обозначается .

Определение. Алгебраическим дополнением элемента определителя называется его минор, взятый со знаком .

Алгебраическое дополнение элемента обозначается через . Следовательно, .

Пример 3. Дан определитель . Найти минор и алгебраическое дополнение элемента (выделен пунктиром).

Решение. Вычеркивая в определителе первую строку и второй столбец, на пересечении которых находится элемент , получим . Тогда .

Теорема 1. Определитель равен сумме произведений элементов какой-нибудь строки или столбца на их алгебраические дополнения, т. е.

, (*)

Где – фиксировано.

Выражение (*) называют разложением определителя по элементам строки с номером .

Вычисление определителя -го порядка сводится к вычислению одного определителя -го порядка, для чего в какой–либо строке (или столбце) получают нулей, а затем разлагают определитель по этой строке, пользуясь формулой (*).

Пример 4. Вычислить определитель

Решение.

Наша задача состоит в том, чтобы, пользуясь свойствами определителя, получить максимальное число нулей в какой-нибудь строке или столбце, а затем применить теорему 1. Во второй строке уже имеются два нуля, получим еще нули в этой строке. Для этого прибавим к элементам второго столбца соответствующие элементы четвертого столбца, умноженные на 2, а к элементам третьего столбца прибавим соответствующие элементы четвертого, умноженные на . Получим определитель, равный исходному

Применим теорему 1 ко второй строке, т. е. разложим определитель по элементам второй строки. Получим определитель 4-го порядка.

Теперь получим нули во втором столбце. Для этого к элементам третьей строки прибавим соответствующие элементы первой строки, умноженные на , а к элементам четвертой – элементы первой, умноженные на .

Получим .

Разлагая его по элементам второго столбца, получим

.

Теперь можно разложить полученный определитель, например, по первому столбцу:

.

Легко вычисляются определители квадратных матриц треугольного или диагонального видов. В этом случае определитель равен произведению элементов, расположенных на диагонали.

Квадратная матрица вида называется диагональной, а квадратные матрицы и называются матрицами треугольного вида.

Пример 5. Вычислить определитель

Решение.

Будем получать нули под главной диагональю.

1-й этап. Берем первую строку и с ее помощью получим нули в первом столбце. Первую строку умножим на и прибавим ко второй, затем первую строку умножим на 2 и прибавим к четвертой. Получим

2-й этап. Работаем со второй строкой и получаем нули во втором столбце. Вторую строку умножаем на и прибавляем к третьей; вторую строку умножаем на 2 и прибавляем к четвертой:

3-й этап. Из четвертой строки вынесем и переставим третью и четвертую строки:

И последний этап.

Третью строку умножим на и прибавим к четвертой:

.

Разлагаем определитель по элементам первого столбца

.

Снова разлагаем определитель D по элементам первого столбца:

.

Действительно, определитель равен произведению элементов, стоящих на диагонали.

Для самостоятельного решения.

1. Вычислить определители

А) . Ответ: .

Б) . Ответ 10.

Указание: Чтобы уменьшить числа, вычтите какую-нибудь строку из остальных. Эту операцию можно проделать несколько раз. Цель: сделать на каком-нибудь месте единицу.

2. Вычислить определитель, приведя его к треугольному виду.

. Ответ: 52.

< Предыдущая   Следующая >

Определитель матрицы — 2×2, 3×3, 4×4…

Каталин Дэвид

Определение

Определитель квадратной матрицы A — это целое число, полученное с помощью ряда методов с использованием элементов матрицы.

Обозначение

Пусть $ А = \begin{pmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \end{pmatrix}$

$дет(А) = \влево|А\вправо| «=» \begin{vmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \end{vmatrix}$

Свойства определителя

  1. Если в матрице есть строка или столбец со всеми элементами, равными 0 , то определитель равен 0 .

    Пример 12
    $\begin{vmatrix} 1 и 4 и 2\\ 0 и 0 и 0\\ 3 и 9 и 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 и 4 и 0\\ 4 и 2 и 0\\ 3 и 9 и 0 \end{vmatrix}=0$

  2. Если матрица имеет две равные строки или два равных столбца , то его определитель равен 0 .

    Пример 13
    $\begin{vmatrix} 1 и 4 и 2\\ 1 и 4 и 2\\ 3 и 9 и 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 и 4 и 1\\ 4 и 2 и 4\\ 3 и 9 и 3 \end{vmatrix}=0$

  3. Если матрица имеет две пропорциональные строки или два пропорциональных столбца , то ее определитель равен 0
    .

    Пример 14
    $\begin{vmatrix} 1 и 4 и 2\\ 2 и 8 и 4\\ 3 и 9& 5 \end{vmatrix}= 0$ (первые две строки пропорциональны)
    или
    $\begin{vmatrix} 8 и 4 и 7\\ 4 и 2 и 3\\ 18 и 9 и 8 \end{vmatrix}=0$ (первые два столбца пропорциональны)

  4. Если строка или столбец есть сумма или разность других строк, соответственно столбцов , то определитель равен 0 .

    Пример 15
    $\begin{vmatrix} 1 и 4 и 2\\ 7 и 2 и 3\\ 8 и 6 и 5 \end{vmatrix}= 0$     $R_{1} +R_{2} =R_{3}$ или

    $ \begin{vmatrix} 9 и 12 и 3\\ 1 и 8 и 7\\ 5 и 7 и 2 \end{vmatrix}=0$     $C_{1}+C_{3}=C_{2}$

  5. В определителе мы можем отдельно выносить целые числа из строк и столбцов.

    Пример 16
    В определителе
    $\begin{vmatrix} 3 и 9 и 12\\ 5 и 1 и 8 \\ 7 и 4 и 2 \end{vmatrix}$, мы умножаем 3 из строки 1 $(R_{1})$ и получаем:

    $3 \cdot \begin{vmatrix} 1 и 3 и 4\\ 5 и 1 и 8\\ 7 и 4 и 2 \end{vmatrix}$, то мы выносим 2 из столбца 3 $(C_{3})$:
    $6\cdot \begin{vmatrix} 1 и 3 и 2\\ 5 и 1 и 4\\ 7 и 4 и 1 \end{vmatrix}$

  6. В определителе мы можем прибавлять или вычитать строки или столбцы к другим строкам, соответственно столбцам, и значение определителя остается прежним.

    Пример 17
    $\begin{vmatrix} 1 и 5\\ 3 и 8 \end{vmatrix}$ $\xlongequal{R_{1}+R_{2}} \begin{vmatrix} 4 и 13\\ 3 и 8 \end{vmatrix}$
    Пример 18
    $\begin{vmatrix} 1 и 5\\ 3 и 8 \end{vmatrix}$ $\xlongequal{C_{1}+C_{2}} \begin{vmatrix} 6 и 5\\ 11 и 8 \end{vmatrix}$

  7. В определителе мы можем складывать или вычитать несколько строк или столбцов.

    Пример 19
    $\begin{vmatrix} 1 и 5\\ 3 и 8 \end{vmatrix}$ $\xlongequal{2R_{1}+3R_{2}} \begin{vmatrix} 11 и 34\\ 3 и 8 \end{vmatrix}$

    Пример 20
    $\begin{vmatrix} 1 и 5\\ 3 и 8 \end{vmatrix}$ $\xlongequal{5C_{1}-C_{2}} \begin{vmatrix} 0 и 5\\ 7 и 8 \end{vmatrix}$

  8. Определитель матрицы равен определителю ее транспонирования.
  9. Определитель произведения двух квадратных матриц равен произведению определителей данных матриц.

Минор матрицы

Определитель, полученный путем удаления некоторых строк и столбцов в квадратной матрице, называется минором этой матрицы.

Пример 21
$A=\begin{pmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \end{pmatrix}$

Один из миноров матрицы A равен $\begin{vmatrix} 1 и 4\\ 5 и 3 \end{vmatrix}$ (получено удалением строки 3 и столбца 3 из матрицы A)

Другой несовершеннолетний $\begin{vmatrix} 1 и 2 \\ 6 и 1 \end{vmatrix}$ (получено удалением строки 2 и столбца 2 из матрицы A)

Пример 22
$B=\begin{pmatrix} 2 и 5 и 1 и 3\\ 4 и 1 и 7 и 9\\ 6 и 8 и 3 и 2\\ 7 и 8 и 1 и 4 \end{pматрица} $

Один из миноров матрицы B равен $ \begin{vmatrix} 1 и 7 и 9\\ 8 и 3 и 2\\ 8 и 1 и 4 \end{vmatrix}$ (получено удалением строки 1 и столбца 1 из матрицы B)

Еще один несовершеннолетний $\begin{vmatrix} 1 и 7 \\ 8 и 3 \end{vmatrix}$ (получено удалением строк 1 и 4 и столбцов 1 и 4 из матрицы B)

Позволять $A= \begin{pmatrix} а_{1,1} и а_{1,2} и а_{1,3} и . & . & a_{1,n}\\ а_{2,1} и а_{2,2} и а_{2,3} и . & . & а_{2,n}\\ а_{3,1} и а_{3,2} и а_{3,3} и . & . & а_{3,n}\\ . & . & . & . & .& .\\ a_{n,1} & a_{n,2} & a_{n,3} & . & . & Анна} \end{pmatrix}$

Мы можем связать минор $\Delta_{i,j}$ (полученный удалением строки i и столбца j) с любым элементом $a_{i,j}$ матрицы A.

Пример 23
$ A = \begin{pmatrix} 4 и 7\\ 2 и 9 \end{pmatrix}$

Нам нужно определить минор, связанный с 2. Так как этот элемент находится в строке 2, столбце 1, то 2 равно $a_{2,1}$.

Мы должны исключить строку 2 и столбец 1 из матрицы A, в результате чего получается

Минор числа 2 равен $\Delta_{2,1} = 7$.

Пример 24
$B=\begin{pmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \end{pmatrix}$

Нам нужно определить минор, связанный с 7. Так как этот элемент находится в строке 2, столбце 3, то 7 равен $a_{2,3}$.

Мы должны исключить строку 2 и столбец 3 из матрицы B, в результате чего получится

Минор числа 7 равен $\Delta_{2,3}= \begin{vmatrix} 1 и 4\\ 6 и 2 \end{vmatrix}$

Пример 25
$C=\begin{pmatrix} 2 и 5 и 1 и 3\\ 4 и 1 и 7 и 9\\ 6 и 8 и 3 и 2\\ 7 и 8 и 1 и 4 \end{pmatrix}$

Нам нужно определить минор, связанный с 5.

Поскольку этот элемент находится в строке 1 столбца 2, то 5 равно $a_{1,2}$.

Мы должны исключить строку 1 и столбец 2 из матрицы C, в результате чего получится

Минор числа 5 равен $\Delta_{1,2}= \begin{vmatrix} 4 и 7 и 9\\ 6 и 3 и 2\\ 7 и 1 и 4\\ \end{vmatrix}$ 9{7}\cdot\Delta_{2,5}= -\Delta_{2,5} $ соответствует элементу $ a_{2.5}$

Приказ определителя

Порядок определителя равен количеству его строк и столбцов.

Пример 26
$\begin{vmatrix} 1 и 4\\ 6 и 2\\ \end{vmatrix}$ (у него 2 строки и 2 столбца, поэтому его порядок равен 2)

Пример 27
$\begin{vmatrix} 4 и 7 и 9\\ 6 и 3 и 2\\ 7 и 1 и 4\\ \end{vmatrix}$ (у него 3 строки и 3 столбца, поэтому его порядок равен 3)

Вычисление определителя матрицы

Определитель матрицы равен сумме произведений элементов любой строки или столбца и их сомножителей.

$\слева| А\право| «=» \begin{vmatrix} а_{1,1} и а_{1,2} и а_{1,3} и . & . & a_{1,n}\\ а_{2,1} и а_{2,2} и а_{2,3} и . & . & а_{2,n}\\ а_{3,1} и а_{3,2} и а_{3,3} и . & . & а_{3,n}\\ . & . & . & . & .& .\\ a_{n,1} & a_{n,2} & a_{n,3} & . & . & Анна}\\ \end{vmatrix}$ 9{3}\cdot\Delta_{1,2}=a_{1,1}\cdot\Delta_{1,1}-a_{1,2}\cdot\Delta_{1,2}$

Однако $ \Delta_{1,1}= a_{2,2} $ и $ \Delta_{1,2}=a_{2,1}$

$ \ влево | А\право| =a_{1.1} \cdot a_{2,2}- a_{1.2} \cdot a_{2,1}$

$\цвет{красный}{ \begin{vmatrix} а и б\\ CD \end{vmatrix} =a \cdot d — b \cdot c}$

Пример 28
$\begin{vmatrix} 2 и 5\\ 3 и 8 \end{vmatrix} =2 \cdot 8 — 3 \cdot 5 = 16 -15 =1$

Пример 29{4}\cdot\Delta_{1,3}=$ $a_{1,1}\cdot\Delta_{1,1}-a_{1.2}\cdot\Delta_{1,2}+a_{1.3}\cdot\Delta_{1,3}$

$\Дельта_{1,1}= \begin{vmatrix} а_{2,2} и а_{2,3}\\ а_{3,2} и а_{3,3} \end{vmatrix} = а_{2,2}\cdot а_{3,3}-a_{2,3}\cdot а_{3,2}$

$\Дельта_{1,2}= \begin{vmatrix} а_{2,1} и а_{2,3}\\ а_{3,1} и а_{3,3} \end{vmatrix} = а_{2,1}\cdot а_{3,3}-a_{2,3}\cdot а_{3,1}$

$\Дельта_{1,3}= \begin{vmatrix} а_{2,1} и а_{2,2}\\ а_{3,1} и а_{3,2} \end{vmatrix} = а_{2,1}\cdot а_{3,2}-a_{2,2}\cdot а_{3,1}$

$\влево| А\право| =a_{1,1}\cdot( a_{2,2}\cdot a_{3,3}-a_{2,3}\cdot a_{3,2})-a_{1,2}\cdot( a_{2,1}\cdot a_{3,3}-a_{2,3}\cdot a_{3,1})+$ $a_{1,3}\cdot(a_{2,1}\cdot а_{3,2}-а_{2,2}\cdot а_{3,1})=$ $a_{1,1}\cdot a_{2,2}\cdot a_{3,3}-a_{1,1}\cdot a_{2,3}\cdot a_{3,2}-a_{1 ,2}\cdot a_{2. 1}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3,1}+$ $a_{1,3}\ cdot a_{2,1}\cdot a_{3,2}-a_{1,3}\cdot a_{2,2}\cdot a_{3,1}=$ $\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3, 1}+a_{1,3}\cdot a_{2,1}\cdot a_{3,2}-}$ $\color{red}{(a_{1,1}\cdot a_{2,3}\cdot a_{3,2}+a_{1,2}\cdot a_{2,1}\cdot a_{3 ,3}+a_{1,3}\cdot a_{2,2}\cdot a_{3,1})}$

Чтобы быстрее достичь последнего отношения, мы можем использовать следующий метод.

Сначала перепишем первые две строки под определителем следующим образом.

$\begin{vmatrix} \color{red}{a_{1,1}} & a_{1,2} & a_{1,3}\\ \color{red}{a_{2,1}} & \color{red}{a_{2,2}} & a_{2,3}\\ \color{red}{a_{3,1}} & \color{red}{a_{3,2}} & \color{red}{a_{3,3}} \end{vmatrix}$
$\hspace{2мм}\begin{массив}{ccc} a_{1,1} & \color{red}{a_{1,2}} & \color{red}{a_{1,3}}\\ a_{2,1} & a_{2,2} & \color{red}{a_{2,3}}\\ \end{массив}$

Мы умножаем элементы на каждой из трех красных диагоналей (главная диагональ и нижние) и суммируем результаты:
$\color{red}{a_{1,1}\cdot a_{2,2}\ cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1,3}+a_{3,1}\cdot a_{1,2}\cdot a_{2 ,3}}$

$\begin{vmatrix} \color{red}{a_{1,1}} & \color{red}{a_{1,2}} & \color{blue}{a_{1,3}}\\ \color{red}{a_{2,1}} & \color{blue}{a_{2,2}} & \color{blue}{a_{2,3}}\\ \color{blue}{a_{3,1}} & \color{blue}{a_{3,2}} & \color{blue}{a_{3,3}} \end{vmatrix}$
$\hпробел{2мм} \begin{массив}{ccc} \color{blue}{a_{1,1}} & \color{blue}{a_{1,2}} & \color{red}{a_{1,3}}\\ \color{blue}{a_{2,1}} & \color{red}{a_{2,2}} & \color{red}{a_{2,3}}\\ \end{массив}$

Мы умножаем элементы на каждой из трех синих диагоналей (второстепенная диагональ и нижняя) и суммируем результаты:

$\color{синий}{a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1, 1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1}}$

Если мы вычтем два отношения, мы получим формулу определителя:

$\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1, 3}+a_{3,1}\cdot a_{1,2}\cdot a_{2,3}-}$ $\color{red}{(a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1 ,1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1})}$

Пример 30
$A=\begin{pmatrix} 1 и 4 и 3 \\ 2 и 1 и 5\\ 3 и 2 и 1\\ \end{pmatrix}$

$\begin{vmatrix} 1 и 4 и 3 \\ 2 и 1 и 5\\ 3 и 2 и 1\\ \end{vmatrix}$
$\hspace{2мм}\begin{массив}{ccc} 1 и 4 и 3\\ 2 и 1 и 5\\ \end{массив}$


$ = 1\cdot1\cdot1 + 2\cdot2\cdot3 + 3\cdot4\cdot5 — (3\cdot1\cdot3 + 5\cdot2\cdot1 + 1\cdot4\cdot2) =$ $1 + 12 + 60 -(9 + 10 + 8)=73-27=46$

Пример 31
$A=\begin{pmatrix} 3 и 5 и 1 \\ 1 и 4 и 2\\ 7 и 1 и 9\\ \end{pmatrix}$

$\begin{vmatrix} 3 и 5 и 1 \\ 1 и 4 и 2\\ 7 и 1 и 9\\ \end{vmatrix}$
$\hspace{2mm}\begin{массив}{ccc} 3 и 5 и 1\\ 1 и 4 и 2\\ \end{массив} $

$= 3\cdot4\cdot9 + 1\cdot1\cdot1 + 7\cdot5\cdot2 — (1\cdot4\cdot7 + 2\cdot1\cdot3 + 9\cdot5\cdot1) =$ 108$ + 1 + 70 -(28 + 6 + 45)=79-79=100$

Существуют определители, элементами которых являются буквы. Их легче вычислить, используя свойства определителей. Например, мы вычисляем определитель матрицы, в которой есть одни и те же элементы в любой строке или столбце, но переупорядоченные.

$\begin{vmatrix} а и б и в \\ такси\\ б и в и а \end{vmatrix}$ $ \xlongequal{C_{1}+C_{2}+C_{3}} \begin{vmatrix} а + б + с и б и с\\ с + а + б & а & ​​б \\ б + в + а и в и а \end{vmatrix} = (а + б + с) \cdot \begin{vmatrix} 1 и б и в\\ 1 и а и б\\ 1 и с и а \end{vmatrix}$ 9{2} \end{vmatrix}= $

$\begin{vmatrix} а-в и б-в \\ (а-с) (а+с) и (б-с)(б+с) \end{vmatrix}=$ $(а-в)(б-в)\begin{vmatrix} 1 и 1\\ а+с и б+с \end{vmatrix}=$

$=(a-c)(b-c)[(b+c)-(a+c)]=$ $(a-c)(b-c)(b+c-a-c)=(a-c)(b-c)(b-a)$

Вычисление определителя 4×4

Для вычисления определителей 4×4 используем общую формулу.

Перед применением формулы с использованием свойств определителей:

  1. проверяем, выполняется ли какое-либо из условий для того, чтобы значение определителя было равно 0.
  2. Мы проверяем, можем ли мы выделить любую строку или столбец.
  3. Проверяем, является ли определитель матрицей Вандермонда и имеет ли он те же элементы, но переупорядоченные, в любой строке или столбце.

В любом из этих случаев воспользуемся соответствующими методами вычисления определителей 3×3. Мы модифицируем строку или столбец, чтобы заполнить его 0, за исключением одного элемента. Определитель будет равен произведению этого элемента и его кофактора. В этом случае кофактор представляет собой детерминант 3×3, который рассчитывается по специальной формуле.

Пример 33
$\begin{vmatrix} 1 и 3 и 9 и 2\\ 5 и 8 и 4 и 3\\ 0 и 0 и 0 и 0\\ 2 и 3 и 1 и 8 \end{vmatrix}$

Заметим, что все элементы в строке 3 равны 0, поэтому определитель равен 0.

Пример 34
$\begin{vmatrix} 1 и 3 и 1 и 2\\ 5 и 8 и 5 и 3\\ 0 и 4 и 0 и 0\\ 2 и 3 и 2 и 8 \end{vmatrix}$
Заметим, что $C_{1}$ и $C_{3}$ равны, поэтому определитель равен 0.

Пример 35
$\begin{vmatrix} 1 и 3 и 9 и 2\\ 5 и 8 и 4 и 3\\ 10 и 16 и 18 и 4\\ 2 и 3 и 1 и 8 \end{vmatrix}$
Заметим, что строки 2 и 3 пропорциональны, поэтому определитель равен 0.

Пример 36
$\begin{vmatrix} \цвет{красный}{4} & 3 & 2 & 2\\ 0 и 1 и -3 и 3\\ 0 и -1 и 3 и 3\\ 0 и 3 и 1 и 1 \end{vmatrix}$

Поскольку в столбце 1 есть только один элемент, отличный от 0, мы применяем общую формулу, используя этот столбец. Кофакторы, соответствующие элементам, равным 0, не нужно вычислять, потому что произведение их и этих элементов будет равно 0.

=
$=4(1\cdot3\cdot1 +(-1)\cdot1\cdot3+3\cdot(-3)\cdot3$ $-(3\cdot3\cdot3+3\cdot1\cdot1 +1\cdot( -3)\cdot(-1)))$ $=4(3-3-27-(27+3+3))=4\cdot(-60)=-240$

Пример 37
$\begin{vmatrix} 4 и 3 и 2 и 2\\ 0 и 1 и 0 и -2\\ 1 и -1 и 3 и 3\\ 2 и 3 и 1 и 1 \end{vmatrix}$

Чтобы изменить строки так, чтобы в них было больше нулей, мы оперируем столбцами и наоборот. Мы выбираем строку или столбец, содержащие элемент 1, потому что мы можем получить любое число путем умножения.

Мы замечаем, что в строке 2 уже есть два элемента, равных 0. Мы делаем только один другой 0, чтобы вычислить только сомножитель 1.

$\begin{vmatrix} 4 и 3 и 2 и 2\\ 0 и 1 и 0 и -2\\ 1 и -1 и 3 и 3\\ 2 и 3 и 1 и 1 \end{vmatrix} \xlongequal{C_{4}+2C_{2}}$ $\begin{vmatrix} 4 и 3 и 2 и 8\\ 0 & \цвет{красный}{1} & 0 & 0\\ 1 и -1 и 3 и 1\\ 2 и 3 и 1 и 7 \end{vmatrix}=$ $=$
9{2+2}\cdot \begin{vmatrix} 4 и 2 и 8\\ 1 и 3 и 1\\ 2 и 1 и 7 \end{vmatrix}=$
$=4\cdot3\cdot7 + 1\cdot1\cdot8 + 2\cdot2\cdot1$ $-(8\cdot3\cdot2 + 1\cdot1\cdot4 + 7\cdot2\cdot1) = $ 84$ + 8 + 4- 48-4-14=30$

Пример 38
$\begin{vmatrix} 1 и -2 и 3 и 2\\ 2 и 3 и 1 и -1\\ 3 и 3 и 3 и 3\\ -1 и 4 и 2 и 1\\ \end{vmatrix}$

Мы можем разложить 3 из строки 3:
$3\cdot \begin{vmatrix} 1 и -2 и 3 и 2\\ 2 и 3 и 1 и -1\\ 1 и 1 и 1 и 1\\ -1 и 4 и 2 и 1\\ \end{vmatrix}$ 9{3+4}\cdot$ $=(-1)\cdot \begin{vmatrix} -1 и -4 и 1\\ 3 и 4 и 2 \\ -2 и 3 и 1\\ \end{vmatrix}$
$=-((-1)\cdot 4\cdot 1 +3 \cdot 3\cdot1 + (-2)\cdot (-4)\cdot 2$ $- (1\cdot 4 \cdot (-2) + 2\cdot 3\cdot (-1) + 1\cdot (-4)\cdot3))$ $=-(-4 + 9 + 16 + 8 + 6 + 12) =-47 $

Пример 39
$\begin{vmatrix} 2 и 5 и 1 и 4\\ 4 и 1 и 6 и 3\\ 5 и 3 и 7 и 2\\ 1 и 0 и 2 и 4 \end{vmatrix}$

В этом примере мы можем использовать последнюю строку (которая содержит 1) и можем сделать нули в первом столбце. 9{4+1}\cdot \begin{vmatrix} 5 и -3 и -4\\ 1 и -2 и -13\\ 3 и -3 и -18 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 5 и -3 и -4\\ 1 и -2 и -13\\ 3 и -3 и -18 \end{vmatrix}$

Мы умножаем -1 из столбца 2 и -1 из столбца 3.
$ (-1)\cdot(-1)\cdot(-1)\cdot \begin{vmatrix} 5 и 3 и 4\\ 1 и 2 и 13\\ 3 и 3 и 18 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 5 и 3 и 4\\ 1 и 2 и 13\\ 3 и 3 и 18 \end{vmatrix}=$ $-[5\cdot 2\cdot 18 + 1\cdot 3\cdot 4+ 3\cdot 3\cdot 13 — (4\cdot 2\cdot 3\cdot + 13\cdot 3\cdot 5 + 18\cdot 3 \cdot 1)]=$ $-(180+12+117-24-195-54)=36$

Пример 40
$\begin{vmatrix} 4 и 7 и 2 и 3\\ 1 и 3 и 1 и 2\\ 2 и 5 и 3 и 4\\ 1 и 4 и 2 и 3 \end{vmatrix}$

В столбце 3 стоит 1, поэтому мы обнулим строку 2.

$\begin{vmatrix} 4 и 7 и 2 и 3\\ 1 и 3 и 1 и 2\\ 2 и 5 и 3 и 4\\ 1 и 4 и 2 и 3 \end{vmatrix}$ $\xlongequal{C_{1}-C_{3}, C_{2}-3C_{3},C_{4}-2C_{3}} \begin{vmatrix} 2 и 1 и 2 и -1\\ 0 и 0 и \цвет{красный}{1} и 0 \\ -1 и -4 и 3 и -2\\ -1 и -2 и 2 и -1 \end{vmatrix}=$ $=1\cdot(-1)^{2+5}\cdot \begin{vmatrix} 2 и 1 и -1\\ -1 и -4 и -2\\ -1 и -2 и -1 \end{vmatrix}$

Мы умножаем -1 из строки 2 и -1 из строки 3.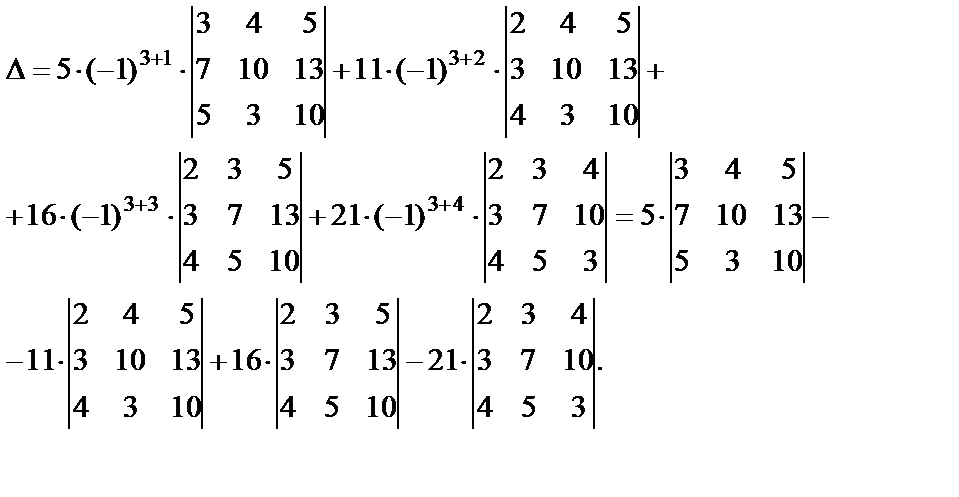
$ (-1)\cdot(-1)\cdot(-1)\cdot \begin{vmatrix} 2 и 1 и -1\\ 1 и 4 и 2\\ 1 и 2 и 1 \end{vmatrix}=$ $(-1)\cdot \begin{vmatrix} 2 и 1 и -1\\ 1 и 4 и 2\\ 1 и 2 и 1 \end{vmatrix}=$ $-[2\cdot 4\cdot 1 + 1\cdot 2\cdot (-1)+ 1\cdot 1\cdot 2 — ((-1)\cdot 4\cdot 1 + 2\cdot 2\cdot 2 + 1\cdot 1\cdot 1)]=$ $-(8-2+2+4-8-1)=-3$

Пример 41
$\begin{vmatrix} 2 и 1 и 3 и 4\\ 1 и 3 и 4 и 2\\ 3 и 4 и 2 и 1\\ 4 и 2 и 1 и 3\\ \end{vmatrix}$

Мы замечаем, что в любой строке или столбце есть одни и те же элементы, но в другом порядке. В этом случае мы складываем все строки или все столбцы.

$\begin{vmatrix} 2 и 1 и 3 и 4\\ 1 и 3 и 4 и 2\\ 3 и 4 и 2 и 1\\ 4 и 2 и 1 и 3 \end{vmatrix}$ $\xlongequal{L_{1}+L_{2}+L_{3}+L_{4}} \begin{vmatrix} 10 и 10 и 10 и 10\\ 1 и 3 и 4 и 2\\ 3 и 4 и 2 и 1\\ 4 и 2 и 1 и 3 \end{vmatrix} =$ $10\cdot \begin{vmatrix} 1 и 1 и 1 и 1\\ 1 и 3 и 4 и 2\\ 3 и 4 и 2 и 1\\ 4 и 2 и 1 и 3 \end{vmatrix}$ $\xlongequal{C_{1} — C_{4},C_{2}-C_{4},C_{3}-C_{4}}10\cdot \begin{vmatrix} 0 & 0 & 0 & \цвет{красный}{1}\\ -1 и 1 и 2 и 2\\ 2 и 3 и 1 и 1\\ 1 и -1 и -2 и 3 \end{vmatrix}=$ 9{1+4}$

$ = (-10)\cdot \begin{vmatrix} -1 и 1 и 2\\ 2 и 3 и 1\\ 1 и -1 и -2 \end{vmatrix}=$ $(-10)\cdot((-1)\cdot 3\cdot (-2) +2 \cdot (-1)\cdot2 + 1\cdot 1\cdot 1$ $-(2\cdot 3\cdot 1 + 1\cdot (-1)\cdot (-1) + (-2)\cdot1\cdot2))$ $= -10\cdot(6 -4 +1 -6 — 1 + 4) =0$

Матрицы Умножение матриц Ранг матриц Обратные матрицы Матричные уравнения Системы уравнений Матричные калькуляторы Матрицы и определители — задачи с решениями

Вычисление определителей матрицы 4-го порядка?

JavaScript отключен. Для лучшего опыта, пожалуйста, включите JavaScript в вашем браузере, прежде чем продолжить.

Состояние
Закрыто для дальнейших ответов.

  • #1

      • Добавить закладку