определения, формулы и примеры решения
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Определение
Последовательность $\left\{x_{n}\right\}$ называется ограниченной сверху, если существует такое число , что для любого номера $n$ , $x_{n} \leq M$
Последовательность $\left\{x_{n}\right\}$ называется ограниченной снизу, если существует такое число $m \in R$ , что для любого номера $n$ , $x_{n} \geq m$
Последовательность $\left\{x_{n}\right\}$ называется ограниченной , если она ограниченная сверху и ограниченная снизу, то есть существует такое число $M \geq 0$ , что для любого номера $n$ , $\left|x_{n}\right| \leq M$
Последовательность $\left\{x_{n}\right\}$ называется неограниченной, если существует такое число $M \geq 0$ , что существует такой номер $n$ , что $\left|x_{n}\right| \geq M$
Пример
Задание. {2}+1}}\right\}, n \in N$ ограничена
{2}+1}}\right\}, n \in N$ ограничена
Читать дальше: бесконечно малые и бесконечно большие последовательности.
Свойства функции, для 9 класса по алгебре
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:Свойства функции (PPTX)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 9 класса
Интерактивное учебное пособие для 9 класса «Правила и упражнения по геометрии»
Электронное учебное пособие «Понятная геометрия» для 7-9 классов
Ребята, мы продолжаем изучать числовые функции. Сегодня мы остановимся на такой теме, как свойства функции. Функции обладают многими свойствами. Вспомните, какие свойства мы с вами совсем недавно изучили. Правильно, область определения и область значений, они являются одними из ключевых свойств.
В этом разделе, мы с вами определим некоторые свойства функций. Порядок, в котором мы будем их определять, рекомендую соблюдать и при решении задач.
Возрастание и убывание функции
Первое свойство, которое мы определим, это возрастание и убывание функции.
Функция называется возрастающей на множестве Х⊂D(f), если для любых х1 и х2, таких, что х1 < x2 — выполняется неравенство f(x1) < f(x2). То есть большему значению аргумента, соответствует большее значение функции.Функция называется убывающей на множестве Х⊂D(f), если для любых х1 и х2, таких, что х1 < x2 — выполняется неравенство f(x1)>f(x2). То есть большему значению аргумента, соответствует меньшее значение функции.
Понятия «возрастание» и «убывание» функции очень легко понять, если внимательно посмотреть на графики функции. Для возрастающей функции: мы как бы поднимаемся в горку, для убывающей соответственно — спускаемся.
Возрастание и убывание функции в общем случае называется монотонностью. То есть, наша задача -это найти промежутки убывания и возрастания функции. В общем случае это формулируется так: найти промежутки монотонности или исследовать функцию на монотонность.
Пример
Исследовать на монотонность функцию $y=3x+2$.Решение: Проверим функцию для любых х1 и х2 и пусть х1 < x2.
$f(x1)=3×1+2$
$f(x2)=3×2+2$
Поскольку, х1< x2, то f(x1) < f(x2), т. е. большему значению аргумента, соответствует большее значение функции.
Ограниченность функции
Функцию $y=f(x)$ называют ограниченной снизу на множестве Х⊂D(f), если существует такое число а, что для любых хϵХ выполняется неравенство f(x) < a.
Функцию $y=f(x)$ называют ограниченной сверху на множестве Х⊂D(f), если существует такое число а, что для любых хϵХ выполняется неравенство f(x) < a.
Если промежуток Х не указывается, то считают, что функция ограничена на всей области определения. 2}≤4$, но это значит ограниченность сверху.
2}≤4$, но это значит ограниченность сверху.Ответ: наша функция ограниченна двумя прямыми $у=0$ и $у=4$.
Наибольшее и наименьшее значение
Наименьшим значение функции y= f(x) на множестве Х⊂D(f), называется некоторое число m, такое, что:
a) Существует некоторое х0, что $f(x0)=m$.
б) Для любого хϵХ, выполняется $f(x)≥f(x0)$.
Наибольшим значение функции y=f(x) на множестве Х⊂D(f), называется некоторое число m, такое что:
a) Существует некоторое х0, что $f(x0)=m$.
б) Для любого хϵХ, выполняется $f(x)≤f(x0)$.
Наибольшее и наименьшее значение принято обозначать y
Понятия ограниченности и наибольшего с наименьшим значением функции тесно связаны. Выполняются следующие утверждения:
а) Если существует наименьшее значение у функции, то она ограничена снизу.
б) Если существует наибольшее значение у функции, то она ограничена сверху.
в) Если функция не ограничена сверху, то наибольшего значения не существует. 2+16x≥0$. Найдем корни квадратного трехчлена $(2х+1)(2х-9)≥0$. При $х=-0,5$ и $х=4,5$ функция обращается в ноль, во всех остальных точках она больше нуля. Тогда, по определению, наименьшее значению функции равно нулю.
2+16x≥0$. Найдем корни квадратного трехчлена $(2х+1)(2х-9)≥0$. При $х=-0,5$ и $х=4,5$ функция обращается в ноль, во всех остальных точках она больше нуля. Тогда, по определению, наименьшее значению функции равно нулю.
Ответ: yнаиб.=5 и yнаим.=0.
Ребята мы с вами еще изучали понятия выпуклости функции. При решении некоторых задач, нам это свойство может понадобиться. Это свойство, также легко определяется с помощью графиков.
Функция выпукла вниз, если любые две точки графика исходной функции соединить, и график функции окажется ниже линии соединения точек.
Функция выпукла вверх, если любые две точки графика исходной функции соединить, и график функции окажется выше линии соединения точек.
Функция непрерывна, если график нашей функции не имеет разрывов, например, как график функции выше.
Если требуются найти свойства функции, то последовательность поиска свойств такова:
а) Область определения.
б) Монотонность. 2$,
2$,
в) $y=\frac{4}{x}$.
Какие есть примеры ограниченных функций?
Ответ
Проверено
183,6 тыс.+ просмотров
Подсказка : Прежде чем приводить примеры ограниченных функций, ограниченная функция — это функция, ограниченная некоторым диапазоном, т. е. $ a \leqslant f\left( x \right) \leqslant b $ . Ниже мы подробно обсудили определение ограниченных функций и их примеры.
Полное пошаговое решение:
В этом вопросе мы рассмотрим, что такое ограниченные функции, и рассмотрим их примеры.
Прежде всего, давайте посмотрим, что такое ограниченные функции.
Функции, которые имеют хотя бы одну пару a и b, так что область значений этой функции находится между a и b, называются ограниченными функциями. Само название объясняет, что функции, ограниченные некоторым диапазоном, называются ограниченными функциями.
$ a \leqslant f\left( x \right) \leqslant b $ , где $ a,b \in R $ .
Наибольшее значение $ a $ называется наибольшей наименьшей границей (GLB), а наименьшее значение $ b $ называется наименьшей верхней границей (LUB). 9{ — 1}}x $ . Здесь мы видим, что график остается в пределах горизонтальной оси.
Приведенный выше график является примером неограниченной функции. Здесь $ f\left( x \right) = x $ . Здесь мы видим, что график не остается в пределах горизонтальной оси.
Недавно обновленные страницы
Если пружина имеет период T и разрезана на n равных 11 класс физики CBSE
Планета движется вокруг Солнца по почти круговой орбите 11 класс физики CBSE
В любом треугольнике AB2 BC4 CA3 а D — середина математики 11 класса JEE_Main
В треугольнике ABC 2asin dfracAB+C2 равно IIT Математика класса 11 JEE_Main
Если в треугольнике ABCangle A 45circ угол C 60circ, то математика класса 11 JEE_Main
Если в треугольнике rmABC сторона a sqrt 3 + 1rmcm и угол класс 11 математика JEE_Main
Если пружина имеет период T и разрезана на n равных 11 класс физики CBSE
Планета движется вокруг Солнца по почти круговой орбите 11 класс физики CBSE
В любом треугольнике AB2 BC4 CA3 и D это середина математики 11 класса JEE_Main
В треугольнике ABC 2asin dfracAB+C2 равно IIT Математика класса 11 JEE_Main
Если в треугольнике ABCangle A 45circ угол C 60circ, то математика класса 11 JEE_Main
Если в треугольнике rmABC сторона a sqrt 3 + 1rmcm и угол математика класса 11 JEE_Main
Тенденции сомнений
Ограниченная функция и неограниченная: определение, примеры
Типы функций >
Содержание (Нажмите, чтобы пропустить этот раздел 9):0003
- Определение ограниченной функции
- Верхняя граница
- Наименьшая верхняя граница (LUB)
- Ограниченная последовательность
- Ограниченная вариация
Ограниченные функции имеют некоторые границы или ограничения, наложенные на них. Большинство вещей в реальной жизни имеют естественные границы: автомобили имеют длину от 6 до 12 футов, людям требуется от 2 до 20 часов, чтобы пробежать марафон, длина кошек варьируется от нескольких дюймов до нескольких футов. Когда вы накладываете такие ограничения на функцию, она становится ограниченная функция .
Большинство вещей в реальной жизни имеют естественные границы: автомобили имеют длину от 6 до 12 футов, людям требуется от 2 до 20 часов, чтобы пробежать марафон, длина кошек варьируется от нескольких дюймов до нескольких футов. Когда вы накладываете такие ограничения на функцию, она становится ограниченная функция .
Чтобы функция была классифицирована как «ограниченная», ее диапазон должен иметь как нижнюю границу (например, 7 дюймов), так и , а также и верхнюю границу (например, 12 футов).
Любая неограниченная функция неограничена . Функция может быть ограничена с одной стороны и неограничена с другой.
Если функция имеет только диапазон с верхней границей (т. е. функция имеет число, которое фиксирует, насколько высоким может быть диапазон), то функция вызывается ограниченный сверху . Обычно нижняя граница диапазона указывается как -∞.
Более формально верхняя граница определяется следующим образом:
Множество A ∈ ℝ действительных чисел ограничено сверху, если существует действительное число M ∈ R, называемое верхней границей A, такое, что x ≤ M для каждого x ∈ A (Hunter, n.
d.).
По сути, приведенное выше определение говорит о том, что существует действительное число M, которое мы назовем верхней границей
Точное определение немного отличается в зависимости от того, где вы используете этот термин.
- Функция, интервал или установка
- Интеграция
- Оценка
Верхней границей функции (U) является наибольшее число этой функции. Более формально можно сказать, что функция f имеет U , если f(x) ≤ U для всех x в области определения функции.
Если вы работаете с интервалом (т.
f(x) ≤ U для всех x на [a, b].
Таким же образом верхняя граница набора (U) является наибольшим числом в наборе. Другими словами, это число, которое больше или равно всем элементам в наборе. Например, 132 — это U для набора {3, 7, 39, 75, 132}.
Верхняя граница интеграла — это место, где вы перестаете интегрировать. Это над интегральным символом:
См.: Интегральные границы.
При оценке «верхняя граница» — это наименьшее значение, которое округляется до следующего значения .
Например, предположим, что у вас есть объект длиной 7 см, округленный до ближайшего сантиметра. Верхняя граница равна 7,5 см, потому что 7,5 см — это наименьшая длина, которую можно округлить до следующего приращения — 8 см. Точно так же нижняя граница — это наименьшее значение, которое округляется до 7 см — 6,5 см.
Вы утверждаете, что 7-сантиметровый объект на самом деле находится где-то между 6,5 см (нижняя граница) и 7,5 см (верхняя граница).
Наименьшая верхняя граница (LUB) относится к числу, которое служит минимально возможным пределом для набора чисел.
Если набор чисел имеет наибольшее число, , то это число также является наименьшей верхней границей (верхней гранью). Например, предположим, что у вас есть множество, определяемое закрытым интервалом [0,2]. Число 2 включено в набор и, следовательно, является наименьшей верхней границей.
Немного интереснее становится, когда набор чисел не имеет верхней границы . В этом случае супремум — это число, которое « хочет, чтобы был величайшим элементом» (Хауленд, 2010). Возьмем открытый интервал {0,2}. Хотя набор ограничен числами 0 и 2, на самом деле они не входят в набор. Однако 2 хочет быть наибольшим элементом, поэтому это наименьшая верхняя граница.
Когда не существует наименьшей верхней границы
Действительные числа (ℝ) включают рациональные (ℚ), которые включают целые числа ( Z ), которые включают натуральные числа (N).
Любой набор действительных чисел, упорядоченный знаком <, имеет наименьшую верхнюю границу. Некоторые наборы не имеют супремум. Например (Holmes, nd):
- Рациональные числа , упорядоченные по <. Допустим, у вас есть набор рациональных чисел, в котором все элементы меньше √2. Вы можете найти верхнюю границу (например, число 2), но единственным кандидатом на наименьшую верхнюю границу является √2, и это число не является рациональным числом (это действительное число). И действительное число не может быть супремумом для набора рациональных чисел. *
- Если набор не имеет верхней границы , то этот набор не имеет верхней границы. Например, множество всех действительных чисел неограниченно.
- Пустой набор не имеет наименьшей верхней границы.
 Это потому, что на каждое число является потенциальной верхней границей для пустого множества.
Это потому, что на каждое число является потенциальной верхней границей для пустого множества.
* Рациональные числа создают всевозможные проблемы, подобные этой, которые делают их «…непригодными для использования в качестве основы исчисления» (Блох, стр. 64).
Более формальное определение
В случае открытого интервала {0,2} это число является наименьшим числом, которое больше, чем каждый элемент в наборе. Другими словами, 2 на самом деле не входит в сам набор, но это наименьшее число вне набора, большее 1,999…
В более формальных терминах:
Если М является набором чисел, а М является числом, мы можем сказать, что М является наименьшей верхней границей или супремумом М , если верны следующие два утверждения. :
- M является верхней границей M и
- ни один элемент M , который меньше M , не может быть верхней границей для M .

Предположим, что M является наименьшей верхней границей для M . Это означает, что для каждого числа x ∈ M мы имеем x ≤ M . Для любого набора чисел, который имеет верхнюю границу, набор ограничен сверху .
Нижняя граница
Если у функции есть диапазон с нижней границей, она называется ограниченной снизу . Обычно нижняя граница диапазона указывается как +∞. Формальное определение почти такое же, как и для верхней границы, за исключением другого неравенства.
Набор A ∈ ℝ действительных чисел ограничено снизу, если существует действительное число M ∈ R, называемое нижней границей числа A, такое, что x ≥ M для каждого x ∈ A (Hunter, nd).
Ограниченная последовательность является частным случаем ограниченной функции; тот, где абсолютное значение каждого термина меньше или равно конкретному действительному положительному числу.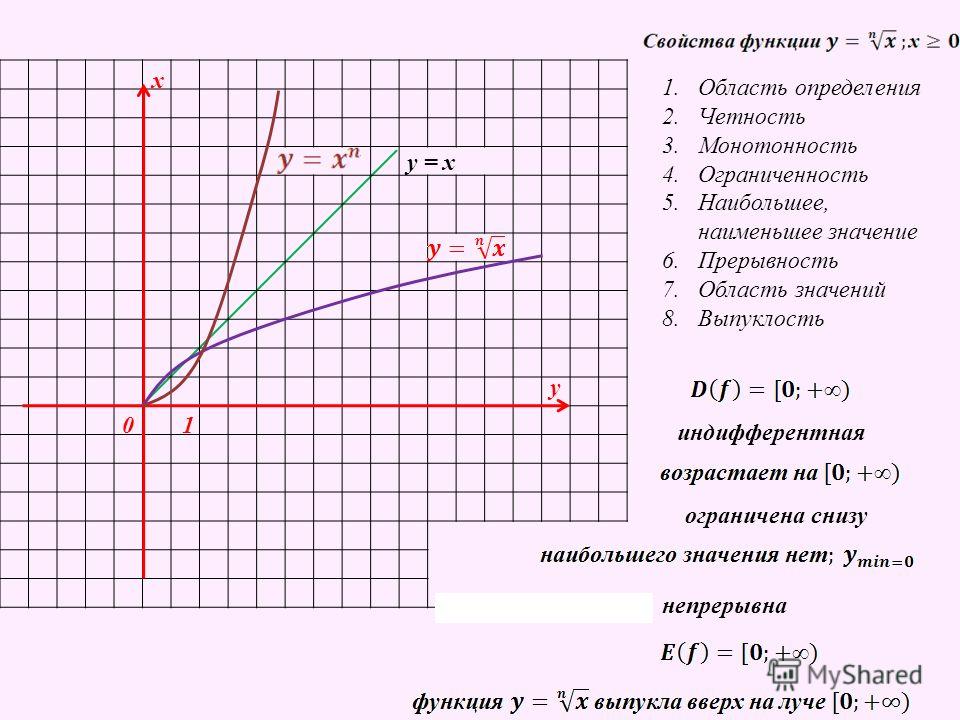 Вы можете думать об этом как о четко определенной граничной линии, так что ни один член последовательности не может быть найден на окраинах этой линии.
Вы можете думать об этом как о четко определенной граничной линии, так что ни один член последовательности не может быть найден на окраинах этой линии.
Формально последовательность X ограничена, если существует действительное число M больше 0, такое |x н | ≤ M для всех n ∈ N.
Синие точки на изображении ниже показывают бесконечную последовательность. Как видите, последовательность не сходится, потому что красные граничные линии никогда не сходятся. Однако он ограничен.
Примеры ограниченных последовательностей
Одним из примеров ограниченной последовательности является та, которая определяется как
Правая часть этого уравнения говорит нам, что n имеет индекс от 1 до бесконечности. Это превращает последовательность в последовательность дробей, где числители всегда равны единице, а знаменатели всегда являются числами больше единицы. Основное алгебраическое тождество говорит нам, что x -к = 1 / х к . Таким образом, каждый термин в последовательности является дробной частью единицы, и мы можем сказать, что для каждого члена в нашей последовательности |x n | ≤ 1,
Таким образом, каждый термин в последовательности является дробной частью единицы, и мы можем сказать, что для каждого члена в нашей последовательности |x n | ≤ 1,
Вспомните теперь наше определение ограниченной последовательности: последовательность X является ограниченной, если существует действительное число M больше 0, такое как |x n | ≤ M для всех n ∈ N . Пусть M = 1, и тогда M — действительное число больше нуля, такое что |x n | ≤ M для всех n от 1 до бесконечности. Итак, наша последовательность ограничена.
Ограниченные последовательности и сходимость
Каждая абсолютно сходящаяся последовательность ограничена, поэтому, если мы знаем, что последовательность сходится, мы сразу знаем, что она ограничена. Обратите внимание, что это ничего не говорит нам о том, сходится ли ограниченная последовательность: может быть, а может и нет. Например, нарисованная выше последовательность не сходится, хотя и ограничена.
Ограничено сверху и снизу
Если мы говорим, что последовательность ограничена, то она ограничена сверху и снизу. Однако некоторые последовательности ограничены только с одной стороны.
Если все члены последовательности больше или равны числу K, последовательность ограничена снизу, и K называется нижней границей. Максимально возможное значение K равно инфимуму .
Если все члены последовательности меньше или равны числу K’, говорят, что последовательность ограничена сверху, а K’ — это верхняя граница. Наименьшее возможное K — это супремум .
Ограниченная функция ограниченной вариации (также называемая BV-функцией ) «колеблется» или колеблется между границами, почти так же, как синусоидальная функция колеблется между границами 1 и -1; Вертикальное (движение вверх и вниз) этих функций ограничено интервалом. Другими словами, вариация не бесконечна: мы можем вычислить для нее значение.
Эти функции могут быть описаны как интегрируемые функции с производной (в смысле распределений), которая представляет собой знаковую меру с конечной полной вариацией [1]. Концепция была первоначально разработана в контексте рядов Фурье [2], когда математики пытались доказать сходимость рядов.
Примеры функций ограниченной вариации
Все монотонные функции и абсолютно непрерывные функции имеют ограниченную вариацию; Вещественнозначные функции с вариацией на компактном интервале могут быть выражены как разность между двумя монотонными (неубывающими) функциями [3], называемая разложением Жордана . Интересно, что эти функции не обязательно должны быть непрерывными функциями и могут иметь конечное число разрывов (хотя они должны быть интегрируемыми по Риману). Они также могут быть аппроксимированы конечными ступенчатыми функциями или разложены на часть непрерывную и часть скачкообразную.
Нормализованные функции могут быть описаны как имеющие ограниченную вариацию на интервале [0,1] с h(0) = 0 и h(c) = h(c + 0) для 0 < c < 1.
Более формально, вещественнозначная функция α ограниченной вариации на замкнутом интервале [a, b] имеет константу M > 0 такую, что [4]: вопрос очевиден [5].
Ссылки (ограниченный вариант)
[1] Цимер В.П. (1989) Функции ограниченной вариации. В кн.: Слабо дифференцируемые функции. Тексты для выпускников по математике, том 120. Спрингер, Нью-Йорк, штат Нью-Йорк. https://doi.org/10.1007/978-1-4612-1015-3_5
[2] Monteiro, G. et al. Серия в реальном анализе. Том 15-Интеграл Курцвейла – Стилтьеса: теория и приложения. Всемирная научная.
[3] Бриджес, Д. (2016). Конструктивный взгляд на функции BV. Бюллетень Лондонского математического общества. Том 32, Выпуск 3 с. 316-324
[4] Бриджес, Д. (2016). Функции ограниченной вариации. получено 8 апреля 2021 г. из:
http://www.math.ubc.ca/~feldman/m321/variation.pdf
[5] Функции BV. Получено 8 апреля 2021 г. с: https://www.diva-portal.org/smash/get/diva2:5850/FULLTEXT01.pdf
Другие ссылки на ограниченные функции
Блох, Э. (2011). Реальные цифры и реальный анализ. Springer Science and Business Media.
(2011). Реальные цифры и реальный анализ. Springer Science and Business Media.
Гэллап, Натаниэль. Mat25 Лекция 9 Заметки: Ограниченность последовательностей. Получено с https://www.math.ucdavis.edu/~npgallup/m17_mat25/lecture_notes/lecture_9/m17_mat25_lecture_9_notes.pdf от 25 января 2018 г.
Холмс (без даты). Заметки о классе. Получено 16 января 2018 г. с: https://math.boisestate.edu/~holmes/math414/M314F09lubnotes.pdf
Howland, J. (2010). Базовый реальный анализ. Джонс и Бартлетт Обучение.
Хантер, Дж. Супремум и Инфиним. Получено 8 декабря 2018 г. с: https://www.math.ucdavis.edu/~hunter/m125b/ch3.pdf
Ларсон и Эдвардс. Исчисление.
Лаваль П. Ограниченные функции. Получено 8 декабря 2018 г. с: http://ksuweb.kennesaw.edu/~plaval/math5381/real_bdfunctions.pdf
Кинг, М. и Моди, Н. (2010). Численные и статистические методы биоинженерии: приложения в MATLAB. Издательство Кембриджского университета.
Центр обучения математике: Последовательности. Получено с https://www3.

 d.).
d.).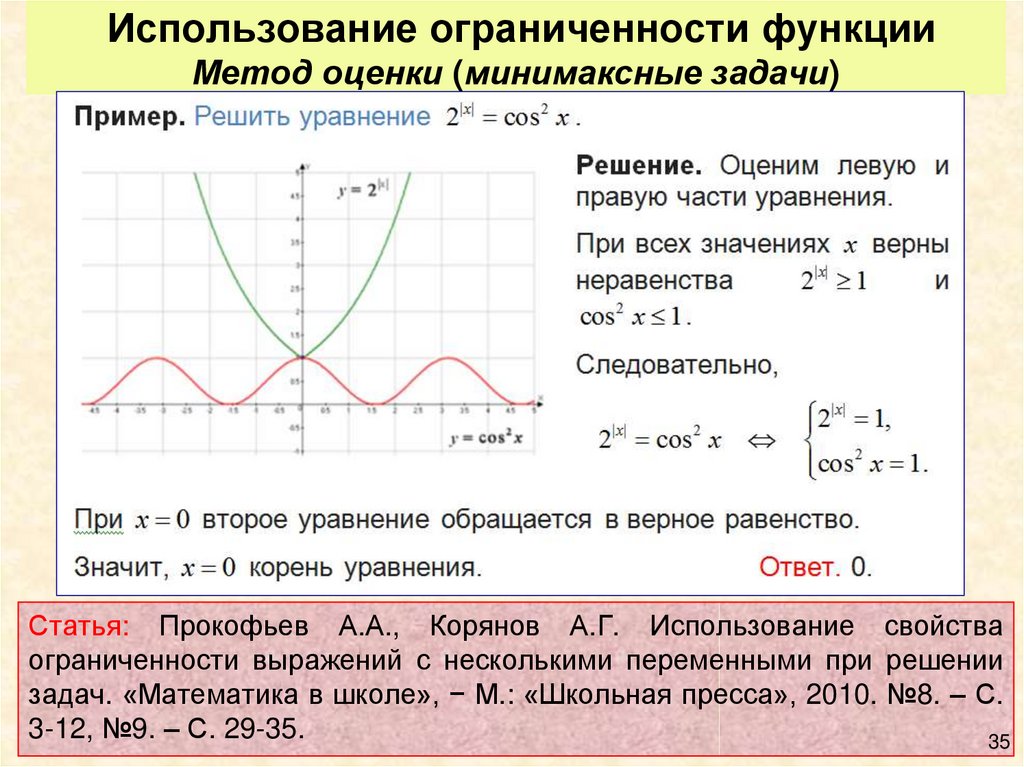 Это потому, что на каждое число является потенциальной верхней границей для пустого множества.
Это потому, что на каждое число является потенциальной верхней границей для пустого множества.