Нахождение точек локального экстремума функции онлайн
| Функция: | |
Локальный экстремум
Определение 1. Пусть существует число 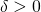 такое, что функция
такое, что функция 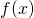 определена в
определена в 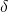 -окрестности точки
-окрестности точки 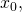 то есть на множестве
то есть на множестве 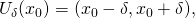 и пусть для всех
и пусть для всех 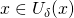
![\[f(x) \ge f(x_0).\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-2f1ef704cc6a01399e19e1798624f0a8_l3.png)
Тогда говорят, что функция 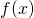 имеет в точке
имеет в точке 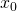 локальный минимум.
локальный минимум.
Аналогично, если существует число 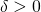 такое, что для всех
такое, что для всех 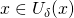 выполняется неравенство
выполняется неравенство
![\[\f(x) \le f(x_0),\]](/800/600/https/umath.ru/wp-content/ql-cache/quicklatex.com-eb99cda2b1aa5bdadda05d28c9c847b3_l3.png)
то говорят, что функция 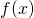 имеет в точке
имеет в точке 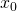 локальный максимум.
локальный максимум.
Определение 2. Если точка 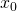 является точкой локального минимума или локального максимума функции
является точкой локального минимума или локального максимума функции 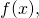 то говорят, что
то говорят, что 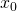 — точка локального экстремума
— точка локального экстремума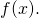
Теорема Ферма
Теорема (Ферма). Если функция 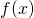 имеет локальный экстремум в точке
имеет локальный экстремум в точке 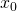 и дифференцируема в этой точке, то
и дифференцируема в этой точке, то
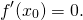
Этой теоремой пользуются для нахождения точек локального экстремума.
экстремум функции двух переменных — 22 Июля 2014 — Примеры решений задач
Ключевые слова: калькулятор экстремумов, найти экстремум функции двух переменных, частные производные первого и второго порядков, стационарные точки, калькулятор частных производных.
Пример 1. Исследовать на экстремум функцию:
Алгоритм решения следующий:
1) находим частные производные первого порядка:
Примечание: найти частные производные онлайн (первого и второго порядка) можно с помощью калькулятора.
2). Решаем систему уравнений:
и таким образом находим стационарные точки функции.
Точки, в которых значение производной функции равно нулю, называются стационарными точками.
Для данного примера получаем систему уравнений:
стационарная точка: (-1;1)
3) Находим вторые частные производные
Вычисляем значения этих частных производных второго порядка в каждой из найденных в п.2 стационарных точках M(x0;y0).
Для данного примера, получаем
4) Делаем вывод о наличии экстремумов:
а) если AC – B2 > 0 и A < 0 , то в точке M имеется максимум;
в) если AC – B2 < 0, то экстремума нет;
г) если AC – B2 = 0, то вопрос о наличии экстремума остается открытым;
Тогда в точке x=-1, y=1
Следовательно в точке x=-1, y=1 функция имеет локальный минимум
Ответ: min{z}=0
Проверить правильность решения можно с помощью калькулятора «экстремум функции».
Экстремумы функции двух переменных
Определение. Точками экстремума функции двух переменных называются точки минимума и максимума этой функции. Значения самой функции в точках экстремума называются экстремумами функции двух переменных.
Определение. Точка P(x0, y0) называется точкой максимума функции двух переменных z = z(x, y), если значение функции в этой точке больше, чем в точках её окрестности. Значение функции в точке максимума называется максимумом функции двух переменных.
Определение. Точка P(x0, y0) называется точкой максимума функции двух переменных z = z(x, y), если значение функции в этой точке больше, чем в точках её окрестности. Значение функции в точке максимума называется максимумом функции двух переменных.
Теорема (необходимый признак экстремума функции двух переменных).
Если точка P(x0, y0)
— точка экстремума функции двух переменных z = z(x, y),
то первые
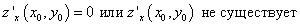
и
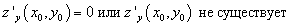 .
.
Определение. Точки, в которой первые частные производные функции двух переменных равны нулю, называются стационарными точками.
Определение. Точки, в которой первые частные производные функции двух переменных равны нулю или не существуют, называются критическими точками.
Как и в случае с функцией одной переменной, необходимое условие существования экстремума функции двух переменных не является достаточным. Встречаются немало функций, в случаях которых первая частная производная функции равна нулю или не существует, но экстремумов в соответствующих точках нет. Каждая точка экстремума является критической точкой, но не каждая критическая точка является экстремумом.
Достаточный признак существования экстремума функции двух переменных. В точке P существует экстремум функции двух переменных, если в окрестности этой точки полное приращение функции не меняет знак. Так как в критической точке первый полный дифференциал равен нулю, то приращение функции определяет второй полный дифференциал
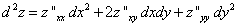 .
.
Наилучшее понимание применения полного дифференциала придёт при изучении и практическом применении шагов 3 и 4 алгоритма нахождения экстремумов функции двух переменных, который следует вторым пунктом этого урока.
Локальный характер экстремумов функции двух переменных
Наибольший интерес представляет алгоритм нахождения экстремумов функции двух переменных, так как он, во-первых, отличается от алгоритма нахождения экстремумов функции одной переменных, а во-вторых, по аналогии с ним можно составить алгоритм нахождения функции трёх переменных. В частности, потребуется вычислять определители.
Итак, алгоритм нахождения экстремумов функции двух переменных.
Дана функция двух переменных  .
.
Шаг 2. Составляем систему уравнений из равенств этих производных нулю (их равенство нулю и есть необходимый признак существования экстремума):
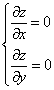
Решения этой системы уравнений 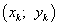 являются точками возможного экстремума — критическими точками.
являются точками возможного экстремума — критическими точками.
Шаг 3. Пусть  является критической точкой, найденной на шаге 2. Чтобы убедиться, что в ней существует экстремум функции двух переменных,
находим частные производные второго порядка
является критической точкой, найденной на шаге 2. Чтобы убедиться, что в ней существует экстремум функции двух переменных,
находим частные производные второго порядка
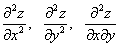
как частные производные от частных производных первого порядка, найденных на шаге 1.
Шаг 4. Присваиваем частным производным второго порядка, найденным на шаге 3, буквенные обозначения:
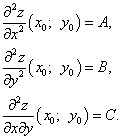
Находим определитель 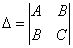 и проверяем достаточный признак существования экстремума.
и проверяем достаточный признак существования экстремума.
Если 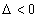 , то экстремума в найденной критической точке нет,
, то экстремума в найденной критической точке нет,
если 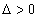 , то экстремум в найденной критической точке есть,
, то экстремум в найденной критической точке есть,
если 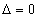 , то требуются дополнительные исследования.
, то требуются дополнительные исследования.
Если экстремум в найденной точке есть и если 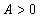 , то в этой точке существует минимум функции двух переменных, если
, то в этой точке существует минимум функции двух переменных, если 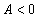 , то максимум.
, то максимум.
Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных  и получаем значение экстремума функции двух переменных (минимума или максимума).
и получаем значение экстремума функции двух переменных (минимума или максимума).
Примеры начнём с более сложного, в котором составленная система уравнений имеет несколько решений, а, значит, найдено несколько критических точек.
Пример 1. Найти экстремумы функции двух переменных 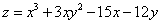 .
.
Решение. Следуем изложенному выше алгоритму.
Шаг 1. Находим частные производные: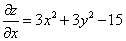
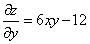 .
.
Шаг 2. Составляем систему уравнений из равенств этих производных нулю:
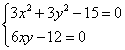
Делим первое уравнение системы на 3, а второе на 6 и получаем
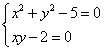
Из второго уравнения выражаем 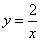 , подставляем в первое уравнение и получаем
, подставляем в первое уравнение и получаем

Умножаем это уравнение на 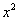 и получаем
и получаем
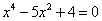 .
.
Производим замену переменной: 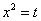 и получаем
и получаем
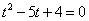 .
.
Решаем полученное квадратное уравнение: 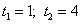 .
.
Так как 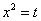 и
и 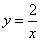 , то
, то
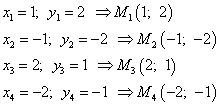
Таким образом, получили четыре критических точки — точки возможного экстремума.
Шаг 3. Находим частные производные второго порядка
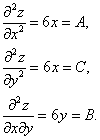
Шаг 4. Находим определитель 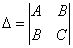 :
:
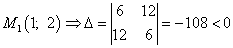 , т. е. экстремума в найденной критической точке нет,
, т. е. экстремума в найденной критической точке нет,
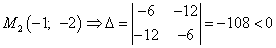 , т. е. экстремума в найденной критической точке нет,
, т. е. экстремума в найденной критической точке нет,
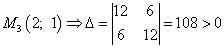 и
и  , т. е. в найденной критической точке есть минимум функции двух переменных,
, т. е. в найденной критической точке есть минимум функции двух переменных,
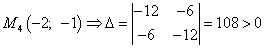 и
и 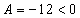 , т. е. в найденной критической точке есть максимум функции двух переменных.
, т. е. в найденной критической точке есть максимум функции двух переменных.
Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных и получаем значения экстремума функции двух переменных:
 ,
,
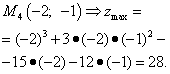
В следующем примере — только одна критическая точка.
Пример 2. Найти экстремумы функции двух переменных 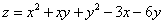 .
.
Шаг 1. Находим частные производные: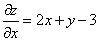
 .
.
Шаг 2. Составляем систему уравнений из равенств этих производных нулю:
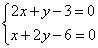
Решаем систему уравнений:
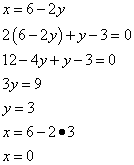
Таким образом, получили критическую точку 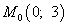 — точку возможного экстремума.
— точку возможного экстремума.
Шаг 3. Находим частные производные второго порядка
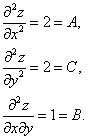
Шаг 4. Находим определитель  , т. е. в найденной критической точке есть экстремум, причём так как
, т. е. в найденной критической точке есть экстремум, причём так как 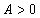 , то это минимум.
, то это минимум.
Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных и получаем значение экстремума функции двух переменных:
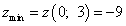 .
.

Функции нескольких переменных
Как найти условные экстремумы функции двух и более переменных
В задачах оптимизации возникает необходимость найти экстремумы функции двух и более
переменных 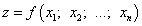 при условии,
что существует связь между переменными этой связи, заданная уравнением
при условии,
что существует связь между переменными этой связи, заданная уравнением
 . В
этом случае говорят, что требуется найти условный экстремум.
. В
этом случае говорят, что требуется найти условный экстремум.
Для того чтобы найти условный экстремум требуется находить частные производные и решать системы уравнений Существует алгоритм нахождения условного экстремума из трёх шагов, который сейчас и разберём на примере, и геометрический смысл условного экстремума, который должен дойти до каждого при разборе этого самого примера.
Итак, алгоритм, который разберём на примере самой распространённой задачи — нахождение условного экстремума функции двух переменных..
Шаг 1. Вводится функция Лагранжа
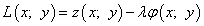 ,
,
где первое слагаемое — сама исходная функция, а второе слагаемое со знаком минус —
левая часть уравнения условия связи, умноженная на  (лямбда) — множитель Лагранжа.
(лямбда) — множитель Лагранжа.
Пример 1. Найти условные экстремумы функции двух переменных 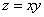 ,
выражающей площадь прямоугольника через его стороны x и y при условии
,
выражающей площадь прямоугольника через его стороны x и y при условии 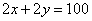 ,
означающем, что существует верёвка, которой можно ограничить этот прямоугольник, и длина этой верёвки равна 100.
,
означающем, что существует верёвка, которой можно ограничить этот прямоугольник, и длина этой верёвки равна 100.
Шаг 1. Решение. Приведём уравнение условия связи к требуемому виду с нулём в правой части:
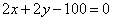 .
.
Составим функцию Лагранжа:
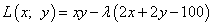 .
.
Шаг 2. Составляем систему уравнений из равенств частных производных нулю и уравения условия связи (необходимый признак существования условного экстремума):
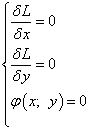
Решения этой системы уравнений являются точками возможного условного экстремума — стационарными точками или, как ещё говорят, критическими точками.
Пример 1. Шаг 2.
Решение. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:
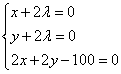
Из первого и второго уравнений выразим соответственно x и y:
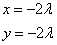
Подставим эти выражения в третье уравнение и найдём значение множителя Лагранжа:
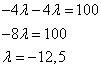
Подставим теперь значение множителя Лагранжа в выражения для x и y и найдём значения переменных исходной функции:
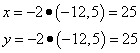
Получили 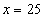 и
и
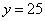 . Эти значения
являются также координатами стационарной точки. Таким образом, получили стационарную точку
. Эти значения
являются также координатами стационарной точки. Таким образом, получили стационарную точку
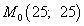 .
.
Шаг 3. Пусть  является стационарной точкой,
найденной на шаге 2. Чтобы определить, является ли условный экстремум минимумом или максимумом, нужно
найти второй дифференциал функции Лагранжа
является стационарной точкой,
найденной на шаге 2. Чтобы определить, является ли условный экстремум минимумом или максимумом, нужно
найти второй дифференциал функции Лагранжа
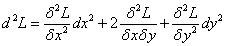
и в полученном выражении подставить вместо «лямбды» её значения (значения множителя Лагранжа), найденные на шаге 2.
Если значение второго дифференциала функции Лагранжа меньше нуля
(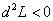 ), то стационарная
точка является точкой максимума, если больше нуля (
), то стационарная
точка является точкой максимума, если больше нуля (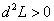 ),
то стационарная точка является точкой минимума. Если значение второго дифференциала функции Лагранжа
равно нулю, то требуются дополнительные исследования, но такие случаи практически не попадаются в
задачах, задаваемых студентам.
),
то стационарная точка является точкой минимума. Если значение второго дифференциала функции Лагранжа
равно нулю, то требуются дополнительные исследования, но такие случаи практически не попадаются в
задачах, задаваемых студентам.
Координаты стационарных точек подставляются в исходную точку и, таким образом, мы окончательно находим условные экстремумы (или минимум и максимум или что-то одно из этих экстремумом).
Пример 1. Шаг 3.
Решение. Найдём второй дифференциал функции Лагранжа:
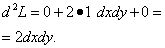
В нашем случае, так как первое и третье составляющие равны нулю, нам не придётся подставлять в них значения множителя Лагранжа. Зато нужно найти отношения между дифференциалами dx и dy:
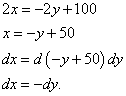
Так как полученные значения — противоположные по знаку, то получаем, что в любом
случае 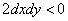 .
.
Теперь можем найти значение условного экстремума исходной функции, являющееся максимумом:
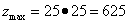 .
.
Это заданная исходной функцией максимальная площадь прямоугольника, который можно ограничить верёвкой, длина которой равна 100.
Пример 2. Найти условные экстремумы функции двух переменных 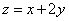 при условии
при условии  .
.
Решение.
Шаг 1. Составим функцию Лагранжа:
 .
.
Шаг 2. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:
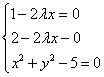
Из первого и второго уравнений выразим соответственно x и y:
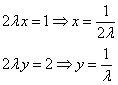
Подставим эти выражения в третье уравнение и найдём значения множителя Лагранжа:

Подставим теперь значение множителя Лагранжа в выражения для x и y и найдём значения переменных исходной функции при двух значениях множителя Лагранжа:
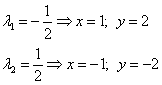
Эти значения икса и игрека
являются координатами двух стационарных точек. Таким образом, получили стационарные точки
 .
.
Шаг 3. Найдём частные производные второго порядка функции Лагранжа:
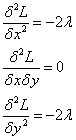 :
:
Найдём второй дифференциал функции Лагранжа по формуле
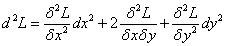 :
:
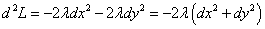 .
.
Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа  :
:
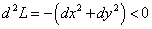
Получили значение, меньшее нуля, следовательно, точка
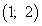 — точка условного максимума:
— точка условного максимума:
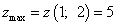 .
.
Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа 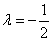 :
:
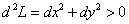
Получили значение, большее нуля, следовательно, точка
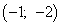 — точка условного минимума:
— точка условного минимума:
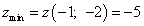 .
.
Таким образом, условные экстремумы заданной функции найдены.
Пример 3. Найти условные экстремумы функции двух переменных 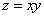 при условии
при условии 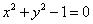 .
.
Решение.
Шаг 1. Составим функцию Лагранжа:
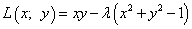 .
.
Шаг 2. Найдём частные производные функции Лагранжа и составим из их равенств нулю и уравнения условия связи систему уравнений:
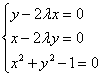
Из первого и второго уравнений выразим соответственно x и y:
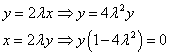
Получаем, что 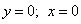 ,
однако подстановка этих значений переменных в третье уравнение системы не даёт верного равенства. Поэтому
считаем, что на самом деле второй сомножитель равенства
,
однако подстановка этих значений переменных в третье уравнение системы не даёт верного равенства. Поэтому
считаем, что на самом деле второй сомножитель равенства 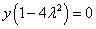 равен нулю:
равен нулю: 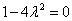 . Отсюда получаем
. Отсюда получаем
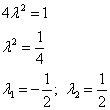
Ищем координаты стационарных точек при значении множителя Лагранжа 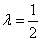 .
Тогда из выражений для икса и игрека из системы уравнений следует, что
.
Тогда из выражений для икса и игрека из системы уравнений следует, что 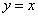 .
Из третьего уравнения системы получаем:
.
Из третьего уравнения системы получаем:
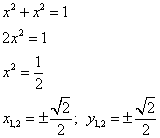
Получили две стационарные точки:
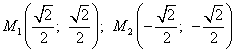
Ищем координаты стационарных точек при значении множителя Лагранжа 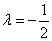 .
Тогда из выражений для икса и игрека из системы уравнений следует, что
.
Тогда из выражений для икса и игрека из системы уравнений следует, что 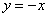 .
.
На основании вычислений двух первых стационарных точек получилаем ещё две стационарные точки:
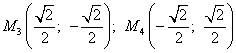
Шаг 3. Найдём частные производные второго порядка функции Лагранжа:
 :
:
Найдём второй дифференциал функции Лагранжа по формуле
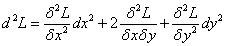 :
:
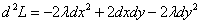 .
.
Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа  :
:
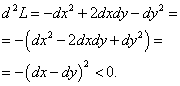
Получили значение, меньшее нуля, следовательно, точки
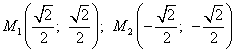 — точки условного максимума:
— точки условного максимума:
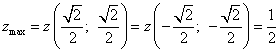 .
.
Установим знак второго дифференциала функции Лагранжа при значении множителя Лагранжа 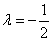 :
:
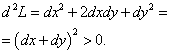
Получили значение, большее нуля, следовательно, точки
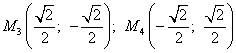 — точки условного минимума:
— точки условного минимума:
 .
.
Таким образом, условные экстремумы заданной функции найдены.
Аналогичным образом можно находить условные экстремумы функций трёх и более переменных.

Функции нескольких переменных
Функция \(z=f(x,y)\) имеет максимум (минимум) в точке \(M_0(x_0;y_0)\) , если значение функции в этой точке больше (меньше), чем ее значение в лююой другой точке \(M(x;y)\) некоторой окресности точки \(M_0\) т.е. \(f(x_0;y_0)>f(x,y)\) для всех точек \(M(x;y)\) , удовлетворящих условию \(\left|M_0M \right|Максимум или минимум функции называется ее экстремумом. Точка \(M_0\), в которой функция имеет экстремум, называется точкой экстремума.
Если дифференцируемая функция \(z=f(x,y)\) достигает экстремума в точке \(M_0(x_0;y_0)\) то ее частные производные первого порядка в этой точке равны нулю, т.е.
$$\frac{\partial f(x_0,y_0)}{\partial x}=0;\frac{\partial f(x_0,y_0)}{\partial y}=0$$
необходимые условия экстремума.
Точки, в которых частные производные равны нулю, называются стационарными точками. Не всякая стационарная точка является точкой экстремума.
Пример 1. Найти экстремум функции \(z=x^2+xy+y^2-3x-6y.\)
Находим частные производные первого порядка :
$$\frac{\partial z}{\partial x}=2x+y-3,\frac{\partial z}{\partial y}=x+2y-6.$$
Воспользовавшись необходимыми условиями экстремума, находим стационарные точки :
$$\begin{cases} & \text{ } 2x+y-3= 0 \\ & \text{ } x+2y-6=0 \end{cases}$$
Откуда \(x=0,y=3; M(0;3).\)
Находим значения частных производных второго порядка в точке \(M\) :
$$\frac{\partial ^2z}{\partial x^2}=2,\frac{\partial ^2z}{\partial y^2}=2,\frac{\partial ^2z}{\partial x\partial y}=1$$
и составляем дискриминант
$$\triangle=AC-B^2=2\cdot 2-1=3>0;A>0.$$
Следовательно, в точке \(M(0;3)\) заданная функция имеет минимум. Значение в этой точки \(z_{min}=-9.\)
Пример 2. Найти экстремум функции
$$z=\frac{1}{2}xy+(47-x-y)\left(\frac{x}{3}+\frac{y}{4} \right).$$
Находим частные производные первого порядка :
$$\frac{\partial z}{\partial x}=-\frac{1}{12}y-\frac{2}{3}x+\frac{47}{3},\frac{\partial z}{\partial y}=-\frac{1}{2}y-\frac{1}{12}x+\frac{47}{4}.$$
Воспользовавшись необходимыми условиями экстремума, находим стационарыне точки:
$$\begin{cases} & \text{ }-\frac{1}{12}y-\frac{2}{3}x+\frac{47}{3}=0 \\ & \text{ }-\frac{1}{2}y-\frac{1}{12}x+\frac{47}{4}= 0 \end{cases}$$
или
$$\begin{cases} & \text{ }8x+y=188 \\ & \text{ }x+6y= 141. \end{cases}$$
Отсюда \(x=21,y=20;\) стационарная точка \(M(21;20)\).
Найдем значения вторых производных в точке \(M :\)
$$\frac{\partial ^2z}{\partial x^2}=-\frac{2}{3},\frac{\partial ^2z}{\partial y^2}=-\frac{1}{2},\frac{\partial ^2z}{\partial x\partial y}=-\frac{1}{12}.$$
Тогда
$$\triangle=AC-B^2=(-2/3)(-1/2)-(-1/12)^2=1/3-1/144>0.$$
Так как \(AУсловный экстремум. Наибольшее и наименьшее значения функции в замкнутой области
Условный экстремум функции \(z=f(x,y)\) называется экстремум этой функции, достигнутый при условии, что переменные \(x\) и \(y\) связаны уравнением \(\varphi (x,y)=0\) (уравнение связи).
Отыскание условного экстремума можно свести к исследованию на обычный экстремум так называемой функции Лагранжа \(u=f(x,y)+\lambda \varphi (x,y)\) , где \(\lambda\) — неопределенный постоянный множитель.
Необходимые условия экстремума функции Лагранжа имеют вид
$$\frac{\partial u}{\partial x}\equiv \frac{\partial f}{\partial x}+\lambda\frac{\partial \varphi }{\partial x}=0,$$
$$\frac{\partial u}{\partial y}\equiv \frac{\partial f}{\partial y}+\lambda\frac{\partial \varphi }{\partial y}=0,$$
$$\varphi (x,y)=0.$$
Из этих трьех уравнений можно найти неизвестные \(x,y,\lambda\).
Для того что бы найти наибольшее и наименьшее значения функции в замкнутой области, надо :
1) найти стационарные точки, расположенные в данной области, и вычислить значения функции в этих точках;
2) найти наибольшее и наименьшее значения функции на линиях, образующих границу области;
3) из всех найденных значений выбрать наибольшее и наименьшее.
Пример 1. Найти экстремум функции \(z=xy\) при условии, что \(x\) и \(y\) связаны уравнением \(2x+3y-5=0.\)
Рассмотрим функцию Лагранжа \(u=xy+\lambda(2x+3y-5)=0.\) Имеем
$$\frac{\partial u}{\partial x}=y+2\lambda, \frac{\partial u}{\partial y}=x+3\lambda.$$
Из системы уравнений (необходимые условия экстремума)
$$\begin{cases} & \text{ } y+2\lambda =0, \\ & \text{ } x+3\lambda =0, \\ & \text{ } 2x+3y-5= 0 \end{cases}$$
находим \(\lambda=-5/12, x=5/4, y=5/6.\) Нетрудно видеть, что в точке \((5/4;5/6)\) функция \(z=xy\) достигает наибольшего значения \(z_{max}=25/24.\)
2012-12-15 • Просмотров [ 18469 ]
Экстремальные значения (минимум / максимум) Калькулятор функции

Поиск инструмента
Экстремум функции
Инструмент для вычисления экстремумов функции. Экстремальное значение функции — это минимальное или максимальное значение, которое может принимать функция.
Результаты
Экстремум функции — dCode
Тег (и): Функции
Поделиться

dCode и вы
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Инструмент для вычисления экстремумов функции.Экстремальное значение функции — это минимальное или максимальное значение, которое может принимать функция.
Ответы на вопросы
Как рассчитать экстремум?
Чтобы найти крайние значения функции (наивысшие или самые низкие точки на интервале, в котором функция определена), сначала вычислите производную функции и изучите знак.
Экстремум функции достигается, когда ее производная равна нулю и меняет знак.2 $, определенная над $ \ mathbb {R} $, функция имеет минимум в $ x = 0 $ и $ f (x)> = 0 $ в области определения $ \ mathbb {R} $.
Максимум функции $ M $ (верхний регистр M) существует, когда для всех $ x $, $ f (x)
В чем разница между относительным / локальным экстремумом и абсолютным / глобальным экстремумом?
Экстремум функции обязательно определяется на интервале. Если интервал — это вся область определения функции, то это глобальный / абсолютный экстремум , в противном случае это локальный / относительный экстремум .
Что такое экстремум?
Extrema — это множественное число от extremum (от латинского, что означает крайность).
Задайте новый вопросИсходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Экстремум функции». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любая функция (преобразование, решение, дешифрование / encrypt, decipher / cipher, decode / encode, translate), написанные на любом информатическом языке (PHP, Java, C #, Python, Javascript, Matlab и т. д.)) доступ к данным, скриптам или API не будет бесплатным, то же самое касается загрузки Экстремума функции для автономного использования на ПК, планшете, iPhone или Android!
Нужна помощь?
Пожалуйста, заходите в наше сообщество в Discord для получения помощи!
Вопросы / комментарии
Сводка
Инструменты аналогичные
Поддержка
Форум / Справка

Рекламные объявления
Ключевые слова
экстремум, функция, производная, вычислитель, максимум, минимум, полином
Ссылки
Источник: https: // www.dcode.fr/extremum-function
© 2020 dCode — Лучший «инструментарий» для решения любых игр / загадок / геокешинга / CTF. .Таблица функций (2 переменные) Калькулятор
- Цель использования
- Студент, изучающий линейную алгебру просмотр старого свойства алгебры, создание двух таблиц результатов для сравнения (вместо этого я должен был использовать калькулятор двух функций). Я проверял, сохраняется ли сложение векторов для преобразования, чтобы доказать линейность, когда я сделал ошибку типа: 2 | u + v | = 2 | u | + 2 | v |.Мне следовало разделить константу, чтобы увидеть, что это | x + y | = | x | + | y | , что, как я знаю, ложно. Но утомительное создание таблицы 5×5 с осями x и y для {-2,2} было забавным в странном и занудном смысле.
В заключение: все преобразования, содержащие абсолютное значение переменной, являются нелинейными, поскольку сложение векторов не сохраняется. Спасибо за услугу. Раньше я все время делал такие тестовые примеры в алгебре старших классов. Это круто, потому что вам не нужно верить кому-то на слово, что важно, когда ваш вопрос слишком непонятный или конкретный, чтобы на него легко найти ответ.
[1] 2020/07/24 19:51 Мужчина / 20-летний уровень / Средняя школа / Университет / Аспирант / Полезно /
- Цель использования
- Школа
- Комментарий / запрос
- нужно вычислить уравнение
[2] 2020/07/23 03:59 Женский / Моложе 20 лет / Высшая школа / Университет / аспирант / Не совсем /
- Цель использования
- Домашнее задание во время этот карантин
[3] 2020/06/18 16:48 Мужчина / До 20 лет / Средняя школа / Университет / аспирант / Немного /
- Цель использования
- для задания по математике
[4] 2020/06/16 15:50 Мужчина / Моложе 20 лет / Начальная школа / Ученик неполной средней школы / Совсем нет /
- Цель использования
- Помощь в школьной работе
[5] 2020/05/13 04:15 Женский / До 20 лет / Начальная школа / Неполный средний класс / Маленький /
- Цель использования
- Домашнее задание по математике во время виртуального обучения
[6 ] 2020/05/06 04:55 Женский / До 20 лет / Средняя школа / Университет / Высшее образование nt / Useful /
- Цель использования
- для работы
- Комментарий / запрос
- хорошо использовать для математики
[7] 2020/04/26 00:43 Женский / До 20 лет / Начальная школа / Ученица неполной средней школы / Полезно /
- Цель использования
- , чтобы помочь мне с дельта-математикой
[8] 2020.04.16 01:36 Мужчина / До 20 лет / Средняя школа / Университет / Выпускник / Очень /
- Цель использования
- Мне это было нужно, чтобы «помочь мне» с моей домашней работой.2
[9] 2020/04/09 01:31 Мужчина / До 20 лет / Начальная школа / Ученик неполной средней школы / Очень /
- Цель использования
- Для помощи в работе в классе
[10] 2020/03/27 02:05 Мужской / До 20 лет / Другое / Не совсем /
Калькулятор линейных уравнений в двух переменных
- Классы
- Класс 1-3
- Класс 4-5
- Класс 6-10
- Класс 11-12
- КОНКУРСНЫЙ ЭКЗАМЕН
- BNAT 000 NC
- 000 NC Книги
- Книги NCERT для класса 5
- Книги NCERT для класса 6
- Книги NCERT для класса 7
- Книги NCERT для класса 8
- Книги NCERT для класса 9
- Книги NCERT для класса 10
- Книги NCERT для класса 11
- Книги NCERT для класса 12
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT 9000 9000
- NCERT Exemplar Class
- Решения RS Aggarwal, класс 12
- Решения RS Aggarwal, класс 11
- Решения RS Aggarwal, класс 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- RD Sharma Class 6 Решения
- Решения RD Sharma Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- 000 NC Книги
- PHYSICS
- Механика
- Оптика
- Термодинамика Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- MATHS
- Теорема Пифагора 0004
- 000300030004
- Простые числа
- Взаимосвязи и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Деление фракций
- BNAT 000 NC
- 000
- 000
- 000
- 000
- 000
- 000 Microology
- 000
- 000 Microology
- 000 BIOG3000
- FORMULAS
- Математические формулы
- Алгебраические формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- 0003000 PBS4000
- 000300030002 Примеры калькуляторов химии Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образцы документов CBSE чел для класса 12
- Классы
- CBSE Контрольный документ за предыдущий год
- CBSE Контрольный документ за предыдущий год Класс 10
- Контрольный документ за предыдущий год CBSE, класс 12
- HC Verma Solutions
- HC Verma Solutions Class 11 Physics
- Решения HC Verma, класс 12, физика
- Решения Лакмира Сингха
- Решения Лакмира Сингха, класс 9
- Решения Лакмира Сингха, класс 10
- Решения Лакмира Сингха, класс 8
- Заметки CBSE
- , класс
- CBSE Notes
- Примечания CBSE класса 7
- Примечания CBSE класса 8
- Примечания CBSE класса 9
- Примечания CBSE класса 10
- Примечания CBSE класса 11
- Примечания CBSE класса 12
- Примечания к редакции
- CBSE
- Примечания к редакции класса 10 CBSE
- Примечания к редакции класса 11 CBSE 9000 4
- Примечания к редакции класса 12 CBSE
- Дополнительные вопросы по математике класса 8 CBSE
- Дополнительные вопросы по науке 8 класса CBSE
- Дополнительные вопросы по математике класса 9 CBSE
- Дополнительные вопросы по науке класса 9 CBSE
- , класс 3
- , класс 4
- , класс 5
- , класс 6
- , класс 7
- , класс 8
- , класс 9 Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для класса 11 по физике
- Решения NCERT для класса 11 Химия Решения для биологии класса 11
- Решения NCERT для математики класса 11 9 0003 NCERT Solutions Class 11 Accountancy
- NCERT Solutions For Класс 12 по физике
- Решения NCERT для химии класса 12
- Решения NCERT для класса 12 по биологии
- Решения NCERT для класса 12 по математике
- Решения NCERT Класс 12 Бухгалтерия
- Решения NCERT, класс 12, бизнес-исследования
- Решения NCERT, класс 12 Экономика
- NCERT Solutions Class 12 Accountancy Part 1
- NCERT Solutions Class 12 Accountancy Part 2
- NCERT Solutions Class 12 Micro-Economics
- NCERT Solutions Class 12 Commerce
- NCERT Solutions Class 12 Macro-Economics
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для математики класса 6
- Решения NCERT для науки класса 6
- Решения NCERT для социальных наук класса 6
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для класса 7 Наука
- Решения NCERT для класса 7 по социальным наукам
- Решения NCERT для класса 7 Английский
- Решения NCERT для класса 8 Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для социальных наук 8 класса
- Решение NCERT ns для класса 8 Английский
- Решения NCERT для социальных наук класса 9
- Решения NCERT для математики класса 9 Глава 1
- Решения NCERT для Математика класса 9 Глава 2
- Решения NCERT для математики класса 9 Глава 3
- Решения NCERT для математики класса 9 Глава 4 Решения NCERT
- для математики класса 9 Глава 5
- Решения NCERT для математики класса 9 Глава 6
- Решения NCERT для Математика класса 9 Глава 7
- Решения NCERT для математики класса 9 Глава 8 Решения NCERT
- для математики класса 9 Глава 9 Решения NCERT
- для математики класса 9 Глава 10
- Решения NCERT для математики класса 9 Глава 11
- Решения NCERT для Математика класса 9 Глава 12
- Решения NCERT для математики класса 9 Глава 13 Решения
- NCERT для математики класса 9 Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT для науки класса 9 Глава 1
- Решения NCERT для науки класса 9 Глава 2
- Решения NCERT для класса 9 Наука Глава 3
- Решения NCERT для Науки Класса 9 Глава 4
- Решения NCERT для Науки Класса 9 Глава 5
- Решения NCERT для Науки Класса 9 Глава 6
- Решения NCERT для Науки Класса 9 Глава 7
- Решения NCERT для Класса 9 Наука Глава 8
- Решения NCERT для Науки Класса 9 Глава 9
- Решения NCERT для Науки Класса 9 Глава 10
- Решения NCERT для Науки Класса 9 Глава 12
- Решения NCERT для Науки Класса 9 Глава 11
- Решения NCERT для Класса 9 Наука Глава 13
- Решения NCERT для класса 9 Наука Глава 14
- Решения NCERT для класса 9 по науке Глава 15
- Решения NCERT для класса 10 по социальным наукам
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- Решения NCERT для математики класса 10 Глава 3
- Решения NCERT для математики класса 10 Глава 4
- Решения NCERT для математики класса 10 Глава 5
- Решения NCERT для математики класса 10 Глава 6
- Решения NCERT для математики класса 10 Глава 7
- Решения NCERT для математики класса 10 Глава 8
- Решения NCERT для математики класса 10 Глава 9 Решения NCERT
- для математики класса 10 Глава 10 Решения
- NCERT для математики класса 10 Глава 11
- Решения NCERT для математики класса 10 Глава 12
- Решения NCERT для математики класса 10 Глава 13
- NCERT Sol Решения NCERT для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки класса 10 Глава 1
- Решения NCERT для науки класса 10 Глава 2
- Решения NCERT для науки класса 10, глава 3
- Решения NCERT для науки класса 10, глава 4
- Решения NCERT для науки класса 10, глава 5
- Решения NCERT для науки класса 10, глава 6
- Решения NCERT для науки класса 10, глава 7
- Решения NCERT для науки 10 класса, глава 8
- Решения NCERT для науки класса 10 Глава 9
- Решения NCERT для науки класса 10 Глава 10
- Решения NCERT для науки класса 10 Глава 11
- Решения NCERT для науки класса 10 Глава 12
- Решения NCERT для науки 10 класса Глава 13
- Решения NCERT для науки 10 класса Глава 14
- Решения NCERT для науки класса 10 Глава 15 Решения NCERT
- для науки класса 10 Глава 16
- Class 11 Commerce Syllabus
- ancy Account
- Учебная программа по бизнесу 11 класса
- Учебная программа по экономике 11 класса
- Учебная программа по коммерции 12 класса
- Учебная программа по бухгалтерии 12 класса
- Учебная программа по бизнесу 12 класса
- Учебная программа по экономике
- 9000
- Образцы документов по коммерции класса 11
- Образцы документов по коммерции класса 12
- TS Grewal Solutions
- TS Grewal Solutions Class 12 Accountancy
- TS Grewal Solutions Class 11 Accountancy
- Отчет о движении денежных средств
- Что такое Entry eurship
- Защита прав потребителей
- Что такое основной актив
- Что такое баланс
- Формат баланса
- Что такое акции
- Разница между продажей и маркетингом
- ICSE
- Документы ICSE
- Вопросы ICSE
- ML Aggarwal Solutions
- ML Aggarwal Solutions Class 10 Maths
- ML Aggarwal Solutions Class 9 Maths
- ML Aggarwal Solutions Class 8 Maths
- ML Aggarwal Solutions Class 7 Maths
- ML 6 Maths
- ML Aggarwal Solutions Class 6 Maths
- ML Aggarwal Solutions Class
- Selina Solutions
- Selina Solutions для класса 8
- Selina Solutions для Class 10
- Selina Solutions для Class 9
- Frank Solutions
- Frank Solutions для математики класса 10
- Frank Solutions для математики класса 9
- Класс ICSE 9000 2
- ICSE Class 6
- ICSE Class 7
- ICSE Class 8
- ICSE Class 9
- ICSE Class 10
- ISC Class 11
- ISC Class 12
- Exam
- IAS
- Civil
- Сервисный экзамен
- Программа UPSC
- Бесплатная подготовка к IAS
- Текущие события
- Список статей IAS
- Пробный тест IAS 2019
- Пробный тест IAS 2019 1
- Пробный тест IAS 2019 2
- Экзамен KPSC KAS
- Экзамен UPPSC PCS
- Экзамен MPSC
- Экзамен RPSC RAS
- TNPSC Group 1
- APPSC Group 1
- Экзамен BPSC
- WBPS3000 Экзамен 9000 MPC 9000 9000 MPC4000 Jam
- Ключ ответов UPSC 2019
- IA S Coaching Бангалор
- IAS Coaching Дели
- IAS Coaching Ченнаи
- IAS Coaching Хайдарабад
- IAS Coaching Мумбаи
- BYJU’SEE
- 9000 JEE 9000 Основной документ JEE 9000 JEE 9000
- Вопросник JEE
- Биномиальная теорема
- Статьи JEE
- Квадратичное уравнение
- Программа BYJU NEET
- NEET 2020
- NEET Приемлемость 9000 Критерии 9000 NEET4 9000 Пример 9000 NEET 9000 9000 NEET
- Поддержка
- Разрешение жалоб
- Служба поддержки
- Центр поддержки
- GSEB
- GSEB Syllabus
- GSEB4
- GSEB3 Образец статьи GSEB3
004 - MSBSHSE
- MSBSHSE Syllabus
- MSBSHSE Учебники
- Образцы статей MSBSHSE
- Вопросники MSBSHSE
- AP Board
- APSCERT
- APS4
- Syll
- AP
- Syll 9000SC4
- Syll
- AP 9000S4 9000 Syll
- Syll
- MP Board
- MP Board Syllabus
- MP Board Образцы документов
- Учебники MP Board
- Assam Board
- Assam Board Syllabus
- Assam Board Учебники 9000 9000 Board4 BSEB
- Bihar Board Syllabus
- Bihar Board Учебники
- Bihar Board Question Papers
- Bihar Board Model Papers
- BSE Odisha
- Odisha Board Syllabus
- Odisha Board Syllabus
- Программа PSEB
- Учебники ПОЭБ
Калькулятор множественной регрессии для 2 переменных-предикторов
Этот простой калькулятор множественной линейной регрессии использует метод наименьших квадратов, чтобы найти линию наилучшего соответствия для данных, содержащих два независимых значения X и одно зависимое значение Y , что позволяет оценить значение зависимой переменной ( Y ) от двух заданных независимых (или объясняющих) переменных ( X 1 и X 2 ).
Линия наилучшего соответствия описывается уравнением ŷ = b 1 X 1 + b 2 X 2 + a , где b 1 и b 2 — это коэффициенты, которые определяют наклон линии, а a — это точка пересечения (т. Е. Значение Y , когда X = 0). Этот калькулятор определит значения b 1 , b 2 и a для набора данных, состоящего из трех переменных, и оценит значение Y для любых заданных значений X 1. и X 2 .
Для начала вам необходимо добавить данные в три текстовых поля непосредственно ниже (либо по одному значению в строке, либо в виде списка, разделенного запятыми), с вашими независимыми переменными в двух полях значений X и вашей зависимой переменной в Y Поле значений. Например, если вы хотите создать линию, наиболее подходящую для связи между ростом, весом и размером обуви, позволяющую прогнозировать размер обуви на основе роста и веса человека, тогда рост и вес будут вашими независимыми переменными ( X 1 и X 1 ) и размер обуви вашей зависимой переменной ( Y ).
X1 Значения
X2 Значения
Y Значения
Этот калькулятор множественной регрессии может оценить значение зависимой переменной ( Y ) для заданных значений двух независимых переменных-предикторов ( X 1 и X 2 ).Просто добавьте значения X , для которых вы хотите создать оценку, в поля предиктора ниже (либо по одному значению в строке, либо в виде списка, разделенного запятыми).
Примечание : Если вы просто хотите сгенерировать уравнение регрессии, которое описывает линию наилучшего соответствия, оставьте поля ниже пустыми.
Предиктор X1
Предиктор X2
