Логарифм 0 чему равен – Логарифм 0 | Логарифмы

Логарифм 0 | Логарифмы

Когда логарифм равен 0?

Каким бы ни было основание логарифма, логарифм равен нулю в единственном случае — когда под знаком логарифма стоит единица.

Например,

   

   

   

   

Если логарифм, под знаком которого стоит выражение с переменной,  равен 0, то это выражение может быть равным только единице:

   

При этом дополнительно накладывать условие на выражение под знаком логарифма не нужно — поскольку оно равно единице, то оно автоматически больше нуля.

Если основание a — число, то область допустимых значений: x — любое число (x∈R).

Если a=a(x), то ОДЗ: a(x)>0, a(x)≠1.

Например,

   

ОДЗ: x∈R

   

   

   

Ответ: ±2.

   

ОДЗ:

   

Так как логарифм равен нулю, выражение, стоящее под знаком логарифма, равно единице:

   

   

   

ОДЗ удовлетворяет только 5.

Ответ: 5.

www.logarifmy.ru

Mathway | Популярные задачи

1	Найти производную — d/dx	квадратный корень x
2	Найти производную — d/dx	натуральный логарифм x
3	Вычислить	интеграл натурального логарифма x по x
4	Найти производную — d/dx	e^x
5	Вычислить	интеграл e^(2x) относительно x
6	Найти производную — d/dx	1/x
7	Найти производную — d/dx	x^2
8	Вычислить	интеграл e^(-x) относительно x
9	Найти производную — d/dx	1/(x^2)
10	Найти производную — d/dx	sin(x)^2
11	Найти производную — d/dx	sec(x)
12	Вычислить	интеграл e^x относительно x
13	Вычислить	интеграл x^2 относительно x
14	Вычислить	интеграл квадратного корня x по x
15	Вычислить	натуральный логарифм 1
16	Вычислить	e^0
17	Вычислить	sin(0)
18	Найти производную — d/dx	cos(x)^2
19	Вычислить	интеграл 1/x относительно x
20	Вычислить	cos(0)
21	Вычислить	интеграл sin(x)^2 относительно x
22	Найти производную — d/dx	x^3
23	Найти производную — d/dx	sec(x)^2
24	Найти производную — d/dx	1/(x^2)
25	Вычислить	интеграл arcsin(x) относительно x
26	Вычислить	интеграл cos(x)^2 относительно x
27	Вычислить	интеграл sec(x)^2 относительно x
28	Найти производную — d/dx	e^(x^2)
29	Вычислить	интеграл в пределах от 0 до 1 кубического корня 1+7x по x
30	Найти производную — d/dx	sin(2x)
31	Вычислить	интеграл натурального логарифма x по x
32	Найти производную — d/dx	tan(x)^2
33	Вычислить	интеграл e^(2x) относительно x
34	Вычислить	интеграл 1/(x^2) относительно x
35	Найти производную — d/dx	2^x
36	График	натуральный логарифм a
37	Вычислить	e^1
38	Вычислить	интеграл 1/(x^2) относительно x
39	Вычислить	натуральный логарифм 0
40	Найти производную — d/dx	cos(2x)
41	Найти производную — d/dx	xe^x
42	Вычислить	интеграл 1/x относительно x
43	Вычислить	интеграл 2x относительно x
44	Найти производную — d/dx	( натуральный логарифм x)^2
45	Найти производную — d/dx	натуральный логарифм (x)^2
46	Найти производную — d/dx	3x^2
47	Вычислить	натуральный логарифм 2
48	Вычислить	интеграл xe^(2x) относительно x
49	Найти производную — d/dx	2e^x
50	Найти производную — d/dx	натуральный логарифм 2x
51	Найти производную — d/dx	-sin(x)
52	Вычислить	tan(0)
53	Найти производную — d/dx	4x^2-x+5
54	Найти производную — d/dx	y=16 корень четвертой степени 4x^4+4
55	Найти производную — d/dx	2x^2
56	Вычислить	интеграл e^(3x) относительно x
57	Вычислить	интеграл cos(2x) относительно x
58	Вычислить	интеграл cos(x)^2 относительно x
59	Найти производную — d/dx	1/( квадратный корень x)
60	Вычислить	интеграл e^(x^2) относительно x
61	Вычислить	sec(0)
62	Вычислить	e^infinity
63	Вычислить	2^4
64	Найти производную — d/dx	x/2
65	Вычислить	4^3
66	Найти производную — d/dx	-cos(x)
67	Найти производную — d/dx	sin(3x)
68	Вычислить	натуральный логарифм 1/e
69	Вычислить	интеграл x^2 относительно x
70	Упростить	1/( кубический корень от x^4)
71	Найти производную — d/dx	1/(x^3)
72	Вычислить	интеграл e^x относительно x
73	Вычислить	интеграл tan(x)^2 относительно x
74	Вычислить	интеграл 1 относительно x
75	Найти производную — d/dx	x^x
76	Найти производную — d/dx	x натуральный логарифм x
77	Вычислить	интеграл sin(x)^2 относительно x
78	Найти производную — d/dx	x^4
79	Вычислить	предел (3x-5)/(x-3), если x стремится к 3
80	Вычислить	интеграл от x^2 натуральный логарифм x по x
81	Найти производную — d/dx	f(x) = square root of x
82	Найти производную — d/dx	x^2sin(x)
83	Вычислить	интеграл sin(2x) относительно x
84	Найти производную — d/dx	3e^x
85	Вычислить	интеграл xe^x относительно x
86	Найти производную — d/dx	y=x^2
87	Найти производную — d/dx	квадратный корень x^2+1
88	Найти производную — d/dx	sin(x^2)
89	Вычислить	интеграл e^(-2x) относительно x
90	Вычислить	интеграл натурального логарифма квадратного корня x по x
91	Вычислить	2^5
92	Найти производную — d/dx	e^2
93	Найти производную — d/dx	x^2+1
94	Вычислить	интеграл sin(x) относительно x
95	Вычислить	2^3
96	Найти производную — d/dx	arcsin(x)
97	Вычислить	предел (sin(x))/x, если x стремится к 0
98	Вычислить	e^2
99	Вычислить	интеграл e^(-x) относительно x
100	Вычислить	интеграл 1/x относительно x

www.mathway.com

Натуральные логарифмы чисел (Таблица)

I. Таблица натуральные логарифмы чисел ¹⁾

¹⁾Натуральный логарифм числа, не содержащегося среди аргументов таблицы, находится следующим образом. Пусть ищется ln 753. Имеем: ln 753 = ln (7,53 • 10²) = ln 7,53 4- 2 ln 10. Первое слагаемое находим по таблице натуральных логарифмов, второе — по таблице III. Получаем: ln 753 = 2,0189 + 4,6052 = 6,6241. Таким же образом находим ln 0,00753 = ln (7,53 • 10″³) = 2,0189 — 6,9078 = -4,8889.

N	0	1	2	3	4	5	6	7	8	9
1,0	0,0000	0,0100	0,0198	0,0296	0,0392	0,0488	0,0583	0,0677	0,0770	0,0862
1,1	0,0953	0,1044	0,1133	0,1222	0,1310	0,1398	0,1484	0,1570	0,1655	0,1740
1,2	0,1823	0,1906	0,1989	0,2070	0,2151	0,2231	0,2311	0,2390	0,2469	0,2546
1,3	0,2624	0,2700	0,2776	0,2852	0,2927	0,3001	0,3075	0,3148	0,3221	0,3293
1,4	0,3365	0,3436	0,3507	0,3577	0,3646	0,3716	0,3784	0,3853	0,3920	0,3988
1,5	0,4055	0,4121	0,4187	0,4253	0,4318	0,4383	0,4447	0,4511	0,4574	0,4637
1,6	0,4700	0,4762	0,4824	0,4886	0,4947	0,5008	0,5068	0,5128	0,5188	0,5247
1,7	0,5306	0,5365	0,5423	0,5481	0,5539	0,5596	0,5653	0,5710	0,5766	0,5822
1,8	0,5878	0,5933	0,5988	0,6043	0,6098	0,6152	0,6206	0,6259	0,6313	0,6366
1,9	0,6419	0,6471	0,6523	0,6575	0,6627	0,6678	0,6729	0,6780	0,6831	0,6881
2,0	0,6931	0,6981	0,7031	0,7080	0,7129	0,7178	0,7227	0,7275	0,7324	0,7372
2,1	0,7419	0,7467	0,7514	0,7561	0,7608	0,7655	0,7701	0,7747	0,7793	0,7839
2,2	0,7885	0,7930	0,7975	0,8020	0,8065	0,8109	0,8154	0,8198	0,8242	0,8286
2,3	0,8329	0,8372	0,8416	0,8459	0,8502	0,8544	0,8587	0,8629	0,8671	0,8713
2,4	0,8755	0,8796	0,8838	0,8879	0,8920	0,8961	0,9002	0,9042	0,9083	0,9123
2,5	0,9163	0,9203	0,9243	0,9282	0,9322	0,9361	0,9400	0,9439	0,9478	0,9517
2,6	0,9555	0,9594	0,9632	0,9670	0,9708	0,9746	0,9783	0,9821	0,9858	0,9895
2,7	0,9933	0,9969	1,0006	1,0043	1,0080	1,0116	1,0152	1,0188	1,0225	1,0260
2,8	1,0296	1,0332	1,0367	1,0403	1,0438	1,0473	1,0508	1,0543	1,0578	1,0613
2,9	1,0647	1,0682	1,0716	1,0750	1,0784	1,0818	1,0852	1,0886	1,0919	1,0953
3,0	1,0986	1,1019	1,1053	1,1086	1,1119	1,1151	1,1184	1,1217	1,1249	1,1282
3,1	1,1314	1,1346	1,1378	1,1410	1,1442	1,1474	1,1506	1,1537	1,1569	1,1600
3,2	1,1632	1,1663	1,1694	1,1725	1,1756	1,1787	1,1817	1,1848	1,1878	1,1909
3,3	1,1939	1,1969	1,2000	1,2030	1,2060	1,2090	1,2119	1,2149	1,2179	1,2208
3,4	1,2238	1,2267	1,2296	1,2326	1,2355	1,2384	1,2413	1,2442	1,2470	1,2499
3,5	1,2528	1,2556	1,2585	1,2613	1,2641	1,2669	1,2698	1,2726	1,2754	1,2782
3,6	1,2809	1,2837	1,2865	1,2892	1,2920	1,2947	1,2975	1,3002	1,3029	1,3056
3,7	1,3083	1,3110	1,3137	1,3164	1,3191	1,3218	1,3244	1,3271	1,3297	1,3324
3,8	1,3350	1,3376	1,3403	1,3429	1,3455	1,3481	1,3507	1,3533	1,3558	1,3584
3,9	1,3610	1,3635	1,3661	1,3686	1,3712	1,3737	1,3762	1,3788	1,3813	1,3838
4,0	1,3863	1,3888	1,3913	1,3938	1,3962	1,3987	1,4012	1,4036	1,4061	1,4085
4,1	1,4110	1,4134	1,4159	1,4183	1,4207	1,4231	1,4255	1,4279	1,4303	1,4327
4,2	1,4351	1,4375	1,4398	1,4422	1,4446	1,4469	1,4493	1,4516	1,4540	1,4563
4,3	1,4586	1,4609	1,4633	1,4656	1,4679	1,4702	1,4725	1,4748	1,4770	1,4793
4,4	1,4816	1,4839	1,4861	1,4884	1,4907	1,4929	1,4951	1,4974	1,4996	1,5019
4,5	1,5041	1,5063	1,5085	1,5107	1,5129	1,5151	1,5173	1,5195	1,5217	1,5239
4,6	1,5261	1,5282	1,5304	1,5326	1,5347	1,5369	1,5390	1,5412	1,5433	1,5454
4,7	1,5476	1,5497	1,5518	1,5539	1,5560	1,5581	1,5602	1,5623	1,5644	1,5665
4,8	1,5686	1,5707	1,5728	1,5748	1,5769	1,5790	1,5810	1,5831	1,5851	1,5872
4,9	1,5892	1,5913	1,5933	1,5953	1,5974	1,5994	1,6014	1,6034	1,6054	1,6074
5,0	1,6094	1,6114	1,6134	1,6154	1,6174	1,6194	1,6214	1,6233	1,6253	1,6273
5,1	1,6292	1,6312	1,6332	1,6351	1,6371	1,6390	1,6409	1,6429	1,6448	1,6467
5,2	1,6487	1,6506	1,6525	1,6544	1,6563	1,6582	1,6601	1,6620	1,6639	1,6658
5,3	1,6677	1,6696	1,6715	1,6734	1,6752	1,6771	1,6790	1,6808	1,6827	1,6845
5,4	1,6864	1,6882	1,6901	1,6919	1,6938	1,6956	1,6974	1,6993	1,7011	1,7029
5,5	1,7047	1,7066	1,7084	1,7102	1,7120	1,7138	1,7156	1,7174	1,7192	1,7210
5,6	1,7228	1,7246	1,7263	1,7281	1,7299	1,7317	1,7334	1,7352	1,7370	1,7387
5,7	1,7405	1,7422	1,7440	1,7457	1,7475	1,7492	1,7509	1,7527	1,7544	1,7561
5,8	1,7579	1,7596	1,7613	1,7630	1,7647	1,7664	1,7681	1,7699	1,7716	1,7733
5,9	1,7750	1,7766	1,7783	1,7800	1,7817	1,7834	1,7851	1,7867	1,7884	1,7901
6,0	1,7918	1,7934	1,7951	1,7967	1,7984	1,8001	1,8017	1,8034	1,8050	1,8066
6,1	1,8083	1,8099	1,8116	1,8132	1,8148	1,8165	1,8181	1,8197	1,8213	1,8229
6,2	1,8245	1,8262	1,8278	1,8294	1,8310	1,8326	1,8342	1,8358	1,8374	1,8390
6,3	1,8405	1,8421	1,8437	1,8453	1,8469	1,8485	1,8500	1,8516	1,8532	1,8547
6,4	1,8563	1,8579	1,8594	1,8610	1,8625	1,8641	1,8656	1,8672	1,8687	1,8703
6,5	1,8718	1,8733	1,8749	1,8764	1,8779	1,8795	1,8810	1,8825	1,8840	1,8856
6,6	1,8871	1,8886	1,8901	1,8916	1,8931	1,8946	1,8961	1,8976	1,8991	1,9006
6,7	1,9021	1,9036	1,9051	1,9066	1,9081	1,9095	1,9110	1,9125	1,9140	1,9155
6,8	1,9169	1,9184	1,9199	1,9213	1,9228	1,9242	1,9257	1,9272	1,9286	1,9301
6,9	1,9315	1,9330	1,9344	1,9359	1,9373	1,9387	1,9402	1,9416	1,9430	1,9445
7,0	1,9459	1,9473	1,9488	1,9502	1,9516	1,9530	1,9544	1,9559	1,9573	1,9587
7,1	1,9601	1,9615	1,9629	1,9643	1,9657	1,9671	1,9685	1,9699	1,9713	1,9727
7,2	1,9741	1,9755	1,9769	1,9782	1,9796	1,9810	1,9824	1,9838	1,9851	1,9865
7,3	1,9879	1,9892	1,9906	1,9920	1,9933	1,9947	1,9961	1,9974	1,9988	2,0001
7,4	2,0015	2,0028	2,0042	2,0055	2,0069	2,0082	2,0096	2,0109	2,0122	2,0136
7,5	2,0149	2,0162	2,0176	2,0189	2,0202	2,0215	2,0229	2,0242	2,0255	2,0268
7,6	2,0281	2,0295	2,0308	2,0321	2,0334	2,0347	2,0360	2,0373	2,0386	2,0399
7,7	2,0412	2,0425	2,0438	2,0451	2,0464	2,0477	2,0490	2,0503	2,0516	2,0528
7,8	2,0541	2,0554	2,0567	2,0580	2,0592	2,0605	2,0618	2,0631	2,0643	2,0656
7,9	2,0669	2,0681	2,0694	2,0707	2,0719	2,0732	2,0744	2,0757	2,0769	2,0782
8,0	2,0794	2,0807	2,0819	2,0832	2,0844	2,0857	2,0869	2,0882	2,0894	2,0906
8,1	2,0919	2,0931	2,0943	2,0956	2,0968	2,0980	2,0992	2,1005	2,1017	2,1029
8,2	2,1041	2,1054	2,1066	2,1078	2,1090	2,1102	2,1114	2,1126	2,1138	2,1150
8,3	2,1163	2,1175	2,1187	2,1199	2,1211	2,1223	2,1235	2,1247	2,1258	2,1270
8,4	2,1282	2,1294	2,1306	2,1318	2,1330	2,1342	2,1353	2,1365	2,1377	2,1389
8,5	2,1401	2,1412	2,1424	2,1436	2,1448	2,1459	2,1471	2,1483	2,1494	2,1506
8,6	2,1518	2,1529	2,1541	2,1552	2,1564	2,1576	2,1587	2,1599	2,1610	2,1622
8,7	2,1633	2,1645	2,1656	2,1668	2,1679	2,1691	2,1702	2,1713	2,1725	2,1736
8,8	2,1748	2,1759	2,1770	2,1782	2,1793	2,1804	2,1815	2,1827	2,1838	2,1849
8,9	2,1861	2,1872	2,1883	2,1894	2,1905	2,1917	2,1928	2,1939	2,1950	2,1961
9,0	2,1972	2,1983	2,1994	2,2006	2,2017	2,2028	2,2039	2,2050	2,2061	2,2072
9,1	2,2083	2,2094	2,2105	2,2116	2,2127	2,2138	2,2148	2,2159	2,2170	2,2181
9,2	2,2192	2,2203	2,2214	2,2225	2,2235	2,2246	2,2257	2,2268	2,2279	2,2289
9,3	2,2300	2,2311	2,2322	2,2332	2,2343	2,2354	2,2364	2,2375	2,2386	2,2396
9,4	2,2407	2,2418	2,2428	2,2439	2,2450	2,2460	2,2471	2,2481	2,2492	2,2502
9,5	2,2513	2,2523	2,2534	2,2544	2,2555	2,2565	2,2576	2,2586	2,2597	2,2607
9,6	2,2618	2,2628	2,2638	2,2649	2,2659	2,2670	2,2680	2,2690	2,2701	2,2711
9,7	2,2721	2,2732	2,2742	2,2752	2,2762	2,2773	2,2783	2,2793	2,2803	2,2814
9,8	2,2824	2,2834	2,2844	2,2854	2,2865	2,2875	2,2885	2,2895	2,2905	2,2915
9,9	2,2925	2,2935	2,2946	2,2956	2,2966	2,2976	2,2986	2,2996	2,3006	2,3016

II. Таблица для перехода от натуральных логарифмов к десятичным 

(таблица умножения на М = log е = 0,4342945…)

	0	10	20	30	40	50	60	70	80	90
0	0,0000	4,3430	8,6859	13,0288	17,3718	21,7147	26,0577	30,4006	34,7436	39,0865
1	0,4343	4,7772	9,1202	13,4631	17,8061	22,1490	26,4920	30,8349	35,1779	39,5208
2	0,8686	5,2115	9,5545	13,8974	18,2404	22,5833	26,9263	31,2692	35,6122	39,9551
3	1,3029	5,6458	9,9888	14,3317	18,6747	23,0176	27,3606	31,7035	36,0464	40,3894
4	1,7372	6,0801	10,4231	14,7660	19,1090	23,4519	27,7948	32,1378	36,4807	40,8237
5	2,1715	6,5144	10,8574	15,2003	19,5433	23,8862	28,2291	32,5721	36,9150	41,2580
6	2,6058	6,9487	11,2917	15,6346	19,9775	24,3205	28,6634	33,0064	37,3493	41,6923
7	3,0401	7,3830	11,7260	16,0689	20,4118	24,7548	29,0977	33,4407	37,7836	42,1266
8	3,4744	7,8173	12,1602	16,5032	20,8461	25,1891	29,5320	33,8750	38,2179	42,5609
9	3,9086	8.2516	12,5945	16,9375	21,2804	25,6234	29,9663	34,3093	38,6522	42,9952

 

III. Таблица для перехода от десятичных логарифмов к натуральным

(таблица умножения на i = In 10 = 2,302585)

	0	10	20	30	40	50	60	70	80	90
0	0,0000	23,026	46,052	69,078	92,103	115,129	138,155	161,181	184,207	207,233
1	2,3026	25,328	48,354	71,380	94,406	117,431	140,458	163,484	186,509	209,535
2	4,6052	27,631	50,657	73,683	96,709	119,734	142,760	165,786	188,812	211,838
3	6,9078	29,934	52,959	75,985	99,011	122,037	145,062	166,089	191,115	214,140
4	9,2103	32,236	55,262	78,288	101,314	124,340	147,365	170,391	193,417	216,443
5	11,513	34,539	57,565	80,590	103,616	126,642	149,668	172,694	195,720	218,746
6	13,816	36,841	59,867	82,893	105,919	128,945	151,971	174,997	198,022	221,048
7	16,118	39,144	62,170	85,196	108,221	131,247	154,273	177,299	200,325	223,351
8	18,421	41,447	64,472	87,498	110,524	133,550	156,576	179,602	202,627	225,653
9	20,723	43,749	66,775	89,801	112,827	135,853	158,878	181,904	204,930	227,956

_______________

Источник информации: Справочник по высшей математике / М. Я. Выгодский. — М.: ACT: Астрель, 2006.

infotables.ru

Логарифм. Как вычислить логарифм?

Логарифмом положительного числа \(c\) по основанию \(a\) \((a>0, a\neq1)\) называется показатель степени \(b\), в которую надо возвести основание \(a\), чтобы получить число \(c\) \((c>0)\), т.е.

\(a^{b}=c\)       \(\Leftrightarrow\)       \(\log_{a}{c}=b\)

Объясним проще. Например, \(\log_{2}{8}\) равен степени, в которую надо возвести \(2\), чтоб получить \(8\). Отсюда понятно, что \(\log_{2}{8}=3\).

Примеры:		\(\log_{5}{25}=2\)		т.к. \(5^{2}=25\)
		\(\log_{3}{81}=4\)		т.к. \(3^{4}=81\)
		\(\log_{2}\)\(\frac{1}{32}\)\(=-5\)		т.к. \(2^{-5}=\)\(\frac{1}{32}\)

Аргумент и основание логарифма

Любой логарифм имеет следующую «анатомию»:

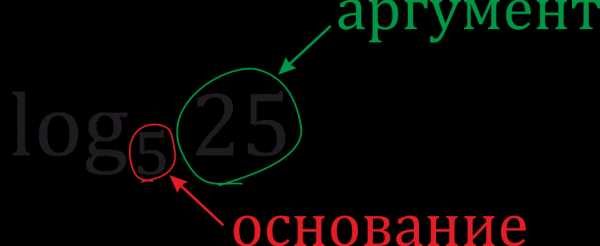
Аргумент логарифма обычно пишется на его уровне, а основание — подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».

Как вычислить логарифм?

Чтобы вычислить логарифм — нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?

Например, вычислите логарифм:  а) \(\log_{4}{16}\)     б) \(\log_{3}\)\(\frac{1}{3}\)     в) \(\log_{\sqrt{5}}{1}\)     г) \(\log_{\sqrt{7}}{\sqrt{7}}\)      д) \(\log_{3}{\sqrt{3}}\)

а) В какую степень надо возвести \(4\), чтобы получить \(16\)? Очевидно во вторую. Поэтому: 

\(\log_{4}{16}=2\)

б) В какую степень надо возвести \(3\), чтобы получить \(\frac{1}{3}\)? В минус первую, так как именно отрицательная степень «переворачивает дробь» (здесь и далее пользуемся свойствами степени).

\(\log_{3}\)\(\frac{1}{3}\)\(=-1\)

в) В какую степень надо возвести \(\sqrt{5}\), чтобы получить \(1\)? А какая степень делает любое число единицей? Ноль, конечно!

\(\log_{\sqrt{5}}{1}=0\)

г) В какую степень надо возвести \(\sqrt{7}\), чтобы получить \(\sqrt{7}\)? В первую – любое число в первой степени равно самому себе.

\(\log_{\sqrt{7}}{\sqrt{7}}=1\)

д) В какую степень надо возвести \(3\), чтобы получить \(\sqrt{3}\)? Из свойств степени мы знаем, что корень – это дробная степень, и значит квадратный корень — это степень \(\frac{1}{2}\).

\(\log_{3}{\sqrt{3}}=\)\(\frac{1}{2}\)

Пример: Вычислить логарифм \(\log_{4\sqrt{2}}{8}\)

Решение:

\(\log_{4\sqrt{2}}{8}=x\)		Нам надо найти значение логарифма, обозначим его за икс. Теперь воспользуемся определением логарифма: \(\log_{a}{c}=b\)       \(\Leftrightarrow\)       \(a^{b}=c\)
\((4\sqrt{2})^{x}=8\)		Что связывает \(4\sqrt{2}\) и \(8\)? Двойка, потому что и то, и другое число можно представить степенью двойки: \(4=2^{2}\)         \(\sqrt{2}=2^{\frac{1}{2}}\)         \(8=2^{3}\)
\({(2^{2}\cdot2^{\frac{1}{2}})}^{x}=2^{3}\)		Слева воспользуемся свойствами степени: \(a^{m}\cdot a^{n}=a^{m+n}\) и \((a^{m})^{n}=a^{m\cdot n}\)
\(2^{\frac{5}{2}x}=2^{3}\)		Основания равны, переходим к равенству показателей
\(\frac{5x}{2}\)\(=3\)		Умножим обе части уравнения на \(\frac{2}{5}\)
\(x=1,2\)		Получившийся корень и есть значение логарифма

Ответ: \(\log_{4\sqrt{2}}{8}=1,2\)

Зачем придумали логарифм?

Чтобы это понять, давайте решим уравнение: \(3^{x}=9\). Просто подберите \(x\), чтобы равенство сработало. Конечно, \(x=2\).

А теперь решите уравнение: \(3^{x}=8\).Чему равен икс? Вот в том-то и дело.

Самые догадливые скажут: «икс чуть меньше двух». А как точно записать это число? Для ответа на этот вопрос и придумали логарифм. Благодаря ему, ответ здесь можно записать как \(x=\log_{3}{8}\).

Хочу подчеркнуть, что \(\log_{3}{8}\), как и любой логарифм — это просто число. Да, выглядит непривычно, но зато коротко. Потому что, если бы мы захотели записать его в виде десятичной дроби, то оно выглядело бы вот так: \(1,892789260714…..\)

Пример: Решите уравнение \(4^{5x-4}=10\)

Решение:

\(4^{5x-4}=10\)		\(4^{5x-4}\) и \(10\) никак к одному основанию не привести. Значит тут не обойтись без логарифма. Воспользуемся определением логарифма: \(a^{b}=c\)       \(\Leftrightarrow\)       \(\log_{a}{c}=b\)
\(\log_{4}{10}=5x-4\)		Зеркально перевернем уравнение, чтобы икс был слева
\(5x-4=\log_{4}{10}\)		Перед нами линейное уравнение. Перенесем \(4\) вправо. И не пугайтесь логарифма, относитесь к нему как к обычному числу.
\(5x=\log_{4}{10}+4\)		Поделим уравнение на 5
\(x=\)\(\frac{\log_{4}{10}+4}{5}\)		Вот наш корень. Да, выглядит непривычно, но ответ не выбирают.

Ответ: \(\frac{\log_{4}{10}+4}{5}\)

Десятичный и натуральный логарифмы

Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы \((a>0, a\neq1)\). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:

Натуральный логарифм: логарифм, у которого основание — число Эйлера \(e\) (равное примерно \(2,7182818…\)), и записывается такой логарифм как \(\ln{a}\).

То есть, \(\ln{a}\) это то же самое, что и \(\log_{e}{a}\), где \(a\) — некоторое число.

Десятичный логарифм: логарифм, у которого основание равно 10, записывается \(\lg{a}\).

То есть, \(\lg{a}\) это то же самое, что и \(\log_{10}{a}\), где \(a\) — некоторое число.

Основное логарифмическое тождество

У логарифмов есть множество свойств. Одно из них носит название «Основное логарифмическое тождество» и выглядит вот так:

\(a^{\log_{a}{c}}=c\)

Это свойство вытекает напрямую из определения. Посмотрим как именно эта формула появилась.

Вспомним краткую запись определения логарифма:

если     \(a^{b}=c\),    то   \(\log_{a}{c}=b\)

То есть, \(b\) – это тоже самое, что \(\log_{a}{c}\). Тогда мы можем в формуле \(a^{b}=c\) написать \(\log_{a}{c}\) вместо \(b\). Получилось \(a^{\log_{a}{c}}=c\) – основное логарифмическое тождество.

Остальные свойства логарифмов вы можете найти здесь. С их помощью можно упрощать и вычислять значения выражений с логарифмами, которые «в лоб» посчитать сложно.

Пример: Найдите значение выражения \(36^{\log_{6}{5}}\)

Решение:

\(36^{\log_{6}{5}}=\)		Сразу пользоваться свойством \(a^{\log_{a}{c}}=c\) мы не можем, так как в основании степени и в основании логарифма – разные числа. Однако мы знаем, что \(36=6^{2}\)
\(=(6^{2})^{\log_{6}{5}}=\)		Зная формулу \((a^{m})^{n}=a^{m\cdot n}\), а так же то, что множители можно менять местами, преобразовываем выражение
\(=6^{2\cdot\log_{6}{5}}=6^{log_{6}{5}\cdot2}=(6^{log_{6}{5}})^{2}=\)		Вот теперь спокойно пользуемся основным логарифмическим тождеством.
\(=5^{2}=25\)		Ответ готов.

Ответ: \(25\)

Как число записать в виде логарифма?

Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что \(\log_{2}{4}\) равен двум. Тогда можно вместо двойки писать \(\log_{2}{4}\). 

Но \(\log_{3}{9}\) тоже равен \(2\), значит, также можно записать \(2=\log_{3}{9}\)  . Аналогично и с \(\log_{5}{25}\), и с \(\log_{9}{81}\), и т.д. То есть, получается  

\(2=\log_{2}{4}=\log_{3}{9}=\log_{4}{16}=\log_{5}{25}=\log_{6}{36}=\log_{7}{49}…\)

Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.

Точно также и с тройкой – ее можно записать как \(\log_{2}{8}\), или как \(\log_{3}{27}\), или как \(\log_{4}{64}\)… Здесь мы как аргумент пишем основание в кубе:

\(3=\log_{2}{8}=\log_{3}{27}=\log_{4}{64}=\log_{5}{125}=\log_{6}{216}=\log_{7}{343}…\)

И с четверкой:

\(4=\log_{2}{16}=\log_{3}{81}=\log_{4}{256}=\log_{5}{625}=\log_{6}{1296}=\log_{7}{2401}…\)

И с минус единицей:

\(-1=\) \(\log_{2}\)\(\frac{1}{2}\)\(=\) \(\log_{3}\)\(\frac{1}{3}\)\(=\) \(\log_{4}\)\(\frac{1}{4}\)\(=\) \(\log_{5}\)\(\frac{1}{5}\)\(=\) \(\log_{6}\)\(\frac{1}{6}\)\(=\) \(\log_{7}\)\(\frac{1}{7}\)\(…\)

И с одной третьей:

\(\frac{1}{3}\)\(=\log_{2}{\sqrt[3]{2}}=\log_{3}{\sqrt[3]{3}}=\log_{4}{\sqrt[3]{4}}=\log_{5}{\sqrt[3]{5}}=\log_{6}{\sqrt[3]{6}}=\log_{7}{\sqrt[3]{7}}…\)

И так далее.

Любое число \(a\) может быть представлено как логарифм с основанием \(b\):       \(a=\log_{b}{b^{a}}\)

Пример: Найдите значение выражения \(\frac{\log_{2}{14}}{1+\log_{2}{7}}\)

Решение:

\(\frac{\log_{2}{14}}{1+\log_{2}{7}}\)\(=\)		Превращаем единицу в логарифм с основанием \(2\): \(1=\log_{2}{2}\)
\(=\)\(\frac{\log_{2}{14}}{\log_{2}{2}+\log_{2}{7}}\)\(=\)		Теперь пользуемся свойством логарифмов: \(\log_{a}{b}+\log_{a}{c}=\log_{a}{(bc)}\)
\(=\)\(\frac{\log_{2}{14}}{\log_{2}{(2\cdot7)}}\)\(=\)\(\frac{\log_{2}{14}}{\log_{2}{14}}\)\(=\)		В числителе и знаменателе одинаковые числа – их можно сократить.
\(=1\)		Ответ готов.

Ответ: \(1\)

Смотрите также:
Логарифмические уравнения
Логарифмические неравенства

cos-cos.ru

Логарифм больше нуля | Логарифмы

Когда логарифм больше нуля?

Это зависит от основания логарифма и от числа, стоящего под знаком логарифма.

Если основание логарифмической функции

   

— число, большее единицы, то функция принимает положительные значения при x>1:

   

Если в основании стоит число, меньшее единицы (положительное), то функция принимает положительные значения при 0<x<1:

   

То есть, логарифм больше нуля, если число под знаком логарифма и число в основании логарифма оба больше единицы или оба меньше единицы (но больше нуля).

Например,

   

   

   

   

   

   

Соответственно, десятичный логарифм больше нуля при x>1.

Например,

   

   

Натуральный логарифм также принимает положительные значения при x>1.

Например,

   

   

Логарифм единицы по любому основанию равен нулю.

www.logarifmy.ru

Логарифм 1 | Логарифмы

Нулевая степень любого положительного числа равна единице:

   

 Из определения логарифма следует, что логарифм единицы по любому основанию равен нулю.

Таким образом, натуральный логарифм 1, десятичный логарифм 1 и логарифм по любому другому основанию равен нулю:

   

   

   

Например,

   

   

   

Как другие свойства логарифмов, это свойство является тождеством.

В ходе решения логарифмических уравнений и неравенств часто требуется некоторое число представить в виде логарифма по определенному основанию.

Нуль может быть заменён на логарифм 1 с нужным основанием:

   

Например,

   

   

   

Логарифм 1 также можно использовать при определении знака логарифма. Как это сделать, рассмотрим позже.

 

www.logarifmy.ru

Десятичные логарифмы | Справочник по математике

В дальнейшем десятичный логарифм именуется просто логарифмом.

Логарифм единицы равен нулю.

Логарифмы чисел 10, 100, 1000 и т.д. равны 1,2,3 и т.д., т.е. имеют столько положительных единиц, сколько нулей стоит после единицы.

Логарифмы чисел 0,1; 0,01; 0,001 и т.д. равны -1, -2, -3 и т.д., т.е. имеют столько отрицательных единиц, сколько нулей стоит перед единицей (считая и нуль целых).

Логарифмы остальных чисел имеют дробную часть, именуемую мантиссой. Целая часть логарифма называется характеристикой.

Числа, большие единицы, имеют положительные логарифмы. Положительные числа, меньшие единицы¹, имеют отрицательные логарифмы.

Например², lg0,5=-0,30103, lg0,005=-2,30103.

Отрицательные логарифмы для большего удобства нахождения логарифма по числу и числа по логарифму представляются не в вышеприведенной «естественной» форме, а в «искусственной«. Отрицательный логарифм в искусственной форме имеет положительную мантиссу и отрицательную характеристику.

Например, lg0,005=3,69897. Эта запись означает, что lg0,005=-3+0,69897=-2,30103.

Чтобы перевести отрицательный логарифм из естественной формы в искусственную, нужно:

1. На единицу увеличить абсолютную величину его характеристики;
2. Полученное число снабдить знаком минус сверху;
3. Все цифры мантиссы, кроме последней из цифр, не равных нулю, вычитать из девяти; последнюю, не равную нулю цифру вычитать из десяти. Получаемые разности записываются на тех же местах мантиссы, где стояли вычитаемые цифры. Нули на конце остаются нетронутыми.

Пример 1. lg0,05=-1,30103 привести к искусственной форме:
1. Абсолютную величину характеристики 1 увеличиваем на 1; получаем 2;
2. Пишем характеристику искусственной формы в виде 2 и отделяем ее запятой;
3. Вычитаем первую цифру мантиссы 3 из 9; получаем 6; записываем 6 на первом месте после запятой. Таким же образом на следующих местах появляются цифры 9(=9-0), 8(=9-1), 9(=9-0) и 7(=10-3).
В результате получаем:

-1,30103=2,69897.

Пример 2. -0,18350 представить в искусственной форме:
1. Увеличиваем 0 на 1, получаем 1;
2. Имеем 1;
3. Вычитаем цифры 1,8,3 из 9; цифру 5 из 10; нуль на конце остается не тронутым.
В результате получаем:

-0,18350=1,81650.

Чтобы перевести отрицательный логарифм из искусственной формы в естественную, нужно:
1. На единицу уменьшить абсолютную величину его характеристики;
2. Полученное число снабдить знаком минус слева;
3. С цифрами мантиссы поступать, как в случае перехода от естественной формы к искусственной.

Пример 3. 4,689 00 представить в естественной форме:
1. 4-1=3;
2. Имеем -3;
3. Вычитаем цифры из мантиссы 6,8 и 9; цифру 9 из 10; два нуля остаются не тронутыми.
В результате получаем:

4,689 00=-3,311 00.

¹Отрицательные числа вовсе не имеют действительных логарифмов.
²Все дальнейшие равенства — приближенные с точностью до половины единицы последнего выписанного знака.

totangens.ru