Курс лекций (часть вторая «Интегральное исчисление функции одной переменной»), страница 14
Причем, если хотя бы один из интегралов, стоящих в правой части последнего равенства расходится, то расходится и интеграл, стоящий в левой части.
{ — неограниченна в точках и }
, .
Причем, если хотя бы один из интегралов, стоящих в правой части последнего равенства расходится, то расходится и интеграл, стоящий в левой части.
Примеры:
1. Исследовать на сходимость интеграл .
Решение
.
Интеграл сходится.
2. Исследовать на сходимость интеграл .
Решение
{подынтегральная функция в т. неограниченна}
.
Интеграл сходится.
3. Исследовать на сходимость интеграл .
Решение
Интеграл сходится.
4. Исследовать на сходимость интеграл .
Решение
;
;
.
Интеграл расходится.
5. Основной пример
5. 1. При каких интеграл сходится?
Решение
.
Имеем:
.
5. 2. При каких интеграл сходится?
Решение
.
Имеем:
.
5. 3. Аналогично можно показать:
,
.
3.1. Критерий Коши сходимости несобственных интегралов
Теорема: Пусть функция определена на промежутке , и интегрируема по Риману на
, . Для того чтобы несобственный интеграл сходился, необходимо и достаточно, чтобы.
Доказательство:
Рассмотрим функцию , . Для того чтобы эта функция имела предел при , необходимо и достаточно, чтобы
,
(критерий Коши существования предела функции).
Но
.
.
А .
3.2. Признаки сходимости несобственных интегралов
3.2.1. Сходимость интегралов
от неотрицательных функций
Теорема: Пусть функция неотрицательна на промежутке , и интегрируема на любом отрезке , . Для того чтобы сходился, необходимо и достаточно, чтобы функция была ограниченна сверху на . В случае выполнения этого условия
Доказательство:
Рассмотрим функцию , . В силу того, что , функция не убывает.
В самом деле, если , то
.
Несобственный интеграл сходится, тогда и только тогда, когда существует конечный предел
,
а последний существует тогда и только тогда, когда функция ограничена сверху, (из теоремы о пределе монотонной функции) и при этом
.
Признак сравнения
Теорема: Пусть функции и неотрицательны на и интегрируемы на любом отрезке , . Пусть (в частности).
Тогда:
1) если — сходится, то сходится и ;
2) если — расходится, то расходится и .
Доказательство:
1) Пусть — сходится, тогда по доказанной выше теореме , .
Из следует, что выполняется неравенство . Из следует, что .
Следовательно, .
По доказанной выше теореме , а, следовательно, и — сходятся.
2) Если — расходится, то очевидно расходится и интеграл , так как в противном случае по доказанному — сходился бы.
Следствие: (предельная форма признака сравнения)
Пусть функции и неотрицательны на и интегрируемы на любом отрезке , , и существует .
Тогда:
1) Если , то из сходимости следует сходимость .
2) Если , то из расходимости следует расходимость .
В частности если — число отличное от нуля, то интегралы и — сходятся или расходятся одновременно.
Доказательство:
1) Пусть . Тогда из , т.е. . Это означает, что , и утверждение 1) следствия следует из 1) признака сравнения.
2) Пусть
Примеры:
1. Исследовать на сходимость интеграл .
Решение
сравним с .
Известно, что сходится при и расходится при .
— сходится т.к. .
Поскольку , то по следствию из признака сравнения
— сходится.
2. Исследовать на сходимость интеграл .
Решение
сравним с .
Известно, что сходится при и расходится при .
— сходится, т.к. .
Поскольку , то по следствию из признака сравнения — сходится.
3. Определить, при каких интеграл сходится, а при каких — расходится.
Решение
vunivere.ru
8.8. Исследование сходимости несобственных интегралов с помощью признаков сравнения
Сформулируем без доказательства теоремы, позволяющие, не находя первообразной, сделать заключение о сходимости или расходимости несобственного интеграла.
ТЕОРЕМА (признак сравнения сходимости несобственных интегралов).
Пусть неотрицательные функции непрерывны, кроме того,. Тогда
если сходится
 ,
то сходится и
,
то сходится и ;
;если расходится
 ,
то расходится и
,
то расходится и .
.
Геометрический
смысл этой теоремы ясен из рис. 33:
сходимость несобственного интеграла 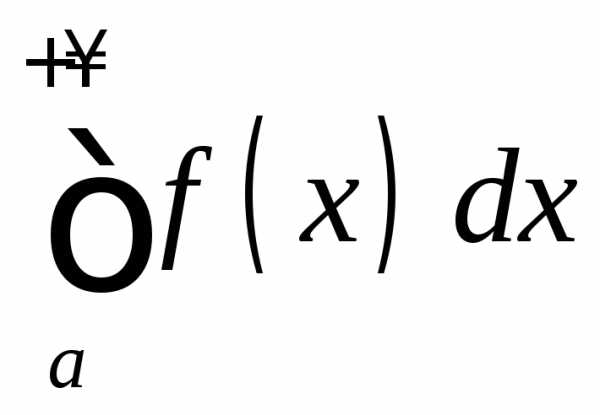 означает, что площадь неограниченной
области между графиком функции
означает, что площадь неограниченной
области между графиком функции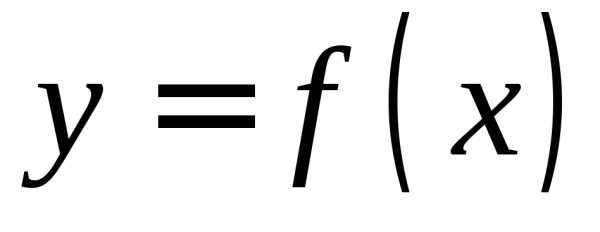 и осью
и осью конечна, поэтому, если большая
площадь конечна, то меньшая конечна и
подавно. Также, если меньшая площадь
бесконечна, то большая
бесконечна тоже.
конечна, поэтому, если большая
площадь конечна, то меньшая конечна и
подавно. Также, если меньшая площадь
бесконечна, то большая
бесконечна тоже.
В качестве интеграла,
с которым сравнивается исследуемый
несобственный интеграл, часто выбирают 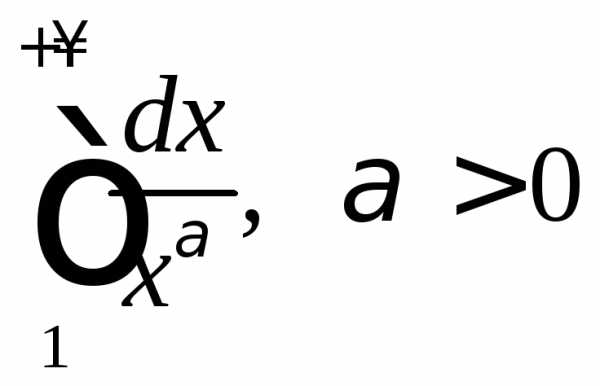 .
.
ПРИМЕР. Исследовать на сходимость несобственный интеграл
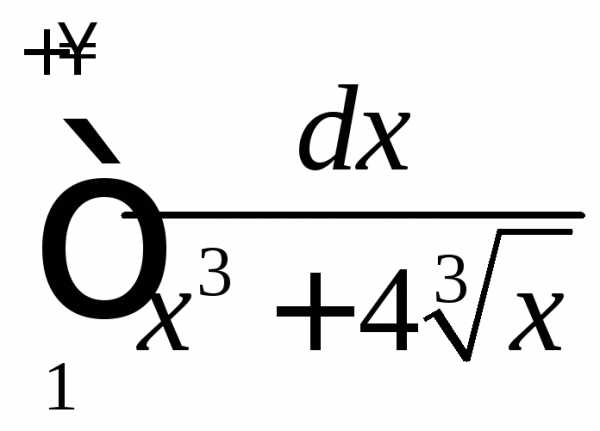
Очевидно, что
и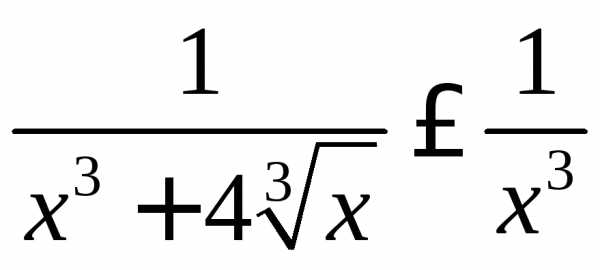 ,
при этом
,
при этом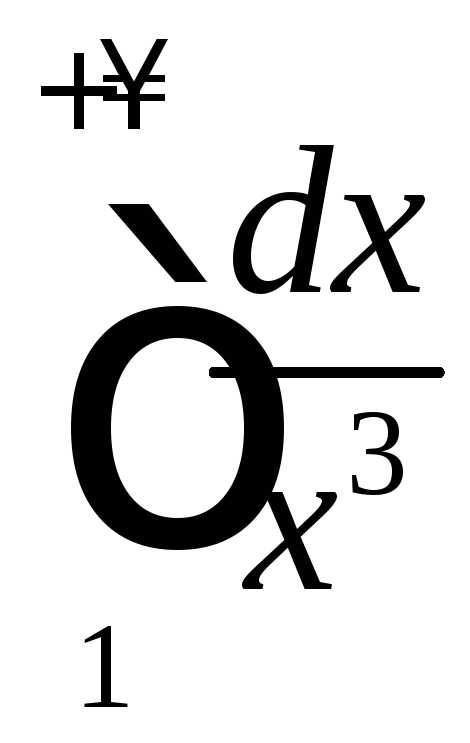 сходится: см. (8.12) при
сходится: см. (8.12) при .
Таким образом, больший интеграл
.
Таким образом, больший интеграл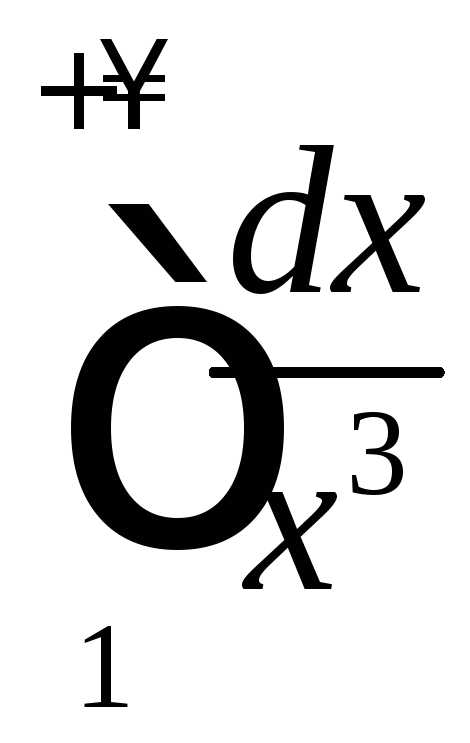 сходится, значит, меньший
сходится, значит, меньший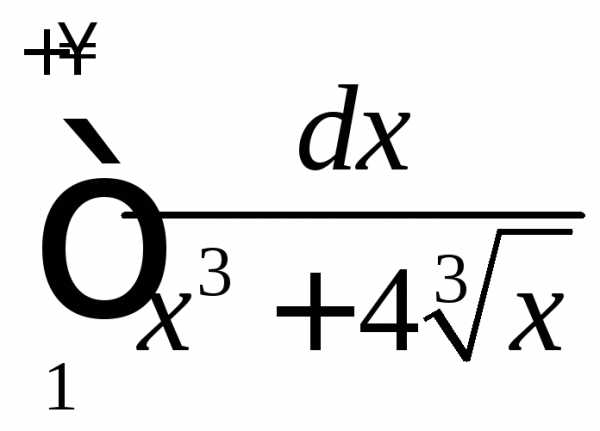 по признаку сравнения тоже сходится.
по признаку сравнения тоже сходится.
Однако, для данной подынтегральной функции справедлива и такая оценка:
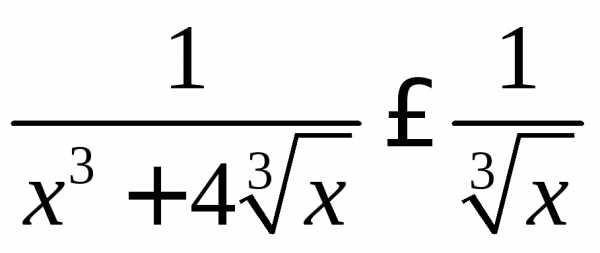 на промежутке
на промежутке 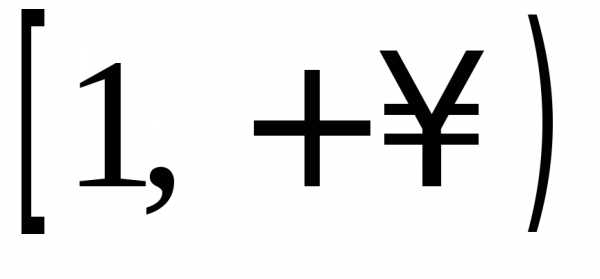 ,
причём
,
причём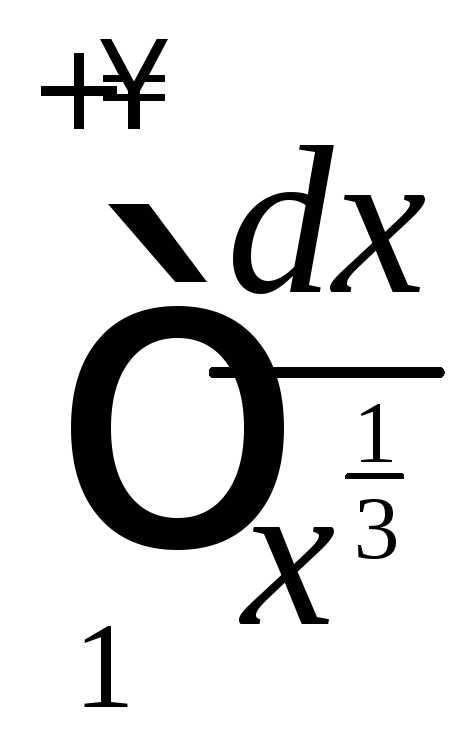 расходится ((8.12),
расходится ((8.12),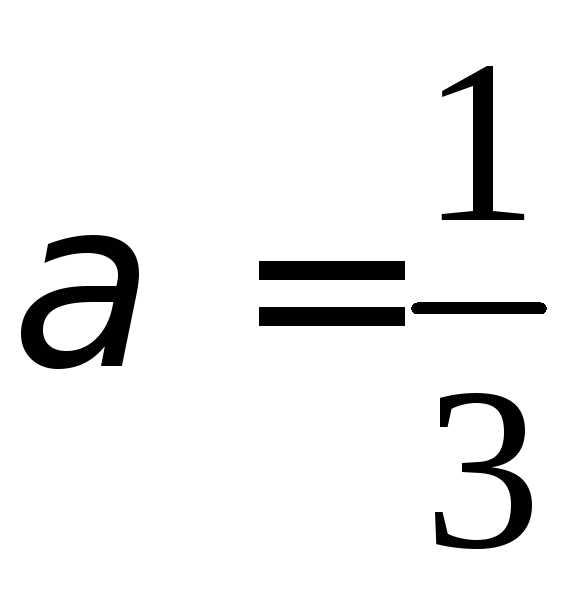
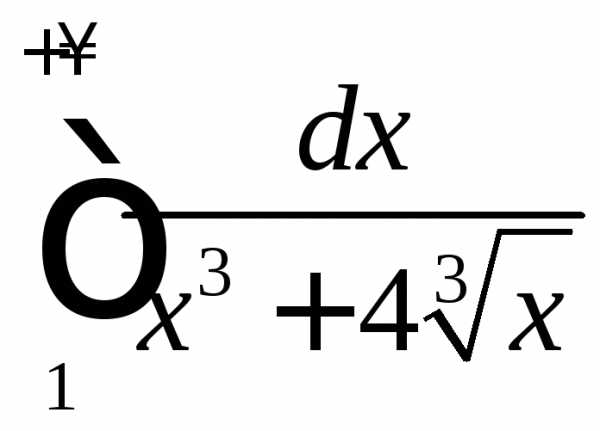 :
если больший интеграл
:
если больший интеграл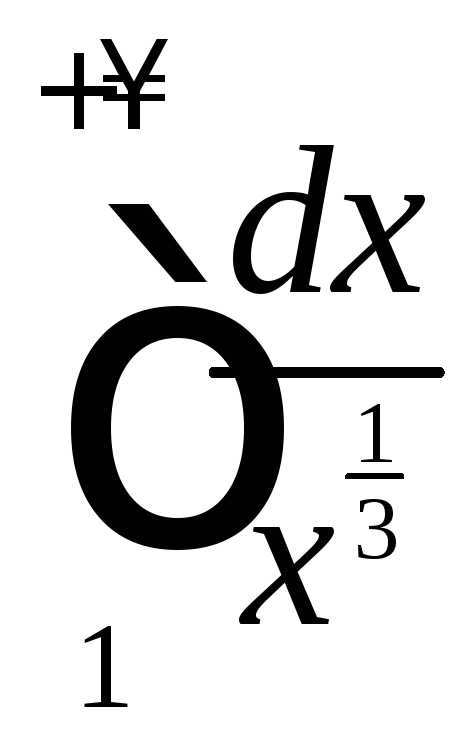 расходится, то меньший, может быть и
сходящимся, и расходящимся.
расходится, то меньший, может быть и
сходящимся, и расходящимся.Это означает, что при исследовании поведения несобственного интеграла с помощью признака сравнения важно правильно сделать оценку подынтегральной функции и правильно выбрать функцию для сравнения.
Часто это бывает сделать не очень просто. Поэтому во многих случаях удобней пользоваться другой теоремой.
ТЕОРЕМА (предельный признак сравнения сходимости
несобственных интегралов). Пусть неотрицательные функции
непрерывныи существуетконечный 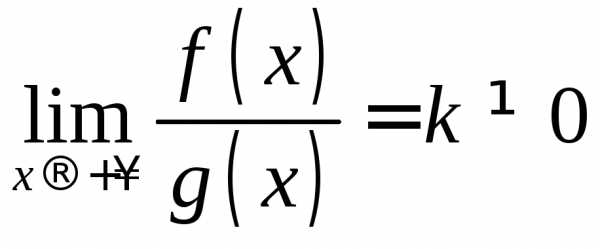 .
Тогда несобственные интегралы
.
Тогда несобственные интегралы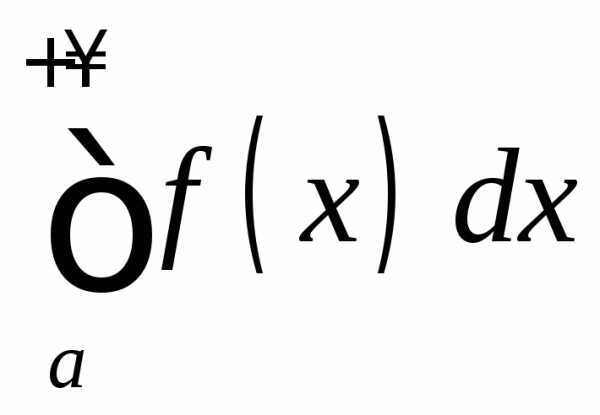
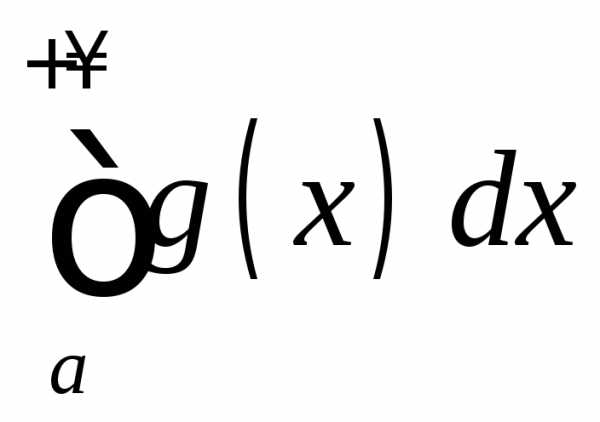 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.ПРИМЕР. Исследовать на сходимость несобственный интеграл
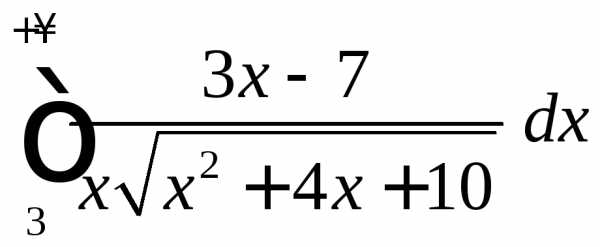 .
.
По условию
.
Выберем функцию для сравнения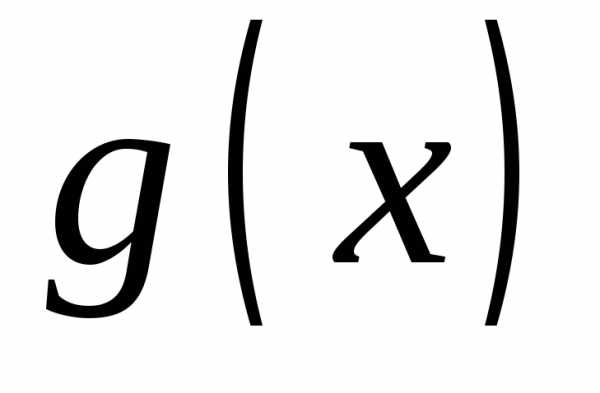 :
так как,
то отбросим в числителе и знаменателе
этой дроби слагаемые, несущественные
при очень больших значениях
:
так как,
то отбросим в числителе и знаменателе
этой дроби слагаемые, несущественные
при очень больших значениях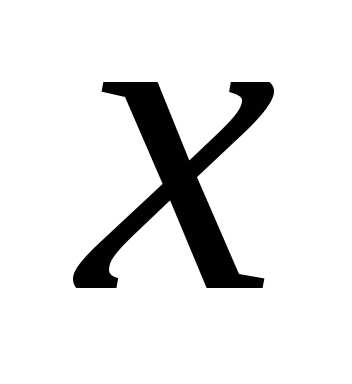 .
Тогда получим,
а
.
Тогда получим,
а
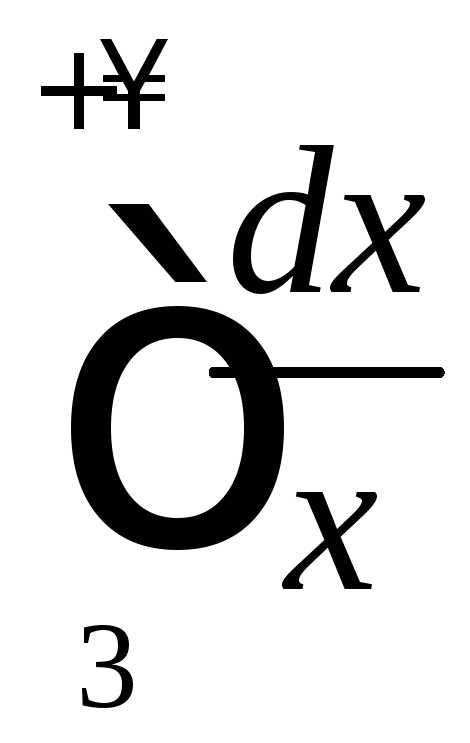 расходится ((8.12),
расходится ((8.12),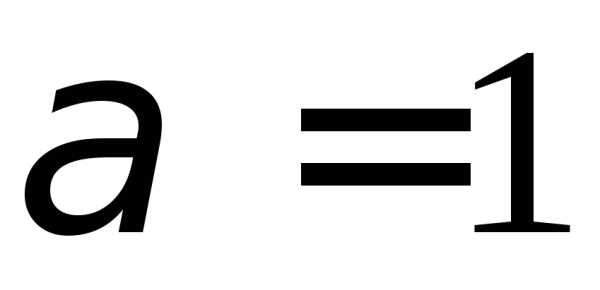 ).
).
Вычислим
(см. гл.4). Полученный предел конечен,
значит, данный интеграл ведет себя так
же, как и интеграл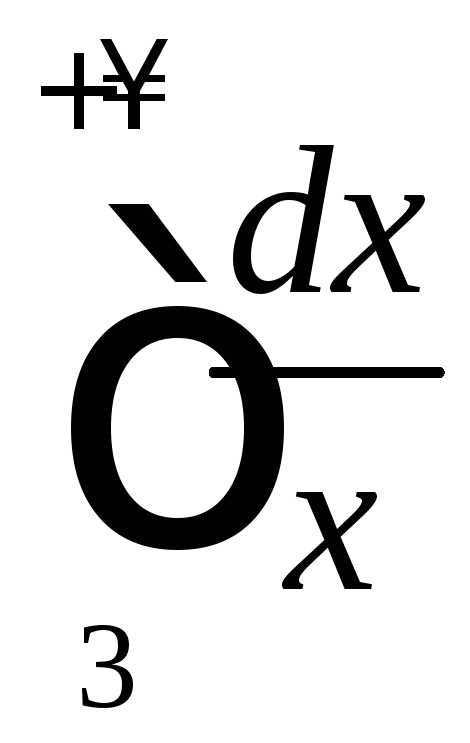
Рассмотрим еще раз предыдущий пример.
ПРИМЕР. Исследовать на сходимость несобственный интеграл
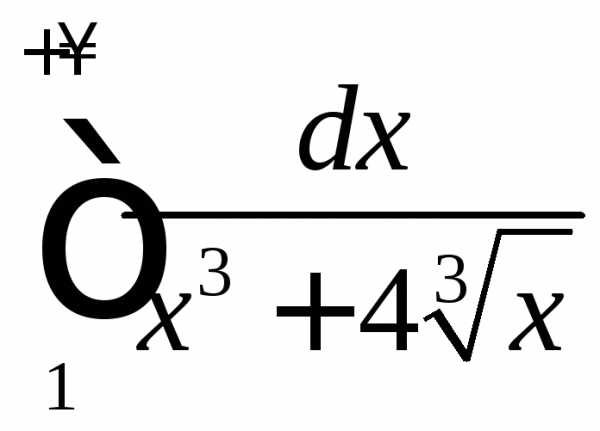 .
.
По условию 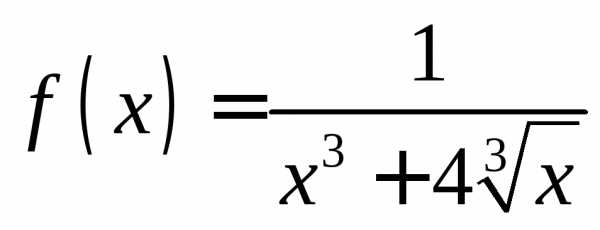 .
При больших значениях
.
При больших значениях поведение знаменателя определяется
слагаемым
поведение знаменателя определяется
слагаемым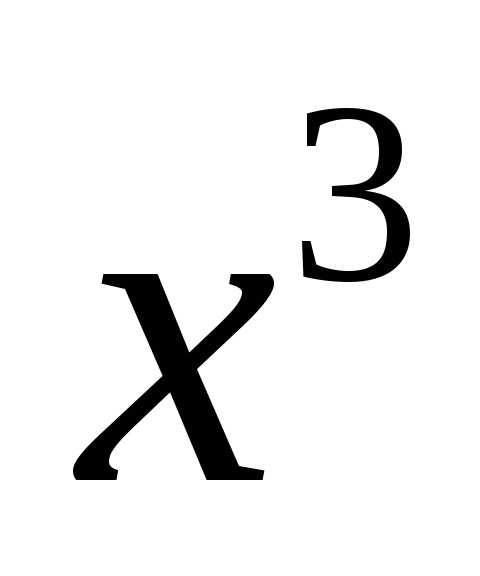 ,
поэтому
,
поэтому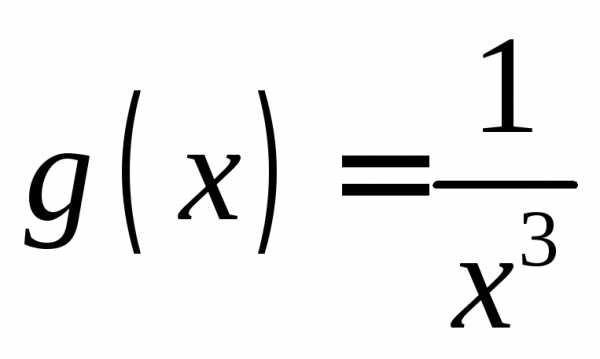 – функция для сравнения. Найдем.
Так как
– функция для сравнения. Найдем.
Так как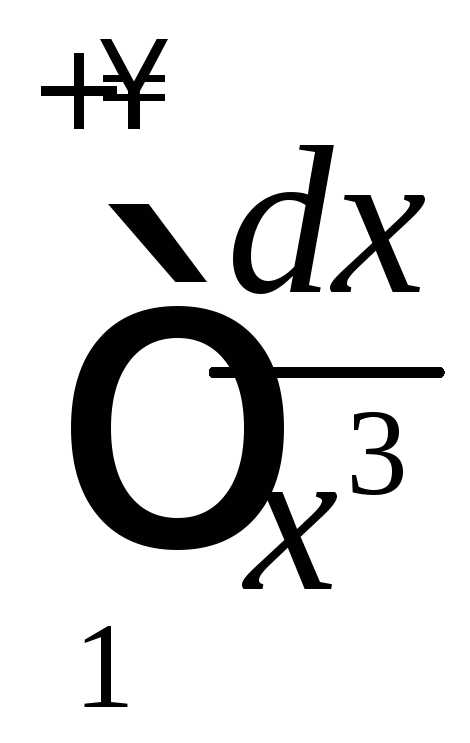 сходится, то данный интеграл сходится
тоже по предельному признаку сравнения.
сходится, то данный интеграл сходится
тоже по предельному признаку сравнения.
ЗАМЕЧАНИЕ.
Если 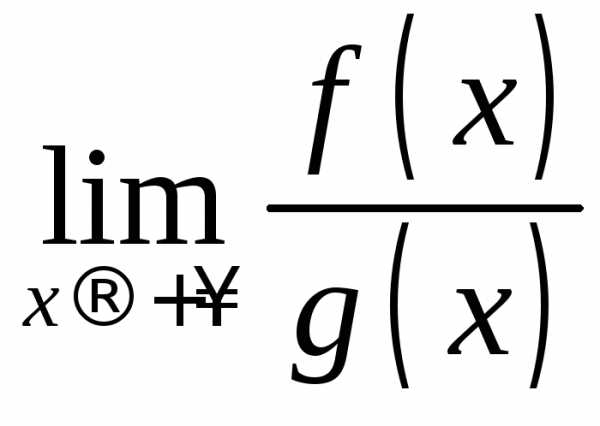 окажется нулевым или бесконечным, это
будет означать, что функция для сравнения
выбрана неверно.
окажется нулевым или бесконечным, это
будет означать, что функция для сравнения
выбрана неверно.
Предельным признаком сравнения сходимости очень удобно пользоваться, если подынтегральная функция представляет собой отношение степенных функций. Если же она содержит, например, показательную функцию, то чаще всего результат можно получить лишь с помощью признака сравнения.
ПРИМЕР.
Исследовать на сходимость несобственный
интеграл  .
.
Так как числитель
дроби 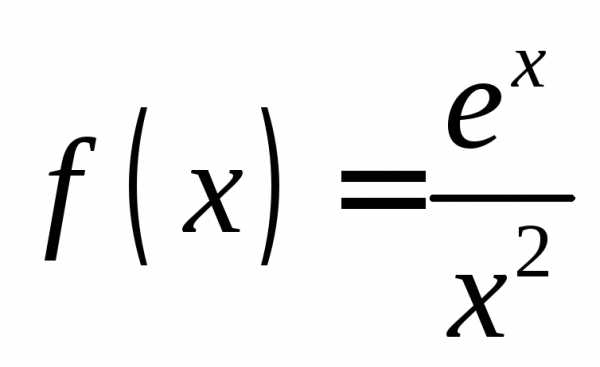 при увеличении
при увеличении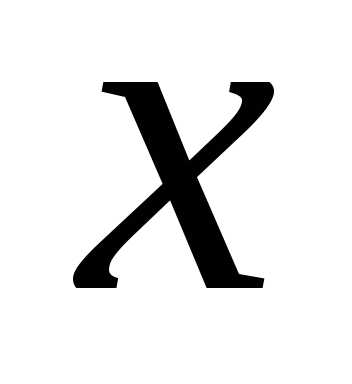 растёт быстрее знаменателя, то естественно
предположить, что этот интеграл
расходится. Исходя из этого предположения,
сделаем такую оценку подынтегральной
функции: при
растёт быстрее знаменателя, то естественно
предположить, что этот интеграл
расходится. Исходя из этого предположения,
сделаем такую оценку подынтегральной
функции: при
 .
Вследствие того, что
.
Вследствие того, что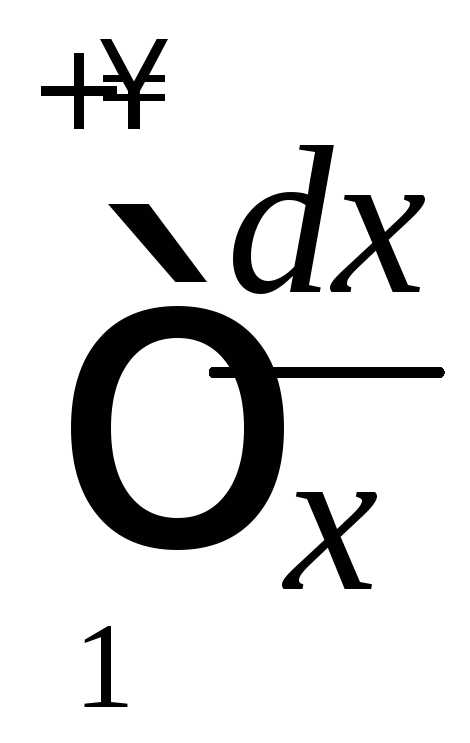 расходится ((8.12),
расходится ((8.12),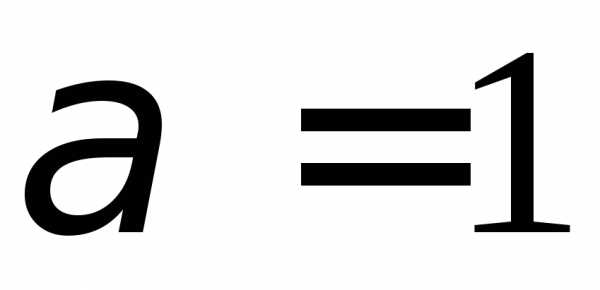 ),
данный интеграл также расходится по
признаку сравнения.
),
данный интеграл также расходится по
признаку сравнения.
ЗАМЕЧАНИЕ. Для несобственных интегралов 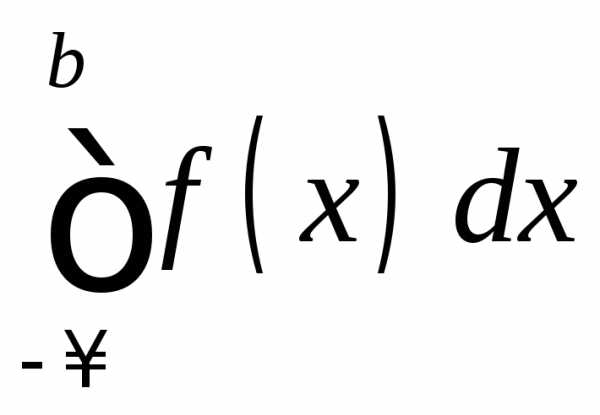 и
и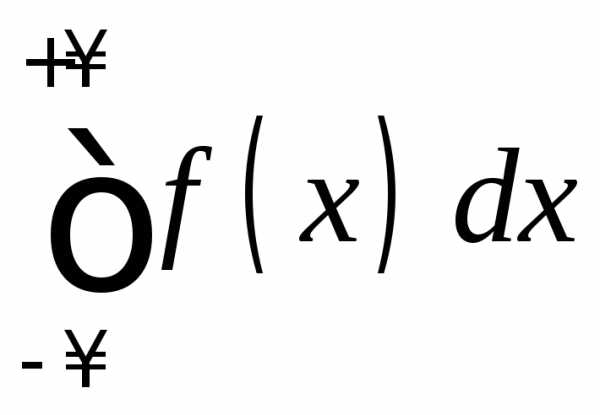 признаки сравнения сходимости
формулируются и применяются аналогично.
признаки сравнения сходимости
формулируются и применяются аналогично.
Подчеркнем, что эти теоремы верны лишь для функций, неотрицательных (или не меняющих знак) на промежутке интегрирования.
ОПРЕДЕЛЕНИЕ.
Пусть непрерывная функция 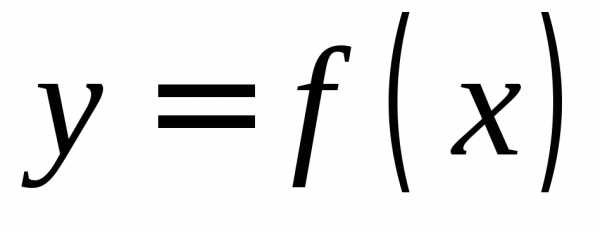 меняет знак на
меняет знак на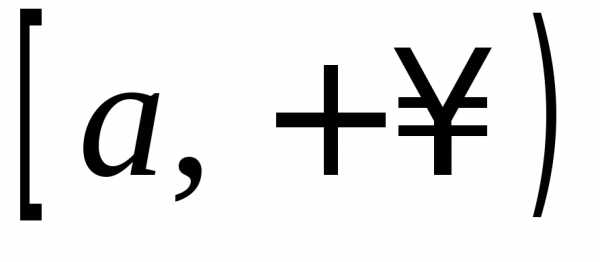 .
Тогда несобственный интеграл
.
Тогда несобственный интеграл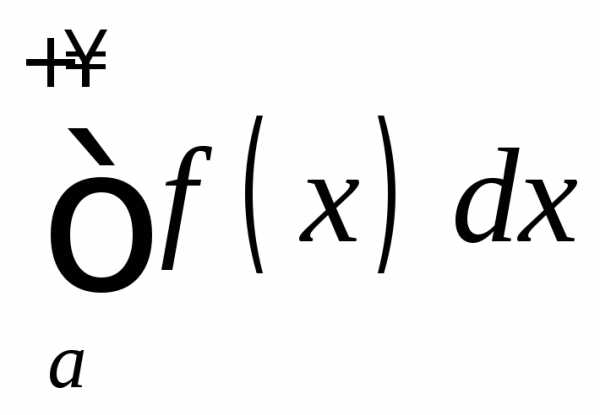 называетсяабсолютно
сходящимся,
если сходится
называетсяабсолютно
сходящимся,
если сходится 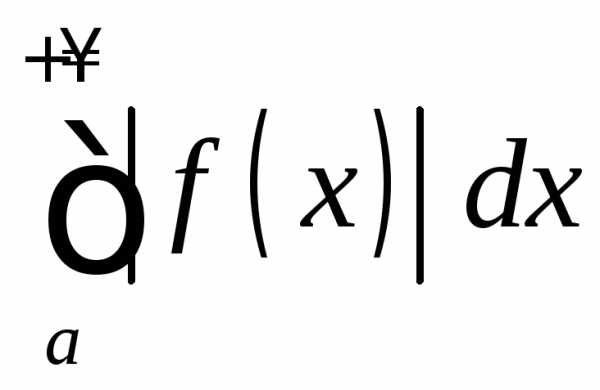 .
Если же
.
Если же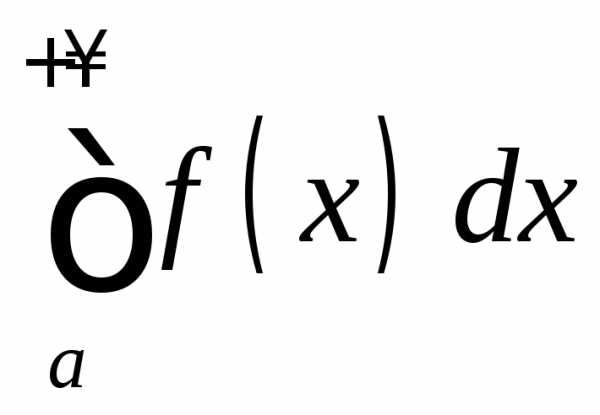 сходится, а
сходится, а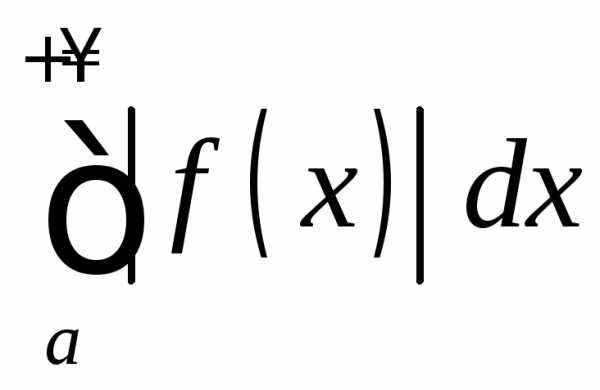 расходится, то
расходится, то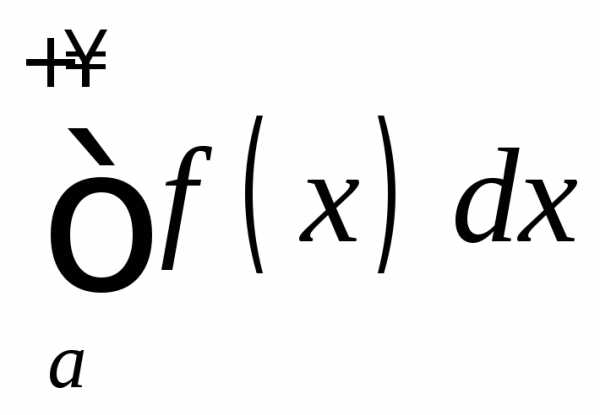 называетсяусловно
сходящимся.
называетсяусловно
сходящимся.
Можно доказать, что абсолютно сходящийся несобственный интеграл сходится.
ПРИМЕР. Исследовать на сходимость несобственные интегралы
а) 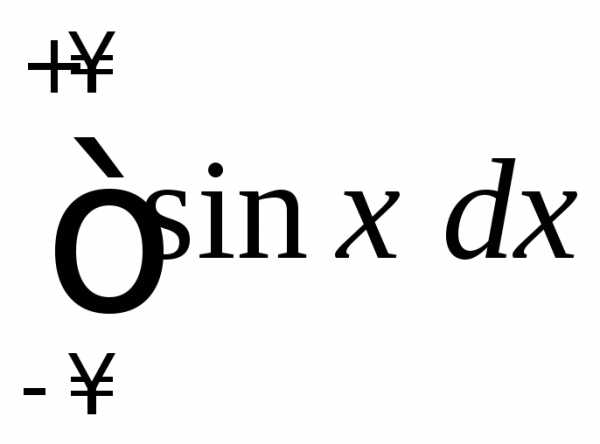 ,
б)
,
б)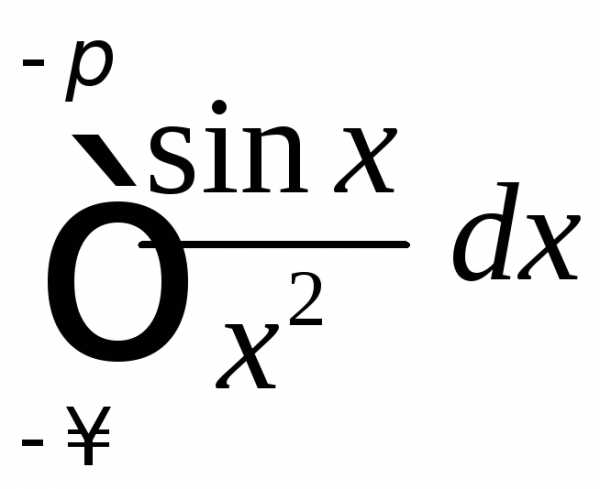 .
.
Заметим, что в обоих случаях подынтегральные функции меняют знак на промежутке интегрирования.
а)
,
но 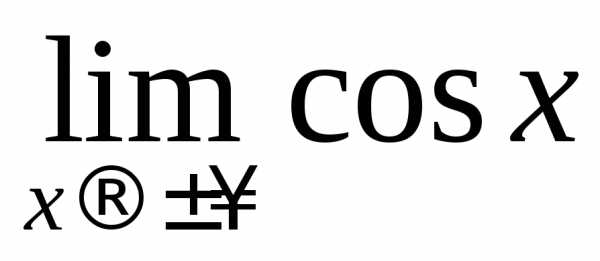 не существует (см. гл. 4), значит, интеграл
расходится.
не существует (см. гл. 4), значит, интеграл
расходится.
б) Функция 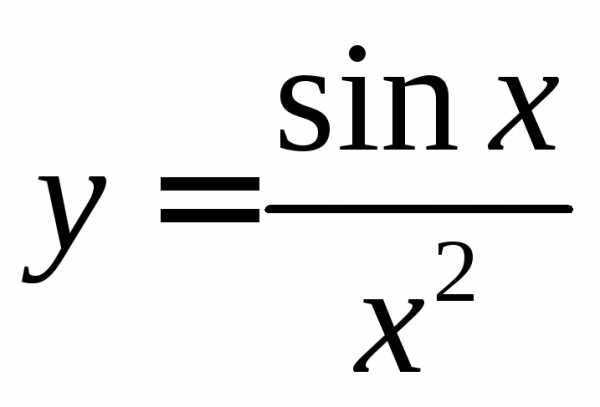 непрерывна при,
но не имеет элементарной первообразной,
поэтому исследовать сходимость этого
интеграла, как предыдущего, непосредственно
по определению невозможно.
непрерывна при,
но не имеет элементарной первообразной,
поэтому исследовать сходимость этого
интеграла, как предыдущего, непосредственно
по определению невозможно.
Рассмотрим 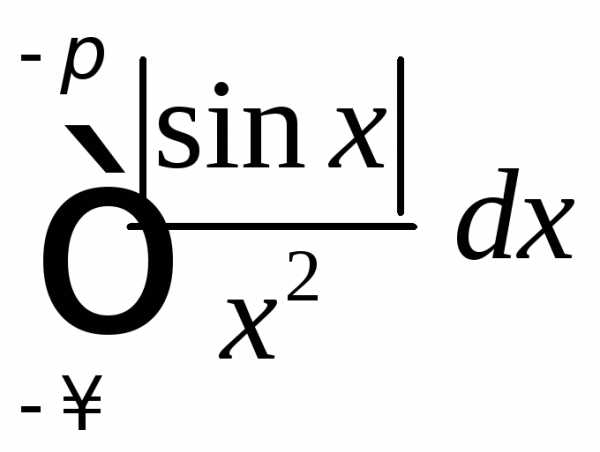 .
Подынтегральная функция в этом интеграле
неотрицательна и
.
Подынтегральная функция в этом интеграле
неотрицательна и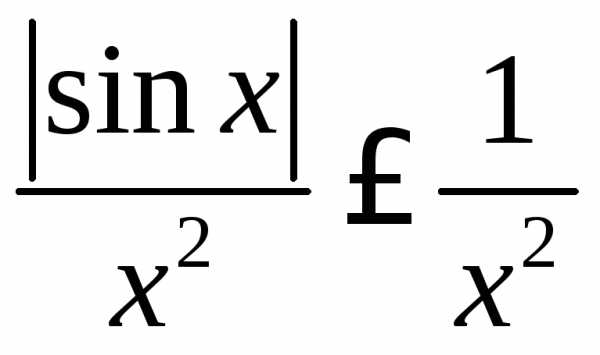 ,
так как.
Кроме того, интеграл
,
так как.
Кроме того, интеграл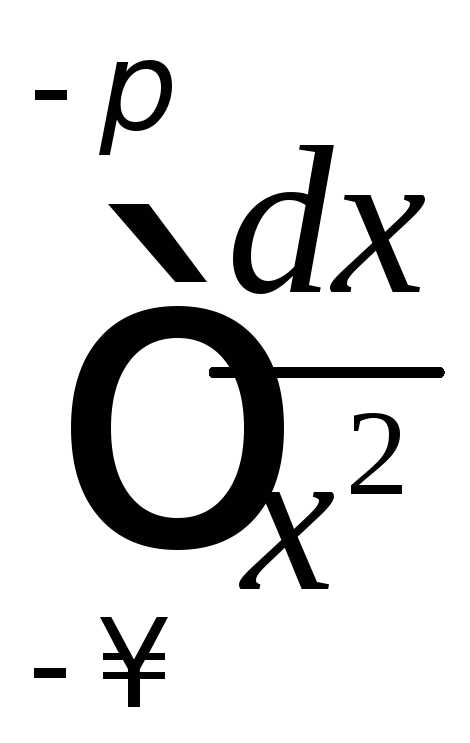 сходится(8.12.
сходится(8.12. 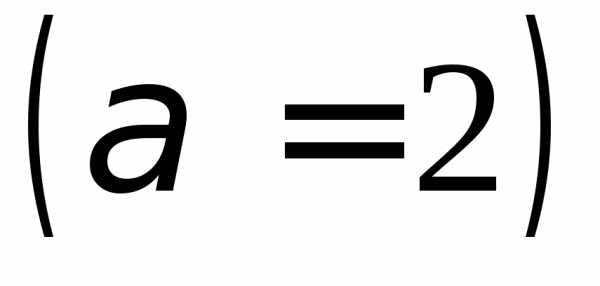 ),
следовательно,
),
следовательно, 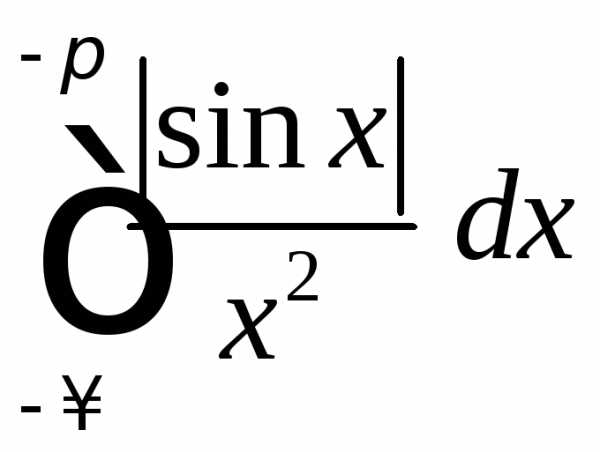 также сходится по признаку сходимости,
а это означает, что
также сходится по признаку сходимости,
а это означает, что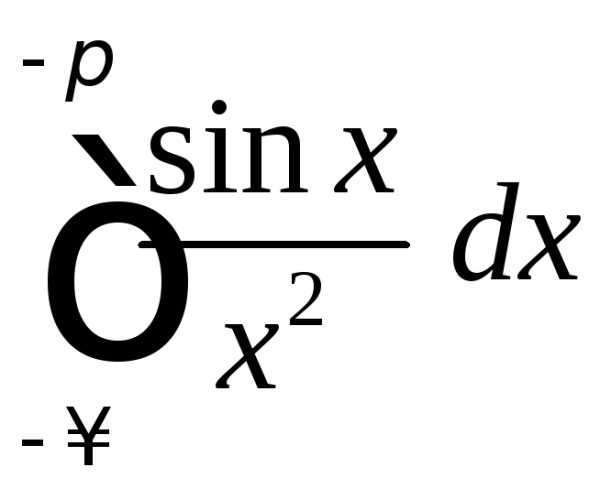 сходится абсолютно.
сходится абсолютно.
studfiles.net
Абсолютная и условная сходимость несобственных интегралов — ПриМат
Введём понятия абсолютно и условно сходящихся несобственных интегралов.
Пусть дан несобственный интеграл :
В случае абсолютной сходимости интеграла говорят, что функция абсолютно интегрируема на полусегменте .
Пример
Теорема 1
Пусть для всех . Тогда из сходимости несобственного интеграла следует сходимость несобственного интеграла и справедливо неравенство:
Теорема 2
Если функция абсолютно интегрируема на промежутке , то несобственные интегралы и сходятся или расходятся одновременно.
Ни на сходимость, ни на характер сходимости прибавление или вычитание под знаком интеграла абсолютно интегрируемой функции не влияет.
Пример
В качестве примера, исследуем интеграл на абсолютную и условную сходимость. Возьмём интеграл .
Спойлер
Рассмотрим три ситуации:
- Пусть . , следовательно, в силу сходимости интеграла , сходится интеграл , т.е. интеграл сходится абсолютно. Отсюда, по теореме 1, следует сходимость интеграла .
- Рассмотрим второй случай. Интегрируя по частям, получим
,
где , а сходится абсолютно. Следовательно, сходится и интеграл сходится при . Интеграл при расходится, а значит, что при интеграл сходится условно.
- Рассмотрим . Используя критерий Коши, докажем расходимость интеграла . Пусть . Выберем число таким, чтобы , и положим
.
Т.к. при выполняется неравенство и при и , то
Очевидно, что условие Коши не выполняется и интеграл расходится при .
Ответ::
- абсолютно сходится при ;
- условно сходится при ;
- расходится при .
[свернуть]
Литература
- А.М. Тер-Крикоров, М.И. Шабунин, Курс математического анализа, физмат-лит, 2001, стр. 375-377
- Л.Д. Кудрявцев «Курс математического анализа», том №1, Высшая школа, 1988-1989, стр. 666-672
- Г.М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том №2, стр. 559-563
- Конспект лекций Лысенко З.М.
Тесты
Абсолютная и условная сходимость несобственных интегралов
Лимит времени: 0
Информация
Проверьте свои знание по теме «Абсолютная и условная сходимость несобственных интегралов».
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 3
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
Рубрики
- Математический анализ 0%
- С ответом
- С отметкой о просмотре
Поделиться ссылкой:
Похожее
ib.mazurok.com
05. Абсолютная и условная сходимость несобственных интегралов по беск
До сих пор рассматривались интегралы от знакоположительных (знакопостоянных) функций. Теперь пусть подынтегральная функция таких ограничений не имеет, то есть может быть и знакочередующейся функцией.
Если наряду с собственным интегралом по бесконечному промежутку Сходится и интеграл по этому же промежутку, то первый интеграл называется Абсолютно сходящимся.
Если интеграл Сходится, а интеграл расходится, то первый интеграл называется Условно сходящимся.
Пример 8. Исследовать на абсолютную сходимость интеграл: .
Решение. В начале исследуется данный интеграл вообще на сходимость, для чего проведем интегрированние по частям: пусть тогда , далее . Так как последний интеграл сходится, то по признаку сравнения сходится и интеграл , причем абсолютно. Исходный интеграл при этом является сходящимся (кстати, сходимость этого можно определить быстрее с помощью признака сходимости Дирихле, который будет рассмотрен позже). Чтобы исследовать исходный интеграл на абсолютную сходимость, надо рассмотреть интеграл: . Так как при , то имеем: . Интеграл аналогично исходному интегралу сходится, а интеграл расходится; стало быть, и интеграл является расходящимся. При этом исходный интеграл является условно сходящимся.
Упражнение 8. Установить условную сходимость интеграла: .
Пример 9. Исследовать на абсолютную сходимость интеграл: .
Решение:
; стало быть, интеграл сходится абсолютно.
Упражнение 9. Установить абсолютную сходимость интеграла: .
Установить условную сходимость при отсутствии абсолютной сходимости в ряде случаев позволяет так называемый Признак сходимости Дирихле, в котором исследуется структура подынтегральной функции, если ее можно представить в виде произведения двух функций, а именно: , где интегрируема и ограничена, то есть:
(7) ;
А функция при непрерывно дифференцируема и монотонна, причем:
(8) .
При выполнении условий, налагаемых на функции и интеграл
(9)
Сходится.
С помощью этого признака условную сходимость интеграла в примере 8 при отсутсвии абсолютной сходимости можно определить следующим образом:
Имеем интеграл , который не является абсолютно сходящимся.
Представим подынтегральную функцию этого интеграла в виде произведения двух функций, то есть: , где , а . Функция интегрируема и ограничена на бесконечном промежутке, так как: , а . Поскольку все условия признака Дирихле (Формулы (7) И (8)) выполнены, то исследуемый интеграл сходится условно, ибо абсолютная сходимость этого интеграла места не имеет, что было показано в примере 8.
Пример 10. Исследовать на абсолютную и условную сходимость интеграл:
Решение. Сначала сделаем в исследуемом интеграле замену переменной:
Пусть , тогда ; если ; если ; итак, имеем: где является функцией интегрируемой и ограниченной на бесконечном промежутке (формула (7)), а (выполняется формула (8)). Поскольку все условия признака Дирихле (формулы (7) и (8)) выполнены, то исследуемый интеграл сходится. Исследуем интеграл на абсолютную сходимость, для чего рассмотрим интеграл . Т. к. при , то . Интеграл сходится по признаку Дирихле, а интеграл расходящийся; стало быть, интеграл тоже расходящийся, при этом исследуемый интеграл сходится условно.
Упражнение 10. Установить условную сходимость интегралов Фронеля:
; .
Интеграл типа (9) можно исследовать на условную сходимость ещё и с помощью так называемого Признака сходимости Абеля, в котором так же исследуется структура подынтегральной функции, если её можно представить в виде произведения двух функций и , на которые теперь наклкдываются следующие ограничения: интеграл от функции по бесконечному промежутку, то есть:
(10)
Сходится, а функция при непрерывно дифференциируема, монотонна и непрерывна, а потому имеет конечный предел, то есть:
(11) , .
При выполнении указанных условий ((10) и (11)) интеграл типа (9) сходится.
Пример 11. Установить сходимость интеграла: , используя признак Абеля.
Решение. Исследуемый интеграл представим следующим образом: , где , а . Так как интеграл от функции по бесконечному промежутку сходится (см. пример (8)), а , то все условия признака Абеля выполнены; стало быть, исследуемый интеграл сходящийся. Характер сходимости исходного итеграла (сходится условно или абсолютно) определится после исследования данного интеграла на абсолютную сходимость, для чего надо исследовать интеграл: . Так как , то .
Интеграл сходится по признаку Дирихле, так как , а . Интеграл расходится, что можно установить по предельному признаку сравнения: при ; тогда в кочестве сопоставляемой функции имеем , а , что означает расходимость интеграла . Стало быть, интеграл тоже расходящийся. Теперь ясен и характер сходимости исходного интеграла : он сходится условно.
Упражнение 11. Исследовать характер сходимости интеграла: .
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Исследовать интеграл на сходимость.
Поиск ЛекцийКОНТРОЛЬНАЯ РАБОТА № 2
Введение в математический анализ.
Производная и ее приложения.
Найти пределы функций, не пользуясь правилом Лопиталя.
а) ;
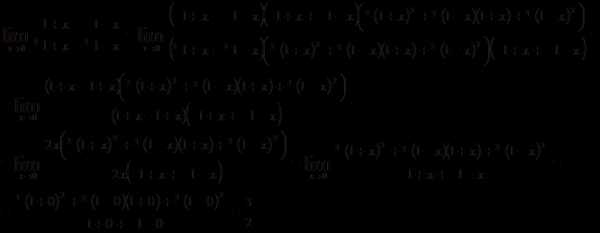
б) ;
в) ;
г)
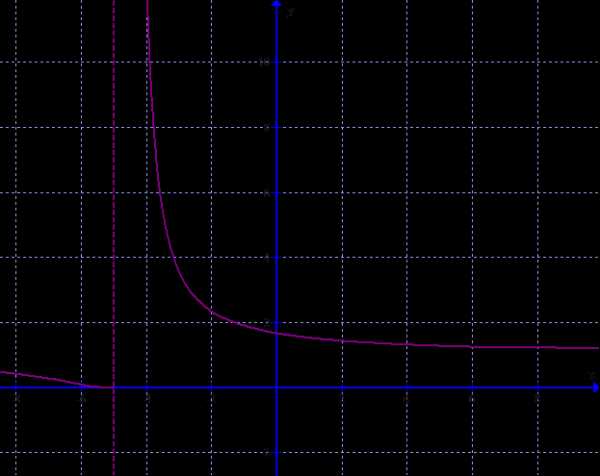
6.3.10. Задана функция у=f(х)и два значения аргумента x1и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
Данная функция определена и непрерывна на интервалах (-∞;-5),(-5;+∞).
Исследуем поведение функции в точках х1=-5, х2=-3. Найдём односторонние пределы.
При х=-3 функция имеет одинаковые односторонние пределы и , значит, в этой точке функция непрерывна. При х=-5 функция имеет с одной стороны бесконечный предел, значит, в этой точках функция разрывна.
Сделаем схематический чертеж:
7.1.30. Найти производные данных функций.
a) ;
б) при ;
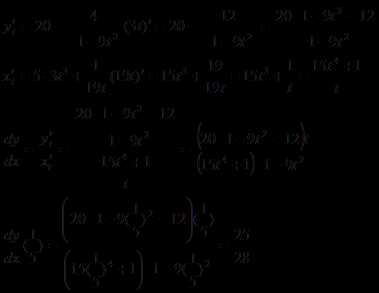
в) .
Прологарифмируем обе части равенства:
Теперь продифференцируем обе части равенства:
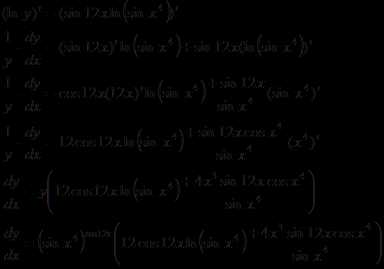
Найти пределы функции, применяя правило Лопиталя.
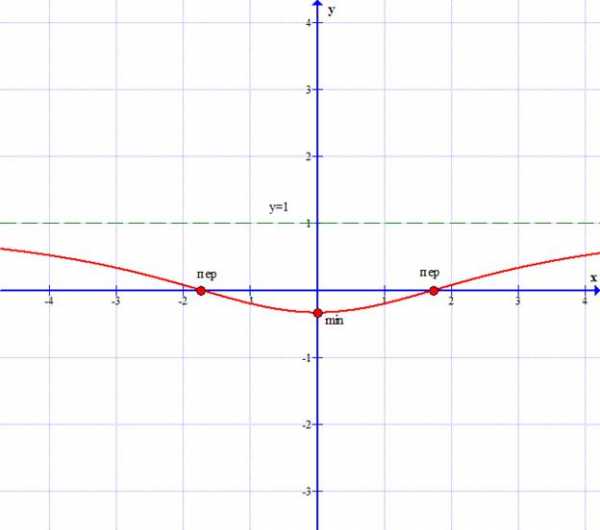
7.3.30. Методами дифференциального исчисления: а) исследовать функцию y = f (x) для и по результатам исследования построить ее график; б) Найти наименьшее и наибольшее значения заданной функции на отрезке [a; b].
а) б) [–2; 2] .
1. Очевидно D(y) = (-¥;+¥).
2. .Функция является чётной.
3. Найдем точки пересечения с осями координат:
с осью Оу: x = 0, то у=-3;
с осью Ох: y = 0, то .
4. Определим критические точки. Для этого найдем производную y’.
Тогда y’ = 0 имеет решение х =0 –абсцисса точки экстремума. Определим знак первой производной на интервалах.
y'(x)
– +
Значит, на промежутке (0,+¥) функция возрастает, на промежутке (-¥,0) функция убывает.
5. Определим точки перегиба. Для этого найдем вторую производную y» функции:
, тогда y» = 0 имеет решение при — это абсциссы точек перегиба.
Определим знак второй производной на области определения.
y»(x)
– + –
Таким образом, при x Î(-¥ , ), ( , +¥) график функции выпуклый, при хÎ( , ) –вогнутый.
6. Функция определена и непрерывна на всей области определения. Выясним, имеет ли график функции наклонную асимптоту у=кх+в.
У=1 – горизонтальная асимптота.
По результатам исследования строим график функции:
б) Функция непрерывна на отрезке [-2;2]. Найдём производную
В данном случае критической является точка при х=0, причём точка принадлежит отрезку [-2;2]. Вычислим значение на концах отрезка:
Таким образом, наименьшее значение данной функции равно -0,333 и получаем его при х=0 в критической точке, наибольшее равное 0,077 получаем при х=-2 и х=2 на правой и левой границах.
КОНТРОЛЬНАЯ РАБОТА № 3
Неопределенный и определенный интегралы.
Функции нескольких переменных. Кратные интегралы.
Криволинейные и поверхностные интегралы.
Найти неопределенные интегралы. Результаты проверить дифференцированием.
а)
Проверим результат дифференцированием:
б) ;
Проверим результат дифференцированием:
в) ;
Проверим результат дифференцированием:
г)
Проверим результат дифференцированием:
Исследовать интеграл на сходимость.
.
Значит, интеграл расходится.
9.1.40. Дана функция двух переменных . Найти все частные производные первого и второго порядков. Обосновать равенство .
.
Равенство верно.
9.2.10. Дана функция и точка . С помощью полного дифференциала вычислить приближенно значение функции в данной точке. Вычислить точное значение функции в точке и оценить относительную погрешность вычислений.
; .
Будем рассматривать z(М)как частное значение функции при x = 0,96 = x1, у =2,05 = у1. За x0 принимаем число 1, за у0 –число 2.
Тогда z(x0,y0) = ;
Переведём dx в радианы:
dx = x1 – x0 =0,96-1=-0,04,
dy = y1 –y0 =2,05-2=0,05
Тогда получим:
» z(x0,y0) + (x0,y0)dx+ (x0,y0)dy=-3+(-2)(-0.04)-3*0.05=-3,07
Оценим погрешность: %
10.1.10. Вычислить криволинейный интеграл. Сделать чертеж дуги кривой L.
, где L – верхняя половина эллипса x = 3sin 2t, y = 4cos 2t. Интегрировать против часовой стрелки.
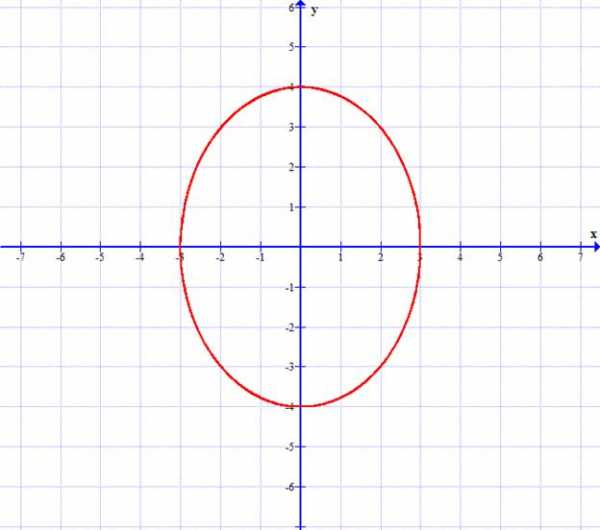
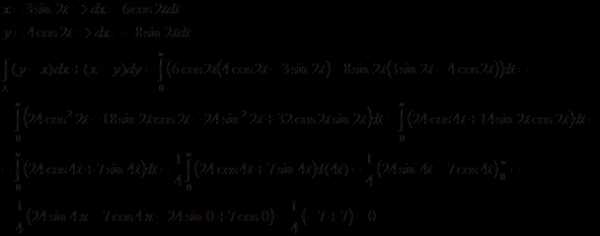
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru
Несобственный интеграл
Несобственный интегралТема «Несобственный интеграл»
Пример
1. Исследовать
на сходимость интеграл
.
Сначала установим, имеет ли подынтегральная функция точки разрыва на интервале
интегрирования. Для этого найдем корни квадратного уравнения .
Вычислим дискриминант: .
Так как ,
то на множестве действительных чисел это уравнение решений не имеет. Следовательно,
и точек разрыва нет.
Таким образом, данный интеграл есть интеграл с бесконечным верхним пределом
от непрерывной функции. Для ответа на вопрос о сходимости этого интеграла нужно
найти предел:
.
Выделим полный квадрат в знаменателе подынтегральной функции:
.
Подставим полученное выражение в последний интеграл и применим метод замены
переменной:
Ответ: несобственный интеграл сходится и равен .
Пример
2. Исследовать
на сходимость интеграл .
Данный интеграл есть интеграл с бесконечным нижним пределом от непрерывной функции.
Для ответа на вопрос о сходимости этого интеграла нужно найти предел:
.
Чтобы вычислить интеграл, стоящий под знаком предела, используем формулу интегрирования
по частям для определенного интеграла :
В нашем случае получим:
Найдем отдельно третий и первый пределы, используя для удобства замену причем
при :
.
Для раскрытия неопределенности в последнем пределе используем правило Лопиталя
:
Подставим полученные значения в исходный предел:
Следовательно, .
Ответ: несобственный интеграл
сходится и равен .
Пример 3. Исследовать на сходимость
интеграл .
Данный интеграл есть интеграл с бесконечным верхним пределом от непрерывной
функции. Для ответа на вопрос о сходимости этого интеграла нужно найти предел:
.
Чтобы вычислить интеграл, стоящий под знаком предела, используем метод замены
переменной. Поскольку множитель ,
стоящий под интегралом, есть, с точностью до константы, производная от выражения
,
то для нахождения интеграла воспользуемся заменой:
Тогда
Поскольку предел равен конечному числу, то несобственный интеграл сходится и
равен :
Ответ: несобственный интеграл
сходится и равен .
Пример 4. Исследовать на сходимость
интеграл .
В данном примере подынтегральная функция терпит разрыв в нижнем пределе (т.е.
при ),
так как в знаменателе .
Следовательно, для ответа на вопрос о сходимости интеграла от разрывной функции,
необходимо найти предел:
.
Чтобы вычислить интеграл, стоящий под знаком предела, используем метод замены
переменной. Поскольку множитель ,
стоящий под интегралом, есть производная от ,
то для нахождения интеграла воспользуемся заменой:
Тогда
Так как
при
не имеет конечного предела, то интеграл
не существует или расходится.
Ответ: интеграл
расходится.
Пример 5. Исследовать
на сходимость интеграл .
Выражение, стоящее в знаменателе подынтегральной функции, обращается в 0 при
(т.е. в нижнем пределе). Следовательно, для ответа на вопрос о сходимости интеграла
от разрывной функции, необходимо найти предел:
.
Чтобы вычислить интеграл, стоящий под знаком предела, можно воспользоваться
метод замены переменной или применить для нахождения первообразной следующее
правило интегрирования:
если , то .
Воспользуемся вышеприведенным правилом, тогда: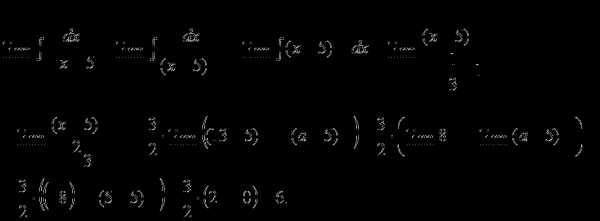
Следовательно, .
Ответ: несобственный интеграл
сходится и равен 6.
Пример 6. Исследовать на сходимость интеграл .
В данном примере подынтегральная функция терпит разрыв в верхнем пределе (т.е.
при ),
так как в знаменателе .
Следовательно, для ответа на вопрос о сходимости интеграла от разрывной функции,
необходимо найти предел:
.
Чтобы вычислить интеграл, стоящий под знаком предела, преобразуем знаменатель
с использованием основного тригонометрического тождества, записанного для половинного
аргумента (),
и формулы для косинуса двойного угла для аргумента
():
Таким образом,
При вычислении первообразной для интеграла
можно воспользоваться методом замены переменной или правилом интегрирования:
если ,
то .
Так как
при
не имеет конечного предела, то интеграл
не существует или расходится.
Ответ: интеграл
расходится.
pgsksaa07.narod.ru

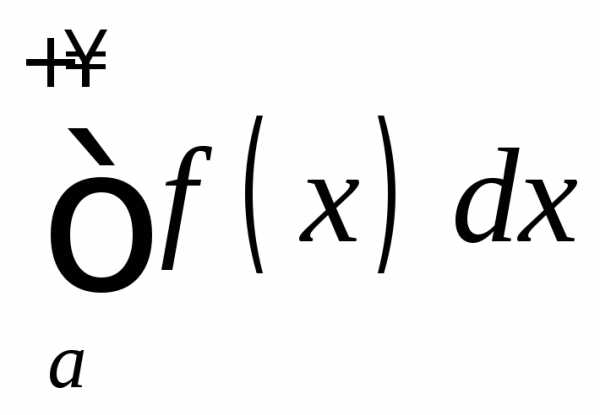 ,
то сходится и
,
то сходится и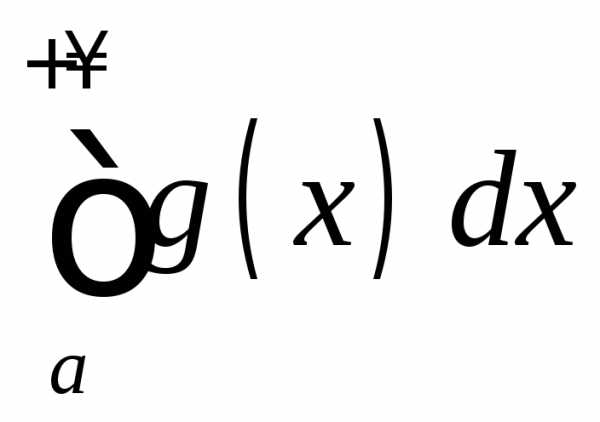 ;
;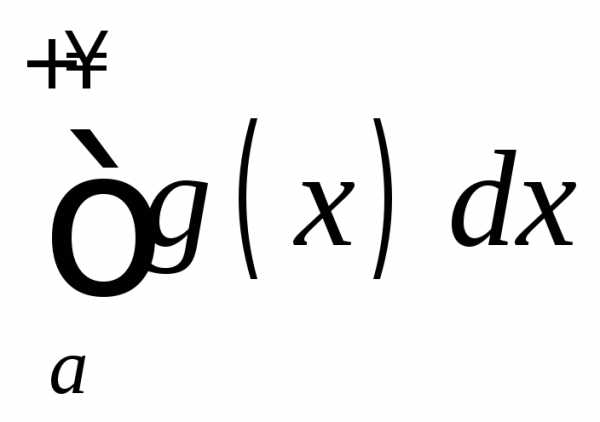 ,
то расходится и
,
то расходится и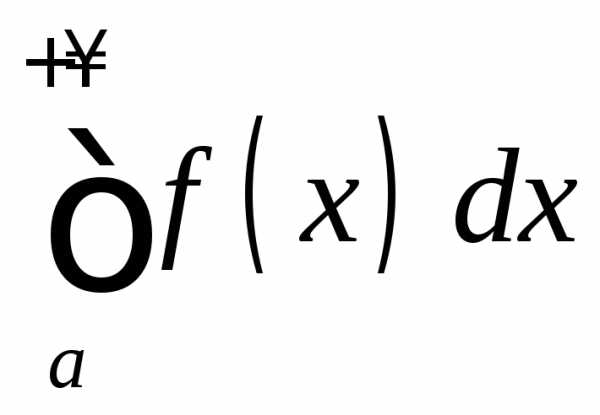 .
.