«Сложение и вычитание, деление и умножение обыкновенных дробей»
Например:
1.
2.
3.
4.
Умножение смешанного числа на целое число.
При умножении смешанного числа на целое в большинстве случаев проще отдельно умножить целое и дробь на целое число.
Например:
1.
2.
3.
Умножение дробь на дробь
Чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:
Например:
1.
2.
3.
4.
.5.
Деление обыкновенных дробей на целое число.
При делении дроби на целое число достаточно числитель разделить на целое число, оставив прежний знаменатель.
Например:
1.
2.
Как поступать в том случае, когда числитель данной дроби не делится на целое число. Тогда существует следующее правило
Чтобы разделить дробь на целое число, достаточно знаменатель дроби умножить на это число, оставив числитель прежним.
Например:
1.
2.
Деление дроби на дробь.
Чтобы разделить дробь на дробь, нужно первую дробь переписать, а вторую дробь перевернуть (это важно!) и их перемножить, т.е. знаменатель на знаменатель, числитель на числитель.:
Например:
1.
2.
3.
4.
5.
.3. Примеры на сложение, вычитание, умножение и деление обыкновенных дробей.
Реши самостоятельно:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19. ;
20. ;
21.
22.
23. ;
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
СПИСОК ЛИТЕРАТУРЫ.
1. Живая математика/Я. И. Перельман;
2. За страницами учебника математики/ И. Я. Депман, Н. Я. Виленкин. – М.: Просвещение, 1988;
3. Математика: Учеб. для 5 классса ср. школы/ Н. Я. Виленкин, А. С. Чесноков, И. Шварцвурд. – 3 изд. – М.: Просвещение, 1988;
4. Элементы историзма в преподавании математики в средней школе/
К. А. Малыгин. – М.: Просвещение, 1958.
5. Черкасов Р.С., Столяр А.А. Методика преподавания математики в средней школе / 1985.
mirznanii.com
Операции с дробями
Автор Сергей Валерьевич
Четверг, Январь 14, 2016
В данной статье репетитором по математике и физике рассказано о том, как производить элементарные операции с обыкновенными дробями: сложение и вычитание, умножение и деление. Рассказано о том, как представить смешанное число в виде неправильной дроби и наоборот, а также о том, как сокращать дроби.
Сложение и вычитание обыкновенных дробей
| Чтобы сложить (или вычесть) две обыкновенные дроби нужно: 1) Привести обе дроби к общему знаменателю. 2) Записать результат в виде дроби с числителем, равным сумме числителей исходных дробей, и найденным общим знаменателем. |
Напомним, что знаменателем дроби называется число, которое находится снизу, а числителем — число, которое находится сверху от дробной черты. Например, у дроби число является числителем, а число — знаменателем.
Общим знаменателем является наименьшее возможное число, которое делится и на знаменатель первой дроби, и на знаменатель второй дроби.
Пример 1. Сложить две дроби: .
Воспользуемся описанным выше алгоритмом:
1) Наименьшее число, которое делится и на знаменатель первой дроби, и на знаменатель второй дроби, равно . Это число и будет являться общим знаменателем. Теперь нужно привести обе дроби к общему знаменателю.
- С первой дробью ничего делать не нужно, поскольку ее знаменатель уже равен .
- Числитель и знаменатель второй дроби нужно умножить на , тогда дробь примет вид: .
2) Складываем полученные дроби: .
Умножение обыкновенных дробей
| Для умножения двух обыкновенных дробей нужно: 1) Вычислить числитель дроби. Для этого нужно перемножить числители исходных дробей. 2) Вычислить знаменатель дроби. Для этого нужно перемножить знаменатели исходных дробей. 3) Записать полученную дробь. |
Иными словами, для всех действительных чисел , , , , справедливо равенство:
Пример 2. Перемножить дроби: .
Для решения данной задачи воспользуемся представленной выше формулой:
yourtutor.info
Сложение, вычитание, умножение и деление обыкновенных дробей
Тема: Сложение, вычитание, умножение и деление обыкновенных дробей.
(Урок по математике в 6 классе)
Тип урока:урок – повторения и закрепления ЗУН.
Цели урока:
— отрабатывать умения складывать, вычитать, умножать, делить дроби, решения простейших задач жизненной практики, способствовать умению рассуждать и логически мыслить, проверить ЗУН обучающихся по теме «Сложение и вычитание дробей с разными знаменателями», «Умножение и деление обыкновенных дробей»;
— способствовать воспитанию умения работать в парах и группах;
— способствовать развитию умения рассуждать и логически мыслить.
Задачи:
Способствовать овладению навыками критического и креативного мышления для генерации новых идей при решении задач динамично изменяющегося мира.
Оборудование: номера столов и участников, карточки с логическими задачами.
На уроке применяются элементы сингапурской методики обучения.
Ход урока:
Организационный момент.
ХАЙ ФАЙВ (СИГНАЛ ТИШИНЫ).
Учитель: Здравствуйте, садитесь. Сегодня мы проведём урок, применяя сингапурские структуры урока. Сообщение темы, цели, плана урока.
Повторение.
Цель: повторение изученного.
ФИНК-РАЙТ-РАУНД РОБИН (ПОДУМАЙТЕ – ЗАПИШИТЕ – ОБСУДИТЕ)
Учитель: Подумайте, запишите и обсудите в группах ответ на вопрос:
— Какие темы мы изучили в этом полугодии?
Запишите как можно больше тем и математических терминов, которые вы узнали в этом учебном году.
Время по 1 минуте каждому подумать и записать на листочках, обсудить по очереди и выслушать друг друга, записать новые идеи команды.
По команде учителя выслушать 2-3 учеников команды.
(Ответы: Делитель, Кратное, Сокращение дробей, Признаки делимости, НОД, НОК, Простые числа, Сравнение, сложение, вычитание, дробей с разными знаменателями, Сравнение, сложение, вычитание смешанных чисел, Умножение, деление дробей.)
Проверка домашнего задания.
Цель: повторение сложения, вычитания, умножения, деления дробей.
Учитель: Домашним заданием было записать на одной стороне листочка любой пример или вопрос, а на обратной стороне – ответ. КУИЗ – КУИЗ – ТРЕЙД (ОПРОСИ – ОПРОСИ – ОБМЕНЯЙСЯ КАРТОЧКАМИ).
Учитель: Ребята, вы будете проверять и обучать друг друга по пройденному материалу, используя карточки с вопросами и ответами.
Учитель: 1)Ребята, встаньте, задвиньте стулья, возьмите свои карточки, поднимите руку и найдите ближайшую пару.
2)Ученик А у которого день рождения ближе к 19 декабрю спрашивает ученика В (задаёт вопрос из своей карточки).
3)Ученик В отвечает.
4)Ученик А помогает и хвалит (подскажи, научи, переспроси, похвали).
5)Ученики меняются ролями (ученик В спрашивает ученика А).
6)Ученики меняются карточками и благодарят друг друга.
Можно повторить шаги 1-6 несколько раз.
Учитель: контролирует время процесса.
4. Математический диктант. (в тетрадях по вариантам, с последующей взаимопроверкой, чётные номера – 1 вариант, не чётные номера – 2 вариант)
Цель: проверить знания по сложению, вычитанию, умножению, делению дробей.
В-1
+
—
·
В — 2
+
—
·
Ответы записаны на обратной стороне доски.
Учитель: — Поменяйтесь тетрадями с партнёром по лицу, оцените работу партнёра.
5. Физминутка.— А теперь ребята встали,
Дружно руки вверх подняли,
В стороны, вперёд, назад,
Наклонились вправо, влево,
Тихо сели вновь за дело.
6. Домашнее задание Составить и записать по 2 примера на сложение вычитание, умножение, деление дробей.
7. Занимательные задачи.
Цель: способствовать развитию логического мышления.
Учитель: Раздаёт карточки с заданиями (или уже они на столе). Учащиеся каждый сам решают задачи. Через определённое время учитель проверяет ответы. ТЭЙК – ОФ – ТАЧ ДАУН ( ВСТАТЬ – СЕСТЬ) для получения информации о классе.
Учитель: Встаньте, пожалуйста, те, у кого ответ в первой задаче ответ = 4 . Спасибо, садитесь.
Встаньте, пожалуйста, те, у кого ответ во второй задаче ответ – одной девочке дали клетку с кроликом. Спасибо, садитесь.
Встаньте, пожалуйста, те, у кого ответ в третьей задаче ответ — всего 3 человека: сын, отец и дед . Спасибо, садитесь.
Встаньте, пожалуйста, те, у кого ответ в четвёртой задаче ответ = 2,3 . Спасибо, садитесь.
Встаньте, пожалуйста, те, у кого ответ в пятой задаче ответ = на 12 равных частей. Спасибо, садитесь.
Задачи:
1.В каждом из четырёх углов комнаты сидит кошка. Напротив каждой из этих кошек сидит кошка. Сколько всего в этой комнате кошек?
2.В клетке находится три кролика. Три девочки попросили дать им по одному кролику. Просьба девочек была удовлетворена, каждой из них дали кролика. И всё же в клетке остался один кролик. Как могло такое случиться?
3.Два отца и два сына разделили между собой три апельсина так, что каждому досталось по одному апельсину. Как такое могло случиться?
4.Какой знак надо поставить между 2 и 3, чтобы число стало больше 2, но меньше 3?
5. Как разрезать торт на части, чтобы его можно было разделить поровну как на трёх, так и на четырёх человек?
8. Рефлексия.
Учитель: Ребята, перед вами новогодняя ёлка и ёлочные украшения. Если вы сегодня получили удовольствие от урока, выберите яркую красную игрушку, если вам не понравился урок – тёмную, если вам было всё равно – зелёную. Нарядите нашу ёлку.
xn--j1ahfl.xn--p1ai
Сложение, вычитание и умножение обыкновенных дробей.
Урок математики
в 6 классе
Тема: «Сложение, вычитание и умножение
обыкновенных дробей».
Цели урока.
Систематизировать и обобщить знания учащихся по данной теме.
Повысить интерес к предмету в процессе повторения пройденного материала.
Развитие логического мышления, внимания, познавательной активности учащихся, самостоятельного применения знаний в различных ситуациях.
Воспитание чувства ответственности каждого школьника за собственную деятельность.
Воспитание у учащихся навыков учебного труда, формирование ответственности за конечный результат.
Воспитание интереса к предмету; формирование доброго отношения друг к другу.
Тип урока. Урок применения знаний и умений, повторительно – обобщающий.
Оборудование:
учебник математики 6–й класс, автор Виленкин Н. А.;
компьютеры;
проекционное оборудование;
экран;
раздаточный материал ( тесты, карточки).
План урока.
I. Организационный момент.
II. Сообщение темы и цели урока.
III. Устный счёт.
IV. Решение упражнений.
V. Физминутка.
VI. Проверка знаний и умений учащихся по пройденному материалу.
VII. Итог урока.
VIII. Домашнее задание.
Ход урока.
Организационный момент.
Взаимное приветствие, проверка рабочих мест учеников.
— Прежде чем перейти к работе по пройденному материалу, нужно сосредоточить своё внимание и слух, настроиться на работу.
Сообщение темы и цели урока.
Итак, открыли тетради, отступите от домашней работы 4 клетки, запишите на полях: число, месяц, классная работа и тему нашего урока «Сложение, вычитание и умножение обыкновенных дробей». Сегодня мы с вами продолжим формировать умения и навыки в данной теме, будем развивать у себя внимание, память, само и взаимоконтроль, а также воспитывать в себе чувство ответственности и товарищества.
III. Устный счёт. ( Фронтальный опрос, индивидуальная работа за компьютером и у доски ).
Фронтальный опрос.
Давайте вспомним некоторые знания, которые помогут нам при выполнении заданий.
Какие дроби вы знаете?
-Десятичные и обыкновенные.
Какие обыкновенные дроби вы знаете?
-Правильные, неправильные и смешанные дроби.
Какие действия мы выполняем с обыкновенными дробями?
А теперь перейдём к устному счёту.
Слайд 1. Устный счёт мы проведём и рекорды все побьём.
Слайд 2. Вопрос. Как найти целую и дробную части неправильной
дроби?
Слайд 3. Пример. Выдели целую часть из неправильной дроби:
а) 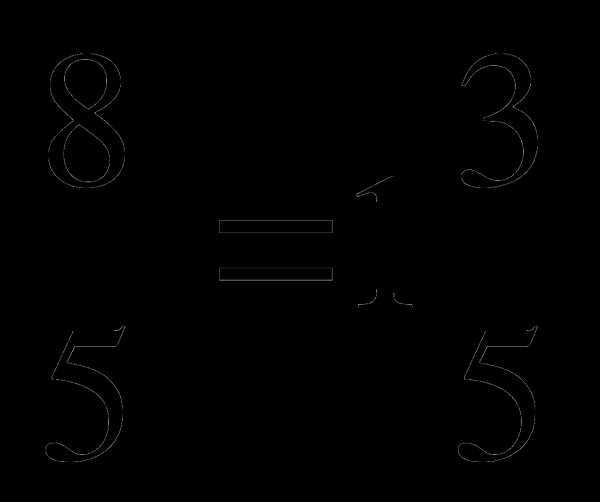 ; б)
; б) 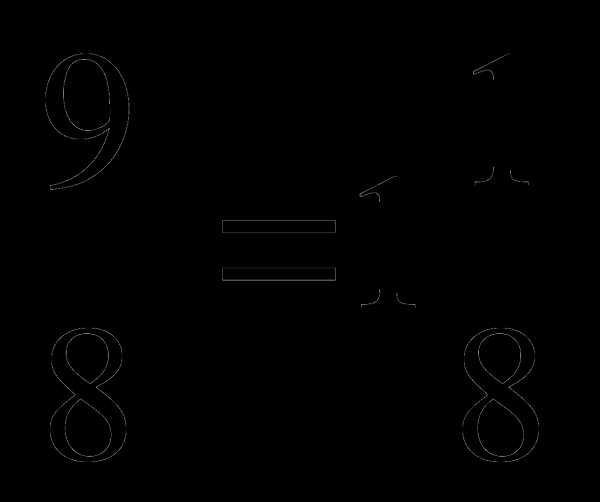 ; в)
; в) 
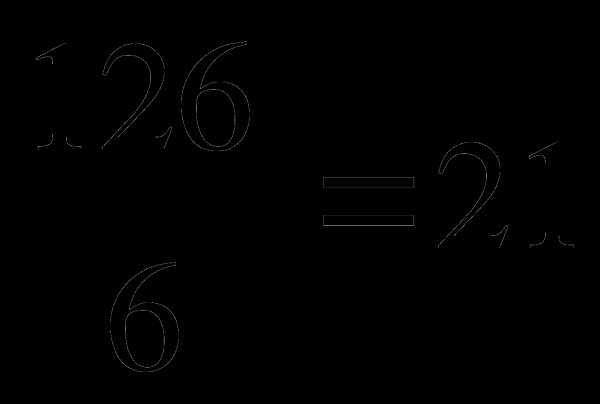 .
.
Слайд 4. Вопрос. Как представить смешанное число в виде неправильной дроби?
Слайд 5. Пример. Представь в виде неправильной дроби:
а) 2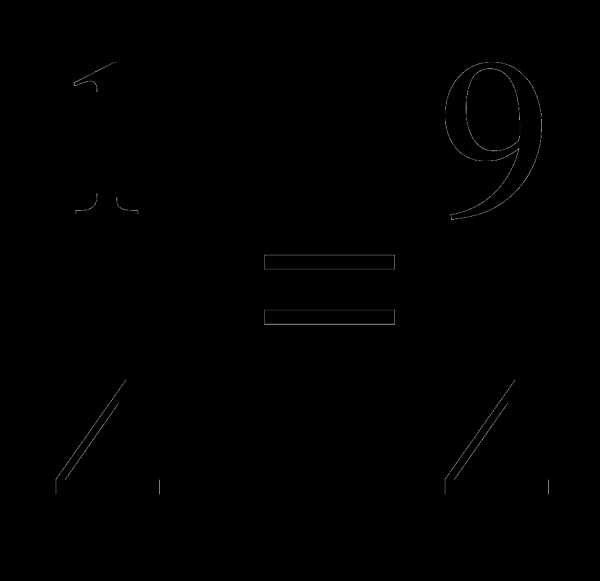 ; б) 3
; б) 3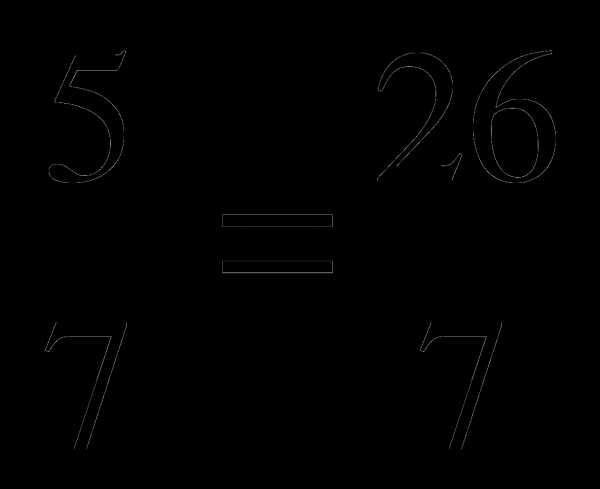 ; в) 12
; в) 12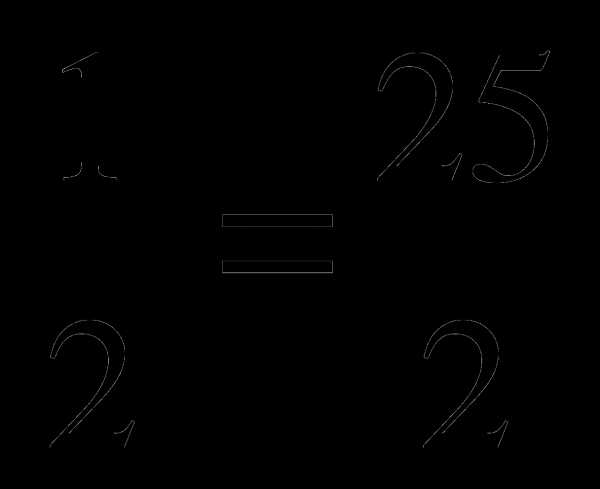 .
.
Слайд 6. Вопрос. Как сложить смешанные числа?
Слайд 7. Пример. Выполните действие:
3.
Слайд 8. Вопрос. Как выполнить вычитание смешанных чисел?
Слайд 9. Пример. Вычислите:
.
Слайд 10. Вопросы.
Как умножить дробь на натуральное число?
Как выполнить умножение двух дробей?
Как выполнить умножение смешанных чисел?
Слайд 11 Пример. Вычислите:
а) 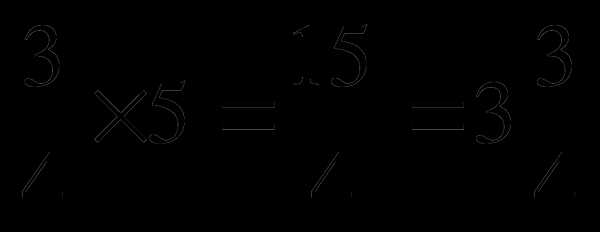 ; б)
; б) 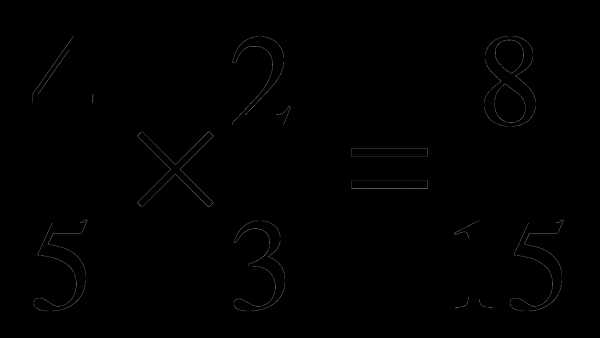 ; в) .
; в) .
2. А в это время …, вычислив и расставив буквы шифра в клетки с ответами, должна расшифровать слово (задание записано на доске).
Д Вычислите объём прямоугольного параллелепипеда, если его измерения  м,
м,  м и
м и  м.
м.
И 4 ( 1 —
( 1 — 
Б (  )
)  7 =
7 =
Р 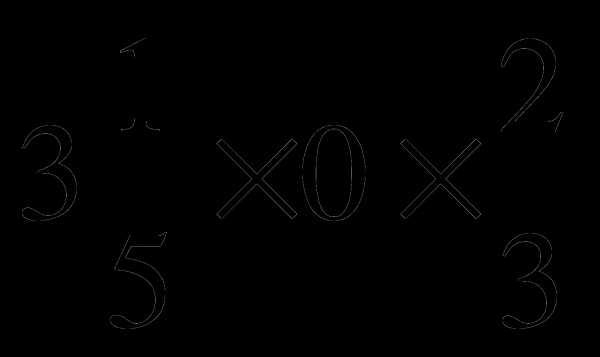 =
=
3.Работа на компьютерах ( 2 — 3 человека, с последующей проверкой учителя по локальной сети).
Вариант 1. Вариант 2.
Выполните вычитание: 1. Выполните вычитание:
3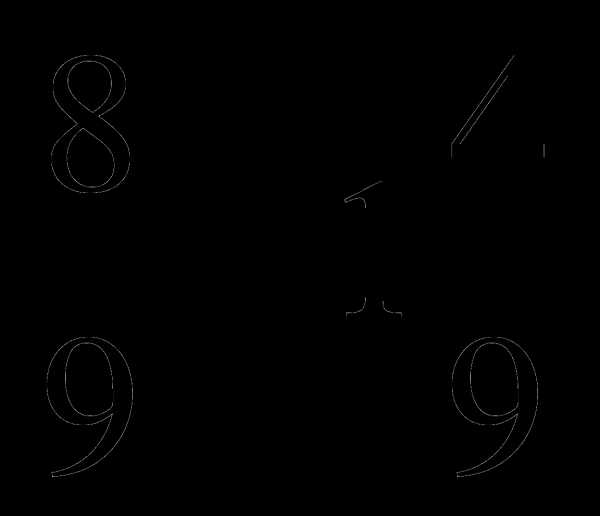 . 8
. 8 .
.
1) 2 ; 2) 2
; 2) 2 ; 3) 2
; 3) 2 ; 4) 2. 1) 7; 2) 2
; 4) 2. 1) 7; 2) 2 ; 3) 6
; 3) 6 ; 4) 6
; 4) 6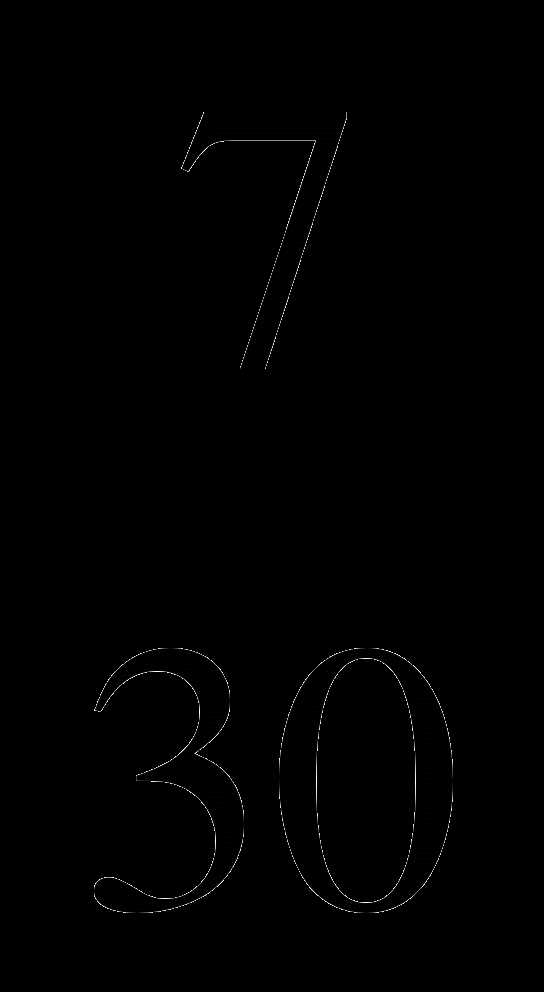 .
.
Ответ: 2. Ответ: 3.
2. Выполните сложение: 2. Выполните сложение:
5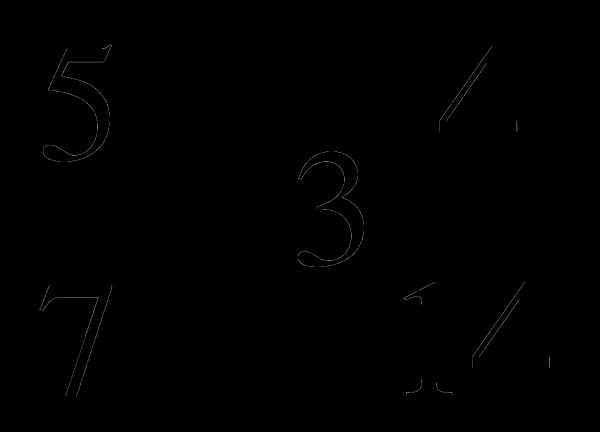 . 7
. 7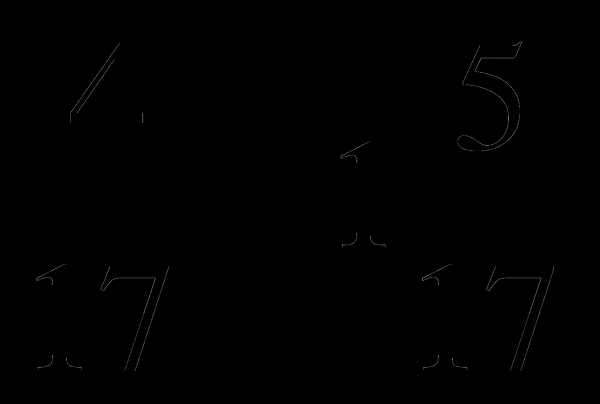 .
.
1) 8 ; 2) 9; 3) 8
; 2) 9; 3) 8 ; 4) 8
; 4) 8 . 1) 8
. 1) 8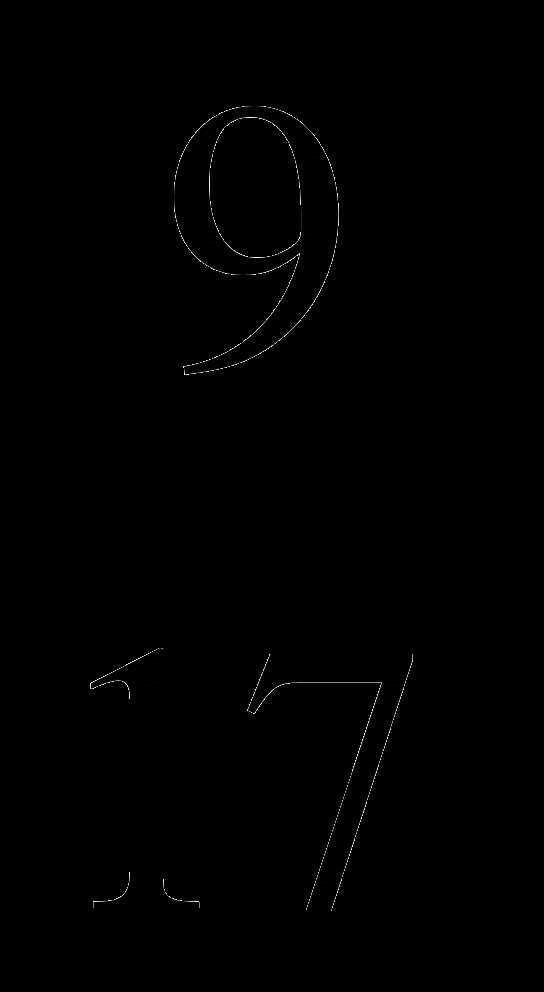 ; 2) 8
; 2) 8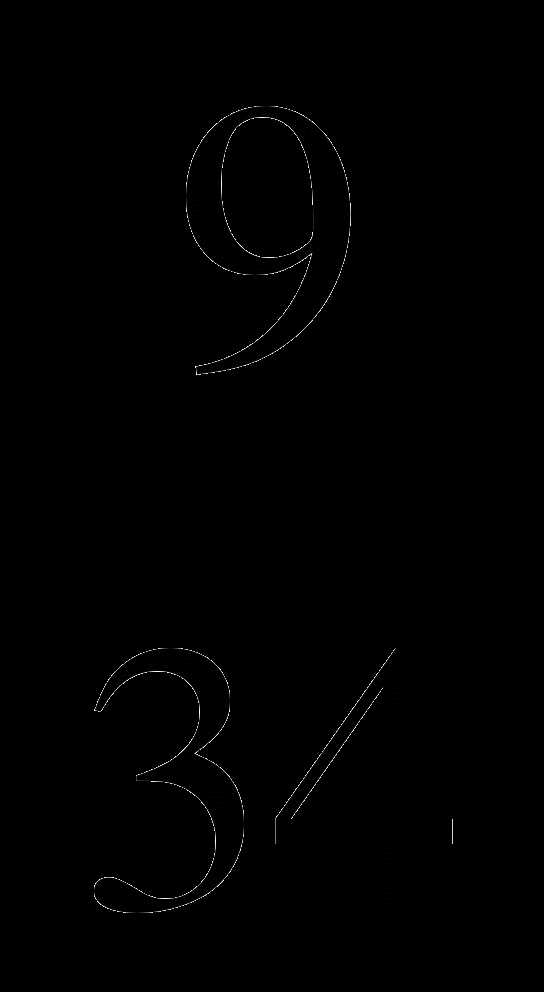 ; 3) 8; 4) 8
; 3) 8; 4) 8 .
.
Ответ: 2. Ответ: 1.
3.Решите уравнение: 3. Решите уравнение:
х-1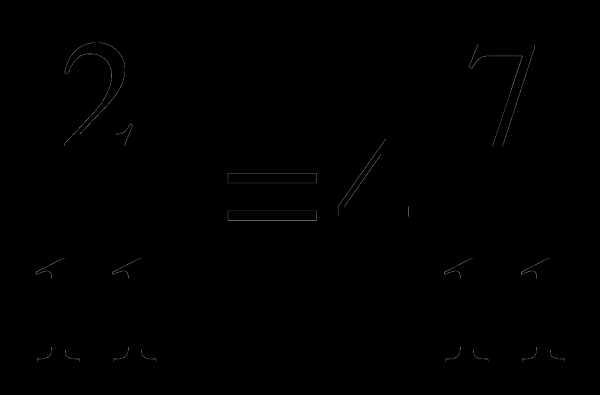 . 12-х=6
. 12-х=6 .
.
1) 3 ; 2) 5
; 2) 5 ; 3) 3
; 3) 3 ; 4) 5
; 4) 5 . 1) 5
. 1) 5 ; 2) 3
; 2) 3 ; 3) 3
; 3) 3 ; 4) 5
; 4) 5 .
.
Ответ: 4. Ответ: 4.
4. Увеличьте в 3 раза число  . 4. Выполните умножение:
. 4. Выполните умножение: 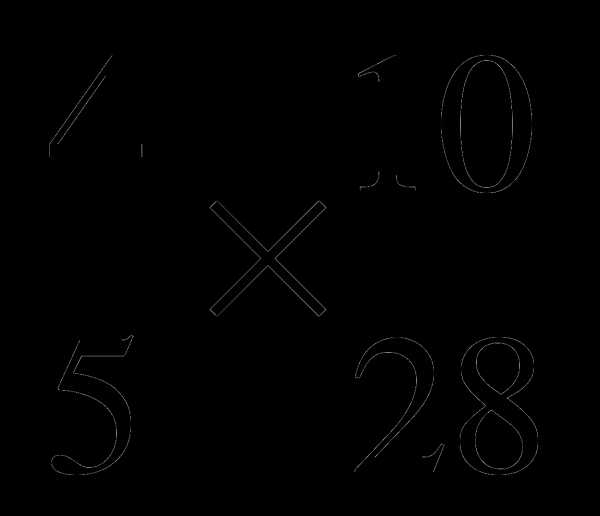 .
.
1)  ; 2) 3
; 2) 3 ; 3)
; 3) 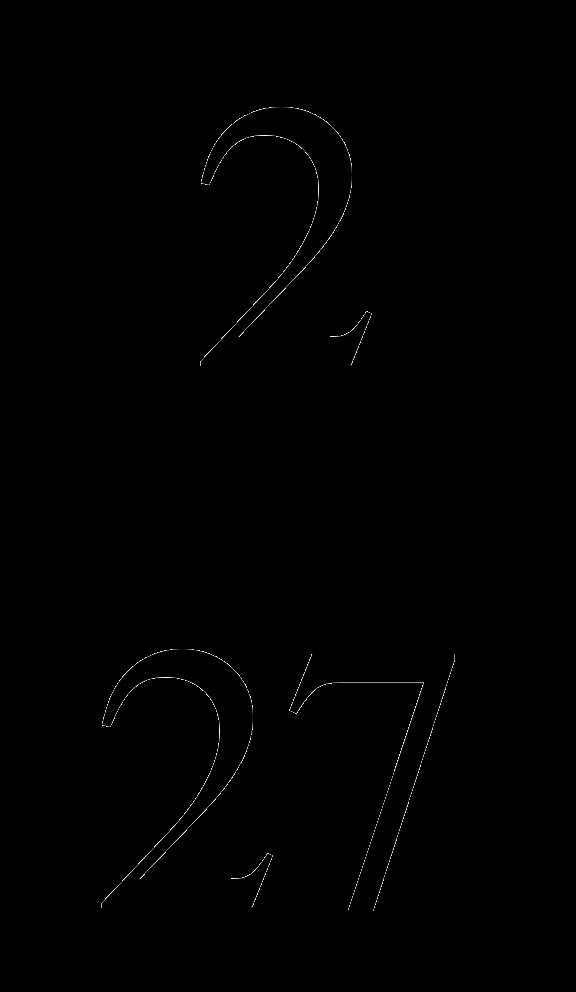 ; 4)
; 4)  . 1)
. 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4) 2.
; 4) 2.
Ответ: 4. Ответ: 2.
Вариант 3.
1. Выполните вычитание: 15 . 2. Выполните сложение: 6
. 2. Выполните сложение: 6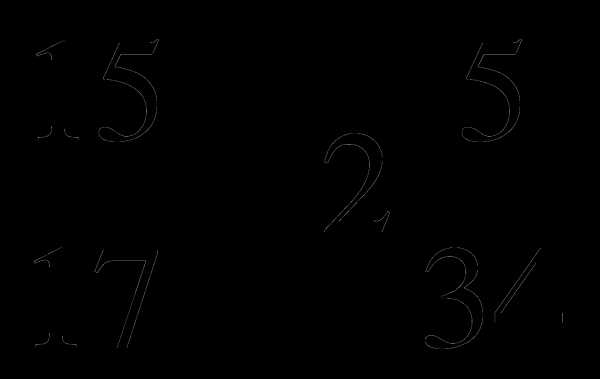 .
.
1) 2 ; 2) 2
; 2) 2 ; 3) 2; 4) 2
; 3) 2; 4) 2 . 1) 8
. 1) 8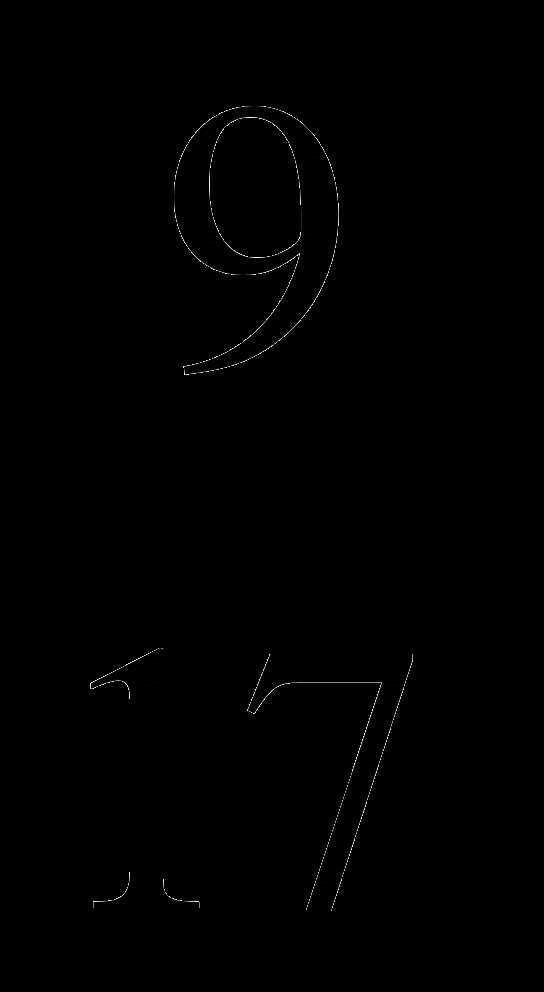 ; 2) 8
; 2) 8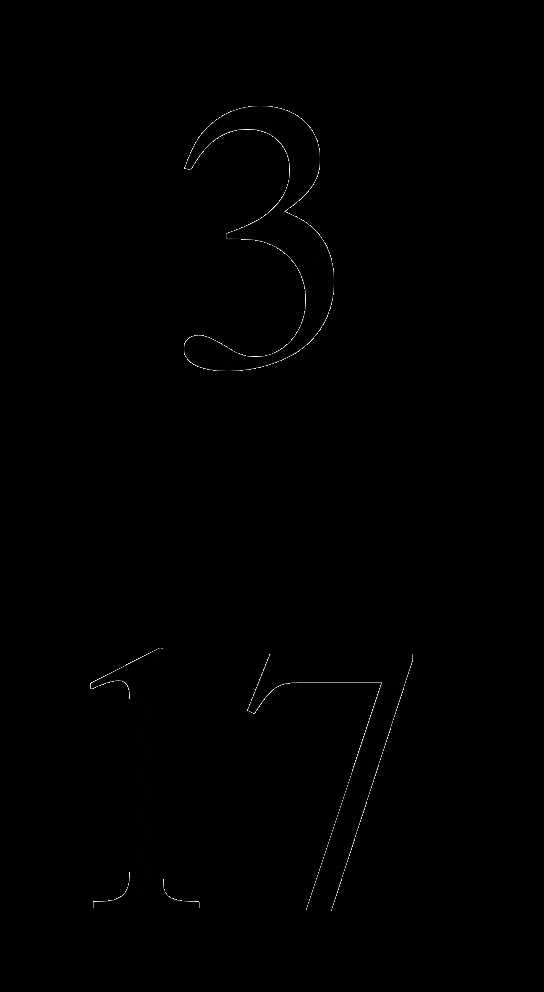 ; 3) 9
; 3) 9 ; 4) 8.
; 4) 8.
Ответ: 2. Ответ: 3.
3.Решите уравнение: 15 х = 10
х = 10 .
.
4; 2) 8
 ; 3) 4
; 3) 4 ; 4) 5
; 4) 5 .
.
Ответ: 3.
Выполните умножение: 3
 .
.12
 ; 2) 12
; 2) 12 ; 3) 12
; 3) 12 ; 4) 15
; 4) 15 .
.
Ответ: 4.
IV.Решение упражнений: (работа с учебником) № 454 (г), № 518.
№ 454 (г).
г) ( 1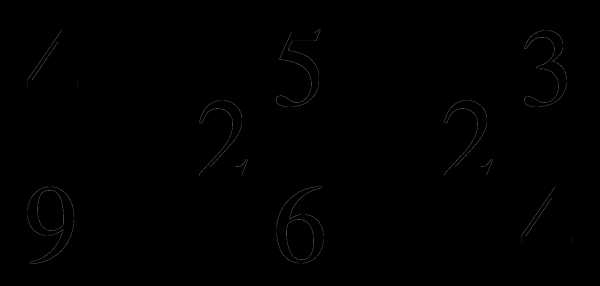 )
)  ( 2
( 2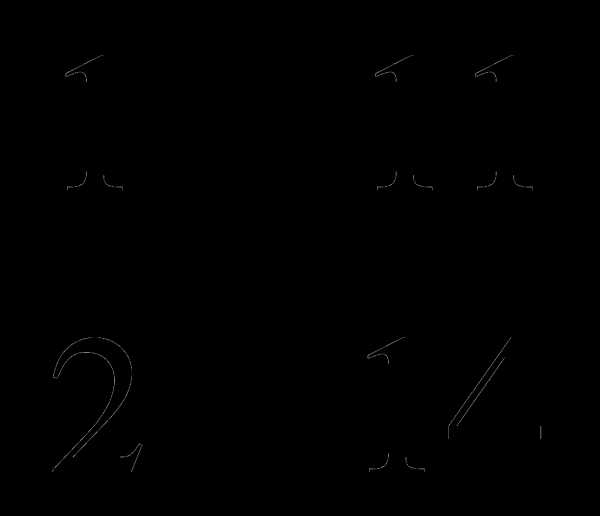 ) = 2
) = 2 .
.
1;
4;
2;
4) 1 .
№ 518.
40
 48 ( км/ч)-скорость скворца
48 ( км/ч)-скорость скворца48
 56 ( км/ч)-скорость голубя
56 ( км/ч)-скорость голубя
Ответ: 56 км/ч.
Карточки для учащихся на партах, как дополнительное задание (выполняется в тетрадях).
Карточка № 1. Карточка № 2.
1. Решите уравнение: 1. Решите уравнение:
1 – k = 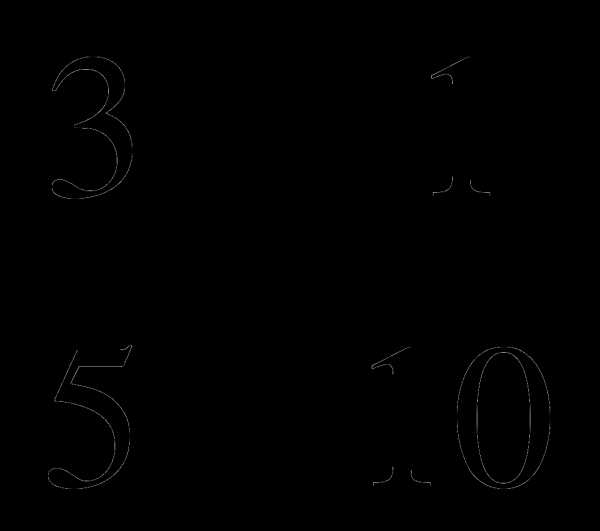 . t + 1 =
. t + 1 = 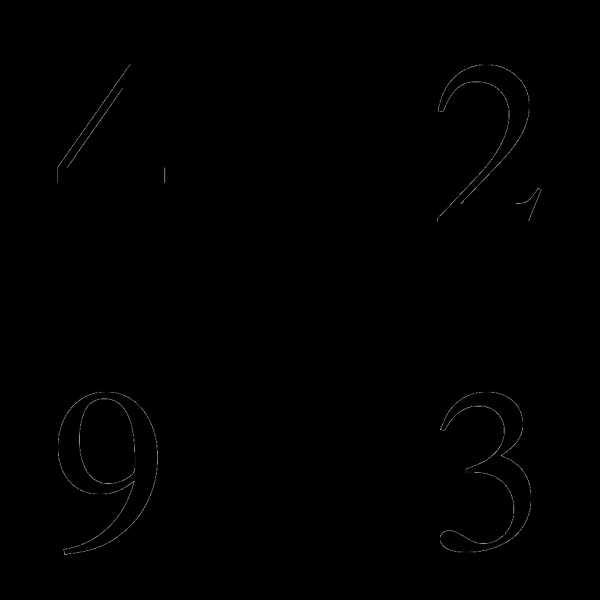 .
.
2. Вычислите: 2. Вычислите:
а) 5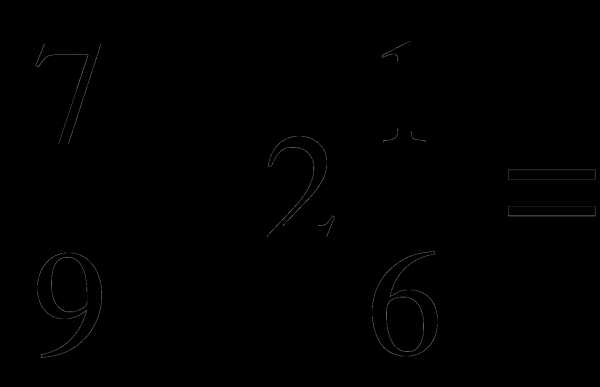 а) 5
а) 5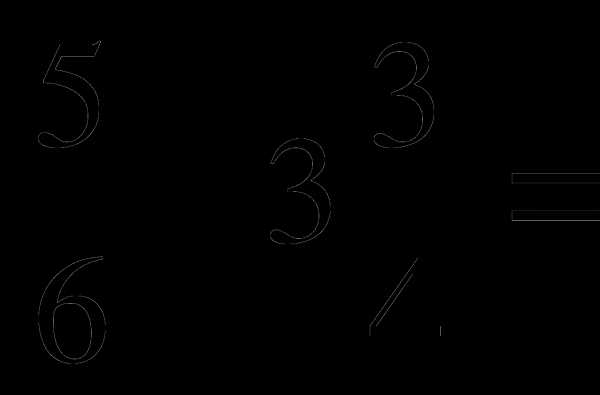
б) 4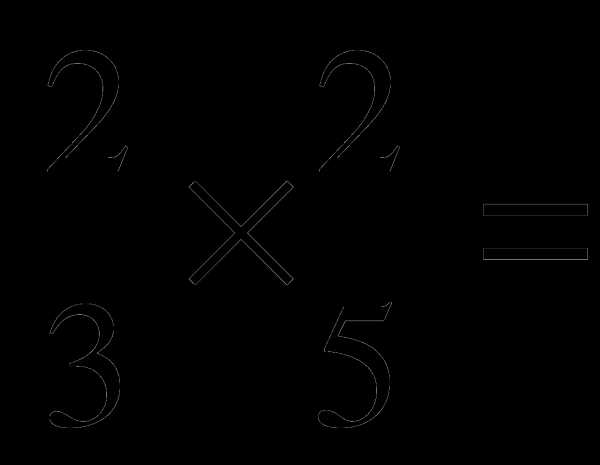 б)
б) 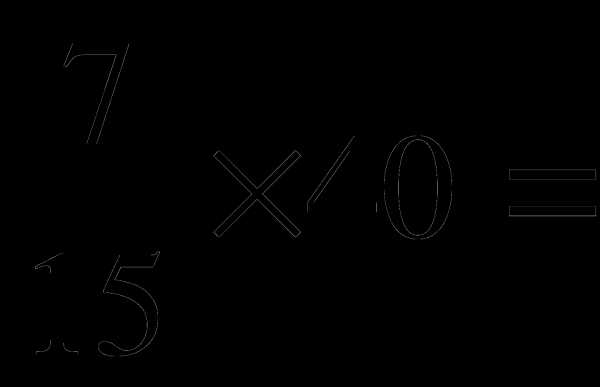
Карточка № 3.
1.Решите уравнение:
X + 2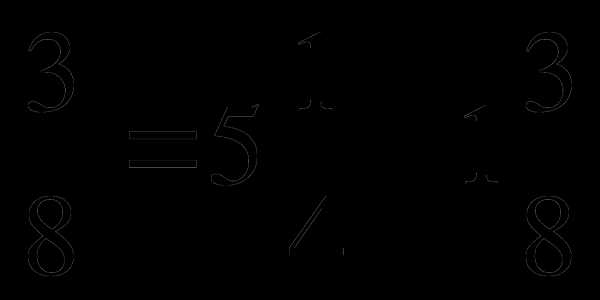 .
.
Вычислите:
а) 
б) 1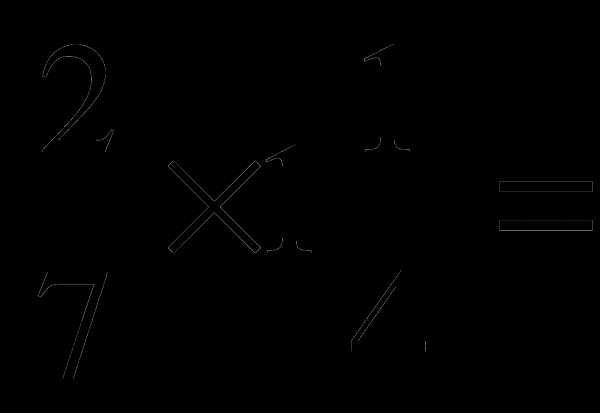
V.Физминутка. ( кроссворд ). А сейчас мы с вами немного отдохнём.
По горизонтали:
Деление числителя и знаменателя на одно и тоже число. ( Сокращение.)
Дробь, у которой числитель и знаменатель взаимно простые числа. ( Несократимая.)
На сколько сокращается дробь
 ? (Двенадцать.)
? (Двенадцать.)
По вертикали:
Название дроби, у которой числитель больше или равен знаменателю. ( Неправильная.)
Для нахождения общего знаменателя надо находить НОД или НОК? ( НОК).
Для сокращения дроби нужно находить НОД или НОК? ( НОД).
Проверка знаний и умений по пройденному материалу ( тестовая работа по карточкам: взаимоконтроль, ответы записаны на доске ). Итак, мы повторили все действия с дробями, а теперь проверим себя.
Вариант 1.
Вычислите сумму
 .
.
Ответ:
2. Собственная скорость катера 20
 км/ч. А скорость течения реки 2
км/ч. А скорость течения реки 2 км/ч. Какова скорость катера по течению реки ?
км/ч. Какова скорость катера по течению реки ?А. 22
 км/ч; Б. 22
км/ч; Б. 22 км/ч; В. 18
км/ч; В. 18 км/ч; Г. 23
км/ч; Г. 23 км/ч.
км/ч.3. Найдите значение выражения: 1
 — (
— (  ).
).А.
 ; Б. 1
; Б. 1 ; В.
; В.  ; Г. 1.
; Г. 1.4. Из 7
 т картофеля магазин продал 3
т картофеля магазин продал 3 т. Сколько тонн картофеля осталось?
т. Сколько тонн картофеля осталось?А. 3
 т; Б. 3
т; Б. 3 т; В. 4
т; В. 4 т; Г. 4
т; Г. 4 т.
т.5. Найдите произведение чисел
 .
.А.
 ; Б.
; Б.  ; В.
; В.  ; Г.
; Г.  .
.Ответы: 1. 1
 ; 2. Г; 3. В; 4. Б; 5. Б.
; 2. Г; 3. В; 4. Б; 5. Б.Вариант 2.
Вычислите сумму
 .
.
Ответ:
2. Собственная скорость катера 20
 км/ч, а скорость течения реки 2
км/ч, а скорость течения реки 2 км/ч. Какова скорость катера против течения реки?
км/ч. Какова скорость катера против течения реки? 
А. 22
 км/ч; Б. 18
км/ч; Б. 18 км/ч; В. 18
км/ч; В. 18 км/ч; Г. 23
км/ч; Г. 23 км/ч.
км/ч.3. Найдите значение выражения:
 .
.А.
 ; Б.
; Б.  ; В.
; В.  ; Г. 1.
; Г. 1.4. В одной корзине 7
 кг яблок, а в другой на 2
кг яблок, а в другой на 2 кг меньше. Сколько яблок во второй корзине?
кг меньше. Сколько яблок во второй корзине?А. 4
 кг; Б. 4
кг; Б. 4 кг; В. 4
кг; В. 4 кг; Г. 5
кг; Г. 5 кг.
кг.5. Найдите произведение чисел
 и
и  .
.А.
 ; Б.
; Б.  ; В.
; В.  ; Г.
; Г.  .
.Ответы: 1. 1
 ; 2. В; 3.Г; 4. А; 5. Б.
; 2. В; 3.Г; 4. А; 5. Б.Подведение итогов. Оценивается работа каждого ученика, подчёркивается знание правил, самостоятельность, грамотность при выполнении заданий, взаимопомощь, активность.
Слайд 12.
Дроби.
Дроби всякие нужны,
Дроби всякие важны.
Дробь учи, тогда сверкнёт удача.
Если дроби будешь знать,
Точно смысл их понимать,
Станет лёгкой даже сложная задача.
Слайд 13.
Самооценка знаний.
Домашнее задание. Повторить правила из п. 12,13; выполнить № 478 (е,з), № 451. Провести инструктаж по выполнению д/з; указать на что обратить внимание.
infourok.ru
Сложение, вычитание, умножение и деление обыкновенных дробей»
Урок по математике в 6 классе (по сингапурской методике обучения).
Учитель математики и физики 1 квалификационной категории МБОУ «СОШ №7 г. Азнакаево» РТ Салимшина Резеда Фандасовна
Тема: Повторение: Сложение, вычитание, умножение и деление обыкновенных дробей.
Урок – повторения и закрепления ЗУН
Цель урока:
— отрабатывать умения складывать, вычитать, умножать, делить дроби, решения простейших задач жизненной практики, способствовать умению рассуждать и логически мыслить, проверить ЗУН обучающихся по теме «Сложение и вычитание дробей с разными знаменателями», «Умножение и деление обыкновенных дробей»;
— способствовать воспитанию умения работать в парах и группах;
— способствовать развитию умения рассуждать и логически мыслить.
Задачи:
Способствовать овладению навыками критического и креативного мышления для генерации новых идей при решении задач динамично изменяющегося мира.
Оборудование: номера столов и участников, карточки с логическими задачами.
Ход урока:
Организационный момент.
ХАЙ ФАЙВ (СИГНАЛ ТИШИНЫ).
Учитель: Здравствуйте, садитесь. Сегодня мы проведём урок, применяя сингапурские структуры урока. Сообщение темы, цели, плана урока.
Повторение.
Цель: повторение изученного.
ФИНК-РАЙТ-РАУНД РОБИН (ПОДУМАЙТЕ – ЗАПИШИТЕ – ОБСУДИТЕ)
Учитель: Подумайте, запишите и обсудите в группах ответ на вопрос:
— Какие темы мы изучили в этом полугодии?
Запишите как можно больше тем и математических терминов, которые вы узнали в этом учебном году.
Время по 1 минуте каждому подумать и записать на листочках, обсудить по очереди и выслушать друг друга, записать новые идеи команды.
По команде учителя выслушать 2-3 учеников команды.
(Ответы: Делитель, Кратное, Сокращение дробей, Признаки делимости, НОД, НОК, Простые числа, Сравнение, сложение, вычитание, дробей с разными знаменателями, Сравнение, сложение, вычитание смешанных чисел, Умножение, деление дробей.)
Проверка домашнего задания.
Цель: повторение сложения, вычитания, умножения, деления дробей.
Учитель: Домашним заданием было записать на одной стороне листочка любой пример или вопрос, а на обратной стороне – ответ. КУИЗ – КУИЗ – ТРЕЙД (ОПРОСИ – ОПРОСИ – ОБМЕНЯЙСЯ КАРТОЧКАМИ).
Учитель: Ребята, вы будете проверять и обучать друг друга по пройденному материалу, используя карточки с вопросами и ответами.
Учитель: 1)Ребята, встаньте, задвиньте стулья, возьмите свои карточки, поднимите руку и найдите ближайшую пару.
2)Ученик А у которого день рождения ближе к 19 декабрю спрашивает ученика В (задаёт вопрос из своей карточки).
3)Ученик В отвечает.
4)Ученик А помогает и хвалит (подскажи, научи, переспроси, похвали).
5)Ученики меняются ролями (ученик В спрашивает ученика А).
6)Ученики меняются карточками и благодарят друг друга.
Можно повторить шаги 1-6 несколько раз.
Учитель: контролирует время процесса.
4.Математический диктант. (в тетрадях по вариантам, с последующей взаимопроверкой, чётные номера – 1 вариант, не чётные номера – 2 вариант)
Цель: проверить знания по сложению, вычитанию, умножению, делению дробей.
В-1
+
—
·
В — 2
+
—
·
Ответы записаны на обратной стороне доски.
Учитель: — Поменяйтесь тетрадями с партнёром по лицу, оцените работу партнёра.
5.Физминутка.— А теперь ребята встали,
Дружно руки вверх подняли,
В стороны, вперёд, назад,
Наклонились вправо, влево,
Тихо сели вновь за дело.
6.Домашнее задание Составить и записать по 2 примера на +, -, ·, : дробей.
7.Занимательные задачи.
Цель: способствовать развитию логического мышления.
Учитель: Раздаёт карточки с заданиями (или уже они на столе). Учащиеся каждый сам решают задачи. Через определённое время учитель проверяет ответы. ТЭЙК – ОФ – ТАЧ ДАУН ( ВСТАТЬ – СЕСТЬ) для получения информации о классе.
Учитель: Встаньте, пожалуйста, те, у кого ответ в первой задаче ответ = 4 . Спасибо, садитесь.
Встаньте, пожалуйста, те, у кого ответ во второй задаче ответ – одной девочке дали клетку с кроликом. Спасибо, садитесь.
Встаньте, пожалуйста, те, у кого ответ в третьей задаче ответ — всего 3 человека: сын, отец и дед . Спасибо, садитесь.
Встаньте, пожалуйста, те, у кого ответ в четвёртой задаче ответ = 2,3 . Спасибо, садитесь.
Встаньте, пожалуйста, те, у кого ответ в пятой задаче ответ = на 12 равных частей. Спасибо, садитесь.
Задачи:
1.В каждом из четырёх углов комнаты сидит кошка. Напротив каждой из этих кошек сидит кошка. Сколько всего в этой комнате кошек?
2.В клетке находится три кролика. Три девочки попросили дать им по одному кролику. Просьба девочек была удовлетворена, каждой из них дали кролика. И всё же в клетке остался один кролик. Как могло такое случиться?
3.Два отца и два сына разделили между собой три апельсина так, что каждому досталось по одному апельсину. Как такое могло случиться?
4.Какой знак надо поставить между 2 и 3, чтобы число стало больше 2, но меньше 3?
5. Как разрезать торт на части, чтобы его можно было разделить поровну как на трёх, так и на четырёх человек?
8.Рефлексия.
Учитель: Ребята, перед вами новогодняя ёлка и ёлочные украшения. Если вы сегодня получили удовольствие от урока, выберите яркую красную игрушку, если вам не понравился урок – тёмную, если вам было всё равно – зелёную. Нарядите нашу ёлку.
Занимательные задачи.
1.В каждом из четырёх углов комнаты сидит кошка. Напротив каждой из этих кошек сидит кошка. Сколько всего в этой комнате кошек?
2.В клетке находится три кролика. Три девочки попросили дать им по одному кролику. Просьба девочек была удовлетворена, каждой из них дали кролика. И всё же в клетке остался один кролик. Как могло такое случиться?
3.Два отца и два сына разделили между собой три апельсина так, что каждому досталось по одному апельсину. Как такое могло случиться?
4.Какой знак надо поставить между 2 и 3, чтобы число стало больше 2, но меньше 3?
5. Как разрезать торт на части, чтобы его можно было разделить поровну как на трёх, так и на четырёх человек?
Занимательные задачи.
1.В каждом из четырёх углов комнаты сидит кошка. Напротив каждой из этих кошек сидит кошка. Сколько всего в этой комнате кошек?
2.В клетке находится три кролика. Три девочки попросили дать им по одному кролику. Просьба девочек была удовлетворена, каждой из них дали кролика. И всё же в клетке остался один кролик. Как могло такое случиться?
3.Два отца и два сына разделили между собой три апельсина так, что каждому досталось по одному апельсину. Как такое могло случиться?
4.Какой знак надо поставить между 2 и 3, чтобы число стало больше 2, но меньше 3?
5. Как разрезать торт на части, чтобы его можно было разделить поровну как на трёх, так и на четырёх человек?
Занимательные задачи.
1.В каждом из четырёх углов комнаты сидит кошка. Напротив каждой из этих кошек сидит кошка. Сколько всего в этой комнате кошек?
2.В клетке находится три кролика. Три девочки попросили дать им по одному кролику. Просьба девочек была удовлетворена, каждой из них дали кролика. И всё же в клетке остался один кролик. Как могло такое случиться?
3.Два отца и два сына разделили между собой три апельсина так, что каждому досталось по одному апельсину. Как такое могло случиться?
4.Какой знак надо поставить между 2 и 3, чтобы число стало больше 2, но меньше 3?
5. Как разрезать торт на части, чтобы его можно было разделить поровну как на трёх, так и на четырёх человек?
1
2
3
4
5
6
7
8
Ответы математического диктанта:
В-1
4
3
В-2
1
1
videouroki.net
Сложение и вычитание, деление и умножение обыкновенных дробей
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ КАЗАХСТАН
КОСТАНАЙСКИЙ
ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ
Реферат
На
тему: «Сложение
и вычитание, деление
и умножение обыкновенных
дробей».
Костанай
2011 год
СОДЕРЖАНИЕ
- Из истории обыкновенных дробей ………………………………………..3
- Действия с обыкновенными дробями …………..…………………………..5
2.1. Сложение
и вычитание обыкновенных
2.2. Умножение
и деление обыкновенных дробей
3. Примеры на сложение, вычитание, умножение и деление дробей ……. 10
4. Список
литературы ……………………………………………………………11
1. Из истории возникновения обыкновенных дробей.
Дроби появились в глубокой древности. При разделе добычи, при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести дроби.
Древние египтяне уже знали, как поделить 2 предмета на троих, для этого числа –2/3- у них был специальный значок. Между прочим, это была единственная дробь в обиходе египетских писцов, у которой в числителе не стояла единица – все остальные дроби непременно имели в числителе единицу (так называемые основные дроби): 1/2; 1/3; 1/28; … . Если египтянину нужно было использовать другие дроби, он представлял их в виде суммы основных дробей. Например, вместо 8/15 писали 1/3+1/5. Иногда это бывало удобно. В папирусе Ахмеса есть задача :
«Разделить 7 хлебов между 8 людьми». Если резать каждый хлеб на 8 частей, придётся провести 49 разрезов.
А по-египетски эта задача решалась так: Дробь 7/8 записывали в виде долей: 1/2+1/4+1/8. Значит каждому человеку надо дать полхлеба, четверть хлеба и восьмушку хлеба; поэтому четыре хлеба разрезали пополам, два хлеба- на 4 части и один хлеб на 8 долей, после чего каждому дали его часть.
Но складывать такие дроби было неудобно. Ведь в оба слагаемых могут входить одинаковые доли, и тогда при сложении появится дробь вида 2/n. А таких дробей египтяне не допускали. Поэтому, папирус Ахмеса начинается с таблицы, в которой все дроби такого вида от 2/5 до 2/99 записаны в виде суммы долей. С помощью этой таблицы выполняли и деление чисел. Вот, например, как 5 делили на 21: 5/21
Умели египтяне также умножать и делить дроби. Но для умножения приходилось умножать доли на доли, а потом, быть может, снова использовать таблицу. Ещё сложнее обстояло с делением.
В древнем Вавилоне предпочитали наоборот, — постоянный знаменатель, равный 60-ти. Шестидесятеричными дробями, унаследованными от Вавилона, пользовались греческие и арабские математики и астрономы. Но было неудобно работать над натуральными числами, записанными по десятичной системе, и дробями, записанными по шестидесятеричной. А работать с обыкновенными дробями было уже совсем трудно. Поэтому голландский математик Симон Стевин предложил перейти к десятичным дробям.
Интересная система дробей была в Древнем Риме. Она основывалась на делении на 12 долей единицы веса, которая называлась асс. Двенадцатую долю асса называли унцией. А путь, время и другие величины сравнивали с наглядной вещью- весом. Например, римлянин мог сказать, что он прошел семь унций пути или прочел пять унций книги. При этом, конечно, речь шла не о взвешивании пути или книги. Имелось в виду, что пройдено 7/12 пути или прочтено 5/12 книги. А для дробей, получающихся сокращением дробей со знаменателем 12 или раздроблением двенадцатых долей на более мелкие, были особые названия.
Даже сейчас иногда говорят:”Он скрупулёзно изучил этот вопрос.” Это значит, что вопрос изучендо конца, что не одной самой малой неясности не осталось. А происходит странное слово “скрупулёзно” от римского названия 1/288 асса — “скрупулус”. В ходу были и такие названия: ”семис”- половина асса, “секстанс”- шестая его доля, “семиунция”- половина унции, т.е. 1/24 асса и т.д. Всего применялось 18 различных названий дробей. Чтобы работать с дробями, надо было помнить для этих дробей таблицу сложения и таблицу умножения. Поэтому римские купцы твёрдо знали, что при сложении триенса (1/3 асса) и секстанса получается семис, а при умножении беса (2/3 асса) на сескунцию( 2/3 унции, т.е.1/8 асса) получается унция. Для облегчения работы составлялись специальные таблицы, некоторые из которых дошли до нас.
Современную систему записи дробей с числителем и знаменателем создали в Индии. Только там писали знаменатель сверху, а числитель — снизу, и не писали дробной черты. А записывать дроби в точности, как сейчас, стали арабы.
Обыкновенная дробь – это число вида , где m и n – натуральные числа, например . Число m называется числителем дроби, n – знаменателем. Среди обыкновенных дробей различают правильные и неправильные дроби. Дробь называется правильной, если ее числитель меньше знаменателя, и неправильной, если ее числитель больше знаменателя или равен ему.
2. Действия с обыкновенными дробями.
2.1. Сложение и вычитание обыкновенных дробей.
Сложение обыкновенных дробей выполняется так:
а) если знаменатели дробей одинаковы, то к числителю первой дроби прибавляют числитель второй дроби и оставляют тот же знаменатель, т.е. ;
б) если знаменатели дробей различны, то дроби сначала приводят к общему знаменателю, предпочтительнее к наименьшему, а затем к числителю первой дроби прибавляют числитель второй дроби, т.е. .
Вычитание обыкновенных дробей выполняют следующим образом:
а) если знаменатели дробей одинаковы, то от числителя первой дроби вычитают числитель второй дроби и оставляют тот же знаменатель, т.е.
.
б) если знаменатели различны, то сначала дроби приводят к общему знаменателю, а затем от числителя первой дроби вычитают числитель второй дроби, т.е. .
Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же.
Например:
1.
2.
3.
4.
5.
6.
Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.
Например:
1.
2.
3.
4.
5.
6.
7.
8.
2.2. Умножение и деление обыкновенных дробей.
Умножение обыкновенных дробей выполняется следующим образом:
т.е. перемножаются отдельно числители, отдельно знаменатели, первое произведение делают числителем, второе – знаменателем.
При умножении дроби на натуральное число, числитель дроби умножают на это число, а знаменатель оставляют без изменения.
Если множители являются смешанными числами, то сначала их нужно записать в виде неправильных дробей, затем воспользоваться правилом умножения дробей.
Деление обыкновенных дробей выполняют следующим образом:
т.е. делимое умножают на дробь , обратную делителю .
Умножение обыкновенной дроби на целое число.
Чтобы умножить дробь на целое число, достаточно числитель дроби умножить на это число, оставив прежний знаменатель.
Например:
1.
2.
3.
4.
Умножение смешанного числа на целое число.
При умножении смешанного числа на целое в большинстве случаев проще отдельно умножить целое и дробь на целое число.
Например:
1.
2.
3.
Умножение дробь на дробь
Чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:
Например:
1.
2.
3.
4. .
5.
Деление обыкновенных дробей на целое число.
При делении дроби на целое число достаточно числитель разделить на целое число, оставив прежний знаменатель.
Например:
1.
2.
Как поступать в том случае, когда числитель данной дроби не делится на целое число. Тогда существует следующее правило
Чтобы разделить дробь на целое число, достаточно знаменатель дроби умножить на это число, оставив числитель прежним.
Например:
1.
2.
Деление дроби на дробь.
Чтобы разделить дробь на дробь, нужно первую дробь переписать, а вторую дробь перевернуть (это важно!) и их перемножить, т.е. знаменатель на знаменатель, числитель на числитель.:
Например:
1.
2.
3.
4.
3. Примеры на сложение, вычитание, умножение и деление обыкновенных дробей.
Реши
самостоятельно:
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
stud24.ru

 ; 3) 4
; 3) 4 ; 4) 5
; 4) 5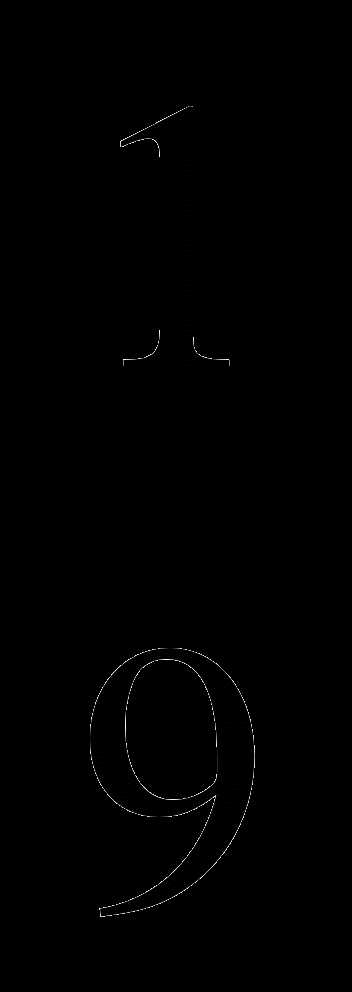 .
.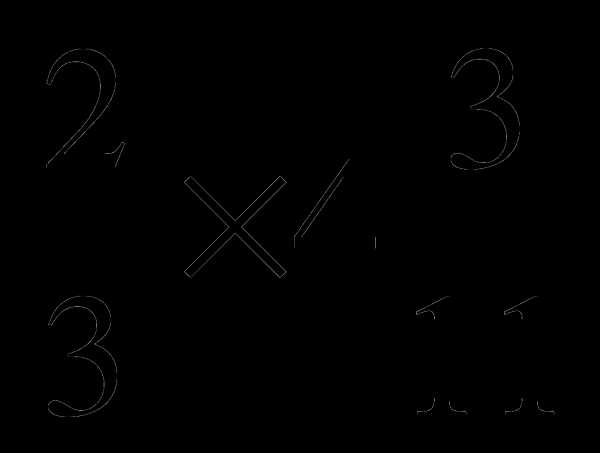 .
. ; 2) 12
; 2) 12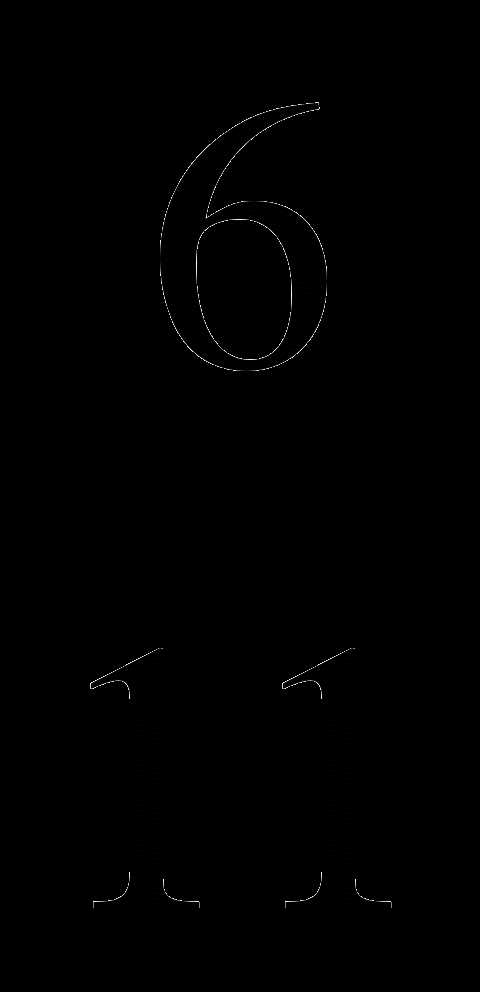 ; 4) 15
; 4) 15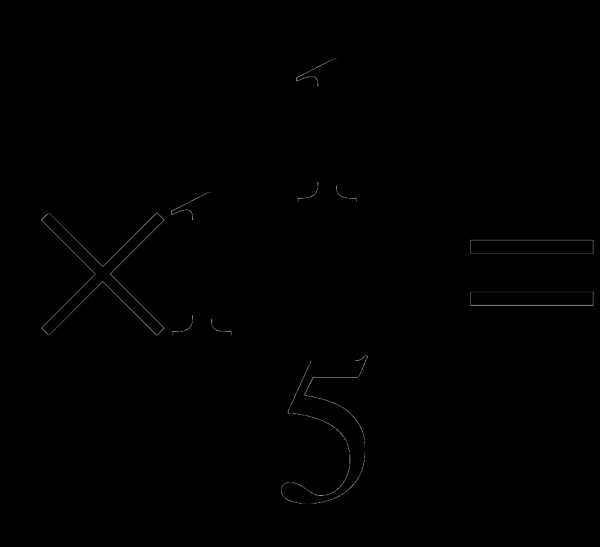 48 ( км/ч)-скорость скворца
48 ( км/ч)-скорость скворца 56 ( км/ч)-скорость голубя
56 ( км/ч)-скорость голубя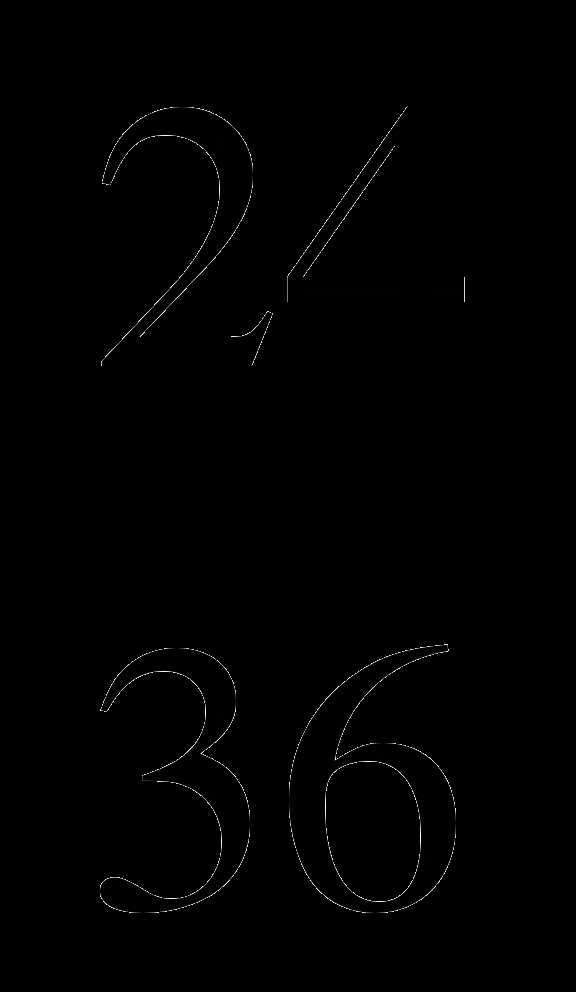 ? (Двенадцать.)
? (Двенадцать.) .
. км/ч. Какова скорость катера по течению реки ?
км/ч. Какова скорость катера по течению реки ? км/ч; В. 18
км/ч; В. 18 км/ч; Г. 23
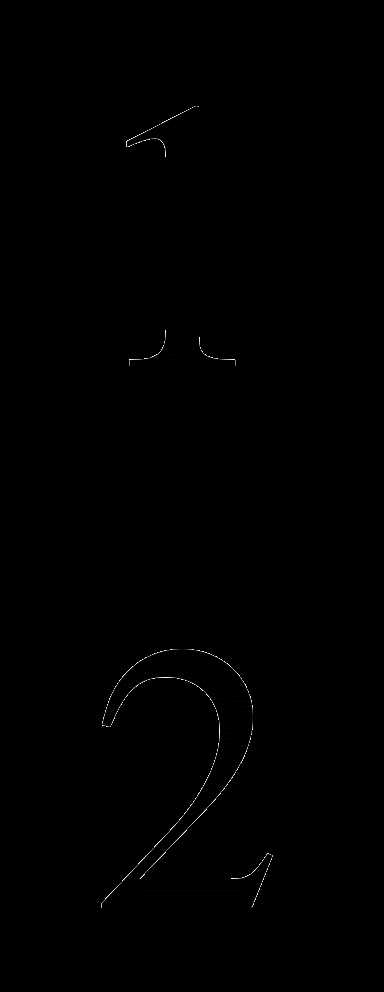
км/ч; Г. 23 — (
— ( 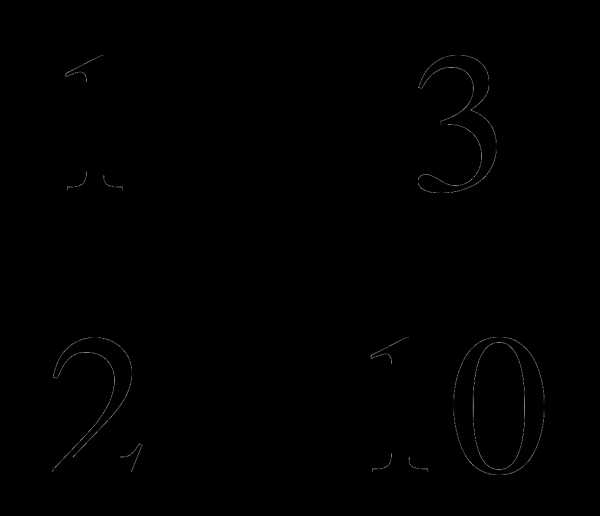 ).
).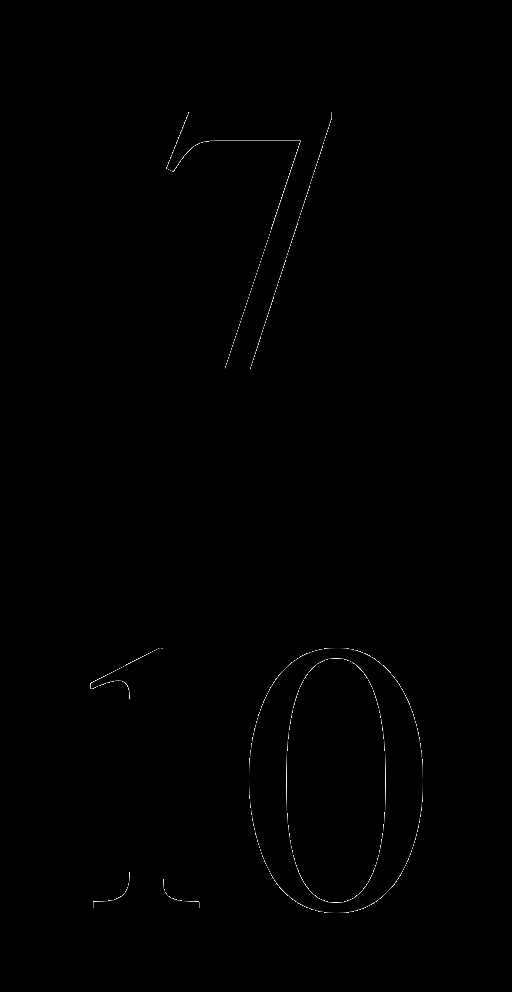 ; Б. 1
; Б. 1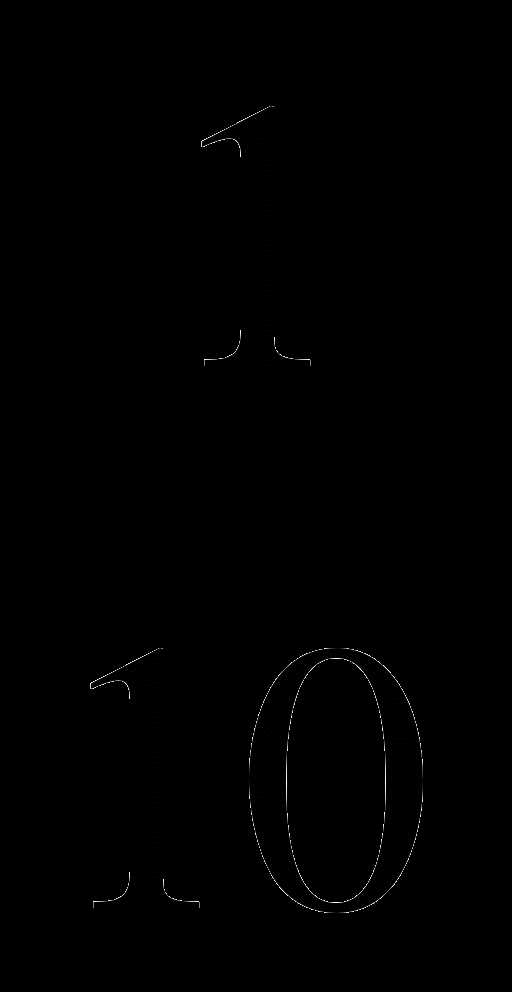 ; В.
; В.  ; Г. 1.
; Г. 1. т; Б. 3
т; Б. 3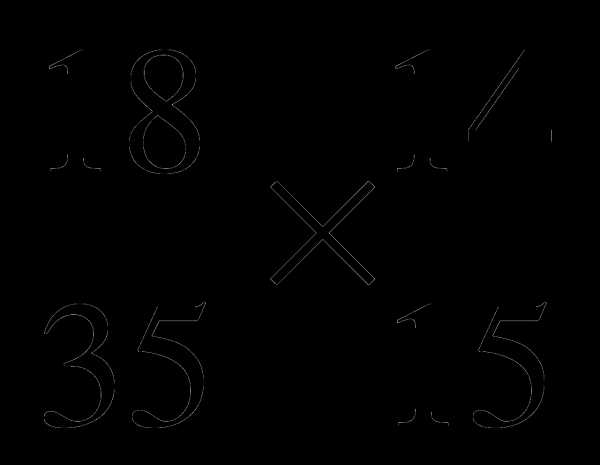 .
. ; Б.
; Б.  ; В.
; В. 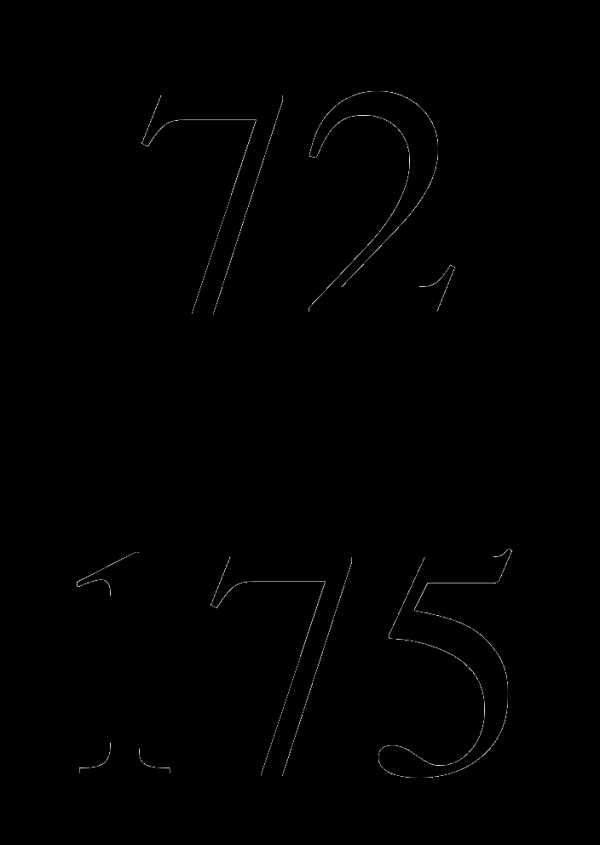 ; Г.
; Г.  ; 2. Г; 3. В; 4. Б; 5. Б.
; 2. Г; 3. В; 4. Б; 5. Б. .
. .
.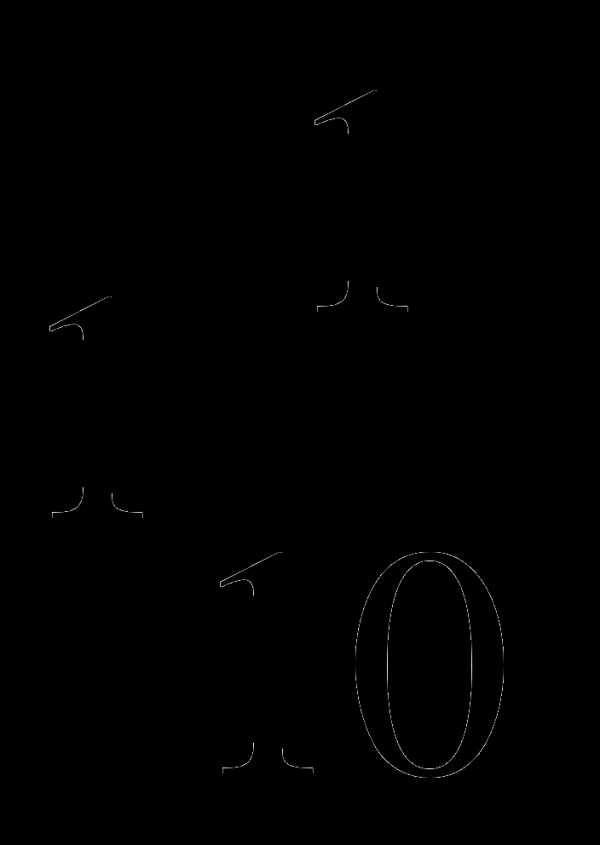 ; В.
; В.  кг яблок, а в другой на 2
кг яблок, а в другой на 2 кг; Б. 4
кг; Б. 4 кг; В. 4
кг; В. 4 и
и  .
.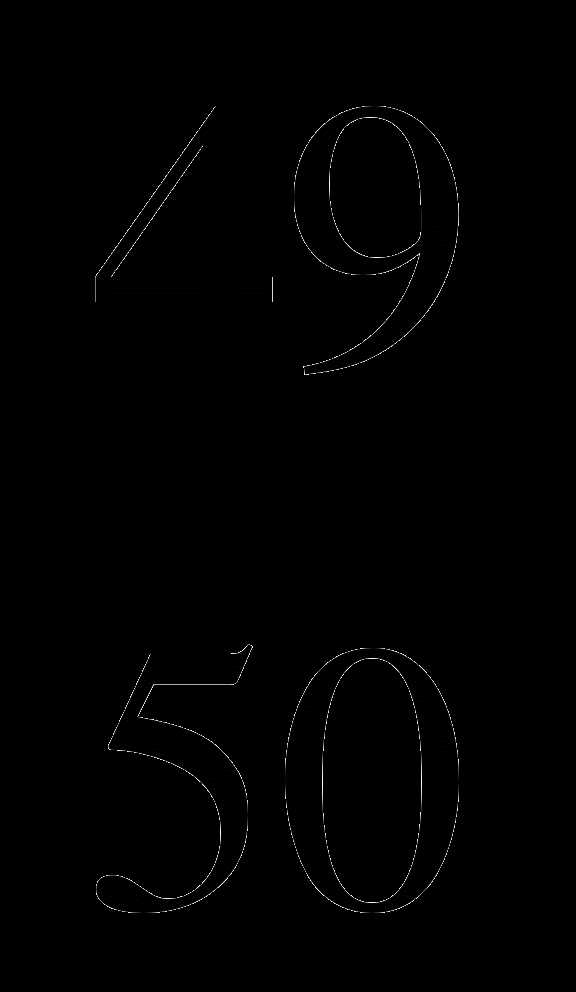 ; Б.
; Б. 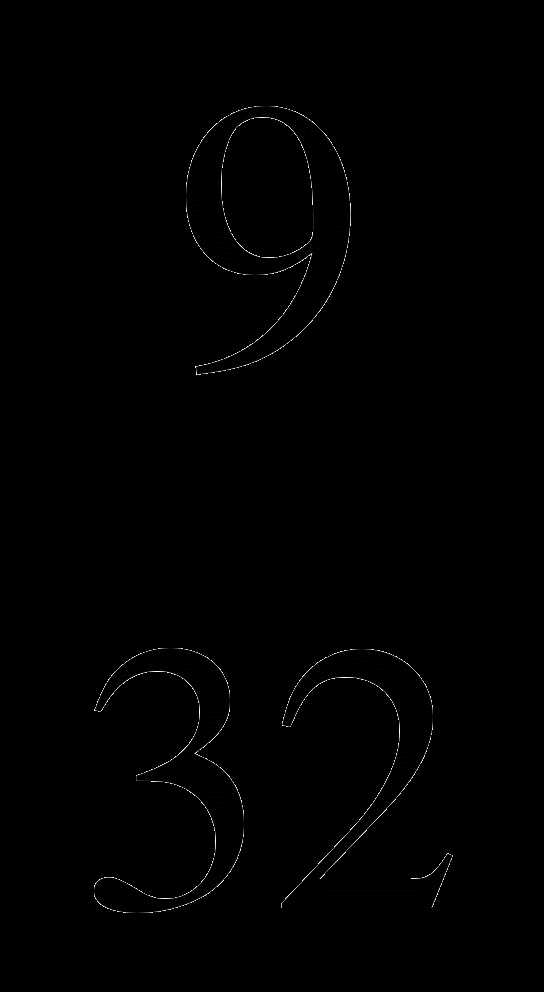 ; В.
; В. 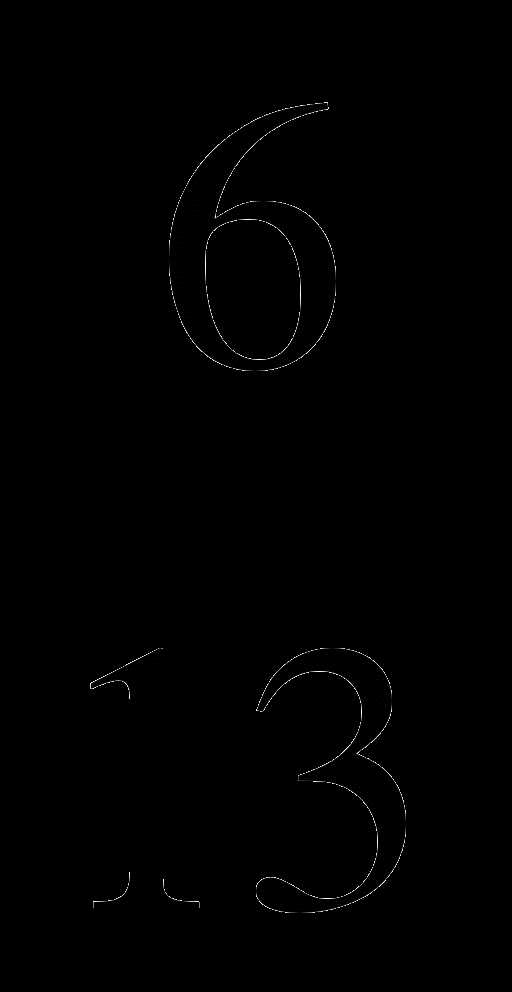 ; Г.
; Г.