Непрерывность функций с примерами решения и образцами выполнения
Оглавление:
Непрерывность функции:
Непрерывные функции, точки разрыва и их классификация, действия над непрерывными функциями, свойства функций, непрерывных на сегменте.
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если:
- функция определена в точке x₀ и в некоторой ее окрестности, содержащей эту точку;
- функция имеет предел при х → x₀;
- предел функции при х → x₀ равен значению функции в точке x₀:
(10.1)
Если в точке x₀ функция непрерывна, то точка x₀ называется точкой непрерывности функции.
Пример:
Исследовать на непрерывность функцию в точке х = 1.
Решение:
Чтобы доказать, что функция непрерывна в точке х = 1, необходимо проверить выполнение трех следующих условий (определение непрерывности):
- функция определена в точке х = 1 ⇒ f(1) = e;
- существует ;
- этот предел равен значению функции в точке х = 1 :
Таким образом, доказано, что функция непрерывна в точке х = 1.
Замечание:
Формулу (10.1) можно записать в виде
(10.2)
так как . Это значит, что при нахождении предела непрерывной функции можно переходить к пределу под знаком функции.
Введем понятие непрерывности функции в точке х₀ справа и слева.
Если, существует f(x) = f(x₀), то функция называется непрерывной в точке x₀ слева. Аналогично определяется непрерывность функции справа.
Так как ∆x = x-x₀, a ∆y = f(x)-(x₀), то условие (10.1) равносильно следующему:
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции
(10.3)
Пример:
Показать, что функция у = х³ непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y.
∆y= (x+∆x)³-x³ = x³+3x²∆x+3x∆x²+∆x³-x³ = 3x²∆x+3x∆x²+∆x³.
Используя теоремы о пределе суммы и произведения функции, получим
(3x²∆x 4- 3x∆x² + ∆x³) = 0.
Следовательно, функция у = х³ непрерывна при — ∞< х < ∞.
Точки разрыва функции и их классификацияОпределение:
Точка х₀ называется точкой разрыва функции у = f(x), если она принадлежит области определения функции или ее границе и не является точкой непрерывности.
Так, например, функция (рис. 89) терпит разрыв при х = 1. Эта функция не определена в точке х = 1, и не существует предела функции в этой точке.
Рис. 89. График функцииОпределение:
Точка разрыва x₀ функции у = f(x) называется точкой устранимого разрыва, если существуют оба односторонних предела в точке x₀ и они равны, т. е.
Пример:
Исследовать на непрерывность функцию
Решение:
В точке x=-1 функция не определена, так как, выполнив подстановку, получаем неопределенность . В других точках дробь можно сократить на (1 + х), так как в них 1 + х ≠ 0. Легко видеть, что односторонние пределы слева и справа в точке х = — 1 равны между собой и их можно вычислить:
В других точках дробь можно сократить на (1 + х), так как в них 1 + х ≠ 0. Легко видеть, что односторонние пределы слева и справа в точке х = — 1 равны между собой и их можно вычислить:
Таким образом, при x = -1 данная функция имеет устранимый разрыв.
Он будет устранен, если положить, что при x = -1 ⇒ у == 3.
Определение:
Если в точке x₀ односторонние пределы слева и справа существуют, но не равны, точка x₀ называется точкой разрыва I рода.
Пример:
Исследовать на непрерывность функцию
(рис. 90).
Решение: Вычислим односторонние пределы функции в точке ее разрыва х = 4.
Предел слева —.
Предел справа — .
Пределы слева и справа существуют, но не равны, следовательно, точка x = 4 для данной функции — точка разрыва I рода (точка скачка).
Определение:
Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода.
В точках разрыва II рода не существует хотя бы один из односторонних пределов. Функция , представленная на рис. 89, не имеет ни левого, ни правого конечного предела в точке х = 1. Следовательно, для данной функции x = 1 является точкой разрыва II рода.
Действия над непрерывными функциямиТеорема:
Непрерывность суммы, произведения и частного непрерывных функций. Если функции ϕ(x) и ψ(x) непрерывны в точке Хо, то их сумма и произведение также непрерывны в точке x₀. Если, кроме того, знаменатель в рассматриваемой точке не равен нулю, то частное непрерывных функций есть функция непрерывная.
Докажем непрерывность произведения.
Дано: непрерывность функций в точке x₀:
и
Доказать, что f(x) — ϕ(x) ∙ ψ(x) есть функция непрерывная в точке x₀, т. е. f(x) — f(x₀).
Доказательство:
f(x) = [ϕ(x) ∙ ψ(x)] = ϕ(x) ∙ ψ(x) = ϕ(x₀) ∙ ψ(x₀) = f(x₀).
Можно строго доказать, что все основные элементарные функции непрерывны при всех значениях х, для которых они определены.
Например, степенная у = xⁿ, показательная у = , тригонометрические у = sin х и у = cos х функции непрерывны на всей числовой оси (х ∈ R), логарифмическая функция непрерывна при х > 0, а тригонометрическая у = tg x непрерывна в каждом из интервалов и терпит разрыв II рода в точках (k = 0; ±1; ±2;…).
Теорема:
Непрерывность сложной функции. Если функция и = ϕ(x) непрерывна в точке x₀, а функция у = f(u) непрерывна в точке и₀ = ϕ(x₀), то сложная функция у = f [ϕ(x)] непрерывна в точке x₀.
Без доказательства.
В заключение этого раздела рассмотрим два предела, которые нам понадобятся в дальнейшем.
Пример:
Вычислить
Решение:
Заметим, что при х → 0 числитель и знаменатель одновременно стремятся к нулю, т.е. имеет место неопределенность вида . Выполним преобразование
Так как данная логарифмическая функция непрерывна в окрестности точки х = 0, то можно перейти к пределу под знаком функции (f(x)= f (x)).
но — второй замечательный предел.
Следовательно,
(10.4)
В частности, при а = е
(10.5)
Таким образом, у = ln( 1 + х) и у = х — эквивалентные бесконечно малые функции при х → 0.
Пример:
Вычислить
Решение:
Здесь мы имеем дело с неопределенностью вида . Для нахождения предела сделаем замену переменной, положив — 1 = t. Тогда . При х → 0 также и t → 0.
Так как на основании результата, полученного в предыдущем примере, то
(10.6)
В частности, если а = е, имеем
т.е. у = — 1 и y = x — эквивалентные бесконечно малые функции при х → 0.
Определение:
Функция у = f(x) непрерывна на сегменте [а, b], если она непрерывна во всех внутренних точках Этого сегмента, а на концах сегмента (в точках a и b) непрерывна соответственно справа и слева.
Теорема:
Если функция у = f(x) непрерывна на сегменте [а, b], то она достигает на этом сегменте своего наибольшего и(или) наименьшего значения.
Простым доказательством этой теоремы, является геометрическая иллюстрация функции у = f(x) на рисунке 91. Непрерывная на сегменте [α, b] функция достигает наименьшего своего значения в точке х = x₁= а, а наибольшего значения в точке х₂.
Рис. 91. Геометрическая иллюстрация условий теоремы 10.3Следствие:
Если функция у = f(x) непрерывна на сегменте [a, b], то она ограничена на этом сегменте.
Действительно, если по теореме 10.3 функция достигает на сегменте наибольшего M и наименьшего т значений, то имеет место неравенство m ≤ f(x) ≤ M для всех значений функции на рассматриваемом сегменте. Т. е. |f(x)| ≤ M и, следовательно, функция у = f(x) ограничена на сегменте [а, b].
Теорема:
Теорема Больцано-Коши. Если функция у = f(x) непрерывна на сегменте [а, b] и на ее концах принимает значения разных знаков, то внутри этого сегмента найдется, по крайней мере, одна тонка С, в которой функция равна нулю.
Геометрический смысл теоремы заключается в следующем: если точки графика функции у = f(x), соответствующие концам сегмента [a, b], лежат по разные стороны от оси ОХ, то этот график хотя бы в одной точке сегмента пересекает ось OX. На данном рисунке 92 это три точки x₁, x₂, x₃.
Рис. 92. Геометрическая иллюстрация условий теоремы 10.4Теорема:
О промежуточных значениях функции. Если функция у = f(x) непрерывна на сегменте [α, b] и f(α) = A и f(b) = В, то для любого числа С, заключенного между A и B, найдется внутри этого сегмента такая точка с, что f(c) = С.
Из графика на рисунке 93 видно, что непрерывная функция, переходя от одного значения к другому, обязательно проходит через все промежуточные значения.
Рис. 93. Геометрическая иллюстрация условий теоремы 10.5Теорема:
О непрерывности обратной функции.) Если функция у = f(x) непрерывна на сегменте [а, b] в возрастает (убывает) на этом сегменте, то обратная функция х = f⁻¹(y) на соответствующем сегменте оси OY существует и является также непрерывной возрастающей (убывающей) функцией.
Эту теорему мы принимаем без доказательства.
Решение на тему: Непрерывная функция
Пример:
Показать, что функция у = 4x² непрерывна в точке х = 2.
Решение:
Для этого необходимо показать, что в точке х = 2 выполняется все три условия непрерывности функции:
1) функция у = 4х² определена в точке х = 2 ⇒ f(2) = 16;
2) существует f(x) = 4x²= 16;
3) этот предел равен значению функции в точке х = 2
f(x) = f(2) = 16.
Пример:
Показать, что функция у = sin x непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y, используя формулы тригонометрических тождеств
Так как то при любом х имеем
Следовательно, функция у = sin x непрерывна при -∞ < х < ∞.
Пример:
Исследовать на непрерывность функцию
Решение:
Рис. 94. График функции примера 10.3
94. График функции примера 10.3Эта функция (рис. 94) определена во всех точках сегмента [0,4] и ее значение при х = 3 ⇒ у = 2. Функция терпит разрыв, так как она не имеет предела при х → 3 :
Следовательно, точка х = 3, точка разрыва первого рода. При этом в граничных точках исследуемого сегмента [0,4], функция f(x) непрерывна справа (х = 0) и непрерывна слева (х = 4).
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 5 функция не определена, т.к., выполнив подстановку, получаем неопределенность вида 0/0. Легко доказать, что
Следовательно, точка х = 5 точка устранимого разрыва.
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 0 функция (рис. 95) терпит разрыв, так как она не определена в этой точке. Пределы функции слева и справа от точки х = 0 равны ∞. Следовательно, точка х = 0 для данной функции является точкой разрыва второго
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 0 функция терпит разрыв 1-го рода, так как односторонние пределы существуют в этой точке, но не равны:
предел слева
предел справа
 95. График функции
95. График функцииПример:
Исследовать на непрерывность функцию .
Решение:
Функция определена для всех значений х, кроме x = 0.B этой точке она имеет разрыв. Точка х = 0 есть точка разрыва II рода, так как при х → 0 как справа, так и слева, функция , колеблясь между -1 и 1, не приближается ни к какому числовому значению. График ее приведен на рис. 96.
Рис. 96. График функцииПример:
Исследовать на непрерывность функцию
Решение:
Функция не определена в точке х = 0. Точка х = 0 является точкой разрыва I рода, так как при х → 0 существуют пределы справа и слева:
Если доопределить функцию в точке х = 0, полагая f(0) = 1, то получим уже непрерывную функцию, определенную так:
f(х) =, если х ≠ 0; f(0) = 1.
Доопределив функцию в точке х = 0, мы устранили разрыв.
Непрерывность функций
Смотрите также:
Предмет математический анализ
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Непрерывность функций и точки разрыва с примерами решения
Содержание:
Непрерывность функции
Определение: Функция
- — она определена в этой точке и ее некоторой -окрестности;
- — существуют конечные лево- и правосторонние пределы от функции в этой точке и они равны между собой, т.
 е.
е.
— предел функции в точке равен значению функции в исследуемой точке, т.е.
Пример:
Найти область непрерывности функции
Решение:
Данная функция непрерывна так как в каждой точке указанного интервала функция определена, в каждой точке существуют конечные и равные лево- и правосторонние пределы, а предел функции в каждой точке равен значению функции в этой точке.
Замечание: Всякая элементарная функция непрерывна в области своего определения.
Точки разрыва
Определение: Точки, в которых не выполняется хотя бы одно из условий непрерывности функции, называются точками разрыва. Различают точки разрыва первого и второго родов.
Определение: Точкой разрыва I рода называется точка, в которой нарушается условие равенства лево- и правостороннего пределов, т.е.
Пример:
Доказать, что функция в точке имеет разрыв первого рода.
Решение:
Нарисуем график функции в окрестности нуля (Рис. 64): Рис. 64. График функции Область определения функции: т.е. точка является точкой подозрительной на разрыв. Вычислим лево- и правосторонние пределы в этой точке: Следовательно, в изучаемой точке данная функция терпит разрыв первого рода.
Замечание: По поводу точки разрыва I рода иначе говорят, что в этой точке функция испытывает конечный скачок (на Рис. 64 скачок равен 1).
Определение: Точка, подозрительная на разрыв, называется точкой устранимого разрыва, если в этой точке левосторонний предел равен правостороннему.
Пример:
Доказать, что функция имеет в точке устранимый разрыв.
Решение:
В точке функция имеет неопределенность поэтому эта точка является точкой, подозрительной на разрыв. Вычислив в этой точке лево- и правосторонний пределы убеждаемся, что данная точка является точкой устранимого разрыва.
Определение: Все остальные точки разрыва называются точками разрыва II рода.
Замечание: Для точек разрыва второго рода характерен тот факт, что хотя бы
один из односторонних пределов равен т.е. в такой точке функция терпит бесконечный разрыв.
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: т.е. точка
является точкой подозрительной на разрыв. Вычислим лево- и правосторонние пределы в этой точке: Так как левосторонний предел конечен, а правосторонний предел бесконечен, то в изучаемой точке данная функция терпит разрыв II рода.
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: т.е. точка является точкой подозрительной на разрыв. Вычислим лево- и правосторонние пределы в этой точке: Так как левосторонний и правосторонний пределы бесконечены, то в изучаемой точке данная функция терпит разрыв II рода.
Операции над непрерывными функциями
Теорема: Сумма (разность) непрерывных функций есть непрерывная функция.
Доказательство: Докажем приведенную теорему для суммы двух функций которые определены в некоторой -окрестности точки в которой лево- и правосторонние пределы равны между собой. Так как функции непрерывны в некоторой -окрестности точки то выполняются равенства: В силу того, что существуют конечные пределы обеих функций, то по теореме о пределе суммы двух функций имеем, что Аналогично теорема доказывается для суммы (разности) любого конечного числа непрерывных функций. Нижеприведенные теоремы доказываются так же, как и теорема.
Теорема: Произведение непрерывных функций есть непрерывная функция.
Теорема: Частное двух непрерывных функций при условии, что во всех точках общей области определения функция , есть непрерывная функция.
Теорема: Сложная функция от непрерывных функций есть непрерывная функция.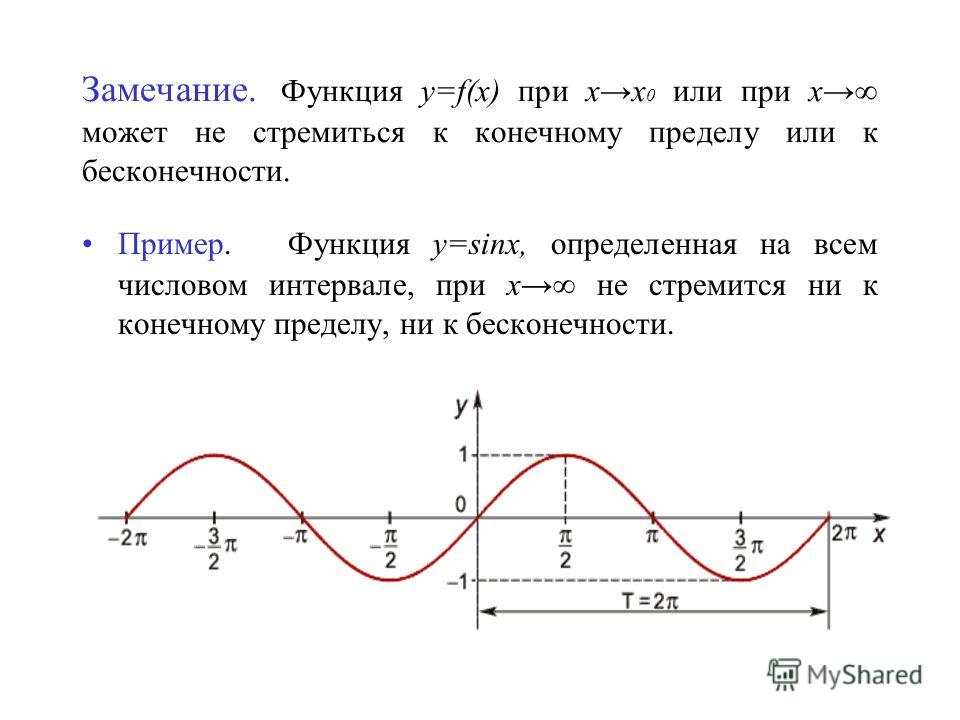
- Заказать решение задач по высшей математике
Схема исследования функции на непрерывность
Исследование функции на непрерывность проводят по следующей схеме:
- находят область определения функции; точки, в которых функция не определена, являются точками подозрительными на разрыв: если функция задана словесным образом, т.е. описывается разными формулами на разных интервалах, то точками подозрительными на разрыв являются точки, определяющие границы интервалов;
- исследуют подозрительные на разрыв точки, для чего вычисляют лево- и правосторонние пределы; классифицируют точки разрыва;
- при наличии точек разрыва строят график функции в малой -окрестности точки .
Пример:
Исследовать на непрерывность функцию
Решение:
Согласно схеме исследования функции на непрерывность имеем:
- точка является точкой подозрительной на разрыв.

- вычислим левосторонний и правосторонний пределы; так как пределы бесконечные, то точка является точкой разрыва второго рода;
- построим график функции в небольшой окрестности точки разрыва (Рис. 65).
Рис. 65. Поведение графика функции в малой окрестности точки разрыва второго рода
Из рисунка видно, что график функции —неограниченно приближается к вертикальной прямой нигде не пересекая эту прямую.
Свойства непрерывных функций на отрезке (a; b)
Свойства непрерывных функций на отрезке .
Определение: Замкнутый интервал будем называть сегментом.
Приведем без доказательства свойства непрерывных функций на сегменте .
Теорема: Если функция непрерывна на сегменте , то она достигает своего наименьшего () и наибольшего () значения либо во внутренних точках сегмента, либо на его концах.
Пример:
Привести примеры графиков функций, удовлетворяющих условиям теорем(см.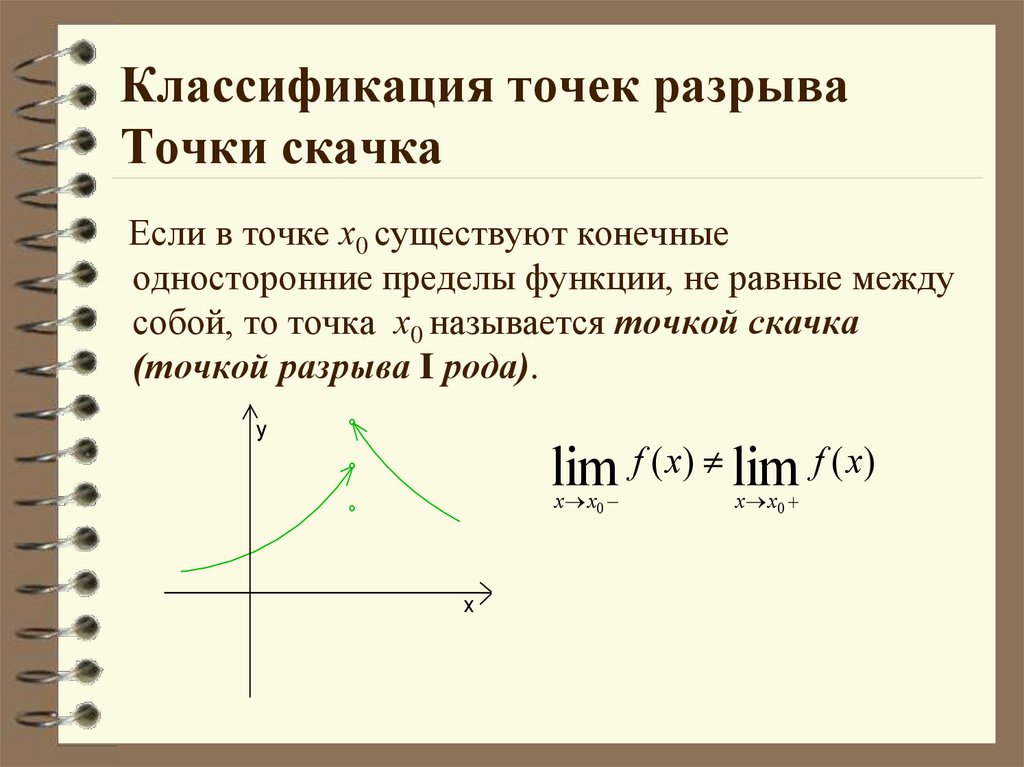 Рис. 66).
Рис. 66).
Рис. 66. Графики функций, удовлетворяющих условиям теоремы.
Решение:
На графике а) функция достигает своего наименьшего и наибольшего значений на концах сегмента На графике б) функция достигает своего наименьшего и наибольшего значения во внутренних точках сегмента На графике в) функция достигает своего наименьшего значения на левом конце сегмента а наибольшего значения во внутренней точке сегмента
Тб. Если функция непрерывна на сегменте и достигает своего наименьшего () и наибольшего () значений, то для любого вещественного числа С, удовлетворяющего неравенству , найдется хотя бы одна точка такая, что .
Пример:
Изобразить графики функций, удовлетворяющих условиям Тб (см. Рис. 67).
Рис. 67. Графики функций, удовлетворяющих условиям Тб.
Теорема: Если функция непрерывна на сегменте и на его концах принимает значения разных знаков, то найдется хотя бы одна точка такая, что.
Пример:
Изобразить графики функций, удовлетворяющих условиям теоремы(см. Рис. 68).
Рис. 68. Графики функций, удовлетворяющих условиям теоремы.
На графике а) существует единственная точка, в которой выполняются условия теоремы. На графиках б) и в) таких точек две и четыре, соответственно. Однако в случаях б) и в) для удовлетворения условий теоремы надо разбивать сегмент на отдельные отрезки.
Непрерывность функции в точке
Справочный материал
§ Если и , то — левосторонний предел функции в точке ; если и , то — правосторонний предел функции в точке .
§ Функция называется непрерывной в точке , если функция удовлетворяет следующим условиям: 1) определена в точке ; 2) имеет конечный предел при ; 3) значение предела совпадает со значением функции в этой точке, т.е. . Если хотя бы одно из условий не выполняется, то — точка разрыва.
- Элементарные функции непрерывны на своей области определения.

- Если в точке функция имеет конечные равные односторонние пределы но значения пределов не равны значению функции в точке , то точка называется точкой устранимого разрыва.
Если в точке функция имеет конечные неравные односторонние пределы , причем значения не имеет, совпадает ли значение функции в точке с одним из этих пределов), то точка называется точкой разрыва с конечным скачком функции.
Точки устранимого разрыва и точки разрыва с конечным скачком функции называются точками разрыва первого рода.
Все другие точки разрыва функции называются точками разрыва второго рода. Каждая точка разрыва второго рода функции характеризуется тем, что в этой точке функция не имеет конечного предела, по крайней мере, с одной стороны, — слева или справа
Примеры
1.Исследовать непрерывность функции , найти точки разрыва, определить их характер.
Решение.
Область определения функции:
Функция элементарная, является непрерывной на своей области определения. Функция непрерывна при .
Точка х0 =2 – точка разрыва графика функции. Установим характер точки разрыва, для этого найдем односторонние пределы функции в этой точке:
;
.
Односторонние пределы бесконечны, х0 = 2 – точка разрыва второго рода.
2. Исследовать функцию на непрерывность, найти точки разрыва, определить их характер и построить график функции.
Решение.
Функция задана тремя различными формулами на промежутках изменения аргумента (внутри каждого промежутка функция определена и непрерывна).
Исследуем непрерывность функции в точках: , .
Проверим точку :
1) ;
— функция определена в точке .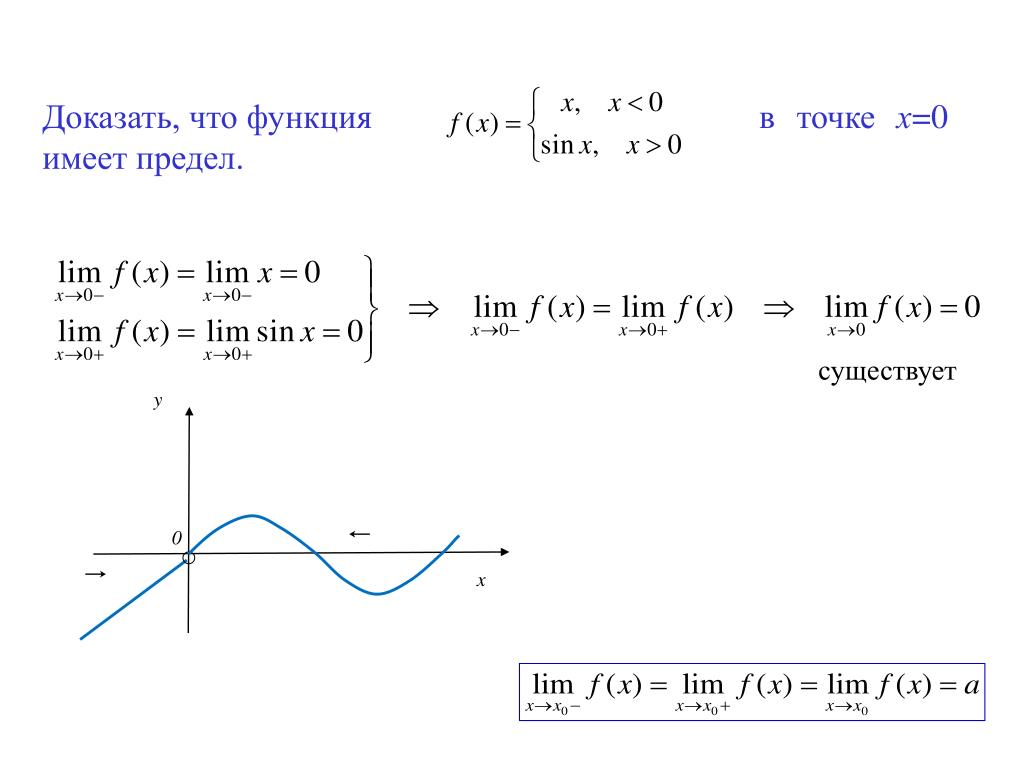
Найдем односторонние пределы в этой точке:
; .
В точке значение функции, левый и правый пределы совпадают, следовательно, функция непрерывна в этой точке.
2) Проверим точку :
;
; .
Односторонние пределы функции в точке конечны и не равны, следовательно, точка разрыва первого рода, точка скачка графика функции.
Задания для самостоятельного решения
№1. Вычислить односторонние пределы
; ;
Ответы.1) 3; 2) -1;
№2. По графику функции y=f(x) определить точки разрыва, провести их классификацию.
y=f(x)
y=f(x)
а) б)
№3. Исследовать непрерывность функции в указанной точке:
Исследовать непрерывность функции в указанной точке:
3)
№4. Исследовать непрерывность функции, найти точки разрыва, определить их характер.
1) ; 2)
№5.* Исследовать непрерывность функции , найти точки разрыва, определить их характер.
.
№6. Исследовать непрерывность функции и построить график:
1) 2)
3) 4)
№7. Исследовать непрерывность функции в указанных точках 2) , а – число букв имени, в – число букв фамилии.
№8. Исследовать непрерывность функции и построить график:
а – число букв имени, в – число букв фамилии.
Дифференцирование функции
Справочный материал
§ Производной функции в точке называется предел отношения приращения функции к приращению аргумента , если , при условии, что этот предел существует: .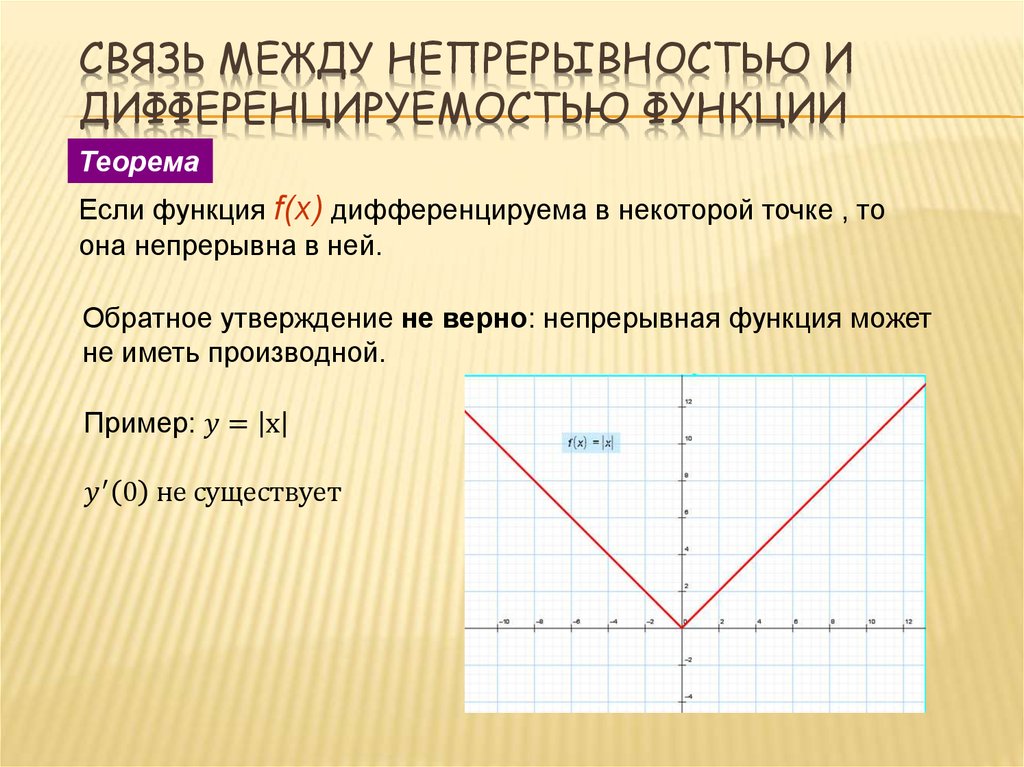
§ Функция , имеющая производную в каждой точке интервала , называется дифференцируемой на этом интервале; операция нахождения производной функции называется дифференцированием.
§ Правила дифференцирования:
u=u(x), v=v(x), w=w(x) — дифференцируемые на некотором числовом множестве функции.
§ Производная сложной функции:
Если y=f(u), u=u(x), т.е. y=f(u(x)), где f(u), u(x) – имеют производные, то .
§ Формулы дифференцирования основных элементарных функций
1) , С-const; , х – аргумент; ;
u– промежуточный аргумент:
2) = ; =
3) = ; = ;
4) = ; = ;
5) = ; 6) = ;
7) = ; 8) = ;
9) = ; 10) = ;
11) = ; 12) = .
Примеры
1. Найти производную функции в точке пользуясь определением производной.
Решение.
—приращение аргумента, — приращение функции.
=
=
2. Вычислить производные функций:
а) б)
Решение.
а) Применяем правило дифференцирования дроби: .
б)
Это сложная функция, ее производную найдем по формуле:
, где .
= = == = =
= =
= = .
3. Вычислить производную второго порядка функции .
Решение.
По правилу дифференцирования произведения: .
= .
Производную второго порядка найдем, применяя правила дифференцирования суммы и произведения:
.
4. Вычислить производную функции
Решение.
Прологарифмируем равенство по основанию : , тогда
Далее продифференцируем полученное равенство по переменной (левая часть представляет сложную функцию, правая — произведение). По таблице производных: .
.
=
Заменяя на выражение и умножив равенство
= на , получим
.
5. Найти производную функции , заданной неявно:
Решение.
Дифференцируем равенство по переменной х:
Вычисляем производную суммы и произведения.
;
;
Сгруппируем относительно и вынесем за скобки:
;
;
Выразим :
.
6. Найти производную функции, заданной параметрически:
Решение.
Найдем производную функции по формуле: .
Вычислим производные .
.
.
.
Задания для самостоятельного решения
№1. Вычислить производные функций, применяя формулы:
1) 2)
№2. Вычислить производные функций и выбрать правильный ответ из предложенных:
1) ; 2) ; 3) ; 4) ;
5) ; 6) .
Ответы.
1)
2)
3)
4)
5)
6)
№3. Найти производные указанных функций:
1)2) 3)
4) 5) 6)
7) 8) ; 9)
10) 11) ; 12)
13) ; 14) ; 15) 16)
17) ; 18) ;
19)* ; 20)* .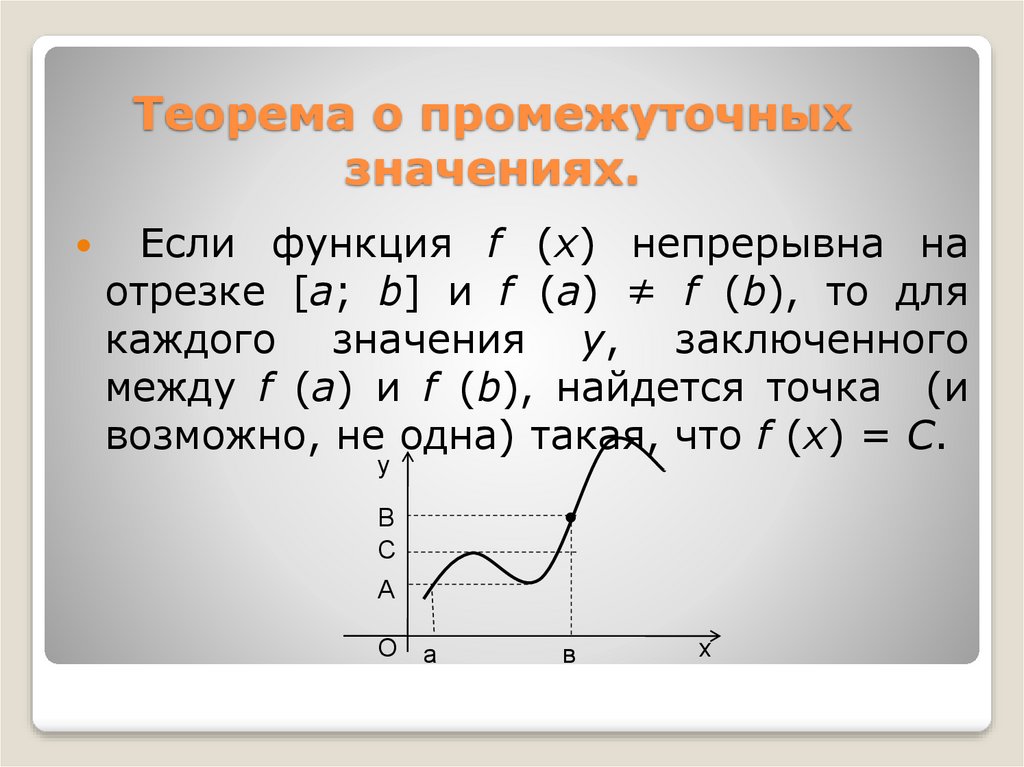
№4. Найти производную функции: и вычислить .
№5. а) Показать, что функция удовлетворяет уравнению .
б) Показать, что функция удовлетворяет уравнению .
в) Показать, что функция удовлетворяет уравнению .
№6. При каких значениях x выполняется условие если ?
№7. Вычислить если .
№8. Вычислить значение производной функции в точках, в которых значение этой функции равно 0.
№9.Вычислить производную функции, заданной неявно:
1) ;2)
№10. Найти производную показательно-степенной функции:
1) 2) ; 3)
(Замечание. Производную показательно-степенной функции можно также найти по формуле: )
№11.Вычислить производную функции, заданной параметрически:
№12. Вычислить производную второго порядка заданной функции.
1) ; 2) .
№13.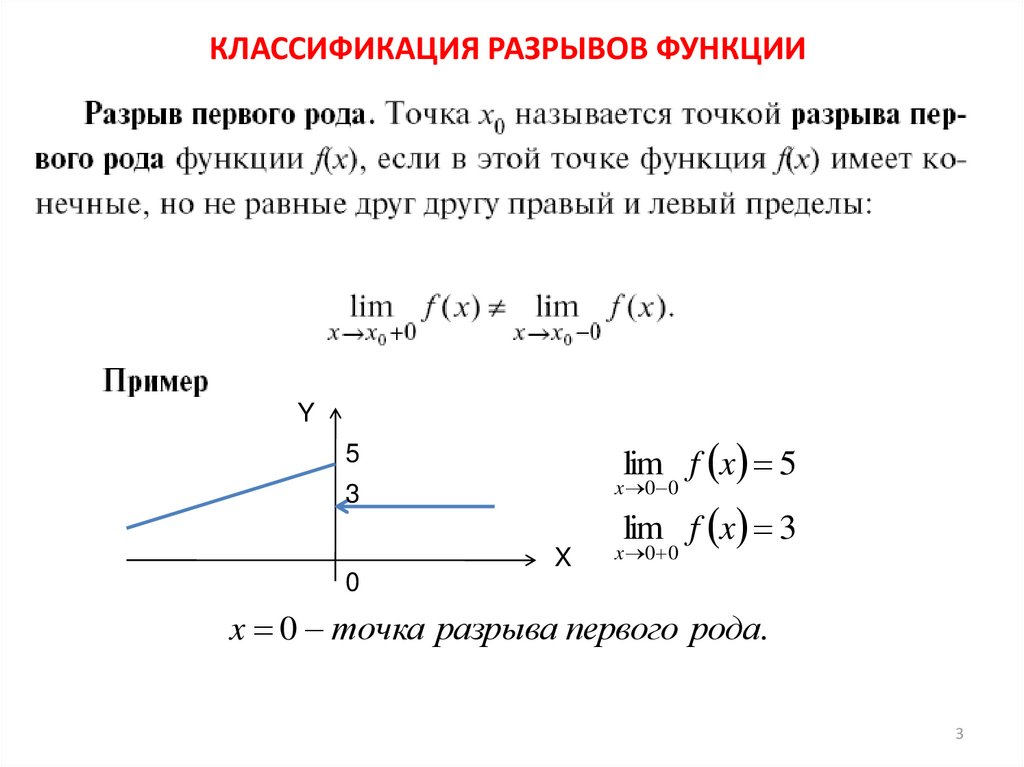 * Доказать, что производная функции равна
* Доказать, что производная функции равна
Ответы.
№3. 4) ; 8) ; 9) ; 10) ; 11) ; 12) ;
13) ; 14) ; 15) ; 16) ;
17) ; 18) ; 19) ;
20)
№4. .
№6. или .
№7. .
№8. .
№9. 1) ; 2) .
№10. 1) ; 2) ;
3) .
№11.
№12. 1) ; 2) .
ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры…
Что делает отдел по эксплуатации и сопровождению ИС? Отвечает за сохранность данных (расписания копирования, копирование и пр.)…
ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования…
Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам. ..
..
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Исследование функции на непрерывность — Мегаобучалка
Для исследования функции на непрерывность необходимо:
1. Найти область определения функции;
2. Рассмотреть односторонние пределы в точках, где функция не существует; если функция кусочная, то рассмотреть односторонние пределы в точках «склейки»;
3. Исследовать функцию на бесконечности;
4. Построить эскиз графика функции.
Для классификации точек разрыва функции можно пользоваться таблицей, приведенной ниже.
Пусть – заданная функция, – исследуемая точка, – соответственно левый и правый пределы функции.
| Тип разрыва | Условия |
| Функция непрерывна | |
| Устранимый разрыв | |
| Разрыв первого рода (скачок) | – конечны |
| Разрыв второго рода |
Рассмотрим примеры.
Пример 1. Задана функция .
Областью определения функции является множество . Действительно, функция не существует в единственной точке , следовательно, эта точка и будет точкой разрыва. Именно в ней мы должны найти односторонние пределы (левосторонний и правосторонний).
· Если отыскивается предел функции в точке при условии, что и , то этот предел, если он существует, называется левосторонним пределом функции и обозначается .
· Если отыскивается предел функции в точке при условии, что и , то этот предел, если он существует, называется правосторонним пределом функции и обозначается .
Найдем односторонние пределы в точке .
· Если левосторонний предел и правосторонний предел функции в точке существуют, но не равны между собой, то есть то точка называется точкой разрыва первого рода.
Согласно теории, точка является точкой разрыва первого рода, то есть в ней функция претерпевает скачок.
Далее исследуем поведение функции на бесконечности, для этого найдем пределы при
Следовательно, – прямая, которая является для функции горизонтальной асимптотой.
Сделаем эскиз графика.
Пример 2. Задана функция .
Областью определения функции является множество . Действительно, функция не существует в единственной точке , следовательно, эта точка и будет точкой разрыва. Определим с помощью односторонних пределов тип разрыва в этой точке.
· — это неопределенность, которую можно раскрыть, разложив на множители числитель и знаменатель.
· Если в точке функция имеет левосторонний и правосторонний пределы, и эти пределы равны между собой, но их значения не совпадают со значением функции в этой точке, то эта точка называется точкой устранимого разрыва:
Делаем вывод, что точка будет точкой устранимого разрыва.
Графиком функции является прямая с выколотой точкой при .
Построим график функции, для этого подберем кроме точки (3,1) еще одну произвольную. Пусть это будет (0,–2).
Пусть это будет (0,–2).
Сделаем эскиз графика функции.
Устранимый разрыв можно ликвидировать, если доопределить функцию в точке разрыва, задав:
Пример 3. Функция имеет две точки разрыва: и . Найдем односторонние пределы в этих точках.
Рассмотрим Разложив знаменатель на множители и сократив, получим следующее: – это гипербола, с точками разрыва и .
Тогда
Делаем вывод, что точка является точкой устранимого разрыва.
· Если в точке не существует левосторонний или правосторонний предел функции (или оба одновременно), то эта точка называется точкой разрыва второго рода (бесконечный разрыв).
Найдем предел функции на бесконечности:
Следовательно, прямая y= 0 будет горизонтальной асимптотой для заданной функции.
Построим график функции:
Рассмотрим примеры кусочных функций.
Пример 4.
Функции являются непрерывными всюду, кроме, может быть, точек «склейки», то есть в , . Исследуем поведение функции в окрестности этих точек:
Исследуем поведение функции в окрестности этих точек:
При функция определена и равна нулю, а функция в эту точку не заходит по условию.
· Функция называется непрерывной в , если ее левосторонний и правосторонний пределы существуют, между собой равны и равны значению функции в этой точке, то есть
Следовательно, точка x= 0 является точкой непрерывности функции.
Делаем вывод, что точка x= 2 является точкой разрыва первого рода и непрерывна слева (по условию).
Строим график склеенной функции:
Пример 5.
Элементарные непрерывные функции и не определены в точке , а функции и «склеены» в точке , которая, быть может, также является точкой разрыва. Исследуем поведение функции в этих точках.
Точка является точкой устранимого разрыва.
При функция принимает значение, равное 2. Следовательно, точка является точкой непрерывности.
Строим график заданной функции:
Пример 6.
Функция задана несколькими аналитическими выражениями, поэтому точки разрыва могут быть как в точках склейки , , так и в точках , , , где знаменатели дробей обращаются в нуль.
Сделаем некоторые упрощения: Далее будем рассматривать функцию с точками разрыва , .
Исследуем все точки:
Точка – точка разрыва второго рода.
Точка – точка разрыва первого рода, функция непрерывна справа (по условию).
Точка – точка разрыва первого рода, функция непрерывна справа (по условию).
Точка является точкой устранимого разрыва.
Точка является точкой разрыва второго рода.
Исследуем поведение функции при , а функции при .
Сделаем эскиз графика функции:
Как исследовать функцию на непрерывность? — Студопедия
Поделись
Исследование функции на непрерывность в точке проводится по уже накатанной рутинной схеме, которая состоит в проверке трёх условий непрерывности:
Пример 1
Исследовать функцию на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
Определить характер разрывов функции, если они существуют. Выполнить чертёж.
Решение:
1) Под прицел попадает единственная точка , в которой функция не определена.
2) Вычислим односторонние пределы:
Односторонние пределы конечны и равны.
Таким образом, в точке функция терпит устранимый разрыв.
Как выглядит график данной функции?
Хочется провести упрощение , и вроде бы получается обычная парабола. НО исходная функция не определена в точке , поэтому обязательна следующая оговорка:
Выполним чертёж:
Ответ: функция непрерывна на всей числовой прямой кроме точки , в которой она терпит устранимый разрыв.
Функцию можно доопределить хорошим или не очень способом, но по условию этого не требуется.
Вы скажете, пример надуманный? Ничуть. Десятки раз встречалось на практике. Почти все задачи сайта родом из реальных самостоятельных и контрольных работ.
Разделаемся с любимыми модулями:
Пример 2
Исследовать функцию на непрерывность. Определить характер разрывов функции, если они существуют. Выполнить чертёж.
Определить характер разрывов функции, если они существуют. Выполнить чертёж.
Решение: почему-то студенты боятся и не любят функции с модулем, хотя ничего сложного в них нет. Таких вещей мы уже немного коснулись на уроке Геометрические преобразования графиков. Поскольку модуль неотрицателен, то он раскрывается следующим образом: , где «альфа» – некоторое выражение. В данном случае , и наша функция должна расписаться кусочным образом:
Но дроби обоих кусков предстоит сократить на . Сокращение, как и в предыдущем примере, не пройдёт без последствий. Исходная функция не определена в точке , так как знаменатель обращается в ноль. Поэтому в системе следует дополнительно указать условие , и первое неравенство сделать строгим:
Теперь об ОЧЕНЬ ПОЛЕЗНОМ приёме решения: перед чистовым оформлением задачи на черновике выгодно сделать чертёж (независимо от того, требуется он по условию или нет). Это поможет, во-первых, сразу увидеть точки непрерывности и точки разрыва, а, во-вторых, 100%-но убережёт от ошибок при нахождении односторонних пределов.
Выполним чертёж. В соответствии с нашими выкладками, слева от точки необходимо начертить фрагмент параболы (синий цвет), а справа – кусок параболы (красный цвет), при этом функция не определена в самой точке :
Если есть сомнения, возьмите несколько значений «икс», подставьте их в функцию (не забывая, что модуль уничтожает возможный знак «минус») и сверьтесь с графиком.
Исследуем функцию на непрерывность аналитически:
1) Функция не определена в точке , поэтому сразу можно сказать, что не является в ней непрерывной.
2) Установим характер разрыва, для этого вычислим односторонние пределы:
Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке . Заметьте, что не имеет значения, определена функция в точке разрыва или нет.
Теперь остаётся перенести чертёж с черновика (он сделан как бы с помощью исследования ;-)) и завершить задание:
Ответ: функция непрерывна на всей числовой прямой кроме точки , в которой она терпит разрыв первого рода со скачком.
Иногда требуют дополнительно указать скачок разрыва. Вычисляется он элементарно – из правого предела нужно вычесть левый предел: , то есть в точке разрыва наша функция прыгнула на 2 единицы вниз (о чём нам сообщает знак «минус»).
Пример 3
Исследовать функцию на непрерывность. Определить характер разрывов функции, если они существуют. Сделать чертёж.
Это пример для самостоятельного решения, примерный образец решения в конце урока.
Перейдём к наиболее популярной и распространённой версии задания, когда функция состоит из трёх кусков:
Пример 4
Исследовать функцию на непрерывность и построить график функции
.
Решение: очевидно, что все три части функции непрерывны на соответствующих интервалах, поэтому осталось проверить только две точки «стыка» между кусками. Сначала выполним чертёж на черновике, технику построения я достаточно подробно закомментировал в первой части статьи. Единственное, необходимо аккуратно проследить за нашими особенными точками: в силу неравенства значение принадлежит прямой (зелёная точка), и в силу неравенство значение принадлежит параболе (красная точка):
Ну вот, в принципе, всё понятно =) Осталось оформить решение. Для каждой из двух «стыковых» точек стандартно проверяем 3 условия непрерывности:
Для каждой из двух «стыковых» точек стандартно проверяем 3 условия непрерывности:
I) Исследуем на непрерывность точку
1) – функция определена в данной точке.
2) Найдём односторонние пределы:
Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке .
Вычислим скачок разрыва как разность правого и левого пределов:
, то есть, график рванул на одну единицу вверх.
II) Исследуем на непрерывность точку
1) – функция определена в данной точке.
2) Найдём односторонние пределы:
– односторонние пределы конечны и равны, значит, существует общий предел.
3) – предел функции в точке равен значению данной функции в данной точке.
Таким образом, функция непрерывна в точке по определению непрерывности функции в точке.
На завершающем этапе переносим чертёж на чистовик, после чего ставим финальный аккорд:
Ответ: функция непрерывна на всей числовой прямой, кроме точки , в которой она терпит разрыв первого рода со скачком.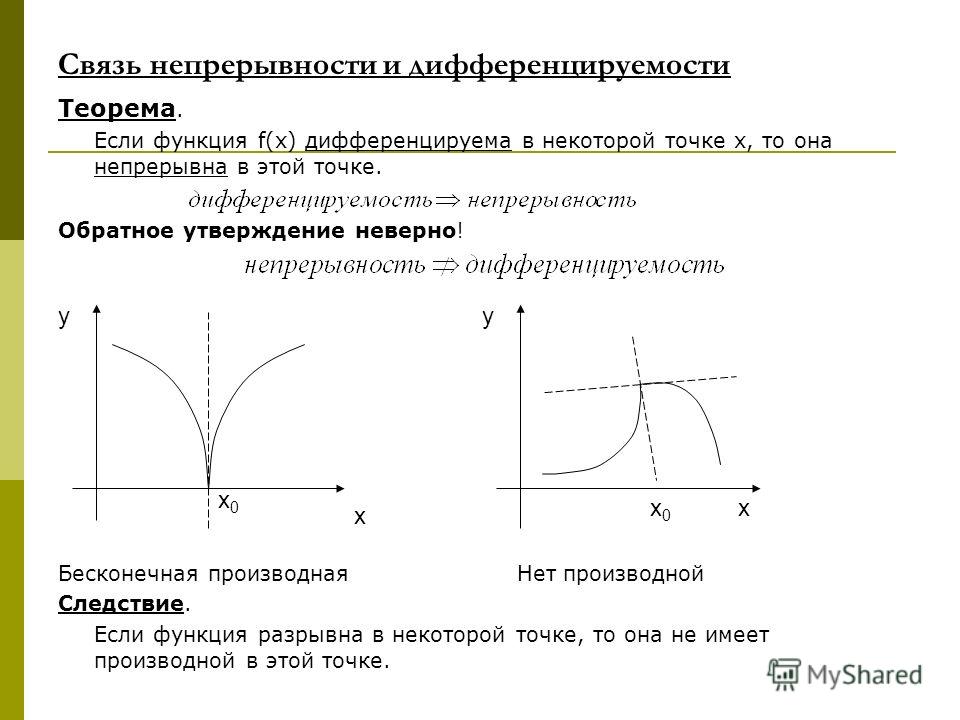
Готово.
Пример 5
Исследовать функцию на непрерывность и построить её график .
Это пример для самостоятельного решения, краткое решение и примерный образец оформления задачи в конце урока.
Может сложиться впечатление, что в одной точке функция обязательно должна быть непрерывной, а в другой – обязательно должен быть разрыв. На практике это далеко не всегда так. Постарайтесь не пренебрегать оставшимися примерами – будет несколько интересных и важных фишек:
Пример 6
Дана функция . Исследовать функцию на непрерывность в точках . Построить график.
Решение: и снова сразу выполним чертёж на черновике:
Особенность данного графика состоит в том, что при кусочная функция задаётся уравнением оси абсцисс . Здесь данный участок прорисован зелёным цветом, а в тетради его обычно жирно выделяют простым карандашом. И, конечно же, не забываем про наших баранов: значение относится к ветке тангенса (красная точка), а значение принадлежит прямой .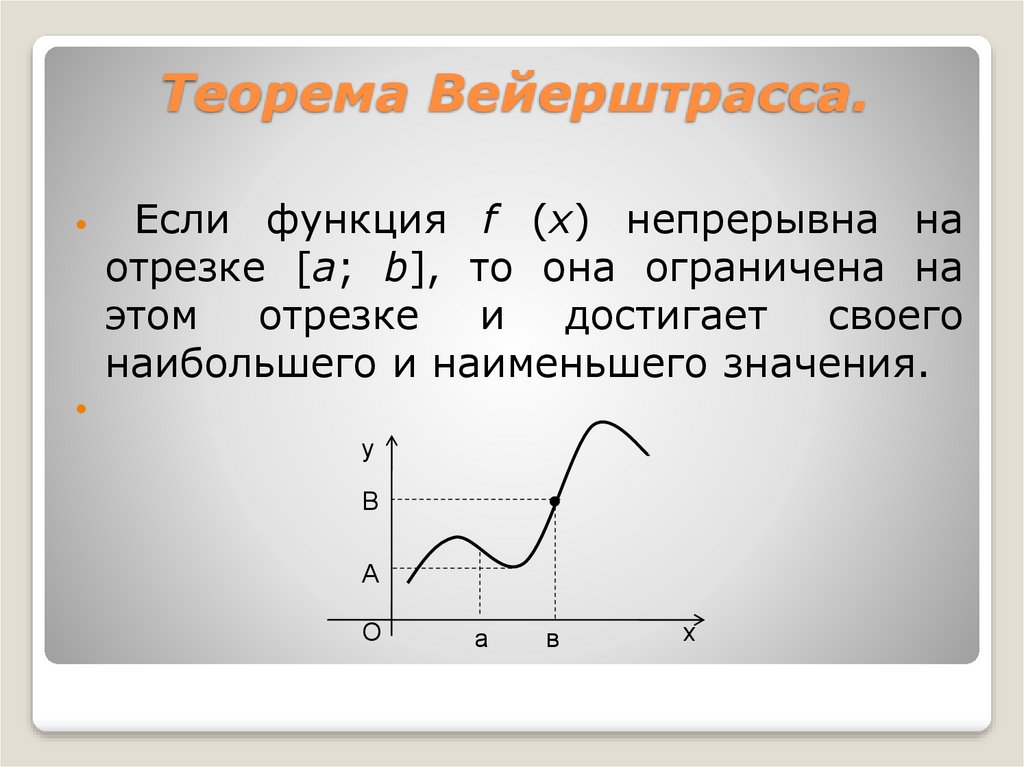
Из чертежа всё понятно – функция непрерывна на всей числовой прямой, осталось оформить решение, которое доводится до полного автоматизма буквально после 3-4-х подобных примеров:
I) Исследуем на непрерывность точку
1) – функция определена в данной точке.
2) Вычислим односторонние пределы:
, значит, общий предел существует.
Случился тут небольшой курьёз. Дело в том, что я создал немало материалов о пределах функции, и несколько раз хотел, да несколько раз забывал об одном простом вопросе. И вот, невероятным усилием воли таки заставил себя не потерять мысль =) Скорее всего, некоторые читатели-«чайники» сомневаются: чему равен предел константы? Предел константы равен самой константе. В данном случае предел нуля равен самому нулю (левосторонний предел).
Едем дальше:
3) – предел функции в точке равен значению данной функции в данной точке.
Таким образом, функция непрерывна в точке по определению непрерывности функции в точке.
II) Исследуем на непрерывность точку
1) – функция определена в данной точке.
2) Найдём односторонние пределы:
И здесь, в правостороннем пределе – предел единицы равен самой единице.
– общий предел существует.
3) – предел функции в точке равен значению данной функции в данной точке.
Таким образом, функция непрерывна в точке по определению непрерывности функции в точке.
Как обычно, после исследования переносим наш чертёж на чистовик.
Ответ: функция непрерывна в точках .
Обратите внимание, что в условии нас ничего не спрашивали про исследование всей функции на непрерывность, и хорошим математическим тоном считается формулировать точный и чёткий ответ на поставленный вопрос. Кстати, если по условию не требуется строить график, то вы имеете полное право его и не строить (правда, потом преподаватель может заставить это сделать).
Небольшая математическая «скороговорка» для самостоятельного решения:
Пример 7
Дана функция .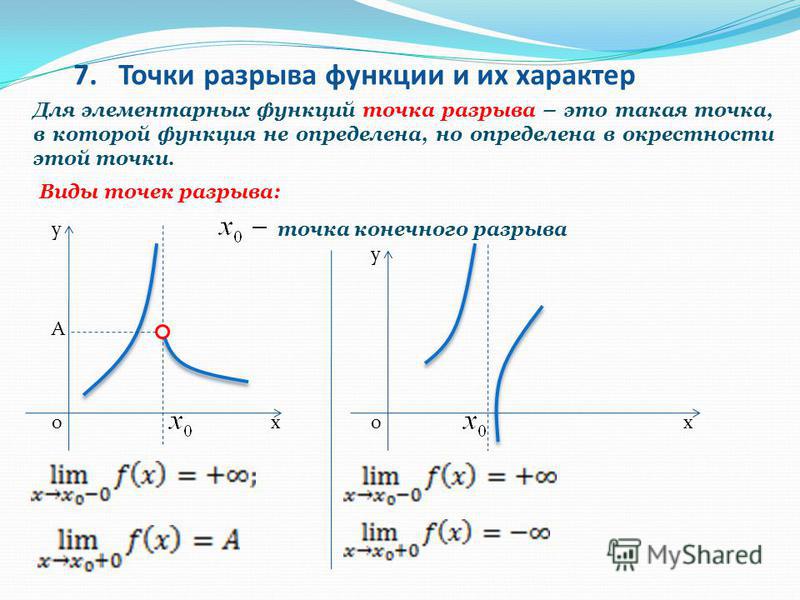
Исследовать функцию на непрерывность в точках . Классифицировать точки разрыва, если они есть. Выполнить чертёж.
Постарайтесь правильно «выговорить» все «слова» =) И график нарисовать поточнее, точность, она везде лишней не будет 😉
Как вы помните, я рекомендовал незамедлительно выполнять чертёж на черновике, но время от времени попадаются такие примеры, где не сразу сообразишь, как выглядит график. Поэтому в ряде случаев выгодно сначала найти односторонние пределы и только потом на основе исследования изобразить ветви. В двух заключительных примерах мы, кроме того, освоим технику вычисления некоторых односторонних пределов:
Пример 8
Исследовать на непрерывность функцию и построить её схематический график.
Решение: нехорошие точки очевидны: (обращает в ноль знаменатель показателя) и (обращает в ноль знаменатель всей дроби). Малопонятно, как выглядит график данной функции, а значит, сначала лучше провести исследование:
I) Исследуем на непрерывность точку
1) Функция не определена в данной точке.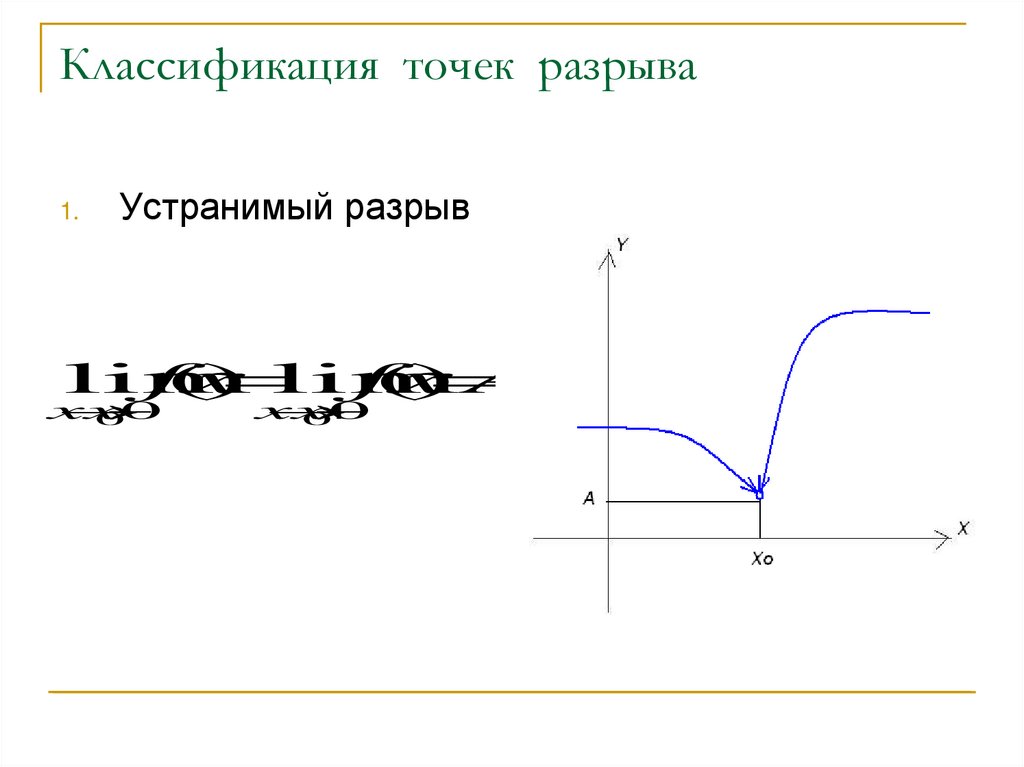
2) Найдём односторонние пределы:
Обратите внимание на типовой приём вычисления одностороннего предела: в функцию вместо «икса» мы подставляем . В знаменателе никакого криминала: «добавка» «минус ноль» не играет роли, и получается «четыре». А вот в числителе происходит небольшой триллер: сначала в знаменателе показателя убиваем –1 и 1, в результате чего получается . Единица, делённая на бесконечно малое отрицательное число, равна «минус бесконечности», следовательно: . И, наконец, «двойка» в бесконечно большой отрицательной степени равна нулю: . Или, если ещё подробнее: .
Вычислим правосторонний предел:
И здесь – вместо «икса» подставляем . В знаменателе «добавка» снова не играет роли: . В числителе проводятся аналогичные предыдущему пределу действия: уничтожаем противоположные числа и делим единицу набесконечно малое положительное число:
Правосторонний предел бесконечен, значит, функция терпит разрыв 2-го рода в точке .
II) Исследуем на непрерывность точку
1) Функция не определена в данной точке.
2) Вычислим левосторонний предел:
Метод такой же: подставляем в функцию вместо «икса» . В числителе ничего интересного – получается конечное положительно число . А в знаменателе раскрываем скобки, убираем «тройки», и решающую роль играет «добавка» .
По итогу, конечное положительное число, делённое на бесконечно малое положительное число, даёт «плюс бесконечность»: .
Правосторонний предел, как брат близнец, за тем лишь исключением, что в знаменателе выплывает бесконечно малое отрицательное число:
Односторонние пределы бесконечны, значит, функция терпит разрыв 2-го рода в точке .
Таким образом, у нас две точки разрыва, и, очевидно, три ветки графика. Для каждой ветки целесообразно провести поточечное построение, т.е. взять несколько значений «икс» и подставить их в . Заметьте, что по условию допускается построениесхематического чертежа, и такое послабление естественно для ручной работы. Я строю графики с помощью проги, поэтому не имею подобных затруднений, вот достаточно точная картинка:
Я строю графики с помощью проги, поэтому не имею подобных затруднений, вот достаточно точная картинка:
Прямые являются вертикальными асимптотами для графика данной функции.
Ответ: функция непрерывна на всей числовой прямой кроме точек , в которых она терпит разрывы 2-го рода.
Более простая функция для самостоятельного решения:
Пример 9
Исследовать на непрерывность функцию и выполнить схематический чертёж.
Примерный образец решения в конце, который подкрался незаметно.
До скорых встреч!
Решения и ответы:
Пример 3: Решение: преобразуем функцию: . Учитывая правило раскрытия модуля и тот факт, что , перепишем функцию в кусочном виде:
Исследуем функцию на непрерывность.
1) Функция не определена в точке .
2) Вычислим односторонние пределы:
Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке . Выполним чертёж:
Выполним чертёж:
Ответ: функция непрерывна на всей числовой прямой кроме точки , в которой она терпит разрыв первого рода со скачком. Скачок разрыва: (две единицы вверх).
Пример 5: Решение: каждая из трёх частей функции непрерывна на своём интервале.
I) Исследуем на непрерывность точку
1) – функция определена в данной точке.
2) Вычислим односторонние пределы:
, значит, общий предел существует.
3) – предел функции в точке равен значению данной функции в данной точке.
Таким образом, функция непрерывна в точке по определению непрерывности функции в точке.
II) Исследуем на непрерывность точку
1) – функция определена в данной точке.
2) Найдём односторонние пределы:
Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке .
Скачок разрыва: (пять единиц вниз).
Чертёж можно найти в первой части статьи.
Ответ: функция непрерывна на всей числовой прямой, кроме точки , в которой она терпит разрыв первого рода со скачком.
Пример 7: Решение:
I) Исследуем на непрерывность точку
1) – функция определена в данной точке.
2) Найдём односторонние пределы:
Левосторонний предел бесконечен, значит, функция терпит разрыв 2-го рода в точке .
II) Исследуем на непрерывность точку
1) – функция определена в данной точке.
2) Найдём односторонние пределы:
Односторонние пределы конечны и различны, значит, функция терпит разрыв 1-го рода со скачком в точке .
Выполним чертёж:
Ответ: В точке функция терпит разрыв 2-го рода, в точке функция терпит разрыв 1-го рода со скачком.
Пример 9: Решение: исследуем на непрерывность точку :
1) Функция не определена в данной точке.
2) Вычислим односторонние пределы:
Левосторонний предел бесконечен, значит, функция терпит разрыв 2-го рода в точке .
Выполним чертёж:
Ответ: функция непрерывна на всей числовой прямой кроме точки , в которой она терпит разрыв 2-го рода.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Как найти область определения функции?
Примеры решений
Если где-то нет чего-то, значит, где-то что-то есть
Продолжаем изучение раздела «Функции и графики», и следующая станция нашего путешествия – Область определения функции.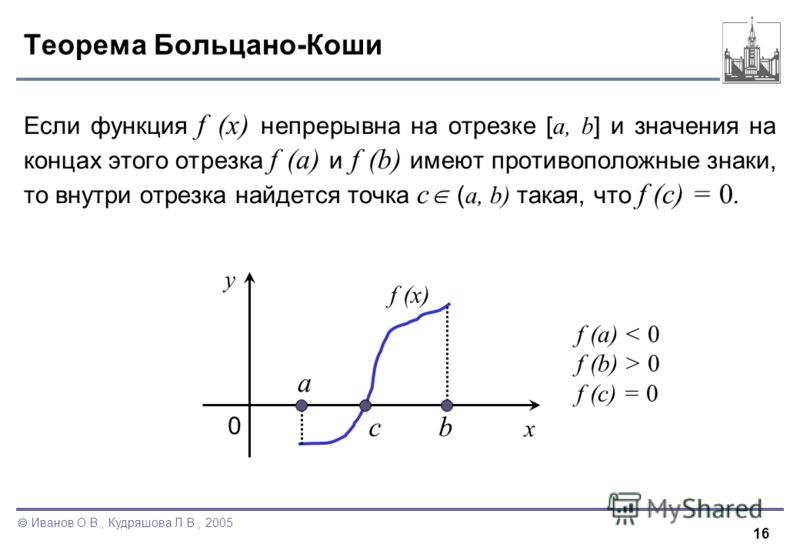 Активное обсуждение данного понятия началось на первом же уроке о графиках функций, где я рассмотрел элементарные функции, и, в частности, их области определения. Поэтому чайникам рекомендую начать с азов темы, поскольку я не буду вновь останавливаться на некоторых базовых моментах.
Активное обсуждение данного понятия началось на первом же уроке о графиках функций, где я рассмотрел элементарные функции, и, в частности, их области определения. Поэтому чайникам рекомендую начать с азов темы, поскольку я не буду вновь останавливаться на некоторых базовых моментах.
Предполагается, читатель знает области определения основных функций: линейной, квадратичной, кубической функции, многочленов, экспоненты, логарифма, синуса, косинуса. Они определены на . За тангенсы, арксинусы, так и быть, прощаю =) Более редкие графики запоминаются далеко не сразу.
Область определения – вроде бы вещь простая, и возникает закономерный вопрос, о чём же будет статья? На данном уроке я рассмотрю распространённые задачи на нахождение области определения функции. Кроме того, мы повторим неравенства с одной переменной, навыки решения которых потребуются и в других задачах высшей математики. Материал, к слову, весь школьный, поэтому будет полезен не только студентам, но и учащимся. Информация, конечно, не претендует на энциклопедичность, но зато здесь не надуманные «мёртвые» примеры, а жареные каштаны, которые взяты из настоящих практических работ.
Информация, конечно, не претендует на энциклопедичность, но зато здесь не надуманные «мёртвые» примеры, а жареные каштаны, которые взяты из настоящих практических работ.
Начнём с экспресс-вруба в тему. Коротко о главном: речь идёт о функции одной переменной . Её область определения – это множество значений «икс», для которых существуют значения «игреков». Рассмотрим условный пример:
Область определения данной функции представляет собой объединение промежутков:
(для тех, кто позабыл: – значок объединения). Иными словами, если взять любое значение «икс» из интервала , или из , или из , то для каждого такого «икс» будет существовать значение «игрек».
Грубо говоря, где область определения – там есть график функции. А вот полуинтервал и точка «цэ» не входят в область определения, поэтому графика там нет.
Да, кстати, если что-нибудь не понятно из терминологии и/или содержания первых абзацев, таки лучше вернуться к статье Графики и свойства элементарных функций.
Как найти область определения функции? Многие помнят детскую считалку: «камень, ножницы, бумага», и в данном случае её можно смело перефразировать: «корень, дробь и логарифм». Таким образом, если вам на жизненном пути встречается дробь, корень или логарифм, то следует сразу же очень и очень насторожиться! Намного реже встречаются тангенс, котангенс, арксинус, арккосинус, и о них мы тоже поговорим. Но сначала зарисовки из жизни муравьёв:
Сообщество Экспонента
- вопрос
- 22.09.2022
Математика и статистика, Системы управления, Изображения и видео, Робототехника и беспилотники, Глубокое и машинное обучение(ИИ), Другое
Коллеги, добрый день. Необходимо использовать corrcoef, а массивы разной длины. Как сделать кол-во элементов одинаково?
Коллеги, добрый день. Необходимо использовать corrcoef, а массивы разной длины. Как сделать кол-во элементов одинаково?
8 Ответов
- вопрос
- 20.
 09.2022
09.2022
Другое, Встраиваемые системы, Цифровая обработка сигналов, Системы управления
Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…
Здравствуйте!Возникла необходимость менять некоторое строчки в сишном файле автоматически, используя матлабовский скрипт. Прошерстил весь интернет, в т.ч. англоязычные форумы, не смог ничего найт…
- MATLAB
20.09.2022
- Публикация
- 15.09.2022
Системы управления, Другое
Видел видос на канале экспоненты по созданию топливной системы. Вопрос заключается в наличии более полного описания готового примера или соответсвующее документации. Я новичок в симулинке и ещё многого не знаю. Адекватных и раскрытых пособий по созданию гидрав…
Моделирование гидравлических систем в simulink
- Публикация
- 10.
 09.2022
09.2022
Системы управления, Электропривод и силовая электроника, Другое
Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов. В этой книге в научно-практическо-методической форме я план…
Планирую написать книгу про модельно-ориентированное программирование с автоматическим генерированием кода применительно к разработке разнообразных микропроцессорных систем управления электроприводов.
- Публикация
- 24.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
&…
Здесь собрана литература по комбинированным методам множественного доступа, в которых используется разделение пользователей в нескольких ресурсных пространствах.
- вопрос
- 23.
 08.2022
08.2022
Математика и статистика, Радиолокация, Цифровая обработка сигналов
Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?
Есть записанный сигнал с датчика (синус с шумом). Как определить соотношение сигнал/шум?
4 Ответа
- ЦОС
- цифровая обработка сигналов
23.08.2022
- Публикация
- 23.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
&…
Здесь соборана литература по методам множественного доступа с поляризационным разделением и разделением по орбитальном угловому моменту.
- Публикация
- 16.08.2022
Цифровая обработка сигналов, Системы связи, Математика и статистика
Здесь собрана литература по методам множественного доступа с пространственным разделением.
- вопрос
- 22.07.2022
Изображения и видео, Цифровая обработка сигналов, Математика и статистика, Биология, Встраиваемые системы, Глубокое и машинное обучение(ИИ), Автоматизация испытаний, ПЛИС и СнК, Системы управления, Другое
Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например: file_1_1.txt file_1_2.txt file_1_3.txt file_1_4.txt fil…
Здравствуйте. Мне нужно обработать большое количество файлов с похожими названиями, каждый блок файлов относится к отдельному объекту, например: file_1_1.txt file_1_2.txt file_1_3.txt file_1_4.txt fil…
2 Ответа
- чтение
22.07.2022
- вопрос
- 17.07.2022
Математика и статистика, Цифровая обработка сигналов
Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…
Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…
Уважаемые коллеги, добрый вечер! В общем, возникла проблема следующего характера. Имеется сигнал, достаточно большой объем точек, длительность порядка 35-40 секунд. Он представлят собой последовательн…
- MATLAB
- Signal Processing
17.07.2022
2} = 2-t,$$ снова для $t \neq 0$. Что происходит, когда $t \to 0$? Это показывает, что $f$ не является непрерывным в $(0,0)$.С другой стороны, $f$ непрерывна везде, где $f$ определена, поскольку числитель и знаменатель, очевидно, непрерывны.
$\endgroup$
$\begingroup$
Чтобы функция была непрерывной в точке $(x_0,y_0)$, нужно доказать, что
$$ \lim f(x,y) = f(x_0,y_0)\quad \mathrm{as} \quad (x,y)\to (x_0,y_0). $$ 92-xy}{x+y}=x\frac{x+y-2y}{x+y}=x-2\frac{1}{\frac{1}{x}+\frac{1}{ у}}. $$
Очевидно, $\lim_{(x,y)\to(0,0)}x=0$. Если мы можем выбрать $y:=y(x)$, ($y(x)\neq -x$), такое, что $\lim_{x\to 0}\left(\frac{1}{x}+ \frac{1}{y(x)} \right)\neq\pm\infty$, то $f$ не является непрерывным в $(0,0)$. Выберите, например, $\frac{1}{x}+\frac{1}{y(x)}=1$, то есть $y(x):=\frac{x}{x-1} $, где можно предположить, что $x\neq 1$, поскольку $x\to 0$. ($y(x)\neq -x$ для любого $x\neq 0$.)
$$
Очевидно, $\lim_{(x,y)\to(0,0)}x=0$. Если мы можем выбрать $y:=y(x)$, ($y(x)\neq -x$), такое, что $\lim_{x\to 0}\left(\frac{1}{x}+ \frac{1}{y(x)} \right)\neq\pm\infty$, то $f$ не является непрерывным в $(0,0)$. Выберите, например, $\frac{1}{x}+\frac{1}{y(x)}=1$, то есть $y(x):=\frac{x}{x-1} $, где можно предположить, что $x\neq 1$, поскольку $x\to 0$. ($y(x)\neq -x$ для любого $x\neq 0$.)
$\endgroup$
$\begingroup$ 92(1-м)}{х(1+м)}$$ $$ \lim_{x \rightarrow \alpha} \frac{x(1-m)}{(1+m)}=\frac{\alpha (1-m)}{(1+m)}$$ $$\text{ответ предела зависит от пути (m), поэтому } \mathcal{f} \text{ не является непрерывным} $$
$\endgroup$
1
$\begingroup$
Еще один способ показать непрерывность в $(0,0)$ состоит в том, чтобы показать, что $f$ неограничена в любой окрестности $(0,0)$:
Пусть $\epsilon > 0 $ и $ x\in\mathbb{R}$ такой, что $0
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Модуль 8 — Непрерывность — Урок 1
На этом уроке вы изучите непрерывность в точке, исследуете разрыв в точке, отобразите разрывы и узнаете, как переопределить функцию для устранения разрыва в точке. Затем вы будете использовать TI-83 для построения графиков кусочно определенных функций.
Неформально функция называется непрерывной на отрезке, если вы можете начертить ее график на отрезке, не отрывая карандаша от бумаги. Формальное определение непрерывности начинается с определения непрерывности в точке, а затем распространяется на непрерывность на интервале. Может показаться, что формальное определение не имеет много общего с концепцией рисования графика, не отрывая карандаша от бумаги, но после изучения нескольких примеров с помощью TI-83 связь между формальным и неформальным определениями должна стать более очевидной.
Непрерывность в точке и на интервале
Формальное определение непрерывности в точке имеет три условия, которые должны быть выполнены.
Функция f ( x ) непрерывна в точке, где x = c , если
- существуют
- ф ( c ) существует (то есть c находится в домене f .)
Функция непрерывна на отрезке, если она непрерывна в каждой точке отрезка.
Разрыв в точке
Определение непрерывности в точке может иметь больше смысла, поскольку вы видите, что оно применяется к функциям с разрывами. Если какое-либо из трех условий определения непрерывности нарушается при x = c , в этой точке функция разрывна. Изучите непрерывность когда х = 0.
Проверка условий непрерывности
- Предел функции как x приближается к 0, обсуждалось в Уроке 6.3, где было показано, что . Следовательно, первое условие непрерывности выполнено.
- Функция не определено при x = 0, потому что деление на 0 не определено.
 Функция не удовлетворяет второму условию непрерывности, потому что 0 не находится в домене f .
Функция не удовлетворяет второму условию непрерывности, потому что 0 не находится в домене f . - Нет необходимости проверять третье условие, поскольку второе условие не выполнено.
По определению непрерывности можно сделать вывод, что не является непрерывным в х = 0.
Отображение разрывов
Разрыв в точке можно проиллюстрировать графиком функции в соответствующем окне. Разрыв проявляется только в том случае, если он имеет значение 90 103 x 90 104, используемое на графике. Трудно (а может и невозможно) заставить его появиться в такой момент, как или же .
- Введите Y 1 = sin(X)/X в редакторе Y=.
Ось y должна быть отключена, чтобы увидеть разрыв в x = 0.
- Откройте меню Формат, нажав [ФОРМАТ], который выше .
- С помощью клавиш со стрелками выделите «AxesOff» и нажмите .
- График функции в окне [-6, 6, 1] x [-1, 2, 1] с Xres = 1.

- Исследуйте функцию с функцией трассировки, чтобы увидеть, что не определяется при x = 0.
Разрыв изображается дырой на графике в точке с координатами (0,1).
| |||
Удаление разрыва
Ниже показано, как можно переопределить, чтобы создать новую функцию, точно такую же, как исходная функция для всех ненулевых значений x , но непрерывен при x = 0.
Определите новую функцию g ( x ) как функцию, значения которой за и y = 1 для x = 0.
То есть,
Эта новая функция называется кусочной функцией , поскольку к разным частям области применяются разные формулы. График г ( x ) совпадает с графиком за исключением того, что он включает точку (0,1), точку, которая заполняет отверстие.
График кусочной функции
Вы можете построить график кусочной функции, введя две части в Y 1 и Y 2 . Первая часть уже должна быть в Y 1 . (Y 1 = sin(X)/X)
- Введите Y 2 = 1/(X=0).
Символ «=» можно вставить в редактор Y= из меню «Тест», нажав [ТЕСТ] .
| gif»> | |||
Логическое выражение Знаменатель Y 2 = 1/(X=0) является логическим выражением , потому что оно либо истинно, либо ложно. Когда логическое выражение истинно, оно возвращает значение 1. Если оно ложно, логическое выражение возвращает значение 0. Это означает, что Y 2 будет равно 1, когда x = 0, и будет неопределенным, когда потому что деление на ноль не определено. |
- Отобразите новый непрерывный график, нажав .
Отверстие в (0, 1) было заполнено.
Включение осей обратно
Прежде чем покинуть этот урок, вы должны включить оси графика.
- Вернитесь в меню Формат, нажав [ФОРМАТ].
- Используйте клавиши со стрелками, чтобы выделить «AxesOn».

- Выберите эту настройку, нажав .
- Выйдите из меню Формат, нажав [ПОКИДАТЬ].
8.1.1 Переопределить чтобы сделать его непрерывным при x = 2. Щелкните здесь, чтобы получить ответ.
Непрерывность: определение, примеры и типы
Один из способов взглянуть на непрерывность — начать с технического определения, а затем выполнить ряд примеров, чтобы увидеть, что является или не является непрерывным, используя определение. Вместо этого мы начнем с интуитивного понимания непрерывных функций и построим то, что хотели бы видеть в определении.
Интуитивно непрерывная
Вы, наверное, слышали, как кто-то сказал, что «функция непрерывна, если вы можете нарисовать ее, не поднимая карандаш». Итак, давайте посмотрим, что должно быть правдой, чтобы это произошло, начиная с одной точки p .
Если вы попытаетесь нарисовать эту функцию, не поднимая карандаш, у вас не получится, потому что в функции есть отверстие на p . На самом деле он даже не определен в p ! Таким образом, вам определенно нужно будет предположить, что функция, о которой вы думаете, определена в точке p, и это делается с помощью фразы «предположим, что существует».
На самом деле он даже не определен в p ! Таким образом, вам определенно нужно будет предположить, что функция, о которой вы думаете, определена в точке p, и это делается с помощью фразы «предположим, что существует».
Эта функция не определена в точке p | StudySmarter Originals
Но достаточно ли функции, имеющей значение p , чтобы убедиться, что вы можете нарисовать ее, не поднимая карандаш? Давайте рассмотрим другой случай.
Эта функция определена по адресу p , но ограничения слева и справа не совпадают. Другими словами,
, значит,
не существует. Итак, предел как x приближается к p тоже должен существовать!
Ограничения слева и справа не совпадают | StudySmarter Originals
Таким образом, даже определения функции недостаточно. Вам также нужно, чтобы предел слева и справа имел одинаковое значение. Но достаточно ли этого, чтобы убедиться, что вы можете рисовать, не поднимая карандаш? Посмотрим!
Приведенная ниже функция определяется по адресу p . Предел существует, поскольку x приближается к p . Но оно не равно значению функции! Вы можете записать эти два значения не так, как
Предел существует, поскольку x приближается к p . Но оно не равно значению функции! Вы можете записать эти два значения не так, как
Значение функции не совпадает с пределом функции | StudySmarter Originals
Теперь давайте объединим все это в определение.
Определение непрерывности
Функция непрерывна в точке p тогда и только тогда, когда все верны следующие три вещи:
- существует
2. существует (предел слева и справа равны)
3.
Если функция не удовлетворяет любому из этих трех условий, то говорят, что она прерывистая на p, или просто не непрерывна на p .
Выражение «тогда и только тогда» — это биусловный логический оператор, означающий, что если A истинно, то B истинно, а если B истинно, то A истинно.
Простые шаги для проверки непрерывности функции
Вы можете использовать определение, чтобы выполнить пошаговый процесс проверки непрерывности функции на стр.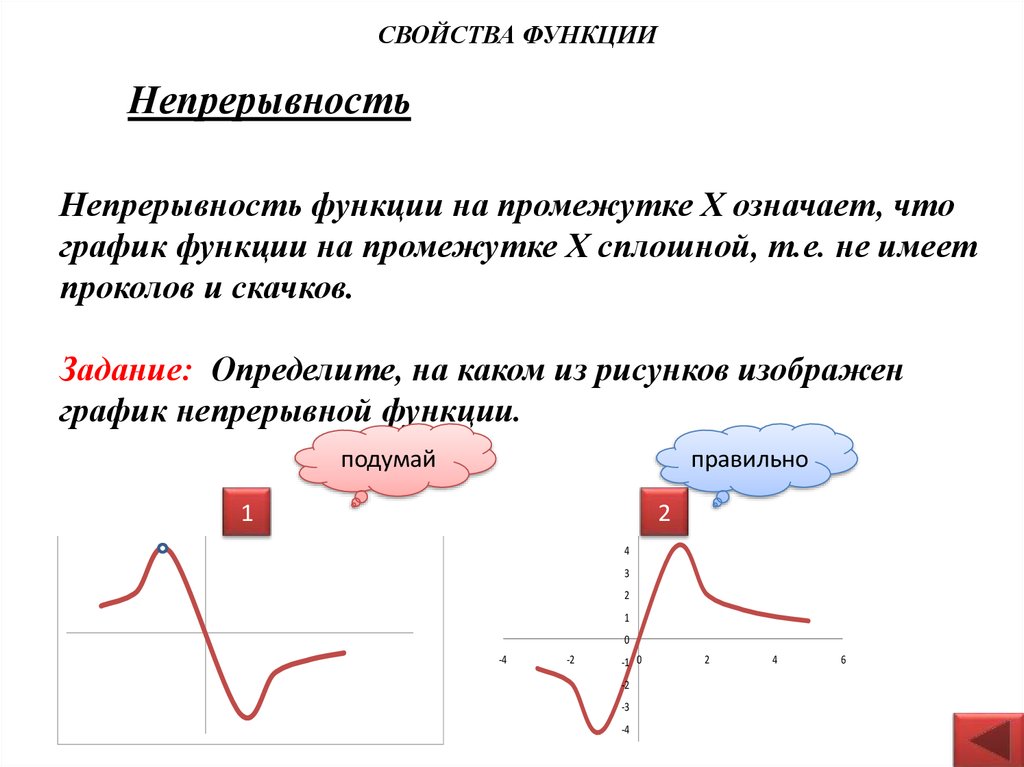 .
.
Шаг 1: Убедитесь, что функция определена по адресу p . Если это не так, остановитесь, потому что функция определенно не непрерывна на p .
Шаг 2: Убедитесь, что он существует. Если это не так, вы можете остановиться, потому что функция определенно не является непрерывной на p .
Шаг 3: Убедитесь, что предел и значение функции равны. Если это не так, то функция определенно не является непрерывной на p .
Обратите внимание: иногда, если функция в какой-то точке имеет разрыв, люди говорят, что она имеет разрыв в этой точке. Эти две фразы означают одно и то же.
Примеры непрерывных функций
Давайте потренируемся определять, является ли функция непрерывной в определенной точке!
Определите, является ли функция
непрерывной при .
Ответ:
Если вы попытаетесь вычислить функцию в 2, вы получите деление на ноль. Так что на самом деле эта функция не определена в точке , поэтому она не может быть непрерывной и в этой точке. Вы можете построить график функции, чтобы увидеть, что в точке есть вертикальная асимптота, поэтому она здесь не определена.
Вы можете построить график функции, чтобы увидеть, что в точке есть вертикальная асимптота, поэтому она здесь не определена.
Эта функция не является непрерывной при x=2 | StudySmarter Originals
Таким образом, сложность предыдущего примера заключалась в том, что функция не была определена, когда . Предположим вместо этого, что ваша функция определяется числом
, которое определенно определено при . Является ли эта функция непрерывной при ?
Ответ:
В этом случае
но
,
так что предел не существует в . Поэтому, хотя функция и определена при , она не непрерывна там.
Давайте еще немного подправим предыдущий пример. Если проблема в том, что предел слева и справа не совпадает, вы можете немного изменить функцию, чтобы посмотреть, что произойдет. Возьмите
, который все еще определен, когда . Теперь функция непрерывна в точке
. Ответ:
. Теперь, когда вы посмотрите на предел, приближающийся к 2, вы получите
Но , что, конечно же, не бесконечность! Таким образом, функция по-прежнему не является непрерывной при .
Решите, будет ли функция
является непрерывным, когда .
Ответ:
Хитрость заключается в том, чтобы внимательно прочитать вопрос. Мы не обязательно смотрим на точку, где функция меняет определение, мы смотрим на то, что задает вопрос!
В этом случае функция меняет определение при x=2, но нас спрашивают, является ли она непрерывной при x=3. Таким образом, все, что вам нужно учитывать, это то, является ли функция непрерывной в точке . Но это всего лишь линия, так что вы знаете
,
и функция непрерывна в .
Давайте разберемся шаг за шагом:
Шаг 1: Убедитесь, что функция определена в . . Поэтому он определен.
Шаг 2: Убедитесь, что ограничение на существует. То есть проверьте, равны ли пределы слева и справа от.
и .
Пределы слева и справа действительно равны.
Шаг 3: Наконец, проверьте, равен ли предел значению функции в . То есть:
Это последнее условие выполнено. Следовательно, функция непрерывна при .
Следовательно, функция непрерывна при .
В предыдущем примере точка p не находилась там, где у функции был переключатель, в котором использовалась формула. Что, если вместо этого вас интересовала точка ?
Определите, является ли функция
непрерывной в точке .
Ответ:
Давайте проделаем те же шаги, что и в предыдущем примере.
Шаг 1: Проверьте, определена ли функция в .
.
Таким образом, функция определена в .
Шаг 2: Теперь вы проверяете, существует ли ограничение. Предел слева дает
, а предел справа равен
, что означает, что
Шаг 3: Наконец, проверьте, равны ли значение функции из шага 1 и предел из шага 2. Они оба равны 5!
Итак, вы проверили:
- Что функция определена в точке,
- В этой точке существует предел функции, и
- Значение функции в этой точке имеет то же значение, что и предел.
Следовательно, функция непрерывна при .
Что, если мы немного изменим функцию в предыдущем примере?
Определите, является ли функция
непрерывной в точке .
Ответ:
Шаг 1:
Так же, как и в предыдущем примере,
Шаг 2: Проверка левого и правого пределов:
Предел слева:
Но теперь предел справа
, поэтому
не существует. Поэтому функция не является непрерывной в точке .
Здесь, поскольку критерий шага 2 не выполнен, нам не нужно переходить к шагу 3!
Непрерывность в исчислении
Почему вас должно волновать, является ли функция непрерывной? Предположим, что вы моделируете население размером 90 375 x 90 376, измеренным в годах, и обнаруживаете, что формула для него дается как
, что, исходя из работы, которую вы проделали выше, не является непрерывной при . Взглянув на график этой функции,
Кусочная функция, не являющаяся непрерывной при p=2 | StudySmarter Originals
Знание того, что функция не является непрерывной, позволяет вам понять, что с изучаемой вами группой населения произошло что-то серьезное. В данном случае это внезапное отмирание, и это проблема, которую вы хотели бы исследовать.
В данном случае это внезапное отмирание, и это проблема, которую вы хотели бы исследовать.
Типы непрерывности
Здесь вы явно рассмотрели непрерывность в точке. Но как насчет непрерывности на интервале или даже на всей реальной линии? Информацию об интервалах см. в разделе «Непрерывность на интервале», а дополнительные теоремы о непрерывности см. в разделе «Теоремы о непрерывности».
Непрерывность — основные выводы
- Интуитивно функция является непрерывной, если вы можете нарисовать ее, не поднимая карандаш.
- Функция непрерывна в точке тогда и только тогда, когда функция определена в , предел функции существует в , а значение функции и предел в обоих имеют одно и то же значение.
- Функция, не являющаяся непрерывной в данной точке, называется разрывной.
- Функция не может быть непрерывной в точке, если
- функция там не определена, или
- если там не существует предела,
- или если там предел и значение функции не совпадают
Объяснение урока: Непрерывность в точке
В этом объяснителе мы узнаем, как проверить непрерывность функции в заданной точке.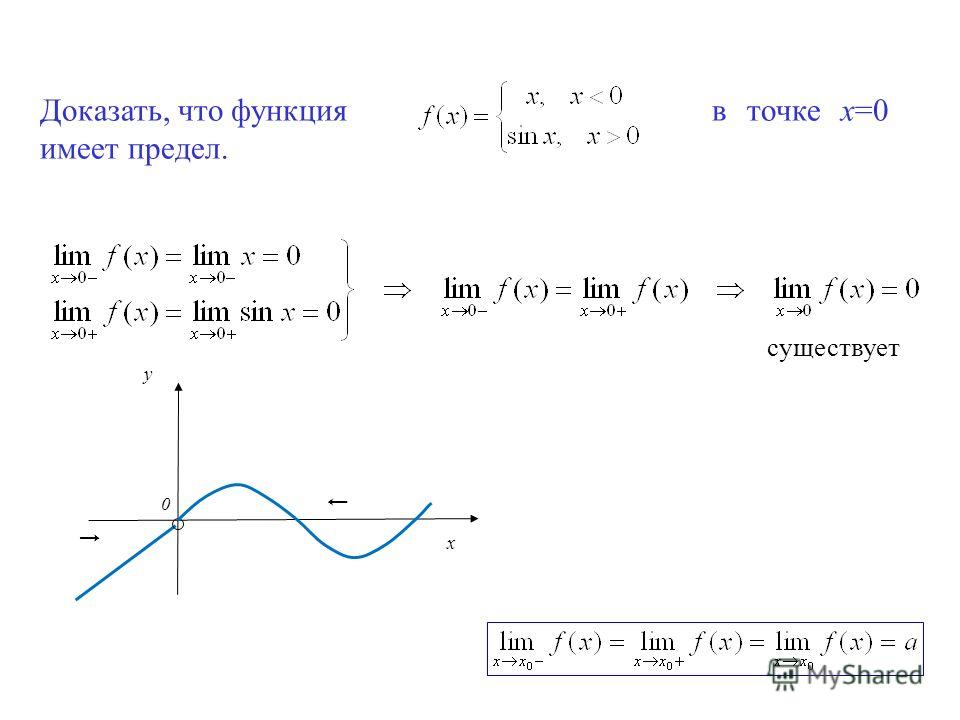
Оценка предела функции в точке — полезный способ получить информацию о том, что происходит с выходами этой функции вблизи (но не в) точки, и является неотъемлемой частью исчисления. Другими словами, предел сообщает нам значение, к которому приближается функция по мере того, как входные данные становятся все ближе и ближе к некоторой точке или числу.
Для некоторых функций оценка этих пределов может быть затруднена и может потребовать перезаписи предела в другой форме. Однако часто мы можем оценить эти пределы, непосредственно подставив эту точку в нашу функцию. Когда это верно, мы называем функцию непрерывной в этой точке.
Определение: Непрерывность функции в точке
Пусть 𝑎∈ℝ. Мы говорим, что вещественнозначная функция 𝑓(𝑥) непрерывна в точке 𝑥=𝑎, если lim→𝑓(𝑥)=𝑓(𝑎).
Полезное свойство непрерывности в точке 𝑥=𝑎 состоит в том, что мы можем нарисовать график 𝑓(𝑥) вблизи 𝑥=𝑎, не отрывая ручки от бумаги.
Для изучения непрерывности функций в точке введем сначала понятие разрыва. Если функция не удовлетворяет определению непрерывности в точке 𝑥=𝑎, то говорят, что 𝑓(𝑥) разрывна в точке 𝑥=𝑎.
Если функция не удовлетворяет определению непрерывности в точке 𝑥=𝑎, то говорят, что 𝑓(𝑥) разрывна в точке 𝑥=𝑎.
Тогда мы можем задать вопрос: «Как может функция не быть непрерывной при 𝑥=𝑎?» Для этого нам понадобится уравнение lim→𝑓(𝑥)=𝑓(𝑎) не соответствовать действительности. Это может произойти тремя способами:
- 𝑓(𝑎) не определено;
- lim→𝑓(𝑥) не существует;
- lim→𝑓(𝑥)≠𝑓(𝑎).
Следовательно, чтобы определить непрерывность функции в точке 𝑥=𝑎, мы должны проверить все три этих свойства.
Практическое руководство. Проверка непрерывности функции в точке
Чтобы проверить непрерывность функции 𝑓(𝑥) в 𝑥=𝑎, нам нужно проверить, выполняются ли следующие три условия.
- 𝑓 должен быть определен в 𝑎 (𝑎 находится в домене 𝑓).
- lim→𝑓(𝑥) должен существовать. (Это эквивалентно утверждению, что левый и правый пределы 𝑓(𝑥) при 𝑥=𝑎 существуют и равны.)
- lim→𝑓(𝑥) и 𝑓(𝑎) должны иметь одинаковое значение.

Например, проверим непрерывность 𝑓(𝑥)=|𝑥| в 𝑥=𝑎.
Во-первых, мы знаем, что 𝑓(0)=|0|=0, поэтому 𝑥=0 находится в домене 𝑓.
Во-вторых, нам нужно определить lim→|𝑥|. Чтобы оценить этот предел, вспомним, что мы можем определить, существует ли предел, проверив, существуют ли и равны ли левый и правый пределы в этой точке. Нам нужно вспомнить кусочное определение модульной функции: |𝑥|=−𝑥𝑥0,𝑥𝑥≥0.
Мы можем использовать это для оценки левого и правого пределов. Во-первых, при вычислении lim→|𝑥| все значения 𝑥 отрицательны, поэтому |𝑥|=−𝑥 в этом пределе. Затем мы можем оценить этот предел прямой подстановкой: limlim→→|𝑥|=(−𝑥)=0.
Аналогично, для правого предела все значения 𝑥 положительны, поэтому limlim→→|𝑥|=𝑥=0.
Итак, мы показали, что limlim→→|𝑥|=|𝑥|=0.
Следовательно, левый и правый пределы |𝑥| в 0 равны, поэтому lim→|𝑥|=0.
В-третьих, мы нашли значения 𝑓(0) и lim→𝑓(𝑥) и показали, что оба они равны одному и тому же значению, 0.
Поскольку выполняются все три условия, мы показали, что 𝑓(𝑥)=|𝑥| непрерывна в точке 0.
В нашем первом примере мы определим непрерывность кусочно определенной функции в концах ее подобластей.
Пример 1. Обсуждение непрерывности кусочно-определенной функции, включающей тригонометрические отношения, в точке 𝑓(𝑥)=−7𝑥+7𝑥,𝑥≤𝜋2,62𝑥−1,𝑥>𝜋2.sincoscos
Ответ
Чтобы функция 𝑓(𝑥) была непрерывной в 𝑎, необходимо выполнение трех условий:
- 𝑓 должно быть определено в 𝑎 (𝑎 находится в области определения 𝑓).
- lim→𝑓(𝑥) должен существовать.
- lim→𝑓(𝑥) и 𝑓(𝑎) должны иметь одинаковое значение.
В нашем случае 𝑎=𝜋2 из определения 𝑓 видно, что 𝑓𝜋2=−7𝜋2+7𝜋2=−7+0=−7.sincos
Следовательно, 𝜋2 находится в области определения 𝑓 и 𝑓𝜋2=−7. Итак, первое условие непрерывности в точке 𝑥=𝜋2 выполнено.
Чтобы проверить второе условие непрерывности, проверим, существуют ли и равны ли левый и правый пределы 𝑓 при 𝑥=𝜋2. Начнем с левого предела и заметим, что при 𝑥≤𝜋2 имеем 𝑓(𝑥)=−7𝑥+7𝑥sincos, что дает нам
limlimsincos→→𝑓(𝑥)=(−7𝑥+7𝑥).
Начнем с левого предела и заметим, что при 𝑥≤𝜋2 имеем 𝑓(𝑥)=−7𝑥+7𝑥sincos, что дает нам
limlimsincos→→𝑓(𝑥)=(−7𝑥+7𝑥).
Поскольку это тригонометрическое выражение, мы можем вычислить этот предел прямой подстановкой: limsincossincos→−7𝑥+7𝑥=−7𝜋2+7𝜋2=−7+0=−7.
Мы можем сделать то же самое для правого предела, отметив, что когда 𝑥>𝜋2, мы имеем 𝑓(𝑥)=62𝑥−1cos, что дает нам limlimcos→→𝑓(𝑥)=(62𝑥−1).
Затем мы можем оценить этот предел прямой подстановкой: limcoscos→(62𝑥−1)=62𝜋2−1=−6−1=−7.
Следовательно, и левый, и правый пределы существуют и равны −7, поэтому мы показали lim→𝑓(𝑥)=−7.
Следовательно, второе условие непрерывности 𝑓 при 𝑥=𝜋2 также выполняется.
Наконец, поскольку это также равно 𝑓𝜋2, мы можем заключить, что третье условие непрерывности также выполняется, и поэтому функция 𝑓 непрерывна в точке 𝑥=𝜋2.
Давайте рассмотрим пример, в котором мы используем определение непрерывности в точке, чтобы определить, как мы можем расширить функцию, чтобы она была непрерывной при значении вне ее области определения.
Пример 2. Использование непрерывности для нахождения значения, необходимого для расширения области определения функции 𝑥=1.
Ответ
Для того, чтобы функция 𝑓(𝑥) была непрерывной в точке a, необходимо выполнение трех условий:
- 𝑓 должно быть определено в 𝑎 (𝑎 находится в области определения 𝑓).
- lim→𝑓(𝑥) должен существовать.
- lim→𝑓(𝑥) и 𝑓(𝑎) должны иметь одинаковое значение.
Нам разрешено определять 𝑓(1) как любое желаемое значение, поэтому первое условие гарантированно выполняется.
Чтобы определить lim→𝑓(𝑥), можно попробовать прямую замену, поскольку 𝑓 — рациональная функция; Однако, 𝑓(1)=1+1−21−1=00, поэтому мы не можем оценить этот предел прямой подстановкой. Вместо этого мы проверим, что левый и правый пределы существуют и равны. Первый, limlim→→→𝑓(𝑥)=𝑥+𝑥−2𝑥−1=(𝑥−1)(𝑥+2)𝑥−1.
Поскольку мы берем предел, когда 𝑥 приближается к 1 слева, значения 𝑥 никогда не равны 1, поэтому мы можем отменить общий множитель 𝑥−1; это не изменит значение этого предела:
limlim→→(𝑥−1)(𝑥+2)𝑥−1=(𝑥+2).
Поскольку это многочлен, мы можем вычислить его прямой подстановкой: lim→(𝑥+2)=1+2=3.
Таким же образом можно вычислить правый предел: limlimlim→→→→𝑓(𝑥)=𝑥+𝑥−2𝑥−1=(𝑥−1)(𝑥+2)𝑥−1=( 𝑥+2)=3.
Поскольку левый и правый пределы существуют и оба равны 3, мы можем заключить lim→𝑓(𝑥)=3.
Для выполнения третьего условия нужно, чтобы 𝑓(1) было равно lim→𝑓(𝑥). Мы показали, что этот предел дает нам три, поэтому мы должны определить 𝑓(1)=3. Тогда это будет гарантировать выполнение всех трех условий непрерывности в этой точке.
Следовательно, 𝑓(1)=3 делает 𝑓 непрерывным в 𝑥=1.
В нашем следующем примере мы определим, можем ли мы сделать обратную функцию непрерывной при 𝑥=0, расширив ее область определения.
Пример 3. Определение возможности расширения области определения обратной функции так, чтобы она была непрерывной =0.
Ответ
Чтобы функция 𝑓(𝑥) была непрерывной в 𝑎, нам нужно выполнить три условия:
- 𝑓 должен быть определен в 𝑎 (𝑎 находится в домене 𝑓).

- lim→𝑓(𝑥) должен существовать.
- lim→𝑓(𝑥) и 𝑓(𝑎) должны иметь одинаковое значение.
Нам сказали, что мы можем определить 𝑓(0) как любое желаемое значение, что позволит выполнить первое условие.
Поскольку 𝑓 — рациональная функция, мы можем попытаться вычислить предел 𝑓(𝑥) при приближении 𝑥 к 0 путем прямой подстановки: lim→𝑓(0)=10, поскольку это не определено, мы не можем оценить этот предел прямой подстановкой. Вместо этого мы проверим, существуют ли и равны ли левый и правый пределы. Мы можем понять, почему эти пределы не существуют, рассмотрев график 𝑦=1𝑥.
По мере того, как входные значения нашей функции приближаются к нулю справа, знаменатель дроби становится все меньшим и меньшим положительным числом; он растет без ограничений. Точно так же, когда 𝑥 приближается к нулю слева, выходы будут приближаться к отрицательной бесконечности.
Как и ожидалось, левый и правый пределы 𝑓(𝑥) в точке 0 не существуют, и мы заключаем, что lim→𝑓(𝑥) не существует. Однако это означает, что второе условие непрерывности 𝑓(𝑥) в 0 не выполняется.
Однако это означает, что второе условие непрерывности 𝑓(𝑥) в 0 не выполняется.
Следовательно, функцию нельзя сделать непрерывной при 𝑥=0, определив 𝑓(0) как lim→𝑓(𝑥) не существует.
В следующем примере мы проверим непрерывность кусочно-определенной функции в точке.
Пример 4. Определение непрерывности функции в точке
Is 𝑓(𝑥)=⎧⎪⎨⎪⎩2𝑥+4𝑥+2𝑥−2,0𝑥=−2,𝑥+6𝑥+8𝑥+2𝑥>−2ififif непрерывный при 𝑥=−2?
Ответ
Напомним, что для того, чтобы 𝑓(𝑥) было непрерывным при −2, нам необходимо выполнение трех условий:
- 𝑓 должно быть определено при −2.
- lim→𝑓(𝑥) должен существовать.
- lim→𝑓(𝑥) и 𝑓(−2) должны иметь одинаковое значение.
Из определения 𝑓(𝑥) видно, что 𝑓(−2)=0, поэтому выполняется первое условие.
Чтобы проверить, выполняется ли второе условие, покажем, что левый и правый пределы существуют и равны. Во-первых, при 𝑥−2 имеем 𝑓(𝑥)=2𝑥+4𝑥+2, поэтому
limlim→→𝑓(𝑥)=2𝑥+4𝑥+2.
Попытка оценить это путем прямой подстановки дает неопределенное значение, поэтому вместо этого мы упрощаем ограничение: limlim→→→2𝑥+4𝑥+2=2(𝑥+2)𝑥+2=(2)=2.
Мы можем сделать то же самое для оценки правого предела: limlimlimlim→→→→𝑓(𝑥)=𝑥+6𝑥+8𝑥+2=(𝑥+2)(𝑥+4)𝑥+ 2=(𝑥+4)=2.
Поскольку и левый, и правый пределы существуют и равны 2, имеем lim→𝑓(𝑥)=2.
Однако это , а не равно 𝑓(−2), что равно 0; следовательно, третье условие непрерывности в точке 𝑥=−2 не выполняется.
Следовательно, 𝑓(𝑥) разрывно в точке 𝑥=−2, поскольку lim→𝑓(𝑥) и 𝑓(−2) имеют разные значения.
Решение : Нет
В нашем последнем примере мы будем использовать определение непрерывности для определения возможных значений переменной, которые позволяют функции быть непрерывной в этой точке.
Пример 5: Поиск значений переменной, которые делают кусочно-определенную функцию непрерывной
Найдите значения 𝑐, которые делают функцию 𝑓 непрерывной в 𝑥=𝑐, если
𝑓(𝑥)=2+𝑥𝑥≤𝑐,−3𝑥𝑥>𝑐. ifif
ifif
Ответ
Напомним, что для непрерывности 𝑓(𝑥) в точке 𝑐 необходимо выполнение трех условий:
- 𝑐 должен быть в домене 𝑓.
- lim→𝑓(𝑥) должен существовать.
- lim→𝑓(𝑥) и 𝑓(𝑐) должны иметь одинаковое значение.
Все три из этих условий должны быть истинными для значений 𝑐, которые мы ищем. Мы можем проверить каждое условие отдельно, начиная с первого условия.
Из определения 𝑓(𝑥) видно, что 𝑓(𝑐)=2+𝑐, поэтому любое реальное значение 𝑐 находится в области 𝑓, что говорит нам о выполнении первого условия.
Чтобы проверить второе условие, нам нужно будет оценить левый и правый пределы 𝑓 в 𝑐. Во-первых, поскольку 𝑓(𝑥)=2+𝑥 при 𝑥≤𝑐, limlim→→𝑓(𝑥)=2+𝑥=2+𝑐.
Во-вторых, поскольку 𝑓(𝑥)=−3𝑥, когда 𝑥>𝑐, limlim→→𝑓(𝑥)=(−3𝑥)=−3𝑐.
Нам нужно, чтобы оба этих предела были равны, что дает нам уравнение 2+𝑐=−3𝑐.
Мы можем найти 𝑐, разложив квадратное выражение на множители: 2+𝑐=−3𝑐𝑐+3𝑐+2=0(𝑐+1)(𝑐+2)=0,
Следовательно, 𝑐=−1 и 𝑐=−2 — единственные действительные значения 𝑐, выполняется второе условие.
Нам еще нужно проверить, позволяют ли эти значения выполнять третье условие.
Если 𝑐=−1, 𝑓(−1)=2+(−1)=3𝑓(𝑥)=2+(−1)=3.→andlim
Если 𝑐=−2, 𝑓(−2)=2+(−2)=6𝑓(𝑥)=2+(−2)=6.→andlim
Следовательно, 𝑓 непрерывно в 𝑐 только тогда, когда 𝑐=−1 или 𝑐=−2.
Давайте закончим повторением некоторых важных моментов этого объяснения.
Ключевые моменты
- Мы говорим, что функция 𝑓(𝑥) непрерывна в 𝑎, если lim→𝑓(𝑥)=𝑓(𝑎).
- Если функция непрерывна в 𝑎, то мы можем вычислить ее предел в 𝑎 прямой подстановкой.
- Мы можем проверить непрерывность 𝑓(𝑥) в 𝑎, проверив выполнение трех условий:
- 𝑓 должно быть определено в 𝑎 (𝑎 находится в домене 𝑓).
- lim→𝑓(𝑥) должны существовать (это эквивалентно утверждению, что левый и правый пределы 𝑓(𝑥) при 𝑥=𝑎 существуют и равны).
- lim→𝑓(𝑥) и 𝑓(𝑎) должны иметь одинаковое значение.
Непрерывность
Функция f ( x ) называется непрерывной в точке ( c , f ( c )), если выполняется каждое из следующих условий:
Геометрически это означает, что для f ( x ) в точке c нет разрыва, разделения или недостающей точки и что карандаш можно перемещать по графику f ( x ) через ( c , f ( c )) без отрыва от графика. Функция называется непрерывной в точке ( c , f ( c )) справа, если и непрерывной в точке ( c , f ( c )) слева, если . Многие из знакомых нам функций, таких как линейные, квадратичные и другие полиномиальные функции, рациональные функции и тригонометрические функции, непрерывны в каждой точке своей области определения.
Функция называется непрерывной в точке ( c , f ( c )) справа, если и непрерывной в точке ( c , f ( c )) слева, если . Многие из знакомых нам функций, таких как линейные, квадратичные и другие полиномиальные функции, рациональные функции и тригонометрические функции, непрерывны в каждой точке своей области определения.
Специальная функция, которая часто используется для иллюстрации односторонних пределов, — это функция наибольшего целого числа. Функция наибольшего целого числа , [ x ], определяется как наибольшее целое число, меньшее или равное x (см. рис. 1).
Рисунок 1 График функции наибольшего целого числа y = [ x ].
Некоторые значения [ x ] для определенных значений x равны
Наибольшая целочисленная функция непрерывна при любом целом числе n справа только потому, что
, следовательно, и f ( x ) не является непрерывным на n слева. Обратите внимание, что функция наибольшего целого числа непрерывна справа и слева при любом нецелом значении x .
Обратите внимание, что функция наибольшего целого числа непрерывна справа и слева при любом нецелом значении x .
Пример 1: Обсудите непрерывность f ( x ) = 2 x + 3 в х = -4.
Когда определение непрерывности применяется к f ( x ) при x = −4, вы обнаружите, что
, следовательно, f непрерывно при x = -4.
Пример 2: Обсудить непрерывность
Когда определение непрерывности применяется к f ( x ) при x = 2, вы обнаружите, что f (2) не существует; следовательно, f не является непрерывным (прерывистым) при x = 2,
Пример 3: Обсудить непрерывность
Когда определение непрерывности применяется к f ( x ) при x = 2, вы обнаружите, что
, следовательно, f непрерывно при x = 2,
Пример 4: Обсудите непрерывность .
Когда определение непрерывности применяется к f ( x ) при x = 0 вы обнаружите, что
, следовательно, f является непрерывным при x = 0 только справа.
Пример 5: Обсудить непрерывность
Когда определение непрерывности применяется к f ( x ) при x = −3, вы обнаружите, что
Многие теоремы исчисления требуют, чтобы функции были непрерывны на интервалах действительных чисел. Функция f ( x ) называется непрерывным на открытом интервале ( a , b ), если f непрерывно в каждой точке c ∈ ( a , b 90). Функция f ( x ) называется непрерывной на отрезке [ a , b ], если f непрерывна в каждой точке c ∈ ( a , b) и если f непрерывен в a справа и непрерывен в б слева.
Пример 6:
а. f ( x ) = 2 x + 3 непрерывно на (−∞, +∞), потому что f непрерывно в каждой точке c ∈ (−∞, +∞).
б . f ( x ) = ( x − 3)/( x + 4) непрерывно на (−∞, −4) и (−4, +∞), поскольку f непрерывно в каждой точке c ∈ (−∞,−4) и c ∈ (−4,+∞)
с . f ( x ) = ( x − 3)/( x + 4) не непрерывно на (−∞,−4] или [−4,+∞), потому что f не непрерывно на −4 слева или справа.
д. непрерывна на [0, +∞), так как f непрерывно в каждой точке c ∈ (0,+∞) и непрерывно в 0 справа.
и . f ( x ) = cos x непрерывно на (−∞,+∞), потому что f непрерывно в каждой точке c ∈ (−∞,+∞).
ф . f ( x ) = tan x непрерывно на (0,π/2), потому что f непрерывно в каждой точке c ∈ (0,π/2).
г . f ( x ) = tan x не является непрерывным на [0,π/2], потому что f не является непрерывным на π/2 слева.
ч . f ( x ) = tan x непрерывно на [0,π/2), потому что f непрерывно в каждой точке c ∈ (0,π/2) и непрерывна в 0 справа.
и . f ( x ) = 2 x /( x 2 + 5) непрерывна на (−∞,+∞), потому что f непрерывно в каждой точке c ∈ (−∞, +∞).
и . ж ( x ) = | x − 2|/( x − 2) непрерывно на (−∞, 2) и (2, +∞), поскольку f непрерывно в каждой точке c ∈ (−∞, 2) и с ∈ (2,+∞).
к . ж ( x ) = | x — 2|/( x — 2) не непрерывно на (-∞, 2] или [2, +∞), потому что f не непрерывно на 2 слева или справа.
Непрерывность функций — в реальном мире
Непрерывность функций — в реальном мире | Шмуп Магазин не будет работать корректно в случае, если куки отключены.
Похоже, в вашем браузере отключен JavaScript. Для наилучшего взаимодействия с нашим сайтом обязательно включите Javascript в своем браузере.
ПредыдущийВ реальном мире
Непрерывный функции, хотите верьте, хотите нет, очень полезны. Для одной вещи, они являются секретом цифровой записи, включая CD и DVD.
Вот краткое объяснение того, как непрерывные функции используются для записи. Предположим, вы хотите использовать цифровое записывающее устройство, чтобы записать свое пение в душе. Песня выходит как непрерывная функция. Цифровое записывающее устройство не может записывать то, как вы звучите в каждый момент времени (моментов бесконечно много!), но оно может записывать небольшие кусочки того, как вы звучите, несколько раз в секунду (на самом деле, гораздо чаще). .
.
Поскольку песня представляет собой непрерывную функцию, а непрерывные функции хороши (во всех отношениях, о которых мы говорили ранее, и во многих других отношениях), запись несколько раз в секунду содержит достаточно информации, чтобы компьютер мог воспроизвести больше или больше. -меньше того, как ты звучала все время, пока пела. Если небольшие фрагменты записывались достаточно часто и достаточно тщательно, воспроизведение будет звучать точно так же, как вы.
Узнайте, как работает цифровая запись.
Чтобы увидеть, насколько математически это может быть, проверьте это.
Страница: Мне нравятся абстрактные вещи; Почему я должен волноваться?
Непрерывные функции в том виде, в каком мы их здесь представили, — это лишь верхушка айсберга.
 Поле топологии множества точек определяет более общие понятия открытых и закрытых множеств, а затем определяет непрерывность в терминах этих открытых и закрытых множеств. Непрерывные функции, которые принимают действительные числа в качестве входных данных и выдают действительные числа в качестве выходных данных, являются лишь одним из видов непрерывных функций. У нас могут быть гораздо более странные функции, которые не имеют чисел в качестве входных или выходных данных, но при этом остаются непрерывными.
Поле топологии множества точек определяет более общие понятия открытых и закрытых множеств, а затем определяет непрерывность в терминах этих открытых и закрытых множеств. Непрерывные функции, которые принимают действительные числа в качестве входных данных и выдают действительные числа в качестве выходных данных, являются лишь одним из видов непрерывных функций. У нас могут быть гораздо более странные функции, которые не имеют чисел в качестве входных или выходных данных, но при этом остаются непрерывными.Страница: Как решить математическую задачу
Решение математической задачи состоит из трех шагов.
- Выясните, в чем проблема.
- Решите проблему.
- Проверьте ответ.
Пример. Определите все значения x , при которых функция
разрывна.

Ответ:
- Выясните, в чем проблема.
Мы хотим убедиться, что понимаем проблему. Что значит прерывистый означает? Это означает «не непрерывно», но что это значит?
A function is continuous at a value x = c if three things happen:
- f ( c ) exists,
- exists, and
For the чтобы функция была прерывистой при x = c , одна из трех вышеперечисленных вещей должна пойти не так. Либо
- f ( c ) не определено,
- не существует или
- f ( c ) и оба существуют, но они не совпадают.
Эта проблема требует от нас изучить функцию f и найти места, где что-то одно (или несколько) из того, что нам нужно для непрерывности, идет не так.
- Решить проблему.
- Где f ( x ) undefined?
Поскольку мы рассматриваем рациональную функцию, f не определено везде, где его знаменатель равен 0.
 Чтобы найти, где это, нам нужно разложить числитель и знаменатель на множители.
Чтобы найти, где это, нам нужно разложить числитель и знаменатель на множители.Когда знаменатель равен 0, либо x = -3, либо x = 4.
- Где не существует?
Эта рациональная функция имеет дырку в x = -3 и вертикальную асимптоту в x = 4, поэтому не существует. Это дает нам еще одну причину того, что f ( x ) прерывисто на x = 4.
- Где f ( c ) и оба существуют, но не совпадают?
У этой функции нет таких мест! Поскольку рациональная функция непрерывна везде, где она определена, мы нашли все разрывные места, о которых нам нужно беспокоиться.
Подводя итог, можно сказать, что эта функция прерывается только при x = -3 и x = 4.
- Проверьте ответ.
Помимо повторных арифметических действий, возможно, лучше всего будет построить график на калькуляторе. Убедитесь, что он выглядит непрерывным, кроме х = 4, где должна быть асимптота.
 Если мы спросим у калькулятора, что это за функция для x = -3, он должен сказать «ОШИБКА», потому что f (-3) не определено.
Если мы спросим у калькулятора, что это за функция для x = -3, он должен сказать «ОШИБКА», потому что f (-3) не определено.- Выясните, в чем проблема.
Приложение: Интервалы и обозначения интервалов
Интервал на реальной линии представляет собой набор всех чисел, попадающих между двумя заданными конечными точками.
Пусть a и b будут вещественными числами, где a < b . У нас могут быть следующие типы конечных интервалов:
- Открытый интервал ( a , b ) — это множество всех действительных чисел , попадающих строго между a и b . То есть все действительные числа x с a < x < b . Значения a и b не включены в этот интервал.

- Замкнутый интервал [ a , b ] представляет собой множество всех действительных чисел x , которые попадают (не строго) между a и b . То есть все действительные числа x , где a ≤ x ≤ b . В этот интервал включены значения a и b .
- Интервал [ a , b ) представляет собой набор всех действительных чисел x , где a ≤ x < b . и включены в этот интервал, а б нет.
- Интервал ( A , B ] — это набор всех реальных чисел x с A < x ≤ B < x ≤ B . не a .
Значения a и b называются конечными точками , потому что они являются точками на обоих концах интервала.
Чтобы запомнить, какой из двух интервалов—( a , b ) или [ a , b ] — включает в себя конечные точки a и b , попробуйте думать об обозначении интервала как о плечах.
 Если рычаги похожи на кронштейны [ a , b ], то они надежно удерживают a и b . Если плечи похожи на скобки ( a , b ), то концы a и b выскальзывают.
Если рычаги похожи на кронштейны [ a , b ], то они надежно удерживают a и b . Если плечи похожи на скобки ( a , b ), то концы a и b выскальзывают.Интервал ( a , b ) называется открытым, а интервал [ a , b ] — закрытым. Интервалы [ a , b ) и ( a , b ] не являются ни открытыми, ни закрытыми. Мы могли бы услышать, что эти интервалы называются «полузамкнутыми», «полузамкнутыми», «полуоткрытыми». , или «полуоткрытый».
У нас также могут быть бесконечные интервалы. Поскольку ∞ не является числом, у нас всегда будут круглые скобки вокруг ∞ или -∞, а не закрытые скобки. Вот типы бесконечных интервалов, которые мы можем есть, если предположить, что a — некоторое конечное число:
- (-∞, ∞), которое представляет собой всю действительную прямую. Другими словами, это множество всех действительных чисел.

- (-∞, a ) — это множество действительных чисел x , где x < a . Этот интервал не включает a .
- (-∞, a ] — множество действительных чисел x , где x ≤ a . Этот интервал действительно включает a .
- ( a , ∞) — это множество действительных чисел x , где a < x . Этот интервал не включает a .
- [ a , ∞) — это множество действительных чисел x , где a ≤ x . Этот интервал действительно включает a .
Бесконечные интервалы (-∞, ∞), (-∞, a ] и [ a , ∞) являются закрытыми интервалами. Бесконечные интервалы (-∞, a ) и ( a , ∞) открыты.
Бесконечные интервалы (-∞, ∞), (-∞, a ] и [ a , ∞) являются закрытыми интервалами. Бесконечные интервалы (-∞, a ) и ( a , ∞) открыты.

- Открытый интервал ( a , b ) — это множество всех действительных чисел , попадающих строго между a и b . То есть все действительные числа x с a < x < b . Значения a и b не включены в этот интервал.

 е.
е.
 09.2022
09.2022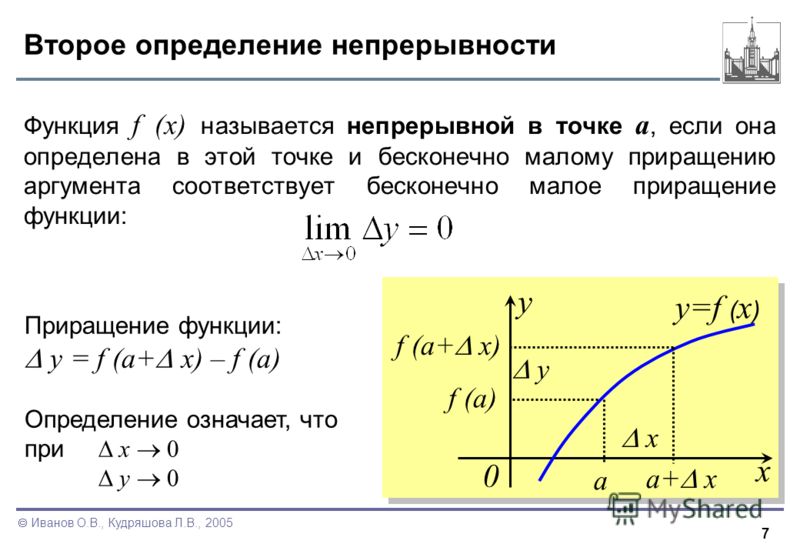 09.2022
09.2022 08.2022
08.2022 Функция не удовлетворяет второму условию непрерывности, потому что 0 не находится в домене f .
Функция не удовлетворяет второму условию непрерывности, потому что 0 не находится в домене f .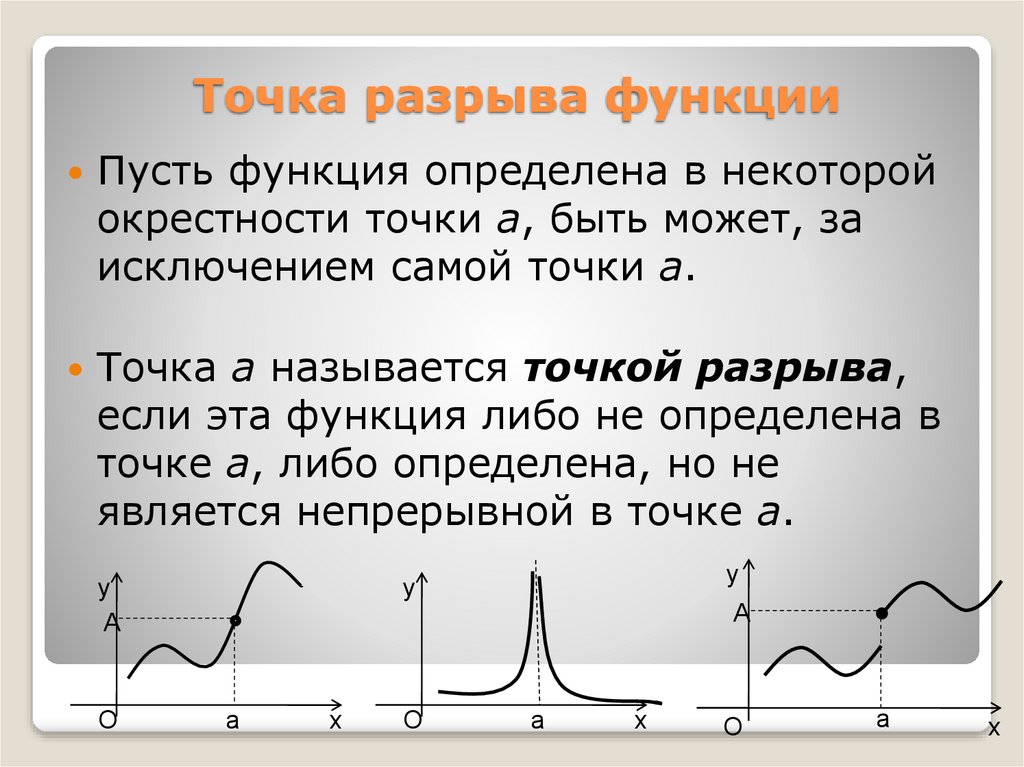


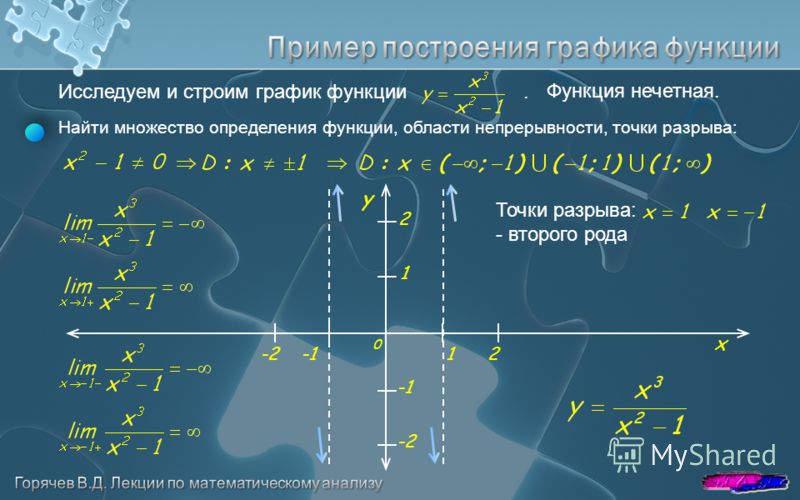
 Поле топологии множества точек определяет более общие понятия открытых и закрытых множеств, а затем определяет непрерывность в терминах этих открытых и закрытых множеств. Непрерывные функции, которые принимают действительные числа в качестве входных данных и выдают действительные числа в качестве выходных данных, являются лишь одним из видов непрерывных функций. У нас могут быть гораздо более странные функции, которые не имеют чисел в качестве входных или выходных данных, но при этом остаются непрерывными.
Поле топологии множества точек определяет более общие понятия открытых и закрытых множеств, а затем определяет непрерывность в терминах этих открытых и закрытых множеств. Непрерывные функции, которые принимают действительные числа в качестве входных данных и выдают действительные числа в качестве выходных данных, являются лишь одним из видов непрерывных функций. У нас могут быть гораздо более странные функции, которые не имеют чисел в качестве входных или выходных данных, но при этом остаются непрерывными.
 Чтобы найти, где это, нам нужно разложить числитель и знаменатель на множители.
Чтобы найти, где это, нам нужно разложить числитель и знаменатель на множители. Если мы спросим у калькулятора, что это за функция для x = -3, он должен сказать «ОШИБКА», потому что f (-3) не определено.
Если мы спросим у калькулятора, что это за функция для x = -3, он должен сказать «ОШИБКА», потому что f (-3) не определено.
 Если рычаги похожи на кронштейны [ a , b ], то они надежно удерживают a и b . Если плечи похожи на скобки ( a , b ), то концы a и b выскальзывают.
Если рычаги похожи на кронштейны [ a , b ], то они надежно удерживают a и b . Если плечи похожи на скобки ( a , b ), то концы a и b выскальзывают.
