Пример. Исследовать сходимость ряда, применяя необходимый признак сходимости и признак сравнения:
| 1 |
|
| 1 |
|
|
| 1 |
|
| 1 |
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
| … |
|
| … | ||||||
(2n 1) 2 | n |
|
|
| 2 |
| 5 2 | 3 | (2n 1) | 2 | n | |||||||
n 1 |
| 1 2 |
| 3 2 |
|
|
|
|
|
|
| |||||||
|
|
| limu |
|
| lim |
|
| 1 |
|
| 0 |
|
|
| |||
|
|
| n |
|
|
|
|
|
|
|
| |||||||
|
|
| (2n 1) | 2n |
|
|
| |||||||||||
|
|
| n |
| n |
|
|
|
|
| ||||||||
Необходимый признак сходимости ряда выполняется.
Для признака сравнения сравним данный ряд с геометрическим:
| 1 | 1 | 1 |
| 1 | … | 1 | … |
n | 2 | 2 | n | |||||
n 0 2 |
|
| 2 |
| 2 |
| ||
который сходится, так как q=1/2<1.
Сравнивая члены нашего ряда с соответствующими членами геометрического ряда, получим неравенства:
1 | 1; | 1 |
| 1 | ; | 1 |
| 1 | ;. | 1 |
| 1 | ;… | |
2 | 3 22 | 22 | 5 23 | 23 | (2n 1) 2n | 2n | ||||||||
|
|
|
|
|
|
|
..;Т.е. члены данного ряда соответственно меньше членов геометрического ряда. Следовательно, данный ряд сходится.
Пример. Исследовать сходимость ряда, используя признак Даламбера:
Следовательно, данный ряд сходится.
Контрольная работа по мат. анализу 08
А=4
Задача 1. Исследовать ряд на сходимость с помощью необходимого условия сходимости
.
Решение:
По необходимому условию сходимости общий член ряда должен стремиться к 0.
Имеем:
.
Следовательно, данный ряд расходится.
Задача 2. Исследовать ряд на сходимость с помощью признака Даламбера:
А) ; б) .
Решение:
А) . Тогда ряд сходится
Б) . Тогда ряд сходится
Задача 3. Исследовать ряд на сходимость с помощью признаков сравнения
А) б)
Решение:
А) Сравним данный ряд с рядом :
.
Ряд является обобщенным гармоническим рядом , тогда он сходится. По признаку сравнения в предельной форме исходный ряд также сходится.
Б) Сравним данный ряд с рядом :
.
Ряд является обобщенным гармоническим рядом , тогда он расходится. По признаку сравнения в предельной форме исходный ряд также сходится.
Задача 4. Исследовать знакочередующийся ряд на абсолютную и условную сходимость:
А) ; б)
Решение:
А) То, что абсолютной сходимости нет, было показано в задаче 3 (б). Условная сходимость выполняется по признаку Лейбница: последовательность монотонно убывает к 0.
Б) Исследуем на абсолютную сходимость по признаку Даламбера:
.
Итак, данный ряд сходится абсолютно.
Задача 5. Найти радиус и область сходимости степенного ряда:
.
Решение:
Радиус сходимости:
.
Итак, ряд сходится при . Исследуем сходимость на концах интервала:
– сходится по признаку Лейбница;
– расходится (показано в задаче 3(б)).
Итак, ряд сходится при .
Задача 6. Разложить в ряд Маклорена функцию , используя стандартные разложения функций в степенной ряд:
А) ; б) ; в) .
Решение:
А) ;
Б)
В) , тогда
.
Задача 7. Вычислить приближенно с точностью , используя разложение функции В степенной ряд.
Решение:
Известно разложение:
Задача 8. Используя разложение подынтегральной функции в степенной ряд, вычислить определенный интеграл с точностью
.
Решение:
Известно разложение:
Задача 9.
Разложить в ряд Фурье -периодическую функцию
Решение:
Разложение в ряд Фурье -периодической функции имеет вид:
Итак,
.
Задача 10. Разложить в ряд Фурье по синусам с периодом функцию , заданную на .
Решение:
Так как функцию нужно разложить по синусам, то предполагаем ее продление на интервале нечетным образом. Тогда
Итак,
.
Задача 11. Разложить в ряд Фурье по косинусам с с периодом функцию , заданную на .
Решение:
Так как функцию нужно разложить по косинусам, то предполагаем ее продление на интервале четным образом. Тогда
Итак,
.
Задача 12. Найти , если .
Решение:
Задача 13. Найти модуль и аргумент комплексного числа и записать в тригонометрической и показательной формах.
Решение:
Тогда тригонометрическая форма:
.
Экспоненциальная форма:
.
Задача 14. Для функции найти ее действительную и мнимую части и проверить на аналитичность:
а) ; б) .
Решение:
А) Пусть
Функция аналитическая, если выполняются условия Коши-Римана:
.
Итак, условия Коши-Римана выполнены, тогда данная функция аналитическая.
Б) Пусть
Функция аналитическая, если выполняются условия Коши-Римана:
.
Итак, условия Коши-Римана выполнены, тогда данная функция аналитическая.
Задача 15. А) Вычислить вычеты функции в ее изолированных особых точках. б) С помощью вычетов вычислить интеграл (обход контура против часовой стрелки):
,
Где – круг .
Решение:
А) Особыми точками данной функции будут точки . Первая будет полюсом второго порядка:
Вторая точка будет простым полюсом:
Вычислим вычеты в найденных точках:
Б) В круг попадают обе особые точки: . Тогда
.
Задача 16.
Найти изображение функции , используя таблицу изображений и свойство линейности преобразования Лапласа.
А) ; б) .
Решение:
По таблице преобразований Лапласа:
Тогда в силу линейности преобразования Лапласа:
А) ;
Б) .
Задача 17. Решить задачи Коши с помощью преобразования Лапласа:
А) б)
Решение:
А)
Итак, решением задачи Коши будет функция .
Б)
Итак, решением задачи Коши будет функция .
| < Предыдущая | Следующая > |
|---|
Ratio Test — Расчет 2
Все ресурсы расчета 2
9 Диагностические тесты 308 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 Следующая →
Исчисление 2 Помощь » Серия по исчислению » Конвергенция и дивергенция » Тест отношения
Какой из этих рядов нельзя проверить на сходимость/расхождение должным образом с помощью теста отношения? (Какая из этих серий не проходит тест на соотношение?)
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Объяснение:
Тест соотношения не пройден, когда . В противном случае ряд сходится абсолютно, если , и расходится, если .
При тестировании серии у нас есть
Следовательно, здесь тест отношения не проходит. (Вероятно, для читателя очевидно, что этот ряд уже расходится. Однако мы должны помнить, что всякая интуиция в математике требует строгого обоснования. Мы пытаемся сделать это здесь.)
Сообщить об ошибке
Предположим, что . Что мы можем сказать о ряде, используя тест отношения:
Возможные ответы:
Мы не можем сделать вывод, используя тест отношения.
Сходится.
Правильный ответ:
Мы не можем сделать вывод, используя тест отношения.
Объяснение:
В соответствии с требованиями этого вопроса нам придется использовать тест отношения. если L<1, то ряд сходится абсолютно, L>1, ряд расходится, а если L=1, ряд может либо сходиться, либо расходиться.
Для этого нам нужно вычислить: . В нашем случае:
Следовательно,
.
Мы знаем, что
Это означает, что
Поскольку L=1 по признаку отношения, мы не можем сделать вывод о сходимости ряда.
Сообщить об ошибке
Мы рассматриваем ряд : , используем критерий соотношения для определения типа сходимости ряда.
Возможные ответы:
Мы не можем сделать вывод о природе ряда.
Ряд быстро сходится.
Он явно расходится.
Правильный ответ:
Мы не можем сделать вывод о природе ряда.
Объяснение:
Чтобы иметь возможность сделать вывод с использованием теста отношения, нам нужно сначала вычислить отношение, а затем использовать если L<1 ряд сходится абсолютно, L>1 ряд расходится, и если L=1 ряд может либо сходятся, либо расходятся.
Вычисляя отношение, мы получаем,
.
Тогда имеем:
Следовательно имеем :
Понятно, что .
По тесту отношения мы не можем сделать вывод о характере ряда.
Сообщить об ошибке
Используя тест отношения,
что мы можем сказать о серии.
где целое число, удовлетворяющее условию:
Возможные ответы:
Мы не можем использовать тест отношения для изучения этой серии.
Мы не можем сделать вывод, используя тест отношения.
Правильный ответ:
Мы не можем сделать вывод, используя тест отношения.
Пояснение:
Позвольте быть общим членом ряда. Для проверки сходимости ряда воспользуемся тестом отношений.
Тест отношений утверждает:
тогда, если
1) L<1 ряд сходится абсолютно.
2) L>1 ряд расходится.
3) L=1 ряд либо сходится, либо расходится.
Значит надо вычислить,
имеем,
следовательно:
.
Мы знаем, что
и, следовательно,
Это означает, что:
Из теста отношения мы не можем сделать вывод о характере ряда. Нам придется использовать другой тест.
Сообщить об ошибке
Рассмотрим следующий ряд:
где дается:
. Используя тест отношения, найти характер ряда.
Возможные ответы:
Мы не можем сделать вывод, используя тест отношения.
Ряд сходится.
Правильный ответ:
Мы не можем сделать вывод, используя тест отношения.
Пояснение:
Позвольте быть общим членом ряда.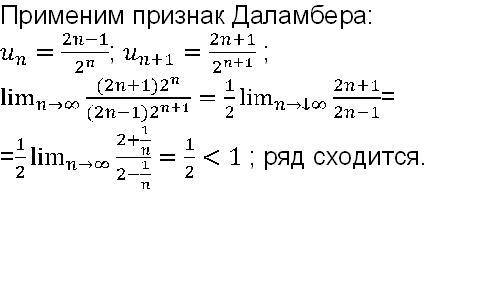
Для проверки сходимости ряда воспользуемся тестом отношений.
если L<1, то ряд сходится абсолютно, L>1, то ряд расходится, а если L=1, то ряд может либо сходится, либо расходиться.
Нам нужно оценить,
имеем:
.
Следовательно:
. Мы знаем, что
и, следовательно,
Это означает, что:
.
По тесту отношения мы не можем сделать вывод о характере ряда. Нам придется использовать другой тест.
Сообщить об ошибке
Используйте тест отношений, чтобы определить, является ли приведенный ниже ряд сходящимся или расходящимся.
Возможные ответы:
Ряд сходится.
Ряд расходится.
Правильный ответ:
Ряд расходится.
Объяснение:
Чтобы использовать тест отношения, нам нужно вычислить отношение
.
Тогда если L<1, то ряд сходится абсолютно, L>1 – ряд расходится, а если L=1 – ряд либо сходится, либо расходится.
У нас есть тогда:
.
Поскольку мы можем написать:
Таким образом и потому, что ряды должны расходиться.
Отсюда заключаем, что ряд расходится.
Сообщить об ошибке
Используя тест отношения, что вы можете сказать о следующем ряде:
Возможные ответы:
Ряд имеет два предела.
Ряд расходится.
Ряд сходится.
Ряд будет сходиться и расходиться, когда он приблизится к .
Правильный ответ:
Ряд сходится.
Объяснение:
Мы будем использовать сравнительный тест, чтобы сделать вывод о сходимости этого ряда. Чтобы показать, что мажорантный ряд сходится, нам придется воспользоваться критерием отношения.
если L<1, то ряд сходится абсолютно, L>1, то ряд расходится, а если L=1, то ряд либо сходится, либо расходится.
Прежде всего заметим, что
где n — натуральное число.
У нас есть . Если с помощью сравнительного теста мы можем показать, что ряд сходится, то с помощью сравнительного теста ряд также сходится.
Рассмотрим теперь ряд:. У нас есть:
и так как , мы заключаем, что ряд сходится по критерию отношения.
Это показывает, что наш ряд сходится.
Сообщить об ошибке
Предположим, что ряд имеет положительные члены.
Если что уж говорить о сходимости ряда.
Возможные ответы:
Нам нужно знать первые два термина.
Нам нужно знать явную формулу для .
Ряд расходится.
Ряд сходится.
Мы не можем сделать вывод.
Правильный ответ:
Ряд расходится.
Пояснение:
Нам дано, что ряд имеет положительные члены. Мы знаем, что
. Это значит, что .
Теперь отметим, что .
Тогда если L<1, то ряд сходится абсолютно, L>1, то ряд расходится, а если L=1, то ряд либо сходится, либо расходится.
Так как ряд будет расходиться.
Тест отношения позволяет сделать вывод, что ряд расходится.
Сообщить об ошибке
Мы будем рассматривать следующие серии:
.
Что вы можете сказать о характере этого ряда, используя тест отношения? Предположим, что .
Возможные ответы:
Нам нужно знать точное значение .
Ряд сходится.
Ряд сходится к .
Характер ряда зависит от .
Мы не можем сделать вывод о характере серии.
Правильный ответ:
Мы не можем сделать вывод о природе ряда.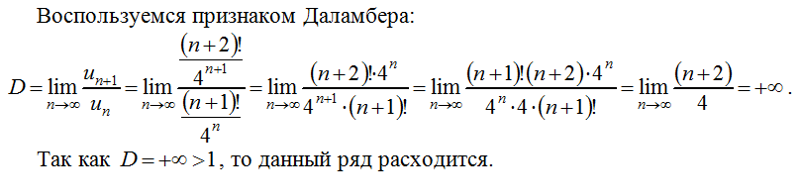
Объяснение:
Обратите внимание, что ряд для и всегда положителен.
Чтобы иметь возможность использовать тест соотношения, нам нужно вычислить соотношение:
. Затем найдите . Если L<1, то ряд сходится абсолютно, L>1 — ряд расходится, а если L=1, то ряд либо сходится, либо расходится.
Отсюда имеем:
Следовательно:
, так как
С помощью теста отношения мы не можем сделать вывод о природе ряда.
Сообщить об ошибке
Мы рассматриваем следующий ряд:
где .
Используя тест отношения, что вы можете сказать о характере ряда?
Сходится или расходится?
Возможные ответы:
Ряд сходится.
Мы не можем сделать вывод, используя тест соотношения.
Ряд расходится.
Правильный ответ:
Мы не можем сделать вывод, используя тест отношения.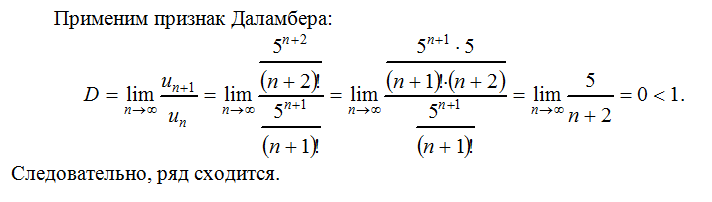
Объяснение:
Мы будем использовать тест отношения, заметив сначала, что ряд положителен.
Вычислим отношение:
. Обратите внимание, что:
Следовательно:
Теперь у нас есть и
и у нас есть
если L<1, то ряд сходится абсолютно, L>1, ряд расходится, а если L=1, ряд либо сходится, либо расходится.
Следовательно, тест отношения не дает результатов. Нам нужно будет использовать другой тест.
Сообщить об ошибке
← Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 Следующая →
Уведомление об авторских правах
Все ресурсы Calculus 2
9 Диагностические тесты 308 практических тестов Вопрос дня Карточки Learn by Concept
| Колледж науки и математики (CSM) готовит студентов к успеху благодаря инновационному и качественному академическому опыту в области физических наук, наук о жизни и математических процессов. | КГУ предлагает более 180 бакалаврских, магистерских, докторских степеней и программ. Выполните поиск ниже, чтобы найти свой. | События | Колледж науки и математики Новости Подробнее Новости
|
| Свяжитесь с нами |
Сочетая исследовательскую деятельность высокого уровня, современные учебные заведения и междисциплинарные курсы, наши студенты готовы к учебе в аспирантуре и карьере, чтобы справиться с задачами завтрашнего дня. Откройте для себя свое будущее среди наших программ для выпускников и бакалавров , специально разработанных для того, чтобы выделиться!
КГУ предлагает специальности
в областях STEM, сестринском деле, искусстве, кибербезопасности, бизнесе и многом другом.