Вариант № 05
1. Найти область определения функции :.
Область определения данной функции определяется неравенством . Корнями уравнения являются числа . Так как ветви параболы направлены вниз, то неравенство выполняется при . Ответ: .
2. Построить график функции: .
Данная функция определена на всей числовой оси. Преобразуем функцию: если , то .
Если , то . Таким образом, .
Ответ: график представлен на рисунке.
3. Построить график функции:
Данная функция определена при или . Преобразуем функцию. Вынесем за скобки множитель 3: Последовательно строим сначала , затем , «сжимая» график в три раза по оси ОХ, затем сдвигаем график вправо по оси ОХ на величину 1/3. Ответ: построения представлены на рисунках (Y – в радианах).
4. Построить график функции:
Исключим параметр T. Подставим во вторую формулу, получим: или . Функция определена при , так как всегда .
5. Построить график функции: .
Функция существует, если , т. е. или . Функция монотонно возрастает от 0 до 4 в интервале и монотонно убывает от 4 до 0 в интервале . Ответ: График представлен на рисунке.
6. Вычислить предел: .
Возведём все скобки в квадраты, получим:
.
Ответ: .
7. Вычислить предел: (неопределённость вида (0/0)).
Разлагаем числитель и знаменатель на простые множители: .
Ответ: .
8. Вычислить предел: (неопределённость вида (0/0)).
Умножим числитель и знаменатель на выражение: . . Ответ: .
9. Вычислить предел: (неопределённость вида (∞/∞)).
Воспользуемся первым замечательным пределом: :
.
Ответ: .
10. Вычислить предел: (неопределённость вида (1∞)).
Приведём предел ко второму замечательному пределу: :
. Ответ:
.11. Вычислить предел: (неопределённость вида (0/0)).
Воспользуемся эквивалентными величинами:
| Ln(1-2X)~-2X, Arctg3X~3X|. Ответ: .
12. Исследовать функцию на непрерывность и построить эскиз графика: .
Область определения – все действительные числа, кроме X=0. В точке X=0 функция имеет разрыв, во всех других точках является непрерывной (как элементарная функция). Исследуем поведение функции в окрестности точки разрыва: . Таким образом, в точке X=0 имеют место устранимый разрыв. Полагая , можно считать функцию непрерывной на всей числовой оси. Для построения эскиза графика функции рассмотрим поведение функции в бесконечности: . Ответ: В точке X=0 функция имеет устранимый разрыв, в остальных точках она непрерывна. Эскиз графика представлен на рисунке.
13. Исследовать функцию на непрерывность и построить эскиз графика: .
Область определения функции: . Ось ОХ разбивается на три интервала, на каждом из которых функция F(X) совпадает с одной из указанных непрерывных функций. Поэтому точками разрыва могут быть только точки, разделяющие интервалы. Вычислим односторонние пределы:
Поэтому точками разрыва могут быть только точки, разделяющие интервалы. Вычислим односторонние пределы:
. Таким образом, в точке X=0 функция непрерывна, а в точке X=1 функция терпит разрыв первого рода. Величина скачка функции в точке X=1 равна 2.
Ответ: В точке X=0 функция имеет разрыв первого рода, в остальных точках она непрерывна. Эскиз графика представлен на рисунке.
14. Исходя из определения производной, найти :
.
По определению . Заменим ΔX на X—X0:
. Но , поэтому . В данном случае , так как при любых значениях X. Ответ: .
15. Найти производную показательно-степенной функции: . Прологарифмируем функцию: . Берём производную, как производную неявной функции: . Подставляем сюда Y:
Ответ: .
16. Составить уравнения касательной и нормали к кривой в данной точке, вычислить :
.
Уравнения касательной и нормали к кривой имеют вид и , где и — координаты точки касания. Вычислим сначала эти координаты:
Вычислим сначала эти координаты:
. Найдём производные и : . Тогда . Далее, , следовательно, . Таким образом, уравнение касательной , уравнение нормали . Или и .
Ответ:
17. Функция Y(X), заданная неявно уравнением , принимает в точке значение . Найти .
Дифференцируем уравнение по X, предполагая, что Y= Y(X): . Из этого равенства находим: . Находим вторую производную: . Вычислим производные в точке : .
18. Вычислить приближённое значение функции в заданной точке с помощью дифференциала: .
По определению дифференциала или, в других обозначениях, . Отсюда получаем формулу для приближённых вычислений: . В данном случае . Тогда . Ответ:
19. Вычислить предел с помощью правила Лопиталя: .
Это неопределённость вида (∞0). Преобразуем предел:
. Найдём предел в показателе степени:
, так как предел знаменателя равен ∞. Следовательно, . Ответ: .
Ответ: .
20. Вычислить предел с помощью правила Лопиталя: .
Это неопределённость вида (∞-∞). Преобразуем предел, делая замену :
. Ответ: .
21. Многочлен по степеням X представить в виде многочлена по степеням : .
Запишем формулу Тейлора для многочлена четвёртой степени: .
Найдём все производные: , . Тогда . Подставив это в формулу, получим: .
Ответ: .
22. Найти многочлен, приближающий заданную функцию в окрестности точки X0 с точностью до : .
Применяем формулу Тейлора:
.
Вычисляем последовательно:
.
Ответ:
23. Исследовать поведение функции в окрестности точки с помощью формулы Тейлора: .
Найдём значение функции и её первых трёх производных в заданной точке:
. По формуле Тейлора . Ответ: В окрестности точки (1, 3) функция ведёт себя как кубическая функция. Точка (1, 3) является точкой перегиба: слева – интервал вогнутости, справа – интервал выпуклости.
24. Вычислить предел с помощью формулы Тейлора: .
По формуле Тейлора . Аналогично, . Подставим это в предел:
.
Ответ: .
25. Найти асимптоты и построить эскиз графика функции: .
Область определения функции: . Функция непрерывна в каждой точке области определения. Найдём односторонние пределы в граничных точках области определения:
. Отсюда следует, что прямые и являются вертикальными асимптотами. Исследуем функцию при : . Следовательно, прямые и являются наклонными односторонними асимптотами. Ответ: Эскиз графика представлен на рисунке.
26. Провести полное исследование поведения функции и построить её график:.
1. Область определения: . 2. Функция чётная, периодичность отсутствует.
3. Функция непрерывна. Вертикальных асимптот нет. 4. , наклонных асимптот нет. 5. Первая производная . Производная в нуль не обращается ни в одной точке. В точке разрыва производной X=0 изменяется. При X<0 производная — функция убывает, При X>0 производная — функция возрастает, следовательно, в точке X=0 имеет место минимум функции, причём .
6. .
В точках и Вторая производная равна нулю. Кроме того, в точке вторая производная не существует. Имеем три интервала: в интервале производная — интервал вогнутости, в интервалах и Производная — интервалы выпуклости, в интервале производная — интервал вогнутости. Таким образом, точки и являются точками перегиба. 7. При функция равна . Точка (0, 3/2) – точка пересечения оси ОУ. С осью ОХ график не пересекается. Ответ: График функции представлен на рисунке, экстремум в точке (0, 3/2) — минимум, точки перегиба и . Значение функции в точках перегиба одинаковы и равны .
| < Предыдущая | Следующая > |
|---|
Вариант № 03
1. Найти область определения функции :.
Область определения данной функции определяется неравенством . Освободимся от знака модуля: при неравенство Никогда не выполняется; при неравенство выполняется всегда. Объединяя результаты, получим: .
2. Построить график функции: .
Так как всегда, то данная функция определена на всей числовой оси. Преобразуем функцию: . Таким образом, .
Ответ: график представлен на рисунке.
3. Построить график функции:
Данная функция определена для X, удовлетворяющих неравенству или . Преобразуем функцию. Вынесем за скобки множитель −3: Последовательно строим сначала , затем (переворачивая график вокруг оси ОY и «сжимая» его в три раза по оси ОХ), затем сдвигаем график вправо по оси ОХ на величину 2/3. Ответ: построения представлены на рисунках.
4. Построить график функции:
Исключим параметр T, применяя формулу . Подставляя сюда (), получим: . Так как по определению , то область определения функции будет . Ответ: График представлен на рисунке.
5. Построить график функции: .
Поскольку , то функция существует для тех значений φ, для которых . Это наблюдается при или .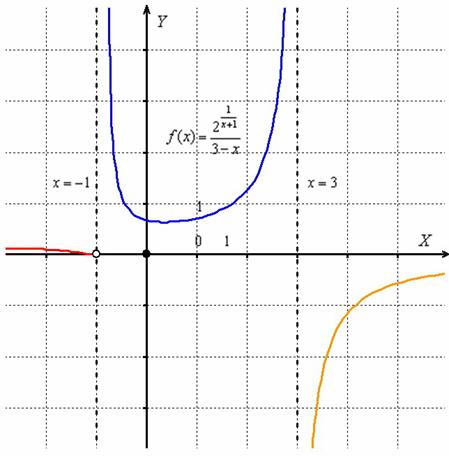 Полагая , получим шесть интервалов для φ, в которых изменяется одинаково, возрастая с нуля до двух, затем убывая с 2 до нуля. Таким образом, графиком будет шестилепестковая роза. Ответ: График представлен на рисунке.
Полагая , получим шесть интервалов для φ, в которых изменяется одинаково, возрастая с нуля до двух, затем убывая с 2 до нуля. Таким образом, графиком будет шестилепестковая роза. Ответ: График представлен на рисунке.
6. Вычислить предел: .
Воспользуемся формулой бинома Ньютона , где . Получим:
. Ответ: .
7. Вычислить предел: (неопределённость вида (0/0)).
Разлагаем числитель и знаменатель на простые множители:
. Ответ: .
8. Вычислить предел: (неопределённость вида (0/0)).
Преобразуем выражение:
.
Ответ: .
9. Вычислить предел: (неопределённость вида (0/0)).
Воспользуемся формулой и первым замечательным пределом: : . Ответ: .
10. Вычислить предел: (неопределённость вида (1∞)).
Приведём предел ко второму замечательному пределу: :
, где . Таким образом,
Ответ: .
11. Вычислить предел: (неопределённость вида (0/0)).
Воспользуемся эквивалентными величинами (при x→∞): Arctg(X)~Tg(X)~X,
~. Тогда .
Ответ: .
12. Исследовать функцию на непрерывность и построить эскиз графика: .
Область определения – все действительные числа, кроме X=−1. В точке X=−1 функция имеет разрыв, во всех других точках является непрерывной (как элементарная функция). Исследуем поведение функции в окрестности точки разрыва: . Таким образом, в точке X=−1 имеют место разрыв первого рода. Скачёк функции в точке разрыва равен (-2). Для построения эскиза графика функции рассмотрим поведение функции в бесконечности: . Ответ: В точке X=−1 функция имеет разрыв первого рода, в остальных точках она непрерывна. Эскиз графика представлен на рисунке.
13. Исследовать функцию на непрерывность и построить эскиз графика: .
Область определения функции: . Ось ОХ разбивается на три интервала, на каждом из которых функция F(X) совпадает с одной из указанных непрерывных функций.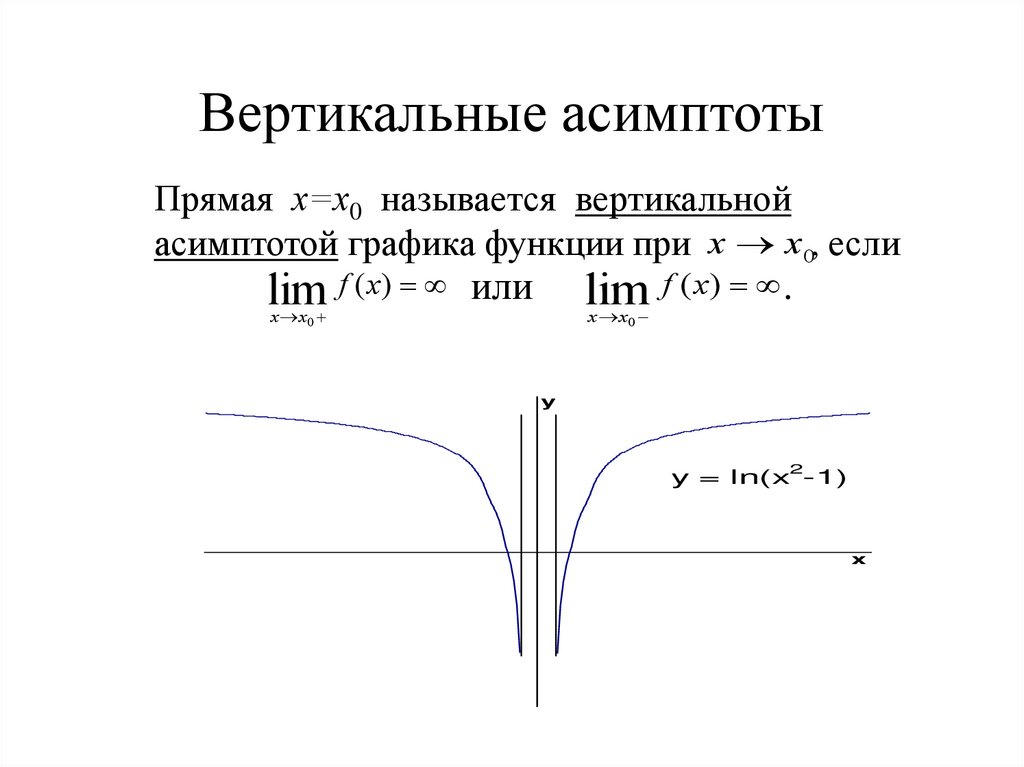 Поэтому точками разрыва могут быть только точки, разделяющие интервалы. Вычислим односторонние пределы:
Поэтому точками разрыва могут быть только точки, разделяющие интервалы. Вычислим односторонние пределы:
. Таким образом, в точке X=4 функция непрерывна, а в точке X=0 функция терпит разрыв первого рода. Величина скачка функции в точке X=0 равна 4.
Ответ: В точке X=0 функция имеет разрыв первого рода, в остальных точках она непрерывна. Эскиз графика представлен на рисунке.
14. Исходя из определения производной, найти :
.
По определению . Заменим ΔX на X—X0:
. Но , поэтому . В данном случае . Но Tg(T) ~T, а 2T-1~t∙ln(2) при T→0 . Поэтому
, так как при любом X. Ответ: .
15. Найти производную показательно-степенной функции: . Прологарифмируем функцию: . Берём производную, как производную неявной функции: . Подставляем сюда Y:
Ответ: .
16. Составить уравнения касательной и нормали к кривой в данной точке, вычислить :
.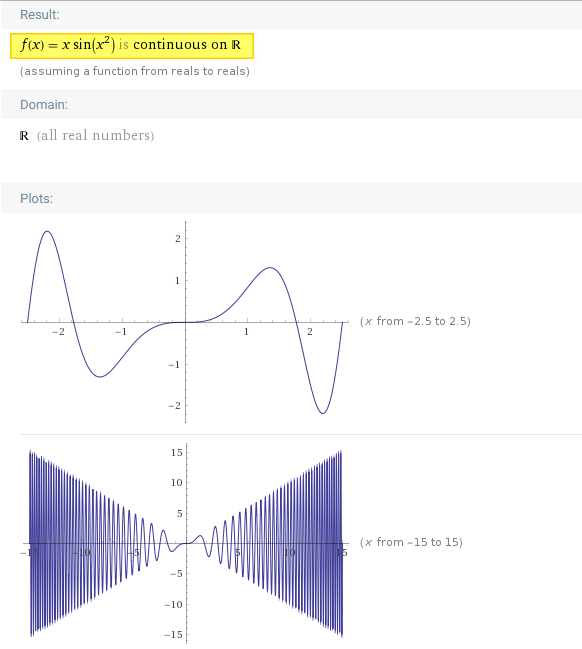
Уравнения касательной и нормали к кривой имеют вид и , где и — координаты точки касания. Вычислим сначала эти координаты:
. Найдём производные и : . Тогда . Далее, , следовательно, . Таким образом, уравнение касательной , уравнение нормали . Или и . Ответ:
17. Функция Y(X), заданная неявно уравнением , принимает в точке Значение . Найти .
Дифференцируем уравнение по X, предполагая, что Y= Y(X): . Из этого равенства находим: . Находим вторую производную: . Вычислим производные в точке : .
Ответ: , , .
18. Вычислить приближённое значение функции в заданной точке с помощью дифференциала: .
По определению дифференциала или, в других обозначениях, . Отсюда получаем формулу для приближённых вычислений: . В данном случае . Тогда . Ответ:
19. Вычислить предел с помощью правила Лопиталя: .
Это неопределённость вида (1∞). Преобразуем предел: . Найдём предел в показателе степени: . Следовательно, . Ответ: .
Следовательно, . Ответ: .
20. Вычислить предел с помощью правила Лопиталя: .
Это неопределённость вида (∞-∞):
. Но ~X. Поэтому
. Ответ: .
21. Многочлен по степеням X представить в виде многочлена по степеням : .
Запишем формулу Тейлора для многочлена четвёртой степени: .
Найдём все производные: , . Тогда . Подставив это в формулу, получим: .
Ответ: .
22. Найти многочлен, приближающий заданную функцию в окрестности точки X0 с точностью до : .
Применяем формулу Тейлора:
.
Вычисляем последовательно:
.
Ответ:
23. Исследовать поведение функции в окрестности точки с помощью формулы Тейлора: .
Найдём значение функции и её первых четырёх производных в заданной точке:
. По формуле Тейлора . Ответ: В окрестности точки (2, -2) функция ведёт себя как степенная функция четвёртой степени. Точка (2, -2) является точкой минимума функции.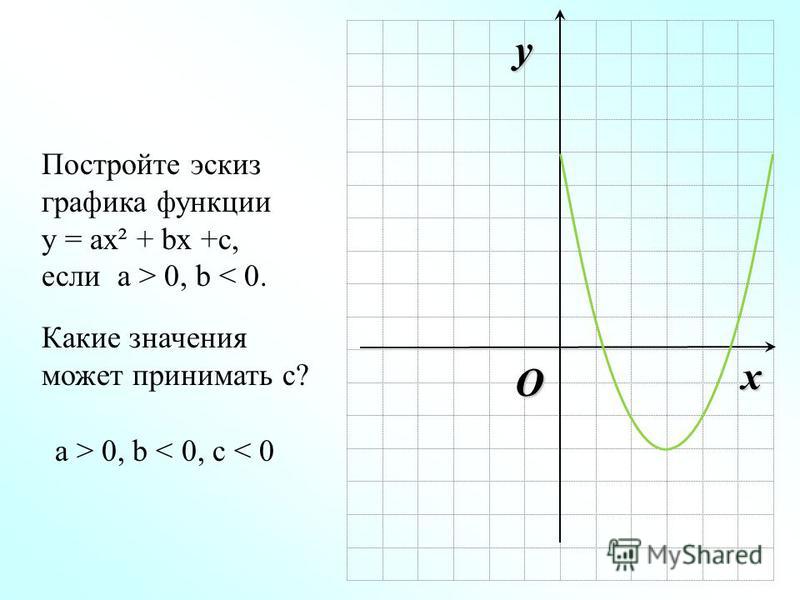
24. Вычислить предел с помощью формулы Тейлора: .
По формуле Тейлора . Аналогично, . Подставим это в предел:
.
Ответ: .
25. Найти асимптоты и построить эскиз графика функции: .
Область определения функции: . Функция непрерывна в каждой точке области определения. Найдём односторонние пределы в точке разрыва функции: . Отсюда следует, что прямая является вертикальной асимптотой. Исследуем функцию при : . Из этого следует, что имеется наклонная асимптота , где K=1. Действительно,
. Тогда
. Таким образом, прямая является на-
Клонной асимптотой. Ответ: Эскиз графика представлен на рисунке.
26. Провести полное исследование поведения функции и построить её график:.
1. Область определения: . 2. Чётность, нечётность, периодичность отсутствуют. 3. Функция непрерывна. Вертикальных асимптот нет. 4.
, следовательно, — односторонняя горизонтальная асимптота, наклонных асимптот нет. 5. Первая производная
Первая производная
. Производная обращается в нуль в точке . При производная , следовательно, функция возрастает, При производная , следовательно, функция убывает. Точка является точкой максимума функции, причём . 6. . В точке вторая производная равна нулю. Имеем два интервала: в интервале производная — интервал выпуклости, в интервале производная — интервал вогнутости. Точка — точка перегиба. 7. При функция равна , точка – точка пересечения оси ОУ. При получим , точка – точка пересечения оси ОХ. Ответ: График функции представлен на рисунке, экстремум (максимум) в точке (-2, 1), точки перегиба – точка .
| < Предыдущая | Следующая > |
|---|
15-16
1. | |||||||||||||||
Постройте графики функций: 2. | 3. | 4. | 5. cos | ||||||||||||
Вычислите пределы: | 6. | 7. | 8. | ||||||||||||
9. | 10. | 11. | |||||||||||||
Исследуйте функции на непрерывность и постройте эскизы графиков: | 12. | 13. | |||||||||||||
14. Исходя из определения производной, найдите : | |||||||||||||||
15. Найдите производную функции . | |||||||||||||||
16. Составьте уравнения касательной и нормали к кривой в заданной точке, вычислите в этой точке . | |||||||||||||||
17. xy2 + y +x2 = 3, x0 =1, y0 =1. | |||||||||||||||
18. Вычислите приближенное значение функции в заданной точке с помощью дифференциала: | y =, x = 4,16 | ||||||||||||||
Вычислите пределы с помощью правила Лопиталя. | 19. | 20. | |||||||||||||
21. Многочлен по степеням x представьте в виде многочлена по степеням разности (x–x0): | f(x) = 3x4 – 11x3 – 66, x0 = –2 | ||||||||||||||
22. | f(x) =, x0 = –1 | ||||||||||||||
23. Исследуйте с помощью формулы Тейлора и изобразите графически поведение функции в окрестности точки: | f(x) = 4x – x2+(x – 2)sin(x – 2), x0 = 2 | ||||||||||||||
24. Вычислите предел с помощью формулы Тейлора: | |||||||||||||||
25. | |||||||||||||||
26. Проведите полное исследование поведения функции и постройте ее график: | |||||||||||||||
1. Найдите область определения функции | |||||||||||||||
Постройте графики функций: | 2. | 3. | 4. | 5. | |||||||||||
Вычислите пределы: | 6. | 7. | 8. | ||||||||||||
9. | 10. | 11. | |||||||||||||
Исследуйте функции на непрерывность и постройте эскизы графиков: | 12. | 13. | |||||||||||||
14. | |||||||||||||||
15. Найдите производную функции | |||||||||||||||
16. Составьте уравнения касательной и нормали к кривой в заданной точке, вычислите в этой точке . | |||||||||||||||
17. Найдите производные неявно заданной функции y(x): x2 + xsiny – ey= 3, x0 = 2, y0 = 0. | |||||||||||||||
18. Вычислите приближенное значение функции в заданной точке с помощью дифференциала: | y = x7, x = 2,002 | ||||||||||||||
Вычислите пределы с помощью правила
Лопиталя. | 19. | 20. | |||||||||||||
21. Многочлен по степеням x представьте в виде многочлена по степеням разности (x–x0): | f(x) = x4 – 3x3, x0 =2 | ||||||||||||||
22. Найдите многочлен, приближающий заданную функцию f(x) в окрестности точки x0 с точностью до о((x–x0)3): | f(x) = sin lnx, x0 = e/6 | ||||||||||||||
23. и изобразите графически поведение функции в окрестности точки: | f(x) = ln(x+3) – sin(x+2)+x2/2 + 2x, x0 = –2 | ||||||||||||||
24. Вычислите предел с помощью формулы Тейлора: | |||||||||||||||
25. Найдите асимптоты и постройте эскиз графика функции: | |||||||||||||||
26. Проведите полное исследование поведения функции и постройте ее график: | |||||||||||||||
Соседние файлы в папке TR_1_Varianty_zadaniy
- #
03.
 07.2016279.55 Кб341-2.doc
07.2016279.55 Кб341-2.doc - #
03.07.2016290.3 Кб2611-12.doc
- #
03.07.2016286.72 Кб3113-14.doc
- #
03.07.2016262.14 Кб2715-16.doc
- #
03.07.2016260.61 Кб3117-18.doc
- #
03.07.2016262.14 Кб2819-20.doc
- #
03.07.2016262.14 Кб3121-22.doc
- #
03.07.2016268.8 Кб2523-24.doc
- #
03.07.2016199.17 Кб2325-25.doc
Как начертить график и найти непрерывность функций
О «Как начертить график и найти непрерывность функций»
Как нарисовать график и найти непрерывность функций:
Здесь мы увидим несколько примеров задач, чтобы понять концепцию рисования графика и проверки непрерывности функции.
Нарисуйте график и проверьте непрерывность функции — Практические вопросы
Вопрос 1:
Найдите точки, в которых функция f разрывна. В какой из этих точек f непрерывна справа, слева или ни там, ни там? Нарисуйте график f.
Решение:
Сначала проверим непрерывность в точке x = -1
lim x-> -1- f(x) = lim x-> -1- 2x + 1
Применяя предел, получаем
= 2(-1) + 1
= -2 + 1
= -1 ——(1)
lim x-> -1+ f(x) = lim x-> -1+ 3x
Применяя предел, получаем
= 3(-1)
= -3 — —(2)
lim x-> -1- f(x) ≠ lim x-> -1+
Итак, функция не является непрерывной при x = -1.
Теперь проверим непрерывность в точке x = 1
lim x-> 1- f(x) = lim x-> 1- 3x
Применяя предел, получаем
= 3(1)
= 3 ——(1)
lim x-> -1+ f(x) = lim x-> -1+ 2x — 1
8 Применяя предел, получаем
= 2(1) — 1
= 1 ——(2)
lim x-> 1- f(x) ≠ lim x-> 1+
Итак, функция не является непрерывной в точке x = 1.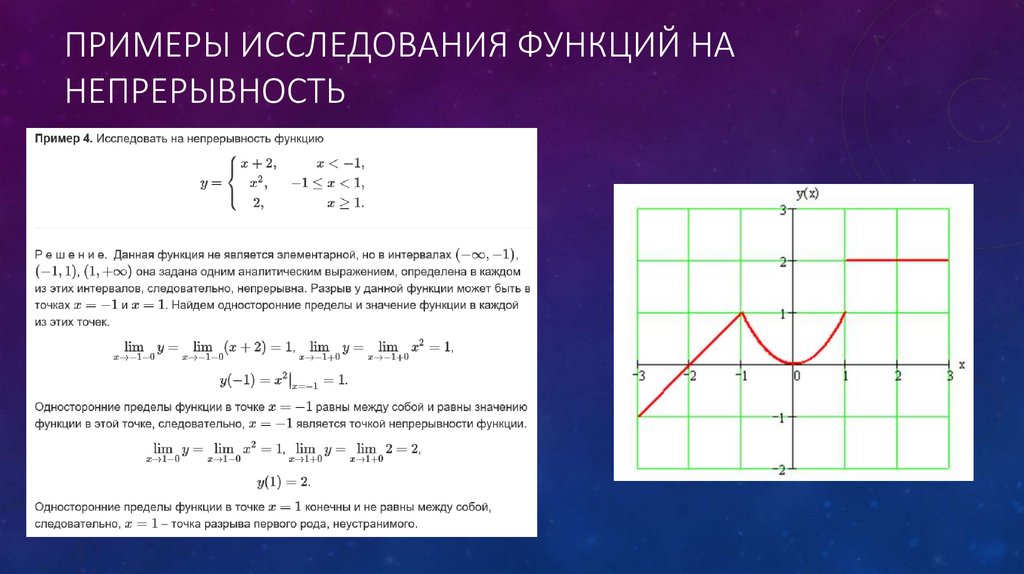
Чтобы найти, в какой из этих точек f непрерывна справа, слева или ни в одной, мы должны провести числовую прямую.
let x 0 ∈ (-∞, -1]
lim x-> x0 f(x) = lim x-> x0 2x + 1
Применяя предел, получаем 8 9000 4 900 2x 0 + 1 ——(1)
f(x 0 ) = 2x 0 + 1 ——(2)
(1) = (2)
Непрерывно в (-∞, -1].
let x 0 ∈ (-1, -1)
lim x-> x0 f(x) = lim x-> x0 3x
Применяя предел, получаем
= 3x 0 ——(1)
f(x 0 ) = 3x 0 ——(2)
(1) = (2)
8 Он непрерывен в (-1, 1).
Пусть x 0 ∈ [1, ∞)
Lim x-> x0 F (x) = Lim x-> x0 2x-1
Применить предел, мы получаем
= 2x 0 — 1 ——(1)
f(x 0 ) = 2x 0 — 1 ——(2)
(1) = (2)
Он непрерывен в [1, ∞).
График f(x) = 2x + 1 :
x = -1 f(-1) = -1 | x = -2 f(-2) = -3 | x = -3 f(-3) = -5 |
График f(x) = 3x :
-1 < x < 1
x = -0,5 f(-0,5) = -1,5 | x = -0,7 f(-0,7) = -2,1 | x = 0,5 f(0,5) = 1,5 |
График f(x) = 2x — 1:
x > = 1
х = 1 f(1) = 1 | x = 2 f(2) = 3 | x = 3 f(3) = 5 |
Вопрос 2 :
Найдите точки, в которых f разрывна. В какой из этих точек f непрерывна справа, слева или ни там, ни там? Нарисуйте график f.
Решение :
Сначала проверим непрерывность в точке х = 0 Применяя предел, получаем = lim x-> 0+ (x + 1) 3
Применяя предел, получаем
= ( 0 + 1) 3
= 1 ——(2)
lim x-> 0- f(x) ≠ lim x-> 0+
Итак, функция не является непрерывной в точке x = 0.
Чтобы найти, в какой из этих точек f непрерывна справа, слева или ни в одной, мы должны провести числовую прямую.
let x 0 ∈ (-∞, 0]
lim x-> x0 f(x) = lim x-> x0 (x — 1) 90 277 4 90 ограничение мы получаем
= (x 0 — 1) 3 ——(1)
f(x 0 ) = (x 0 — 1) 3 —- 90-277 (2)
(1) = (2)
Непрерывно в (-∞, 0]. ) = lim x-> x0 (x + 1) 3
Применяя предел, получаем
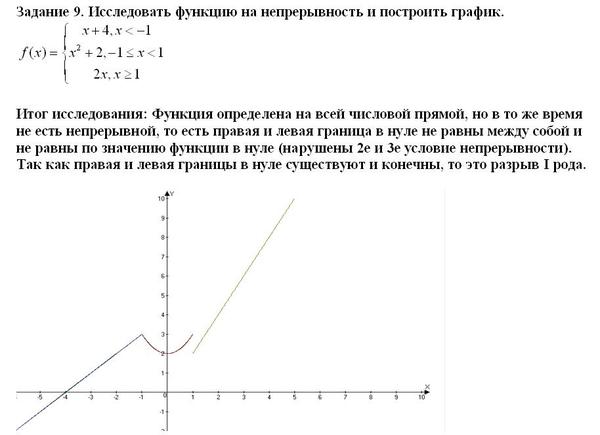
= (x 0 + 1) 3 9-08(0) 9-0271 ф(х 0 ) = (x 0 + 1) 3 ——(2) (1) = (2) Непрерывно в [0, ∞). График f(x) = (x — 1) 3 x < 0 x = -1 f(-1) = -8 x = -2 f(-2) = -27 x = -3 f(-3) = -64 График f(x) = (x + 1) 3 х >= 0 x = 1 f(1) = 8 х = 2 f(2) = 27 x = 3 f(3) = 64 Мы надеемся, что после изучения вышеизложенного материала учащиеся поняли, «Как начертить график и найти непрерывность функций» Непрерывность функций», если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь. Пожалуйста, отправьте ваш отзыв на [email protected] Мы всегда ценим ваши отзывы. ©Все права защищены. onlinemath5all.com Нарисуйте график и проверьте непрерывность функции: Здесь мы мы увидим несколько примеров задач, чтобы понять концепцию построения графика и проверки непрерывности функции. Вопрос 1 : Пусть f(x) Нарисуйте график функции. Покажите, что f(x) непрерывна на (- ∞, ∞). Решение: В кусочной функции есть три раздела. Для проверки непрерывности в точке 0 нужно доказать следующее. lim x-> 0- f(x) = lim x->0+ f(x) = lim x->0 f(0) lim x-> 0- f(x) = 0 —-(1) lim x->0+ f(x) = 0 — —(2) f(0) = 0 —-(3) (1) = (2) = (3) Следовательно, функция непрерывна при x = 0. Теперь пусть проверим непрерывность в точке 2. lim х-> 2- f(x) = 2 2 = 4 —-(1) lim x->2+ f(x) = 4 —-(2) f(2) = 4 —-(3) (1) = (2) = (3) Следовательно, функция непрерывна при x = 2. Значит, данная кусочная функция непрерывна на (- ∞, ∞). Вопрос 2 : Если f и g непрерывные функции с f(3) = 5 и lim x->3 [2 f(x) — g(x)] = 4, найдите g(3). Решение: лим x->3 [2 f(x) — g(x)] = 4 Применим 3 в функции вместо x. [2 f(3) — g(3)] = 4 2(5) — g(3) = 4 10 — g(3) = 9 4
Нарисуйте график и проверьте непрерывность функции
О разделе «Нарисуйте график и проверьте непрерывность функции»
Нарисуйте график и проверьте непрерывность функции. Практические вопросы
6
(3) = 10 — 4
g(3) = 6
Следовательно, значение g(3) равно 6.
Вопрос 3:
. . В какой из этих точек f непрерывна справа, слева или ни там, ни там? Нарисуйте график f.
Решение:
Сначала проверим непрерывность в точке x = -1
lim x-> -1- f(x) = lim x-> -1- 2x + 1
Применяя предел, получаем (x) = lim x-> -1+ 3xПрименяя предел, получаем
= 3(-1)
= -3 ——(2)
lim x-> -1- f(x) ≠ lim x-> -1+
Итак, функция не является непрерывной при x = -1.
Теперь проверим непрерывность в точке x = 1
lim x-> 1- f(x) = lim x-> 1- 3x
Применяя предел, получаем
3(1)
= 3 ——(1)
lim x-> -1+ f(x) = lim x-> -1+ 2x — 1
предел, мы получаем 9Так, функция не является непрерывной в точке x = 1.
Чтобы найти, в какой из этих точек f непрерывна справа, слева или ни в одной, мы должны провести числовую прямую.
let x 0 ∈ (-∞, -1]
lim x-> x0 f(x) = lim x-> x0 2x + 1
Применяя предел, получаем 9000 80004 = 2x 0 + 1 ——(1)
f(x 0 ) = 2x 0 + 1 ——(2)
(1) = (2 )
Непрерывно в (-∞, -1].
let x 0 ∈ (-1, -1)
lim x-> x0 f(x) = lim x-> x0 Применяя предел, получаем (1) = (2) Непрерывно в (-1, 1).0008 Пусть x 0 ∈ [1, ∞) Lim x-> x0 F (x) = Lim x-> x0 2x-1 Применить предел, мы получаем = 2x 0 — 1 ——(1) f(x 0 ) = 2x 0 — 1 ——(2) (1) = (2) It непрерывна в [1, ∞). График f(x) = 2x + 1 : x = -1 f(-1) = -1 х = -2 f(-2) = -3 x = -3 f(-3) = -5 График f(x) = 3x : -1 < x < 1 x = -0,5 f(-0,5) = -1,5 x = -0,7 f(-0,7) = -2,1 x = 0,5 f(0,5) = 1,5 График f(x) = 2x — 1: x > = 1 х = 1 f(1) = 1 x = 2 f(2) = 3 x = 3 f(3) = 5 Мы надеемся, что после изучения материалов, приведенных выше, учащиеся поняли, что такое «Нарисовать график и проверить непрерывность функции». функции», если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь. Пожалуйста, отправьте ваш отзыв на [email protected] Мы всегда ценим ваши отзывы. ©Все права защищены. onlinemath5all.com На этом уроке вы изучите непрерывность в точке, исследуете разрыв в точке, отобразите разрывы и узнаете, как переопределить функцию для устранения разрыва в точке. Затем вы будете использовать функцию «когда» для построения графика кусочно определенных функций. Неформально функция называется непрерывной на отрезке, если вы можете начертить ее график на отрезке, не отрывая карандаша от бумаги. Формальное определение непрерывности начинается с определения непрерывности в точке, а затем распространяется на непрерывность на интервале. Непрерывность в точке Формальное определение гласит, что функция f ( x ) непрерывна в точке, где x = c , если Функция непрерывна на отрезке, если она непрерывна в каждой точке отрезка. Определение непрерывности можно использовать, чтобы показать, что непрерывен при x = . На главном экране Потому что , непрерывен при x = . Разрыв в точке Если какое-либо из трех условий в определении непрерывности не выполняется при x = k , функция в этой точке разрывна. 6.1.1 Есть непрерывный в х = 0? Обосновать ответ. Щелкните здесь, чтобы получить ответ. Отображение разрывов Вы можете визуализировать разрыв в точке, построив график функции в соответствующем окне. Функция f ( x ) уже определена как . Ось y должна быть отключена, чтобы увидеть разрыв в x = 0. Разрыв представлен в виде отверстия с координатами (0,1). Хотя разрыв выглядит как дыра на графике, можно утверждать, что дыры не должно быть, потому что недостающая точка бесконечно мала. На TI-89 недостающая точка представлена отсутствующим пикселем только в том случае, если значение x отверстия является одним из значений x, используемых на графике. Удаление разрыва Ниже показано, как можно переопределить так, чтобы он был непрерывным при x = 0. Использование функции «когда» Функцию «когда» на TI-89 можно использовать для переопределения f ( x ) на для х 0 и 1 для x = 0. То есть . Чтобы переопределить f ( x ), Синтаксис «когда» Синтаксис функции «когда»: символ находится в подменю MATH Test, которое можно найти, нажав 
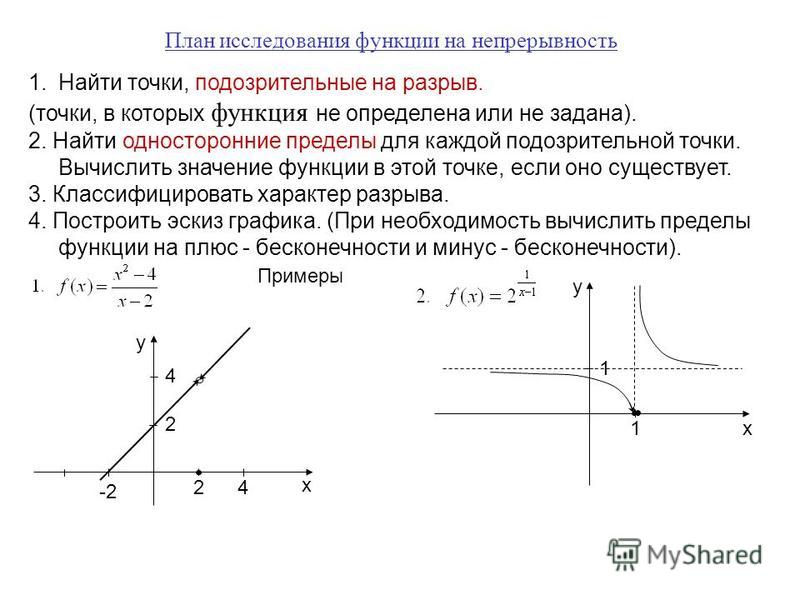
Модуль 6 — Непрерывность — Урок 1
Модуль 6 — Непрерывность Введение |
Урок 1 |
Урок 2 |
Урок 3 |
Самооценочный тест Урок 6.1. Определение непрерывности  Может показаться, что это формальное определение не имеет много общего с концепцией рисования графика, не отрывая карандаша от бумаги, но после изучения нескольких примеров с помощью TI-89, связь между формальными и неформальными определениями может быть более очевидной.
Может показаться, что это формальное определение не имеет много общего с концепцией рисования графика, не отрывая карандаша от бумаги, но после изучения нескольких примеров с помощью TI-89, связь между формальными и неформальными определениями может быть более очевидной.

Вы не увидите дыру, если оставите для xres значение по умолчанию 2. Исследуйте с помощью Trace, чтобы увидеть, что f не определяется при x = 0.
.

 Найти область
определения функции
Найти область
определения функции
 Найдите производные
неявно заданной функции y(x):
Найдите производные
неявно заданной функции y(x): Найдите
многочлен, приближающий заданную
функцию f(x) в окрестности точки x0 с точностью до о((x–x0)3):
Найдите
многочлен, приближающий заданную
функцию f(x) в окрестности точки x0 с точностью до о((x–x0)3): Найдите
асимптоты и постройте эскиз графика
функции:
Найдите
асимптоты и постройте эскиз графика
функции: cos
cos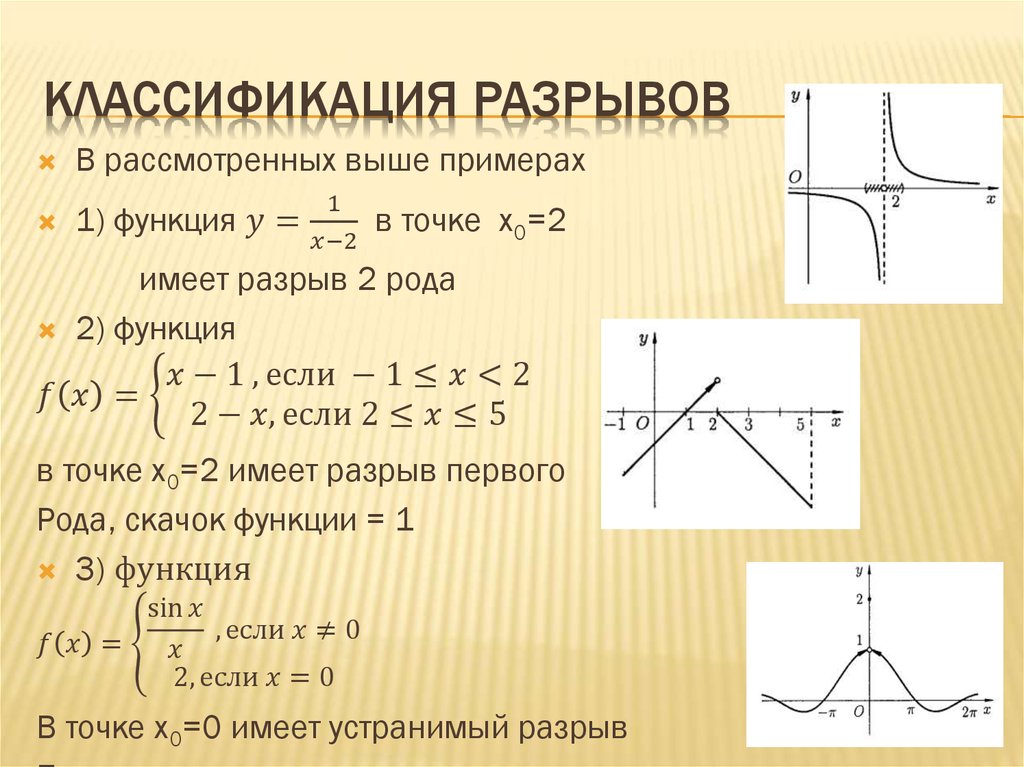 Исходя из
определения производной, найдите
:
Исходя из
определения производной, найдите
:
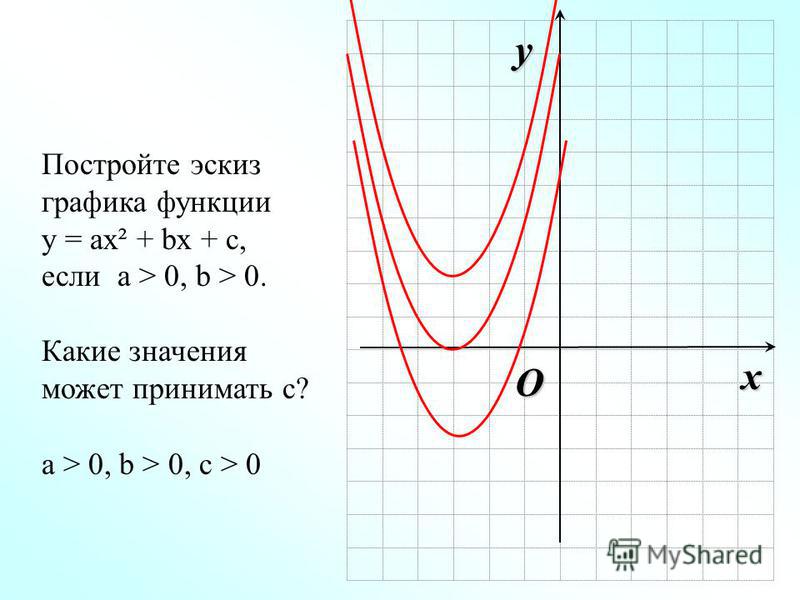 Исследуйте с помощью формулы Тейлора
Исследуйте с помощью формулы Тейлора 07.2016279.55 Кб341-2.doc
07.2016279.55 Кб341-2.doc