Обыкновенные дроби
Определение обыкновенной дроби
Определение 1
Обыкновенные дроби используют для описания числа долей. Рассмотрим пример, с помощью которого можно дать определение обыкновенной дроби.
Яблоко разделили на $8$ долей. В этом случае каждая доля представляет одну восьмую долю целого яблока, т. е. $\frac{1}{8}$. Две доли обозначаются $\frac{2}{8}$, три доли — $\frac{3}{8}$ и т.д., а $8$ долей — $\frac{8}{8}$. Каждая из представленных записей называется обыкновенной дробью.
Приведем общее определение обыкновенной дроби.
Определение 2
Обыкновенной дробью называется запись вида $\frac{m}{n}$, где $m$ и $n$— любые натуральные числа.
Часто можно встретить следующую запись обыкновенной дроби: $m/n$.
Пример 1
Примеры обыкновенных дробей:
\[{3}/{4}, \frac{101}{345},\ \ {23}/{5}, \frac{15}{15}, {111}/{81}.\]
Замечание 1
Числа $\frac{\sqrt{2}}{3}$, $-\frac{13}{37}$, $\frac{4}{\frac{2}{7}}$, $\frac{2,4}{8,3}$ не являются обыкновенными дробями, т.
Числитель и знаменатель
Обыкновенная дробь состоит из числителя и знаменателя.
Определение 3
Числителем обыкновенной дроби $\frac{m}{n}$ называется натуральное число $m$, которое показывает количество взятых равных долей из единого целого.
Определение 4
Знаменателем обыкновенной дроби $\frac{m}{n}$ называется натуральное число $n$, которое показывает, на сколько равных долей разделено единое целое.
Рисунок 1.
Числитель располагается над дробной чертой, а знаменатель —под дробной чертой. Например, числителем обыкновенной дроби $\frac{5}{17}$ является число $5$, а знаменателем — число $17$. Знаменатель показывает, что предмет разделен на $17$ долей, а числитель — что взято $5$ таких долей.
Натуральное число как дробь со знаменателем 1
Знаменателем обыкновенной дроби может быть единица. В таком случае считают, что предмет неделим, т. е. представляет собой единое целое. Числитель такой дроби показывает, сколько целых предметов взято. Обыкновенная дробь вида $\frac{m}{1}$ имеет смысл натурального числа $m$. Таким образом получаем обоснованное равенство $\frac{m}{1}=m$.
е. представляет собой единое целое. Числитель такой дроби показывает, сколько целых предметов взято. Обыкновенная дробь вида $\frac{m}{1}$ имеет смысл натурального числа $m$. Таким образом получаем обоснованное равенство $\frac{m}{1}=m$.
Если переписать равенство в виде $m=\frac{m}{1}$, то оно даст возможность любое натуральное число $m$ представить в виде обыкновенной дроби. Например, число $5$ можно представить в виде дроби $\frac{5}{1}$, число $123 \ 456$ — это дробь $\frac{123\ 456}{1}$.
Таким образом, любое натуральное число $m$ можно представить в виде обыкновенной дроби со знаменателем $1$, а любую обыкновенную дробь вида $\frac{m}{1}$ можно заменить натуральным числом $m$.
Дробная черта как знак деления
Представление предмета в виде $n$ долей является делением на $n$ равных частей. После деления предмета на $n$ долей его можно разделить поровну между $n$ людьми — каждый получит по одной доле.
Пусть имеется $m$ одинаковых предметов, разделенных на $n$ долей. Эти $m$ предметов можно поровну разделить между $n$ людьми, если раздать каждому человеку по одной доле от каждого из $m$ предметов. При этом каждый человек получит $m$ долей $\frac{1}{n}$, которые дают обыкновенную дробь $\frac{m}{n}$. Получаем, что обыкновенная дробь $\frac{m}{n}$ может применяться для обозначения деления $m$ предметов между $n$ людьми.
Эти $m$ предметов можно поровну разделить между $n$ людьми, если раздать каждому человеку по одной доле от каждого из $m$ предметов. При этом каждый человек получит $m$ долей $\frac{1}{n}$, которые дают обыкновенную дробь $\frac{m}{n}$. Получаем, что обыкновенная дробь $\frac{m}{n}$ может применяться для обозначения деления $m$ предметов между $n$ людьми.
Связь между обыкновенными дробями и делением выражается в том, что дробную черту можно понимать как знак деления, т.е. $\frac{m}{n}=m:n$.
Обыкновенная дробь дает возможность записывать результат деления двух натуральных чисел, для которых не выполняется деление нацело.
Пример 2
Например, результат деления $7$ яблок на $9$ человек можно записать как $\frac{7}{9}$, т.е. каждый получит семь девятых долей яблока: $7:9=\frac{7}{9}$.
Равные и неравные обыкновенные дроби, сравнение дробей
Результатом сравнения двух обыкновенных дробей может быть или их равенство, или их не равенство. При равенстве обыкновенных дробей их называют равными, в другом случае обыкновенные дроби называют неравными.
Обыкновенные дроби $\frac{a}{b}$ и $\frac{c}{d}$ называют равными, если справедливым является равенство $a\cdot d=b\cdot c$.
Обыкновенные дроби $\frac{a}{b}$ и $\frac{c}{d}$ называют неравными, если равенство $a\cdot d=b\cdot c$ не выполняется.
Пример 3
Выяснить, являются ли равными дроби $\frac{1}{3}$ и $\frac{2}{6}$.
Проверим, выполняется ли равенство $a\cdot d=b\cdot c$:
\[1\cdot 6=3\cdot 2.\]
Равенство выполняется, значит, дроби $\frac{1}{3}$ и $\frac{2}{6}$ являются равными: $\frac{1}{3}=\frac{2}{6}$.
Данный пример можно рассмотреть на примере яблок: одно из двух одинаковых яблок разделено на три равные доли, второе — на $6$ долей. При этом видно, что две шестых доли яблока составляют $\frac{1}{3}$ долю.
Пример 4
Проверить, являются ли равными обыкновенные дроби $\frac{3}{17}$ и $\frac{4}{13}$.
Проверим, выполняется ли равенство $a\cdot d=b\cdot c$:
\[3\cdot 13\ne 17\cdot 4;\] \[39\ne 58. \]
\]
Равенство не выполняется, значит, дроби $\frac{3}{17}$ и $\frac{4}{13}$ не равны: $\frac{3}{17}\ne \frac{4}{13}$.
При сравнении двух обыкновенных дробей, если выясняется, что они не равны, можно узнать, какая из них больше, а какая — меньше другой. Для этого используют правило сравнения обыкновенных дробей: нужно привести дроби к общему знаменателю и затем сравнить их числители. У какой дроби числитель будет больше, та дробь и будет являться большей.
Дроби на координатном луче
Все дробные числа, которые отвечают обыкновенным дробям, можно отобразить на координатном луче.
Чтобы на координатном луче отметить точку, которая соответствует дроби $\frac{m}{n}$, необходимо от начала координат в положительном направлении отложить $m$ отрезков, длина которых составляет $\frac{1}{n}$ долю единичного отрезка. Такие отрезки получают при делении единичного отрезка на $n$ равных частей.
Чтобы отобразить на координатном луче дробное число, нужно единичный отрезок разделить на части.
Рисунок 2.
Равные дроби описываются одним и тем же дробным числом, т.е. равные дроби представляют собой координаты одной и той же точки на координатном луче. Например, координатами $\frac{1}{3}$, $\frac{2}{6}$, $\frac{3}{9}$, $\frac{4}{12}$ описывается одна и та же точка на координатном луче, так как все записанные дроби равны.
Если точка описывается координатой с большей дробью, то она будет находится правее на горизонтальном направленном вправо координатном луче от точки, координатой которой является меньшая дробь. Например, т.к. дробь $\frac{5}{6}$ больше дроби $\frac{2}{6}$, то и точка с координатой $\frac{5}{6}$ находится правее точки с координатой $\frac{2}{6}$.
Аналогично, точка с меньшей координатой будет лежать левее точки с большей координатой.
определения, обозначения, примеры, действия с дробями, числитель и знаменатель
Рассмотрение данной темы мы начнем с изучения понятия доли в целом, которое даст нам более полное понимание смысла обыкновенной дроби. Дадим основные термины и их определение, изучим тему в геометрическом толковании, т.е. на координатной прямой, а также определим список основных действий с дробями.
Дадим основные термины и их определение, изучим тему в геометрическом толковании, т.е. на координатной прямой, а также определим список основных действий с дробями.
Доли целого
Представим некий предмет, состоящий из нескольких, совершенно равных частей. Например, это может быть апельсин, состоящий из нескольких одинаковых долек.
Определение 1Доля целого или доля – это каждая из равных частей, составляющих целый предмет.
Очевидно, что доли могут быть разные. Чтобы наглядно пояснить это утверждение, представим два яблока, одно из которых разрезано на две равные части, а второе – на четыре. Ясно, что размеры получившихся долей у разных яблок будут различаться.
Доли имеют свои названия, которые зависят от количества долей, составляющих целый предмет. Если предмет имеет две доли, то каждая из них будет определяться как одна вторая доля этого предмета; когда предмет состоит из трех долей, то каждая из них – одна третья и так далее.
Определение 2Половина – одна вторая доля предмета.
Треть – одна третья доля предмета.
Четверть – одна четвертая доля предмета.
Чтобы сократить запись, ввели следующие обозначения долей: половина — 12 или 1/2; треть — 13 или 1/3; одна четвертая доля — 14 или 1/4 и так далее. Записи с горизонтальной чертой используются чаще.
Понятие доли естественно расширяется с предметов на величины. Так, можно использовать для измерения небольших предметов доли метра (треть или одна сотая), как одной из единиц измерения длины. Аналогичным образом можно применить доли других величин.
Обыкновенные дроби, определение и примеры
Обыкновенные дробиприменяются для описания количества долей. Рассмотрим простой пример, который приблизит нас к определению обыкновенной дроби.
Представим апельсин, состоящий из 12 долек. Каждая доля тогда будет – одна двенадцатая или 1/12. Две доли – 2/12; три доли – 3/12 и т.д. Все 12 долей или целое число будет выглядеть так: 12/12. Каждая из используемых в примере записей является примером обыкновенной дроби.
Обыкновенная дробь – это запись вида mn или m/n, где m и n являются любыми натуральными числами.
Согласно данному определению, примерами обыкновенных дробей могут быть записи: 4/9, 1134, 91754. А такие записи: 115, 1,94,3 не являются обыкновенными дробями.
Числитель и знаменатель
Определение 4Числителем обыкновенной дроби mn или m/n является натуральное число m.
Знаменателем обыкновенной дроби mn или m/n является натуральное число n.
Т.е. числитель – число, расположенное сверху над чертой обыкновенной дроби (или слева от наклонной черты), а знаменатель – число, расположенное под чертой (справа от наклонной черты).
Какой же смысл несут в себе числитель и знаменатель? Знаменатель обыкновенной дроби указывает на то, из скольких долей состоит один предмет, а числитель дает нам информацию о том, каково рассматриваемое количество таких долей. К примеру, обыкновенная дробь 754 указывает нам на то, что некий предмет состоит из 54 долей, и для рассмотрения мы взяли 7 таких долей.
Натуральное число как дробь со знаменателем 1
Знаменатель обыкновенной дроби может быть равен единице. В таком случае возможно говорить, что рассматриваемый предмет (величина) неделим, являет собой нечто целое. Числитель в подобной дроби укажет, какое количество таких предметов взято, т.е. обыкновенная дробь вида m1 имеет смысл натурального числа m. Это утверждение служит обоснованием равенства m1 = m.
Запишем последнее равенство так: m = m1. Оно даст нам возможность любое натуральное число использовать в виде обыкновенной дроби. К примеру, число 74 – это обыкновенная дробь вида 741.
Любое натуральное число m возможно записать в виде обыкновенной дроби, где знаменатель – единица: m1.
В свою очередь, любая обыкновенная дробь вида m1 может быть представлена натуральным числом m.
Черта дроби как знак деления
Использованное выше представление данного предмета как n долей является не чем иным, как делением на n равных частей. Когда предмет разделен на n частей, мы имеем возможность разделить его поровну между n людьми – каждый получит свою долю.
В случае, когда мы изначально имеем m одинаковых предметов (каждый разделен на n частей), то и эти m предметов возможно поровну разделить между n людьми, дав каждому из них по одной доле от каждого из m предметов. При этом у каждого человека будет m долей 1n, а m долей 1n даст обыкновенную дробь mn. Следовательно, обыкновенную дробь mn можно использовать, чтобы обозначать деление m предметов между n людьми.
Полученное утверждение устанавливает связь между обыкновенными дробями и делением. И эту связь можно выразить следующим образом: черту дроби возможно иметь в виду в качестве знака деления, т.е. m/n = m : n.
При помощи обыкновенной дроби мы можем записать итог деления двух натуральных чисел. К примеру, деление 7 яблок на 10 человек запишем как 710: каждому человеку достанется семь десятых долей.
Равные и неравные обыкновенные дроби
Логичным действием является сравнение обыкновенных дробей, ведь очевидно, что, к примеру, 18 яблока отлична от 78.
Результатом сравнения обыкновенных дробей может быть: равны или неравны.
Определение 6Равные обыкновенные дроби – обыкновенные дроби ab и cd, для которых справедливо равенство: a · d = b · c.
Неравные обыкновенные дроби — обыкновенные дроби ab и cd, для которых равенство: a · d = b · c не является верным.
Пример равных дробей: 13 и 412 – поскольку выполняется равенство 1 ·12 = 3 · 4.
В случае, когда выясняется, что дроби не являются равными, обычно необходимо также узнать, какая из данных дробей меньше, а какая – больше. Чтобы дать ответ на эти вопросы, обыкновенные дроби сравнивают, приводя их к общему знаменателю и затем сравнив числители.
Дробные числа
Каждая дробь – это запись дробного числа, что по сути — просто «оболочка», визуализация смысловой нагрузки. Но все же для удобства мы объединяем понятия дроби и дробного числа, говоря просто – дробь.
Дроби на координатном луче
Все дробные числа, как и любое другое число, имеют свое уникальное месторасположение на координатном луче: существует однозначное соответствие между дробями и точками координатного луча.
Чтобы на координатном луче найти точку, обозначающую дробь mn, необходимо от начала координат отложить в положительном направлении m отрезков, длина каждого из которых составит 1n долю единичного отрезка. Отрезки можно получить, разделив единичный отрезок на n одинаковых частей.
Как пример, обозначим на координатном луче точку М, которая соответствует дроби 1410. Длина отрезка, концами которого является точка О и ближайшая точка, отмеченная маленьким штрихом, равна 110 доле единичного отрезка. Точка, соответствующая дроби 1410, расположена в удалении от начала координат на расстояние 14 таких отрезков.
Если дроби равны, т.е. им соответствует одно и то же дробное число, тогда эти дроби служат координатами одной и той же точки на координатном луче. К примеру, координатам в виде равных дробей 13, 26, 39, 515, 1133 соответствует одна и та же точка на координатном луче, располагающаяся на расстоянии трети единичного отрезка, отложенного от начала отсчета в положительном направлении.
Здесь работает тот же принцип, что и с целыми числами: на горизонтальном, направленном вправо координатном луче точка, которой соответствует большая дробь, разместится правее точки, которой соответствует меньшая дробь. И наоборот: точка, координата которой – меньшая дробь, будет располагаться левее точки, которой соответствует бОльшая координата.
Правильные и неправильные дроби, определения, примеры
В основе разделения дробей на правильные и неправильные лежит сравнение числителя и знаменателя в пределах одной дроби.
Определение 7Правильная дробь – это обыкновенная дробь, в которой числитель меньше, чем знаменатель. Т.е., если выполняется неравенство m < n, то обыкновенная дробь mn является правильной.
Неправильная дробь — это обыкновенная дробь, числитель которой больше или равен знаменателю. Т.е., если выполняется неравенство undefined, то обыкновенная дробь mn является неправильной.
Приведем примеры: — правильные дроби:
Пример 15/9, 367, 138514;
— неправильные дроби:
Пример 213/13, 573, 901112, 167.
Также возможно дать определение правильных и неправильных дробей, опираясь на сравнение дроби с единицей.
Определение 8Правильная дробь – обыкновенная дробь, которая меньше единицы.
Неправильная дробь – обыкновенная дробь, равная или бОльшая единицы.
Например, дробь 812 – правильная, т.к. 8 12< 1. Дроби 532 и 1414 являются неправильными, т.к. 532 > 1, а 1414 = 1.
Немного углубимся в размышление, почему дроби, в которых числитель больше или равен знаменателю получили название «неправильных».
Рассмотрим неправильную дробь 88: она сообщает нам, что взято 8 долей предмета, состоящего из 8 долей. Таким образом, из имеющихся восьми долей мы можем составить целый предмет, т.е. заданная дробь 88 по сути представляет целый предмет: 88=1. Дроби, в которых числитель и знаменатель равны, полноценно заменяет натуральное число 1.
Рассмотрим также дроби, в которых числитель превосходит знаменатель: 115 и 363. Понятно, что дробь 115 сообщает о том, что из нее мы можем составить два целых предмета и еще останется одна пятая доля.
Указанные примеры дают возможность сделать вывод, что неправильные дроби возможно заменить натуральными числами (если числитель без остатка делится на знаменатель: 88 = 1; 363 = 12) или суммой натурального числа и правильной дроби (если числитель не делится на знаменатель без остатка: 115 = 2 + 15). Вероятно, потому такие дроби и получили название «неправильных».
Здесь также мы сталкиваемся с одним из важнейших навыков работы с числами.
Определение 9Выделение целой части из неправильной дроби – это запись неправильной дроби в виде суммы натурального числа и правильной дроби.
Также отметим, что существует тесная взаимосвязь между неправильными дробями и смешанными числами.
Положительные и отрицательные дроби
Выше мы говорили о том, что каждой обыкновенной дроби соответствует положительное дробное число. Т.е. обыкновенные дроби – это положительные дроби. Например, дроби 517, 698, 6479 – положительные, и, когда необходимо особо подчеркнуть «положительность» дроби, она записывается с использованием знака плюс: +517, +698, +6479.
Например, дроби 517, 698, 6479 – положительные, и, когда необходимо особо подчеркнуть «положительность» дроби, она записывается с использованием знака плюс: +517, +698, +6479.
Если же обыкновенной дроби присвоить знак минус, то полученная запись будет являться записью отрицательного дробного числа, и мы говорим в таком случае об отрицательных дробях. Например, -817, -7814 и т.д.
Положительная и отрицательная дробиmn и -mn – противоположные числа. Например, дроби 78 и -78 являются противоположными.
Положительные дроби, как и любые положительные числа в целом, означают прибавление, изменение в сторону увеличения. В свою очередь, отрицательные дроби соответствуют расходу, изменению в сторону уменьшения.
Если мы рассмотрим координатную прямую, то увидим, что отрицательные дроби расположены левее точки начала отсчета. Точки, которым соответствуют дроби, являющиеся противоположными (mn и -mn), располагаются на одинаковом расстоянии от начала отсчета координат О, но по разные стороны от нее.
Здесь также отдельно скажем о дробях, записанных в виде 0n. Такая дробь равна нулю, т.е. 0n= 0.
Суммируя все вышесказанное, мы подошли к важнейшему понятию рациональных чисел.
Определение 10Рациональные числа – это множество положительных дробей, отрицательных дробей и дробей вида 0n.
Действия с дробями
Перечислим основные действия с дробями. В общем и целом, суть их та же, что имеют соответствующие действия с натуральными числами
- Сравнение дробей – данное действие мы рассмотрели выше.
- Сложение дробей – результатом сложения обыкновенных дробей является обыкновенная дробь (в частном случае сокращаемая до натурального числа).
- Вычитание дробей – действие, обратно сложению, когда по одной известной дроби и заданной сумме дробей определяется неизвестная дробь.
- Умножение дробей – это действие можно описать как нахождение дроби от дроби. Результат умножения двух обыкновенных дробей – обыкновенная дробь (в частном случае равная натуральному числу).

- Деление дробей – действие, обратное умножению, когда мы определяем дробь, на которую необходимо умножить заданную, чтобы получить известное произведение двух дробей.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Обыкновенные дроби
Обыкновенные дроби — определение, примеры, правильные и неправильные дроби, смешанные дроби, основное свойство дроби
Обыкновенной дробью называется число вида
, где m и n – натуральные числа, а дробная черта означает деление. Число m – называется числителем дроби, а n – знаменателем.
Правильные и неправильные дроби
Обыкновенная дробь называется правильной, если числитель этой дроби меньше ее знаменателя, и неправильной, если числитель больше либо равен знаменателю. Например,
3/5
,
7/15
,
20/21
— правильные дроби, а
6/5
,
15/15
,
42/13
— неправильные дроби.
Калькуляторы для решение примеров и задач по математике
Лучшие математические приложения для школьников и их родителей, студентов и учителей. Подробнее …
Cмешанные дроби
Дробь, записанная в виде целого числа и правильной дроби, называется смешанной.
Например,
3
3/5
, 2
7/15
, 1
20/21
— смешанные дроби.
Смешанную дробь можно представить в виде неправильной дроби, так как целое число всегда можно представить в виде неправильной дроби с любым знаменателем, например,
5 =
5/1
=
5*2/1*2
=
10/2
;
5 =
5/1
=
5*3/1*3
=
15/3
;
5 =
5/1
=
5*4/1*4
=
20/4
;
Тогда
5
1/3
= 5 +
1/3
=
15/3
+
1/3
=
16/3
;
1
11/17
= 1 +
11/17
=
17/17
+
11/17
=
28/17
.
Таким образом, получаем формулу для представления смешанных дробей в виде неправильной дроби
k
m/n
=
(k*n + m)/n
.
Пример 1. Записать смешанную дробь
в виде неправильной дроби.
3
3/5
=
3*5+3/5
=
18/5
.
Пример 2. Записать смешанную дробь
в виде неправильной дроби.
7
1/12
=
7*12+1/12
=
85/12
.
Пример 3. Представить смешанную дробь
4
11/25
в виде неправильной дроби.
4
11/25
=
4*25+11/25
=
111/25
.
Основное свойство дроби. Сокращение дробей.
Основное свойство обыкновенной дроби состоит в том, что если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной дроби. На этом свойстве основано сокращение дробей.
Если числитель и знаменатель дроби делятся на одно и то же натуральное число не равное 1, то сократить дробь — значит разделить на это число и числитель, и знаменатель дроби. Если такого числа не существует, то дробь называется несократимой. В ходе выполнения арифметических операций с дробями часто получаются сократимые дроби, их необходимо сокращать. Если в ответе получается неправильная дробь, то ее надо представить в виде смешанной, выделив целую часть.
Примеры.
1)
— сократимая дробь, так как и числитель 15, и знаменатель 25 дроби
делятся на 5.
Следовательно,
15/25
=
3*5/5*5
=
3/5
.
2)
— сократимая дробь, так как и числитель, и знаменатель дроби
делятся на 4.
Следовательно,
24/20
=
6*4/5*4
=
6/5
.
3)
— сократимая дробь, так как и числитель, и знаменатель дроби
делятся на 7.
Следовательно,
14/21
=
2*7/3*7
=
2/3
.
4)
— несократимая дробь, так как числитель 14, и знаменатель 27 дроби
не имеют общих делителей
14/27
=
2*7/3*3*3
.
5)
— неправильная дробь, представим ее в виде смешанной. Для этого разделим 5 на 2, получим 2 и 1 в остатке, то есть
5/2
= 2
1/2
.
6)
— неправильная дробь, представим ее в виде смешанной. Для этого разделим 23 на 5, получим 4 и 3 в остатке, то есть
23/5
= 4
3/5
.
Типов Дробей — Примеры
Прежде чем исследовать Типов Дробей , давайте вспомним дроби. Дробь — это часть или часть любого количества из целого, где целым может быть любое число, определенное значение или вещь. Во многих ситуациях реального времени каждая измеряемая величина не может быть абсолютным целым числом. Следовательно, нам, возможно, придется иметь дело с частями целого или частями целого. Вот тут-то и появляется концепция дробей. В этом уроке давайте узнаем о различные виды дробей с примерами, такими как правильные и неправильные дроби, смешанные дроби, эквивалентные дроби, подобные и неодинаковые дроби.
Во многих ситуациях реального времени каждая измеряемая величина не может быть абсолютным целым числом. Следовательно, нам, возможно, придется иметь дело с частями целого или частями целого. Вот тут-то и появляется концепция дробей. В этом уроке давайте узнаем о различные виды дробей с примерами, такими как правильные и неправильные дроби, смешанные дроби, эквивалентные дроби, подобные и неодинаковые дроби.
| 1. | Какие существуют типы дробей? |
| 2. | Неправильная дробь в смешанной дроби |
| 3. | Смешанная дробь в неправильную дробь |
| 4. | Часто задаваемые вопросы о типах фракций |
Какие существуют типы дробей?
различных типа дробей различаются в основном на основе их числителя и знаменателя. Дробь состоит из двух частей, числителя и знаменателя. Числитель — это число, расположенное над дробной чертой, а число, расположенное внизу, называется знаменателем. В числителе указано количество рассматриваемых частей, а в знаменателе — общее количество частей в целом.
Числитель — это число, расположенное над дробной чертой, а число, расположенное внизу, называется знаменателем. В числителе указано количество рассматриваемых частей, а в знаменателе — общее количество частей в целом.
Хотя существует много типов дробей, три основных типа дробей, которые различаются на основе числителя и знаменателя:
- Правильные дроби
- Неправильные дроби
- Смешанные фракции
Правильные дроби
Дробь, числитель которой меньше знаменателя, называется правильной дробью. Например, 3/12 и 2/5 — правильные дроби, потому что 3 < 12 и 2 < 5. Пример: Сэм взял плитку шоколада и разделил ее на 3 равные части. Он взял 1 часть и отдал 2 части своей сестре Саре. Мы можем представить долю Сэма как 1/3, а долю Сары как 2/3. Обе эти дроби считаются правильными дробями.
Неправильные дроби
Дробь, числитель которой больше или равен знаменателю, называется неправильной дробью. Например, 5/2 и 8/7 — неправильные дроби, потому что 5 > 2 и 8 > 7.
Смешанные дроби
Смешанная дробь — это смесь целого числа и правильной дроби. Например, \(1 \dfrac{3}{4}\) и \(3 \dfrac{4}{7}\) — это смешанные числа или смешанные дроби. В первом примере 1 — это целая часть числа, а 3/4 — правильная дробь. Во втором примере 3 — это целая часть числа, а 4/7 — правильная дробь.
Теперь давайте изучим типы дробей, которые классифицируются по группам. Когда классифицируется группа дробей , они помогают сравнивать дроби. Они классифицируются следующим образом:
- Подобные дроби
- В отличие от дробей
- Эквивалентные дроби
Подобные дроби
Если знаменатели двух или более дробей одинаковы, то они называются однотипными. Например, 1/6, 2/6, 3/6, 5/6 известны как подобные дроби. Мы можем выполнять сложение и вычитание дробей только с одинаковыми дробями. В некоторых случаях нам нужно преобразовать разные дроби в похожие дроби, чтобы сложить или вычесть.
Отличные дроби
Если знаменатели двух или более дробей различны, то дроби называются неодинаковыми дробями. Например 1/2, 1/3, 2/5, 3/6 и т.д. Если дроби разные, то при сложении или вычитании дробей мы преобразуем их в подобные дроби.
Например 1/2, 1/3, 2/5, 3/6 и т.д. Если дроби разные, то при сложении или вычитании дробей мы преобразуем их в подобные дроби.
Равные дроби
Равные дроби — это дроби, которые имеют разные числители и разные знаменатели, но при упрощении или сокращении равны одному и тому же значению. Например, 2/4, 3/6, 4/8 — эквивалентные дроби, потому что все они уменьшаются до 1/2.
Кроме них, есть дроби с 1 в числителе. Давайте прочитаем о них.
Дроби единиц
Дроби единиц – это те дроби, в которых числитель равен 1, а знаменатель – положительное целое число. Например, 1/3, 1/8, 1/19, 1/23 и так далее называются единичными дробями.
Неправильная дробь в смешанной дроби
Чтобы преобразовать неправильные дроби в смешанные, нужно разделить числитель на знаменатель. Затем мы записываем его в форме смешанного числа, помещая частное как целое число, остаток как числитель и делитель как знаменатель. Давайте рассмотрим следующий пример, чтобы лучше понять это. Пусть неправильная дробь будет 12/5. Чтобы преобразовать его в смешанную дробь, мы выполняем следующие шаги:
Пусть неправильная дробь будет 12/5. Чтобы преобразовать его в смешанную дробь, мы выполняем следующие шаги:
- Шаг 1: Разделите 12 на 5.
- Шаг 2: При делении мы получаем частное как 2 и остаток как 2.
- Шаг 3: Частное становится целой частью числа, а остаток 2 становится новым числителем, а знаменатель остается прежним.
- Шаг 4: Таким образом, неправильная дробь 12/5 записывается как смешанная дробь и представляется как \(2\dfrac{2}{5}\)
Смешанная дробь в неправильную дробь
Смешанная дробь представляет собой смесь целого числа и правильной дроби. Чтобы смешанную дробь преобразовать в неправильную, нужно знаменатель умножить на целую часть, а затем прибавить к произведению числитель. Результатом будет новый числитель, тогда как знаменатель останется прежним. Давайте рассмотрим следующий пример, чтобы лучше понять это. Пусть смешанная дробь будет \(7\dfrac{3}{5}\). Чтобы преобразовать это в неправильную дробь, мы выполняем следующие шаги:
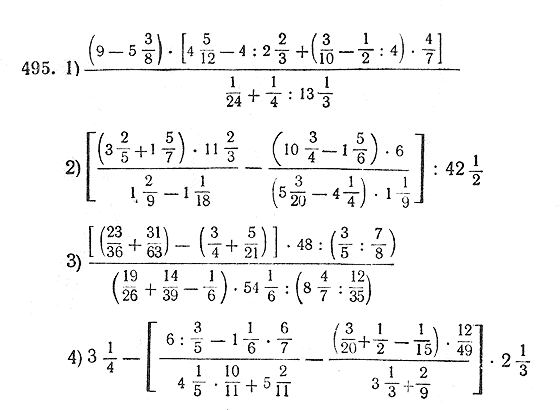
- Шаг 1: Умножаем целое число 7 на знаменатель 5.
 Итак, получаем 7 × 5 = 35
Итак, получаем 7 × 5 = 35 - Шаг 2: Добавьте произведение с числителем: 35 + 3 = 38
- Шаг 3: Представьте дробь со знаменателем 5, то есть 38/5
Советы по типам дробей
Ниже приведены несколько важных моментов, связанных с различными типами дробей:
- Значение неправильной дроби всегда больше 1,
- Значение правильной дроби всегда меньше 1.
- Смешанная дробь — это комбинация целого числа и дроби.
- Смешанную дробь можно преобразовать в неправильную и наоборот. Например, \(2\dfrac{1}{2}\) = 5/2.
☛ Похожие темы
- Умножение дробей
- Деление дробей
- Связь между дробями и десятичными знаками
- Сложение и вычитание дробей
- Как калькулятор дробей
- Калькулятор умножения дробей
- Калькулятор деления дробей
- Калькулятор преобразования неправильных дробей в смешанные числа
- Калькулятор эквивалентных дробей
Часто задаваемые вопросы о типах фракций
Сколько существует типов дробей?
Существует 7 различных типов фракций, которые классифицируются по различным категориям.
- Когда дроби классифицируются на основе числителя и знаменателя, они подразделяются на правильные дроби, неправильные дроби, смешанные дроби.
- Когда они классифицируются по группам, они классифицируются как похожие дроби, в отличие от дробей и эквивалентных дробей.
- Тогда есть дроби единиц, у которых 1 в числителе.
Какие существуют три типа дробей?
Три типа дробей в зависимости от числителя и знаменателя: правильные, неправильные и смешанные дроби. Например, 2/5, 3/4 называются правильными дробями, потому что здесь числитель меньше знаменателя; 5/2, 8/3 называются неправильными дробями, потому что числитель больше знаменателя; и \(1\dfrac{2}{6}\) и \(3\dfrac{1}{4}\) называются смешанными дробями, поскольку они состоят из целого числа и правильной дроби.
Как решить все виды дробей?
Фракции можно решать в соответствии с категорией, к которой они принадлежат. Различные типы дробей решаются следующими способами.
- Чтобы складывать и вычитать подобные дроби, мы просто решим числители, а знаменатели останутся прежними. Например, 1/3 + 4/3 = 5/3, 9/4 — 3/4 = 6/4
- Для разнородных дробей их сначала преобразуют в подобные дроби, чтобы сложить или вычесть их. Например, чтобы сложить 1/3 + 1/2, нам нужно найти наименьшее общее кратное (НОК) знаменателей и преобразовать данные дроби в подобные дроби, которые им эквивалентны. Здесь они преобразуются и записываются как 2/6 + 3/6, а затем мы складываем их, что дает (2 + 3)/6 = 5/6
- Умножение двух заданных дробей выполняется путем умножения числителей, а затем умножения знаменателей. После этого они сокращаются до самых низких условий, если это необходимо. Например, 1/3 × 1/2 = 1/6 .
- Деление дробей производится путем умножения первой дроби на обратную величину второй дроби. Например, 1/3 ÷ 1/2 = 1/3 × 2/1 = 2/3
Что такое правильные дроби?
Дробь, у которой числитель меньше знаменателя, называется правильной дробью. Например, 5/12 и 3/8 — правильные дроби.
Например, 5/12 и 3/8 — правильные дроби.
Что такое две части дроби?
Дробь состоит из двух частей: числителя и знаменателя.
- Числитель: Числитель представляет собой число, стоящее над дробью. Он представляет собой часть, которая считается из целого. Например, в 5/6 числитель 5.
- Знаменатель: Знаменатель указывает часть, которая находится в нижней части дроби. Он представляет собой общее количество частей. Например, в 5/6 6 является знаменателем.
Что такое смешанная фракция?
Дробь, представляющая собой комбинацию целого числа и правильной дроби, называется смешанной дробью. Например, \(2\dfrac{1}{3}\) — смешанная дробь, где 2 — целая часть числа, а 1/2 — правильная дробь.
Что такое подобные дроби?
Подобные фракции также известны как подобные фракции. Две или более дроби, имеющие одинаковый знаменатель, называются подобными дробями или подобными дробями. Другими словами, дроби с одинаковыми знаменателями называются одинаковыми дробями. Например, 1/7, 2/7, 5/7, 6/7 — все как дроби с одним и тем же знаменателем, то есть 7.
Например, 1/7, 2/7, 5/7, 6/7 — все как дроби с одним и тем же знаменателем, то есть 7.
Какие есть 7 типов дробей с примерами?
7 типов дробей с примерами приведены следующим образом:
- Правильные дроби: Правильные дроби — это те дроби, в которых числитель меньше знаменателя. Например, 3/4, 7/19, 67/543 и так далее.
- Неправильные дроби: Неправильными дробями называются те дроби, у которых числитель больше знаменателя. Например, 13/4, 57/9, 567/83 и так далее.
- Смешанные дроби: Смешанные дроби или смешанные числа — это те дроби, которые состоят из целой части числа и дробной части. Например, \(2 \dfrac{6}{7}\) и \(8 \dfrac{3}{4}\).
- Подобные дроби: Подобные дроби представляются группой дробей с одинаковым знаменателем. Например, 8/9, 5/9, 4/9 подобны дробям, потому что у них одинаковые знаменатели.
- Непохожие дроби: Непохожие дроби выражаются в виде группы дробей с разными знаменателями. Например, 6/7, 5/8, 3/5 не похожи на дроби, потому что у них разные знаменатели.

- Равнозначные дроби: Равнозначные дроби — это те дроби, которые имеют разные числители и разные знаменатели, но при упрощении или сокращении равны одному и тому же значению. Например, 13/26, 14/28, 20/40 являются эквивалентными дробями, потому что все они сводятся к одной и той же дроби, то есть к 1/2.
- Дроби единиц: Дроби единиц — это те дроби, в которых числитель равен 1, а знаменатель — положительное целое число. Например, 1/2, 1/27, 1/56 и так далее.
Какие дроби имеют разные знаменатели?
Дроби, имеющие разные знаменатели, называются неодинаковыми. Эти фракции представлены в группах. Например, 7/9, 2/5, 3/6 не похожи на дроби, потому что у них разные знаменатели.
дробей — Дети | Britannica Kids
7-дневная бесплатная пробная версия
Поиск
Посмотреть статью для:
- Дети
- Ученики
- Ученые
2:52
1:57
Связанные статьи
Мы были заняты, усердно работая над тем, чтобы предоставить вам новые функции и обновленный дизайн. Мы надеемся, что вам и вашей семье понравится NEW Britannica Kids. Уделите минутку, чтобы проверить все улучшения!
Мы надеемся, что вам и вашей семье понравится NEW Britannica Kids. Уделите минутку, чтобы проверить все улучшения!
- Один и тот же безопасный и надежный контент для исследователей всех возрастов.
- Доступен на всех современных устройствах: телефонах, планшетах и настольных компьютерах.
- Улучшенные ресурсы для домашних заданий, предназначенные для поддержки различных предметов и стандартов учебной программы.
- Новый, третий уровень контента, разработанный специально для удовлетворения продвинутых потребностей искушенного ученого.
- И многое другое!
Хотите увидеть его в действии?
Ознакомиться
Начать бесплатную пробную версию
Подпишитесь прямо сейчас!
Перевести эту страницу
Выберите язык в меню выше, чтобы просмотреть версию этой страницы с компьютерным переводом. Обратите внимание: текст на изображениях не переводится, некоторые функции после перевода могут работать некорректно, а перевод может неточно передавать предполагаемое значение. Britannica не просматривает преобразованный текст.
Обратите внимание: текст на изображениях не переводится, некоторые функции после перевода могут работать некорректно, а перевод может неточно передавать предполагаемое значение. Britannica не просматривает преобразованный текст.
После перевода статьи все инструменты, кроме увеличения/уменьшения шрифта, будут отключены. Чтобы повторно включить инструменты или преобразовать обратно в английский язык, нажмите «Просмотреть оригинал» на панели инструментов Google Translate.
Этот веб-сайт использует файлы cookie, чтобы помочь предоставлять и улучшать наши услуги и предоставлять вам гораздо больше возможностей во время вашего посещения. Чтобы узнать больше о файлах cookie и ваших возможностях выбора файлов cookie, нажмите здесь.
×
Правильная дробь — определение, отличие, примеры
Дробь называется правильной, если ее числитель меньше знаменателя. Значение правильной дроби всегда меньше 1 . Например, Сэму досталась плитка шоколада, и он разделил ее на четыре равные части. Он взял одну часть и отдал три части своей сестре Рахили. Мы представляем долю Сэма как 1/4, а долю Рэйчел как 3/4. Обе эти дроби правильные, потому что здесь числитель меньше знаменателя.
Он взял одну часть и отдал три части своей сестре Рахили. Мы представляем долю Сэма как 1/4, а долю Рэйчел как 3/4. Обе эти дроби правильные, потому что здесь числитель меньше знаменателя.
| 1. | Что такое правильная дробь? |
| 2. | Правильная дробь и неправильная дробь |
| 3. | Преобразование неправильных дробей в правильные дроби |
| 4. | Как добавить смешанную дробь к правильной дроби? |
| 5. | Часто задаваемые вопросы о правильной дроби |
Что такое правильная дробь?
Дробь, в которой значение числителя всегда меньше значения знаменателя, называется правильной дробью. Например, 18/25, 19/45, 62/78, 1/6, 1/9 — правильные дроби. Дробь состоит из двух частей, числителя и знаменателя, и на основе этих двух значений определяются различные типы дробей. Две первичные дроби, которые различаются по этому критерию, — это правильные и неправильные дроби.
Две первичные дроби, которые различаются по этому критерию, — это правильные и неправильные дроби.
Теперь давайте научимся выполнять основные арифметические операции над правильными дробями.
Сложение правильных дробей
Чтобы сложить две правильные дроби, складываем числители, если данные дроби подобны дробям, т. е. если знаменатели одинаковы. Например, 2/8 + 3/8 можно легко сложить, просто добавив числители, поскольку знаменатели одинаковы. Сумма 2/8 + 3/8 будет 5/8.
Однако, чтобы сложить правильные дроби, которые не похожи друг на друга, у которых разные знаменатели, мы берем НОК (наименьшее общее кратное) знаменателей и переписываем дроби как эквивалентные дроби, используя НОК в качестве общего знаменателя. Теперь, когда все знаменатели станут одинаковыми, мы сложим числители и запишем результат как окончательный числитель поверх общего знаменателя. Например, чтобы сложить 2/3 + 4/5, мы берем НОК знаменателей. НОК 3 и 5 равно 15. Теперь умножим обе дроби на такое число (в данном случае 5 и 3 соответственно) так, чтобы знаменатели стали равными. В результате получается (10 + 12)/15 = 22/15.
Теперь умножим обе дроби на такое число (в данном случае 5 и 3 соответственно) так, чтобы знаменатели стали равными. В результате получается (10 + 12)/15 = 22/15.
Вычитание правильных дробей
Вычитание правильных дробей аналогично сложению. Если нам нужно найти разность правильных дробей, похожих на дроби, мы просто находим разность числителей, сохраняя тот же знаменатель. Например, разница 6/9 — 4/9 будет 2/9.
Теперь, если мы хотим вычесть правильные дроби, которые не похожи друг на друга, у которых разные знаменатели, мы берем НОК (наименьшее общее кратное) знаменателей и переписываем дроби как эквивалентные дроби, используя НОК в качестве общего знаменателя. Когда все знаменатели станут одинаковыми, вычитаем числители и записываем результат в общий знаменатель. Например, чтобы вычесть 8/9- 3/4, берем НОК знаменателей. НОК 9 и 4 равно 36. Теперь умножим обе дроби на такое число (в данном случае 4 и 9 соответственно) так, чтобы знаменатели стали равными. Это приводит к (32 — 27)/36 = 5/36.
Умножение правильных дробей
В отличие от сложения и вычитания, умножение и деление правильных дробей в каком-то смысле проще. Мы просто умножаем данные числители, затем умножаем знаменатели и, наконец, упрощаем или уменьшаем полученную дробь. Например, чтобы умножить 2/6 × 5/4, мы умножаем числители 2 и 5, чтобы получить 10, и мы умножаем знаменатели 6 и 4, чтобы получить 24. Произведение записывается как 10/24, которое можно еще уменьшить. до 5/12.
Деление правильных дробей
Деление правильных дробей аналогично умножению. Единственное отличие состоит в том, что мы меняем знак деления на знак умножения, а затем умножаем первую дробь на обратную (обратную) второй дроби. Например, разделим: 4/9 ÷ 2/3. Это станет 4/9 × 3/2 = 12/18. Это может быть дополнительно уменьшено до 2/3.
Правильная дробь и неправильная дробь
Противоположностью правильной дроби является неправильная дробь. Когда числитель меньше знаменателя, получается правильная дробь, а когда он равен или больше знаменателя, получается неправильная дробь. Таким образом, мы можем решить, какая дробь является правильной, а какая неправильной, сравнив значения числителя и знаменателя. Пример правильной дроби — 5/7, а когда мы возьмем ее обратную, то есть 7/5, получим неправильную дробь. Теперь давайте изучим табличную разницу между правильной дробью и неправильной дробью.
Таким образом, мы можем решить, какая дробь является правильной, а какая неправильной, сравнив значения числителя и знаменателя. Пример правильной дроби — 5/7, а когда мы возьмем ее обратную, то есть 7/5, получим неправильную дробь. Теперь давайте изучим табличную разницу между правильной дробью и неправильной дробью.
Разница между правильной и неправильной дробями
Посмотрите на приведенную ниже таблицу, в которой показаны правильные и неправильные дроби.
| Правильная дробь | Неправильная дробь |
|---|---|
| Дробь, в которой числитель меньше знаменателя, называется правильной дробью. | Дробь, в которой числитель больше или равен знаменателю, называется неправильной дробью. |
| Его значение всегда меньше 1. | Его значение всегда больше или равно 1. |
Примеры: 2/3, 6/7, 10/23 и т. д. д. | Примеры: 3/2, 17/5, 4/3, 5/5 и т. д. |
Преобразование неправильных дробей в правильные дроби
Математически неправильная дробь может быть преобразована в смешанную дробь, представляющую собой комбинацию целого числа и правильной дроби. Например, давайте преобразуем неправильную дробь 13/5 в смешанную дробь, выполнив следующие действия:
- Разделить числитель на знаменатель. Здесь при делении 13 : 5 мы получаем 2 как частное и 3 как остаток.
- Запишите полученное частное как целое число, а остаток как числитель при том же знаменателе. Здесь частное (2) будет целым числом, остаток (3) будет новым числителем, а знаменатель останется прежним.
- Преобразует заданную неправильную дробь в правильную дробь, имеющую целое число. Следовательно, 13/5 можно записать как \(2\dfrac{3}{5}\).
Как добавить смешанную дробь к правильной дроби?
Чтобы сложить смешанную дробь с правильной, мы просто преобразуем смешанную дробь в неправильную, а затем складываем две дроби обычным способом сложения дробей.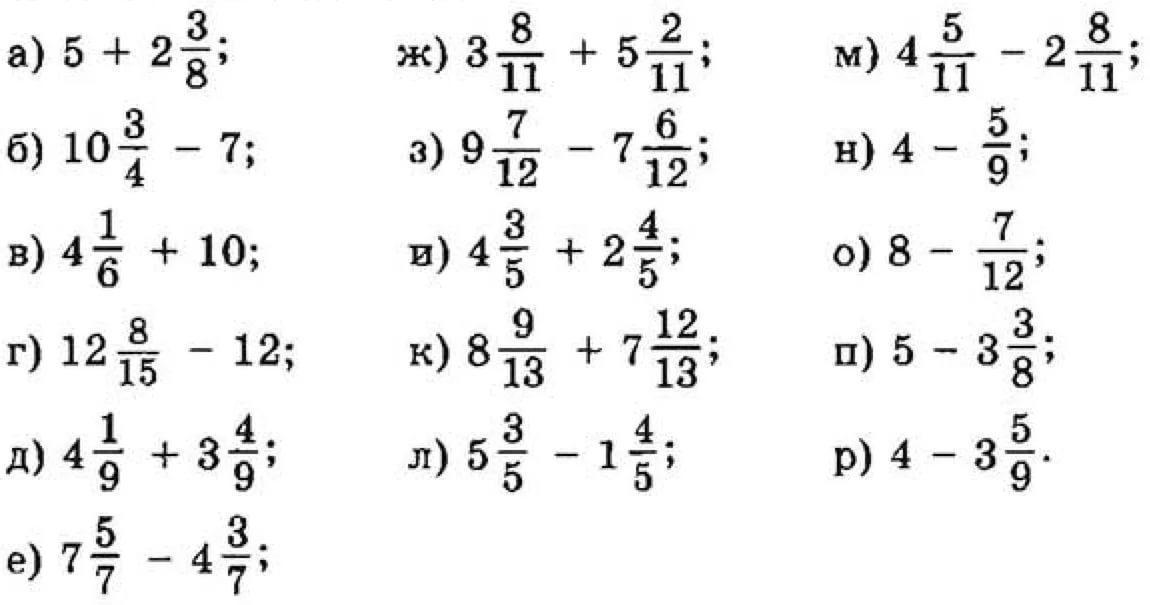 После нахождения ответов снова переводим результат в смешанную дробь. Например, добавим \(2\dfrac{1}{5}\) + \(\dfrac{1}{4}\).
После нахождения ответов снова переводим результат в смешанную дробь. Например, добавим \(2\dfrac{1}{5}\) + \(\dfrac{1}{4}\).
Преобразуйте смешанную дробь в неправильную, то есть \(2\dfrac{1}{5}\) = 11/5.
11/5 + 1/4 = (44 + 5)/20 = 49/20
Теперь преобразуйте 49/20 в смешанную дробь, которая будет = \(2\dfrac{9}{20}\) . Вот как мы прибавляем смешанное число к правильной дроби.
► Статьи по теме
Проверьте эти интересные темы, связанные с правильными дробями.
- Доля единицы измерения
- Десятичные числа и дроби
- Подобные дроби и отличные дроби
- Сравнение дробей
Часто задаваемые вопросы о правильной дроби
Что такое правильная дробь с примером?
Дробь, у которой числитель меньше знаменателя, называется правильной дробью. Например, 7/12, 7/8 — правильные дроби.
В чем разница между правильной дробью и неправильной дробью?
Дробь, у которой знаменатель больше числителя, называется правильной дробью. Например, 3/4, 27/39 — правильные дроби. С другой стороны, дробь, в которой числитель больше или равен знаменателю, называется неправильной дробью. Например, 18/5, 49/23, 46/46 — неправильные дроби.
Например, 3/4, 27/39 — правильные дроби. С другой стороны, дробь, в которой числитель больше или равен знаменателю, называется неправильной дробью. Например, 18/5, 49/23, 46/46 — неправильные дроби.
Как преобразовать неправильную дробь в правильную дробь?
Неправильные дроби можно преобразовать в смешанные дроби, представляющие собой комбинацию целого числа и правильной дроби. Только так можно преобразовать неправильную дробь в правильную. Для этого разделим числитель на знаменатель и запишем частное как целое число, остаток как числитель, а знаменатель останется прежним.
Как складывать правильные дроби с разными знаменателями?
Чтобы сложить правильные дроби с разными знаменателями, мы берем НОК знаменателей и преобразуем данные дроби в их эквиваленты, чтобы сделать знаменатель одинаковым. Затем мы записываем сумму числителей над общим знаменателем.
Как умножать правильные дроби?
Чтобы умножить правильные дроби, мы умножаем заданные числители, затем умножаем знаменатели, а затем приводим дробь к ее наименьшему члену. Например, чтобы умножить 4/9 × 3/6, мы умножаем числители 4 и 3, чтобы получить 12, а знаменатели умножаем на 9.и 6, чтобы получить 54. Произведение равно 12/54, которое можно уменьшить до 2/9.
Например, чтобы умножить 4/9 × 3/6, мы умножаем числители 4 и 3, чтобы получить 12, а знаменатели умножаем на 9.и 6, чтобы получить 54. Произведение равно 12/54, которое можно уменьшить до 2/9.
Как делить правильные дроби?
Мы делим правильные дроби так же, как мы их умножаем. Разница лишь в том, что мы умножаем первую дробь на обратную (обратную) второй дроби. Например, разделим: 2/3 ÷ 4/5. Мы напишем обратную величину второй дроби, а затем перемножим дроби. Это даст нам 2/3 × 5/4 = 10/12. Это может быть дополнительно уменьшено до 5/6.
Является ли 12/8 правильной дробью?
Нет, 12/8 не является правильной дробью, поскольку числитель (12) больше знаменателя (8). Это неправильная дробь.
Является ли 7/7 правильной дробью?
Нет, 7/7 не правильная дробь, потому что числитель равен знаменателю. Считается неправильной дробью.
Является ли 5/8 правильной дробью?
Да, 5/8 — правильная дробь, потому что числитель (5) меньше знаменателя (8).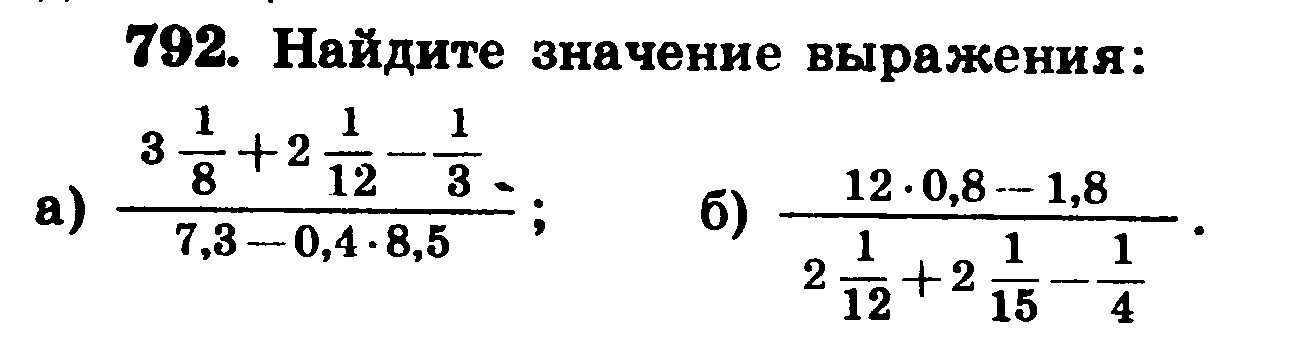


 Итак, получаем 7 × 5 = 35
Итак, получаем 7 × 5 = 35