404 Cтраница не найдена
Размер:
AAA
Цвет: C C C
Изображения Вкл. Выкл.
Обычная версия сайта
Мы на карте Версия для слабовидящих Версия для слабовидящих
СПб ГБ ПОУ «Техникум «Приморский»
- Сведения об образовательной организации
- Основные сведения
- Структура и органы управления образовательной организацией
- Документы
- Образование
- Руководство.
 Педагогический (научно-педагогический состав)
Педагогический (научно-педагогический состав) - Материально-техническое обеспечение и оснащенность образовательного процесса
- Стипендии и иные виды материальной поддержки
- Платные образовательные услуги
- Финансово-хозяйственная деятельность
- Вакантные места для приёма (перевода)
- Энергосбережение и повышение энергетической эффективности
- Доступная среда
- Наш техникум
- Теоретическое и производственное обучение
- Воспитательная работа
- Доступная среда
- Противодействие коррупции
- Абитуриенту
- Приёмная комиссия
- Профессии
- Фото-экскурсия
- Видеогалерея
- Студенту
- Полезные ссылки
- Расписание
- ЕГЭ
- ГИА
- Центр содействия трудоустройству выпускников
- Учебно-методические материалы
- Контакты
- WorldSkills Russia
- О нас
- Чемпионат
- Обращения граждан
- Новости
- Наши профессии
- Преподавателю
- Moodle
- Организация питания в образовательной организации
- Меню (в том числе информация о наличии диетического меню в образовательной организации)
- Организация питания, документы и иная информация
- Родительский контроль
- Обратная связь для родителей (законных представителей), обучающихся
- Международное сотрудничество
- org/ListItem»>Главная
- ›
- raspisanie distancion docum
Исследовать функцию и построить график.
Пример 1:
Исследовать функцию и построить ее график.
Решение от преподавателя:
1) Область определения функции х – любое.
2) Четность или нечетность функции.
y(-x) = y(x), четная функция
3) Точки пересечения кривой с осями координат.
Пересечение с осью 0Y
Пересечение с осью 0X
y=0
x1 = 1, x2 = -1
4) Исследование на экстремум.
1. Находим интервалы возрастания и убывания. Первая производная.
=
Находим нули функции. Для этого приравниваем производную к нулю
x = 0
Откуда:
x1 = 0
(-∞ ;0) | (0; +∞) |
f'(x) > 0 | f'(x) |
функция возрастает | функция убывает |
В окрестности точки x = 0 производная функции меняет знак с (+) на (-). Следовательно, точка x = 0 — точка максимума. Ymax=1
Следовательно, точка x = 0 — точка максимума. Ymax=1
2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.
или
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
Откуда точки перегиба:
f»(x) > 0 | f»(x) | f»(x) > 0 |
функция вогнута | функция выпукла | функция вогнута |
5) Асимптоты кривой.
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. 2+20
2+20
1. Находим интервалы возрастания и убывания. Первая производная.
f'(x) = 3x2+6x
или
f'(x)=3x(x+2)
Находим нули функции. Для этого приравниваем производную к нулю
x(x+2) = 0
Откуда:
x1 = 0
x2 = -2
(-∞ ;-2) | (-2; 0) | (0; +∞) |
f'(x) > 0 | f'(x) | f'(x) > 0 |
функция возрастает | функция убывает | функция возрастает |
В окрестности точки x = -2 производная функции меняет знак с (+) на (-). Следовательно, точка x = -2 — точка максимума. В окрестности точки x = 0 производная функции меняет знак с (-) на (+). Следовательно, точка x = 0 — точка минимума.
2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.
f»(x) = 6x+6
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
6x+6 = 0
Откуда точки перегиба:
x1 = -1
(-∞ ;-1) | (-1; +∞) |
f»(x) | f»(x) > 0 |
функция выпукла | функция вогнута |
6) Асимптоты кривой.
y = x3+3x2+20
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:
Находим коэффициент k:
Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует.
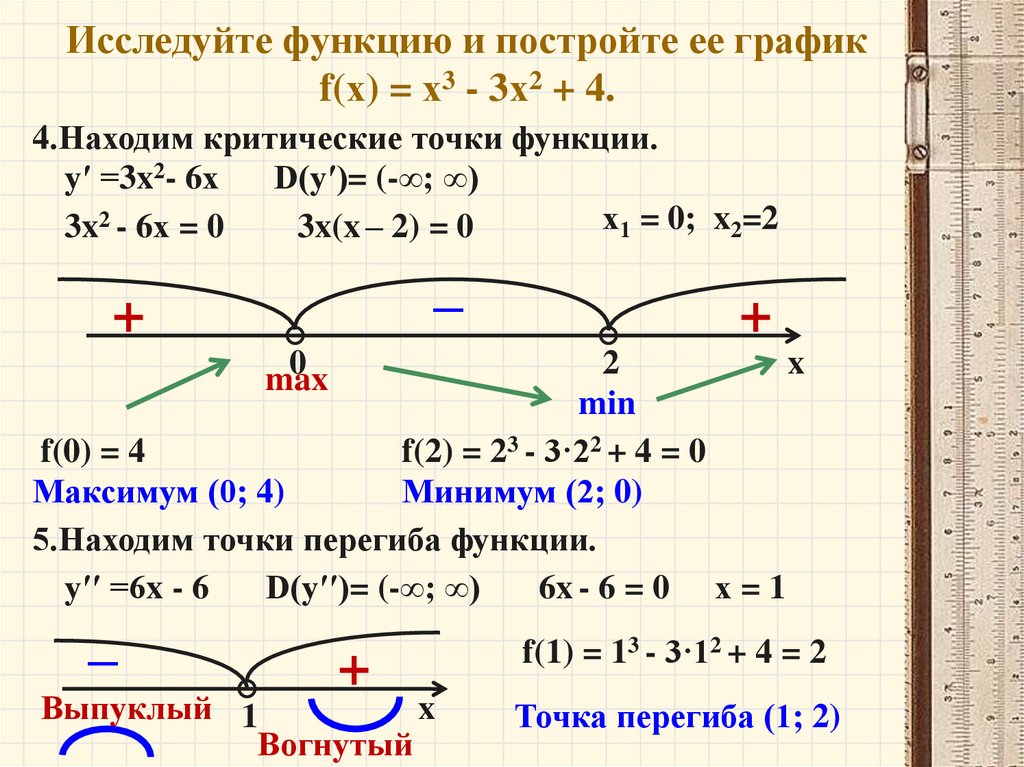
Пример 3:
Исследовать функцию и построить график:
Решение от преподавателя:
1.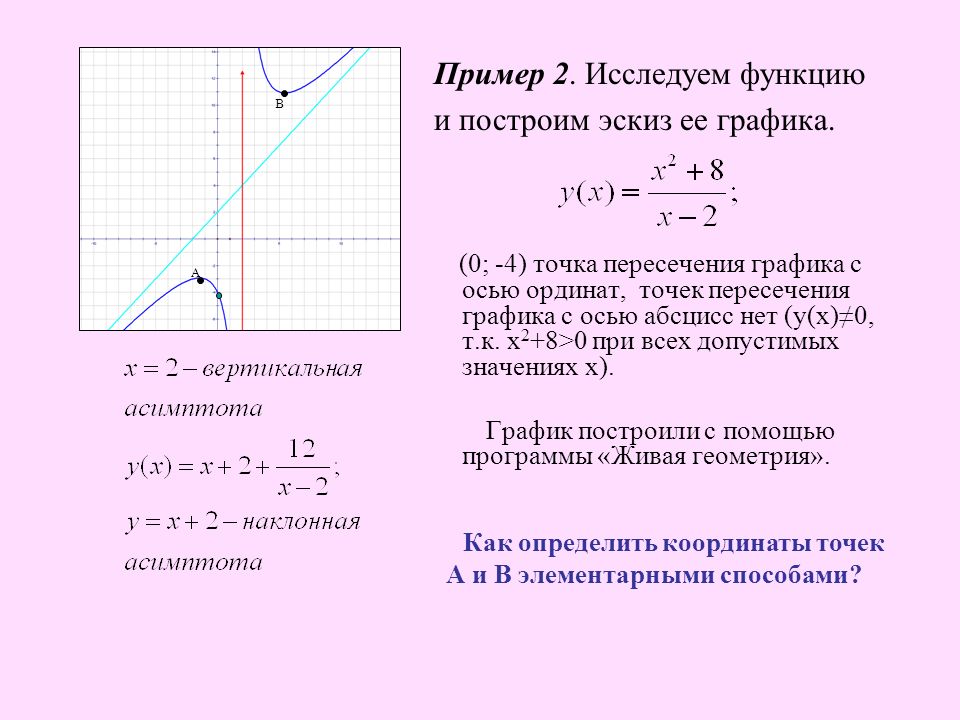 Находим область определения D(x) функции: определена на всей числовой оси.
Находим область определения D(x) функции: определена на всей числовой оси.
2.Асимптоты:
Вертикальных асимптот нет.
Находим наклонную асимптоту:
следовательно график функции не имеет наклонных асимптот.
Горизонтальная асимптота y=0.
3. Функция обладает свойствами четности, а, следовательно, график функции симметричен относительно оси OX.
4.Точек пересечения с осями координат: x=0, y=2.
5.Находим точки экстремума и интервалы монотонности, точки перегиба и интервалы выпуклости и вогнутости.
Первая производная функции:
Вторая производная функции:
Точек перегиба график функции не имеет.
На интервале – функция возрастает.
На интервале – функция убывает.
Точка максимума:
Функция выпуклая вверх на интервале:
Функция вогнута вниз на интервалах:
6. Изображаем график функции:
Пример 4:
Решение от преподавателя:
Пример 5:
Исследовать функцию у = 15х2 – 2х3 – 36х и построить ее график.
Решение от преподавателя:
1) Область определения функции
2) Четность или нечетность функции.
y(-x)=2x3+15x2+36x y(x)
Функция общего вида
3) Точки пересечения кривой с осями координат.
Пересечение с осью 0Y x=0, y=0
Пересечение с осью 0X y=0
15x2-2x3-36x=0, x = 0
5) Исследование на экстремум.
y = -2x3+15x2— 36x
1. Находим интервалы возрастания и убывания. Первая производная.
f'(x) = -6x2+30x-36
Находим нули функции. Для этого приравниваем производную к нулю
-6x2+30x-36 = 0 или x2+5x-6 = 0
Откуда:
x1 = 2
x2 = 3
(-∞ ;2) | (2; 3) | (3; +∞) |
f'(x) | f'(x) > 0 | f'(x) |
функция убывает | функция возрастает | функция убывает |
В окрестности точки x = 2 производная функции меняет знак с (-) на (+). Следовательно, точка x = 2 — точка минимума.
Следовательно, точка x = 2 — точка минимума.
В окрестности точки x = 3 производная функции меняет знак с (+) на (-). Следовательно, точка x = 3 — точка максимума.
Ymin=y(2)=-28, Ymax=y(3)=-27
2. Найдем интервалы выпуклости и вогнутости функции.
Вторая производная f»(x) = -12x+30
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
-12x+30 = 0
Откуда точки перегиба:
x1 = 5/2 y(5/2)=-27,5
(-∞ ;5/2) | (5/2; +∞) |
f»(x) > 0 | f»(x) |
функция вогнута | функция выпукла |
y = kx + b. Находим коэффициент k: Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует. |
Пример 6:
Методами дифференциального исчисления исследовать функцию y = f(x). Построить график этой функции, используя результаты исследования.
Решение от преподавателя:
1) Область определения функции. Точки разрыва функции.
Все действительные числа кроме х = 2
2) Четность или нечетность функции.
Функция общего вида
3) Периодичность функции.
4) Точки пересечения кривой с осями координат.
Пересечение с осью 0Y
x=0, y=0
Пересечение с осью 0X
y=0
x = 0, x = 0
5) Исследование на экстремум. 2)/(x-2)
2)/(x-2)
Найдем точки разрыва функции.
x1 = 2
1. Находим интервалы возрастания и убывания. Первая производная.
или
Находим нули функции. Для этого приравниваем производную к нулю
-2x2+8x-6 = 0
Откуда:
x1 = 1
x2 = 3
(-∞ ;1) | (1; 2) | (2; 3) | (3; +∞) |
f'(x) | f'(x) > 0 | f'(x) > 0 | f'(x) |
функция убывает | функция возрастает | функция возрастает | функция убывает |
В окрестности точки x = 1 производная функции меняет знак с (-) на (+).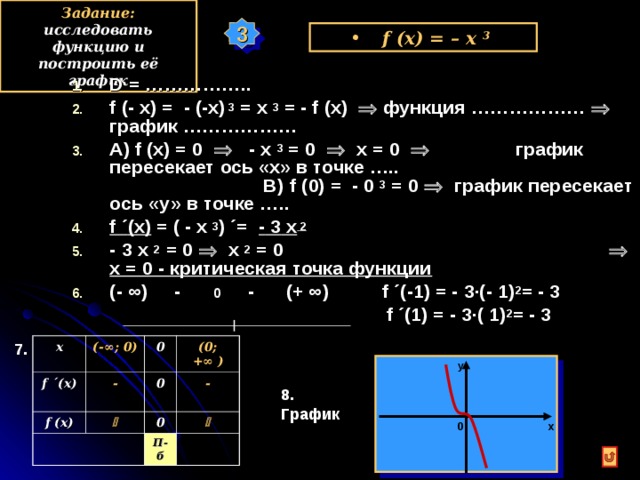 Следовательно, точка x = 1 — точка минимума. В окрестности точки x = 3 производная функции меняет знак с (+) на (-). Следовательно, точка x = 3 — точка максимума.
Следовательно, точка x = 1 — точка минимума. В окрестности точки x = 3 производная функции меняет знак с (+) на (-). Следовательно, точка x = 3 — точка максимума.
2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.
или
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
Для данного уравнения корней нет.
(-∞ ;2) | (2; +∞) |
f»(x) > 0 | f»(x) |
функция вогнута | функция выпукла |
6) Асимптоты кривой.
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:
Находим коэффициент k:
Находим коэффициент b:
Получаем уравнение наклонной асимптоты:
y = -2x-1
Найдем вертикальные асимптоты. Для этого определим точки разрыва:
Для этого определим точки разрыва:
x1 = 2
Находим переделы в точке x=2
x1 = 2 — точка разрыва II рода и является вертикальной асимптотой.
Пример 7:
Исследовать функцию и построить ее график.
Решение от преподавателя:
Пример 8:
Исследовать функцию и построить её схематический график.
Решение от преподавателя:
Пример 9:
Исследовать заданную функцию и начертить ее график.
Решение от преподавателя:
Пример 10:
Провести полное исследование функции и построить график.
Решение от преподавателя:
1) Область определения функции.
2) Четность или нечетность функции.
y(-x) = -y(x), нечетная функция
3) Точки пересечения кривой с осями координат.
Пересечение с осью 0Y
Нет пересечений.
Пересечение с осью 0X
y=0
4) Исследование на экстремум.
1. Находим интервалы возрастания и убывания. Первая производная.
Находим нули функции. Для этого приравниваем производную к нулю
x2+3 = 0
Для данного уравнения корней нет.
(-∞ ;0) | (0; +∞) |
f'(x) > 0 | f'(x) > 0 |
функция возрастает | функция возрастает |
2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
Для данного уравнения корней нет.
(-∞ ;0) | (0; +∞) |
f»(x) > 0 | f»(x) |
функция вогнута | функция выпукла |
6) Асимптоты кривой.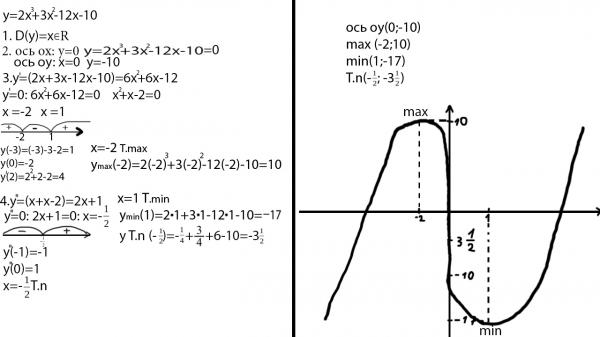
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:
Находим коэффициент k:
Находим коэффициент b:
Получаем уравнение наклонной асимптоты:
y = x
Найдем вертикальные асимптоты. Для этого определим точки разрыва:
x1 = 0
Находим переделы в точке x=0
x1 = 0 — точка разрыва II рода и является вертикальной асимптотой.
Пример 11:
Провести полное исследование и построить график функции .
Найти наибольшее и наименьшее значения функции на отрезке .
Решение от преподавателя:
График:
Пример 12:
Провести полное исследование функции
Решение от преподавателя:
Пример 13:
Провести полное исследование и построить график функции .
Решение от преподавателя:
Пример 14:
Исследовать функцию и построить график:
Решение от преподавателя:
Пример 15:
Провести полное исследование и построить график функции. Найти наибольшее и наименьшее значения функции на отрезке
Найти наибольшее и наименьшее значения функции на отрезке
Решение от преподавателя:
Пример 16:
Исследовать функцию и построить ее график.
Решение от преподавателя:
Пример 17:
Провести полное исследование и построить график функции.
Решение от преподавателя:
Пример 18:
Исследовать данную функцию и построить график:
Решение от преподавателя:
1) Область определения функции – множество всех действительных чисел: .
2) Чётность и нечётность функции:
Функция не обладает свойствами чётности или нечётности. Следовательно, график функции не будет симметричен ни относительно оси Oy, ни относительно начала координат.
3) Периодичности функции.
Функция непериодическая, так как является многочленом.
4) Непрерывность функции.
На всей области определения функция непрерывна как многочлен.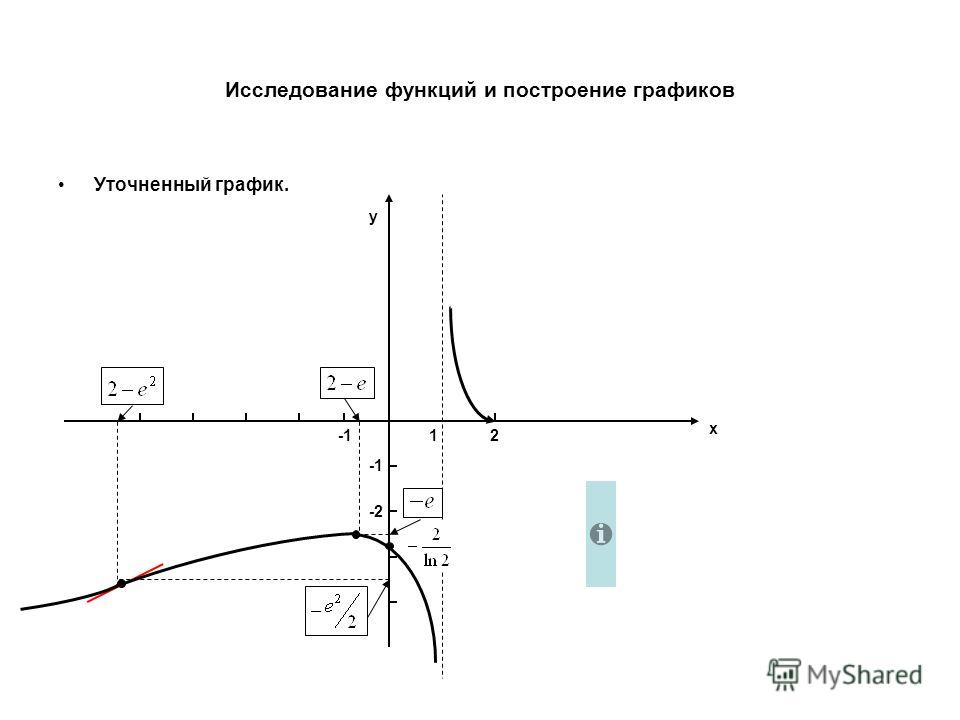
5) Интервалы монотонности и точки экстремума.
Вычислим производную функции и найдём критические точки.
Точки — критические.
Они делят область определения функции на интервалы:
Определим знак производной на каждом из интервалов:
.
Следовательно, на интервале функция возрастает;
.
Следовательно, на интервале функция убывает;
.
Следовательно, на интервале функция возрастает;
При переходе через точку производная меняет свой знак с плюса на минус. Следовательно, — точка максимума функции. При переходе через точку производная меняет свой знак с минуса на плюс. Следовательно, — точка минимума функции.
6) Интервалы выпуклости, вогнутости и точки перегиба.
Найдём производную второго порядка от функции
7) Точки пересечения графика с осями координат.
8) График функции.
Пример 19:
Исследовать функцию и построить график:
Решение от преподавателя:
Пример 20:
Для данной функции требуется:
а) найти точки разрыва;
б) найти скачок функции в каждой точке разрыва;
в) сделать чертеж.
Решение от преподавателя:
При х=0
Разрыва нет
При х=2
Разрыв есть
Определяем пределы слева и справа от данной точки
Т. к. оба пределы конечны, но равны между собой, то получили точку разрыва 1-го рода – точку скачка
Скачок функции составляет 8-3=5 единиц
Пример 21:
Исследовать функцию и построить график
y = 2x·lnx
Решение от преподавателя:
1. Область определения — точек разрыва нет.
2. Область значений — .
3. функция общего вида, пересекает оси координат в точке (1, 0).
4. интервалы монотонности:
Корень х=1\е, это минимум. Функция убывает на участке (0, 1\е) и возрастает на остальной области определения.
5. интервалы выпуклости, вогнутости.
Корней нет – нет и точек перегиба.
Вторая производная положительна на всей области определения (x>0) – функция вогнутая.
6. Асимптоты.
Вертикальных –нет.
Поскольку
, горизонтальной асимптоты нет.
Проверим, есть ли наклонная асимптота вида y=kx+b.
Найдем , наклонной также нет.
7. строим график:
Пример 22:
Исследовать функцию и построить ее график:
Решение от преподавателя:
\
Пример 23:
Исследовать функция и построить её график.
Решение от преподавателя:
Пример 24:
Исследовать функцию и построить график:
y=
Решение от преподавателя:
1) Область определения функции x€(-∞,-4)Ù(-4,+∞)
2) Четность или нечетность функции.
y(-x)≠y(x), y(-x)≠ — y(x),
Функция общего вида
3) Точки пересечения кривой с осями координат.
Пересечение с осью 0Y
Пересечение с осью 0X: y=0
4) Исследование на экстремум.
Найдем точки разрыва функции.
x1 = -4
1. Находим интервалы возрастания и убывания. Первая производная.
Первая производная.
Находим нули функции. Для этого приравниваем производную к нулю
x2+8x+15 = 0
Откуда:
x1 = -5 x2 = -3
(-∞ ;-5) | (-5; -4) | (-4; -3) | (-3; +∞) |
f'(x) > 0 | f'(x) | f'(x) | f'(x) > 0 |
функция возрастает | функция убывает | функция убывает | функция возрастает |
В окрестности точки x = -5 производная функции меняет знак с (+) на (-).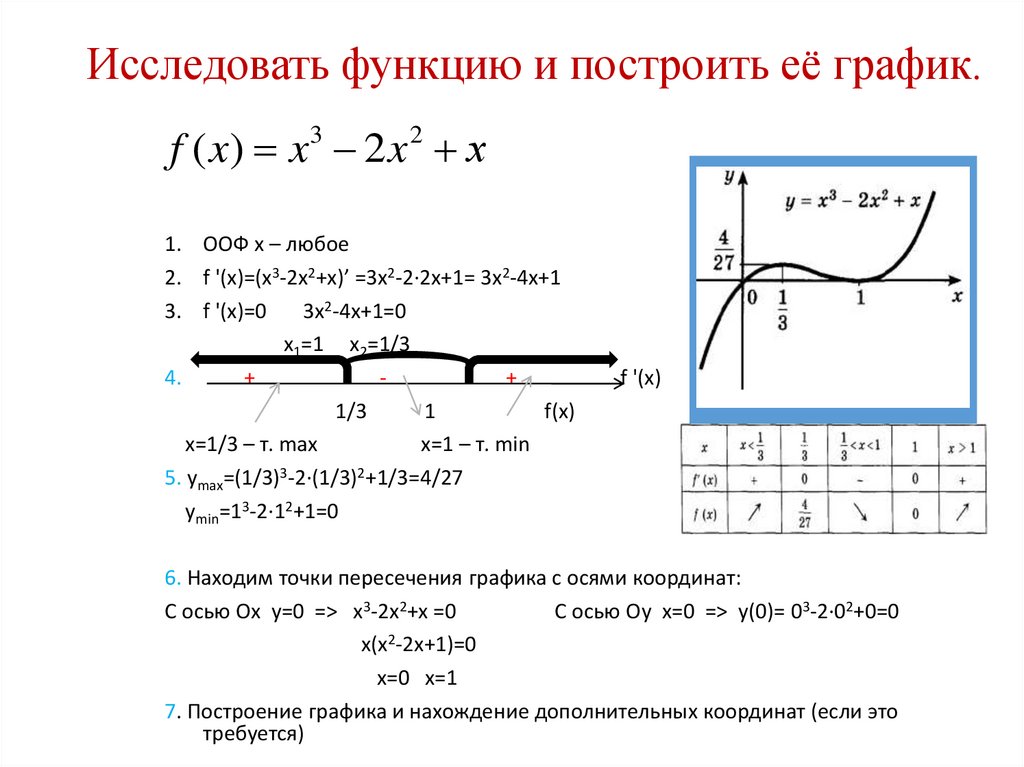 Следовательно, точка x = -5 — точка максимума.
Следовательно, точка x = -5 — точка максимума.
Ymax = y(-5) = -10
В окрестности точки x = -3 производная функции меняет знак с (-) на (+). Следовательно, точка x = -3 — точка минимума.
Ymin = y(-3) = -6
2. Найдем интервалы выпуклости и вогнутости функции.
Вторая производная.
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
Для данного уравнения корней нет.
(-∞ ;-4) | (-4; +∞) |
f»(x) | f»(x) > 0 |
функция выпукла | функция вогнута |
5) Асимптоты кривой.
Уравнения наклонных асимптот обычно ищут в виде y = kx + b.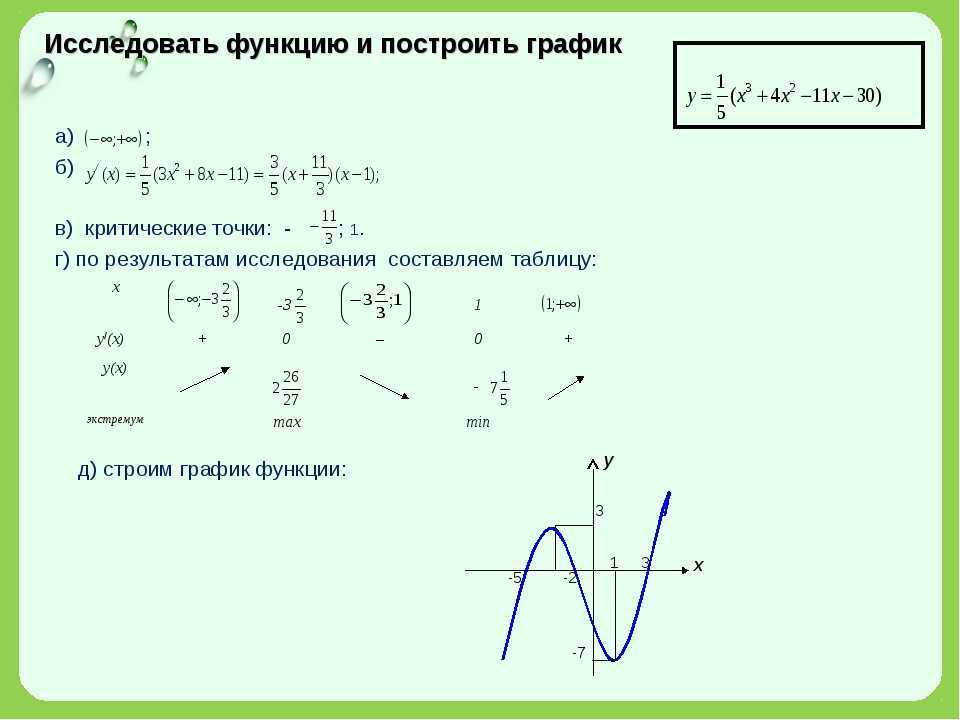 По определению асимптоты:
По определению асимптоты:
Находим коэффициент k:
Находим коэффициент b:
Получаем уравнение наклонной асимптоты:
y = x-4
Найдем вертикальные асимптоты. Для этого определим точки разрыва:
x1 = -4
Находим переделы в точке x=-4
x1 = -4 — точка разрыва II рода и является вертикальной асимптотой.
исчисление — изучить и построить график функции, заданной в параметрической форме
Задать вопрос
спросил
Изменено 5 лет, 9 месяцев назад
Просмотрено 99 раз
$\begingroup$
Мне трудно понять, как исследовать и построить график функции, заданной в параметрической форме. 2+2t,t\in\mathbb R?$$
2+2t,t\in\mathbb R?$$
- вычисления
- графические функции
- параметрические
$\endgroup$
2$\begingroup$
Не общий ответ, но каждый раз, когда вы видите пару уравнений вида \начать{выравнивать*} и &= а + Ь, \\ v &= а — б, \конец{выравнивание*} тихий голос в вашей голове должен спросить: «Что произойдет, если я сложу и вычту (т. е. решу $a$ и $b$ через $u$ и $v$)?» 9{2}$.
Теперь $(u, v)$ представляет собой повернутую и масштабированную декартову систему координат:
Ось $u$ имеет уравнение $v = 0$, т. е. $y = x$;
Ось $v$ имеет уравнение $u = 0$, т. е. $y = -x$;
Обе координаты увеличиваются на $y$;
Точка $(x, y) = (1, 1)$ удовлетворяет условию $(u, v) = (1, 0)$, поэтому одна единица длины в $(u, v)$ равна $\sqrt{ 2}$ единиц длины в $(x, y)$.

Какой вклад дают «антисимметричные» члены $\pm 2t$? Ну, $-2t$ для $x$ заставляет прямую линию расти медленнее в направлении $x$, и то же самое с $y$, только вместо этого с увеличением роста, поэтому график должен иметь наклон, который обычно больше $1$ в начале. 92-2x$). Однако с этого момента $x$ также всегда увеличивается. Зная это, а также тот факт, что через какое-то время график должен напоминать прямую линию, вы можете получить представление о том, как будет выглядеть весь график, а именно:
$\endgroup$
В этом разделе мы узнаем о графиках степенных функций, f ( х ) = топор р . Чтобы исследовать эти графики, мы начнем с рассмотрения a = 1 и p ≥ 0. Примечание.
что когда ф (1) = (1) р = 1. График степенных функций, где x > 0 и p ≥ 0 Во многих биологических приложениях мы имеем дело с положительными значениями x , поэтому мы рассмотрим f ( x ) = x p с x > 0 и p ≥ 0 , просмотрев несколько случаев.
Одной из важных особенностей силовых функций является то, как они сравниваются друг с другом.
когда Что происходит с функцией f ( x ) = x p при p ≥ 0 и x < 0 сложнее. \
График f ( x ), когда x < 0 будет посмотреть одним из двух способов:
|

 Педагогический (научно-педагогический состав)
Педагогический (научно-педагогический состав)


 С другой стороны, если x > 1, p > q подразумевает x p > x q . Например, если x > 1, то x 2 > √ x . Эту особенность силовых функций можно увидеть
на графике ниже.
С другой стороны, если x > 1, p > q подразумевает x p > x q . Например, если x > 1, то x 2 > √ x . Эту особенность силовых функций можно увидеть
на графике ниже.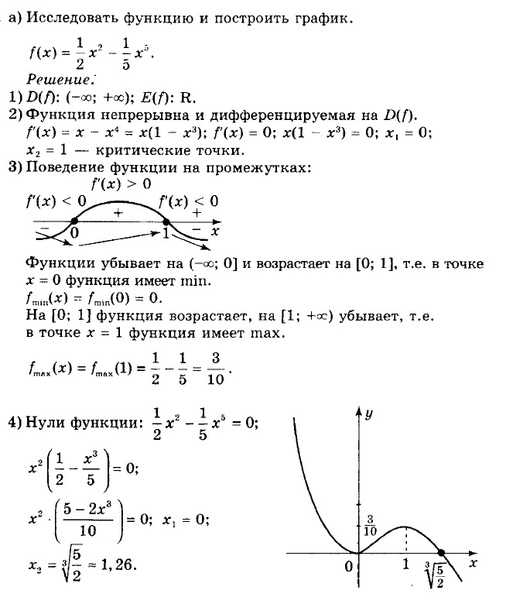
 , если P = R / S (в самых низких условиях) с S ODD и R ODD, F ( x ) → –1 AS x ( x ) → –1 AS x ( x ) → –1 AS x ° → –186 x ° → –186 x ° → –186 x → –186 x → –186 x → –1 ar x °) −1,
и график f ( x ) симметрично относительно начала координат (т.е. f ( x ) нечетно). К
см. это, мы интерпретируем f ( x ) = x p как
, если P = R / S (в самых низких условиях) с S ODD и R ODD, F ( x ) → –1 AS x ( x ) → –1 AS x ( x ) → –1 AS x ° → –186 x ° → –186 x ° → –186 x → –186 x → –186 x → –1 ar x °) −1,
и график f ( x ) симметрично относительно начала координат (т.е. f ( x ) нечетно). К
см. это, мы интерпретируем f ( x ) = x p как/ModulBM/ModBM/Praktika/Rechen/pract(IssF_2pr).files/image212.jpg) Случай a ≠ 1 можно обработать, обратившись к графическому
преобразования. В частности, | и | > 1 вертикально растягивает
граф относительно базового графа y = x p , а | и | < 1 вертикально сжимает граф по отношению к базовому графу. Если a < 0 тоже есть отражение
относительно оси x .
Случай a ≠ 1 можно обработать, обратившись к графическому
преобразования. В частности, | и | > 1 вертикально растягивает
граф относительно базового графа y = x p , а | и | < 1 вертикально сжимает граф по отношению к базовому графу. Если a < 0 тоже есть отражение
относительно оси x . В частности, линия х = 0 является вертикальной асимптотой
график. График f ( x ), когда p < 0 и f ( x ), определенные для x < 0, будут выглядеть
одним из двух способов:
В частности, линия х = 0 является вертикальной асимптотой
график. График f ( x ), когда p < 0 и f ( x ), определенные для x < 0, будут выглядеть
одним из двух способов: