404 Cтраница не найдена
- Сведения об образовательной организации
- Основные сведения
- Структура и органы управления образовательной организацией
- Документы
- Образование
- Образовательные стандарты
- Руководство. Педагогический (научно-педагогический состав)
- Материально-техническое обеспечение и оснащенность образовательного процесса
- Стипендии и иные виды материальной поддержки
- Платные образовательные услуги
- Вакантные места для приёма (перевода)
- Энергосбережение и повышение энергетической эффективности
- Доступная среда
- Наш техникум
- Теоретическое и производственное обучение
- Воспитательная работа
- Доступная среда
- Противодействие коррупции
- Абитуриенту
- Приёмная комиссия
- Профессии
- Фото-экскурсия
- Видеогалерея
- Студенту
- Полезные ссылки
- Расписание
- Библиотека
- ЕГЭ
- ГИА
- Центр содействия трудоустройству выпускников
- Учебно-методические материалы
- Контакты
- WorldSkills Russia
- О нас
- Чемпионат
- Обращения граждан
- Новости
- Наши профессии
- Преподавателю
- Moodle
- Организация питания в образовательной организации
- Меню (в том числе информация о наличии диетического меню в образовательной организации)
- Организация питания, документы и иная информация
- Родительский контроль
- Обратная связь для родителей (законных представителей), обучающихся
- Международное сотрудничество
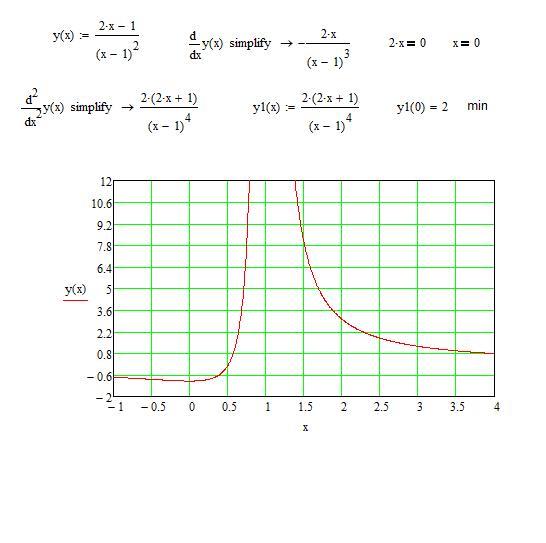
Исследовать функцию на чётность (нечётность) : Школьная алгебра
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| Charlz_Klug |
| ||
01/09/14 |
| ||
| |||
| Ms-dos4 |
| |||
25/02/08 |
| |||
| ||||
| мат-ламер |
| |||
30/01/09 |
| |||
| ||||
| Charlz_Klug |
| ||
01/09/14 |
| ||
| |||
| provincialka |
| |||
18/01/13 |
| |||
| ||||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| provincialka |
| |||
18/01/13 |
| |||
| ||||
| ewert |
| |||
11/05/08 |
| |||
| ||||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| Charlz_Klug |
| ||
01/09/14 |
| ||
| |||
| AlexDem |
| |||
07/08/06 |
| |||
| ||||
| Charlz_Klug |
| ||
01/09/14 |
| ||
| |||
| arseniiv |
| |||
27/04/09 |
| |||
| ||||
| AlexDem |
| |||
07/08/06 |
| |||
| ||||
| AlexDem |
| |||
07/08/06 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 15 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
TANRIC: интерактивная открытая платформа для изучения функции днРНК при раке
. 2015 15 сентября; 75 (18): 3728-37.
2015 15 сентября; 75 (18): 3728-37.
doi: 10.1158/0008-5472.CAN-15-0273. Epub 2015 24 июля.
Джун Ли 1 , Ленг Хань 1 , Пол Робак 1 , Ликсия Диао 1 , Линсян Лю 2 , Юань Юань 1 , Джон Н. Вайнштейн 3 , Хань Лян 4
Принадлежности
- 1 Факультет биоинформатики и вычислительной биологии, Онкологический центр им. М. Д. Андерсона Техасского университета, Хьюстон, Техас.
- 2 Кафедра биоинформатики и вычислительной биологии, Онкологический центр им.
 М. Д. Андерсона Техасского университета, Хьюстон, Техас. Кафедра онкологии Нанкинского медицинского университета, Нанкин, Цзянсу, Китай.
М. Д. Андерсона Техасского университета, Хьюстон, Техас. Кафедра онкологии Нанкинского медицинского университета, Нанкин, Цзянсу, Китай. - 3 Кафедра биоинформатики и вычислительной биологии, Онкологический центр им. М. Д. Андерсона Техасского университета, Хьюстон, Техас. Департамент системной биологии, Онкологический центр им. М. Д. Андерсона Техасского университета, Хьюстон, Техас.
- 4 Кафедра биоинформатики и вычислительной биологии, Онкологический центр им. М. Д. Андерсона Техасского университета, Хьюстон, Техас. Департамент системной биологии, Онкологический центр им. М. Д. Андерсона Техасского университета, Хьюстон, Техас. Высшая школа биомедицинских наук Техасского университета, Хьюстон, Техас. Программа магистратуры по структурной и вычислительной биологии и молекулярной биофизике, Медицинский колледж Бэйлора, Хьюстон, Техас.
 [email protected].
[email protected].
- PMID: 26208906
- PMCID: PMC4573884
- DOI: 10.1158/0008-5472.КАН-15-0273
Бесплатная статья ЧВК
Джун Ли и др. Рак рез. .
Бесплатная статья ЧВК
. 2015 15 сентября; 75 (18): 3728-37.
doi: 10.1158/0008-5472.CAN-15-0273. Epub 2015 24 июля.
Авторы
Джун Ли 1 , Ленг Хань 1 , Пол Робак 1 , Ликсия Диао 1 , Линсян Лю 2 , Юань Юань 1 , Джон Н. Вайнштейн 3 , Хань Лян 4
Вайнштейн 3 , Хань Лян 4
Принадлежности
- 1 Факультет биоинформатики и вычислительной биологии, Онкологический центр им. М. Д. Андерсона Техасского университета, Хьюстон, Техас.
- 2 Кафедра биоинформатики и вычислительной биологии, Онкологический центр им. М. Д. Андерсона Техасского университета, Хьюстон, Техас. Кафедра онкологии Нанкинского медицинского университета, Нанкин, Цзянсу, Китай.
- 3 Кафедра биоинформатики и вычислительной биологии, Онкологический центр им. М. Д. Андерсона Техасского университета, Хьюстон, Техас. Департамент системной биологии, Онкологический центр им. М. Д. Андерсона Техасского университета, Хьюстон, Техас.
- 4 Кафедра биоинформатики и вычислительной биологии, Онкологический центр им.
 М. Д. Андерсона Техасского университета, Хьюстон, Техас. Департамент системной биологии, Онкологический центр им. М. Д. Андерсона Техасского университета, Хьюстон, Техас. Высшая школа биомедицинских наук Техасского университета, Хьюстон, Техас. Программа магистратуры по структурной и вычислительной биологии и молекулярной биофизике, Медицинский колледж Бэйлора, Хьюстон, Техас. [email protected].
М. Д. Андерсона Техасского университета, Хьюстон, Техас. Департамент системной биологии, Онкологический центр им. М. Д. Андерсона Техасского университета, Хьюстон, Техас. Высшая школа биомедицинских наук Техасского университета, Хьюстон, Техас. Программа магистратуры по структурной и вычислительной биологии и молекулярной биофизике, Медицинский колледж Бэйлора, Хьюстон, Техас. [email protected].
- PMID: 26208906
- PMCID: PMC4573884
- DOI: 10.1158/0008-5472.КАН-15-0273
Абстрактный
Длинные некодирующие РНК (днРНК) стали важными игроками в биологии рака. Используя последние крупномасштабные наборы данных секвенирования РНК, особенно из Атласа генома рака (TCGA), мы разработали «Атлас некодирующих РНК в раке» (TANRIC; http://bioinformatics. mdanderson.org/main/TANRIC: Обзор), удобный веб-ресурс с открытым доступом для интерактивного исследования днРНК при раке. Он характеризует профили экспрессии lncRNAs в больших когортах пациентов с 20 типами рака, включая TCGA и независимые наборы данных (всего> 8000 образцов). TANRIC позволяет исследователям быстро и интуитивно анализировать интересующие днРНК (аннотированные днРНК или любые определяемые пользователем) в контексте клинических и других молекулярных данных как внутри, так и между типами опухолей. Используя TANRIC, мы идентифицировали большое количество lncRNAs с потенциальным биомедицинским значением, многие из которых демонстрируют сильную корреляцию с установленными терапевтическими мишенями и биомаркерами для разных типов опухолей или с чувствительностью к лекарствам для разных клеточных линий. TANRIC представляет собой ценный инструмент для исследования функции и клинической значимости днРНК при раке, что значительно облегчает биологические открытия и клинические применения, связанные с днРНК.
mdanderson.org/main/TANRIC: Обзор), удобный веб-ресурс с открытым доступом для интерактивного исследования днРНК при раке. Он характеризует профили экспрессии lncRNAs в больших когортах пациентов с 20 типами рака, включая TCGA и независимые наборы данных (всего> 8000 образцов). TANRIC позволяет исследователям быстро и интуитивно анализировать интересующие днРНК (аннотированные днРНК или любые определяемые пользователем) в контексте клинических и других молекулярных данных как внутри, так и между типами опухолей. Используя TANRIC, мы идентифицировали большое количество lncRNAs с потенциальным биомедицинским значением, многие из которых демонстрируют сильную корреляцию с установленными терапевтическими мишенями и биомаркерами для разных типов опухолей или с чувствительностью к лекарствам для разных клеточных линий. TANRIC представляет собой ценный инструмент для исследования функции и клинической значимости днРНК при раке, что значительно облегчает биологические открытия и клинические применения, связанные с днРНК.
©2015 Американская ассоциация исследований рака.
Заявление о конфликте интересов
Конфликт интересов Авторы заявляют об отсутствии конфликта интересов, связанного с этой работой.
Цифры
Рисунок 1. Обзор архитектуры TANRIC
Рисунок 1. Краткий обзор архитектуры TANRIC
Рисунок 2. Обзор портала данных TANRIC
Рисунок 2. Обзор портала данных TANRIC
Обзор портала данных TANRIC
(i) Панель из шести модулей; (ii)…
Рисунок 2. Обзор портала данных TANRIC(i) Панель из шести модулей; (ii) модуль «Резюме»; (iii) представление «кластерная тепловая карта следующего поколения» в модуле «Визуализация»; (iv) модуль «Скачать»; (v) три модуля анализа предоставляют необработанные данные об экспрессии интересующей днРНК; (vi) модули анализа обеспечивают анализ клинических данных днРНК (включая дифференциальный анализ между подтипами, стадиями и классами опухолей) и анализ корреляции с выживаемостью пациентов; и (vii) модули анализа обеспечивают анализ геномных данных днРНК, включая дифференциальный анализ между мутированными образцами и образцами дикого типа для представляющего интерес гена, кодирующего белок, и анализ корреляций с SCNA, микроРНК, мРНК и экспрессией белка.
Рисунок 3. Большое количество днРНК…
Большое количество днРНК…
Рисунок 3. Большое количество днРНК, имеющих потенциальное биомедицинское значение при различных типах рака
(а) Суммарные столбцы представляют количество экспрессированных днРНК; красные части представляют количество днРНК, дифференциально экспрессируемых между опухолевыми и соответствующими нормальными образцами для разных типов опухолей. ( б ) общее количество столбцов представляет количество экспрессированных днРНК; синие части представляют количество дифференциально экспрессируемых днРНК среди известных подтипов опухолей. (c) Суммарные столбцы представляют количество экспрессированных lncRNAs; зеленые части представляют количество дифференциально экспрессируемых lncRNAs среди клинических стадий, среди которых светло-зеленые части представляют те, у которых характерно постоянное увеличение или уменьшение на разных стадиях. ( d ) Круговая диаграмма, показывающая количество lncRNAs, имеющих биомедицинское значение, по типам опухолей.
( d ) Круговая диаграмма, показывающая количество lncRNAs, имеющих биомедицинское значение, по типам опухолей.
Рисунок 4. Ассоциации днРНК с клинически…
Рисунок 4. Ассоциации днРНК с клинически активными генами или чувствительностью к лекарствам
(а) Номера…
Рисунок 4. Ассоциации днРНК с клинически активными генами или чувствительностью к лекарственным средствам (a) Количество lncRNAs, для которых уровни экспрессии связаны с SCNA, экспрессией мРНК или соматической мутацией клинически активных генов при каждом типе рака. ( б ) Количество пар днРНК-ген при нескольких типах рака. Цветные полосы представляют частоты в соответствии с клинической полезностью активных генов. ( c ) График Манхэттена, показывающий корреляции экспрессии днРНК и IC50 лекарственного средства в клеточных линиях CCLE. Каждая точка представляет одну корреляцию днРНК-лекарство, а корреляции для разных лекарств показаны разными цветами.
Каждая точка представляет одну корреляцию днРНК-лекарство, а корреляции для разных лекарств показаны разными цветами.
Рисунок 5. Экспрессия днРНК проявляется клинически и…
Рисунок 5. Экспрессия днРНК позволяет выявить клинически и биологически значимые подтипы опухолей
(a) Подтипы экспрессии днРНК показывают…
Рисунок 5. Экспрессия днРНК позволяет выявить клинически и биологически значимые подтипы опухолей. (a) Подтипы экспрессии днРНК демонстрируют обширную, сильную согласованность с установленными подтипами опухолей. ( б ) подтипы экспрессии днРНК, по-видимому, коррелируют с общим временем выживания пациентов в BRCA, HNSC, KIRC и LGG. ( c ) Ключевые сигнальные пути по-разному экспрессируются среди подтипов опухолей, определяемых экспрессией lncRNA. Цвета на тепловой карте представляют статистическую значимость (FDR) ассоциаций между подтипами опухолей с экспрессией днРНК и показателями пути экспрессии белка.
Цвета на тепловой карте представляют статистическую значимость (FDR) ассоциаций между подтипами опухолей с экспрессией днРНК и показателями пути экспрессии белка.
См. это изображение и информацию об авторских правах в PMC
Похожие статьи
lnCAR: всеобъемлющий ресурс для lncRNAs из раковых массивов.
Чжэн И, Сюй Цюй, Лю М, Ху Х, Се Ю, Цзо Зи, Рен Дж. Чжэн И и др. Рак рез. 2019 15 апреля; 79(8):2076-2083. doi: 10.1158/0008-5472.CAN-18-2169. Epub 2019 20 февраля. Рак рез. 2019. PMID: 30786995
LncMAP: панраковый атлас нарушений транскрипционной сети, опосредованных длинными некодирующими РНК.
Ли И, Ли Л, Ван З, Пан Т, Сахни Н, Джин Х, Ван Г, Ли Дж, Чжэн Х, Чжан Ю, Сюй Дж, Йи С, Ли Х.
 Ли Ю и др.
Нуклеиновые Кислоты Res. 2018 16 февраля; 46 (3): 1113-1123. дои: 10.1093/нар/gkx1311.
Нуклеиновые Кислоты Res. 2018.
PMID: 29325141
Бесплатная статья ЧВК.
Ли Ю и др.
Нуклеиновые Кислоты Res. 2018 16 февраля; 46 (3): 1113-1123. дои: 10.1093/нар/gkx1311.
Нуклеиновые Кислоты Res. 2018.
PMID: 29325141
Бесплатная статья ЧВК.Lnc2Catlas: атлас длинных некодирующих РНК, связанных с риском развития рака.
Рен С., Ан Г., Чжао С., Оуян З., Бо С., Шу В. Рен С и др. Научный представитель 2018 г. 30 января; 8 (1): 1909. doi: 10.1038/s41598-018-20232-4. Научный представитель 2018. PMID: 29382910 Бесплатная статья ЧВК.
Распутывание lncRNAome рака полости рта: идентификация новых lncRNAs, связанных со злокачественным прогрессированием и инфекцией ВПЧ.
Нохата Н., Абба М.С., Гуткинд Д.С. Нохата Н. и соавт. Оральный онкол. 2016 авг;59:58-66. doi: 10.
 1016/j.oraloncology.2016.05.014.
Оральный онкол. 2016.
PMID: 27424183
Бесплатная статья ЧВК.
Обзор.
1016/j.oraloncology.2016.05.014.
Оральный онкол. 2016.
PMID: 27424183
Бесплатная статья ЧВК.
Обзор.Длинные некодирующие РНК при раке: от открытия до терапевтических мишеней.
Чоудхари Р., Седано М.Дж., Харрисон А.Л., Субрамани Р., Лин К.И., Рамос Э.И., Лакшманасвами Р., Гадад С.С. Чоудхари Р. и др. Adv Clin Chem. 2020;95:105-147. doi: 10.1016/bs.acc.2019.08.003. Epub 2019 31 октября. Adv Clin Chem. 2020. PMID: 32122521 Обзор.
Посмотреть все похожие статьи
Цитируется
Некодирующие РНК в области здоровья и болезней человека: потенциальная функция биомаркеров и терапевтических мишеней.
Loganathan T, Doss C GP. Логанатан Т. и др.
 Функц Интегр Геномикс. 2023 10 января; 23(1):33. дои: 10.1007/s10142-022-00947-4.
Функц Интегр Геномикс. 2023.
PMID: 36625940
Бесплатная статья ЧВК.
Обзор.
Функц Интегр Геномикс. 2023 10 января; 23(1):33. дои: 10.1007/s10142-022-00947-4.
Функц Интегр Геномикс. 2023.
PMID: 36625940
Бесплатная статья ЧВК.
Обзор.Изучение кооперации lncRNA-lncRNA выявило доминирующее влияние на противоопухолевый иммунитет при раке.
Шао Т., Се И., Ши Дж., Ян С., Цзоу Х., Ли И., Сюй Дж., Ли Х. Шао Т. и др. коммун биол. 3 декабря 2022 г .; 5 (1): 1324. doi: 10.1038/s42003-022-04249-0. коммун биол. 2022. PMID: 36463330 Бесплатная статья ЧВК.
Транскриптомное профилирование индийских пациентов с раком молочной железы выявило характерные для подтипа сигнатуры мРНК и днРНК.
Манджунат М., Ниргуде С., Мхатре А., Вемури С.Г., Натарадж М., Тумси Дж., Чоудхари Б. Манджунат М.
 и соавт.
Фронт Жене. 2022 25 окт;13:932060. doi: 10.3389/fgene.2022.932060. Электронная коллекция 2022.
Фронт Жене. 2022.
PMID: 36386805
Бесплатная статья ЧВК.
и соавт.
Фронт Жене. 2022 25 окт;13:932060. doi: 10.3389/fgene.2022.932060. Электронная коллекция 2022.
Фронт Жене. 2022.
PMID: 36386805
Бесплатная статья ЧВК.Клетки рака молочной железы перепрограммируют сети коэкспрессии онкогенных днРНК/мРНК в трехмерном микроокружении.
Нуньес-Ольвера С.И., Агилар-Арнал Л., Сиснерос-Вильянуэва М., Идальго-Миранда А., Марчат Л.А., Салинас-Вера Ю.М., Рамос-Паян Р., Перес-Пласенсиа С., Карлос-Рейес А., Пуэнте-Ривера Х., Лопес-Камарильо К. Нуньес-Ольвера С.И. и соавт. Клетки. 2022 1 ноября; 11 (21): 3458. doi: 10.3390/ячейки11213458. Клетки. 2022. PMID: 36359853 Бесплатная статья ЧВК.
PLK4 является потенциальным биомаркером аномальной пролиферации опухоли, иммунной инфильтрации и прогноза при скПКР.

Hu C, Liu Q, Hu C, Wang Y, Wang P, Zhou X. Ху С и др. Вычислительные математические методы мед. 2022, 20 сентября; 2022:6302234. дои: 10.1155/2022/6302234. Электронная коллекция 2022. Вычислительные математические методы мед. 2022. PMID: 36176741 Бесплатная статья ЧВК.
Просмотреть все статьи «Цитируется по»
Типы публикаций
термины MeSH
вещества
Грантовая поддержка
- P30 CA016672/CA/NCI NIH HHS/США
- CA143883/CA/NCI NIH HHS/США
- CA175486/CA/NCI NIH HHS/США
- R01 CA175486/CA/NCI NIH HHS/США
- U24 CA143883/CA/NCI NIH HHS/США
1.2 Что такое исчисление и зачем мы его изучаем?
Исчисление — это изучение того, как вещи меняются. Он обеспечивает основу для моделирования систем, в которых
изменение и способ вывести прогнозы таких моделей.
Он обеспечивает основу для моделирования систем, в которых
изменение и способ вывести прогнозы таких моделей.
Я здесь уже некоторое время и знаю, как все меняется, более или менее. Что может добавить исчисление который?
Я уверен, что вы много знаете о том, как все меняется. И у вас есть качественное представление об исчислении. Например Понятие скорости движения — понятие прямо из исчисления, хотя оно, несомненно, существовало задолго до появления исчисления. и вы много знаете об этом.
Так что же мне дает исчисление?
Он дает нам возможность построить относительно простые количественные модели изменений и вывести их последствия.
С какой целью?
Благодаря этому вы получаете возможность находить влияние изменяющихся условий на исследуемую систему. От
изучая их, вы можете научиться управлять системой, чтобы заставить ее делать то, что вы хотите. Расчет, по
Предоставление инженерам и вам возможности моделировать системы и управлять ими дает им (и, возможно, вам) исключительные возможности.
власть над материальным миром.
От
изучая их, вы можете научиться управлять системой, чтобы заставить ее делать то, что вы хотите. Расчет, по
Предоставление инженерам и вам возможности моделировать системы и управлять ими дает им (и, возможно, вам) исключительные возможности.
власть над материальным миром.
Развитие исчисления и его приложений в физике и технике, вероятно, является наиболее значительным фактором в развитии современной науки за пределами того, где она была во времена Архимеда. И это было ответственность за промышленную революцию и все, что из нее последовало, включая почти все основные достижения последних столетий.
Вы пытаетесь утверждать, что я достаточно знаю об исчислении, чтобы моделировать системы и делать выводы, чтобы контролировать их?
Если бы вы задали мне этот вопрос в 1990 году, я бы сказал «нет». Сейчас это в пределах возможного, т. к.
некоторые нетривиальные системы с использованием вашего ноутбука или настольного компьютера.
к.
некоторые нетривиальные системы с использованием вашего ноутбука или настольного компьютера.
Хорошо, но как меняются расчетные модели? На что похоже исчисление?
Фундаментальная идея исчисления состоит в том, чтобы изучать изменения, изучая «мгновенные» изменения, под которыми мы понимаем меняется через крошечные промежутки времени.
А что в этом хорошего?
Оказывается, такие изменения, как правило, намного проще, чем изменения за конечные интервалы времени. Это означает их намного легче моделировать. На самом деле исчисление было изобретено Ньютоном, который открыл то ускорение, которое означает, что изменение скорости объектов может быть смоделировано его относительно простыми законами движения.
И так?
Это оставляет нас с проблемой вывода информации о движении объектов из информации об их
скорость или ускорение. А детали исчисления включают взаимосвязь между понятиями, иллюстрируемыми
по скорости и ускорению, а также по положению.
А детали исчисления включают взаимосвязь между понятиями, иллюстрируемыми
по скорости и ускорению, а также по положению.
Итак, что изучается при изучении исчисления?
Для начала у вас должна быть структура для описания таких понятий, как позиционная скорость и ускорение.
Исчисление с одной переменной, с которого мы начнем, может иметь дело с движением объекта по фиксированной траектории. более общая задача, когда движение может происходить на поверхности или в пространстве, может решаться многомерными исчисление. Мы изучаем этот последний предмет, находя хитрые приемы использования одномерных идей и методов. для решения более общих проблем. Таким образом, исчисление с одной переменной также является ключом к общей проблеме.
Когда мы имеем дело с объектом, движущимся по пути, его положение меняется со временем, мы можем описать его положение в
в любое время одним числом, которое может быть расстоянием в некоторых единицах от некоторой фиксированной точки на этом пути, называемом
начало нашей системы координат. (Мы добавляем к этому расстоянию знак, который будет отрицательным, если объект
позади происхождения.)
(Мы добавляем к этому расстоянию знак, который будет отрицательным, если объект
позади происхождения.)
Затем движение объекта характеризуется набором его числовых положений в соответствующие моменты времени.
Набор позиций и времен, которые мы используем для описания движения, мы называем функцией . И подобные функции используются для описания интересующих величин во всех системах, к которым применяется исчисление. применяемый.
Курс здесь начинается с обзора чисел и функций и их свойств. Вы, несомненно, знакомы с большей частью этого, поэтому мы попытались добавить незнакомый материал, чтобы удерживать ваше внимание при просмотре.
Я увязну, если прочитаю о таких вещах. Должен я?
Я хотел бы, чтобы вы посмотрели на него, так как я его написал, но если вы предпочитаете этого не делать, вы, несомненно, могли бы обойтись.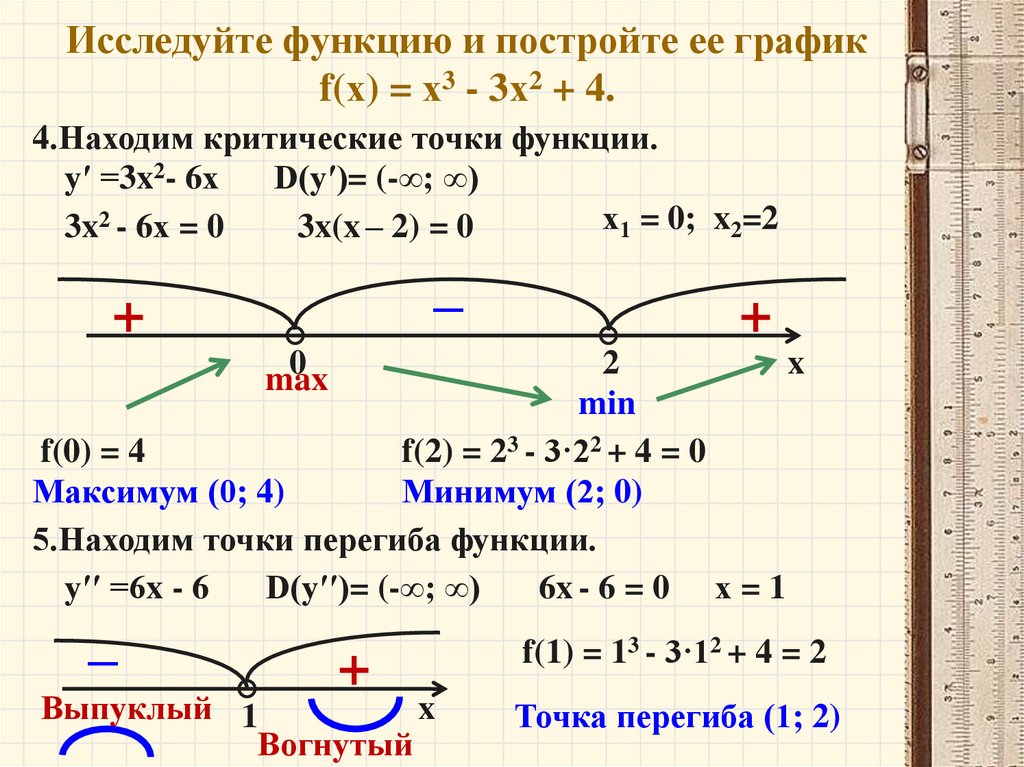 пропустить его и вернуться к нему, когда или если вам нужно это сделать. Однако вы пропустите новую информацию,
и это может испортить вам жизнь навсегда. (Хотя я в этом сомневаюсь.)
пропустить его и вернуться к нему, когда или если вам нужно это сделать. Однако вы пропустите новую информацию,
и это может испортить вам жизнь навсегда. (Хотя я в этом сомневаюсь.)
А что идет после чисел и функций?
Типичный курс исчисления охватывает следующие темы:
1. Как найти мгновенное изменение (называемое «производной») различных функций. (процесс выполнения так называется «дифференциация» .)
2. Как использовать производные для решения разного рода задач.
3. Как вернуться от производной функции к самой функции. (Этот процесс называется «интеграция» .)
4. Изучение подробных методов интегрирования функций некоторых видов.
5. Как использовать интегрирование для решения различных геометрических задач, таких как вычисление площадей и объемов
определенные регионы.
В таком курсе есть еще несколько стандартных тем. К ним относятся описание функций с точки зрения мощности ряд и изучение того, когда бесконечный ряд «сходится» к числу.
Итак, где это дает мне возможность делать что?
На самом деле это не так. Проблема в том, что такие курсы впервые были разработаны столетия назад, и они были нацелены
не на наделении полномочиями (в то время совершенно невозможном), а на ознакомлении своей аудитории с идеями и концепциями
и обозначения, которые позволяют понять более сложную работу. Математики, ученые и инженеры используют
концепции исчисления во всех видах контекстов и использовать жаргон и обозначения, которые без вашего знания о
исчисление, было бы совершенно непостижимым для вас. Изучение исчисления обычно направлено на то, чтобы дать вам
«математическая изощренность» для обозначения такой более продвинутой работы.
Так к чему эта ерунда про наделение полномочиями?
Этот курс попытается быть другим и направлен на расширение прав и возможностей, а также на другие обычные цели. Это может не получится, но по крайней мере попытается.
И как он попытается сотворить это чудо?
Традиционные курсы исчисления делают акцент на алгебраических методах выполнения дифференцирования и интегрирования. Мы будем
описать такие методы, но и показать, как можно выполнять дифференцирование и интегрирование (а также решение
обыкновенные дифференциальные уравнения) в компьютерной таблице с приемлемым усилием. Мы также
поставлять апплеты, которые делают то же самое автоматически с еще меньшими усилиями. С помощью этих апплетов или электронных таблиц вы
может применять инструменты исчисления с большей легкостью и гибкостью, чем это было возможно раньше.
(Часто доступны более продвинутые программы, такие как MAPLE и Mathematica, которые позволяют вам делать гораздо больше с такой же легкостью. С их помощью вы можете вывести последствия моделей разного рода в широком диапазоне. разнообразие контекстов. Как только вы поймете исчисление, они могут сделать его использование намного проще, но они дают ответы вводимые данные, что не дает понимания того, как они это делают.)
Кроме того, мы будем уделять гораздо больше внимания системам моделирования. С идеями по моделированию и методам решения дифференциальных уравнений, к которым они приводят, вы можете достичь того расширения возможностей, на которое мы претендовали.
И я смогу использовать это с какой-нибудь полезной целью?
Ладно, наверное, нет. Но вы могли бы. А также вас могут спровоцировать узнать больше о системах, которые вы хотите
изучения или о математике, чтобы улучшить свои шансы сделать это. Также вы могли бы быть в состоянии понять вероятные
последствия моделей немного лучше, чем у вас сейчас. Также вам могут понравиться концепции и идеи
исчисление.
Также вы могли бы быть в состоянии понять вероятные
последствия моделей немного лучше, чем у вас сейчас. Также вам могут понравиться концепции и идеи
исчисление.
Ну и что во вводной главе о числах?
Начнем с натуральных чисел \((1,2,3,…)\) и заметим, как выполняются операции вычитания, деления и принимая квадратный корень привел нас к расширению нашей системы счисления, включив в нее отрицательные числа, дроби (называемые рациональными числа) и комплексные числа. Мы также описываем десятичные разложения (описывающие «действительные числа») и изучаем в понятие счетности. Мы тоже бормочем о комплексных числах.
А в главе о функциях?
Мы начинаем с абстрактного определения функции (как набора пар аргумент-значение), а затем описываем
стандартные функции. Это те, которые получаются, начиная с функции тождества (значение = аргумент) и
экспоненциальные функции и различные операции над ними.
Операции, какие операции?
Это сложение, вычитание, умножение, деление, замена и инверсия.
Но что такое экспоненциальная функция и что такое подстановка и инверсия?
Вот ответы одним предложением: если вы хотите узнать больше, прочитайте главу!
Экспоненциальная функция загадочным образом определяется с помощью исчисления: это функция, являющаяся собственной производной, определено как имеющее значение 1 в качестве аргумента 0. Однако оказывается, что это то, что вы видели раньше. И это оказывается тесно связанным с синусоидальной функцией тригонометрии. 92 \) имеет обратную функцию квадратного корня.
В бессмертных словах отца Уильяма своему племяннику, написанных Льюисом Кэрроллом, который был математиком:
Я ответил на три вопроса и этого достаточно,
Сказал мудрец, не зазнавайся.

 11.2015, 21:20
11.2015, 21:20  11.2015, 21:26
11.2015, 21:26  11.2015, 21:28
11.2015, 21:28 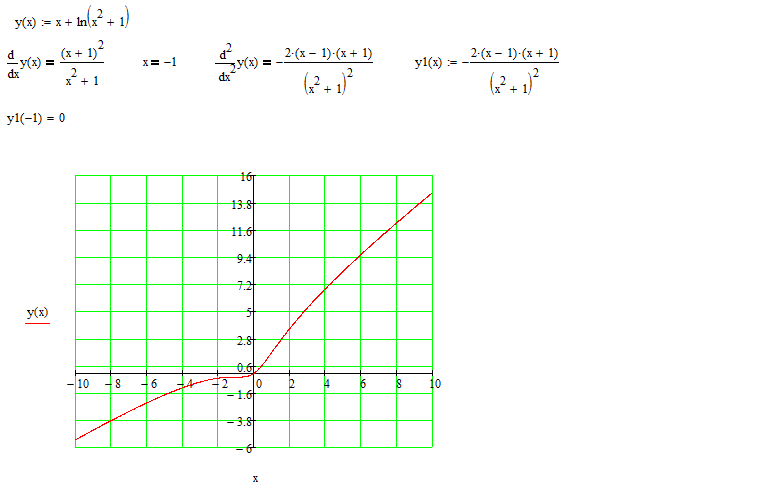 11.2015, 23:46
11.2015, 23:46 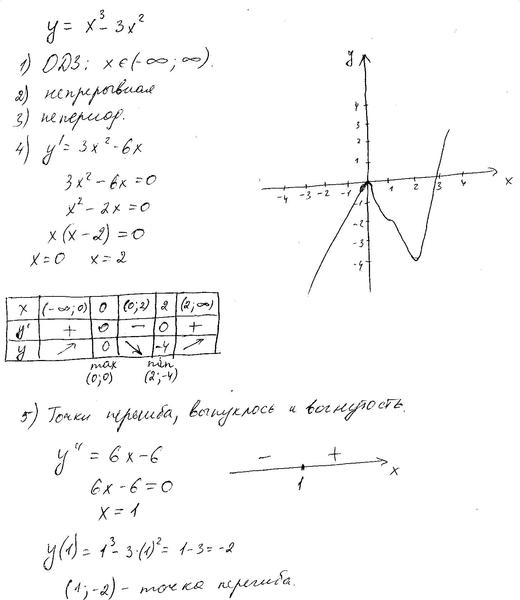

 11.2015, 11:38
11.2015, 11:38  11.2015, 11:54
11.2015, 11:54  11.2015, 12:24
11.2015, 12:24  11.2015, 13:14
11.2015, 13:14 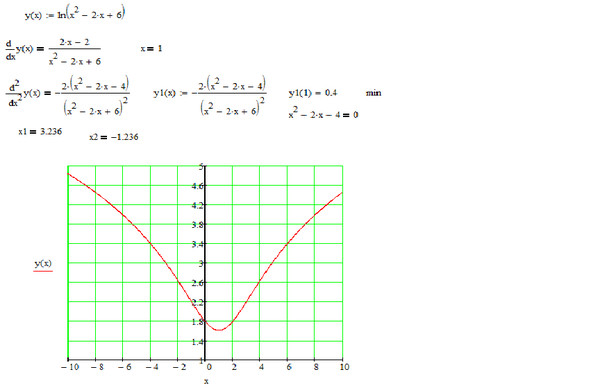 11.2015, 13:26
11.2015, 13:26  Разве она не будет чётной на ?
Разве она не будет чётной на ?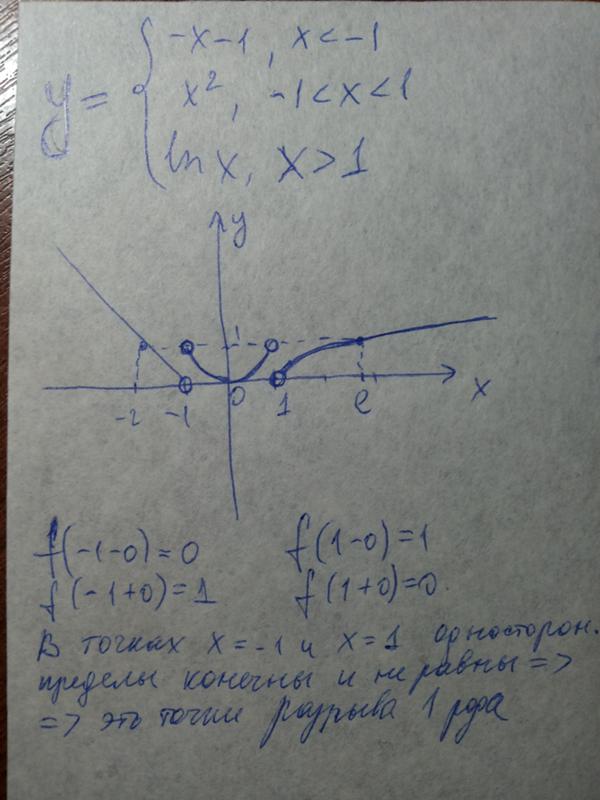
 М. Д. Андерсона Техасского университета, Хьюстон, Техас. Кафедра онкологии Нанкинского медицинского университета, Нанкин, Цзянсу, Китай.
М. Д. Андерсона Техасского университета, Хьюстон, Техас. Кафедра онкологии Нанкинского медицинского университета, Нанкин, Цзянсу, Китай.
 М. Д. Андерсона Техасского университета, Хьюстон, Техас. Департамент системной биологии, Онкологический центр им. М. Д. Андерсона Техасского университета, Хьюстон, Техас. Высшая школа биомедицинских наук Техасского университета, Хьюстон, Техас. Программа магистратуры по структурной и вычислительной биологии и молекулярной биофизике, Медицинский колледж Бэйлора, Хьюстон, Техас.
М. Д. Андерсона Техасского университета, Хьюстон, Техас. Департамент системной биологии, Онкологический центр им. М. Д. Андерсона Техасского университета, Хьюстон, Техас. Высшая школа биомедицинских наук Техасского университета, Хьюстон, Техас. Программа магистратуры по структурной и вычислительной биологии и молекулярной биофизике, Медицинский колледж Бэйлора, Хьюстон, Техас.  Ли Ю и др.
Нуклеиновые Кислоты Res. 2018 16 февраля; 46 (3): 1113-1123. дои: 10.1093/нар/gkx1311.
Нуклеиновые Кислоты Res. 2018.
PMID: 29325141
Бесплатная статья ЧВК.
Ли Ю и др.
Нуклеиновые Кислоты Res. 2018 16 февраля; 46 (3): 1113-1123. дои: 10.1093/нар/gkx1311.
Нуклеиновые Кислоты Res. 2018.
PMID: 29325141
Бесплатная статья ЧВК. 1016/j.oraloncology.2016.05.014.
Оральный онкол. 2016.
PMID: 27424183
Бесплатная статья ЧВК.
Обзор.
1016/j.oraloncology.2016.05.014.
Оральный онкол. 2016.
PMID: 27424183
Бесплатная статья ЧВК.
Обзор. Функц Интегр Геномикс. 2023 10 января; 23(1):33. дои: 10.1007/s10142-022-00947-4.
Функц Интегр Геномикс. 2023.
PMID: 36625940
Бесплатная статья ЧВК.
Обзор.
Функц Интегр Геномикс. 2023 10 января; 23(1):33. дои: 10.1007/s10142-022-00947-4.
Функц Интегр Геномикс. 2023.
PMID: 36625940
Бесплатная статья ЧВК.
Обзор. и соавт.
Фронт Жене. 2022 25 окт;13:932060. doi: 10.3389/fgene.2022.932060. Электронная коллекция 2022.
Фронт Жене. 2022.
PMID: 36386805
Бесплатная статья ЧВК.
и соавт.
Фронт Жене. 2022 25 окт;13:932060. doi: 10.3389/fgene.2022.932060. Электронная коллекция 2022.
Фронт Жене. 2022.
PMID: 36386805
Бесплатная статья ЧВК.