|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 3 из 5Следующая ⇒ Теория Согласно Шеннону, информативность сообщения характеризуется содержащейся в нем полезной информацией — той частью сообщения, которая снимает полностью или уменьшает неопределенность какой-либо ситуации. Неопределенность некоторого события — это количество возможных исходов данного события. Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных (равновозможных) событий. Тогда количество информации i, заключенное в этом сообщении, и число событий N связаны формулой: 2i = N (или i=log2N). Эта формула носит название формулы Хартли. В общем случае, если N – количество возможных событий, pi – вероятности отдельных событий, применяется формула Шеннона:
Энтропия (H) – мера неопределенности, выраженная в битах. Количество информации I и энтропия H характеризуют одну и ту же ситуацию, но с качественно противоположенных сторон. I – это количество информации, которое требуется для снятия неопределенности H. Когда неопределенность снята полностью, количество полученной информации I равно изначально существовавшей неопределенности H.
Примеры 1. Сколько бит информации несет сообщение о том, что из 256 одинаковых по размеру, но разноцветных шаров наугад выбрали красный шар? Решение: Выбор шара любого цвета, в том числе и красного – события равновероятностные, следовательно, i = log2256 = 8(бит). Ответ: сообщение о том, что из 256 одинаковых по размеру, но разноцветных шаров наугад выбрали красный шар, несет 8бит. 2. В гимназический класс школы были отобраны ученики из 128 претендентов. Какое количество учеников было отобрано, если сообщение о том, кто был отобран, содержит 140 битов информации? Решение: Определим, сколько бит содержит сообщение об одном ученике. Ответ: 20 человек было отобрано в гимназический класс. 3. В озере живут караси и окуни. Вероятность попадания на удочку карася – 0,75; окуня – 0,25. Сколько информации содержится в сообщении, что рыбак поймал рыбу? Решение: По формуле Шеннона
Ответ: в сообщении, что рыбак поймал рыбу содержится 0,8 бит информации. Задачи для самостоятельного решения 1. В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержится в сообщении о первом выпавшем номере (например, выпал номер 15)? 2. При угадывании целого числа в диапазоне от 1 до N было получено 6 бит информации. Чему равно N? 3. Сообщение о том, что из корзины с разноцветными шарами (все шары разного цвета) достали зеленый шар, содержит 4 бита информации. 4. Из папки NEW одновременно удалили 10 файлов. Сообщение о названиях удаленных файлов содержит 80 бит информации. Сколько файлов было всего в папке? 5. В доме 4 подъезда, в каждом из которых 16 этажей. Какое количество информации содержится в сообщении о том, что Иван живет на пятом этаже в третьем подъезде? 6. Система может находиться в трех различных состояниях с вероятностями: в первом (худшем) состоянии с вероятностью 0,1; во втором – 0,4; в третьем (лучшем) – 0,5. Чему равно количество информации о произвольном состоянии системы?
⇐ Предыдущая12345Следующая ⇒ Читайте также: Где возникла философия и почему? Относительная высота сжатой зоны бетона Сущность проекции Гаусса-Крюгера и использование ее в геодезии Тарифы на перевозку пассажиров |
||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 1117; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов… Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров… Интересное: Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом… Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным. Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 5Следующая ⇒ Теория Звук может иметь различные уровни громкости. Частота дискретизации — количество измерений уровня входного сигнала в единицу времени (за 1 секунду). Размер цифрового моноаудиофайла вычисляется по формуле А=Д*Т*i, где Д- частота дискретизации; Т- время звучания или записи звука; i — разрядность регистра (глубина звука). Для стереоаудиофайла размер вычисляется по формуле А=2*Д*Т*i
Примеры 1. Подсчитать, сколько места будет занимать одна минута цифрового звука на жестком диске или любом другом цифровом носителе, записанного с частотой 44.1 кГц и разрядностью 16 бит. Решение: Если записывают стереосигнал А = 2*Д*Т*i = 44100*120*16 = 84672000бит = = 10584000байт = 10335,9375Кб = 10,094Мб. Если записывают моносигнал А = 5Мб. Ответ: 10 Мб, 5Мб 2. Объем свободной памяти на диске — 0,01 Гб, разрядность звуковой платы — 16. Какова длительность звучания цифрового аудиофайла, записанного с частотой дискретизации 44100 Гц. Решение: А = Д * Т * i Т =А / Д / i Т = 10737418,24/44100/2 = 121,74(сек) = 2,03(мин) Ответ: 2,03 мин. Задачи для самостоятельного решения 1. Определить размер (в байтах) цифрового аудиофайла, время звучания которого составляет 10 секунд при частоте дискретизации 22,05 кГц и разрешении 8 бит. Файл сжатию не подвержен. 2. В распоряжении пользователя имеется память объемом 2,6 Мб. Необходимо записать цифровой аудиофайл с длительностью звучания 1 минута. Какой должна быть частота дискретизации и разрядность? 3. Объем свободной памяти на диске – 0,01 Гб, разрядность звуковой платы – 16. Какова длительность звучания цифрового аудиофайла, записанного с частотой дискретизации 44100 Гц? 4. Одна минута записи цифрового аудиофайла занимает на диске 1,3 Мб, разрядность звуковой платы – 8. С какой частотой записан звук?
Содержательный подход к измерению информации Теория Согласно Шеннону, информативность сообщения характеризуется содержащейся в нем полезной информацией — той частью сообщения, которая снимает полностью или уменьшает неопределенность какой-либо ситуации. Неопределенность некоторого события — это количество возможных исходов данного события. Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных (равновозможных) событий. Тогда количество информации i, заключенное в этом сообщении, и число событий N связаны формулой: 2i = N (или i=log2N). Эта формула носит название формулы Хартли. В общем случае, если N – количество возможных событий, pi – вероятности отдельных событий, применяется формула Шеннона:
Энтропия (H) – мера неопределенности, выраженная в битах. Количество информации I и энтропия H характеризуют одну и ту же ситуацию, но с качественно противоположенных сторон. I – это количество информации, которое требуется для снятия неопределенности H. Когда неопределенность снята полностью, количество полученной информации I равно изначально существовавшей неопределенности H.
Примеры 1. Сколько бит информации несет сообщение о том, что из 256 одинаковых по размеру, но разноцветных шаров наугад выбрали красный шар? Решение: Выбор шара любого цвета, в том числе и красного – события равновероятностные, следовательно, i = log2256 = 8(бит). Ответ: сообщение о том, что из 256 одинаковых по размеру, но разноцветных шаров наугад выбрали красный шар, несет 8бит. 2. В гимназический класс школы были отобраны ученики из 128 претендентов. Какое количество учеников было отобрано, если сообщение о том, кто был отобран, содержит 140 битов информации? Решение: Определим, сколько бит содержит сообщение об одном ученике. 2i = N, 2i = 128, i = 7(бит). Т.о. было отобрано 140 / 7 = 20 человек. Ответ: 20 человек было отобрано в гимназический класс. 3. В озере живут караси и окуни. Вероятность попадания на удочку карася – 0,75; окуня – 0,25. Сколько информации содержится в сообщении, что рыбак поймал рыбу? Решение: По формуле Шеннона
Ответ: в сообщении, что рыбак поймал рыбу содержится 0,8 бит информации. Задачи для самостоятельного решения 1. В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержится в сообщении о первом выпавшем номере (например, выпал номер 15)? 2. При угадывании целого числа в диапазоне от 1 до N было получено 6 бит информации. Чему равно N? 3. Сообщение о том, что из корзины с разноцветными шарами (все шары разного цвета) достали зеленый шар, содержит 4 бита информации. Сколько шаров было в корзине? 4. Из папки NEW одновременно удалили 10 файлов. Сообщение о названиях удаленных файлов содержит 80 бит информации. Сколько файлов было всего в папке? 5. В доме 4 подъезда, в каждом из которых 16 этажей. Какое количество информации содержится в сообщении о том, что Иван живет на пятом этаже в третьем подъезде? 6. Система может находиться в трех различных состояниях с вероятностями: в первом (худшем) состоянии с вероятностью 0,1; во втором – 0,4; в третьем (лучшем) – 0,5. Чему равно количество информации о произвольном состоянии системы?
⇐ Предыдущая12345Следующая ⇒ Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни. Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… |
Математическая задача: Цветные шарики — вопрос № 62254, алгебра, уравнение
В мешке лежат цветные шарики. Одна треть из них синие, одна шестая зеленые, пять двенадцатых желтые, а остальные десять шаров красные. Сколько желтых шаров в мешке?
Правильный ответ:
Нашли ошибку или неточность? Не стесняйтесь
пишите нам. Благодарю вас!
Советы для связанных онлайн-калькуляторов
Нужна помощь в вычислении суммы, упрощении или умножении дробей? Попробуйте наш калькулятор дробей.
У вас есть линейное уравнение или система уравнений и вы ищете ее решение? Или у вас есть квадратное уравнение?
You need to know the following knowledge to solve this word math problem:
- algebra
- equation
- system of equations
- arithmetic
- multiplication
- numbers
- fractions
Оценка словесной задачи:
- тренировка для 13-летних
- тренировка для 14-летних
- У Буси есть
У Буси есть сумка с двадцатью мячами. Желтых шаров в два раза больше, чем синих, но желтые шары составляют лишь треть красных. Зеленые шары имеют тот же номер, что и синие шары. Сколько шариков каждого цвета?
Желтых шаров в два раза больше, чем синих, но желтые шары составляют лишь треть красных. Зеленые шары имеют тот же номер, что и синие шары. Сколько шариков каждого цвета? - 20 шаров
20 цветных шаров в мешке: Четыре красных Семь зеленых Девять желтых Какова вероятность того, что выпадет желтый шар? - Пули вероятности
В мешочке шесть красных, пять зеленых, голубых и 11 желтых шаров. Какова вероятность того, что мы вытащим зеленую пулю? - Три в пропорции
1/8 шаров в мешке красные, 5/8 синие, а остальные зеленые. Найдите соотношение красных, синих и зеленых шаров. - Мешок с шариками
В мешке, полном шариков, 1/4 этих шариков зеленые, 1/8 — синие, 1/2 — желтые, а остальные 26 — белые. Сколько шариков синего цвета? - Вероятность 29163
В шляпе десять красных, шесть синих и восемь зеленых шаров. Какова вероятность того, что случайно выбранный шар окажется синим или красным? - Вероятность 3835
У нас в мешке четыре красных, три синих, шесть желтых и два черных шара. Найдите вероятность того, что вытащите синий или красный шар.
Найдите вероятность того, что вытащите синий или красный шар. - Прозрачный 5345
Глиняные шарики и несколько прозрачных стеклянных шариков высыпались из сумки Питера. Раскрась шарики один за другим, если знаешь, что 1/6 были красными, 3/8 синими, 7/24 зелеными и 1/12 желтыми. Сколько у него было очков? - Две трети 4450
У Марека есть мячи трех цветов. Две трети шаров зеленые, 2/7 синие и один шар желтый. Сколько мячей у Марека? - Композиции 68764
У нас есть два одинаковых синих шара и два одинаковых красных шара. Располагаем их в ряд всеми способами. Сколько существует различных аранжировок? - Красные шары
В мешочке три красных, 12 синих и восемь зеленых шаров. Сколько красных шаров мы должны положить в мешок, если мы хотим, чтобы вероятность вытащить красные шары была 20%? - Бар
Половина бара зеленая, треть желтая, а оставшиеся 40 см красные. Как долго длится бар? - Флаг
Флаг должен состоять из 3 полос разного цвета — доступные цвета: белый, красный, синий, зеленый и желтый. Укажите: A) количество всех флажков B) количество флажков с синей полосой C) количество флажков с синей полосой посередине D) количество флажков
Укажите: A) количество всех флажков B) количество флажков с синей полосой C) количество флажков с синей полосой посередине D) количество флажков - Одинаковые 63414
У Еничека 4 одинаковых желтых кубика и 3 одинаковых синих игральная кость. Сколько разноцветных змей может их сделать? - Мячи 8358
У нас в мешке пять красных, четыре синих и семь белых мячей. По крайней мере, сколько шаров нам нужно вытащить, чтобы на столе оказался хотя бы один белый шар? - Шарики 3
У Пейсли есть сумка с 16 зелеными, оранжевыми и желтыми шариками. Если есть восемь зеленых шариков, сколько шариков должно быть желтым, чтобы P(желтый) = 1/4? - Всего 80458
Башня из красных кубиков 13/72, синих 25/48, зеленых 516. Сколько всего кубиков?
биномиальное распределение — Вероятность получения не менее 5 шаров одного цвета из равномерно распределенного набора размера 126 с красными, синими и белыми шарами
спросил
Изменено 7 лет, 5 месяцев назад
Просмотрено 2к раз
$\begingroup$
Я пытаюсь решить следующую задачу:
- У меня есть равномерно распределенный набор, состоящий из красных, синих и белых шаров.
 Всего в этом наборе 126 шаров, то есть по 42 (${126 \over 3}$) шаров каждого цвета.
Всего в этом наборе 126 шаров, то есть по 42 (${126 \over 3}$) шаров каждого цвета. - Я вытащу 7 шаров.
Какова вероятность того, что я получу хотя бы 5 шаров одного цвета?
Я пытаюсь сделать следующее:
Подсчитать вероятность того, что я вытащу 5, 6 и 7 шаров каждого цвета, а затем сложу их вместе. Что-то вроде этого: 9{-7} $$
Верно ли это? Моя вероятность немного заржавела.
Моя актуальная проблема связана с вычислением вероятности столкновения многих хешей с использованием открытой адресации, если кто-то в этом заинтересован.
Заранее спасибо.
- вероятность
- биномиальное распределение
$\endgroup$
$\begingroup$
Я интерпретирую проблему как то, что мы рисуем без замены . Представьте, что все мячи имеют идентификационные номера.
Существует $\binom{126}{7}$ равновероятных способов вытянуть «руку» из шаров по $7$.

 Все правила по сольфеджио
Все правила по сольфеджио

 2i = N, 2i = 128, i = 7(бит). Т.о. было отобрано 140 / 7 = 20 человек.
2i = N, 2i = 128, i = 7(бит). Т.о. было отобрано 140 / 7 = 20 человек. Сколько шаров было в корзине?
Сколько шаров было в корзине?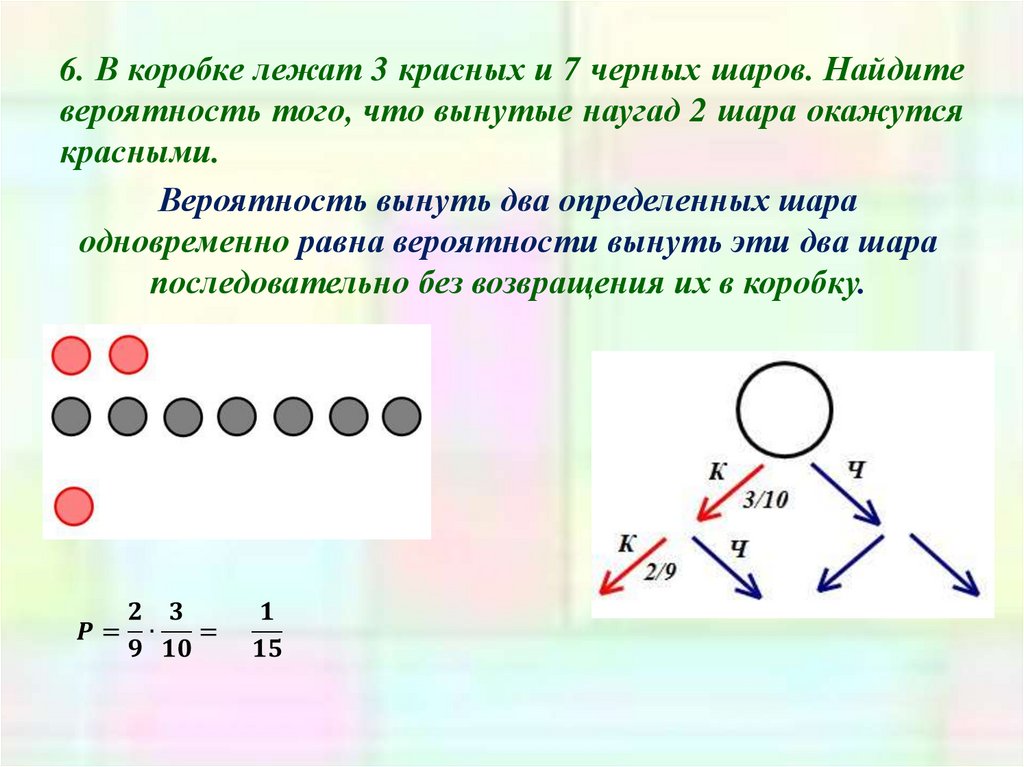 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.003 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.003 с.)
 Количество различных уровней рассчитывается по формуле N = 2i, где i — глубина звука.
Количество различных уровней рассчитывается по формуле N = 2i, где i — глубина звука.



 ..
.. Желтых шаров в два раза больше, чем синих, но желтые шары составляют лишь треть красных. Зеленые шары имеют тот же номер, что и синие шары. Сколько шариков каждого цвета?
Желтых шаров в два раза больше, чем синих, но желтые шары составляют лишь треть красных. Зеленые шары имеют тот же номер, что и синие шары. Сколько шариков каждого цвета? Найдите вероятность того, что вытащите синий или красный шар.
Найдите вероятность того, что вытащите синий или красный шар. Укажите: A) количество всех флажков B) количество флажков с синей полосой C) количество флажков с синей полосой посередине D) количество флажков
Укажите: A) количество всех флажков B) количество флажков с синей полосой C) количество флажков с синей полосой посередине D) количество флажков Всего в этом наборе 126 шаров, то есть по 42 (${126 \over 3}$) шаров каждого цвета.
Всего в этом наборе 126 шаров, то есть по 42 (${126 \over 3}$) шаров каждого цвета.