Задачи на тему сложение и вычитание векторов – Задачи. Сложение векторов — PhysBook

Задачи (1) на сложение и вычитание векторов (9 кл.)

Задачи (1) на сложение и вычитание векторов (9 кл.)

Вопрос 1. Дан вектор . Номер вектора :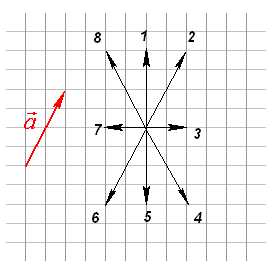 

Вопрос 2. Номер вектора ?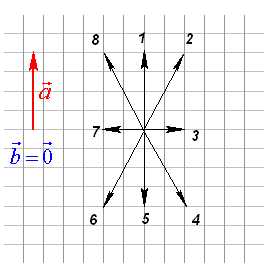 

Вопрос 3. Номер вектора ?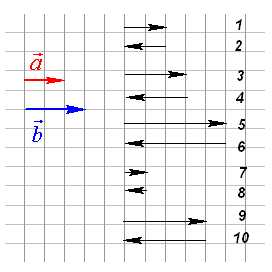 

Вопрос 4. Номер вектора ?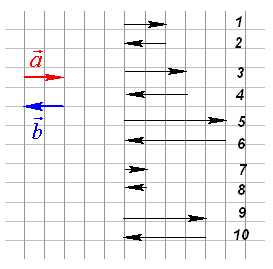 

Вопрос 5. Номер вектора ? 

Вопрос 6. Номер вектора ? 

Вопрос 7. Номер вектора ? 

Вопрос 8. Номер вектора ?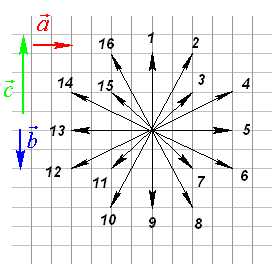 

Вопрос 9. Номер вектора ?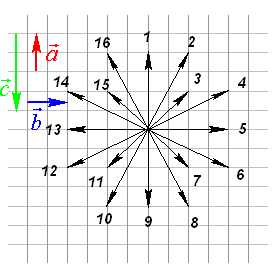 

Вопрос 10. Номер вектора ? 

infourok.ru

Разработка урока по теме «Вычитание векторов. Решение задач».

Г- 9 класс Урок № 5

Тема: «Вычитание векторов»

Цели урока:

1. Дидактическая: ввести понятие разности двух векторов, рассмотреть теорему о разности векторов; сформировать умение находить разность двух векторов двумя способами.

2. Развивающая: развивать воображение – репродуктивное, творческое, образное; абстрактное и логическое мышление, умение обобщать.

3. Воспитательная: нравственное воздействие, воспитание культуры умственного труда, культуры общения.

Обучающиеся должны:

Знать, какой вектор является разностью двух векторов, теорему о разности векторов.

Уметь строить разность двух векторов двумя способами, применять эти знания при решении задач.

Оборудование: проектор, презентация «Вектора».

Ход урока.

1. Организационный момент.

Сообщение темы и целей урока.

2. Актуализация знаний и умений обучающихся.

   1. 1. 1. Проверка выполнения домашнего задания. Разбор нерешенных заданий.

         2. Проверка пройденного материала.

Тестирование:

1. Как называются векторы, имеющие равные модули и противоположно направленные?

А) противоположные

Б) противоположно направленные

В) равные

2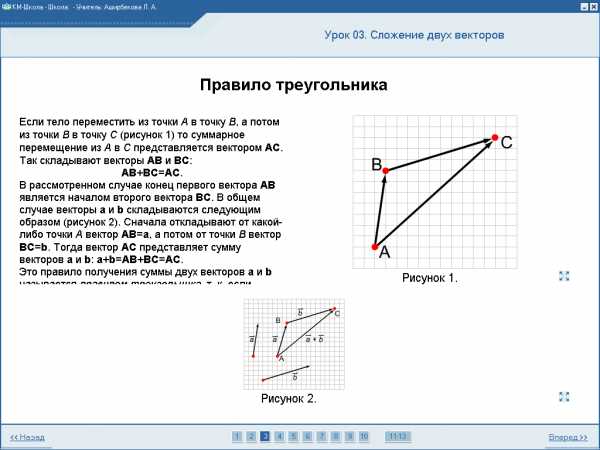. Тело переместили из точки А в точку В, а потом из точки В в точку С. Какой вектор представляет суммарное перемещение тела?

А)

Б)

В)

3. Закончите предложение:

Суммой двух векторов называется вектор, построенный по правилу…. (треугольника)

4. Вставьте пропущенное слово:

Чтобы сложить два неколлинеарных вектора и, нужно отложить от произвольной точки О векторы = и = и построить …. ОАСВ, тогда =+

(параллелограмм)

5. Изображенный на рисунке способ построения суммы нескольких векторов называется правилом…

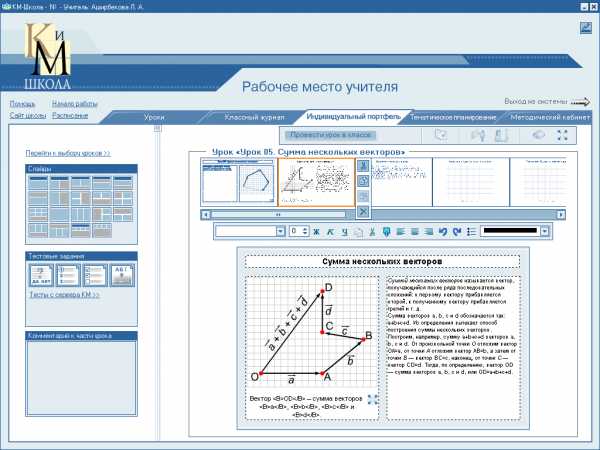
(многоугольника)

III. Объяснение нового материала:

План объяснения:

1. Разность векторов

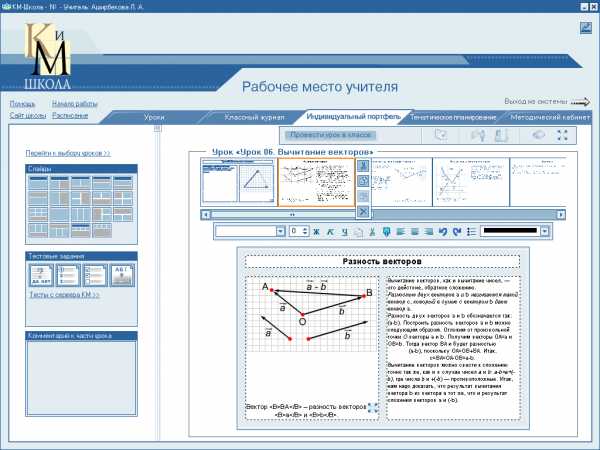
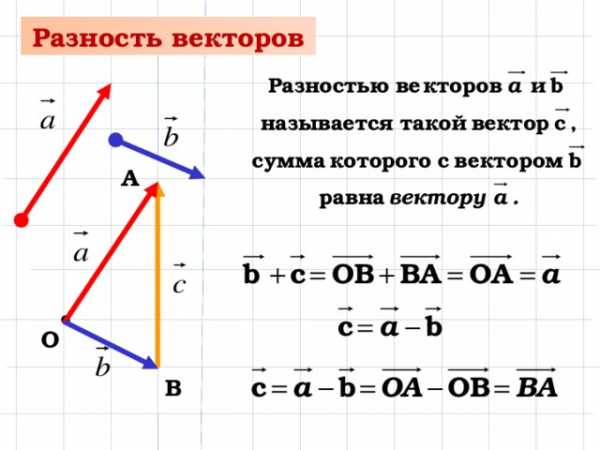
Вычитание векторов, как и вычитание чисел, — это действие, обратное сложению. Разность двух векторов и называется такой вектор , который в сумме с вектором дает вектор . Разность векторов и обозначается так: — . Построить разность векторов и можно следующим образом. Отложим от произвольной точки О векторы и . Получим векторы = и =. Тогда вектор и будет разностью — , поскольку

=+. Итак, == — = — .

Вычитание векторов можно свести к сложению точно так же, как и в случае чисел а и b:

а — b = а + (- b), где числа b и + (- b) — противоположные.

Итак, нам надо доказать, что результат вычитания вектора из вектора тот же, что и результат сложения векторов а + (- b).

2. Теорема о разности двух векторов.

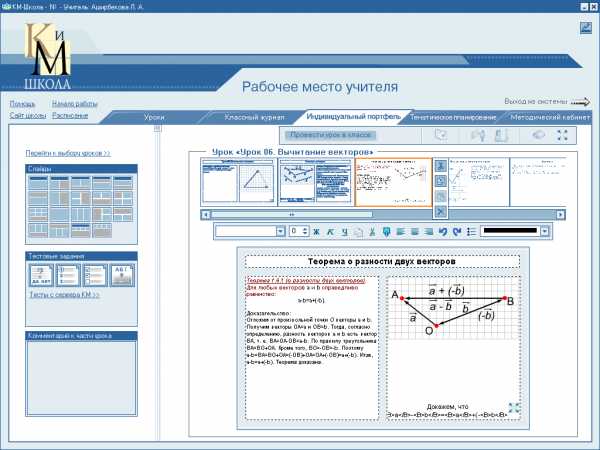
Теорема (о разности векторов)

Для любых векторов и справедливо равенство — = + (- ).

Доказательство:

Отложим от произвольной точки О векторы и . Получим векторы = и =. Тогда, согласно определению, разность векторов и есть вектор , т.е. = — = — . По правилу треугольника = + . Кроме того, = — = -. Поэтому — = = + = (-) + =+(-)=+(-). Теорема доказана.

3. Построение разности векторов.

Доказанная теорема подсказывает еще один способ построения разности векторов и .

Отложим от произвольной точки О вектор = , затем от точки А отложим вектор = -. Тогда по теореме о разности двух векторов — = + (-), поэтому — = + = . Итак, мы построили разность векторов и .

IV. Закрепление полученных знаний.

Тестирование.

1. Какой вектор называется разностью векторов и ?

А) Разностью двух векторов и называется такой вектор , построенный по правилу треугольника.

Б) Разностью двух векторов и называется такой вектор , который получается после ряда последовательных сложений

В) Разностью двух векторов и называется такой вектор , который в сумме с вектором дает вектор

2. Какой вектор, изображенный на рисунке, является разностью векторов и ?

А)

Б)

В)

3. №767. Дан треугольник АВС. Выразите векторы = и = вектор .

а) —

б) —

в) +

4. №762. Сторона равностороннего треугольника АВС равна а .Модуль  —  = а

да нет

V. Подведение итогов.

Выводы по уроку:

1. Разностью двух векторов и называется такой вектор , который в сумме с вектором дает вектор .

2. Теорема ( о разности двух векторов): Для любых векторов и справедливо равенство:

— = + (-).

VI. Домашнее задание: прочитать п.82, решить №№754, 756, 767.

infourok.ru

Вычитание векторов — Математика — 8 класс

Разработка  предназначена для введения понятия разности векторов и способов построения разности векторов. Содержит задачи на нахождение вектора суммы и вектора разности векторов и их длин. Презентация может быть использована при объяснении нового материала по геометрии в 8 классе, либо в 9 классе (учебник Геометрия 7-9, автор Л.С.Атанасян)

Просмотр содержимого документа
«Вычитание векторов»

Вычитание векторов

К учебнику Геометрия 7-9,

автор Л.С.Атанасян и др.

Автор: Софронова Наталия Андреевна,

учитель математики высшей категории

МОУ «Упшинская основная общеобразовательная школа»

Оршанского района Республики Марий Эл

Разность векторов

А

О

В

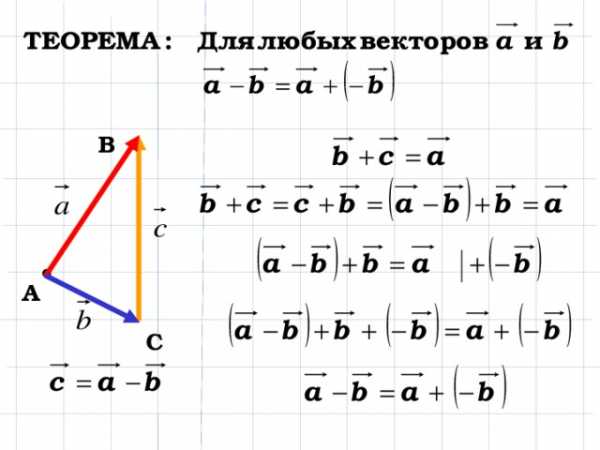
Построения

разности

векторов

А

О

В

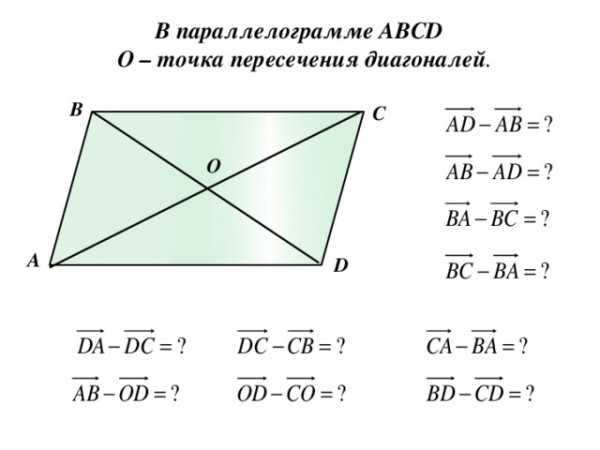
В параллелограмме АВСD

О – точка пересечения диагоналей .

В

С

О

А

D

Противоположные векторы

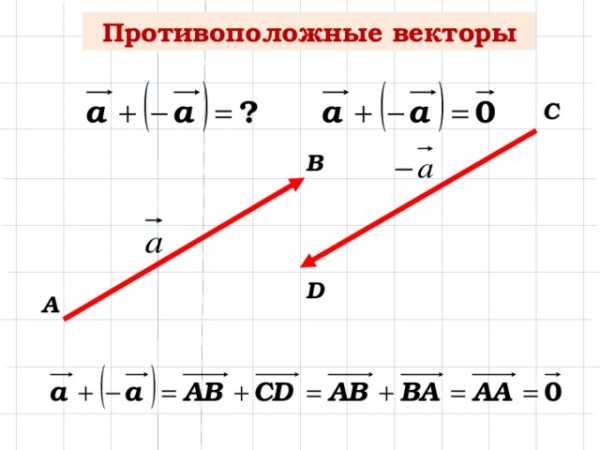
Противоположные векторы

С

В

D

А

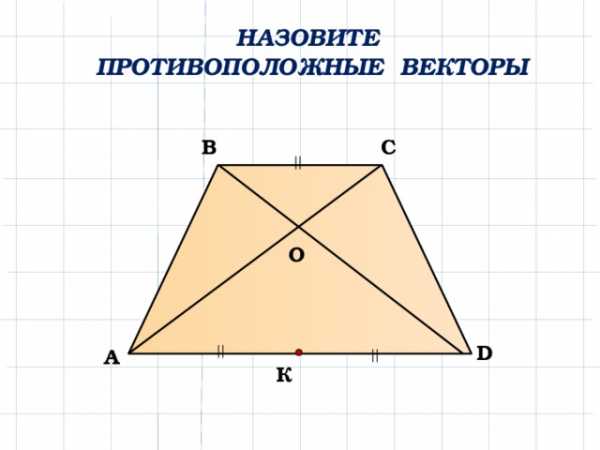
НАЗОВИТЕ

ПРОТИВОПОЛОЖНЫЕ ВЕКТОРЫ

С

В

O

О

D

А

К

B

А

С

Построения

разности

векторов

С

В

А

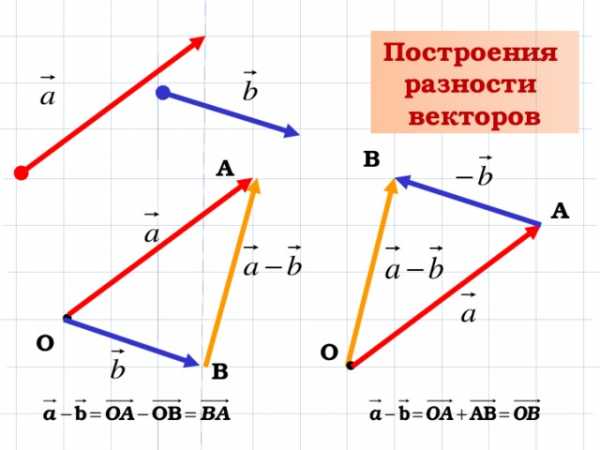
Построения

разности

векторов

В

А

А

О

О

В

Q

U

W

D

I

E

F

C

R

O

E 1

V

G

P

T

R 1

P 1

B

H

Y

A

N 1

A 1

T 1

N

S

J

L

K 1

S 1

Y 1

K

M

Z

D 1

L 1

U 1

Q 1

X

Z 1

B 1

F 1

M 1

G 1

X 1

O 1

C 1

H 1

V 1

ВЫПОЛНИТЕ СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ

Задача 1.

В равнобедренном треугольнике АВС точка D — середина основания АС.

В

С

А

D

РЕШЕНИЕ

8

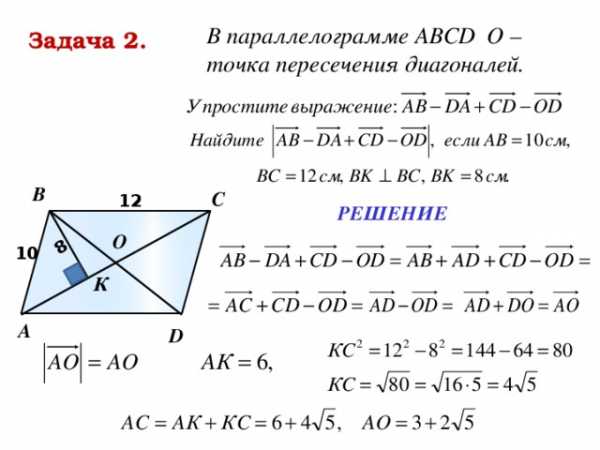
В параллелограмме АВСD О –

точка пересечения диагоналей.

Задача 2.

В

С

12

РЕШЕНИЕ

О

10

К

А

D

30 0

Задача 3.

В равнобедренной трапеции АВСD ∠А=30 0 , меньшее основание равно боковой стороне, а высота, опущенная из вершины тупого угла В на основание АD, равна 4 см.

С

В

РЕШЕНИЕ

4

D

А

К

Н

multiurok.ru

Урок геометрии в 9 классе «Сложение и вычитание векторов»

«Сложение и вычитание векторов»

Цель урока: 1) закрепление теоретического материала;

2) совершенствование навыков решения задач по данной теме.

Ход урока:

. Орг. момент.

. Актуализация знаний учащихся:

1) геометрический диктант

а) Направленный отрезок, для которого указано, какая из его граничных точек считается началом, а какая концом называется … (вектором).

б) Длиной или модулем вектора АВ называется … (длина отрезка АВ).

в) Если вектора лежат на одной прямой или на параллельных прямых, то они называются … (коллинеарными).

г) Одинаково направленные вектора называются … (сонаправленные).

д) Вектора, имеющие противоположное направление, называются … (противоположно направленные).

е) Если векторы сонаправлены и длины их равны, то они называются … (равными).

ж) От любой точки можно отложить вектор … (равный данному и притом только один).

Самопроверка: ответы на доске, ученики оценивают сами себя.

Ошибки Отметка

0 5

1 4

2 – 3 3

более 3 2

2) Устно: на доске параллелограмм АВСD.

. Закрепление изученных знаний:

1) Устно: правила сложения и вычитания векторов.

а) правило треугольника;

б) правило параллелограмма;

в) правило вычитания;

г) теорема о разности векторов.

2) по рисунку параллелограмма АВСD найти суммы и разности векторов.

Учащиеся записывают решение в тетрадях.

3) Задание на доске.

4) Работа с учебником

№764(а) (работают на местах, отвечают с места)

5) Физкультминутка.

а) глаза закрыть (1 – 2 мин), открыть; сильно зажмурить, широко открыть; зажмурить открыть.

б) водить глазами по стрелкам:

6) Работа с учебником.

№768 (по готовому чертежу, чертеж на доске)

Наводящие вопросы:

. Самостоятельная работа.

1 вариант

2 вариант

V. Подведение итогов урока. Д/з: №770, №772.

infourok.ru

Урок геометрии для 9 класса по теме «Сложение и вычитание векторов»

Класс: 9 класс

Цели урока: ввести понятие вектора, равного сумме двух и более векторов, разности двух векторов; сформировать умение выполнять основные действия над векторами: складывать векторы по правилу треугольника и параллелограмма и вычитать векторы.

Этапы урока:

Актуализация опорного материала.

Опрос: решение задач по готовым чертежам.

Изучение нового материала.

Закрепление изученного материала.

Первичный контроль и коррекция.

Постановка домашнего задания.

Использование интерактивного оборудования: на данном уроке используется интерактивная доска, а также компьютер с подключённым выходом в сеть Интернет, позволяющими делать урок более наглядным и динамичным.

На первом этапе обозначена тема урока и поставлены вопросы на повторение, которые помогут учащимся повторить пройденный материал и подготовить к усвоению нового. На этом же слайде методом «перетаскивания» учитель открывает вторую часть, содержащую задачу. Проверяются умения учащихся определять равные векторы, коллинеарные векторы, за счёт чего экономится время на уроке, повышается наглядность, следовательно, усвоение учебного материала.

При изучении нового материала используется метод «копирования», который ещё раз демонстрирует учащимся понятие равных векторов, являющееся основным понятие изучаемой на уроке темы. Используемые на слайдах гиперссылки, делают урок мобильным. Если класс подготовленный, то можно предложить учащимся самостоятельно доказать изучаемые теоремы, если класс более слабый, то показать доказательство на доске и попросить прокомментировать его одного или двух учеников.

На этапе первичного закрепления нового материала учащимся получают тесты в печатном виде. Учитель на доске комментирует раздаточный материал, обращая внимание учащихся на более важные и значимые моменты. Сам тест является интерактивным, что позволяет проверить результаты здесь же на уроке.

Вся информация с урока остаётся на доске и может быть использована на следующем уроке.

Ход урока:

Этапы урока	Учитель	Ученики
Актуализация опорного материала Цели: (повторение того, что надо к изучению нового материала: понятий, формулировок, правил, формул, проверка домашнего задания)	Слайд 1. Разделен на две части: Тема урока. Сформулированы вопросы на повторение.	Отвечая на вопросы, вспоминают понятие вектора, нулевого вектора, длины (модуля) вектора, дают определение коллинеарных векторов.
Опрос Цели: (контроль за усвоением предыдущей изученной темы)	Вторая часть слайда содержит задачу. Докажите, что векторы AD и ВС равны?	Один ученик (слабый) у доски на параллелограмме показывает с помощью инструмента перо (маркер) равные и противоположно направленные вектора. Остальные учащиеся комментируют с места. Доказывает (сильный) ученик. Демонстрирует наложение вектора на равный ему вектор (слабый) ученик.
Изучение нового материала Цели: (основная обучающая цель)	Слайд 2. На примере движения от одного пункта к другому учитель вводит понятие суму векторов. Слайд 3. «Конструктор сложения векторов». Учитель с помощью инструмента копирования и вставки показывает сложение векторов и доказывает, что получившийся вектор не зависит от выбора точки. Слайд 4. «Конструктор законов сложения векторов». Учитель формулирует законы сложения векторов и доказывает их. Переход на доказательство можно оформить по гиперссылке для работы в более подготовленном классе Слайд 5. «Конструктор вычитания векторов»	Один ученик показывает на рисунке направление движения с помощью инструмента стрелка. Учащиеся делают в тетради необходимые записи и новые обозначения. Учащиеся выполняют чертежи в тетрадях. Если класс подготовленный, можно вызвать одного ученика к доске для доказательства свойств.
Первичное закрепление Цели: (отработка до автоматизма минимальных навыков, базовых знаний, может быть выполнение заданий по образцу)	Слайд 3 или 5. «Конструктор»	Для слабого класса в режиме «Конструктор» два – три ученика показывают сложение векторов про правилу треугольника и параллелограмма. Остальные учащиеся выполняют поэтапное построение в тетрадях.
Первичный контроль и коррекция Цели: (контроль за усвоением знаний, умений и навыков, самоконтроль)	Слайд 5. «Проверь себя». По гиперссылке учитель выходит на сайт «ЦОР» на вариант первичного закрепления нового материала.	Учащиеся обсуждают предложенные задания и отвечают на вопросы. После обсуждений заполняют тест на ИД и получают результат.
Определение домашнего задания Цели: (нацеливание на закрепление изученного материала)	Постановка домашнего задания. Индивидуальное домашнее задание: получение раздаточного материала.

Используемая литература:

Геометрия, 7 – 9: Учеб. для общеобразоват. учреждений/Л.С. Атанасян, В.Ф. Бутузов и др. – М.: Просвещение, 2003

Изучение геометрии в 7 – 9 классах: Метод. рекомендации к учеб.: Кн. для учителя / Л.С. Атанасян, В.Ф. Бутузов и др. – М.: Просвещение, 1999

Геометрия. Задачи на готовых чертежах для VII – IX классов. / Э.Н. Балаян. – Ростов н/Д: Феникс, 2006

Тесты для самостоятельной работы: http://files.school-collection.edu.ru/dlrstore/aa9a8892-0e44-4ae5-b192-77d9bbbb6e17/%5BG79_9-09-02%5D_%5BQS_v1%5D.html

Раздаточный материал

Сложение и вычитание векторов

У

В

 

кажите номер того равенства, которое является верным:

А

С

 

 

Может ли модуль суммы двух векторов быть равным разности модулей этих векторов?

У

Q

 

кажите номер того равенства, которое является верным:

P

R

 

 

Назовите вектор, который является разностью векторов и ?

Запишите векторную сумму в виде одного вектора с началом и концом в каких-то из указанных точек.

 

Ответы:

№ 1	№ 2	№ 3	№ 4	№ 5
3	да	3

 

xn--j1ahfl.xn--p1ai

8 класс. Геометрия. Векторы. Применение векторов к решению задач. — Сложение и вычитание векторов.

Комментарии преподавателя

Сло­же­ние и вы­чи­та­ние век­то­ров

На преды­ду­щем уроке мы опре­де­ли­ли по­ня­тие век­то­ра, ска­за­ли, какие век­то­ры на­зы­ва­ют­ся рав­ны­ми, кол­ли­не­ар­ны­ми, со­на­прав­лен­ны­ми и про­ти­во­на­прав­лен­ны­ми.

Те­перь пусть за­да­но два век­то­ра – век­то­ра  и . Най­дем сумму этих двух век­то­ров . Для этого от­ло­жим из неко­то­рой точки А век­тор . Из точки В от­ло­жим век­тор . Тогда век­тор  на­зы­ва­ют сум­мой за­дан­ных век­то­ров:  (см. Рис. 1).

Рис. 1

Дан­ное опре­де­ле­ние можно объ­яс­нить так: пусть был задан груз, и сна­ча­ла на него по­дей­ство­ва­ла сила  – он пе­ре­ме­стил­ся из точки А в точку В, после этого по­дей­ство­ва­ла сила  – груз пе­ре­ме­стил­ся из точки В в точку С. Но в ре­зуль­та­те дей­ствия двух этих сил груз пе­ре­ме­стил­ся из точки А в точку С.

Таким об­ра­зом, мы по­лу­чи­ли опре­де­ле­ние суммы двух век­то­ров – пра­ви­ло тре­уголь­ни­ка.

Пра­ви­ло тре­уголь­ни­ка

Для того чтобы по­лу­чить сумму двух век­то­ров, нужно из про­из­воль­ной точки от­ло­жить пер­вый век­тор, из конца по­лу­чен­но­го век­то­ра от­ло­жить вто­рой век­тор, и по­стро­ить век­тор, со­еди­ня­ю­щий на­ча­ло пер­во­го с кон­цом вто­ро­го – это и будет сумма двух век­то­ров.

Можно про­ве­сти ана­ло­гию с чис­ла­ми. Мы ввели по­ня­тие числа, на­учи­лись скла­ды­вать числа, опре­де­ли­ли за­ко­ны сло­же­ния и так далее. Те­перь мы ввели по­ня­тие век­то­ра, на­учи­лись на­хо­дить рав­ные век­то­ра, скла­ды­вать век­то­ра. Те­перь нужно опре­де­лить за­ко­ны сло­же­ния.

За­ко­ны сло­же­ния век­то­ров

Для любых век­то­ров ,  и  спра­вед­ли­вы сле­ду­ю­щие ра­вен­ства:

 – пе­ре­ме­сти­тель­ный закон.

До­ка­за­тель­ство: от­ло­жим из точки сна­ча­ла век­тор , по­лу­ча­ем точку В, из нее от­кла­ды­ва­ем век­тор , по­лу­ча­ем точку С и век­тор .

Те­перь от­ло­жим из точки А сна­ча­ла век­тор  по­лу­чим точку В, из нее от­ло­жим век­тор, по­лу­чим точку С и век­тор .

Чтобы до­ка­зать ра­вен­ство по­лу­чен­ных век­то­ров, вы­пол­ним оба по­стро­е­ния из одной точки и по­лу­чим таким об­ра­зом пра­ви­ло па­рал­ле­ло­грам­ма (см. Рис. 2).

Рис. 2

От­кла­ды­ва­ем из точки А век­тор  и век­тор . Из точки В от­кла­ды­ва­ем век­тор , век­то­ра  и  равны, а зна­чит, сто­ро­ны ВС и АВ1 че­ты­рех­уголь­ни­ка АВСВ1 па­рал­лель­ны. Ана­ло­гич­но па­рал­лель­ны и сто­ро­ны АВ и В1С, таким об­ра­зом, мы по­лу­чи­ли па­рал­ле­ло­грамм. АС – диа­го­наль па­рал­ле­ло­грам­ма. , таким об­ра­зом, мы до­ка­за­ли пе­ре­ме­сти­тель­ный

Рис. 3

www.kursoteka.ru

Практическая работа по геометрии «Сложение и вычитание векторов» 1

Практическая работа №2

«Сложение и вычитание векторов»

Вариант 1

Цель работы:

• уяснить понятия: сумма двух векторов, сумма нескольких векторов, разность векторов, противоположные векторы;

• научиться выполнять сложение векторов по правилам треугольника, параллелограмма, многоугольника;

• научиться выполнять вычитание векторов.

Ход работы:

Выполните задания:

Задание 1 Выполните сложение векторов 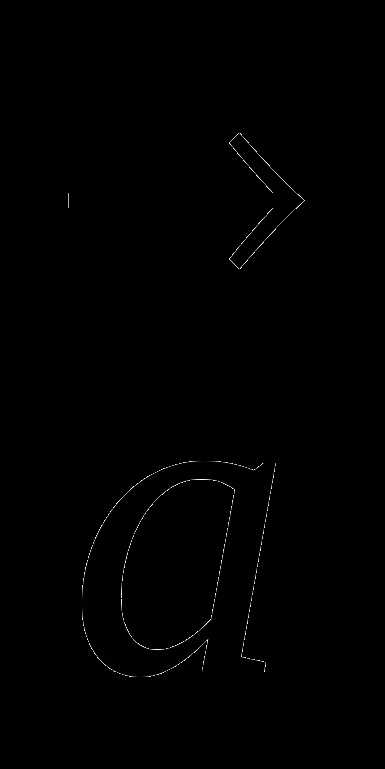и .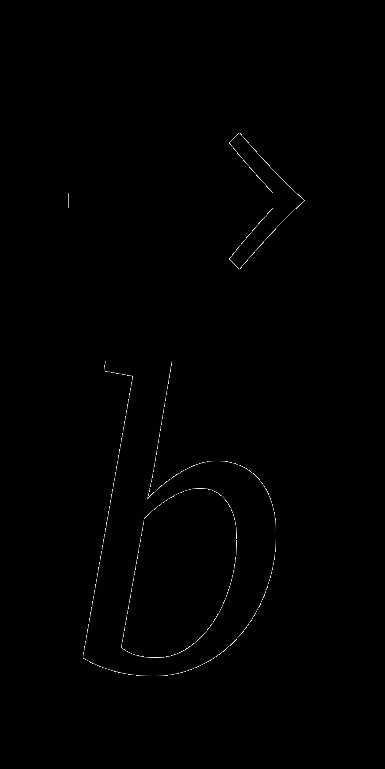

Задание 2 Выполните сложение векторов и .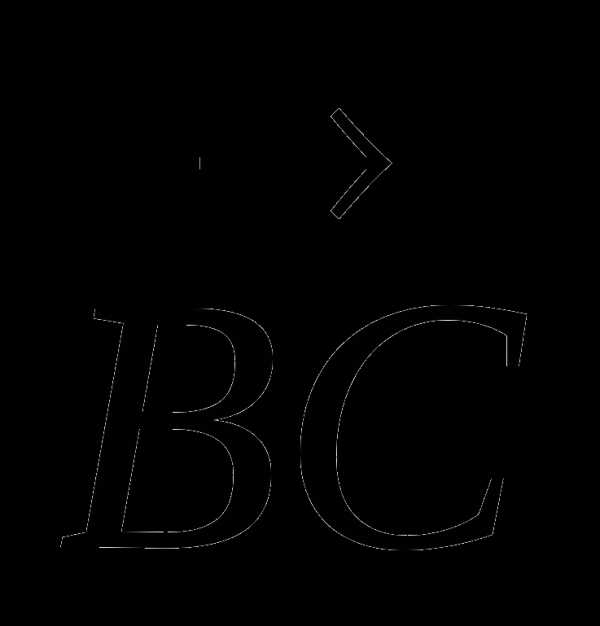

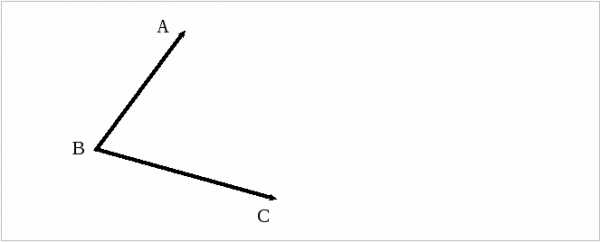
Задание 3 Выполните сложение векторов 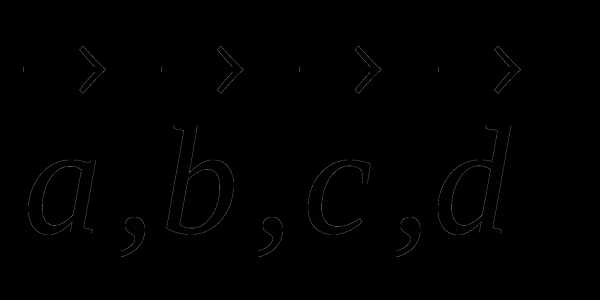и .

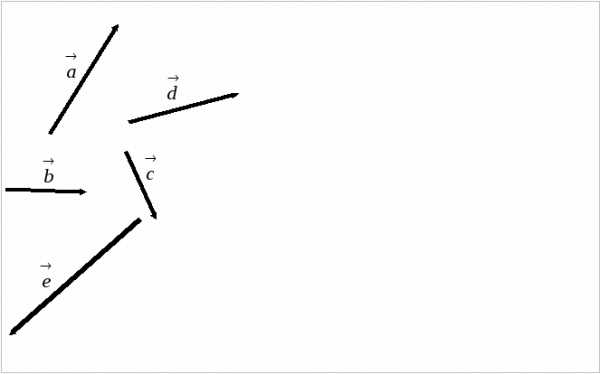
Задание 4 Найдите разность .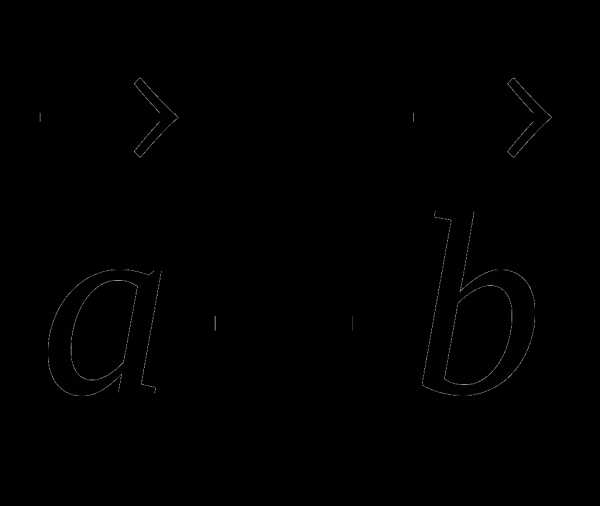

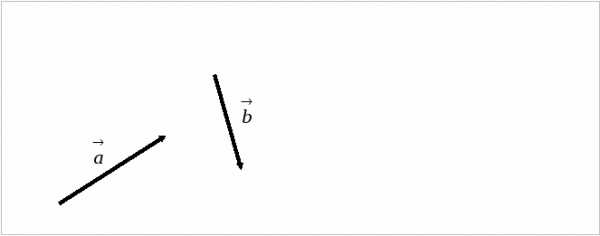
Вывод (По каким правилам можно выполнять сложение векторов? Как найти разность векторов): _______________________________________________________________

____________________________________________________________________________________________________________________________________________

______________________________________________________________________

Работу выполнил учащийся (учащаяся) 9 класса_____________________________

Дата выполнения __________________

infourok.ru