Свойства и способы вычисления двойных интегралов. (Семинар 29)
1. Семинар 29
Двойные интегралы. Свойствадвойных интегралов. Способы
вычисления двойных
интегралов.
Пусть f(x,y) – функция, ограниченная в некоторой замкнутой ограниченной
области D.
i — частичная область области D. i — площадь частичной области i
Pi ( xi , yi ) i , f ( xi , yi ) значение функции в точке Pi ( xi , yi )
n
Составим сумму
i 1
f ( x i , y i ) i (*)
Сумма (*) называется интегральной суммой для функции f(x,y) в области D,
соответствующей данному разбиению области D на n – частичных
областей.
Определение
Двойным интегралом от функции f(x,y) по области D называется предел, к
которому стремится интегральная сумма при стремлении к 0 наибольшего
диаметра частичных
областей
n
Запись lim n f ( xi , yi ) i f ( x, y )d
i 1
D
«Двойной интеграл от функции f(x,y) по области D»
f ( x, y )d — выражение; f(x,y) – подынтегральная функция;
d — элемент площади; D – область интегрирования.
Свойства двойных интегралов
1. Двойной интеграл от суммы конечного числа функций равен сумме
интегралов от слагаемых функций:
f ( x, y) … f
1
n
( x, y) d f1 ( x, y)d … f n ( x, y)d
D
D
D
2. Постоянный множитель подынтегральной функции можно выносить за
символ двойного интеграла:
сf ( x, y)d с f ( x, y)d
D
D
3. Если область D разбита на две области D1 , D2 без общих внутренних
точек, то:
f ( x, y )d f ( x, y )d f ( x, y )d
D
D1
D2
4. Если во всех точках области D функция f ( x, y ) ( x, y ) , то:
f ( x, y)d ( x, y)d
D
D
5. Значение двойного интеграла заключено между произведениями
наименьшего (m) и наибольшего (M) значений подынтегральной функции в
области D на площадь области интегрирования: mS f ( x, y)d MS , где S D
площадь области D.
6. Двойной интеграл равен произведению значения подынтегральной
функции в некоторой точке области интегрирования на площадь области
интегрирования, то есть: f ( x, y)d f ( , )S , f ( , ) — среднее значение
D
функции f(x,y) в области D
При вычислении f ( x, y)d элемент d удобнее представлять в
D
следующем виде.
Область D в плоскости ОХУ разбивается на частичные области посредством
двух систем координатных линий: x=const, y=const. Эти прямые
соответственно параллельны ОХ и ОУ. Частичные области прямоугольники.
Площадь каждой частичной области не примыкающей к границе D , будет
равна произведению x y.
Поэтому запишем
f ( x, y)d f ( x, y)dxdy
D
D
b
V f ( x, y)dxdy dx
D
a
(*)
y2 ( x )
x2 ( y )
d
f ( x, y)dy (**) V f ( x, y )dxdy
y1 ( x )
D
с
dy
f ( x, y )dx
(***)
x1 ( y )
Если область D – прямоугольник со сторонами параллельными осям
координат, то есть имеет вид, представленный на рисунке, то пределы
интегрирования – постоянные величины
b
d
d
b
a
c
c
a
f ( x, y)dxdy dx f ( x, y)dy dy f ( x, y)dx
D
Замена переменных в двойном интеграле
Полярные координаты
При вычислении определенных интегралов важную роль играет правило
замены переменной, согласно
которому
при соблюдении соответствующих
x
u
условий имеет место f ( x)dx f [ (u )] ‘ (u )du
2
2
x1
u1
Обычно функция x (u ) монотонна; тогда она осуществляет
взаимнооднозначное соответствие между точками интервала [u1 , u 2 ] изменения
переменной u и точками интервала [ x1 , x2 ] изменения переменной х.
Заменяя x (u )Правило замены переменной в двойном интеграле достаточно сложное. Приведем
формулу замены.
При переходе в двойном интеграле от переменных x,y к новым переменным u,v:
x=x(u,v), y=y(u,v) (*) формула замены такова
( x, y )
f
(
x
,
y
)
dxdy
f
[
x
(
u
,
v
),
y
(
u
,
v
)]
dudv (**), где
D
*
(u, v)
D
x x
( x, y )
x y x y
u v
y y
(u, v)
u v v u
x dv
Есть функциональный определитель Якоби (Якобиан) составленный из
частных производных функций (*), то есть
( x, y )
d dxdy
dudv
(u, v)
Старая область интегрирования D заменяется на новую область D* по
переменным u,v. Новое выражение для d называется элементом площади в
координатах u,v.
Применим формулу (**) к преобразованию с помощью полярных координат
(обозначения общепринятые)
x r cos , y r sin , r 0,0 2 ( )
( x, y) x y x y
cos r cos ( r sin ) sin r
Якобиан будет равен
(r , ) r r
Тогда
f ( x, y)dxdy f (r cos , r sin )rdrd (***), где
D
D и – D*
D*
соответствующие друг другу области в плоскостях OXY и O1r (здесь r и
рассматриваются как декартовы координаты точки).
Примеры с решениями
1. Вычислить x ln ydxdyесли D – прямоугольник 0 x 4,1 y e
D
4
x2
e
Решение. Имеем x ln ydxdy xdx ln ydy y ln y y 1 8(e e 1) 8
2 0
D
0
1
4
2
x2
1
x
e
2. Вычислить I dx (2 x y )dy
x2
x2
Решение. Имеем I dx (2 x y)dy 2 xy 1 y 2 2 x3 1 x 4 2 x 2 1 x 2 dx
2 x 1
2
2
1
x
1
2
2
2
2
1 5
1 3
1 4
x
x
x 0,9
2
10
2 1
3. Перейдя к полярным координатам вычислить
если D – I четверть круга x 2 y 2 a 2
Решение. Полагая x cos , y sin имеем
D
x y dxdy
2
2
D
x 2 y 2 dxdy
D
12 3 a
a3 2
a 3
cos sin d d d d 0 d d
30
30
6
0
0
2
2
2
2
2
a
2
4. Вычислить
2
2
ln(
x
y
)dxdy,
где D –кольцо между окружностями
D
x y e , x y 2 e4
2
2
2
2
Решение. Перейдем к полярным координатам
ln( x
2
y 2 )dxdy
D
ln
2
2
e2
0
e
d d 2 ln d d 2 d ln d
D
2
e2
Взяв по частям интеграл, зависящий от получим2 1 2 ln 1 2 d e 2 (3e 2 1)
4 e
0 2
5.
Вычислить интеграл ( x y )dxdyпо области D, ограниченной линиямиD
y=x и y x 2
Решение
а) Интегрируем сначала по у, затем по х
1
x
1
1
y2 x
3x 2
x4
x3 x 4 x5 1 3
3
D ( x y)dxdy 0 dx 2 ( x y)dy 0 [ xy 2 ] |x 2 dx 0 ( 2 x 2 )dx ( 2 4 10 ) |0 20
x
b) Интегрируем сначала по х, затем по у
5
y
1
1 2
1
2
2
x
y
3y
y 2 y 2 y3 1 3
y
D ( x y)dxdy 0 dy y ( x y)dx 0 [ 2 xy] |y dy 0 ( 2 y y 2 )dy ( 4 5 2 ) |0 20
Примеры для самостоятельного решения
1. Вычислить y ln xdxdy
, если область D ограничена линиями xy 1, y x , x 2
D
2. Вычислить xdxdy
, если область D – треугольник с вершинами A(2;3),
D
B(7;2), C(4;5).
e
ln x
sin x
3. Изменить порядок интегрирования dx f ( x, y)dy, dx f ( x, y)dy
1
0
0
0
3
2
(
x
y
)
(
x
y
)
dxdy, если D – квадрат, ограниченный
4. Вычислить
D
прямыми x+y=1, x-y=1, x+y=3, x-y=-1
5.
Переходя к полярным координатам, вычислить двойные интегралы:2
y
a) 1 2 dxdy, если область D – круг x 2 y 2 2
D
x
1
2
y
1
x
,
область
D
ограничена
полуокружностью
dxdy
D x 2 y 2 1
и осью ОХ.
x 2 y 2 dxdy , — область D ограничена окружностью x 2 y 2 2ax
с)
b)
D
d)
D
sin x 2 y 2
x2 y2
x2 y 2 2 / 9
dxdy если область D ограничена линиями: 2
x y2 2
Двойной интеграл в прямоугольных координатах. Ответы
Двойной интеграл в прямоугольных координатах. Ответы
Почему так важно бывает подобрать верный порядок интегрирования.
Вот пример, когда расстановка пределов интегрирования в одном порядке приводит к вполне приемлемым по сложности вычислениям, в тот момент как расстановка в другом порядке привела бы к чудовищным вычислительным сложностям.
При вычислении двойного интеграла в прямоугольных координатах мы строим соответствующий повторный интеграл, и, если область интегрирования является правильной в направлении обеих осей, это можно сделать двумя способами.
В нашем случае граница описана при помощи функции арксинус, которая крайне неудобна для интегрирования. Но если изменить порядок интегрирования, то граница буде описана при помощи синуса, и задача вычисление двойного интеграла в прямоугольных координатах путем сведения его к повторному интегралу, становится вполне приемлемой по сложности.
В случае необходимости, если какие-то из данных двойных интегралов в прямоугольных координатах показались вам слишком сложными, еще раз просмотрите тему «Двойной интеграл в прямоугольных координатах», после чего еще раз вернитесь к тем заданиям видео «Двойной интеграл в прямоугольных координатах», с которыми вы не справились. Обязательно добейтесь того, чтобы самостоятельное вычисление двойного интеграла в прямоугольных координатах расстановка пределов интегрирования в повторных интегралах не вызывало у вас затруднений.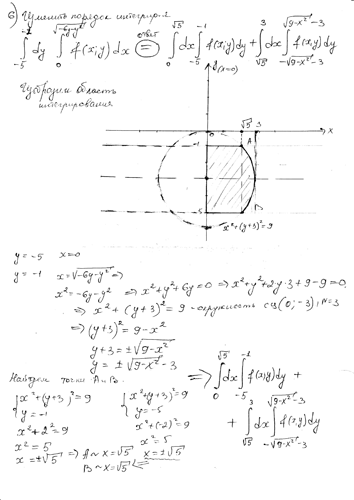
Тема «Двойной интеграл в прямоугольных координатах»
Ответы на вопросы по теме «Двойной интеграл в прямоугольных координатах»
Для того чтобы лучше разобраться с темой «Двойной интеграл в прямоугольных координатах», обязательно решите все задания.
Все лекции здесь.
Популярные сообщения из этого блога
Двойной интеграл в полярных координатах. Вопросы
Даны два двойных интеграла. Требуется вычислить их путем перехода к полярным координатам.
Замена переменных в двойном интеграле. Вопросы
Даны два двойных интеграла.
Репетиторство и консультации по Skype
$ Общее время занятий включает в себя, помимо онлайн-занятия, несколько часов видео для предварительного изучения (которые не оплачиваются). Таким образом, занимаясь фактически 3, 4, 5 и более часов, вы оплачиваете только 2 академических часа. Это выгодно. Ознакомиться с условиями занятий
Исчисление— Как изменить порядок интегрирования, когда предел является функцией?
спросил
Изменено 3 года, 5 месяцев назад
Просмотрено 782 раза
$\begingroup$
Рассмотрим двойной интеграл:
$A=\displaystyle\int_0^5 \left( \int_0^7 {x’}^2x^3 dx \right) dx’$ 93 дх\вправо) дх’$
Как изменить порядок этого интеграла, т.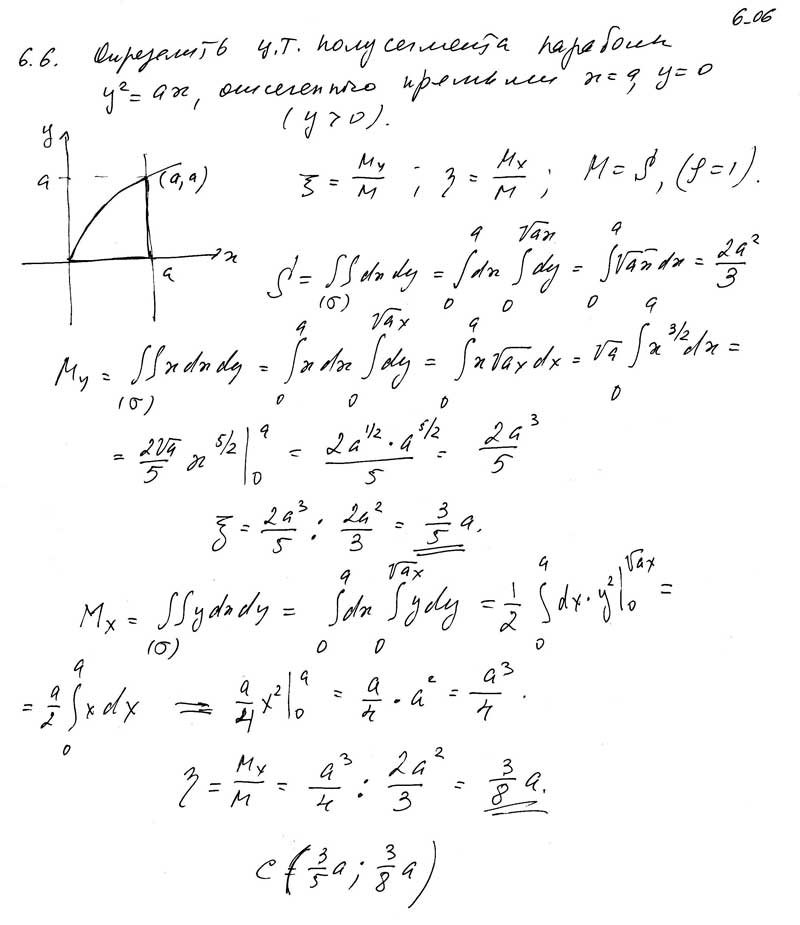
е. когда пределом является произвольная функция $f(x’)$?
- исчисление
- интегрирование
- многомерное исчисление
- функции
- определенные интегралы
$\endgroup$
3
$\begingroup$
Часто, как в вашем случае, очень помогает картинка: 9{-1}$, если $f$ — возрастающая функция, в какой области мы хотим решить это неравенство. И когда это убывающая функция, просто измените направление, чтобы получить ответ. Таким образом, на самом деле нам нужно разбить область $0 \leqslant x’ \leqslant 5$ на некоторое $a_i \leqslant x’ \leqslant b_i$ для $1 \leqslant i \leqslant n$ такое, что $a_1=0, b_i=a_{ i+1}, b_n=5$ такие, что все $a_i,b_i$ являются оптимальными точками $f$, монотонного на каждом интервале. После этого вы можете изменить порядок интеграла, но вам нужно разбить его на выраженные интервалы.
$\endgroup$
кратных интегралов — Криста Кинг Математика | Онлайн-помощь по математике
Сообщения с тегами множественных интегралов Нахождение среднего значения из двойного интегралаМы можем оценить среднее значение области кривых уровня, используя формулу (1/A(R)) int int_R f(x,y) Delta(A), где A(R) — площадь прямоугольника, определенного на R=[x1,x2]x[y1,y2], и где двойной интеграл дает объем под поверхностью f(x,y) в области R.
Читать далее
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, вычисление 3, вычисление iii, множественные интегралы, двойные интегралы, среднее значение, среднее значение из двойных интегралов, функции многих переменных , многомерные функции, кривые уровня, оценка среднего значения с кривыми уровня
Как преобразовать повторные интегралы в полярные координаты 92.
Помните также, что когда вы конвертируете dA или dy dx в полярные координаты, они преобразуются как dA=dy dx=r dr dtheta.Читать далее
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление iii, исчисление 3, исчисление iii, исчисление 3, многомерное исчисление, многомерное исчисление, многомерное исчисление, многомерное исчисление, множественные интегралы, двойные интегралы , повторные интегралы, полярные координаты, преобразование повторных интегралов, преобразование двойных интегралов
Как нарисовать площадь, заданную двойным интегралом в полярных координатах Чтобы набросать область интегрирования двойного полярного интеграла, вам нужно будет проанализировать функцию и оценить оба набора пределов по отдельности. Помните, что вам нужно будет нарисовать полярную функцию на осях полярных координат, где значения r представляют радиус круга, а значения тета будут давать прямые линии.
Читать далее
Learn mathКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление iii, исчисление 3, исчисление iii, вычисление 3, множественные интегралы, двойные интегралы, полярные координаты, двойные полярные интегралы, повторные интегралы, двойные интегралы в полярных координатах, повторные интегралы в полярных координатах, зарисовка области
Нахождение площади двойных интегралов в полярных координатах Вы можете использовать двойной интеграл, чтобы найти площадь внутри полярной кривой. Предполагая, что сама функция и пределы интегрирования уже имеют полярную форму, вы сможете напрямую вычислить повторный интеграл. В противном случае, если функция и/или пределы интегрирования имеют прямоугольную форму, вам нужно будет преобразовать ее в полярную перед оценкой.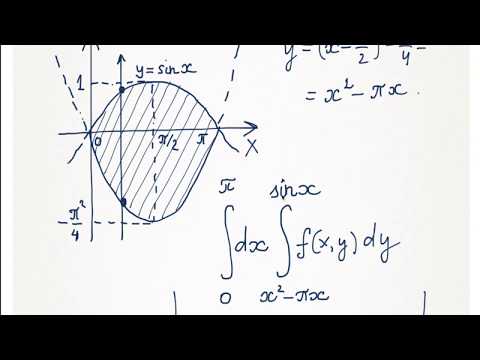
Learn mathКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, исчисление 3, исчисление iii, множественные интегралы, двойные интегралы, полярные координаты, двойные полярные интегралы, объем из двойных интегралов , повторные интегралы, двукратные повторные интегралы
Замена тройных интегралов цилиндрическими координатамиЧтобы перевести тройной интеграл в цилиндрические координаты, нам потребуется перевести пределы интегрирования, саму функцию и dV из прямоугольных координат в цилиндрические. Переменная z остается, но x изменится на rcos(theta), а y изменится на rsin(theta). dV преобразуется в r dz dr d(theta).
Читать далее
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, исчисление 3, исчисление iii, многомерное исчисление, многомерное исчисление, многомерное исчисление, многомерное исчисление, множественные интегралы, тройные интегралы , тройное интегрирование, цилиндрические координаты, преобразование в цилиндрические координаты, преобразование координат, тройные интегралы в цилиндрических координатах Как вычислить повторные тройные интегралыПовторные интегралы — это двойные или тройные интегралы, пределы интегрирования которых уже указаны. В этом уроке мы рассмотрим, как вычислять тройные повторные интегралы, работая изнутри наружу.
Читать далее
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, многомерное исчисление, многомерное исчисление, многомерное исчисление, многомерное исчисление, исчисление iii, исчисление 3, исчисление iii, вычисление 3, повторные тройные интегралы, повторные интегралы, тройные интегралы, кратные интегралы
Нахождение объема из тройных интегралов Мы можем интегрировать в любом порядке, поэтому мы попробуем интегрировать в том порядке, в котором проще всего, в зависимости от пределов интегрирования, которые мы обнаружим, анализируя объект E.
Имейте в виду, что когда дело доходит до пределов интеграции, вам нужны ограничения, выраженные в переменных, которые необходимо интегрировать.
Читать далее
Learn mathКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление 3, исчисление iii, исчисление iii, множественные интегралы, тройные интегралы, объем с тройными интегралами, тройной интегральный объем, порядок интеграция
Нахождение объема двойными интегралами в полярных координатах Если нам дан двойной интеграл в прямоугольных координатах и его попросят оценить как двойной полярный интеграл, нам потребуется преобразовать функцию и пределы интегрирования из прямоугольных координат (x,y) в полярные координаты (r, тета), а затем вычислить интеграл. Мы можем сделать это, используя формулы для преобразования между прямоугольными и полярными координатами.
Читать далее
Learn mathКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, исчисление 3, исчисление iii, множественные интегралы, двойные интегралы, полярные координаты, двойные полярные интегралы, нахождение объема, объема с двойными интегралами, перевод в полярные координаты, объем твердого тела
Нахождение объема в областях типа I и типа II Мы уже знаем, что можем использовать двойные интегралы, чтобы найти объем под поверхностью в некоторой области R=[a,b]x[c,d]. Мы можем определить область R как тип I, тип II или их сочетание. Кривые типа I — это кривые, которые могут быть определены для y через x и располагаются более или менее «над и под» друг другом. С другой стороны, кривые типа II — это кривые, которые могут быть определены для x через y и лежат более или менее «левее и правее» друг друга.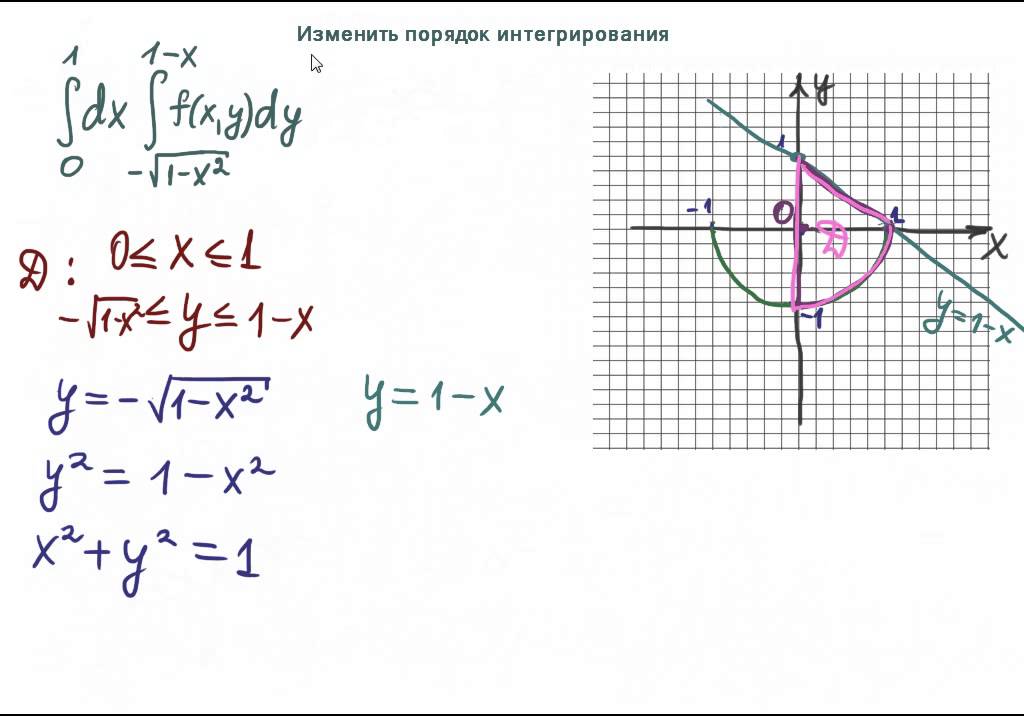
Читать далее
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, исчисление 3, исчисление iii, множественные интегралы, объем, нахождение объема, области типа i и ii, области типа i , регионы типа ii, объем по регионам типа i, объем по регионам типа ii
Использование двойного интеграла для нахождения объема объектаМы уже знаем, что можем использовать двойные интегралы, чтобы найти объем ниже функции по некоторой области, заданной R=[a,b]x[c,d]. Мы используем формулу двойного интеграла V=int int_D f(x,y) dA, чтобы найти объем, где D представляет собой область, по которой мы интегрируем, а f(x,y) – это кривая, ниже которой мы хотим найти объем. .
Читать далее
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, исчисление 3, исчисление iii, множественные интегралы, множественное интегрирование, двойные интегралы, двойное интегрирование, объем, объем с двойным интегралы, двойные интегралы для нахождения объема, объем по области
Нахождение объема тройных интегралов в цилиндрических координатахЧтобы найти объем из тройного интеграла с использованием цилиндрических координат, мы сначала преобразуем тройной интеграл из прямоугольных координат в цилиндрические координаты. Нам нужно преобразовать функцию, дифференциалы и границы каждого из трех интегралов. Как только тройной интеграл выражен в цилиндрических координатах, мы можем интегрировать, чтобы найти объем.
Читать далее
Изучайте математикуКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, исчисление 3, исчисление iii, множественные интегралы, тройные интегралы, объем тройного интеграла, цилиндрические координаты, тройные интегралы в цилиндрических координатах, цилиндрические координаты для тройных интегралов , переводя в цилиндрические координаты
Среднее значение для тройных интеграловЧтобы использовать формулу среднего значения тройного интеграла, нам нужно найти объем объекта, а также область значений x, y и z, чтобы мы могли установить пределы интегрирования, превратить тройной интеграл в повторный интеграл. , и замените dV на dzdydx.
Читать далее
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление 3, исчисление 3, исчисление iii, многомерное исчисление, многомерное исчисление, многомерное исчисление, многомерное исчисление, тройные интегралы, множественные интегралы , среднее значение, среднее значение для тройных интегралов
Правило средней точки для аппроксимации двойных интегралов В прошлом мы использовали правило средней точки для оценки площади под функцией одной переменной.
Мы рисовали прямоугольники под кривой так, чтобы средняя точка в верхней части каждого прямоугольника касалась графика функции. Затем мы суммировали площади каждого прямоугольника, чтобы найти приблизительное значение площади под кривой. Когда мы переводим это в трехмерное пространство, это означает, что мы используем трехмерные прямоугольные призмы вместо двумерных прямоугольников, чтобы аппроксимировать объем под функцией многих переменных.
Читать далее
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, исчисление 3, исчисление iii, множественные интегралы, многомерное исчисление, многомерное исчисление, многомерное исчисление, многомерное исчисление, многомерное, многомерный, двойные интегралы, правило средней точки, правило средней точки для двойных интегралов, аппроксимация двойных интегралов
Якобиан от трех переменных для замены переменных Имея область, определенную в uvw-пространстве, мы можем использовать преобразование Якоби, чтобы переопределить ее в xyz-пространстве или наоборот.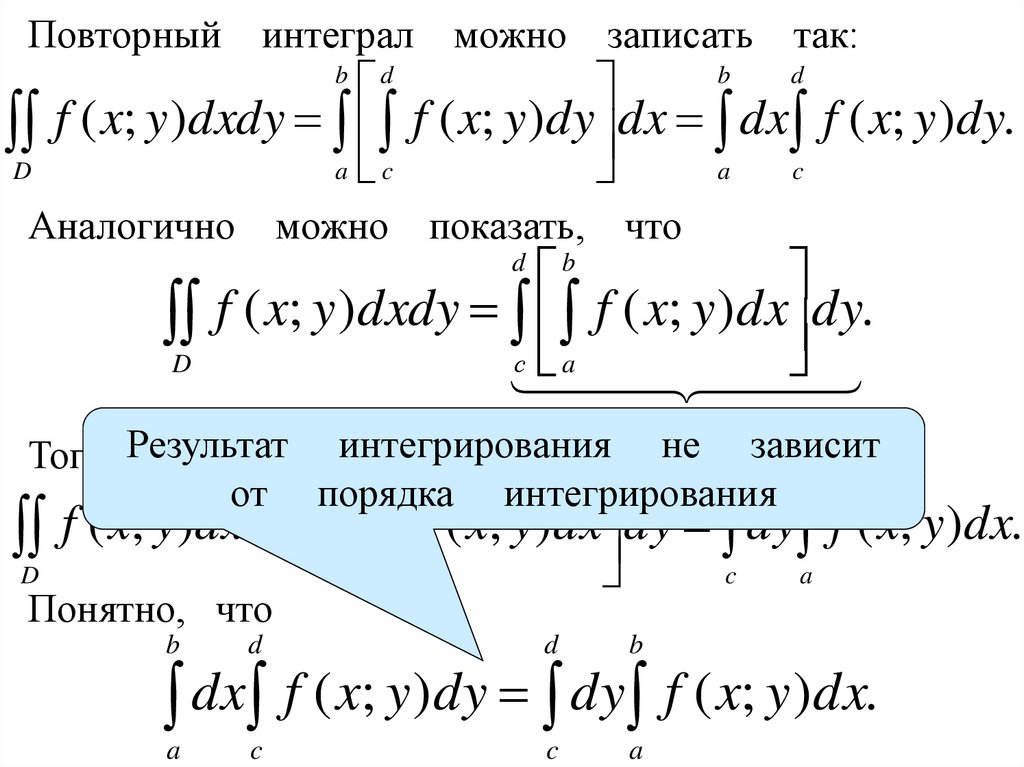
Мы будем использовать формулу определителя 3×3 для вычисления якобиана.
Читать далее
Изучайте математикуКриста Кинг математика, учитесь онлайн, исчисление 3, исчисление iii, исчисление 3, исчисление iii, множественные интегралы, множественное интегрирование, двойные интегралы, тройные интегралы, якобиан, 3×3, 3×3 якобиан, якобиан преобразования , преобразования, преобразование переменных, многомерные функции, многомерное исчисление, онлайн-математика, онлайн-курс
Нахождение объема для тройных интегралов с использованием сферических координатМы можем использовать тройные интегралы и сферические координаты, чтобы найти объем твердой сферы. Чтобы преобразовать прямоугольные координаты в сферические, мы используем набор формул сферического преобразования.
Читать далее
Learn mathКриста Кинг математика, выучить онлайн, онлайн курс, онлайн математика, исчисление 3, исчисление 3, исчисление 3, множественные интегралы, тройные интегралы, сферические координаты, объем в сферических координатах, объем сферы, объем полусферы, переход к сферическим координатам, уравнения перехода, формулы перевода, объем тройного интеграла, пределы интегрирования, границы интеграла, вычисл iii
Нахождение площади поверхности одной функции, ограниченной другой функцией, с помощью двойного интегралаВы можете использовать двойной интеграл, чтобы найти площадь поверхности, ограниченной другой поверхностью. Самой сложной частью этого будет нахождение границ каждого из интегралов в двойном интеграле.
Читать далее
Learn mathКриста Кинг математика, выучить онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, исчисление 3, исчисление iii, множественные интегралы, двойные интегралы, площадь поверхности, площадь поверхности, площадь поверхность внутри функции
Решение тройных интегралов по правилу середины Аналогично тому, как мы использовали средние точки для аппроксимации простых интегралов, взяв среднюю точку на вершине каждого аппроксимирующего прямоугольника, и тому, как мы использовали средние точки для аппроксимации двойных интегралов, взяв среднюю точку на вершине каждой аппроксимирующей призмы, мы можем использовать средние точки, чтобы аппроксимировать тройной интеграл, взяв среднюю точку каждого вложенного куба.
Читать далее
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, исчисление 3, исчисление iii, множественные интегралы, тройные интегралы, правило средней точки, оценка тройных интегралов, средние точки, кубы, суб-кубы
Цилиндрические координаты и тройные интегралыПодобно декартовым (или прямоугольным) координатам и полярным координатам, цилиндрические координаты — это просто еще один способ описания точек в трехмерном пространстве. Цилиндрические координаты точно такие же, как и полярные, только в трехмерном, а не в двухмерном пространстве.
Читать далее
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 3, исчисление iii, исчисление 3, исчисление iii, исчисление с несколькими переменными, вычисление с несколькими переменными, множественные интегралы, тройные интегралы, цилиндрические координаты, преобразование в цилиндрические координаты, тройные интегралы в цилиндрических координатах
Шесть способов записать один и тот же повторный тройной интегралПовторный тройной интеграл можно выразить шестью способами. В то время как функция внутри интеграла всегда остается неизменной, порядок интегрирования изменится, и пределы интегрирования изменятся в соответствии с порядком.
Читать далее
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, множественные интегралы, исчисление 3, исчисление iii, исчисление 3, исчисление iii, тройные интегралы, повторные интегралы, тройные повторные интегралы, повторные тройные интегралы, шесть способов, шесть способов записать тройной интеграл
Вычисление двойных интегралов как повторных интегралов Всякий раз, когда нам дают двойной интеграл, мы хотим превратить его в повторный интеграл, потому что с повторными интегралами мы можем легко вычислять один интеграл за раз, как в исчислении с одной переменной.