1 2 3 > >>
Основные понятия
Делители и кратные
Делителем натурального числа a называют натуральное число, на которое a делится без остатка.
Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем (НОД) этих чисел.
Для того чтобы найти наибольший общий делитель нескольких чисел, нужно:
- Разложить их на простые множители.
- Из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел.
- Найти произведение оставшихся множителей.
Если наибольший общий делитель двух чисел равен 1, то такие числа называются взаимно простыми. Например, числа 13 и 15 – взаимно простые.
Натуральное число называется простым, если оно имеет только два делителя: единицу и самого себя. Если же число имеет больше двух делителей, то оно называется составным. Исключением из этого правила является число 1, оно не является ни простым, ни составным, так как вообще имеет только один делитель.
Кратным натуральному числу а называют натуральное число, которое делится на а без остатка. Любое натуральное число имеет бесконечно много кратных.
Наименьшим общим кратным (НОК) натуральных чисел a и b называют наименьшее натуральное число, которое кратно и a, и b.
Чтобы найти наименьшее общее кратное нескольких чисел, надо:
- Разложить их на простые множители.
- Выделить множители, входящие в разложение одного из чисел.
- Добавить к ним недостающие множители из разложения остальных чисел.
- Найти произведение получившихся чисел.
В серии интерактивных уроков и тренажеров «Обыкновенные дроби» представлены:
- Делители и кратные. Разложение на простые множители.
- Наибольший общий делитель. Взаимно простые числа. Наименьшее общее кратное.
Обыкновенные (или простые) дроби
Запись вида называется обыкновенной (или простой) дробью. Число a при этом называется числителем, а b – знаменателем.
Дробь, в которой числитель меньше знаменателя, называют правильной дробью.
Дробь, в которой числитель больше знаменателя или равен ему, называют неправильной дробью.
Чтобы из неправильной дроби
- разделить с остатком числитель на знаменатель;
- неполное частное будет целой частью
- остаток (если он есть) дает числитель, а делитель — знаменатель дробной части.
Запись числа, содержащую целую и дробную части, называют смешанной. Смешанное число можно представить и в виде неправильной дроби.
Чтобы представить смешанное число в виде неправильной дроби, нужно:
- умножить его целую часть на знаменатель дробной части;
- к полученному произведению прибавить числитель дробной части;
- записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.
Основное свойство дроби: если числитель и знаменатель дроби одновременно умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Правило сокращения дробей: деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.
В серии интерактивных уроков и тренажеров «Обыкновенные дроби» представлены:
- Основное свойство дроби и правило сокращения дробей.
- Приведение дробей к общему знаменателю. Сравнение дробей.
Сложение и вычитание обыкновенных (простых) дробей
При сложении или вычитании дробей с одинаковыми знаменателями числители соответственно складывают или вычитают, а знаменатель оставляют тот же.
Число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель, называют дополнительным множителем. При приведении дроби к новому знаменателю
Чтобы сравнить, сложить или вычесть дроби с разными знаменателями, надо сначала привести данные дроби к общему знаменателю, а потом сравнить, сложить или вычесть их.
В общем виде сложение и вычитание дробей выглядит так:
хотя часто удобнее в качестве общего знаменателя брать не простое произведение знаменателей, а наименьшее общее кратное знаменателей данных дробей.
В серии интерактивных уроков и тренажеров «Обыкновенные дроби» представлены:
- Сложение и вычитание дробей с разными знаменателями.
- Смешанные числа. Сложение и вычитание смешанных чисел
Умножение и деление обыкновенных (простых) дробей
Произведение обыкновенных дробей – это дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей данных дробей
Числа, произведение которых равно 1, называются взаимно обратными.
Чтобы разделить число на дробь, надо умножить эта число на дробь, обратную делителю
В серии интерактивных уроков и тренажеров «Обыкновенные дроби» представлены:
- Умножение и деление обыкновенных дробей
Факторинг рациональных выражений — Алгебра II
Все ресурсы по Алгебре II
10 Диагностических тестов 630 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Алгебра II Помощь » Промежуточная алгебра с одной переменной » Рациональные выражения » Решение рациональных выражений » Факторинг рациональных выражений
Упрощение:
Правильный ответ:
Объяснение:
Если мы факторизуем знаменатель, мы получаем
Следовательно, рациональное выражение становится равным
, что равно
0.
Возможные ответы:
Выражение нельзя упростить.
Правильный ответ:
Пояснение:
а. Упростите числитель и знаменатель по отдельности, выделив общие множители.
б. Уменьшите, если возможно.
в. Фактор трехчлена в числителе.
д. Сократите общие множители между числителем и знаменателем.
Сообщить об ошибке
Преобразуйте следующее уравнение из стандартной формы в вершинную:
Возможные ответы:
Правильный ответ: 52
5
Объяснение:
Чтобы взять это уравнение стандартной формы и преобразовать его в вершинную форму, нам нужно завершить квадрат.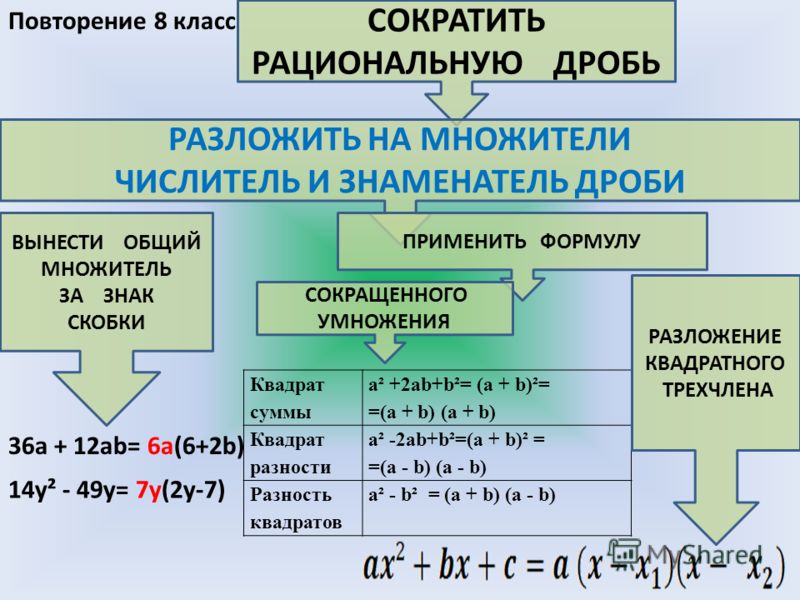
Это можно сделать следующим образом:
Заполним квадрат на . В данном случае это наше в нашем будущем. Поэтому мы хотим нашего, так что.
Так как мы прибавляем с правой стороны (поскольку мы заполняем квадрат внутри круглых скобок), нам нужно прибавлять и к левой стороне. Таким образом, наше уравнение становится:
Наш окончательный ответ, следовательно,
Отчет о ошибке
Оцените следующее выражение:
Возможные ответы:
Правильный ответ:
. Объяснение:
Когда мы умножаем выражения с показателями, нам нужно помнить о некоторых правилах:
Перемножаемые переменные добавляют показатели степени.
Разделенные переменные вычитают показатели степени.
Переменные, возведенные в степень, умножают показатели степени.
Следовательно, когда мы мулитиппий две фракции, мы получаем:
Наш окончательный ответ, следовательно,
Отчет о ошибке
Упрощение:
Возможные ответы:
Правильный ответ:
Объяснение:
Первый множитель числителя. Нам нужны два числа с суммой 3 и произведением 2. Числа 1 и 2 удовлетворяют следующим условиям:
Теперь посмотрим, есть ли общие множители, которые сокращают:
числитель и знаменатель сокращаются, оставляя .
Сообщить об ошибке
Упростите это рациональное выражение:
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Объяснение:
Чтобы увидеть, что можно упростить, разложите квадратные уравнения.
Отмена, как Условия:
Условия комбинации:
Отчет о ошибке
Фактор и упростите это рациональное выражение:
Возможные ответы:
4. Нет.
Правильный ответ:
Объяснение:
Полностью факторизовать все многочлены:
Отменить подобные термины:
Сообщить об ошибке
Фактор .
Возможные ответы:
Правильный ответ:
Объяснение:
Вначале мы можем рассматривать это как две отдельные задачи и независимо множить числитель и знаменатель:
После факторизации мы можем поместить факторизованные уравнения обратно в исходную задачу:
Отсюда мы можем отменить сверху и снизу, оставив:
Отчет Ошибка
Фактор:
Возможные ответы:
Правильный ответ:
Объяснение:
Умножьте два в числителе.
Разложить трехчлен на множители.
Разложите знаменатель на множители.
Разделите термины.
Ответ:
Сообщить об ошибке
Упростите до простейших терминов.
Возможные ответы:
Правильный ответ:
Объяснение:
Правильный ответ . И числитель, и знаменатель можно разложить на более простые члены:
Условия отменяются. Уход . Хотя это вариант ответа, его можно еще больше упростить. Если вычесть a из знаменателя, условия аннулируют уход .
Сообщить об ошибке
← Назад 1 2 Далее →
Уведомление об авторских правах
Все ресурсы Algebra II
10 Диагностические тесты 630 практических тестов Вопрос дня Карточки Учитесь по концепции
Определение и упрощение рациональных выражений
Результаты обучения
- Распознавание и определение рациональных выражений
- Определить область определения рационального выражения
- Упростить рациональное выражение
Рациональные выражения — это дроби, которые имеют многочлен в числителе, знаменателе или в обоих.
2}[/latex] в сочетании с методами разложения полиномов на множители.
Сохраняйте спокойствие и будьте рациональны
Чтобы представить первое важное свойство рациональных выражений и уравнений, мы покажем пример.
Вычислить [латекс]\frac{x}{x-2}[/латекс] вместо [латекс]х=2[/латекс]
Подставить [латекс]х=2[/латекс]
[латекс]\ begin{array}{l}\frac{2}{2-2}\\\text{}\\=\frac{2}{0}\end{array}[/latex]
Помните, что вы можете’ t делить на ноль, поэтому это означает, что для выражения [латекс]\фрак{х}{х-2}[/латекс] х не может равняться 2, потому что это приведет к неопределенной пропорции. В общем, поиск значений переменной, которые не приводят к делению на ноль, называется поиском домена.
Область определения рационального выражения или уравнения
Область определения рационального выражения или уравнения — это набор значений переменной, который не приведет к неопределенной математической операции, такой как деление на ноль. Для a = любое действительное число, мы можем записать домен следующим образом:
x — все действительные числа, где [latex]x\neq{a}[/latex]
Причина, по которой нельзя делить любое число c на ноль [латекс] \left( \frac{c}{0}\,\,=\,\,? \right)[/latex] заключается в том, что вам нужно будет найти число, которое при умножении на 0 вы получите обратно [latex]c \left( ?\,\,\cdot \,\,0\,\,=\,\,c \right)[/latex].
Не существует чисел, которые могут это сделать, поэтому мы говорим «деление на ноль не определено». При упрощении рациональных выражений необходимо обращать внимание на то, при каких значениях переменных в выражении знаменатель будет равен нулю. Эти значения не могут быть включены в домен, поэтому они называются исключенными значениями. Откажитесь от них в самом начале, прежде чем идти дальше.
(Обратите внимание, что хотя знаменатель не может быть эквивалентен 0, числитель может быть эквивалентен — вот почему вы ищете только исключенные значения в знаменателе рационального выражения.)
Для рациональных выражений домен будет исключать значения, для которых значение знаменателя равно 0. Следующие два примера иллюстрируют нахождение домена выражения.
В следующем примере мы идентифицируем область определения рационального выражения, содержащего многочлены в числителе и знаменателе. 92}{10x}=\frac{5\cdot{x}\cdot{x}}{5\cdot{2}\cdot{x}}[/latex]
Общие множители между числителем и знаменателем равны 5 и x, поэтому мы можем «отменить» их, чтобы показать, что [latex]\frac{5}{5}=1\text{ и }\frac{x}{x}=1[/latex].
[латекс]\displaystyle\normalsize\frac{5\cdot{x}\cdot{x}}{5\cdot{2}\cdot{x}}=\frac{\cancel{5}\cdot{\ cancel{x}}\cdot{x}}{\cancel{5}\cdot{2}\cdot{\cancel{x}}}=\frac{x}{2}[/latex]
Следующий пример дает напоминание о том, как упростить моном с переменными и показателями. Затем мы воспользуемся этой идеей, чтобы упростить рациональное выражение и определить его домен.
Мы можем обобщить процесс следующим образом: разложить на множители числитель, разложить на множители знаменатель, определить множители, общие для числителя и знаменателя, сократить их, чтобы представить деление, и упростить.
При упрощении рациональных выражений полезно всегда сначала рассматривать предметную область. Это пригодится, когда вы начнете решать рациональных уравнений чуть позже. При нахождении домена выражения вы всегда начинаете с исходного выражения, потому что переменные термины могут быть исключены как часть процесса упрощения.
В следующих примерах числитель и знаменатель представляют собой многочлены с более чем одним членом, но снова применяются те же принципы упрощения.
Разложите числитель и знаменатель на множители, чтобы упростить рациональное выражение.
Действия по упрощению рационального выражения
Чтобы упростить рациональное выражение, выполните следующие действия:
- Определите домен. Исключенные значения — это те значения переменной, которые приводят к тому, что выражение имеет знаменатель, равный 0,9.0370
- Разложите числитель и знаменатель на множители.
- Найдите общие делители для числителя и знаменателя и упростите.
Дополнительным соображением для рациональных выражений является определение того, какие значения исключаются из домена. Поскольку деление на 0 не определено, любые значения переменных, знаменатель которых равен 0, должны быть исключены. Исключенные значения должны быть идентифицированы в исходном уравнении, а не в его факторизованной форме.