«Как раньше рассчитывали степень числа, к примеру, 2 в степени 1,7?» — Яндекс Кью
Популярное
Сообщества
Сейчас, чтобы возвести 2 в степень 1,7 мы воспользуемся калькулятором, но раньше, в каком-нибудь 16 веке, калькуляторов не было. Наверняка, была потребность в расчете степени числа, но как эту степень рассчитывали.
ИсторияМатематикаНаука
Евгений Пантелеев
·
4,0 K
ОтветитьУточнитьНадежда Шихова
Математика
8,6 K
Редактор, автор и переводчик книг по математике · 1 мая 2021 ·
problemaday
История математики говорит нам, что в 16 веке 2 в степени 1,7 еще не рассчитывали.
В конце 16 века еще только учились записывать десятичные дроби. В 1585 году вышла книга Симона Стевина L’arithmetique, где автор объяснял действия с десятичными дробями. Очень популярная книга для своего времени, но десятичные дроби там автор записывал совсем не так, как мы.
В 16 веке не было общепринятого обозначения для натуральных степеней; записывали кто во что горазд. Вместо х в квадрате долго писали хх, и т.п.
Потребность в сложных расчетах пришла из астрономии и навигации. Чтобы умножать числа, переходили к их логарифмам, складывали логарифмы, а потом переходили обратно. Аналогично можно было бы возводить в степень.
Логарифмы не вычисляли каждый раз, а пользовались таблицами. Первая таблица логарифмов была составлена и опубликована в 1614 году Дж. Непером. Она была предназначена для астрономических расчетов, поэтому в нее входили еще логарифмы синусов и косинусов. Основание логарифмов Непер подобрал так, чтобы удобно было работать именно с синусами и косинусами, позднее стали брать основание 10 или е.
Непер понимал, что если последовательность чисел образует геометрическую прогрессию, то последовательность их логарифмов образует арифметическую прогрессию. На этом основании он и составлял таблицы.
Чтобы возвести 2 в степень 1,7, можно по таблице найти натуральный логарифм 2, умножить его на 1,7, получится примерно 1,18. Потом по таблице возвращались обратно: находили число, логарифм которого равен 1,18.
Владение логарифмами и использование таблиц так и остались основой для расчетов вплоть до последней трети 20 века. Пользоваться логарифмической линейкой и таблицами Брадиса учили в школах где-то до 70-80х годов.
1 эксперт согласен
Евгений Пантелеев
1 мая 2021
Хорошо, а как тогда Непер получил таблицу логарифмов? Ведь логарифм — это операция обратная возведению в степень… Читать дальше
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
POW: Объяснение формул Google Sheets
Как вы используете POW в Google Sheets?
POW — это функция в Google Sheets, которая вычисляет степень числа.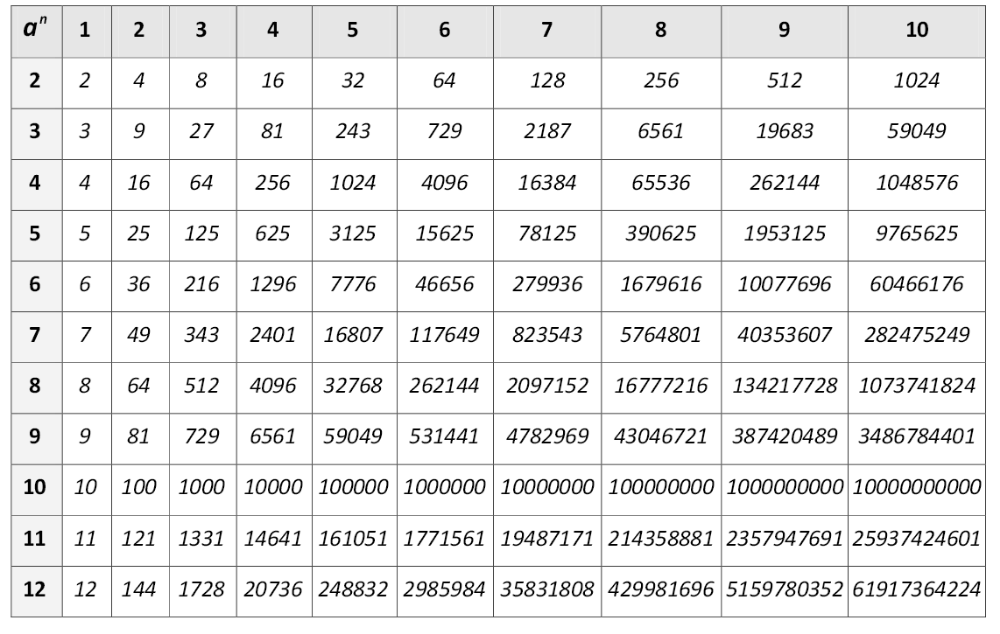 Синтаксис использования POW: POW(число,мощность), где число — это число, мощность которого вы хотите вычислить, а мощность — это количество раз, которое вы хотите вычислить. Например, если вы хотите вычислить степень числа 9 в 3-й степени, вы должны использовать следующую формулу: POW(9,3).
Синтаксис использования POW: POW(число,мощность), где число — это число, мощность которого вы хотите вычислить, а мощность — это количество раз, которое вы хотите вычислить. Например, если вы хотите вычислить степень числа 9 в 3-й степени, вы должны использовать следующую формулу: POW(9,3).
Каков синтаксис POW в Google Таблицах?
Функция POW в Google Таблицах вычисляет степень числа в заданной степени. Синтаксис функции POW:
=POW(число,степень)
Где число — это число, которое нужно возвести в степень степени.
Какой пример использования POW в Google Sheets?
В Google Sheets функция POWER() принимает одно число (основание) и целое число (показатель степени) и вычисляет результат возведения основания в степень степени. Например, формула =СТЕПЕНЬ(4,3) вернет 64.
Когда не следует использовать POW в Google Таблицах?
В некоторых случаях вам не следует использовать функцию POW в Google Таблицах. Один из таких случаев — когда вы пытаетесь вычислить мощность числа, меньшего нуля. В этом случае вместо этого вы должны использовать функцию XOR. В другой раз вам не следует использовать функцию POW, когда вы пытаетесь вычислить степень числа, которое больше или равно 1 000 000. В этом случае вы должны использовать функцию EXP.
В этом случае вместо этого вы должны использовать функцию XOR. В другой раз вам не следует использовать функцию POW, когда вы пытаетесь вычислить степень числа, которое больше или равно 1 000 000. В этом случае вы должны использовать функцию EXP.
Какие формулы похожи на POW в Google Таблицах?
Ниже приведены формулы, аналогичные POW в Google Таблицах: =СУММПРОИЗВ(—(A1:A10>0),A1:A10) =СРЗНАЧ(A1:A10) =MIN(A1:A10) =MAX(A1:A10) )
В этом подробном руководстве мы рассмотрим формулу POW Google Sheets, которая используется для вычисления степени числа. Мы расскажем все, что вам нужно знать об этой формуле, включая ее синтаксис, примеры, советы и рекомендации, распространенные ошибки, устранение неполадок и связанные формулы. К концу этой статьи вы будете иметь полное представление о формуле POW и о том, как эффективно использовать ее в своих проектах Google Sheets.
Синтаксис POW
Синтаксис формулы POW в Google Sheets следующий:
=POW(основание, показатель степени)
Формула принимает два аргумента:
- основание : Число, до которого нужно возвести сила.

- показатель степени : Степень, до которой вы хотите поднять базу.
Результатом формулы является основание, возведенное в степень степени. И основание, и показатель степени могут быть положительными или отрицательными числами, а также ссылками на ячейки или другими формулами, возвращающими числовое значение.
Примеры POW
Давайте рассмотрим несколько примеров использования формулы POW в Google Таблицах:
- Основное использование: Чтобы вычислить 2, возведенное в степень 3, вы должны использовать формулу =POW(2, 3). Это вернет результат 8, как 2 * 2 * 2 = 8.
- Использование ссылок на ячейки: Если у вас есть основание в ячейке A1 и показатель степени в ячейке B1, вы можете использовать формулу =POW(A1, B1 ) для вычисления результата. Например, если A1 содержит значение 3, а B1 содержит значение 4, формула вернет 81, так как 3 * 3 * 3 * 3 = 81,
- Отрицательное основание: Чтобы вычислить мощность отрицательного основания, просто включите знак минус в аргумент основания.
 Например, =POW(-2, 3) вернет -8, так как -2 * -2 * -2 = -8.
Например, =POW(-2, 3) вернет -8, так как -2 * -2 * -2 = -8. - Отрицательная экспонента: Чтобы вычислить степень отрицательной экспоненты, включите знак минус в аргумент экспоненты. Например, =POW(2, -3) вернет 0,125, так как 1 / (2 * 2 * 2) = 1/8 = 0,125.
- Дробная экспонента: Чтобы вычислить степень дробной экспоненты, включите дробь в аргумент экспоненты. Например, =POW(9, 0,5) вернет 3, так как квадратный корень из 9 равен 3.
POW Tips & Tricks
Вот несколько советов и приемов, которые помогут вам максимально эффективно использовать формулу POW в Google Sheets:
- Вычисление квадратных корней: Вы можете использовать формулу POW для вычисления квадратных корней, установив показатель степени равным 0,5. Например, =POW(16, 0,5) вернет 4, так как квадратный корень из 16 равен 4.
- Вычисление кубических корней: Точно так же вы можете вычислить кубические корни, установив показатель степени равным 1/3.
 Например, =POW(27, 1/3) вернет 3, так как кубический корень из 27 равен 3.
Например, =POW(27, 1/3) вернет 3, так как кубический корень из 27 равен 3. - Использование POW с другими формулами: Вы можете комбинировать формулу POW с другими формулами Google Sheets для выполнения более сложных вычислений. Например, вы можете использовать формулу СУММ, чтобы сложить результаты двух формул POW: =СУММ(POW(2, 3), POW(3, 2)) вернет 17, так как 2 * 2 * 2 = 8 и 3 * 3 = 9 и 8 + 9 = 17.
- Расчет сложных процентов: Формула POW может использоваться для расчета сложных процентов. Например, если у вас есть первоначальные инвестиции в размере 1000 долларов США, годовая процентная ставка 5%, и вы хотите рассчитать стоимость инвестиций через 10 лет, вы можете использовать формулу = 1000 * POW (1 + 0,05, 10) . Это вернет 1628,89 долларов США., что представляет собой стоимость инвестиций после 10 лет начисления сложных процентов.
Распространенные ошибки при использовании POW
Вот некоторые распространенные ошибки, которые пользователи допускают при использовании формулы POW в Google Таблицах:
- Неправильный порядок аргументов: Обязательно введите основание в качестве первого аргумента и показатель степени в качестве второй аргумент.
 Ввод аргументов в неправильном порядке приведет к неверным вычислениям.
Ввод аргументов в неправильном порядке приведет к неверным вычислениям. - Использование нечисловых значений: Формула POW требует числовых значений как для основания, так и для показателя степени. Если вы используете нечисловые значения или ссылки на ячейки, содержащие нечисловые значения, формула вернет ошибку.
- Забыли использовать круглые скобки: Если вы используете более сложную формулу в качестве аргумента для формулы POW, обязательно используйте круглые скобки, чтобы обеспечить правильный порядок операций. Например, если вы хотите возвести сумму 2 и 3 в степень 2, вы должны использовать формулу =POW((2 + 3), 2), а не =POW(2 + 3, 2).
Почему моя формула военнопленных не работает?
Если ваша формула POW не работает должным образом, вот несколько шагов по устранению неполадок, которые помогут вам определить и устранить проблему:
- Проверить наличие ошибок: Если ваша формула возвращает ошибку, убедитесь, что вы используете правильный синтаксис и что и основание, и показатель степени являются числовыми значениями или ссылками на ячейки, содержащими числовые значения.

- Проверьте значения аргументов: Дважды проверьте значения основания и показателя степени, чтобы убедиться, что они правильные. Если вы используете ссылки на ячейки, убедитесь, что указанные ячейки содержат правильные значения.
- Проверка циклических ссылок: Если ваша формула ссылается на ячейку, содержащую результат формулы, возможно, вы создали циклическую ссылку, что может привести к ошибкам или неправильным вычислениям. Убедитесь, что ваша формула не ссылается на собственный результат.
- Проверьте другие формулы: Если ваша формула POW является частью более крупного расчета, убедитесь, что другие задействованные формулы работают правильно и возвращают ожидаемые значения.
POW: Родственные формулы
Вот некоторые родственные формулы Google Sheets, которые могут оказаться полезными при работе с формулой POW:
- SQRT: Формула SQRT вычисляет квадратный корень числа.
 2, равное примерно 7,389..
2, равное примерно 7,389.. - LN: Формула LN вычисляет натуральный логарифм числа. Например, =LN(10) вернет натуральный логарифм 10, что приблизительно равно 2,303.
- LOG: Формула LOG вычисляет логарифм числа по указанному основанию. Например, =LOG(100, 10) вернет логарифм 100 по основанию 10, что равно 2.
- LOG10: Формула LOG10 вычисляет логарифм числа по основанию 10. Например, =LOG10(100) вернет логарифм числа 100 по основанию 10, что равно 2,9.0040
В заключение отметим, что формула POW — это мощный и универсальный инструмент в Google Таблицах, позволяющий вычислять степень числа. Поняв его синтаксис, используя его в различных примерах и применяя советы и приемы, представленные в этом руководстве, вы сможете эффективно использовать силу формулы POW в своих проектах Google Sheets.
Учебник по алгебре для среднего уровня 38
Алгебра для среднего уровня
Урок 38: Рациональные показатели
WTAMU > Виртуальная математическая лаборатория > Алгебра среднего уровня
Цели обучения
После завершения этого урока вы сможете:
- Перепишите рациональный показатель в радикальных обозначениях.

- Упростите выражение, содержащее рациональный показатель.
- Используйте рациональные показатели для упрощения подкоренного выражения.
Введение
В этом уроке мы собираемся объединить две идеи, которые обсуждались ранее. в более ранних уроках: экспоненты и радикалы. Мы посмотрим, как переписать, упростить и оценить эти выражения, содержащие рациональные экспоненты. К чему это сводится, если у вас есть знаменатель в вашем показателе это
 23: Экспоненты и научная нотация Часть I и Учебное пособие
24: Экспоненты и научная запись, часть II . Давай двигаться
на рациональные показатели и корни.
23: Экспоненты и научная нотация Часть I и Учебное пособие
24: Экспоненты и научная запись, часть II . Давай двигаться
на рациональные показатели и корни.
Учебник
Рациональные показатели и корни
Если x положительно, то p и q равны целые числа и q положительно,
Другими словами, когда у вас есть рациональный показатель степени, знаменатель этого показателя — ваш индекс или корневой номер и числитель экспонента — экспоненциальная часть.
Мне было легче думать об этом в двух частях. Найдите корень
сначала часть, а затем, если возможно, перейти к экспоненциальной части.
Это значительно упрощает работу с цифрами.
Радикальные показатели следуют точно таким же правилам порядка, как обсуждалось. в Урок 23: Экспоненты и научные Обозначения, Часть I и Учебное пособие 24: Экспоненты и научное обозначение, часть II . В тех два учебника мы имели дело только с целыми числами, но вы можете расширить эти правила к рациональным показателям.
Вот краткий обзор этих экспоненциальных правил:
Обзор экспоненциальных правил
Пример
1 : Используйте радикальное обозначение, чтобы записать выражение и упростить его.
*Переписать показатель степени 1/2 как квадратный корень
Ищем квадратный корень из 4, возведенный в степень 1, который это то же самое, что просто произнести квадратный корень из 4.
Если числитель вашей степени равен 1, вы просто ищете корень (показатель знаменателя).
Наш ответ 2 , так как квадратный корень из 4 равен 2.
Пример 2 : Используйте радикальное обозначение, чтобы написать выражение и упростить его.
*Переписать показатель степени 2/3 как
кубический корень в квадрате
В этой задаче мы ищем кубический корень из -27 в квадрате. Опять же, я думаю, что проще сначала сделать корневую часть, если это возможно.
С цифрами будет легче работать.
Опять же, я думаю, что проще сначала сделать корневую часть, если это возможно.
С цифрами будет легче работать.
Кубический корень из -27 равен -3, а (-3) в квадрате равен 9.
Пример 3 : Используйте радикальное обозначение, чтобы записать выражение и упростить его.
*Запишите показатель степени 3/2 как
квадратный корень в кубе
В этой задаче мы ищем квадратный корень из 36/49 в кубе. Опять же, я думаю, что проще сначала сделать корневую часть, если это возможно.
С цифрами будет легче работать.
Опять же, я думаю, что проще сначала сделать корневую часть, если это возможно.
С цифрами будет легче работать.
Квадратный корень из 36/49 равен 6/7, а 6/7 в кубе равен 216/343.
Пример 4 : Пишите с положительным показателем степени и упрощайте.
*Переписать как получатель. базы
поднят в поз. эксп.
*Переписать показатель степени 5/3 как
кубический корень в 5-й степени
В этой задаче мы ищем кубический корень из 1/8, возведенный в
пятая власть. Опять же, я думаю, что проще сначала сделать корневую часть
если возможно. С цифрами будет легче работать.
Опять же, я думаю, что проще сначала сделать корневую часть
если возможно. С цифрами будет легче работать.
Кубический корень из 1/8 равен 1/2, а 1/2 в пятой степени равен
1/32.
Пример 5 : Упростите выражение. Пишите с положительными показателями только.
* Возведение основания в два порядка,
мульт. эксп.
*Переписать как рецепт. базы
поднят в поз. эксп.
 Пишите только с положительными показателями.
Пишите только с положительными показателями.
* Умножать как основания, доп.
опыт
* Разделить как основания, суб.
опыт
*Переписать как рецепт. базы
поднят в поз. эксп.
Пример 7 : Умножить.
Поскольку это бином, умноженный на бином, мы можем использовать Метод FOIL , описанный в учебном пособии . 26: Умножение многочленов .
26: Умножение многочленов .
* Умножать как основания, доп.
опыт
Пример 8 : Разложите общий множитель из заданного выражения.
По сути, мы выделяем GCF, как обсуждалось в Tutorial. 27: ЗКФ и факторинг по группе . Помните, когда вы вычеркнув GCF, мы делаем обратное распределительному свойству.
*Разложить x на 1/4
Пример
9 : Используйте рациональные показатели, чтобы упростить радикал. Предположим, что переменная представляет положительное число.
Предположим, что переменная представляет положительное число.
*Переписать восьмой корень из x в квадрате как x в степени 2/8
*Упростить показатель степени
*Переписать показатель степени 1/4 как
четвертый корень
Практические задачи
Это практические задачи, которые помогут вам
следующий уровень.
Это позволит вам проверить и понять, понимаете ли вы
эти
виды проблем. Математика работает так же, как
что-либо
иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться
это. Даже лучшие спортсмены и музыканты получали помощь на этом пути и много
практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.
Даже лучшие спортсмены и музыканты получали помощь на этом пути и много
практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.
Чтобы получить максимальную отдачу от этого, вы должны работать проблема на свой собственный, а затем проверьте свой ответ, нажав на ссылку для ответ/обсуждение для этой задачи . По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа.
Практика Задачи 1a — 1c: Используйте подкоренную запись, чтобы записать выражение и упростить его.
1а.
(ответ/обсуждение
к 1а)
1б.
(ответ/обсуждение
к 1b)
1c.
(ответ/обсуждение
к 1с)
Практика Задача 2а: Напишите с положительным показателем степени и упростите.
2а.
(ответ/обсуждение
к 2а)
Практика Задачи 3a — 3b: Упростите выражение, запишите с положительными показателями только.
3а.
(ответ/обсуждение
до 3а)
3б.
(ответ/обсуждение
к 3б)
Практика Задача 4а: Умножить.

4а.
(ответ/обсуждение
к 4а)
Практика Задача 5a: Выразите общий множитель из данного выражения.
5а.
(ответ/обсуждение
к 5а)
Практика Задача 6a: Используйте рациональные показатели, чтобы упростить радикал. Предположим, что переменная представляет положительное число.
6а.
(ответ/обсуждение
к 6а)
Нужна дополнительная помощь по этим темам?
Перейти к получению
Помощь за пределами
Классная комната в Учебнике 1: Как добиться успеха на уроке математики для
некоторый
больше предложений.


 Например, =POW(-2, 3) вернет -8, так как -2 * -2 * -2 = -8.
Например, =POW(-2, 3) вернет -8, так как -2 * -2 * -2 = -8. Например, =POW(27, 1/3) вернет 3, так как кубический корень из 27 равен 3.
Например, =POW(27, 1/3) вернет 3, так как кубический корень из 27 равен 3.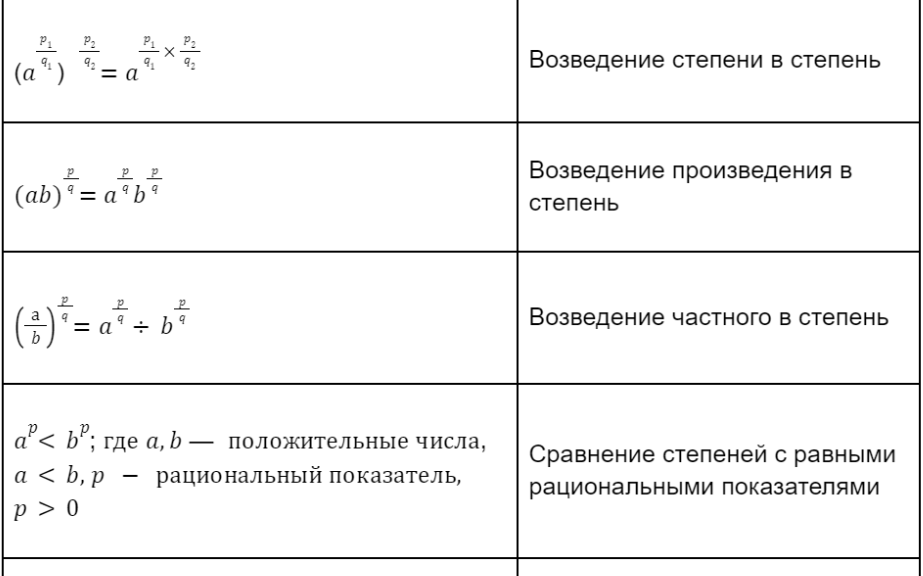 Ввод аргументов в неправильном порядке приведет к неверным вычислениям.
Ввод аргументов в неправильном порядке приведет к неверным вычислениям.
 2, равное примерно 7,389..
2, равное примерно 7,389..
