Как факториал делить на факториал: Факториал — урок. Алгебра, 9 класс.

Занимательная математика, очаровательный python. Эпизод 1: Факториалы

Этот цикл статей я хочу посвятить обзору математических возможностей python 2.7. Вместе с моей любимой змеёй мы окунёмся в тайны математики и напишем такие функции, который просто поразят воображение. Итак, запускайте python, включайте голову, вперёд!

Нам понадобятся:

1. Python (я буду использовать версию 2.7.5 под Windows 64 bit)
2. Мозги (я буду пользовать свои с примесью google и wikipedia)

• Факториал

Факториалы манили меня еще в школе. Красивое слово, необычный (для того времени) синтаксис. Я всегда с некоторой издевкой мог блеснуть талантом, ”вычисляя” факториал простого числа. Став старше, и особенно влюбившись в python, моя страсть к факториалам не просто не уменьшилась, скорее наоборот, именно поэтому эта статья полностью будет посвящена всевозможным факториалам. Но сначала немного математики. Итак,

Факториалом числа n (обозначается n!) называется произведение всех натуральных  чисел от 1 до n.

Иными словами,

6! = 1*2*3*4*5*6 = 720

Физический смысл (если так можно сказать) факториала определяется как число упорядочиваний  множества из n элементов. Переводя с непонятного на русский, давайте представим себе колоду из 36 карт. Каждый раз, когда мы тасуем эту колоду мы создаем уникальное упорядочивание, одно из 36! = 371993326789901217467999448150835200000000. Возможно, именно поэтому карточные игры так популярны! 🙂

Но ближе к делу! Наверняка каждый, кто изучал python, знает как вычислить факториал, причем не одним способом. Когда изучают lambda-функции, пишут так:

factorial = lambda x: factorial(x-1) * x if x > 0 else 1

… и мало кто что понимает!

Когда изучают рекурсию, пишут так:

def factorial(x):
    if x == 0:
        return 1
    elif x > 0:
        return factorial(x-1) * x

Это уже понятней! А те, кто совсем хорошо знают python, вообще не парятся и делают так:

import math
math. factorial(5)

Но мы пойдём своим путём. Мы не будем использовать math, вместо этого мы напишем свой собственный модуль. Откройте свой любимый редактор (я буду пользоваться стандартным IDLE), создайте файл factorials.py и давайте творить! В качестве простейшей задачи сначала давайте определим функцию для вычисления факториала. Я буду делать это с помощью lambda, как в первом примере:

def factorial(x):
    result = lambda x: result(x-1) * x if x > 0 else 1
    return result(x)

Теперь, если запустить скрипт на выполнение, то можно будет прямо в интерактивном интерпретаторе набрать

import factorials
factorials.factorial(5)
120

Казалось бы супер! И все примеры, которые можно найти в интернете здесь заканчиваются на позитивной ноте, однако как обычно все не так просто. На самом деле наша функция абсолютно некорректна и простейший способ проверить это — передать ей неадекватное значение. И если с совсем бредятинкой типа

”str” python справится сам, то вот значение типа ”float” легко пропустит. Не верите? Попробуйте посчитать факториал 4.125. Не бином Ньютона, что наша новорожденная функция должна работать только с целочисленным типом данных, следовательно нужно переписать её так:

def factorial(x):
    if type(x) == int:
        result = lambda x: result(x-1) * x if x > 0 else 1
        return result(x)
    else:
        raise TypeError, "The given value must be integer, not %s"%type(x)

Во-о-о-т! Теперь скормить ересь не получится, так как сразу будет подниматься TypeError. Но и это еще не всё. Если мы попробуем посчитать факториал -5 (минус пяти), то получим в ответ единицу, а это тоже неадекватно. Факториал определяется только для целых и положительных цифр, следовательно нужно ещё раз переписать код.

def factorial(x):
    if type(x) == int and x >= 0:
        result = lambda x: result(x-1) * x if x > 0 else 1
        return result(x)
    else:
        raise TypeError, "The given value must be positive integer, not %s"%(type(x) if type(x) != int else "negative")

Для эстетов еще могу порекомендовать обработать значения типа ”float”, которые по сути являются целыми, типа 25. 0, 12.0 etc. Я этого делать не буду, так как предпочитаю более жёстко обращаться с типами данных.

• Обратный факториал

Простейшая задача выполнена, но я бы не стал городить всё это только ради простейшей задачи! 🙂 Куда более интересно найти обратный факториал.  Легко догадаться, что

Обратным факториалом числа i называется такое число, факториал которого будет равен i.

То есть если 4! = 24, то обратным факториалом 24 будет 4. Функция для обратного факториала несколько сложнее. Для начала нужно понять механизм её работы. Если считая факториал числа мы последовательно умножаем цифры, то, как не сложно догадаться, здесь мы должны последовательно делить. Для себя я написал такой алгоритм работы функции: последовательно делим число на 1, 2, 3, 4 etc., до тех пор, пока не получим 1 и тогда возвращаем последний делитель. Но перед тем как начать писать код небольшое лирическое отступление. С помощью нашей функции вычислите факториал 4000. И получаем мы RuntimeError: maximum recursion depth exceeded. Печально? На самом деле ничего страшного не произошло, просто python ограничивает глубину рекурсии, что на мой взгляд правильно. Для того, чтобы посмотреть глубину рекурсии необходимо либо в интерпретаторе, либо где кому удобно импортировать модуль

sys и выполнить функцию sys.getrecursionlimit(). В ответ вы скорее всего получите 1000, но лично у меня питон падает при вычислении факториала 995, хотя глубина рекурсии стоит 1000. Это на самом деле не важно, так как можно легко увеличить (но будьте разумны!) глубину путем вызова функции sys.setrecursionlimit(5000) например до 5000. Собственно, к чему все это? А к тому, что функция sys.getrecursionlimit() пригодится нам для написания своей функции обратного факториала. Итак, первым делом мы должны проверить поступающее значение на валидность. Также как и с факториалом, мы будем работать только с целыми положительными цифрами, следовательно

def antifactorial(x):
    if type(x) == int and x >= 0:
        # do_something
    else:
        raise TypeError, "The given value must be positive integer, not %s"%(type(x) if type(x) != int else "negative")

Теперь наша задача сводится к тому, чтобы последовательно делить x на числа от 1 и до… догадались? До sys. getrecursionlimit()+1! Решение вполне простое и изящное. Можно было, конечно, задать какое-нибудь произвольное число, например 500. Однако, давайте представим себе, что пользователь вычислил факториал 900, взял это число и подставил его в нашу функцию. Вы поняли что произойдет, я уверен. Наш антифакториал будет делить и делить до тех пор, пока не дойдет до 500, а затем остановится. Но мы должны были делить последовательно до 900! В общем, для того, чтобы не париться с такой фигнёй и было реализовано такое решение. Смысл его прост — посчитать факториал 3000 можно только увеличив глубину рекурсии допустим до 4000, а это в свою очередь одновременно увеличит и нашу последовательность, следовательно, антифакториал также будет найден! А сейчас, волшебным образом я сразу покажу функцию антифакториала!))

def antifactorial(x):
    if type(x) == int and x >= 0:
        for each in range(1, sys.getrecursionlimit()+1):
            x = float(x)/float(each)
            if x != 1. 0 and x > 1.0:
                continue
            elif x != 1.0 and x < 1.0:
                raise ValueError,"The given value is not a factorial"
            else:
                return each
                break
    else:
        raise TypeError, "The given value must be positive integer, not %s"%(type(x) if type(x) != int else "negative")

Теперь логика 🙂 Сначала мы проверяем валидность данных, потом начинаем последовательно делить число, причем важно, что мы делим именно преобразованные во ”float” значения. Для того, чтобы понять смысл этого преобразования прямо в интерпретаторе разделить 8 на 3. Почему вы получаете 2 я расскажу как нибудь потом, для нас же важно точное значение. Разделите 8.0 на 3.0 и увидите разницу. На самом деле цикл работает довольно просто. Мы делим значение на 1, проверяем равно ли получившееся 1.0 или больше 1.0. Если значение не равно 1.0 и больше 1.0, то инструкция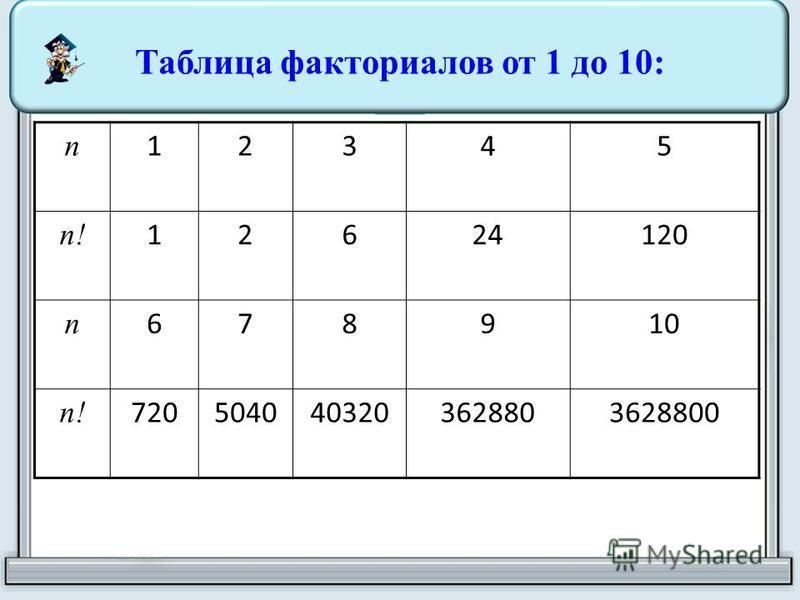

continue продолжает цикл, мы делим значение на 2 , проверяем etc. Если вдруг значение не равно 1.0, и при этом уже меньше 1.0, значит данное число не было факториалом и нам нужно выйти из цикла, возбудив ValueError. Мы выходим из цикла для того, чтобы попусту не заставлять python тратить ресурсы на прогон по всему циклу, что логично. Если же значение строго рано 1.0, то мы опять же выходим из цикла и возвращаем тот делитель, на котором этот выход произошел. Строго говоря, можно (и нужно!) еще сократить цикл — смысла делить на 1 тоже нет. Теперь можно потестировать наш

antifactorial. К примеру:

antifactorial(-2)
TypeError: The given value must be positive integer, not negative
antifactorial(2)
2
antifactorial(12)
ValueError: The given value is not a factorial
antifactorial(720)
6
antifactorial("720")
TypeError: The given value must be positive integer, not <type 'str'>

Таким образом мы написали пару функций — прямую и обратную, которые помогут нам как посчитать факториал числа, так и выяснить факториалом какого числа является (если вообще является) другое число. Дальше будет проще, но интересней!

• Суперфакториал

Суперфакториал придумали в 1995 году Нейл Слоан и Саймон Плоуф (англ.) и определили они его как произведение факториалов. Иными словами,

sf(4) = 1!*2!*3!*4! = 288

Функция для нахождения суперфакториала элементарна до безобразия, я даже не буду особо распинаться:

def superfactorial(x):
    if type(x) == int and x >= 0:
        result = lambda x: result(x-1) * factorial(x) if x > 0 else 1
        return result(x)
    else:
        raise TypeError, "The given value must be integer, not %s"%(type(x) if type(x) != int else "negative")

Знакомо, не правда ли? По сути, это та же самая функция, что и факториал, но только умножение происходит не на x, а на factorial(x)!

• Обратный суперфакториал

Также элементарен и обратный суперфакториал:

def antisuperfactorial(x):
    if type(x) == int and x >= 0:
        for each in range(2, sys. getrecursionlimit()+1):
            x = float(x)/flactorial(each)
            if x != 1.0 and x > 1.0:
                continue
            elif x != 1.0 and x < 1.0:
                raise ValueError,"The given value is not a superfactorial"
            else:
                return each
                break
    else:
        raise TypeError, "The given value must be positive integer, not %s"%(type(x) if type(x) != int else "negative")

Здесь мы делим в свою очередь не на число, а на факториал числа.

• Гиперфакториалы

Энтузиасты не остановились на суперфакториалах и в 2000 году  Генри Боттомли (англ.) создал гиперфакториалы, которые являются произведением суперфакториалов. Я не буду впадать в маразм и функцию мне писать лень, но о произведении гиперфакториалов, произведении произведения гиперфакториалов etc. я умолчу 😛

def hyperfactorial(x):
    if type(x) == int and x >= 0:
        result = lambda x: result(x-1) * superfactorial(x) if x > 0 else 1
        return result(x)
    else:
        raise TypeError, "The given value must be integer, not %s"%(type(x) if type(x) != int else "negative")

 Функция гиперфакториала повторяет суперфакториал, только вместо умножения на factorial(x) мы умножаем на superfactorial(x). Обратный гиперфакториал я предлагаю вам написать самостоятельно, это не составит вообще никакой сложности.

• Двойной факториал

Не намного более сложной задачей является написание функции двойного факториала.  Сначала разберемся, что это собственно такое.

Двойным факториалом числа n (n!!) называется произведение всех натуральных чисел от 1 до n, имеющих ту де чётность, что и n.

Соответственно можно написать такую функцию:

def doublefactorial(x):
    if type(x) == int and x >= 0:
        result = lambda x: result(x-2) * x if x > 0 else 1
        return result(x)
    else:
        raise TypeError, "The given value must be positive integer, not %s"%(type(x) if type(x) != int else "negative")

Смысл такой же как и у обычного факториала, только с одной особенностью — шаг рекурсии не 1, а 2 (так как нам нужно идти строго по чётным или нечётным числам).

• Обратный двойной факториал

Обратный двойной факториал — это ненамного сложнее, чем обычный обратный факториал. Я реализовал её на мой взгляд не самым изящным способом, но пока нет желания как-то сокращать код. Основное отличие от обычных обратных факториалов в том, что мы должны делить не последовательно на 2, 3, 4,5 etc., но последовательно с шагом 2 и начинать деление либо с 2, либо с 3 в зависимости от чётности.  Собственно реализация:

def antiDoubleFactorial(x):
    if type(x) == int and x >= 0:
        if x % 2 == 0:
            for each in [z for z in range(2, sys.getrecursionlimit()) if z % 2 == 0]:
                x = float(x)/float(each)
                if x != 1.0 and x > 1.0:
                    continue
                elif x != 1.0 and x < 1.0:
                    raise ValueError,"The given value is not a factorial"
                else:
                    return each
                    break
        else:
            for each in [z for z in range(1, sys.getrecursionlimit()) if z % 2 != 0]:
                x = float(x)/float(each)
                if x != 1. 0 and x > 1.0:
                    continue
                elif x != 1.0 and x < 1.0:
                    raise ValueError,"The given value is not a factorial"
                else:
                    return each
                    break
    else:
        raise TypeError, "The given value must be positive integer, not %s"%(type(x) if type(x) != int else "negative"

Поскольку произведение чётных факториал есть чётное число, мы можем воспользоваться генераторами списков для создания как чётной, так и нечётной последовательностей. Все остальное элементарно.

Тест на внимательность!

Если вы дочитали до сюда, то наверняка уже не раз нашли ошибки в коде.  Нет? Что же, давайте тогда вычислим 0! и 1!. А теперь antifactorial(1)! Именно! Мы совсем забыли об этой единице. Но давайте обратим на неё внимание теперь. Факториал, суперфакториал, гиперфакториал и двойной факториал нуля и единицы равен одному. Разумеется, нам необходимо научить наши функции возвращать значения, причем сразу два. Новичок начнет сразу переписывать все обратные функции, вводить эти конструкции ”если-то”. Мы — не новички!:-) Мы возьмем и напишем декоратор! Я сейчас не буду вдаваться в подробности о декораторах, этим на примере этого же модуля займусь завтра, когда у меня будет время, а сейчас просто напишу этот декоратор. Просто без комментариев:

def constant(function):
    def wrapper(x):
        if x == 1:
            return [0,1]
    return wrapper

 Теперь перед всеми обратными функциями достаточно прописать инструкцию @constant и все будет в порядке!

На этом разрешите пока остановиться. В следующей части мы познакомимся с праймориалами и факторионами, а также научимся (если вдруг кто не умел) генерировать последовательности всех этих кракозябр. После же того, как мы закончим с математикой, мы преобразим наш код в нечто декорированное! 🙂

Понравилось это:

Нравится Загрузка…

Делимые факториалы | Общество | Селдон Новости

Недавно я был совершенно сбит с толку этим твитом «Библиотеки Ферма»:

«Вот что получится, если в факториале не умножать, а делить. »

Когда я увидел его, мне пришлось бросить свои дела, схватить блокнот и проверить форулу. Результат в черновом виде казался логичным. Так как мультипликативная версия при увеличении стремится к бесконечности, то «делительная» версия должна стремиться к нулю. И ведёт себя именно так; полиномиальная функция растёт медленнее, чем степенная функция для достаточно больших :

Но почему результат деления принимает именно вид

? Откуда берётся

?

Чтобы ответить на этот вопрос, мне пришлось разбередить старую травму, связанную с изучением деления дробей, но я справился с болью. Двигаясь по формуле из твита слева направо, мы сначала получаем

. Затем, поделив эту величину на

, получаем

Продолжая таким образом, мы в результате приходим к:

Чтобы прийти к показанному в твите результату

, мы просто умножим числитель и знаменатель на

. (Хотя на мой вкус, выражение

более понятно.)

Я официально признанный фанат факториалов. Оставьте при себе свои последовательности Фибоначчи; вот моя любимая функция. Каждый раз, когда я изучаю новый язык программирования, моим первым упражнением становится написание нескольких процедур для вычисления факториалов. За многие годы я придумал несколько вариаций этой темы, например, замену в определении на (что даёт нам треугольные числа). Но кажется, что раньше я никогда не задумывался о замене на . Получается странно. Так как умножение коммутативно и ассоциативно, мы можем определить просто как произведение всех целых чисел от до , не беспокоясь о порядке операций. Но при делении порядок игнорировать не получится. В общем случае, и .

В твите «Библиотеки Ферма» делители поставлены в порядке по убыванию: . Очевиднее всего будет заменить это на порядок по возрастанию: . Что произойдёт, если мы зададим факториал деления как ? Ещё один возврат к школьному алгоритму деления дробей даёт нам простой ответ:

Другими словами, когда мы многократно выполняем деление, выполняя подсчёт от

до

, окончательный результат будет равен величине, обратной

. (Мне хотелось бы поставить в конце этого предложения восклицательный знак, но увы!) Если вы ищете канонический ответ на вопрос «Что мы получим при делении вместо умножения в

?», то я бы заявил, что

— лучший кандидат, чем

. Почему бы нам не принять симметрию между

и обратной ему величиной?

Разумеется, есть множество других способов размещения n целочисленных значений во множестве . Но сколько именно? Как оказалось, ровно ! Поэтому, может показаться, что есть уникальных способов задания делительной функции . Однако, изучение ответов двух показанных выше перестановок даёт нам понять, что здесь работает более простой паттерн. Какой бы элемент последовательности не появился первым, он оказывается в числителе большой дроби, а знаменателем оказывается произведение всех других элементов. Поэтому в итоге остаётся всего различных результатов (если предположить, что мы всегда выполняем операции деления строго слева направо). Для любого целочисленного в интервале от до , поставив в начало очереди, мы создаём делительное , равное , поделённому на все другие коэффициенты. Можно записать это следующим образом:

И таким образом мы решили небольшую загадку о том, как в этом твите

превратилось в

.
Стоит заметить, что все эти функции сходятся к нулю при стремлении

к бесконечности. С асимптотической точки зрения,

идентичны.

Та-да! Миссия выполнена. Задача решена. Дело сделано. Теперь мы знаем всё, что нам нужно, о делительных факториалах, верно?

Ну, возможно, есть ещё один вопрос. Что скажет компьютер? Если взять наш любимый алгоритм факториала, и сделать то, что предлагается в твите, заменив все вхождения оператора (или *) на /, то что случится? Какие из вариантов делительного выдаст нам программа?

Вот мой любимый алгоритм для вычисления факториалов в виде программы на Julia:

function mul!(n) if n == 1 return 1 else return n * mul!(n - 1) end end

Этот алгоритм познакомил целые поколения нердов с концепцией рекурсии. В текстовом виде он гласит: если

равно

, то

равно

. В противном случае нужно вычислить функцию

, а затем умножить результат на

.

_{Вы можете спросить, что произойдёт, если будет равным нулю или отрицательным. Спросить вы можете, но лучше не надо. Для наших текущих целей .}

Начав с любого положительного , последовательность рекурсивных вызовов рано или поздно опустится к .

Функцию можно записать более лаконично с помощью однострочного стиля определений Julia:

mul!(n) = n == 1 ? 1 : n * mul!(n - 1)

Правая часть оператора присваивания — это условное выражение, или тернарный оператор, имеющий вид a ? b : c. Здесь a — булево условие теста, которое должно вернуть значение или true, или false. Если a равно true, то вычисляется выражение b, а результат становится значением всего выражения. В противном случае вычисляется c.

Просто чтобы убедиться, что я сделал всё верно, вот первые 10 факториалов, вычисленных этой программой:

[mul!(n) for n in 1:10] 10-element Array{Int64,1}: 1 2 6 24 120 720 5040 40320 362880 3628800

Теперь давайте изменим это определение и преобразуем единственное вхождение * в /, оставив всё остальное неизменным (за исключением названия функции).

div!(n) = n == 1 ? 1 : n / div!(n - 1)

И вот что вернёт программа, если мы запустим её для значений

от

до

:

[div!(n) for n in 1:20] 20-element Array{Real,1}: 1 2.0 1.5 2.6666666666666665 1.875 3.2 2.1875 3.657142857142857 2. 4609375 4.063492063492063 2.70703125 4.432900432900433 2.9326171875 4.773892773892774 3.14208984375 5.092152292152292 3.338470458984375 5.391690662278897 3.523941040039063 5.675463855030418

Что? Это точно не походит на схождение к нулю, как и на

или

. На самом деле значения так не выглядят, потому что и не собираются сходиться. Судя по показанному ниже графику, последовательность состоит из двух перемежающихся компонентов, каждый из которых, похоже, медленно растёт в сторону бесконечности, а также отклоняется от другого.

Разбираясь с тем, что же мы здесь наблюдаем, полезно будет изменить тип выходных данных функции div!. Вместо использования оператора деления /, который возвращает значение как число с плавающей запятой, мы можем заменить его оператором //, возвращающим точное рациональное значение, округлённое до младшего члена.

div!(n) = n == 1 ? 1 : n // div!(n - 1)

Вот последовательность значений для n в интервале 1:20:

20-element Array{Real,1}: 1 2//1 3//2 8//3 15//8 16//5 35//16 128//35 315//128 256//63 693//256 1024//231 3003//1024 2048//429 6435//2048 32768//6435 109395//32768 65536//12155 230945//65536 262144//46189

В списке полно любопытных паттернов. Это двойная спираль, в которой чётные и нечётные числа зигзагами перемещаются в комплементарных нитях. Чётные числа не просто чётные, все они являются степенями

. Кроме того, они появляются в парах — сначала в числителе, затем в знаменателе — и их последовательность неубывающая. Но существуют пробелы; присутствуют не все степени

. Нечётная нить выглядит ещё более сложной, в числах появляются и исчезают разные небольшие простые коэффициенты. (Простые числа должны быть малыми, как минимум, меньше

. )

Этот результат удивил меня. Я ожидал увидеть гораздо более смирную последовательность, наподобие тех, которые я вычислял на бумаге. Все эти изломанные скачки вверх и вниз не имели никакого смысла. Как не имел смысла и общий тренд к неограниченному росту соотношения. Как мы можем постоянно делить, получая при этом всё бОльшие и бОльшие числа?

На этом этапе можете приостановить чтение и попытаться придумать собственную теорию о том, откуда взялись эти зигзагообразные числа. Если вам нужна подсказка, то у вас она есть, и очень сильная, почти спойлер: поищите последовательность числителей или последовательность знаменателей в «Онлайн-энциклопедии целочисленных последовательностей».

Вот ещё одна подсказка. Небольшое изменение в программе div! полностью преобразует выходные данные. Просто изменим последнее выражение, заменив n // div!(n - 1) на div!(n - 1) // n.

div!(n) = n == 1 ? 1 : div!(n - 1) // n

Теперь результаты выглядят вот так:

10-element Array{Real,1}: 1 1//2 1//6 1//24 1//120 1//720 1//5040 1//40320 1//362880 1//3628800

Это обратная функция факториала, которую мы уже видели, ряд значений, сгенерированные при обходе слева направо по возрастающей последовательности делителей

.

Неудивительно, что изменение последнего выражения в процедуре менят результат. В конце концов, мы знаем, что деление не коммутативно и не ассоциативно. Но сложно понять, почему последовательность сгенерированных исходной программой значений даёт такую странную зигзагообразную форму. Какой механизм порождает такие парные степени двойки и попеременные нечётные и чётные значения?

Я обнаружил, что объяснить происходящее в зигзагообразной последовательности проще на итеративной версии процедуры, а не на рекурсивной. (Это заявление может показаться досадным тем, кто считает рекурсивные определения более простыми, но так уж получилось.) Вот как выглядит программа:

function div!_iter(n) q = 1 for i in 1:n q = i // q end return q end

Я заявляю, что эта процедура с циклом по функционалу идентична рекурсивной функции, в том смысле, что если div!(n) и div!_iter(n) возвращают результат для какого-то положительного целого n, то он всегда будет одинаковым. Вот моё доказательство:

[div!(n) for n in 1:20] [div!_iter(n) for n in 1:20] 1 1//1 2//1 2//1 3//2 3//2 8//3 8//3 15//8 15//8 16//5 16//5 35//16 35//16 128//35 128//35 315//128 315//128 256//63 256//63 693//256 693//256 1024//231 1024//231 3003//1024 3003//1024 2048//429 2048//429 6435//2048 6435//2048 32768//6435 32768//6435 109395//32768 109395//32768 65536//12155 65536//12155 230945//65536 230945//65536 262144//46189 262144//46189

Чтобы понять процесс, порождающий эти числа, рассмотрим последовательные значения переменных

и

при каждом выполнении цикла. Изначально

и

равны

; поэтому после первого прохода цикла выражение q = i // q даёт

значение

. Затем

, а

, то есть новое значение

равно

. При третьей итерации

, а

, что даёт нам

. Если это всё ещё сбивает вас с толку, то представьте

как

. Важным наблюдением здесь является то, что при каждом обходе цикла

получает обратное значение, становясь

.

Если развернуть эти операции и посмотреть на умножения и деления, входящие в каждый элемент ряда, то возникает паттерн:

В общем виде:

Функции для нечётного и для чётного имеют собственное название! Они называются двойными факториалами, и записываются как .

_{Ужасная терминология, правда? Лучше бы их назвали «полуфакториалами». И если бы я этого не знал, то прочитал бы как «факториал факториала».}

Двойной факториал n определяется как произведение n и всех меньших положительных целых чисел той же чётности. Таким образом, наша любопытная последовательность зигзагообразных значений — это просто .

В статье 2012 года Генри У. Гулда и Джослин Куэнтенс (увы, находящаяся за paywall) исследуются применения двойных факториалов. Они встречаются гораздо чаще, чем можно подумать. В середине 17-го века Джон Валлис вывел следующее тождество:

Ещё более странный ряд с участием куба значений двойных факториалов суммируется в

. Его обнаружил не кто иной, как Сриниваса Рамануджан.

Гулд и Киэнтенс также рассматривали эквивалент двойного факториала для биномиальных коэффициентов. Стандартный биномиальный коэффициент определяется как:

Двойная версия выглядит так:

Заметьте, что наши зигзагообразные числа соответствуют этому описанию, а потому могут считаться биномиальными коэффициентами двойных факториалов. Говоря конкретнее, они являются такими числами:

Обычный бином

не очень интересен; он просто равен

. Но двойная версия

, как мы видели, танцует более оживлённый танец. И в отличие от обычного бинома она не всегда бывает целочисленной. (Единственные целые значения — это

и

.)

Взгляд на зигзагообразные числа как на частное двойных факториалов объясняет довольно многие их свойства, начиная с попеременных чётных и нечётных значений. Также мы можем увидеть, почему все чётные числа в последовательности являются степенями 2. Рассмотрим пример с . Числитель этой дроби — это , получающий от множитель . Но знаменатель равен . Тройки сверху и снизу сокращаются, оставляя нам . Такие сокращения происходят в каждом из случаев. Каждый раз, когда в последовательности чётных чисел появляется нечётный множитель , он обязательно имеет вид , но к этому времени само уже должно появиться в последовательности нечётных чисел.

Является ли последовательность зигзагообразных чисел разумным ответом на вопрос: «Что произойдёт, если мы будем делить, а не умножать в ?» Или генерирующая их компьютерная программа просто оказалась ошибочным алгоритмом? По моему личному мнению, — более интуитивный ответ, зато — более интересный.

Более того, само существование зигзагообразной последовательности расширяет наши горизонты. Как сказано выше, если вы настаиваете, что алгоритм деления всегда должен по порядку проходить по списку числителей , на каждом шаге деля число слева на число справа, то имеется всего возможных результатов, и все они выглядят очень похожими. Но зигзагообразное решение обеспечивает намного более широкие возможности. Мы можем сформулировать задачу следующим образом: возьмём множество числителей , выберем его подмножество и обратим все элементы этого подмножества; теперь перемножим все числители, как обратные, так и прямые. Если обращённое подмножество пусто, то результатом будет обычный факториал . Если все числители превратились в обратные им значения, то мы получаем обратный . А если обращён каждый второй числитель, начиная с , то результатом будет элемент зигзагообразной последовательности.

Это только некоторые из множества возможных вариантов; в сумме здесь есть подмножеств из элементов. Например, можно брать обратные значения каждого числа, являющегося простым или степенью простого числа . При малых результаты скачут, но постоянно остаются меньше, чем :

Однако если бы я продолжил этот график для бОльших

, он бы взлетел в стратосферу. Степени простых чисел становятся очень разреженными на числовой прямой.

Теперь я задам вопрос. Мы видели вариации факториалов, приближающиеся к нулю при стремлении к бесконечности, например . Мы видели другие вариации, растущие при увеличении безгранично, в том числе сам и зигзагообразные числа. Существуют ли какие-то разновидности процесса факториалов, сходящиеся к какой-то конечной границе, не являющейся нулём?

В первую очередь мне пришёл в голову такой алгоритм:

function greedy_balance(n) q = 1 while n > 0 q = q > 1 ? q /= n : q *= n n -= 1 end return q end

Мы циклически перебираем целые значения от

вниз до

, вычисляя в процессе текущее произведение/частное

. На каждом шаге, если текущее значение

больше

, мы делим его на следующий числитель, в противном случае, выполняем умножение. Эта схема реализует своего рода управление обратной связью или поведение поиска цели. Если

становится слишком большим, мы уменьшаем его; если слишком маленьким, мы увеличиваем его. Я предположил, что при стремлении

к бесконечности,

будет сходиться к постоянно сужающемуся интервалу значений рядом с

.

Но эксперимент подкинул мне ещё один сюрприз:

Такая пилообразная волна — не совсем то, чего я ожидал. Любопытно, что кривая не симметрична около

; отклонения сверху имеют бОльшую амплитуду, чем снизу. Но это искажение больше визуальное, чем математическое. Так как

является частным, расстояние от

до

такое же, как расстояние от

до

, но в линейном масштабе таким не выглядит. Исправить это можно, составив логарифмический график частного:

Теперь график симметричен, или хотя бы приблизительно таков, и центрирован относительно значения

, которое является логарифмом

. Но остаётся более серьёзная тайна. Пилообразная волна очень регулярна и имеет период

, при этом не показывает признаков сжатия по направлению к ожидаемому ограничивающему значению

. Численные значения предполагают, что при стремлении

к бесконечности пики кривой сходятся к значению чуть выше

, а минимумы приближаются к значению чуть ниже

. (Соответствующие логарифмы по основанию

примерно равны

). Мне не удалось разобраться, почему так происходит. Возможно, кто-то сможем объяснить.

Неудача с этим жадным алгоритмом не означает, что мы не сможем делительный факториал, сходящийся к .

_{Если мы будем работать с логарифмами числителей, то эта процедура становится случаем хорошо известной вычислительной задачи под названием «задача разбиения множества чисел». Нам даётся множество вещественных чисел, и мы должны разделить их на два множества, сумма которых равна, или как можно ближе к равенству. Это подтверждённо сложная задача, но её также называют (PDF) «простейшей сложной задачей».}

Для любого мы можем обнаружить, что при использовании обратных значений какого-то другого подмножества числителей даёт нам лучшее приближение к . Для малых мы можем решить эту задачу способом перебора: просто рассмотреть все подмножеств и выбрать самое лучшее.

Я вычислил оптимальные разбиения вплоть до , когда выбирать нужно из миллиарда вариантов.

Очевидно, что график становится всё более плоским. Можно использовать тот же метод для принудительного схождения к любому другому значению в интервале от

до

.

И таким образом мы получаем ещё один ответ на вопрос, заданный твитом и начавший наше путешествие. Что произойдёт, если мы будем делить, а не умножать в ? Всё, что нам угодно.

Факториалы умножения и деления — Математика средней школы

• Войти
• Биографии репетитора
• Подготовка к тесту

  СРЕДНЯЯ ШКОЛА

  • ACT Репетиторство
  • SAT Репетиторство
  • Репетиторство PSAT
  • ASPIRE Репетиторство
  • ШСАТ Репетиторство
  • Репетиторство STAAR

  ВЫСШАЯ ШКОЛА

  • Репетиторство MCAT
  • Репетиторство GRE
  • Репетиторство по LSAT
  • Репетиторство по GMAT

  К-8

  • Репетиторство AIMS
  • Репетиторство по HSPT
  • Репетиторство ISEE
  • Репетиторство ISAT
  • Репетиторство по SSAT
  • Репетиторство STAAR

  Поиск 50+ тестов

• Академическое обучение

  репетиторство по математике

  • Алгебра
  • Исчисление
  • Элементарная математика
  • Геометрия
  • Предварительный расчет
  • Статистика
  • Тригонометрия

  репетиторство по естественным наукам

  • Анатомия
  • Биология
  • Химия
  • Физика
  • Физиология

  иностранные языки

  • французский
  • немецкий
  • Латинский
  • Китайский мандарин
  • Испанский

  начальное обучение

  • Чтение
  • Акустика
  • Элементарная математика

  прочие

  • Бухгалтерия
  • Информатика
  • Экономика
  • Английский
  • Финансы
  • История
  • Письмо
  • Лето

  Поиск по 350+ темам

• О
  • Обзор видео
  • Процесс выбора наставника
  • Онлайн-репетиторство
  • Мобильное обучение
  • Мгновенное обучение
  • Как мы работаем
  • Наша гарантия
  • Влияние репетиторства
  • Обзоры и отзывы
  • Освещение в СМИ
  • О преподавателях университета

Звоните прямо сейчас, чтобы записаться на обучение:

(888) 888-0446

Все ресурсы по математике для старших классов

8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept

Справка по математике для старших классов » Алгебра II » Математические отношения и основные графики » Факториалы » Умножение и деление факториалов

Решите следующее выражение.

Возможные ответы:

Правильный ответ:

Объяснение:

Это выражение можно упростить, потому что все члены выражения для 8! также встречаются в выражении для 10!. Написав приведенное ниже выражение, мы можем сократить 8!.

Сообщить об ошибке

Решить: 

Возможные ответы:

Правильный ответ:

Пояснение:

И числитель, и знаменатель являются факториалами. Если вы развернете оба, все сократится, кроме  в числителе. Умножьте их, чтобы получить 720. 

Сообщить об ошибке

Упростить .

Возможные ответы:

Правильный ответ:

Объяснение:

Таким образом,  , так как остальные члены сокращаются. 56 — это упрощенный результат.

Сообщить об ошибке

У Стьюи есть шарики в мешке. Сколько шариков у Стьюи?

Возможные ответы:

Правильный ответ:

Объяснение:

Упрощая это уравнение, мы замечаем, что тройки, двойки и единицы сокращаются, поэтому

Альтернативное решение

Сообщить об ошибке

Что из следующего НЕ совпадает с ?

Возможные ответы:

Правильный ответ:

Объяснение:

Отменяется все, кроме частей больше 4, остается 6 и 5 для умножения

Сообщить об ошибке

Упростить и решить.

Возможные ответы:

Правильный ответ:

Объяснение:

Запомните число, за которым следует ! является факториалом. Факториал — это произведение заданного числа и всех чисел, меньших его, до нуля. Например, .

Вместо того, чтобы выполнять всю математику, связанную с , обратите внимание, что  то же самое, что и 

Отсюда s отменяется, оставляя нас с .

Сообщить об ошибке

Что из следующего эквивалентно ?

Возможные ответы:

Ни один из других ответов не является правильным.

Правильный ответ:

Объяснение:

Это факторный вопрос. Формула факториала такова.

 

Сообщить об ошибке

Уведомление об авторских правах

Посмотреть репетиторов

Бенджамин
Сертифицированный репетитор

Мичиганский университет в Дирборне, бакалавр искусств, математика. Texas A&M University-Corpus Christi, доктор наук, мате. ..

Посмотреть репетиторов

Хелен
Сертифицированный репетитор

Государственный университет Нью-Мексико, главный кампус, бакалавр наук, общественное здравоохранение. Университет Уолдена, магистр наук, психическое здоровье…

Посмотреть репетиторов

Лела
Сертифицированный репетитор

Университет Вандербильта, бакалавр искусств, испанский язык.

Все ресурсы по математике для старших классов

8 диагностических тестов 613 практических тестов Вопрос дня Карточки Учитесь по концепции

Решение большого деления на множители без записи факториалов

спросил 6 лет, 11 месяцев назад

Изменено 6 лет, 11 месяцев назад

Просмотрено 2к раз

$\begingroup$

Я вычисляю энтропию для задачи по физике, и для этого нужно решить следующее уравнение:

$\ Энтропия = \frac{949!}{899! 50!} $

Однако я не знаю, как решить это математически, не возвращаясь к выписыванию каждого числа в верхнем факториале, пока не достигну 899. Есть ли кратчайший путь к решению деления на множители без записи этих чисел?

• факториал

$\endgroup$

1

$\begingroup$

Можно использовать приближение Стирлинга в логарифмической форме $\log n! \ приблизительно n(\log n-1)+\log\sqrt {2\pi n}$, чтобы избежать переполнения. Это довольно точно.

$\endgroup$

2

$\begingroup$

Можно вычеркнуть одинаковые множители в числителе и знаменателе. Например:

$$\frac{6!}{4! \times2!} = \frac{6\times5\times4\times3\times2\times1}{(4\times3\times2\times1) (2\times1)} $$

Теперь вычеркните все одинаковые множители снизу и сверху . Только по одному фактору одновременно вверху и внизу.