Множества операции над множествами примеры: Множества и операции над множествами

Множества. Операции над множествами — презентация онлайн

1. Множества. Операции над множествами

«Множество есть многое, мыслимое
нами как единое»
основатель теории множеств – Георг Кантор
(1845—1918) — немецкий
математик, логик, теолог, создатель
теории бесконечных множеств,
оказавшей определяющее влияние
на развитие математических наук на
рубеже 19— 20 вв.

3. Примеры множеств из окружающего мира

Например, множество дней
недели состоит из элементов:
понедельник, вторник, среда,
четверг, пятница, суббота,
воскресенье.
Множество месяцев – из
элементов: январь, февраль,
март, апрель, май, июнь, июль,
август, сентябрь, октябрь,
ноябрь, декабрь.
Придумай название для предметов и животных,
собранных вместе:
НАБОР
КОЛЛЕКЦИЯ МАРОК КАРАНДАШЕЙ
ЧАЙНЫЙ СЕРВИЗ
БУКЕТ ЦВЕТОВ
СТАЯ ПТИЦ
СТАДО КОРОВ

5. Примерами множеств в геометрии могут служить:

а) множество видов треугольников,
б) множество многоугольников
Множество – совокупность объектов,
объединенных по какому – нибудь признаку.
Множества обозначают большими буквами
латинского алфавита: А, В, С, D и т. д.
Объекты, составляющие множество,
называются элементами множества.
множество
элемент
Множество
четырехугольников
Трапеция, параллелограмм,
ромб, квадрат, прямоугольник
Пространственные тела
Шар, прямоугольный
параллелепипед, призма,
пирамида, октаэдр
Натуральные числа
Квадраты чисел
Цифры десятичной системы
счисления
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…
1, 4, 9, 16, 25, 36, 49, 64, 81, 100 ..
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
10, 12, 14, 16 … 96, 98
Двузначные четные числа
Примерами множеств в математике могут
служить:
а) множество всех натуральных чисел N,
б) множество всех целых чисел Z
(положительных, отрицательных и нуля),
в) множество всех рациональных чисел Q,
г) множество всех действительных чисел R
Множество
арифметических
действий — из
элементов:
сложение,
вычитание,
умножение,
деление.

9. Множество А называется подмножеством множества В, если все элементы множества А принадлежат множеству В.

10. ВИДЫ МНОЖЕСТВ

Запишите множества букв слов
КОНИ И КИНО
{К, О, Н, И}
{К, И, Н, О}
Равные множества
А=В
(состоящие из одних и
тех же элементов)
множество людей на Солнце
множество прямых углов равностороннего
треугольника
множество точек пересечения двух
параллельных прямых
Пустое множество-
в котором нет элементов

12. ВИДЫ МНОЖЕСТВ

А = {2; 3; 5; 7; 11; 13};
{х | 5< х <12}
Конечные множества

13. ВИДЫ МНОЖЕСТВ

{1; 4; 9; 16; 25; …};
{10; 20; 30; 40; 50; …};
Бесконечные множества
Среди перечисленных ниже множеств укажите
конечные и бесконечные множества:
а) множество чисел, кратных 13;
б) множество делителей числа 15;
в) множество деревьев в лесу;
г) множество натуральных чисел;
д) множество рек Ростовской области;
е) множество корней уравнения х + 3 = 11;
ж) множество решений неравенства х + 1 < 3.

18. ДЕЙСТВИЯ НАД МНОЖЕСТВАМИ

Пересечением двух множеств А и В называется
множество С = А В, которое состоит из всех
элементов х, лежащих одновременно в
множестве А и в множестве В.
А В = {х}, где х А и х В
М= а
с
ЗАДАЧА 1
А
ЗАДАЧА 2
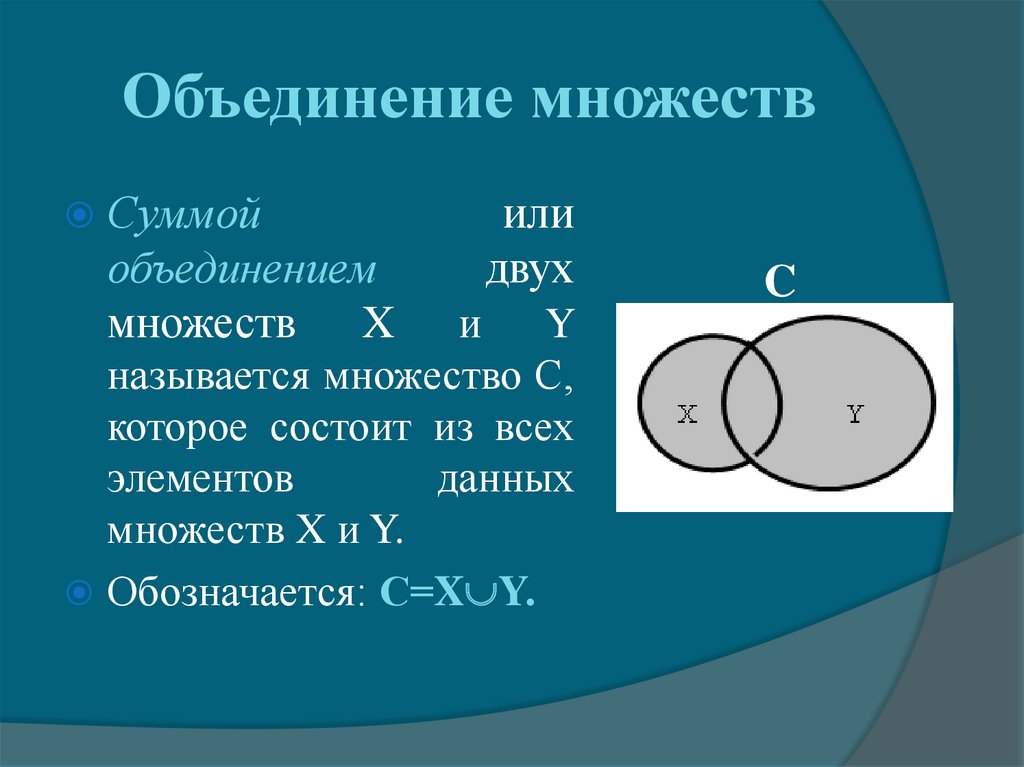
Объединением двух множеств А и В называется
множество А В, которое состоит из всех элементов,
принадлежащих А или В.
С = А В= {х}, где х А или х В.
А – девочки
класса,
В – мальчики
класса,
С – весь класс

22. Разностью множеств – называется множество состоящее из тех и только тех элементов А, которые не принадлежат В.

А\В= {х| х А и х В.
Даны множества
X={1,2,3,4,5},
Y={2,4,6,8},
А
В
Разность
X\Y={1,3,5},
Разность Y\X={6,8}

23. Дополнение к множеству -элементы, которые не принадлежат множеству А (т.е. дополняют его до универсального)

Предположим, что
множество U состоит из всех
букв русского алфавита,
U
Аа
В
А
А
A – из всех согласных
Тогда:
дополнение множества А
до универсального
множества U – из всех
гласных.
№1
Какое множество задано путем
перечисления данных элементов?
А={0,1,2,3,4,5,6,7,8,9}
В={А,Е,И,О,У,Э,Ю,Я}
№2
№3
Задайте
множество крокодилов, летящих в
небе.
Даны множества
А = {3, 5, 0, 11, 12, 19},
В = {2, 4, 8, 12, 18,0}. Найдите множества
AUВ,
А В
Решение задачи
с помощью кругов Эйлера
k
K
́ д Э́йлер —
Леонар
швейцарский, немецкий и
российский математик,
внёсший значительный вклад в
развитие математики, а также
механики, физики, астрономии
и ряда прикладных наук.
В классе 30 человек, каждый из которых поёт
или танцует. Известно, что поют 17 человек,
а танцевать умеют 19 человек. Сколько
человек поёт и танцует одновременно?
Всего 30
11
6
поют 17
17+19=36, всего 30
13
танцуют 19
36-30=6

27. Решение

Пусть А — это множество учеников, умеющих петь.
Количество элементов в нём по условию равно n = 17.
Пусть В — множество учеников, умеющих танцевать.
Количество элементов в нём — m = 18. Множество
совпадает со всем классом, т.к. каждый ученик в
классе поёт или танцует. А В — это множество тех
учеников класса, которые поют и танцуют
одновременно. Пусть их количество равно k.
Согласно формуле доказанной выше
n + m- k = 17+ 19- k = 30 k = 6.
Ответ: 6 учеников в классе поют и танцуют
одновременно.
На фирме работают 67 человек. Из них 47 знают
английский язык, 35 — немецкий язык, а 23 — оба
языка. Сколько человек в фирме не знают ни
английского, ни немецкого языков?
Английский 47
Всего 67
Немецкий 35
35-23=12
47-23=24
12
24
23
24+12+23=59
67- 59=8

29. Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27

учащихся, а два языка —
18 учащихся. Сколько учащихся в классе?
18
Немецкий 27
Английский 25
Только
английский
25 – 18 = 7
7
9
Только немецкий
27 – 18 = 9
7 + 9 + 18 = 34
Ответ: в классе 34 ученика
Расположите 4 элемента в двух множествах
так, чтобы в каждом из них было по 3
элемента.
Множества А и В содержат соответственно 5 и 6
элементов, а множество А ∩ В – 2 элемента. Сколько
элементов в множестве А U В?
Объединение содержит 9 элементов
Каждая семья, живущая в нашем доме, выписывает или
газету, или журнал, или и то и другое вместе. 75 семей
выписывают газету, а 27 семей выписывают журнал и
лишь 13 семей выписывают и журнал, и газету. Сколько
семей живет в нашем доме?
Всего: 14 + 13 + 62 =89
32
МНОЖЕСТВО
ЭЛЕМЕНТ МНОЖЕСТВА
ВИДЫ МНОЖЕСТВ
ОТНОШЕНИЯ МЕЖДУ
МНОЖЕСТВАМИ
ОБЪЕДИНЕНИЕ МНОЖЕСТВ
ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
НАХОДИТЬ
ОБЪЕДИНЕНИЕ
МНОЖЕСТВ
НАХОДИТЬ
ПЕРЕСЕЧЕНИЕ
МНОЖЕСТВ
ИЗОБРАЖАТЬ С
ПОМОЩЬЮ КРУГОВ
ЭЙЛЕРА-ВЕННА
РЕШАТЬ ЗАДАЧИ С
ИСПОЛЬЗОВАНИЕМ
ИМЕЮЩИХСЯ ЗНАНИЙ

объединение, пересечение, дополнение и различие

Редакция Кодкампа

17 авг. 2022 г. читать 2 мин

---

Набор — это набор предметов.

Мы обозначаем набор с помощью заглавной буквы, а элементы в наборе определяем с помощью фигурных скобок. Например, предположим, что у нас есть некоторый набор под названием «A» с элементами 1, 2, 3. Мы запишем это так:

А = {1, 2, 3}

В этом руководстве объясняются наиболее распространенные операции с множествами, используемые в теории вероятностей и статистике.

Союз

Определение: Объединение множеств A и B — это множество элементов, которые находятся либо в A, либо в B.

Обозначение: А ∪ В

Примеры:

• {1, 2, 3} ∪ {4, 5, 6} = {1, 2, 3, 4, 5, 6}
• {1, 2} ∪ {1, 2} = {1, 2}
• {1, 2, 3} ∪ {3, 4} = {1, 2, 3, 4}

Перекресток

Определение: Пересечение множеств A и B — это множество элементов, которые находятся как в A, так и в B.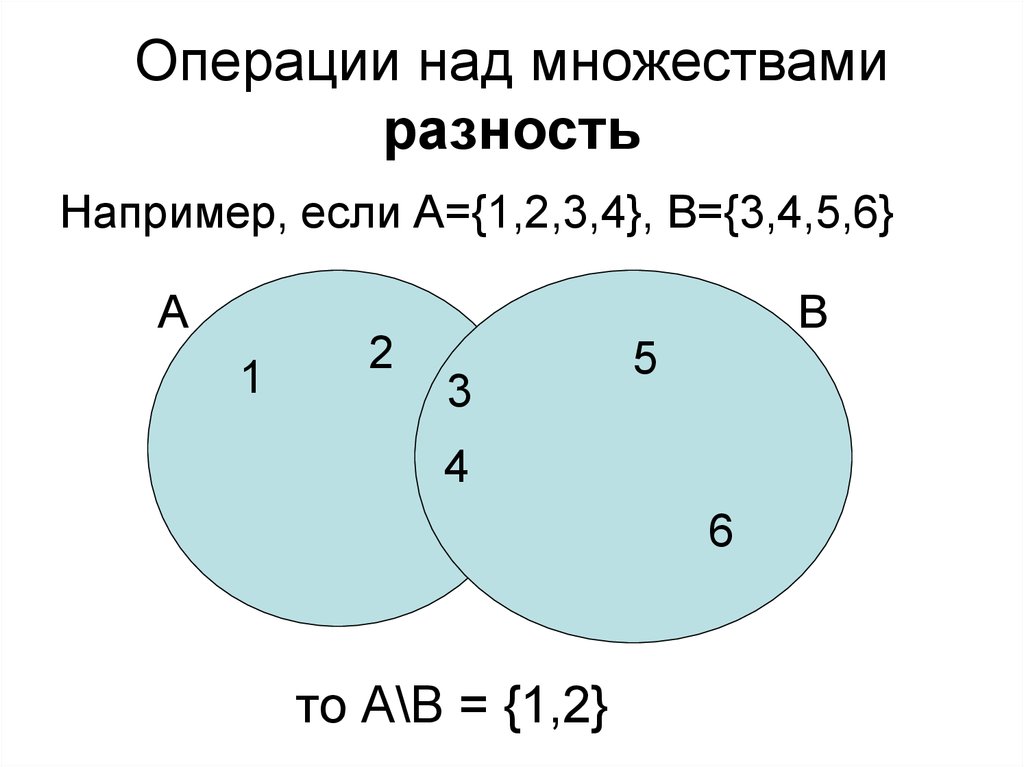

Обозначение: А ∩ В

Примеры:

• {1, 2, 3} ∩ {4, 5, 6} = {∅}
• {1, 2} ∩ {1, 2} = {1, 2}
• {1, 2, 3} ∩ {3, 4} = {3}

Дополнение

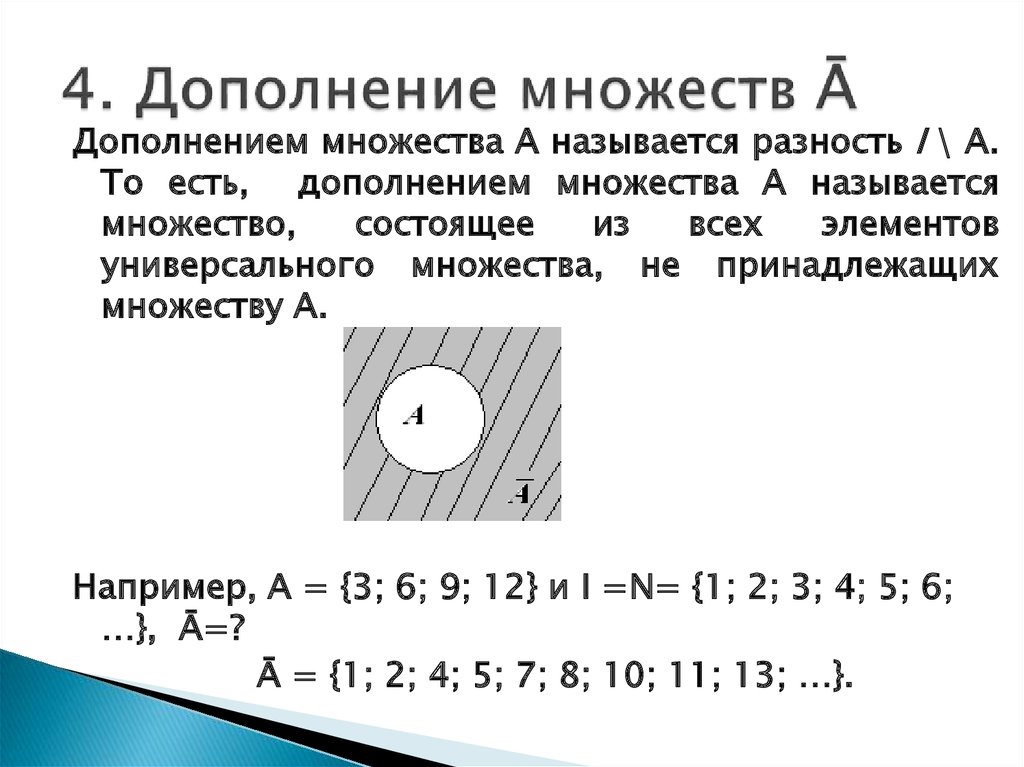
Определение: Дополнением множества A называется множество элементов, которые входят в универсальное множество U, но не входят в A.

Обозначение: A’ или A c

Примеры:

• Если U = {1, 2, 3, 4, 5, 6} и A = {1, 2}, то A c = {3, 4, 5, 6}
• Если U = {1, 2, 3} и A = {1, 2}, то A c = {3}

Разница

Определение: Разность множеств А и В — это множество элементов, которые есть в А, но отсутствуют в В.

Обозначение: А – Б

Примеры:

• {1, 2, 3} – {2, 3, 4} = {1}
• {1, 2} – {1, 2} = {∅}
• {1, 2, 3} – {4, 5} = {1, 2, 3}

Симметричная разница

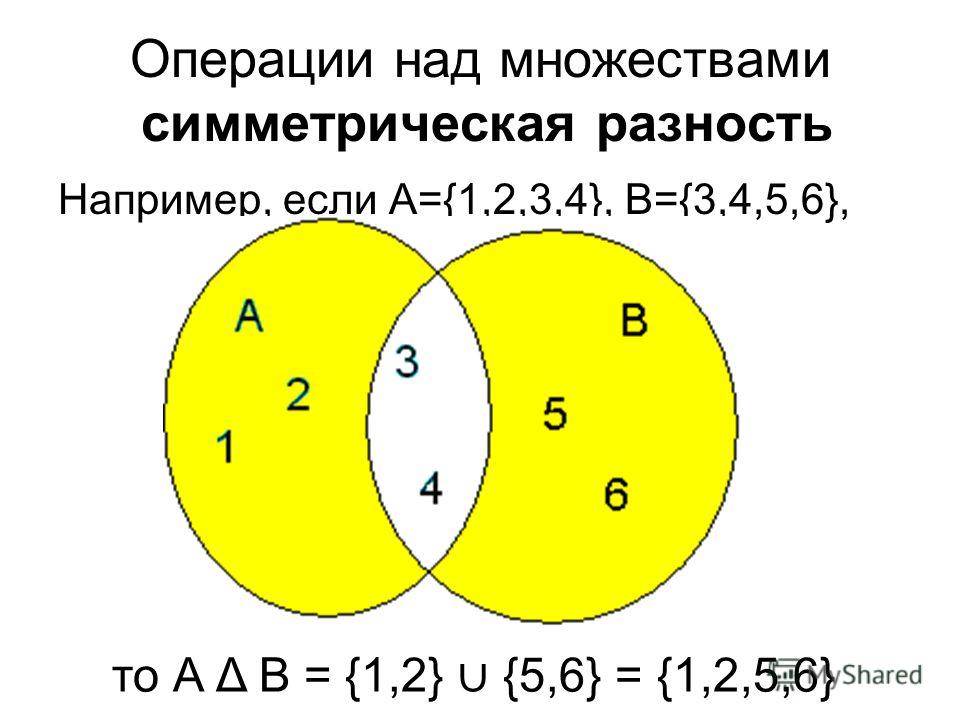
Определение: Симметричная разность множеств A и B — это множество элементов, которые находятся либо в A, либо в B, но не в обоих.

Обозначение: А Δ В

Примеры:

• {1, 2, 3} ∆ {2, 3, 4} = {1, 4}
• {1, 2} ∆ {1, 2} = {∅}
• {1, 2, 3} Δ {4, 5} = {1, 2, 3, 4, 5}

Декартово произведение

Определение: Декартово произведение множеств A и B — это множество упорядоченных пар из A и B.

Обозначение: А х В

Примеры:

• Если A = {H, T} и B = {1, 2, 3}, то A x B = {(H, 1), (H, 2), (H, 3), (T, 1), ( Т, 2), (Т, 3)}
• Если A = {T, H} и B = {1, 2, 3}, то A x B = {(T, 1), (T, 2), (T, 3), (H, 1), ( Н, 2), (Н, 3)}

Документ без названия

Документ без названия

 

В регулярной алгебре мы можем комбинировать простые операции в более сложные операторы; например, мы можем написать выражение, которое включает в себя и сложение, и умножение: 4x+7, потому что у нас есть правила, которые говорят нам, что когда мы сталкиваемся с этим выражением, мы всегда сначала выполняем умножение, а затем сложение.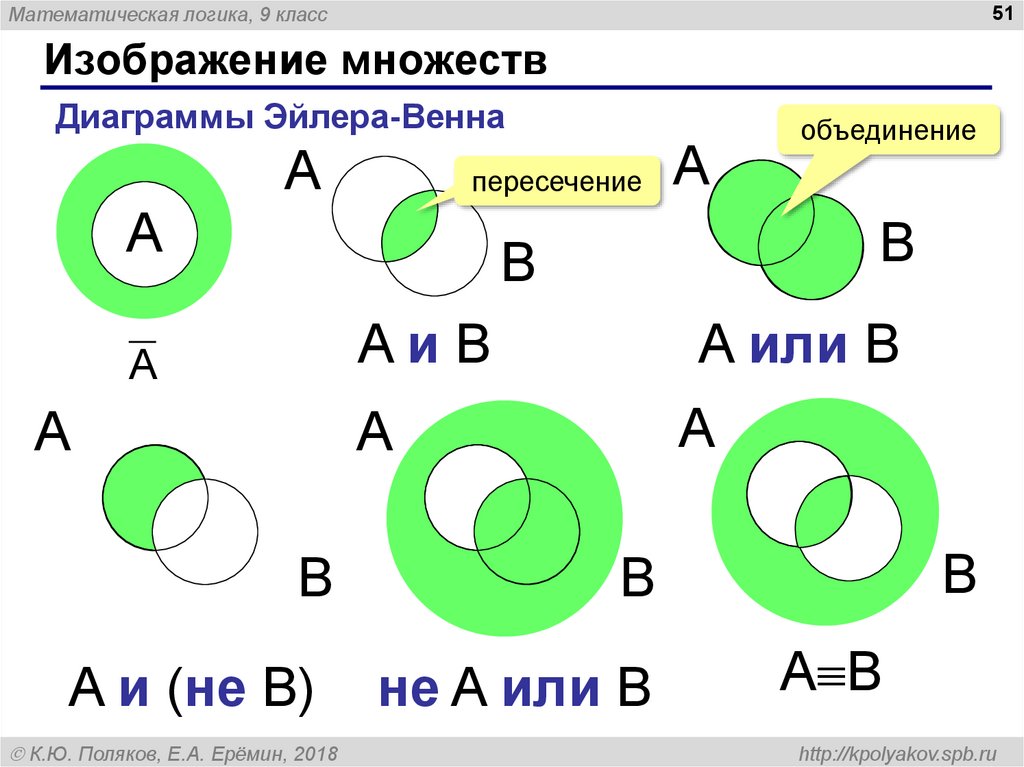

Теперь, когда мы узнали о четырех операциях над множествами: объединении, пересечении, разности и дополнении, мы хотим иметь возможность писать более сложные выражения, такие как, например, (A∪B′)∩A. Мы хотим иметь возможность рисовать диаграммы Венна для этих составных выражений, и мы хотим иметь возможность вычислять результат для этих составных выражений, если нам дано точное содержание каждого из задействованных наборов.

Дополнительная информация о рисовании диаграмм Венна:

Прежде чем мы пойдем дальше в изучении составных операций над множествами, нам нужно убедиться, что мы поняли некоторые важные моменты о том, как рисовать диаграмму Венна.

Как нарисовать диаграмму Венна, содержащую два набора::

При построении диаграмм Венна мы должны быть осторожны, чтобы не делать предположений об отношениях между множествами, когда мы ничего не знаем о самих множествах. Если у нас есть два множества, то они могут быть связаны тремя возможными способами:

Назовем наши два набора A и B.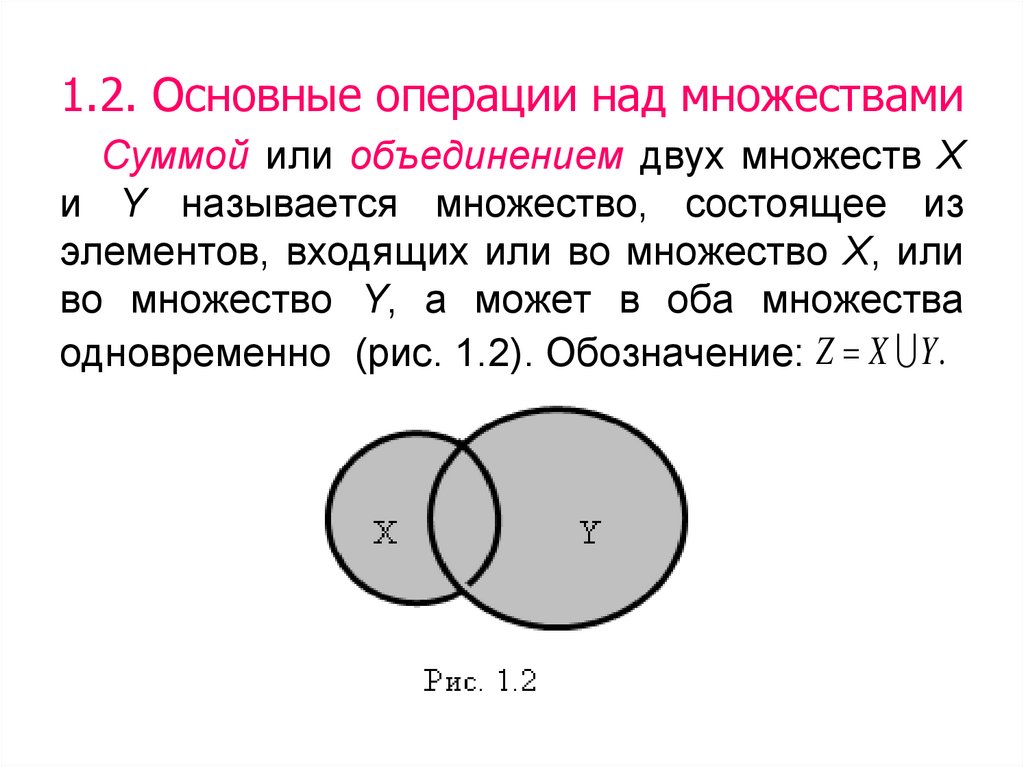

1. Один набор является подмножеством другого: (Здесь B является подмножеством A.)
   

2. Два набора не пересекаются:
   

3. Два набора пересекаются:
   

Когда мы ничего не знаем о наборах, с которыми работаем, мы всегда рисуем их так, как будто они перекрываются :

Почему это работает? Мы на мгновение закрасим некоторые области разными цветами, чтобы объяснить, почему. На следующей диаграмме мы заштриховали множество A красным, а множество B синим; фиолетовый указывает, где были затенены и красный, и синий.

 

• Если два множества НЕ ПЕРЕСЕКАЮТСЯ, эта картина все еще работает, если мы предположим, что A ∩ B ПУСТО. Помните, что A ∩ B — это фиолетовая область в середине, где A и B перекрываются.

• Если A⊆B, то эта картина все еще работает, если мы предположим, что A-B ПУСТОЙ. Помните, что A-B — это просто красная область A слева (не включает фиолетовую область A, где она пересекается с B).

• Если B⊆A, то эта картина все еще работает, если мы предположим, что B-A ПУСТ. Помните, что B-A — это просто синяя область B справа (она не включает фиолетовую область B, где она пересекается с A).

Если вы рисуете диаграмму Венна для решения задачи и понятия не имеете, что это за два множества, обязательно нарисуйте диаграмму так, чтобы эти два множества перекрывались.

Важно понимать, что мы никогда не можем предполагать, что произвольное множество не пусто.

Тот факт, что множество занимает место на диаграмме Венна, не означает, что оно обязательно содержит элементы. Например, если бы A на самом деле было пустым множеством на приведенной выше диаграмме Венна, то это означало бы, что область, заштрихованная красным, и область, заштрихованная фиолетовым цветом (где также имеется красное затенение) будут пустыми. Это означает, что хотя эти заштрихованные области на диаграмме занимают место, в них может ничего не быть.

Диаграммы Венна с 3 наборами:

Во всех примерах, которые мы будем рассматривать в этом разделе, мы часто будем работать с 3 или более множествами. Мы можем нарисовать диаграмму Венна с любым количеством множеств в ней. Общая диаграмма Венна для трех наборов будет выглядеть примерно так:

Важно всегда маркировать ваши диаграммы Венна. Всякий раз, когда вы используете диаграмму Венна для представления набора, вы должны поместить метку, указывающую, что затенение изображает выше или ниже диаграммы Венна. См. некоторые из примеров ниже:

Порядок операций на комплектах:

Иногда нам нужно объединить более двух наборов и более одной операции, чтобы создать более сложное выражение. Но для этого мы должны установить некоторый набор правил, чтобы мы знали, в каком порядке выполнять каждую операцию.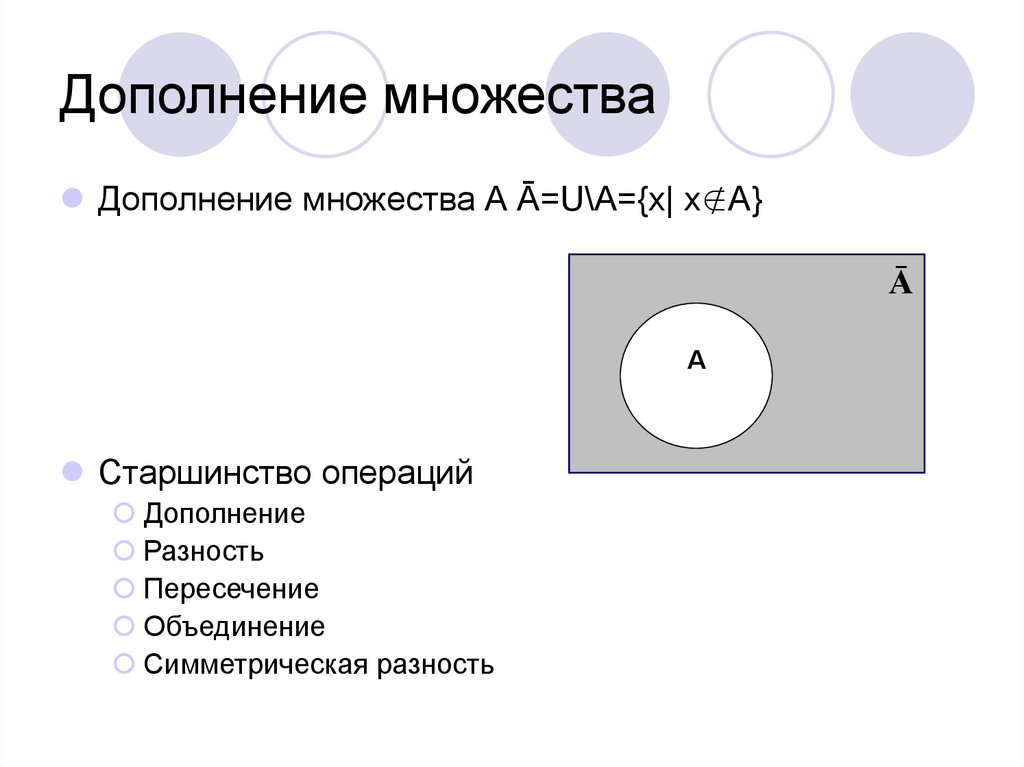 Как и в случае с числами, мы используем круглые скобки, если хотим, чтобы операция была выполнена первой.

1. Как и в случае с числами, мы всегда сначала делаем что-то в скобках. Если имеется более одного набора скобок, мы работаем изнутри наружу.

2. Сначала делаем комплементы.

3. Операции объединения, пересечения и разности равны по порядку. Поэтому, если у нас есть более одной из них одновременно, мы должны использовать круглые скобки, чтобы указать, какая из этих операций должна быть выполнена первой. Например, выражение A∪B-C не имеет никакого смысла, потому что мы не знаем, какую операцию мы должны выполнить в первую очередь: взять сначала объединение, а затем разность, или сначала взять разность, а затем объединение ? Чтобы это было ясно, нам нужно писать либо (A∪B)-C, либо A∪(B-C).

Давайте рассмотрим несколько примеров. Для каждого из этих примеров пусть U={1,2,3,4,5,6,7,8,9}, A={1,2,3,4,5}, B={2,4, 6,8}, С={4,5,6}:

Итак, наша диаграмма Венна будет выглядеть следующим образом: (Каждый элемент я расставил по своим местам на диаграмме Венна.

)

Пример 1:

(А∪В)-С

Сначала находим A∪B. В этом случае A∪B={1,2,3,4,5,6,8}. На диаграмме Венна для A∪B мы получили бы:

А∪В

Помните, что когда мы берем A∪B, мы игнорируем множество C. Не позволяйте тому факту, что существует множество C, отвлекать вас. Это не имеет ничего общего с операцией A ∪ B, поэтому пока мы ее игнорируем; мы будем использовать его на следующем шаге.

Далее находим (A∪B)-C. Поскольку A∪B={1,2,3,4,5,6,8} и C={4,5,6}, мы просто подставляем эти наборы вместо A∪B и C соответственно, чтобы получить:

(А∪В)-С={1,2,3,4,5,6,8}-{4,5,6}={1,2,3,8}

Чтобы создать диаграмму Венна для (A∪B)-C, мы должны сначала иметь диаграммы Венна для A∪B и для C, поэтому вот диаграмма Венна для C, где множество C заштриховано синим цветом:

С

Теперь мы поместим обе эти штриховки для A∪B и C вместе на одну и ту же диаграмму Венна, и мы получим следующую картину; набор C показан синим цветом, набор A∪B красным, а область, где они пересекаются, становится фиолетовой:

A∪B красного цвета, C синего цвета

Теперь, чтобы взять (A∪B)-C, мы просто убираем все, что было закрашено синим цветом (включая фиолетовую часть), потому что мы хотим сохранить все, что есть в множестве A∪B, но избавиться от всего, что есть в наборе. C. То, что осталось, это диаграмма Венна для (A∪B)-C:

А∪В

Обратите внимание, что именно то, что осталось в заштрихованной красным области, — это набор {1,2,3,8}, который мы получили выше, когда вычисляли это, используя только наборы без диаграмм!

Пример 2:

А∪(В∩С′)

Сначала находим C′, потому что сначала делаем то, что в скобках; в скобках у нас есть две операции: пересечение и дополнение, и порядок операций говорит нам, что сначала нужно выполнить дополнение.

В данном случае C={4,5,6}. Итак, C′={4,5,6}′={1,2,3,7,8,9}.

Чтобы найти диаграмму Венна для C′, мы должны сначала нарисовать диаграмму Венна для C: (Здесь C заштриховано синим цветом.)

С

Теперь, чтобы найти C’, мы закрасим любую часть, которая была белой на диаграмме для C, чтобы получить следующую диаграмму C’, где C’ закрашено красным:

С’

Теперь, когда у нас есть C′, теперь мы хотим найти B∩C′.

Поскольку B={2,4,6,8} и C′={1,2,3,7,8,9}, подставляя эти множества в B∩C′, мы получаем:

B∩C′={2,4,6,8}∩{1,2,3,7,8,9}={2,8}

Чтобы построить диаграмму Венна для B∩C′, нам сначала нужны диаграмма Венна для B и диаграмма Венна для C′. На нашей диаграмме Венна для B мы заштриховали B синим цветом:

.

Б

Теперь мы сложим наши диаграммы Венна для B и для C’ вместе; мы заштриховываем C’ красным, а B синим, чтобы область, где B и C’ перекрываются, была фиолетовой. Обратите внимание, что эта фиолетовая область находится там, где пересекаются C′ и B, поэтому числа, заштрихованные фиолетовым, в точности являются элементами множества {2,8}!

C’ красного цвета, B синего цвета

Итак, мы берем только фиолетовую область, где B и C’ пересекаются, и рисуем нашу диаграмму Венна для B∩C’ следующим образом:

Б∩С’

Теперь мы можем взять A∪(B∩C′). Поскольку теперь мы знаем, что B∩C′={2,8}, а A={1,2,3,4,5}, мы можем подставить эти множества в A∪(B∩C′), чтобы получить:

А∪(В∩С′)={1,2,3,4,5}∪{2,8}={1,2,3,4,5,8}.

Будьте осторожны! Помните, что когда мы берем СОЮЗ, мы складываем ВСЕ элементы обоих наборов вместе. Это ПРОТИВОПОЛОЖНО взятию ПЕРЕСЕЧЕНИЯ, когда мы берем только элементы, которые находятся в ОБОИХ наборах одновременно! Будьте осторожны, не перепутайте объединение с пересечением.

Чтобы получить диаграмму Венна для A∪(B∩C′), нам нужны диаграммы Венна для A и для B∩C′. Мы рисуем диаграмму Венна для A, заштриховав A желтым цветом:

.

А

Итак, теперь мы соединим нашу штриховку для A с нашей штриховкой для B ∩ C ‘, так что A будет закрашено желтым, а B ∩ C ‘заштриховано фиолетовым на той же диаграмме Венна. Там, где желтый набор A и фиолетовый набор (B ∩ C′) перекрываются, мы получаем что-то вроде сине-зеленого, так что картина выглядит так:0005

 

A желтого цвета, B∩C′ фиолетового цвета

Поскольку мы хотим взять ОБЪЕДИНЕНИЕ желтого множества A и фиолетового множества B∩C′, мы берем всю заштрихованную область, где есть желтый и фиолетовый, и где желтый и фиолетовый перекрываются, чтобы получить сине-зеленый. . Чтобы сделать нашу окончательную диаграмму Венна ясной, мы закрасим всю область одним цветом (здесь мы выбрали оранжевый):

.

А∪(В∩С′)

Обратите внимание, что наша последняя заштрихованная область — это множество {1,2,3,4,5,8}, точно такой же ответ, который мы получили для A∪(B∩C′) выше!

 

Когда следует использовать диаграммы Венна?

Для любых данных наборов и операций мы можем выполнять операции, либо рисуя несколько диаграмм Венна шаг за шагом, либо мы можем просто работать с элементами самих наборов. Обратите внимание на инструкции, чтобы решить, какой из этих методов вас просят использовать.

Как правило, если мы знаем, что такое множества, мы просто вычисляем ответ, но если мы не знаем, что это за множества, мы рисуем диаграммы Венна, потому что Диаграммы Венна — единственный способ представления абстрактных множеств, о которых мы ничего не знаем!

Использование диаграмм Венна для доказательства равенства двух выражений:

Мы также можем использовать диаграммы Венна, чтобы доказать равенство двух выражений. Если мы хотим показать, что два выражения, включающие множества и операции над множествами, на самом деле равны независимо от того, что представляют собой множества, все, что нам нужно сделать, это нарисовать диаграмму Венна для каждого выражения и показать, что две диаграммы Венна идентичны.

Например, когда мы узнали определения дополнения и различия, мы поняли, что A’ и U-A — это одно и то же. Таким образом, мы можем написать A′=U-A. Лучший способ доказать, что два выражения одинаковы, — нарисовать их диаграммы Венна и показать, что они имеют точно такую ​​же заштрихованную площадь.

Мы знаем, что A’ имеет следующую диаграмму Венна:

А’

Теперь нарисуем диаграмму Венна U-A. Сначала у нас должна быть диаграмма Венна для U и диаграмма Венна для A.

У

Здесь множество U заштриховано красным цветом. Обратите внимание, что это вся диаграмма Венна, потому что универсальное множество всегда включает все.

А

Здесь множество A закрашено желтым цветом.

Теперь мы помещаем U и A вместе на одну и ту же диаграмму Венна так, чтобы A была закрашена желтым цветом, а U — красным, так что места, где красный и желтый перекрываются, были оранжевыми:

А желтый, У красный

Чтобы взять разность U-A, мы должны начать с U, части, заштрихованной красным, и удалить все части, которые были в A или были закрашены желтым цветом. Поскольку оранжевая часть этой диаграммы была закрашена желтым, мы должны удалить ее из диаграммы, чтобы получить диаграмму для UA:

U-A

Обратите внимание, что диаграмма Венна для A′ и диаграмма Венна для U-A идентичны! Это доказывает, что A′=U=A, что бы ни содержали множества U и A!

Будьте осторожны — Вы НЕ МОЖЕТЕ доказать, что два выражения всегда равны, приведя ПРИМЕРЫ определенных множеств, которые сделали бы выражения равными; вы можете сделать это, только показав, что их диаграммы Венна равны. Это очень важное понятие в математике: ПРИМЕР: НЕ ДОКАЗАТЕЛЬСТВО! Убедитесь, что вы знаете разницу между примером и доказательством!

Чтобы проиллюстрировать эту идею, давайте приведем пример и доказательство для нескольких разных задач:

Пример:

А-В=(А’∪В)’

Сначала давайте придумаем пример. Если мы сделаем A={15,20,25} и B={20,30}, и U={5,10,15,20,25,30}, тогда:

А-Б={15,20,25}-{20,30}={15,25}

Чтобы найти (A′∪B)′, нам нужно сначала найти A′, потому что оно находится внутри круглых скобок, а дополнения идут первыми. Здесь А’={5,10,30}.

Далее мы можем найти A′∪B={5,10,30}∪{20,30}={5,10,20,30}.

Тогда мы можем найти (A′∪B)′={5,10,20,30}′={15,25}.

Поскольку AB={15,25} и (A′∪B)′={15,25}, мы можем сказать, что AB=(A′∪B)′.

Но это только ПРИМЕР! Это показывает только, что AB=(A′∪B)′, когда A={15,20,25} и B={20,30}, и U={5,10,15,20,25,30}.

Мы не можем сказать, верно ли A-B=(A′∪B)′ для ВСЕХ ВОЗМОЖНЫХ НАБОРОВ A и B! Так что это НЕ доказательство!

Доказательство:

Теперь попробуем доказательство. Единственный способ доказать, что AB = (A′∪B)′ для всех возможных множеств A и B, — это показать, что диаграмма Венна для AB такая же, как диаграмма Венна для (A′∪B)′.

Сначала напомним, что диаграмма Венна AB выглядит так:

А-Б

Теперь нам нужно шаг за шагом построить диаграмму Венна для (A′∪B)′, чтобы показать, что она точно такая же, как и выше.

Чтобы сделать это, мы должны сначала нарисовать A′ (что мы уже сделали в предыдущем примере, поэтому мы просто воспользуемся этой диаграммой здесь), потому что мы должны сначала сделать то, что указано в скобках, а дополнение идет перед каждой другой операцией. .

Диаграмма Венна для A’:

А’

 

Теперь возьмем диаграмму Венна для B:

Б

Будьте осторожны. Обратите внимание, что у нас есть овал, обозначающий множество B на диаграмме Венна для A′, и овал, обозначающий множество A на диаграмме Венна для B, что в общем случае не обязательно. ОДНАКО, поскольку в этом случае нам нужны эти диаграммы Венна только как шаг для создания диаграммы Венна для (A′∪B)′, а ЭТО ОКОНЧАТЕЛЬНОЕ ВЫРАЖЕНИЕ содержит ОБА множества A и B, то ОБА овал, обозначающий множество A, И овал, указывающий, что множество B должен быть на КАЖДОЙ диаграмме Венна, которую мы делаем, ведущую к нашей диаграмме Венна для (A′∪B)′. Если бы на диаграмме Венна для A’ отсутствовал овал, указывающий на множество B, или на диаграмме Венна для B отсутствовал овал, указывающий на множество A, то мы не смогли бы поместить их вместе на одной диаграмме Венна, чтобы получить объединение .

Теперь закрасим B желтым, а A′ синим на той же диаграмме Венна, чтобы найти A′∪B. Области на диаграмме Венна, где желтая B и синяя A’ перекрываются, становятся зелеными:

A’ синего цвета, B желтого цвета

Мы хотим получить объединение желтого множества B и синего множества A′, поэтому мы берем все, что было закрашено желтым или синим (или зеленым, где перекрываются и желтый, и синий). Чтобы сделать нашу диаграмму более ясной, мы перерисовываем ее, чтобы она была полностью окрашена в один цвет, поэтому диаграмма Венна, которую мы получаем для A′∪B, будет следующей:

А’∪В

 

Теперь нам нужно найти (A′∪B)′ . Итак, мы хотим взять дополнение заштрихованной красным областью выше, которая представляет множество A′∪B. Напомним, что дополнение — это все, что есть в универсальном множестве, но не в A′∪B. Область, которая находится в U, но не в A′∪B, — это точно белая область на диаграмме Венна. Таким образом, чтобы закрасить (A′∪B)′ , все, что нам нужно сделать, это закрасить область, которая была белой на приведенной выше диаграмме Венна, вот так:

(А’∪В)’

Это то же самое, что и диаграмма Венна для AB! Итак, мы ДОКАЗАЛИ, что A-B=(A′∪B)′!

Это доказательство, потому что все диаграммы Венна являются общими и не требуют от нас знания, что такое А и В.

С помощью диаграмм Венна мы показали, что A-B=(A′∪B)′ для ВСЕХ множеств A, B и U.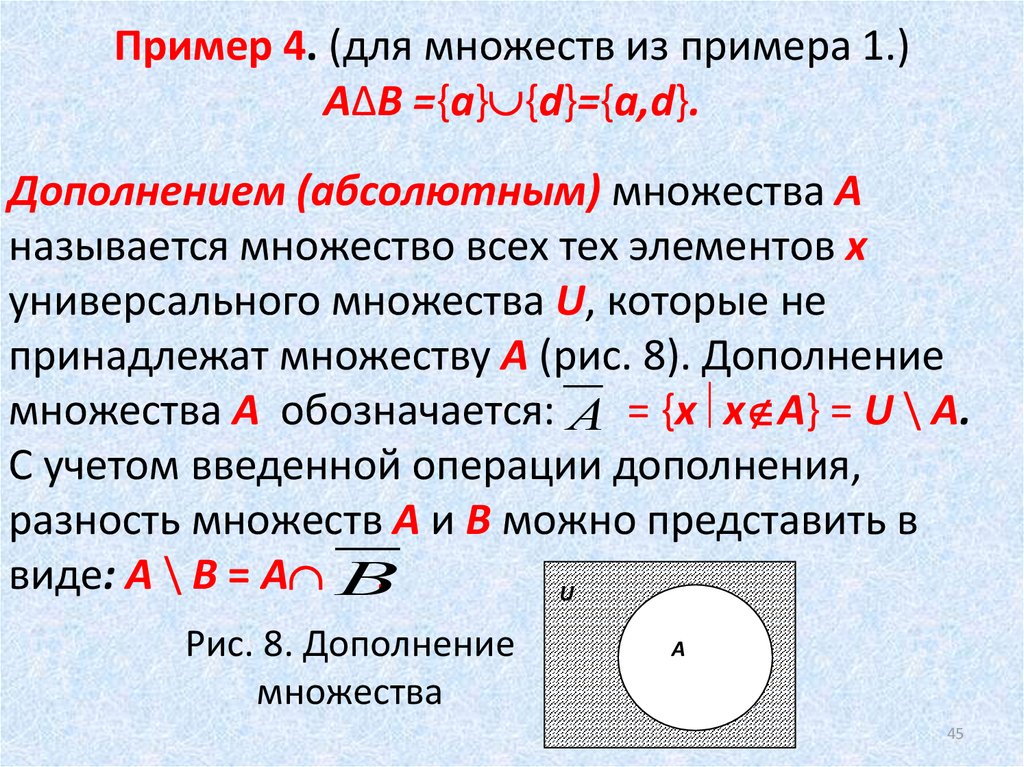 A, B и U могут быть НИЧЕГО, и A-B=(A′∪B )′ все равно будет правдой!

Использование диаграмм Венна для доказательства того, что два множества не равны:

Если мы хотим доказать, что два множества НЕ равны, все, что нам нужно сделать, это показать, что их диаграммы Венна не совпадают:

. Рассмотрим A∪B=A∩B. Всегда ли это так? Иногда правда? Или никогда не правда?

Чтобы проверить, верно ли это в общем случае, нарисуем диаграммы Венна:

Мы помним из предыдущих примеров, что A∪B имеет диаграмму Венна:

А∪В

Мы также помним из предыдущих примеров, что A∩B имеет диаграмму Венна:

А∩В

Эти две диаграммы НЕ совпадают! Это означает, что НЕВЕРНО, что A∪B=A∩B для ВСЕХ ВОЗМОЖНЫХ МНОЖЕСТВ A и B.

Однако могут существовать наборы, для которых A∪B=A∩B.

Ясно, что если A={1,2,3} и B={2,4,6}, A∪B={1,2,3,4,6} и A∩B={2}. Очевидно {1,2,3,4,6}≠{2}.

Но если A={1,2,3} и B={1,2,3}, то A∪B={1,2,3} и A∩B={1,2,3}, поэтому в этом случай А∪В=А∩В.

Итак, A∪B=A∩B верно ИНОГДА, но НЕ ВСЕГДА.

Если вы посмотрите внимательно, то заметите, что A∪B=A∩B будет истинным только тогда, когда A=B. Чтобы убедиться в этом, посмотрите на диаграммы Венна выше. Единственный способ сделать область, заштрихованную красным, и область, заштрихованную желтым цветом, одинаковыми, — это объединить наборы A и B в один набор, чтобы они были точно одним и тем же набором.

Законы ДеМоргана:

Когда можно заменить одно составное выражение, содержащее множества, другим?

Прямо сейчас мы сделаем еще один пример, показывающий, как мы можем доказать эквивалентность двух составных выражений, содержащих множества. Этот пример на самом деле является одним из двух хорошо известных правил теории множеств, называемых законами Де Моргана (по имени математика, открывшего их).

Когда была изобретена теория множеств, и у нас появились составные выражения, включающие множества и множественные операции, становится естественным спросить, действительно ли два разных составных выражения равны. Например, в обычной алгебре, использующей числа и операции над числами, такие как сложение, вычитание, умножение и деление, существуют правила, гласящие, что вы можете переписать 3(4 x +2) как 12 x +6 путем распределения умножения над сложением. Верен ли тот же процесс для множеств?

Например, могу ли я написать (A∪B)′ как A′∪B′? Другими словами, могу ли я распределить дополнение множества по объединению множеств? Единственный способ сказать это — нарисовать диаграмму Венна для (A∪B)′ и диаграмму Венна для A′∪B′ и посмотреть, идентичны ли две диаграммы Венна:

Начнем с рисования диаграммы Венна для (A∪B)′:

Мы помним из предыдущей задачи, что диаграмма Венна для A ∪ B выглядит так: (помните, что, поскольку объединение находится внутри скобок, мы должны сделать это до того, как возьмем дополнение, которое находится вне скобок)

А∪В

Теперь, чтобы взять дополнение к A∪B, мы возьмем только белую область на предыдущей диаграмме Венна, чтобы получить:

(А∪В)’

Теперь нарисуем диаграмму Венна для A′∪B′. Начнем с диаграмм Венна для A′ и B′, которые мы помним из предыдущих примеров:

А’

Б’

Теперь нам нужно поместить A′ и B′ на одну и ту же диаграмму Венна. Поскольку A’ — синий, а B’ — красный, область, где они перекрываются, будет фиолетовой:

.

A’ — синий, B’ — красный

Поскольку мы берем объединение, мы сохраняем все, что было заштриховано синим или красным (или фиолетовым, потому что фиолетовый происходит от красного и синего затенения). Чтобы сделать нашу диаграмму более четкой, мы решили заштриховать все одним цветом, так что это диаграмма A′∪B′:

.

А’∪В’

Это явно , а не то же самое, что и диаграмма Венна для (A∪B)′! Таким образом, мы можем заключить, что в общем случае (A∪B)′ нельзя заменить на A′∪B′ без изменения результирующего множества!

Будьте осторожны! Вы можете НИКОГДА не заменять (A∪B)′ на A′∪B′, потому что эти два множества НЕ (вообще) равны! Если вас попросят нарисовать диаграмму Венна для (A∪B)′, например, убедитесь, что вы следуете порядку операций — НИКОГДА начните с дополнения A и B, потому что это ВНЕ круглых скобок ! Точно так же вы НЕ МОЖЕТЕ заменить (A∩B)′ на A′∩B′, потому что эти два набора НЕ (вообще) равны! (Чтобы убедиться в этом, попробуйте нарисовать диаграмму Венна для каждой стороны и сравнить их. )

Законы ДеМоргана:

Оказывается, на самом деле существует своего рода искаженное правило распределения, которое позволяет вам «распределять» дополнение множества по объединению множеств (или пересечению)

Оказывается, следующие два правила ВСЕГДА верны для ЛЮБЫХ двух множеств A и B:

1) А′∪В′=(А∩В)′

2) А′∩В′=(А∪В)′

Эти правила называются ЗАКОНЫ ДЕМОРГАНА .

Откуда мы знаем, что эти два правила всегда будут верны?

Начнем с первого правила: откуда мы знаем, что A′∪B′ всегда будет равно (A∩B)′, какими бы ни были множества A и B? Мы рисуем диаграммы Венна для каждой части этого уравнения и показываем, что они совпадают.

Сначала мы рисуем диаграмму Венна для A′∪B′; поскольку мы только что сделали это в предыдущем примере, мы можем просто использовать ту же диаграмму здесь:

А’∪В’

Теперь построим диаграмму Венна для (A∩B)′:

Поскольку мы всегда сначала делаем то, что указано в скобках, мы сначала рисуем диаграмму Венна для A ∩ B, которая у нас есть из предыдущего примера:

А∩В

Теперь мы берем дополнение, заштриховав белую область на диаграмме выше (помните, что дополнением является все, что НЕ находится в A ∩ B!):

Таким образом, мы получаем следующую диаграмму Венна для (A∩B)′:

(А∩В)′

Это та же самая диаграмма Венна, которую мы получили для A′∪B′.

Итак, мы доказали первый закон Де Моргана: A′∪B′=(A∩B)′, потому что диаграммы Венна каждой части уравнения идентичны.

Рисование диаграмм Венна нулевого и универсального множеств

Иногда вам может понадобиться нарисовать диаграммы Венна нулевого множества Ø или универсального множества U. Чтобы нарисовать диаграмму Венна нулевого множества, нам нужно только нарисовать любую диаграмму Венна без какой-либо штриховки . Ниже приведены несколько примеров различных диаграмм Венна нулевого набора:

Ø

Ø

Ø

Ø

Чтобы нарисовать диаграмму Венна Универсального набора, заштриховываем все . Ниже приведены несколько различных примеров диаграмм Венна универсального набора:

U

U

U

U

 

 

Операции с базовыми множествами

В математике множество — это совокупность четко определенных и различных объектов, где объект — это то, что определено или может быть формально определено. Числа, целые числа, перестановки, комбинации, функции, точки, линии и отрезки — вот лишь несколько примеров математических объектов.

Теория множеств может использоваться в дедуктивных рассуждениях и математических доказательствах, и как таковая может рассматриваться как основа, на основе которой может быть получена большая часть математики.

В теории множеств есть четыре основных операции: объединение, пересечение, дополнение и декартово произведение.

Объединения

Объединения являются результатом «сложения» двух наборов вместе. Союзы обозначаются символом «∪».

Объединение двух множеств, A и B, обозначаемое как A ∪ B, включает все объекты, являющиеся членами A, B или обоих.

Пример:

Даны следующие множества:

A = {4, 5, 6}

B = {6, 7, 8}

A≈ 6} ∪ {6,7,8} = {4,5,6,7,8}

Ниже показано объединение двух множеств:

Заштрихованная серая область представляет собой объединение A и B.

Пересечения

Пересечения являются результатом определения общих членов между двумя множествами. Пересечения обозначаются как «∩».

Пересечение двух множеств, A и B, обозначаемое как A ∩ B, включает все объекты, находящиеся как в A, так и в B.

Пример:

Даны следующие множества: 6} B = {6, 7, 8} A ∩ B = {4,5,6} ∩ {6,7,8} = {6}

Ниже приведено изображение пересечения двух наборов:

Заштрихованная серая область представляет собой пересечение A и B.

Дополнения

Дополнение множества A относится к элементам, которых нет в A. Среди других обозначений дополнение A может обозначаться как A ^c . Например, в случае, когда рассматриваются все целые числа, если бы A было множеством всех четных целых чисел, A ^c было бы множеством всех нечетных целых чисел.

Наборы можно «вычитать». Разность между двумя множествами, A и B, можно обозначить как A \ B.