Как исследовать ряды на сходимость: Как исследовать ряд на сходимость: примеры решений

Признак сравнения рядов для выяснения их сходимости

Признак сравнения рядов, как и признак Даламбера, радикальный признак Коши и интегральный признак Коши, является достаточным признаком сходимости рядов с положительными членами, так как исследование ряда с помощью этих признаков даёт однозначный ответ на вопрос о том, сходится ряд или расходится.

Применение признака сравнения заключается в том, что исследуемый ряд сравнивают с рядом, сходимость которого заранее известна.

Непосредственное сравнение членов рядов

Пусть даны два ряда с положительными общими членами и . Пусть для этих рядов выполняется неравенство , то есть члены первого ряда не превосходят соответствующих членов второго ряда.

Тогда из сходимости второго ряда (ряда с бОльшим общим членом) следует сходимость первого ряда, а из расходимости первого ряда (ряда с меньшим общим членом) – расходимость второго ряда.

Предел отношения общих членов рядов

Пусть даны два ряда с положительными общими членами и . Если , то есть предел отношения общих членов ряда равен конечному и отличному от нуля числу, то оба ряда ведут себя одинаково: или оба сходятся, или оба расходятся.

Трудность применения на практике признака сравнения состоит в необходимости иметь «запас» рядов, сходимость (или расходимость) которых известна, а среди них подобрать такой, чтобы выполнялось условие. Для сравнения часто используются:

• геометрический ряд , который сходится, если |q| < 1 и расходится, если |q| ≥ 1;
• обобщённый гармонический ряд , который сходится, если p > 1 и расходится, если p ≤ 1;
• ряд .

---

Пример 1. Исследовать сходимость ряда

Решение. Члены данного ряда не превосходят соответствующих членов сходящегося геометрического ряда с общим членом

Согласно признаку сравнения, данный ряд также сходится.

---

Пример 2. Исследовать сходимость ряда

Решение. Так как

то члены данного ряда меньше членов

 

сходящегося ряда. На основании признака сравнения данный ряд также сходится.

Пример 3. Исследовать сходимость ряда

Решение. Сравним данный ряд с гармоническим рядом. Первые их члены совпадают, а остальные члены данного ряда больше соответствующих членов расходящегося гармонического ряда:

поскольку

Согласно признаку сравнения, данный ряд также расходится.

---

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Ряды

Пример 4. Исследовать сходимость ряда

.

Решение. Так как , а ряд сходится как геометрический ряд с , то по признаку сравнения данный ряд также сходится.

---

Пример 5. Исследовать сходимость ряда

.

Решение. Выясним значение предела отношения общих членов данного ряда и гармонического ряда :

Так как предел отношения общих членов данного ряда и второго ряда, который расходится, отличен от нуля и не равен бесконечности, то оба ряда ведут себя одинаково. То есть данный ряд так же расходится.

Пример 6. Исследовать сходимость ряда

.

Решение. Выясним значение предела отношения общих членов данного ряда и гармонического ряда :

Так как предел отношения общих членов данного ряда и второго ряда, который расходится, отличен от нуля и не равен бесконечности, то оба ряда ведут себя одинаково. То есть данный ряд так же расходится.

---

Пример 7. Исследовать сходимость ряда

.

Решение. Выясним значение предела отношения общих членов данного ряда и обобщённого гармонического ряда , который расходится, так как . Искать предел будем, учитывая, что , если , поэтому , если . Итак, предел:

.

Так как предел отношения общих членов данного ряда и второго ряда, который расходится, отличен от нуля и не равен бесконечности, то оба ряда ведут себя одинаково. То есть данный ряд так же расходится.

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Пройти тест по теме Ряды

Всё по теме «Ряды»

• Числовые ряды
• Признак сравнения рядов
• Признак Даламбера сходимости рядов
• Радикальный признак Коши сходимости рядов
• Интегральный признак Коши сходимости рядов
• Знакочередующиеся и знакопеременные ряды. Признак Лейбница
• Функциональные ряды
• Степенные ряды
• Ряды Фурье

Исследовать ряд на сходимость с примерами решения

Содержание:

1. Примеры с решением
2. Интегральный признак сходимости Коши.
3. Примеры исследования рядов на сходимость

Начнем с изучения рядов, все члены которых неотрицательны. Пусть дан ряд вида где все Так как и Это значит, что последовательность частичных сумм данного ряда неубывающая:

В курсе «Введение в анализ» доказывается, что для сходимости неубывающей последовательности необходимо и достаточно, чтобы она была ограничена сверху, т. е. необходимо и достаточно, чтобы существовало такое что для всех Значит, в этом и только в этом случае ряд где сходится.

Мы доказали следующее утверждение:

Теорема 6.1. Для того чтобы ряд с неотрицательными членами сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху. Если последовательность неубывающая, то ее предел не меньше любого из ее членов, т. е. для всех п выполняется неравенство где Доказанное утверждение позволяет установить следующий признак сходимости рядов с неотрицательными членами: Теорема 6.2. Пусть даны два ряда и члены которых неотрицательны, причем для всех выполняется неравенство Тогда если сходится ряд то сходится и ряд причем (из сходимости ряда соответственно с большими членами вытекает сходимость ряда с соответственно меньшими членами).

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Высшая математика: лекции, формулы, теоремы, примеры задач с решением

Доказательство. Обозначим частичные суммы ряда через snt а ряда — через По предположению для всех имеем Далее, так как ряд сходится, а члены этого ряда неотрицательны, то для всех имеем где — сумма этого ряда. Но тогда для всех имеем

Это значит, что частичные суммы sn ряда ограничены сверху числом поскольку члены этого ряда неотрицательны, он по теореме 6.1. сходится. Обозначим через Из неравенства вытекает, что (это вполне естественно — если для всех имеем

Возможно вам будут полезны данные страницы:

Сходимость ряда

Признаки сходимости рядов

Область сходимости ряда

Найти сходимость ряда

Следствие. Если члены рядов и неотрицательны и для всех п выполняется неравенство то из расходимости ряда вытекает, что и ряд расходится. В самом деле, если бы ряд сходился, то по доказанной выше теореме сходился бы и ряд вопреки предположению.

Примеры с решением

Пример 6.1.

Выше (см. пример 1.5) было доказано, что ряд сходится. Но при любом имеет место неравенство т. е. 3нaчит, ряд тоже сходится.

Пример 6.2.

Так как ряд расходится, а при любом имеем то ряд тоже расходится.

Замечание.

Так как сходимость ряда равносильна сходимости любого его остатка, то члены рядов можно сравнивать и лишь начиная с некоторого места (однако если лишь при то, вообще говоря, неравенство может не иметь места).

Иногда удобнее применять другую теорему сравнения рядов с неотрицательными членами. Теорема 6.3 (вторая теорема сравнения рядов с неотрицательными членами). Пусть все члены рядов и неотрицательны и пусть существует предел Тогда при оба ряда либо одновременно сходятся, либо одновременно расходятся. Если же то из сходимости ряда вытекает сходимость ряда а из расходимости ряда — расходимость ряда Доказательство. Пусть Выберем такую окрестность что (рис. 1). Так как то, начиная с некоторого значения все окажутся в этой окрестности, а тогда для всех будут выполняться неравенства где Но тогда из сходимости ряда следует сходимость ряда а тем самым и ряда . Из сходимости же ряда следует сходимость ряда а тогда сходится и ряд Значит, сходимость одного из рядов влечет за собой сходимость другого ряда.

Рис. 1

Если же то аналогичные рассуждения показывают существование такого что при выполняется неравенство Но тогда сходимость ряда влечет за собой сходимость ряда а из расходимости ряда следует расходимость ряда Теорема доказана.

Пример 6.3.

Мы знаем, что ряд сходится.

Так как то и ряд сходится. Признаки сходимости Даламбера и Коши. Чаще всего сравнивают ряды с суммами бесконечных убывающих прогрессий. Имеет место следующая теорема: Теорема 6.4 (признак Даламбера). Пусть все члены ряда положительны и пусть существует предел отношения последующего члена ряда к предыдущему: Тогда: если то ряд сходится, если то ряд расходится, если то возможны как сходимость, так и расходимость ряда. Доказательство. Пусть Выберем такое что Так как то, начиная с некоторого номера будет выполняться неравенство Но тогда при имеем и потому

Таким образом, все члены заданного ряда, начиная с не превосходят членов геометрической прогрессии которая сходится, поскольку Значит, по признаку сравнения сходится и заданный ряд. Рассмотрим теперь случай, когда

В этом случае, начиная с некоторого значения будет выполняться неравенство Это значит, что т. е. члены ряда не убывают, а потому не могут стремиться к нулю (напомним, что все ). Поэтому ряд расходится.

Покажем, наконец, что при ряд может как сходиться, так и расходиться. Для этого заметим, что при любом значении имеем:

Поэтому для любого ряда вида выполнено равенство Но при этот ряд расходится, а при сходится. Пример 6.4. Докажем сходимость ряда Для этого ряда имеем

Значит, Так как то ряд сходится.

Другим признаком сходимости рядов с положительными членами, основанным на сравнении с суммой геометрической прогрессии, является так называемый радикальный признак сходимости Коши. Теорема 6.5. Пусть все члены ряда положительны и пусть существует предел Тогда: а) если то ряд сходится; б) если то ряд расходится; в) если то возможны как сходимость, так и расходимость ряда.

Доказательство. Пусть Выберем число такое, что Так как lim то, начиная с некоторого значения будет выполняться неравенство т. е. Значит, начиная с некоторого номера члены ряда меньше, чем члены прогрессии со знаменателем причем Так как сумма такой прогрессии—сходящийся ряд, то и заданный ряд сходится. Если то, начиная с некоторого, номера выполняется неравенство Из него следует, что т. е. что члены ряда не стремятся к нулю.

Поэтому ряд расходится. Легко убедиться, что при любом имеем По этому для рядов вида всегда Но такие ряды могут как сходиться, так и расходиться. Теорема доказана.

Интегральный признак сходимости Коши.

Во многих случаях члены рассматриваемых рядов не только положительны, но и монотонно стремятся к нулю.

Для таких рядов вопрос о сходимости часто решается путем сравнения ряда с несобственным интегралом. Напомним, что по определению несобственный интеграл сходится, если существует предел и равен в этом случае значению этого предела.

Если функция всюду имеет первообразную то где Таким образом, в случае существования первообразной для функции исследование сходимости эквивалентно исследованию предела при этом если предел существует и конечен, то интеграл сходится, а если предел равен или не существует, то интеграл расходится. Если несобственный интеграл сходится, то для любой последовательности стремящейся к оо, имеем: В случае, когда для сходимости интеграла достаточно существования хотя бы одной последовательности у такой, что и

Это вытекает из того, что при функция монотонно возрастает. В частности, при сходимость интеграла равносильна сходимости ряда: (6.1)

В самом деле, частичные суммы этого ряда имеют вид: а для сходимости интеграла необходимо и достаточно, чтобы существовал предел

Сформулируем признак сходимости рядов с монотонно убывающими положительными членами.

Теорема 6.6 (интегральный признак Коши). Пусть функция задана на луче непрерывна, положительна, монотонно убывает и стремится к нулю, когда Обозначим через Тогда ряд сходится в том и только том случае, когда сходится несобственный интеграл

Доказательство.

Так как функция монотонно убывает на отрезке то на этом отрезке выполняется неравенство т. е. Отсюда следует, что Если сходится интеграл то сходится и ряд (6.1), а тогда в силу признака сравнения рядов сходится ряд получаемый из данного ряда отбрасыванием слагаемого Значит, данный ряд сходится.

При этом имеет место неравенство где сумма данного ряда. Обратно, пусть сходится ряд По признаку сравнения сходится и ряд (6.1), т. е. интеграл При этом Мы доказали теорему, получив при этом следующее неравенство: В случае сходимости ряда эту формулу можно использовать и для его остатка Получаем: (6.2) где, напомним,

Пример 6.5.

Докажем, что ряд расходится при и сходится при

Решение. Функция удовлетворяет условиям теоремы 6.6, причем Значит, ряд сходится или расходится одновременно с интегралом Таким образом, для исследования сходимости ряда достаточно рассмотреть предел первообразной для функции при При Если то и потому В этом случае интеграл, а тем самым и ряд расходятся. Если же то и тогда В этом случае интеграл, а следовательно, и ряд сходятся. Наконец, при а так как то интеграл, а следовательно, и ряд расходятся.

Примеры исследования рядов на сходимость

Рассмотрим дальнейшие примеры на все признаки сходимости.

Пример 6.6.

Исследуем сходимость ряда:

Решение:

Общий член ряда Заметим, что Но ряд с общим членом сходится (это геометрическая прогрессия со знаменателем По первой теореме сравнения заданный ряд сходится.

Пример 6.7.

Исследуем сходимость ряда:

Решение:

Общий член ряда Необходимое условие сходимости ряда выполняется, но ряд расходится. Действительно,

Ряд с общим членом расходится (это гармонический ряд). Поэтому на основании первой теоремы сравнения и заданный ряд расходится. Замечание. Мы использовали неравенство

Для его доказательства рассмотрим функцию Ее производная —больше нуля при положительных значениях

Следовательно, на функция монотонно возрастает, а так как то она положительна на Полагая теперь имеем:

Пример 6.

8.

Исследуем сходимость ряда:

Решение:

Необходимое условие сходимости выполняется. Возьмем гармонический ряд (его общий член и рассмотрим предел Предел существует и отличен от нуля. Поскольку гармонический ряд расходится, то на основании второй теоремы сравнения заданный ряд также расходится.

Пример 6.9.

Оценим остаток ряда:

Решение:

Все члены ряда: начиная со второго, меньше соответствующих членов геометрической прогрессии. Поэтому остаток меньше суммы этой геометрической прогрессии, которую обозначим т. е. Следовательно, Если, например, взять вместо суммы данного ряда частичную сумму то возникающая при этом погрешность и, таким образом, будет допущена ошибка, меньшая, чем

Пример 6.10.

Исследуем сходимость ряда:

Решение:

Воспользуемся признаком Даламбера. Общий член ряда Поэтому и Ряд сходится. Заметим, что мы доказали также соотношение (общий член сходящегося ряда стремится к нулю).

Пример 6.11.

Исследуем сходимость ряда:

Решение:

Как и в предыдущем примере, воспользуемся признаком Даламбера: При имеем и, следовательно, ряд сходится. При ряд расходится, так как При имеем Признак Даламбера формально не дает ответа на вопрос о сходимости ряда, но поскольку в рассматриваемом случае стремится к пределу монотонно возрастая, то

Это означает, что и потому для каждого Таким образом, необходимый признак сходимости нарушается и ряд расходится. Итак, заданный ряд сходится при и расходится при

Пример 6.12.

Исследуем сходимость ряда:

Решение:

Так как в рассматриваемом случае легко найти то воспользуемся признаком Коши: Значит, ряд сходится. Отсюда следует, что, в частности,

Пример 6.13.

Докажем сходимость ряда и оценим погрешность при замене суммы ряда суммой первых десяти членов.

Решение:

Признаки Даламбера и Коши здесь не дают ответа на вопрос о сходимости ряда.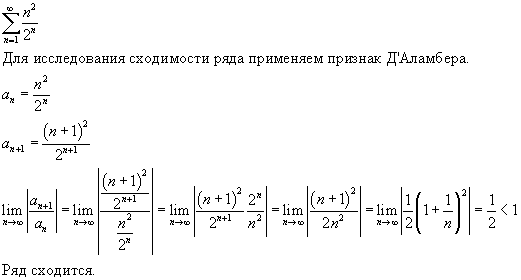 Члены ряда положительны и монотонно убывают. Рассмотрим функцию При она положительна и монотонно убывает. При ее значения совпадают с соответствующими членами ряда. Согласно интегральному признаку Коши, данный ряд сходится или расходится одновременно с несобственным интегралом Подстановка показывает, что Поскольку очевидно, что то интеграл, а следовательно, и ряд сходятся. Для оценки остатка воспользуемся формулой (6.2) Из нее следует, что Имеем:

Точно так же получаем: По таблице логарифмов находим, что

Пример 6.14.

Сколько членов ряда следует взять, чтобы вычислить сумму ряда с точностью до 0,002?

Решение:

Оценим величину

Имеем:

Так как то Поэтому нам нужно выбрать такое значение чтобы выполнялось неравенство Так как то достаточно решить нера венство Подбором находим

I. Необходимый признак сходимости рядов

Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒ Необходимым признаком сходимости рядов является следующая теорема. Теорема. Если ряд сходится, то предел его общего члена при равен нулю, т.е. . Однако на практике в таком виде применять теорему для исследования ряда невозможно, т.к. мы не знаем, сходится ли наш ряд. Поэтому для практического применения необходимый признак сходимости сформулируем в следующем виде: Следствие. Если предел общего члена ряда при не равен нулю, то ряд расходится. Пример. Исследовать на сходимость ряд Решение. Т.к. , то ряд расходится (по необходимому признаку сходимости). Очень важно помнить, что из того, что , не следует ни сходимость, ни расходимость ряда. Говорят, что если , то необходимый признак не работает. Замечание. Смысл или польза этого признака: если общий член ряда стремится к нулю, то ряд может быть как сходящимся, так и расходящимся, а если , то это заведомо расходящийся ряд. Этот признак является необходимым, но не достаточным. В качестве примера рассмотрим ряд , (2.1) называемый гармоническим. Необходимый признак сходимости для этого ряда не работает, т.к. . Докажем, что ряд расходится. Перепишем ряд (2.1) в виде: (2.2) Напишем вспомогательный ряд: (2.3) Ряд (2.3) строится так, что каждый его член меньше либо равен соответствующему члену ряда (2.2). Обозначим через сумму первых членов ряда (2.2), и через частичную сумму ряда (2.3). Т.к. каждый член ряда (2.2) больше либо равен соответствующему ему члену ряда (2.3), то . (2.4) Вычислим несколько частичных сумм ряда (2.3) для значений , равных : …………………………………………………………. следовательно, , а тогда в силу (2.4) , и ряд (2.1) расходится. Далее рассмотрим достаточные признаки сходимости знакоположительных рядов. II. Признак Даламбера Теорема. Пусть для ряда ( ) существует предел отношения ( )-го члена ряда к -му: . Тогда: а) если , то ряд сходится, б) если , то ряд расходится, в) если , то вопрос о сходимости ряда остается нерешенным, т. е. признак не работает. Примеры Исследовать следующие ряды на сходимость: 1) . Решение. Т.к. то по признаку Даламбера ряд сходится. 2) Замечание. Напомним, что , поэтому . Решение. Воспользуемся формулой , тогда: следовательно, по признаку Даламбера ряд сходится. 3) Решение и ряд расходится. Замечание. С помощью признака Даламбера исследовать ряды на сходимость имеет смысл только тогда, когда в выражении для — го члена ряда имеются показательная функция и/или факториал. III. Радикальный признак Коши Теорема. Пусть для ряда , ( ) существует . Тогда а) если , то ряд сходится, б) если , то ряд расходится, в) если , то вопрос о сходимости ряда остается нерешенным, т. е. признак не работает. Примеры. Исследовать следующие ряды на сходимость: 1) Решение. Вычислим , следовательно, по радикальному признаку Коши ряд расходится. 2) Решение. Вычислим , следовательно, по радикальному признаку Коши ряд сходится. Замечание. С помощью радикального признака Коши исследовать ряды на сходимость имеет смысл тогда, когда -й член ряда представляет собой некое выражение, возведенное в -ю степень. IV. Интегральный признак Коши Теорема. Пусть члены ряда положительны и пусть такая непрерывная функция, что , , … , …, причем функция невозрастающая на интервале при некотором . Тогда справедливы следующие утверждения: 1) если несобственный интеграл сходится, то сходится и ряд , 2) если несобственный интеграл расходится, то расходится и ряд . Для краткости говорят: «Ряд и интеграл ведут себя одинаково». Замечание. Для применения интегрального признака к исследованию сходимости ряда надо подобрать такую функцию , что , т.е. попросту говоря, выписать и заменить в нем n на x, и затем исследовать сходимость интеграла . Это имеет смысл делать только тогда, когда полученный интеграл достаточно легко вычисляется. Примеры 1) Применим интегральный признак к исследованию на сходимость ряда вида , , называемого обобщенным гармоническим рядом или рядом Дирихле. Решение. В этом случае требуемой функцией является . Функция является невозрастающей на интервале . Вычислим . Если , то . Если , то . Следовательно, несобственный интеграл сходится при и расходится при . То же самое можно сказать и о данном ряде. Запомнить! Обобщенный гармонический ряд сходитсяпри и расходится при . 2) Исследовать на сходимость ряд . Решение. Выписав и заменив в нем n на x, получим функцию . Внимание! Пока мы не убедились, что функция невозрастающая на некотором интервале вида , к интегрированию переходить рано! Исследуем функцию на монотонность с помощью производной: . Критическая точка , на интервале , т.е. функция невозрастающая. Теперь можно переходить к интегрированию. , интеграл расходится, расходится и данный ряд. V. Признаки сравнения Теорема.Первый признак сравнения (признак сравнения в форме неравенства). Пусть даны два ряда с положительными членами: (2.5) (2.6) причем члены первого ряда не превосходят членов второго при любом , т.е. (2.7) Тогда: а) если сходится ряд (2. 6), то сходится и ряд (2.5) б) если расходится ряд (2.5), то расходится и ряд (2.6). Удобно применять другую формулировку этой теоремы: а) если больший ряд сходится, то меньший ряд тоже сходится; б) если меньший ряд расходится, то больший ряд тоже расходится. Примеры Исследовать сходимость следующих рядов: 1) Решение. Сравним данный ряд с гармоническим , мысленно отбросив его первый член, равный 1 (что, естественно, не повлияет на сходимость ряда). Т.к. , , и вообще, (ведь ), то члены данного ряда больше членов расходящегося гармонического ряда, и, следовательно, на основании признака сравнения данный ряд расходится. Понятно, что для применения признака сравнения в форме неравенства нужно сначала установить подходящее неравенство. При этом часто пользуются следующими стандартными неравенствами: , (2.8) , . Иногда приходится применять более сложные неравенства: , , , , при некотором . 2) Решение. Прежде всего, заметим, что это ряд с положительными членами, т.к. синус возводится в четную степень. Далее очевидное неравенство позволяет заключить, что , а поскольку ряд сходится, то и ряд с меньшими членами тоже сходится. 3) Решение. Преобразуем выражение, стоящее под знаком суммы, следующим образом: (здесь мы учли, что ). Т.к. ряд – сходится (как обобщенный гармонический при ), то исследуемый ряд также сходится. Отметим «эталонные» ряды, часто используемые для сравнения: а) геометрический ряд – сходится при , расходится при , б) обобщенный гармонический ряд сходится при и расходится при . Нестандартность применения признака сравнения заключается в том, что надо не только подобрать соответствующий «эталонный» ряд, но и доказать неравенство (2.7), для чего часто требуется преобразование рядов (например, отбрасывание или приписывание конечного числа членов, умножение на определенные числа и т. п.). Более простым оказывается признак сравнения в предельной форме – ведь вычислять пределы обычно гораздо проще, чем доказывать неравенства. Теорема.Второй признак сравнения (признак сравнения в предельной форме). Если и – ряды с положительными членами и существует предел отношения их общих членов , причем , то ряды ведут себя одинаково: либо одновременно сходятся, либо одновременно расходятся. Чаще всего исследуемый ряд сравнивают с обобщенным гармоническим рядом , причем p удобно подбирать в процессе сравнения, как это сделано ниже в примере 1. Примеры 1) Решение. Сравним данный ряд с обобщенным гармоническим рядом , причем p подберем в процессе сравнения. Выпишем предел и преобразуем его: (2.9) Мы пришли к пределу отношения двух степенных выражений на бесконечности. Если степень числителя меньше степени знаменателя, то предел равен 0, а это тот случай, когда признак сравнения в предельной форме не работает. Если степень числителя больше степени знаменателя, то предел равен , а это опять тот случай, когда признак сравнения в предельной форме не работает. Таким образом, нас устроит только случай, когда степень числителя равна степени знаменателя, т.е. , или (в этом случае предел равен отношению старших коэффициентов, т.е. не 0 и не ). Итак, исследуемый ряд ведет себя так же, как и ряд , т.е. сходится. Разумеется, решение похожих задач не надо расписывать так подробно. Обычно, выписав предел (2.9), далее пишут сходится. Ясно, что слово «сходится» относится сразу к двум рядам и к , и к исходному ряду. Следствием второго (предельного) признака сравнения является третий признак сравнения. Теорема.Третий признак сравнения (признак сравнения в форме эквивалентных б.м. или кратко эквивалентный признак сравнения). В общем члене ряда бесконечно малый множитель или делитель можно заменить на эквивалентный, поведение ряда (сходимость или расходимость) от этого не изменится. Замечание 1. Напомним таблицу эквивалентных бесконечно малых величин (при ): . Замечание 2. При работе с эквивалентным признаком сравнения необходимо помнить, что таблица эквивалентных бесконечно малых величин выписана при , а в рядах всегда , т.е. n является бесконечно большой. А вот бесконечно малыми являются величины вида: (и вообще при ), (и вообще при ). 2) Решение. Т.к. при (т.е. – б.м.), то , и ряд ведет себя так же, как и ряд – обобщенный гармонический ряд при p=1/2<1, т.е. расходится. На практике запись ведут кратко: – расходится. Ясно, что слово «расходится» относится к обоим рядам. 3) . Решение. Т.к. ,то , ряд знакоположительный, и к нему можно применять эквивалентный признак сравнения. Поскольку – б.м. при , то и = . Последний ряд легко исследуется по признаку Даламбера (он сходится). Несмотря на то, что предельный и эквивалентный признаки сравнения более просты по сравнению с признаком сравнения в форме неравенства, иногда без первого признака не обойтись. Покажем это на следующем примере, а заодно продемонстрируем, как надо рассуждать в общем и целом при исследовании рядов на сходимость. 4) Решение. Проверим необходимый признак: – необходимый признак не работает. Попробуем применить признак Даламбера: , т.е. вопрос о сходимости ряда остается открытым. Этого следовало ожидать (см. замечание к признаку Даламбера). Применим признак сравнения в предельной форме. Сравним данный ряд, например, с гармоническим рядом: , т.е. ответа о сходимости ряда нет. Аналогичная картина наблюдается и при использовании других «эталонных» рядов. Применим, наконец, признак сравнения в форме неравенства (первый признак сравнения). Сравним данный ряд с гармоническим, у которого отброшен первый член: . .. Т.к. члены рассматриваемого ряда больше членов расходящегося гармонического , что вытекает из неравенства (2.8), то данный ряд расходится. Отметим, что для исследования сходимости данного ряда неприменим и интегральный признак, т.к. первообразная подынтегральной функции не является элементарной функцией, т.е. соответствующий неопределенный интеграл является «не берущимся». Задачи А) Исследовать ряды с помощью признака Даламбера: 1. 2. 3. 4. 5. 6. B) Исследовать ряды с помощью радикального признака Коши: 7. 8. 9. 10. C) Исследовать ряды с помощью интегрального признака Коши: 11. 12. 13. 14. 15. D) Исследовать ряды с помощью признаков сравнения: 16. 17. 18. 19. 20. 21. Е) Исследовать ряды на сходимость: 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37 . 38. 39. 40. 41. 42. 43. 44. . ⇐ Предыдущая1234Следующая ⇒ Читайте также:  Техника прыжка в длину с разбега Организация работы процедурного кабинета Области применения синхронных машин Оптимизация по Винеру и Калману 

Последнее изменение этой страницы: 2016-04-23; просмотров: 871; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.046 с.)

Какой тест сходимости следует использовать? Часть 1

Студенты, впервые изучающие ряды, часто спрашивают, как узнать, какой тест сходимости использовать с данным рядом. Первый ответ: практика, практика, практика. Второй ответ заключается в том, что часто существует более одного теста сходимости, которые можно использовать с данным рядом.

Я проиллюстрирую это положение рассмотрением одного ряда и нескольких тестов, которые можно использовать для демонстрации его сходимости. Это послужит обзором некоторых тестов и способов их использования. Список тестов на конвергенцию, необходимых для экзамена AP Calculus BC, можно найти здесь.

Чтобы иметь возможность использовать эти тесты, учащиеся должны знать гипотезы каждого теста и убедиться, что они выполняются для рассматриваемой серии. В вопросах с несколькими вариантами ответов учащимся не нужно объяснять, как они работают, но в вопросах со свободным ответом (таких как проверка конечных точек интервала сходимости ряда Тейлора) они должны указать их и сказать, что ряд им соответствует.

В нашем примере мы рассмотрим серию

Спойлер : За исключением первых двух тестов, остальные тесты требуют гораздо больше работы, чем необходимо для этой серии. Суть в том, чтобы показать, что для данной серии можно использовать несколько тестов, и отработать другие тесты.

Тест геометрического ряда является очевидным тестом для использования здесь, так как это геометрический ряд. Обычное отношение равно (–1/3), и, поскольку оно находится между –1 и 1, ряд будет сходиться.

Также можно использовать тест чередующихся серий (критерий Лейбница) . Ряд меняет знаки, убывает по модулю, и предел члена n ^th при стремлении n к бесконечности равен 0, поэтому ряд сходится.

Тест отношения широко используется со степенными рядами для определения радиуса сходимости, но его также можно использовать для определения сходимости. Чтобы использовать тест, мы находим

  Поскольку предел меньше 1, мы заключаем, что ряд сходится.

Абсолютная сходимость

Ряд является абсолютно сходящимся тогда и только тогда, когда этот ряд сходится. Другими словами, если вы сделаете все члены положительными и этот ряд сходится, то исходный ряд также сходится. Если ряд абсолютно сходится, то он сходится. (Ряд, который сходится, но не является абсолютно сходящимся, называется условно сходящимся.)

Преимущество абсолютной сходимости состоит в том, что нам не приходится иметь дело с отрицательными членами; это позволяет нам использовать другие тесты.

Применительно к нашему примеру, если ряд сходится, то наш ряд будет сходиться абсолютно и сходится.

Тест геометрического ряда можно использовать снова, как указано выше.

Интегральный тест говорит, что если несобственный интеграл сходится, то наш исходный ряд сходится абсолютно.

, так как ln(1/3) < 0.

Предел конечен, поэтому наш ряд сходится абсолютно, а значит, сходится.

Можно также использовать тест прямого сравнения . Нам нужно найти положительный сходящийся ряд, члены которого почленно больше, чем члены нашего ряда. Геометрический ряд отвечает этим двум требованиям. Следовательно, исходный ряд сходится абсолютно и сходится.

Сравнительный тест пределов — еще одна возможность. Здесь нам нужен сходящийся положительный ряд; мы можем использовать снова. Мы смотрим на

  а так как ряд в знаменателе сходится, то наш ряд сходится абсолютно.

Итак, для этого примера можно использовать все конвергенции, которые могут быть протестированы на экзамене AP Calculus BC, за единственным исключением теста серии p-, который нельзя использовать с этой серией.

---

Рекомендации по обучению

1. В то время как сходимость ряда, используемого здесь, может быть достигнута всеми этими способами, другие ряды подходят только для одного. Подчеркните форму серии, которая работает с каждым тестом. Например, тест предельного сравнения чаще всего используется для рациональных выражений с числителем меньшей степени, чем знаменатель, и для выражений, содержащих радикалы многочленов. Сравнение производится с p — ряды любой степени сделают числитель и знаменатель одной и той же степени, что позволит найти предел.
2. Большинство учебников, после объяснения каждого теста и выполнения упражнений по ним, включают серию смешанных упражнений, требующих выполнения всего теста, пройденного до этого момента. Хороший способ использовать этот набор — поручить учащимся указать, какой тест они будут пробовать первым в каждой серии. Обсудите мнения класса и проработайте любые вопросы, в которых учащиеся не уверены или по которым предлагается несколько способов.
3. Дайте учащимся указанный выше ряд или подобный ему и попросите их доказать его сходимость, используя каждый из тестов на сходимость, как это было сделано выше.
4. Разделите свой класс на группы и назначьте каждой группе серию и один из тестов сходимости. Попросите их использовать тест для доказательства конвергенции, а затем обсудите результаты в группе.

Конечно, на самом деле я не ответил на вопрос, не так ли? Проверьте, какой тест сходимости следует использовать Часть 2

---

Обновлено 23 февраля 2013 г. 9{\ infty} \ гидроразрыва {1} {к} $$ с $p=1$ называется гармоническим рядом .

Сравнительный тест

Пусть $\sum a_k$ и $\sum b_k$ — ряды с неотрицательными членами. Если $a_k \le b_k$ для всех достаточно больших $k$, то

1. Если $\sum b_k$ сходится, то $\sum a_k$ также сходится.
2. Если $\sum a_k$ расходится, то $\sum b_k$ также расходится.

Неформально, если «больший» ряд сходится, то сходится и «меньше». Если «меньшая» серия ныряет, то и «большая». 9{\infty}a_k $$ сходится, если последовательность частичных сумм сходится и расходится в противном случае.

Для определенного ряда один или несколько общих тестов сходимости может быть наиболее удобным для применения.

---

[Я готов пройти тест.] [Мне нужно просмотреть больше.]

AP Исчисление BC: Тесты на сходимость

Сравнительные тесты

 Сравнительный тест бывает двух видов: ограничение и прямое сравнение.

наверх

Предельный сравнительный тест

Если     где L — конечное число и L > 0, то два ряда сходятся или расходятся вместе.

Пример:

Этот тест может быть полезен для серий, которые не соответствуют простой оценке с помощью предыдущих тестов. Как правило, идеальной серией для этого теста будет та, чьи члены представлены частными многочленами или другими подобными рядами. Как вы можете догадаться, это было бы изнурительной манипуляцией при тестировании с использованием теста прямого сравнения 9.0109 ; вместо этого мы приступаем к тесту предельного сравнения, находя соответствующий референтный ряд (члены которого представлены b _n ) , для которого сходимость/расхождение известна и оценивается.

наверх

Тест прямого сравнения

a. Если сходится и a _n ≤ b _n для всех n, то также сходится.

б. Если расходится и _n  ≥ b _n для всех n, то   также расходится.

Пример:

Мы обычно используем этот критерий, когда связь может быть легко установлена ​​посредством неравенства, чтобы показать, что члены неизвестного ряда всегда больше, чем члены известного расходящегося ряда, или всегда меньше, чем члены известного ряда. сходящийся ряд. Если это нелегко сделать из-за трудностей с алгебраическими манипуляциями или по другим причинам, тест на предельное сравнение или какой-либо другой тест может быть лучшим выбором.

Тест чередующихся рядов

Учитывая знакопеременный ряд ,  переменный ряд будет сходиться, если выполняются следующие два условия: 

i. a _n  ≥ a _n+1 > 0

ii. = 0

Если одно из условий не выполняется, то ряд расходится.

Пример (хотя и не очень тщательно демонстрирующий доказательство условий ):

При обсуждении знакопеременных рядов мы должны отметить различие между абсолютной и условной сходимостью. Когда дело доходит до чередующихся рядов (рядов с коэффициентом (-1) ^n-1  , вызывая чередование положительных и отрицательных членов), мы можем классифицировать сходимость на абсолютно сходящуюся и условно сходящуюся на основе поведения членов a _n . Если мы можем показать, что знакопеременный ряд сходится , как мы делаем с тестом знакопеременного ряда, и что он не сходится без знакопеременного множителя,     (-1) ^n-1 , с помощью какого-либо другого теста , можно сделать вывод, что ряд сходится условно . С другой стороны, если мы воспользуемся тестом чередующихся рядов и обнаружим, что ряд сходится условно, но затем независимо определим, что ряд с | a _n | также сходится, то можно сделать вывод, что ряд сходится абсолютно . В следующих тестах, где берется предел отношения абсолютных значений, результат, указывающий на сходимость, фактически указывает на то, что тестируемый ряд абсолютно сходится.

Тест отношения

Тест отношения полезен для определения сходимости самых разных рядов, особенно тех, которые содержат факториалы.

Для бесконечной серии  вы выполняете этот тест, получая файл .

• Если R < 1, то ряд сходится абсолютно
• Если R > 1, то ряд расходится
• Если R = 1, то критерий не дает результатов

Пример:

Как упоминалось ранее, этот тест может определить, является ли ряд расходящимся или абсолютно сходящимся на основе значения отношения R. В случае, если R = 1, вы должны использовать другой тест ряда, чтобы сделать вывод определенность условие расходимости/сходимости ряда. Если R действительно равно 1, не используйте вместо этого корневой тест, потому что он даст эквивалентный неубедительный результат L = 1!

Корневой тест

Для бесконечной серии вы выполняете корневой тест, находя .

• Если L < 1, то ряд сходится абсолютно
• Если L > 1, то ряд расходится
• Если L = 1, то проверка не дает результатов. используйте тест отношения, чтобы определить расходимость/сходимость рядов, содержащих факториалы, экспоненты и другие более сложные термины. Мы используем The Root Test при условии, что все количество 9 0109 a _n возводится в степень n, чтобы исключить мощность и оценить предел изолированного a _n . Поскольку тест Ratio более широко применим к различным сериям, мы используем его чаще, чем более специализированный Root Test.

  No related posts.