Площадь круга — PeVuz.ru
Длина окружности и площадь круга
Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):
Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C – длина окружности, π – константа, D – диаметр окружности, R – радиус окружности.
Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
следовательно радиус будет равен:
| R | ≈ | 7,85 | = | 7,85 | = 1,25 (м) |
| 2 · 3,14 | 6,28 |
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга:
S = πr2
где S – площадь круга, а r – радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
следовательно, формула нахождения площади круга через диаметр будет выглядеть так:
| S = π( | D | )2 = π | D2 | = π | D2 |
| 2 | 22 | 4 |
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 22 = 3,14 · 4 = 12,56 (см2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7 : 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr2 ≈ 3,14 · 3,52 = 3,14 · 12,25 = 38,465 (см2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D2 | ≈ 3,14 | 72 | = 3,14 | 49 | = | 153,86 | = 38,465 (см2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м2.
Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:
r = √S : π
следовательно радиус будет равен:
r ≈ √12,56 : 3,14 = √4 = 2 (м)
Число π
Длину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно.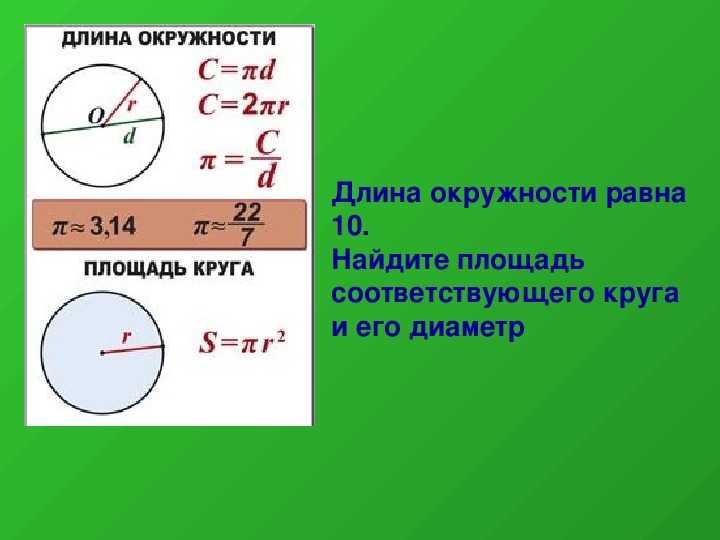
Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге.
В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
| Ведро | Таз | Бочка | Тарелка | Стакан | |
| Окружность | 91 см | 157 см | 220 см | 78,5 см | 23,9 см |
| Диаметр | 29 см | 50 см | 70 см | 25 см | 7,6 см |
| Отношение (с точн. до 0,01) | 3,14 | 3,14 | 3,14 | 3,14 | 3,14 |
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π.
Это отношение и обозначается буквой π.
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π. В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
Источник: https://naobumium.info/planimetriya/dlina_okruzhnosti.php
Площадь круга
Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром.
Формула площади круга рассчитывается с помощью математической константы – числа π. .
.
: Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.
Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров.
Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.
Рассмотрим пример расчета площади круга через диаметр, зная его радиус.
Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.
Теперь используем данные для примера расчета площади круга по приведенной выше формуле:
Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l = 8 см. Подставим значение в выведенную формулу:
Итого площадь круга будет равна 5 кв. см.
см.
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: отсюда .
После того, как найдем диагональ – мы сможем рассчитать радиус: .
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Рассмотрим пример расчета площади круга, описанного вокруг квадрата.
Задача: дан квадрат, вписанный в круг. Его сторона a = 4 см. Найдите площадь окружности.
Для начала рассчитаем длину диагонали d.
Теперь подставляем данные в формулу
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
Сектор кругового кольца – это плоская фигура, которая представляет собой часть плоскости между дугами двух окружностей с общим центром и разным радиусами, ограниченных двумя радиальными линиями, которые проведены к концам дуги с большим радиусом.
Формула площади сектора кольца, выраженная через внешний и внутренний радиусы
Пусть дана окружность радиуса R и окружности радиуса r. Причем R>r. Совместим центры этих окружностей. Возьмем на окружности с большим радиусом две произвольные точки. Проведем к ним радиусы, которые образуют угол α. Эти радиусы отсекут от окружностей некоторые дуги.
Фигура, заключенная между этими дугами окружностей и радиусами, проведенными к концам этих дуг, и будет сектор кольца, у которого R является внешним радиусом, r -внутренним радиусом.Тогда площадь этой фигуры будет равна разницы между площадью сектора круга с большим радиусом и площадью сектора круга с меньшим радиусом.
Площадь сектора круга с радиусом r выражается формулой:
где l–длина дуги равная Подставим выражение длины дуги в формулу площади сектора. Получим:
Площадь круга с радиусом R выражается формулой:
где L–длина дуги равная Подставим выражение длины дуги в формулу площади сектора.
Получим:
Тогда площадь кольца будет равна: Таким образом, площадь сектора кольца равна произведению площади единичного сектора кольца, то есть сектору, соответствующему центральному углу с мерой равной единице на меру центрального угла, соответствующего данному сектору.
Формула имеет вид:
Пример расчета площади сектора кольца, если известны его радиусы.Найдите площадь сектора кольца, образованного углом 30° , если его внешний радиус равен 14, а внутренний – 8.Площадь кольца вычисляется по формуле:
Подставив значения из условия задачи, имеем:
Page 3
Чтобы найти объем конуса необходимо произвести дополнительные построения.
Построим вписанную в конус правильную n-угольную пирамиду и опишем вокруг данного конуса правильную n-угольную пирамиду.Вписанная пирамида содержится в конусе. Из этого следует, что ее объем не больше объема конуса.
Описанная пирамида содержит конус, а это значит, что ее объем не меньше объема конуса.
Впишем в основание вписанной пирамиды окружность.
Если радиус вписанного правильного n-угольника равен R, то радиус вписанной в него окружности будет равен:
Объем вписанной пирамиды вычисляется по формуле:
где S – основание пирамиды.
Площадь данного круга вычисляется по формуле: Площадь основания вписанной пирамиды не меньше площади круга, содержащегося в ней
Поэтому утверждение, что объем вписанной в конус пирамиды не меньше верно.
А следовательно, мы может утверждать, что объем конуса, содержащий эту пирамиду будет больше или равен
V≥
Теперь опишем окружность вокруг основания описанной вокруг конуса пирамиды.
Радиус этой окружности будет равен:
Площадь данного круга вычисляется по формуле:
Основание описанной пирамиды содержится в круге описанном вокруг него. Поэтому площадь основания пирамиды не больше
Поэтому утверждение,что объем описанной пирамиды не больше верно.
А следовательно, мы может утверждать, что объем конуса, содержащий в эту пирамиду будет меньше или равен
Два полученных неравенства равны при любом n.
Если то
Тогда из первого неравенства следует, что V≥
Из второго неравенства
Отсюда следует, что
Объем конуса равен одной трети произведения радиуса на высоту.
Пример расчета объема конусаНайти объем конуса, если его радиус основания равен 3 см, а образующая 5 см.
Объем конуса вычисляется по формуле:
Для того, чтобы воспользоваться данной формулой необходимо найти высоту конуса. Образующая конуса, его высота и радиус основания образуют прямоугольный треугольник.
Воспользовавшись теоремой Пифагора имеем:
Отсюда:
Подставим значение радиуса и высоты в формулу объема конуса.Имеем:
Page 4
При нахождении объема усеченного конуса целесообразней рассматривать разность объема полного конуса и объема отсеченного конуса.
Дополним данный усеченный конус до полного . Пусть его высота будет x . Если высота усеченного конуса – h , то высота отсеченного конуса будет – x-h .
Высота усеченного конуса будет равна разности объема полного конуса с радиусом R1и высотой x и объема полного конуса с радиусом R2. и высотой x-h.
Из подобия этих конусов получаем:
Выразим x:
Тогда объем усеченного конуса можно выразить:
Применив формулу разницы кубов, имеем:
Таким образом, формула объема усеченной пирамиды имеет вид:
Пример расчета объема усеченного конусаРадиусы основания усеченного конуса равны 11 и 27 , образующая относится к высоте как 17:15 . Найдите объем усеченного конуса.
Найдите объем усеченного конуса.
Объем усеченного конуса вычисляется по формуле:
Для того, чтобы воспользоваться данной формулой необходимо найти высоту конуса. Образующая конуса, его высота и разница радиусов оснований образуют прямоугольный треугольник.
Воспользовавшись теоремой Пифагора получаем: Так как образующая относится к высоте как 17:15, то L=17x, H=15x.
Тогда:
Тогда высота усеченного конуса будет равна:
Подставим значения в формулу объема усеченного конуса. Получим:
Page 5
При нахождении объема усеченного конуса целесообразней рассматривать разность объема полного конуса и объема отсеченного конуса. Читать далее
Чтобы найти объем конуса необходимо произвести дополнительные построения. Читать далее
Усеченный конус – это часть конуса, ограниченная между двумя параллельными основаниями перпендикулярными его оси симметрии. Читать далее
Пусть α– плоскость, точка S– точка, не лежащая в этой плоскости. Возьмем на плоскости произвольный круг с радиусом R. Читать далее
Возьмем на плоскости произвольный круг с радиусом R. Читать далее
Сектор кругового кольца – это плоская фигура, которая представляет собой часть плоскости между дугами двух окружностей с общим центром и разным радиусами, ограниченных двумя радиальными линиями, которые проведены к концам дуги с большим радиусом. Читать далее
Кольцо – это плоская геометрическая фигура, которая представляет собой часть плоскости между двумя окружностями с общим центром, но имеющими разный радиус. Читать далее
Очень часто на практике приходится сталкиваться с задачей нахождения длины дуги. Читать далее
Шестиугольной пирамидой называется многогранник, в основании которого лежит правильный шестиугольник, а боковые грани образуются одинаковыми равнобедренными треугольниками. Читать далее
Читать далее
Многогранник, в основании которого лежит правильный треугольник, а остальные грани представлены равнобедренными треугольниками называется треугольной пирамидой. Читать далее
Четырехугольной пирамидой называется многогранник, в основании которого лежит квадрат, а все боковые грани являются одинаковыми равнобедренными треугольниками. Читать далее
Page 6
У большинства детей младшего школьного возраста хорошо развита механическая память, которая задействуется при выучивании правил.
Но для отдельных детей, а особенно творческих личностей, зубрежка является невыносимой.
Родители, думающие, что их чадо не способно освоить изучение таблицы умножения и поэтому в дальнейшем будет отставать в математике, заблуждаются. На самом деле к нему нужен совершенно другой, особый подход.
Читать далее
Ниже представлена таблица степеней от 2 до 10 натуральных чисел от 1 до 20.
Читать далее
Таблица кубов натуральных чисел от 1 до 100
Читать далее
Таблица факториалов от 1 до 40
Читать далее
Page 7
При нахождении объема усеченного конуса целесообразней рассматривать разность объема полного конуса и объема отсеченного конуса.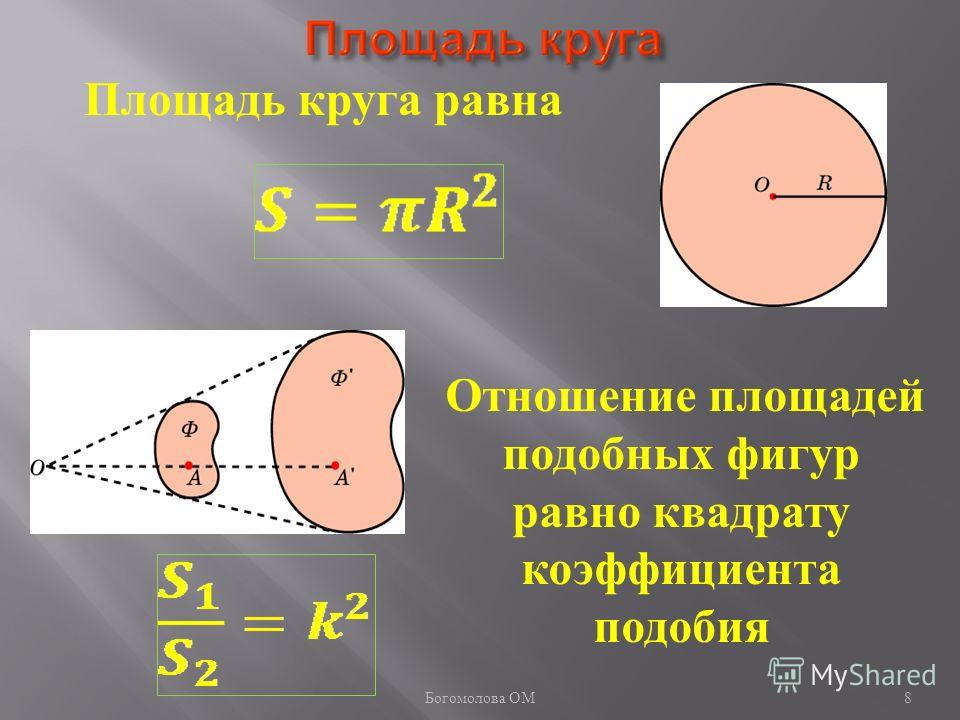 Читать далее
Читать далее
Чтобы найти объем конуса необходимо произвести дополнительные построения. Читать далее
Усеченный конус – это часть конуса, ограниченная между двумя параллельными основаниями перпендикулярными его оси симметрии. Читать далее
Пусть α– плоскость, точка S– точка, не лежащая в этой плоскости. Возьмем на плоскости произвольный круг с радиусом R. Читать далее
Сектор кругового кольца – это плоская фигура, которая представляет собой часть плоскости между дугами двух окружностей с общим центром и разным радиусами, ограниченных двумя радиальными линиями, которые проведены к концам дуги с большим радиусом. Читать далее
Кольцо – это плоская геометрическая фигура, которая представляет собой часть плоскости между двумя окружностями с общим центром, но имеющими разный радиус. Читать далее
Очень часто на практике приходится сталкиваться с задачей нахождения длины дуги. Читать далее
Читать далее
Шестиугольной пирамидой называется многогранник, в основании которого лежит правильный шестиугольник, а боковые грани образуются одинаковыми равнобедренными треугольниками. Читать далее
Многогранник, в основании которого лежит правильный треугольник, а остальные грани представлены равнобедренными треугольниками называется треугольной пирамидой. Читать далее
Четырехугольной пирамидой называется многогранник, в основании которого лежит квадрат, а все боковые грани являются одинаковыми равнобедренными треугольниками. Читать далее
Источник: http://2mb.ru/matematika/geometriya/ploshhad-kruga/
Площадь круга и его частей. Длина окружности и ее дуг
| Справочник по математике | Геометрия (Планиметрия) | Окружность и круг |
| Фигура | Рисунок | Определения и свойства |
| Окружность | Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности | |
| Дуга | Часть окружности, расположенная между двумя точками окружности | |
| Круг | Конечная часть плоскости, ограниченная окружностью | |
| Сектор | Часть круга, ограниченная двумя радиусами | |
| Сегмент | Часть круга, ограниченная хордой | |
| Правильный многоугольник | Выпуклый многоугольник, у которого все стороны равны и все углы равны | |
Около любого правильного многоугольника можно описать окружность |
| Окружность |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки – центра окружности |
| Дуга |
Часть окружности, расположенная между двумя точками окружности |
| Круг |
Конечная часть плоскости, ограниченная окружностью |
| Сектор |
Часть круга, ограниченная двумя радиусами |
| Сегмент |
Часть круга, ограниченная хордой |
| Правильный многоугольник |
Выпуклый многоугольник, у которого все стороны равны и все углы равны youtube.com/embed/2vFZ3vnV3RI?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Около любого правильного многоугольника можно описать окружность |
Определение 1. Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Площадь круга
Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.
Рис.1
Площадь правильного n – угольника, вписанного в окружность радиуса R, равна
Площадь правильного n – угольника, вписанного в окружность радиуса 1, равна
Следовательно,
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1, стремится к π, то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу πR2.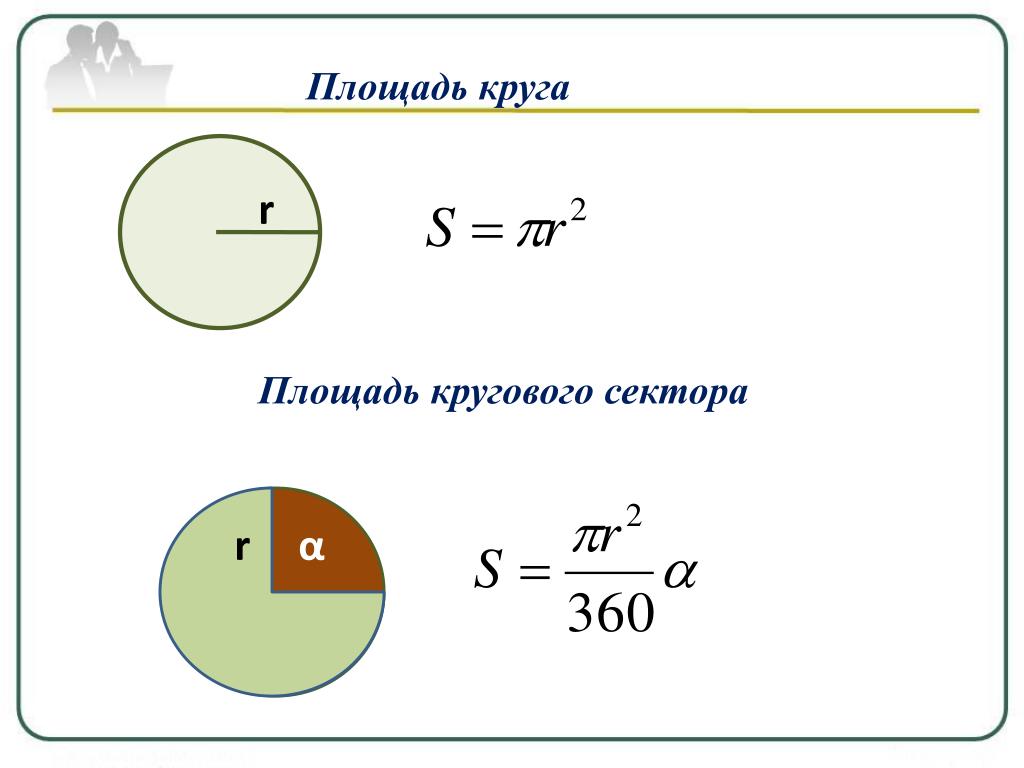
Таким образом, площадь круга радиуса R, обозначаемая S, равна
S = πR2.
Длина окружности
Рассмотрим правильный n – угольник B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центраO окружности перпендикуляры на все стороны многоугольника (рис. 2).
Рис.2
Поскольку площадь n – угольника B1B2…Bn равна
то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R:
C = 2πR.
Следствие. Длина окружности радиуса 1 равна 2π.
Длина дуги
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
Рис.3
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
Рис.4
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
Рис.5
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
Следовательно,
В случае, когда величина α выражена в в радианах, получаем
Следовательно,
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
| подготовительные курсы для школьников 8, 9, 10 и 11 классов |
У нас также для школьников организованы
| индивидуальные занятия с репетиторами по математике и русскому языку |
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
Источник: https://www.resolventa.ru/demo/diaggia6.htm
Как рассчитать площадь круга. Площадь круга
Круг – это видимая совокупность множества точек, которые находятся на одинаковом расстоянии от центра. Чтобы найти его площадь, необходимо знать, что такое радиус, диаметр, число π и окружность.
Величины, участвующие в расчете площади круга
Расстояние, ограниченное центральной точкой круга и любой из точек окружности, называется радиусом этой геометрической фигуры. 2. Другими словами диаметр во 2 степени равен стороне квадрата во 2 степени, умноженной на 2.
2. Другими словами диаметр во 2 степени равен стороне квадрата во 2 степени, умноженной на 2.
Вычислив значение длины диаметра круга, можно узнать и его радиус, после чего воспользоваться одной их формул определения площади круга.
Площадь сектора круга
Сектор – это часть круга, ограниченная 2 радиусами и дугой между ними. Чтобы узнать его площадь, нужно измерить угол сектора. После этого необходимо составить дробь, в числителе которой будет значение угла сектора, а в знаменателе – 360. Чтобы высчитать площадь сектора, значение, полученное в результате деления дроби, нужно умножить на площадь круга, вычисленную по одной из вышеперечисленных формул.
Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.
Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.
Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.
Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.
Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.
Формула нахождения площади круга через радиус:Примеры решения заданий по нахождению S-площади круга через R-радиус:
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².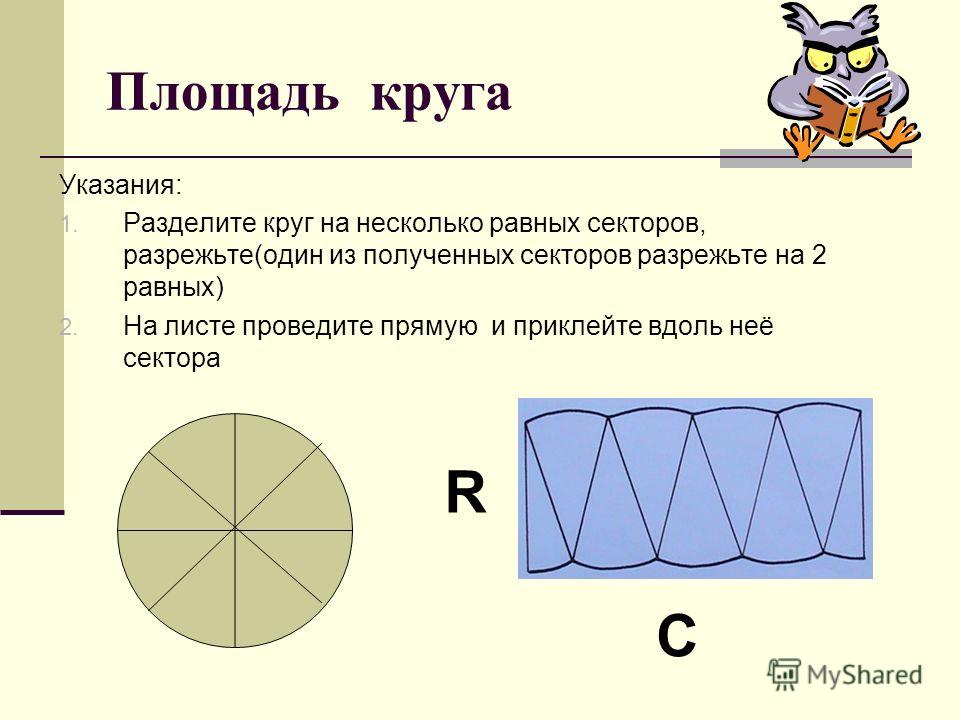
Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².
Ответ: Площадь плоской круглой фигуры равна 78,5 см².
Нахождение S круга, если известна длина окружности:
Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.
Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².
Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.
Формула нахождения площади круга, вписанного в квадрат:
Примеры решения задач по нахождению площади круга, вписанного в квадрат:
———————————————————————————————————————
Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————
Задача №2 : Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.Решайте так : Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².
Немного сложнее находить площадь круглой фигуры, описанной около квадрата.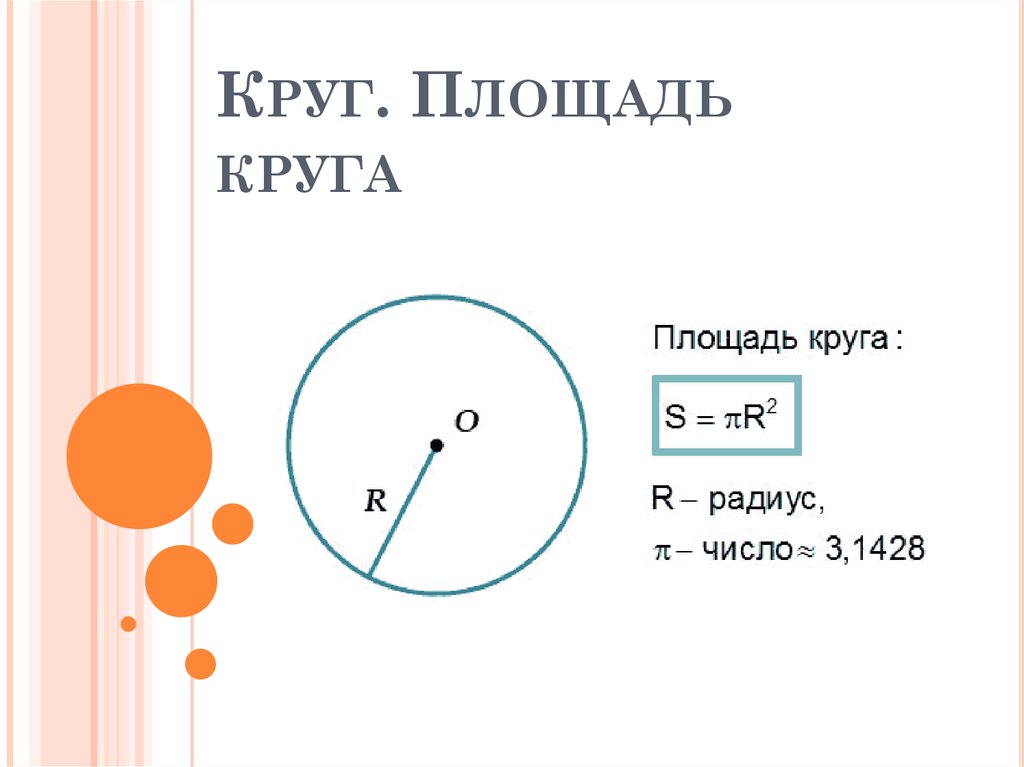 Но, зная формулу, можно быстро подсчитать данное значение.
Но, зная формулу, можно быстро подсчитать данное значение.
Формула нахождения S круга, описанного около квадратной фигуры:
Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:
Задача
Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
Формула нахождения площади круга, вписанного в равнобедренный треугольник:
Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².
Формула нахождения площади круга, вписанного в прямоугольный треугольник:
Примеры решения заданий:
Задача №1
Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²
Задача №2
Решение:
Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.
Формулу смотрите выше по тексту.
Задача №3
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.
Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:
Примеры решения задач:
Вот еще пример решения задачи с использованием формулы Герона.
Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.
Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.
Для решения этой задачи нужно использовать такие формулы:
Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:
Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Примеры решения задач:
Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:
Примеры решения задач:
Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Ответ: Радиус равен 6.
В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Видео: Математика | Вычисление площадей круга и его частей
В геометрии кругом называется некоторое множество всех точек на плоскости, которые удалены от одной точки, называемой его центром, на расстояние, не большее заданного, называемого его радиусом. При этом внешней границей круга является окружность , а в том случае, если длина радиуса равна нулю, круг вырождается в точку.
Определение площади круга
При необходимости площадь круга можно вычислить по формуле:
| S | D 2 |
r — радиус круга
D — диаметр круга
S — площадь круга
π — 3. 14
14
Эта геометрическая фигура очень часто встречается как в технике, так и в архитектуре. Конструкторы машин и механизмов разрабатывают различные детали, сечения многих из которых представляют собой именно круг . К примеру, таковыми являются валы, штоки, тяги, цилиндры, оси, поршни и так далее. При изготовлении этих деталей используются заготовки из различных материалов (металлов, древесины, пластических масс), их сечения также представляют собой именно круг . Само собой разумеется, что разработчикам нередко приходится вычислять площадь круга через диаметр или радиус, используя для этой цели несложные математические формулы, открытые еще в глубокой древности.
Именно тогда круглые элементы стали активно и широко использоваться в архитектуре. Один из самых ярки тому примеров – цирк, представляющий собой разновидность строений, предназначенных для проведения в них различных зрелищных мероприятий. Их арены имеют форму круга , а впервые они стали строиться еще во времена античности. Само слово «circus » в переводе с латинского языка означает «круг ». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить
Само слово «circus » в переводе с латинского языка означает «круг ». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить
Архитектурными элементами, которые могут принимать форму круга, являются окна. Конечно, в большинстве случаев они прямоугольные или же квадратные (причем во многом благодаря тому, что это проще как для зодчих, так и для строителей), но в некоторых зданиях можно встретить и круглые окна.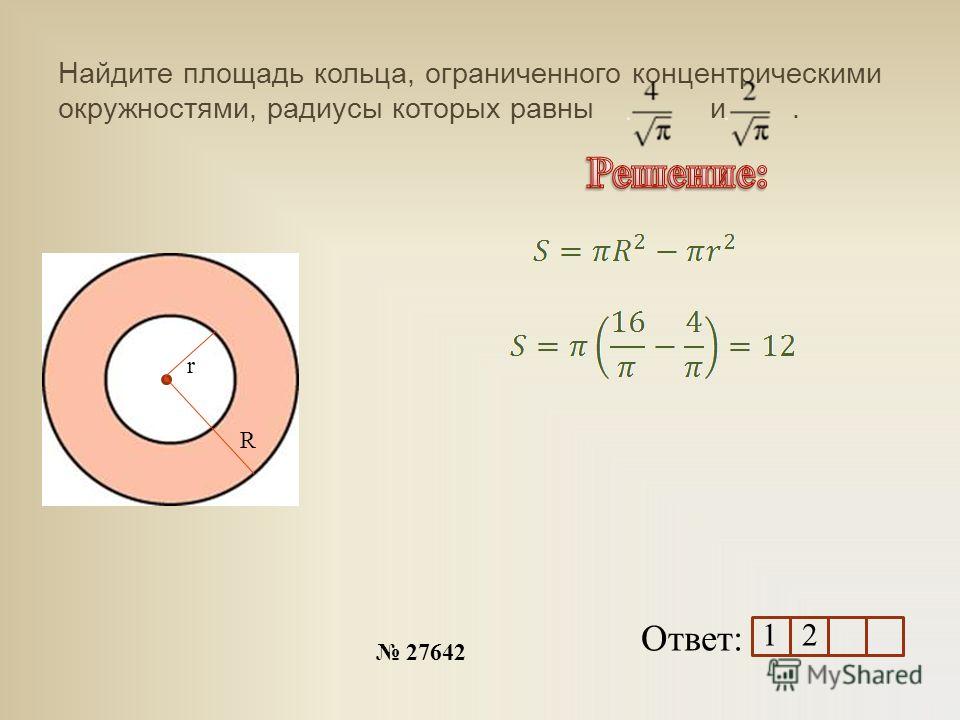 Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.
Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.
Отнюдь не является редкостью использование круглых элементов для производства мебели, например столов и стульев. Существует даже понятие «круглый стол », которое подразумевает конструктивную дискуссию, в ходе которой происходит всестороннее обсуждение различных важных проблем и вырабатывается пути их решения. Что касается изготовления самих столешниц, имеющих круглую форму, то для их производства применяются специализированные инструменты и оборудование, при условии участия рабочих с довольно высокой квалификацией.
Инструкция
Используйте число Пи для нахождения радиуса по известной площади круга. Эта константа задает пропорцию между диаметром круга и длиной его границы (окружности). Длина окружности максимальную площадь плоскости, которую возможно с ее помощью охватить, а диаметр равняется двум радиусам, поэтому и площадь с радиусом тоже соотносятся друг с другом с пропорцией, которую можно выразить через число Пи. Эта константа (π) определяется как площади (S) и возведенного в квадрат радиус (r) круга. Из этого вытекает, что радиус можно выразить, как квадратный корень из частного от деления площади на число Пи: r=√(S/π).
Эта константа (π) определяется как площади (S) и возведенного в квадрат радиус (r) круга. Из этого вытекает, что радиус можно выразить, как квадратный корень из частного от деления площади на число Пи: r=√(S/π).
Долгое время Эрастофен возглавлял Александрийскую библиотеку, самую знаменитую библиотеку древнего мира. Помимо того, что он вычислил размер нашей планеты, сделал еще ряд важных изобретений и открытий. Изобрел нехитрый метод определять простые числа, называемый теперь «решето Эрастофена».
Нарисовал «карту мира», в которой показал все части света, известные на тот момент древним грекам. Карта считалась одной из лучших для своего времени. Разработал систему долготы и широты и календарь, включавший високосные годы. Изобрел армиллярную сферу, механическое устройство, используемое ранними астрономами, чтобы демонстрировать и предсказывать видимое движение звезд на небе. Также составил звездный каталог, включавший в себя 675 звезд.
Источники:
- Греческий ученый Эратосфен Киренский впервые в мире вычислил радиус Земли
- Eratosthenes» Calculation of Earth»s Circumference
- Eratosthenes
формула.
 Чему равна площадь круга, описанного и вписанного в квадрат, прямоугольный и равнобедренный треугольник, прямоугольную, равнобедренную трапецию
Чему равна площадь круга, описанного и вписанного в квадрат, прямоугольный и равнобедренный треугольник, прямоугольную, равнобедренную трапециюИнструкция
Используйте число Пи для нахождения радиуса по известной площади круга. Эта константа задает пропорцию между диаметром круга и длиной его границы (окружности). Длина окружности максимальную площадь плоскости, которую возможно с ее помощью охватить, а диаметр равняется двум радиусам, поэтому и площадь с радиусом тоже соотносятся друг с другом с пропорцией, которую можно выразить через число Пи. Эта константа (π) определяется как площади (S) и возведенного в квадрат радиус (r) круга. Из этого вытекает, что радиус можно выразить, как квадратный корень из частного от деления площади на число Пи: r=√(S/π).
Долгое время Эрастофен возглавлял Александрийскую библиотеку, самую знаменитую библиотеку древнего мира. Помимо того, что он вычислил размер нашей планеты, сделал еще ряд важных изобретений и открытий. Изобрел нехитрый метод определять простые числа, называемый теперь «решето Эрастофена».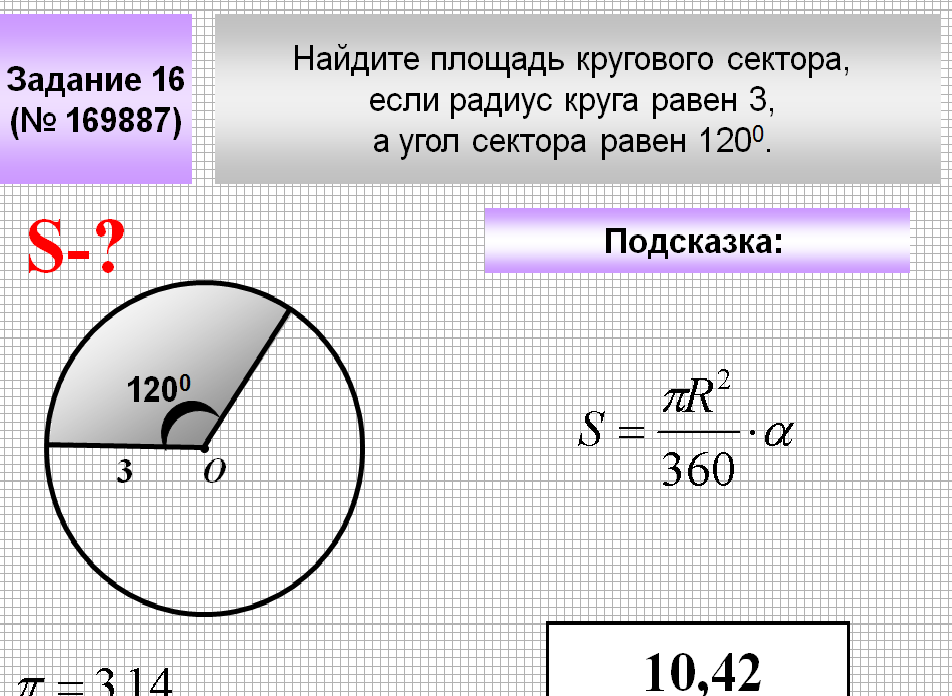
Нарисовал «карту мира», в которой показал все части света, известные на тот момент древним грекам. Карта считалась одной из лучших для своего времени. Разработал систему долготы и широты и календарь, включавший високосные годы. Изобрел армиллярную сферу, механическое устройство, используемое ранними астрономами, чтобы демонстрировать и предсказывать видимое движение звезд на небе. Также составил звездный каталог, включавший в себя 675 звезд.
Источники:
- Греческий ученый Эратосфен Киренский впервые в мире вычислил радиус Земли
- Eratosthenes» Calculation of Earth»s Circumference
- Eratosthenes
Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.
Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.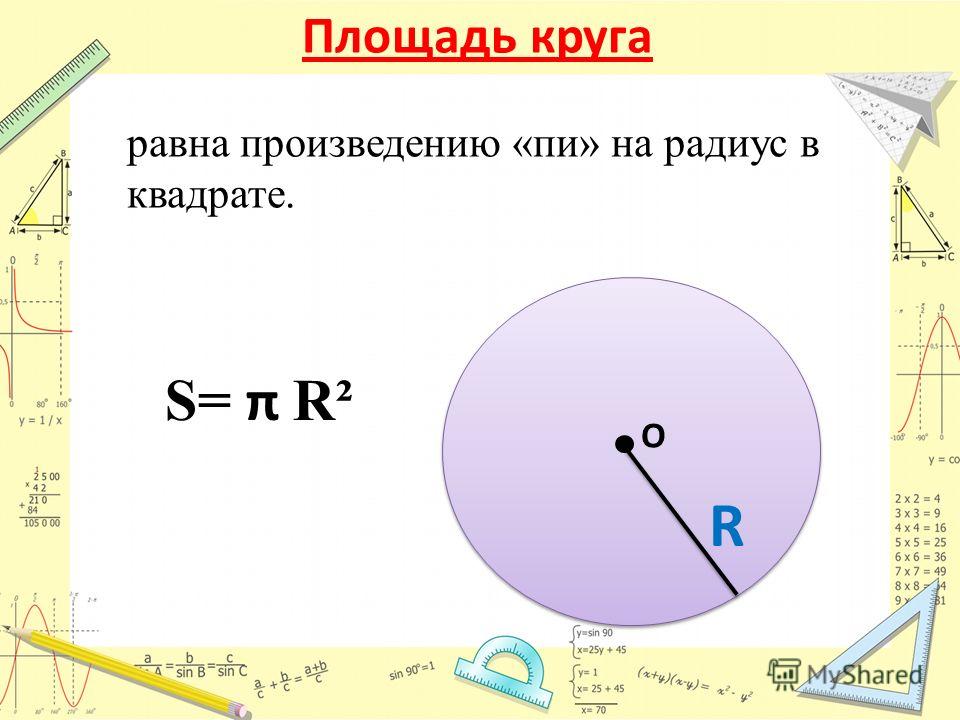
Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.
Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.
Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.
Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.
Формула нахождения площади круга через радиус:Примеры решения заданий по нахождению S-площади круга через R-радиус:
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².
Формула нахождения S-площади круга через D-диаметр:Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².
Ответ: Площадь плоской круглой фигуры равна 78,5 см².
Нахождение S круга, если известна длина окружности:
Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.
Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².
Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.
Формула нахождения площади круга, вписанного в квадрат:
Примеры решения задач по нахождению площади круга, вписанного в квадрат:
———————————————————————————————————————
Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
Найдите S-площадь вписанной окружности.Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————
Задача №2 : Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.Решайте так : Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².
Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.
Формула нахождения S круга, описанного около квадратной фигуры:
Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:
Задача
Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
Формула нахождения площади круга, вписанного в равнобедренный треугольник:
Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².
Формула нахождения площади круга, вписанного в прямоугольный треугольник:
Примеры решения заданий:
Задача №1
Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²
Задача №2
Решение:
Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.
Задача №3
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.
Когда известен радиус, то найти площадь просто, как было описано выше.
Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:
Примеры решения задач:
Вот еще пример решения задачи с использованием формулы Герона.
Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.
Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.
Для решения этой задачи нужно использовать такие формулы:
Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:
Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Примеры решения задач:
Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:
Примеры решения задач:
Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Ответ: Радиус равен 6.
В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Видео: Математика | Вычисление площадей круга и его частей
Круг – это видимая совокупность множества точек, которые находятся на одинаковом расстоянии от центра. Чтобы найти его площадь, необходимо знать, что такое радиус, диаметр, число π и окружность.
Величины, участвующие в расчете площади круга
Расстояние, ограниченное центральной точкой круга и любой из точек окружности, называется радиусом этой геометрической фигуры. Длины всех радиусов одного круга одинаковы. Отрезок между 2 любыми точками окружности, который проходит через центральную точку, называется диаметром. Длина диаметра равна длине радиуса, умноженной на 2.
Для подсчета площади круга применяется значение числа π. Эта величина равна отношению длины окружности к длине диаметра круга и имеет неизменное значение. Π = 3,1415926. Длина окружности высчитывается по формуле L=2πR. 2. Другими словами диаметр во 2 степени равен стороне квадрата во 2 степени, умноженной на 2.
2. Другими словами диаметр во 2 степени равен стороне квадрата во 2 степени, умноженной на 2.
Вычислив значение длины диаметра круга, можно узнать и его радиус, после чего воспользоваться одной их формул определения площади круга.
Площадь сектора круга
Сектор – это часть круга, ограниченная 2 радиусами и дугой между ними. Чтобы узнать его площадь, нужно измерить угол сектора. После этого необходимо составить дробь, в числителе которой будет значение угла сектора, а в знаменателе – 360. Чтобы высчитать площадь сектора, значение, полученное в результате деления дроби, нужно умножить на площадь круга, вычисленную по одной из вышеперечисленных формул.
– это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом . В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром . Формула площади круга рассчитывается с помощью математической константы – числа π..
Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром . Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно : Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.
Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр . Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения .
Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R
= 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.
Для начала найдем диаметр, который, как известно, в два раза больше радиуса.
Теперь используем данные для примера расчета площади круга по приведенной выше формуле:
Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l
= 8 см. Подставим значение в выведенную формулу:
Итого площадь круга будет равна 5 кв. см.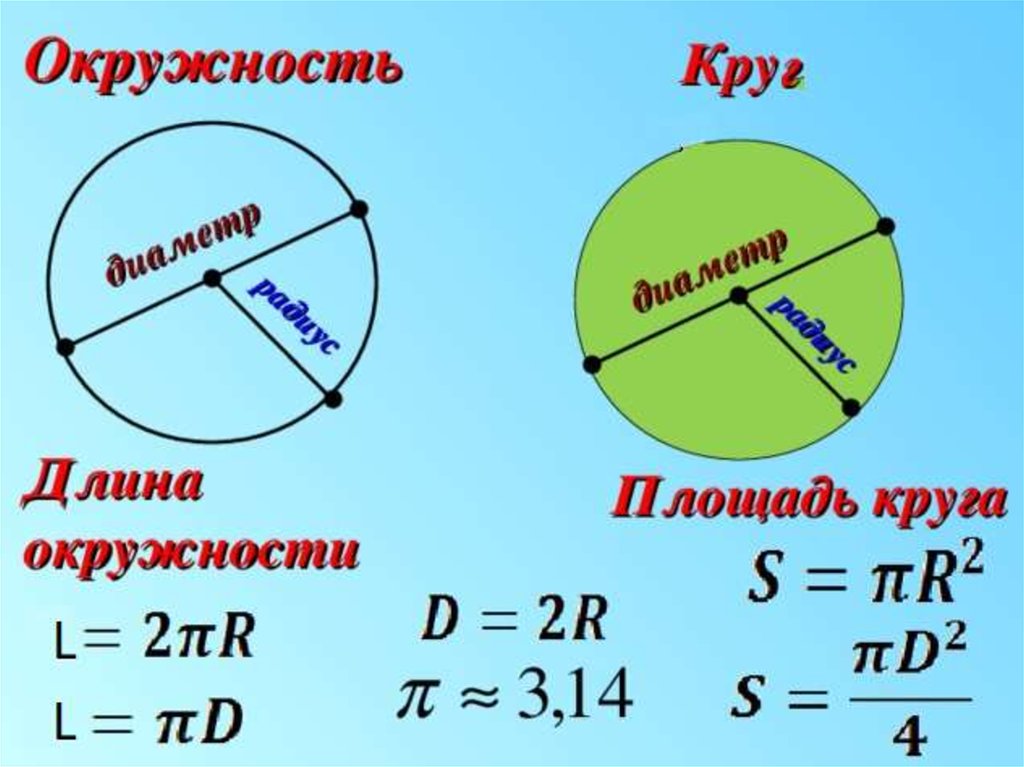
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a
ее можно найти по теореме Пифагора: отсюда .
После того, как найдем диагональ – мы сможем рассчитать радиус: .
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга.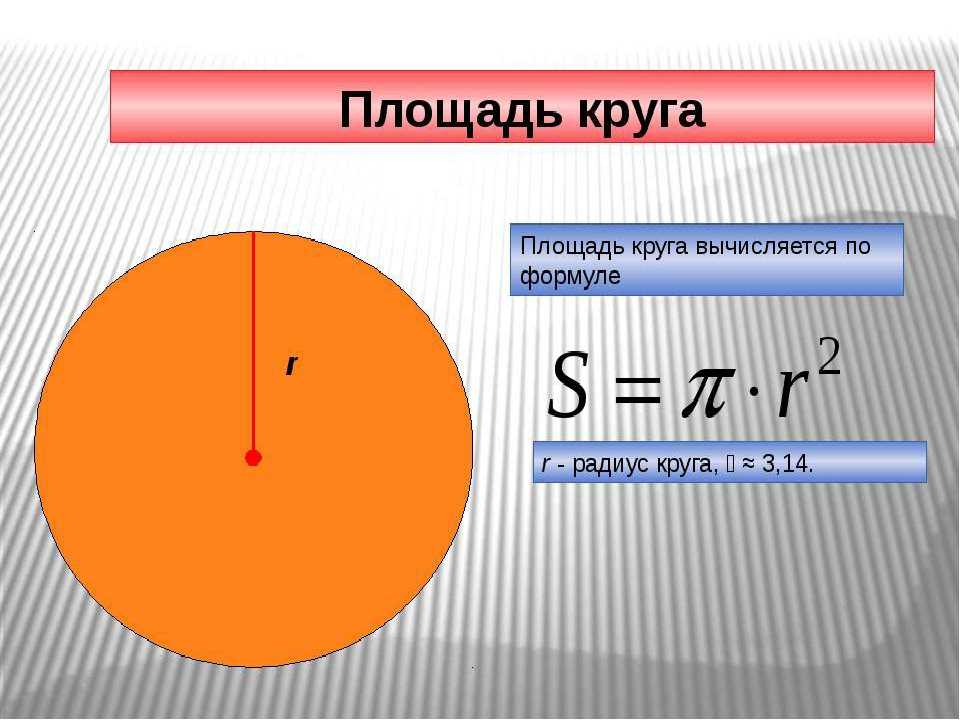 Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Как найти площадь круга
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 9 … 15 16 Следующая →
Справка по основам геометрии » Плоская геометрия » Круги » Радиус » Как найти площадь круга
Радиус круга 4см, чему равна площадь?
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь круга находится по формуле: , где r — радиус.
.
Площадь круга .
Сообщить об ошибке
Радиус круга ниже составляет 18 единиц. Какова площадь круга?
Какова площадь круга?
Возможные ответы:
квадраты
квадраты
Невозможно определить
Квадратные единицы
Квадратные единицы
Правильный ответ:
Квадратные единицы
Объяснение:
Формула площади круга с радиусом:
Мы можем заполнить
Вы можете произвести арифметические действия, чтобы получить площадь около 1017,876 квадратных единиц, но это хорошо, а точнее оставить так, как показано.
Сообщить об ошибке
Укажите площадь круга диаметром 13.
Возможные ответы:
Правильный ответ:
Объяснение:
Половина диаметра 13 – это радиус .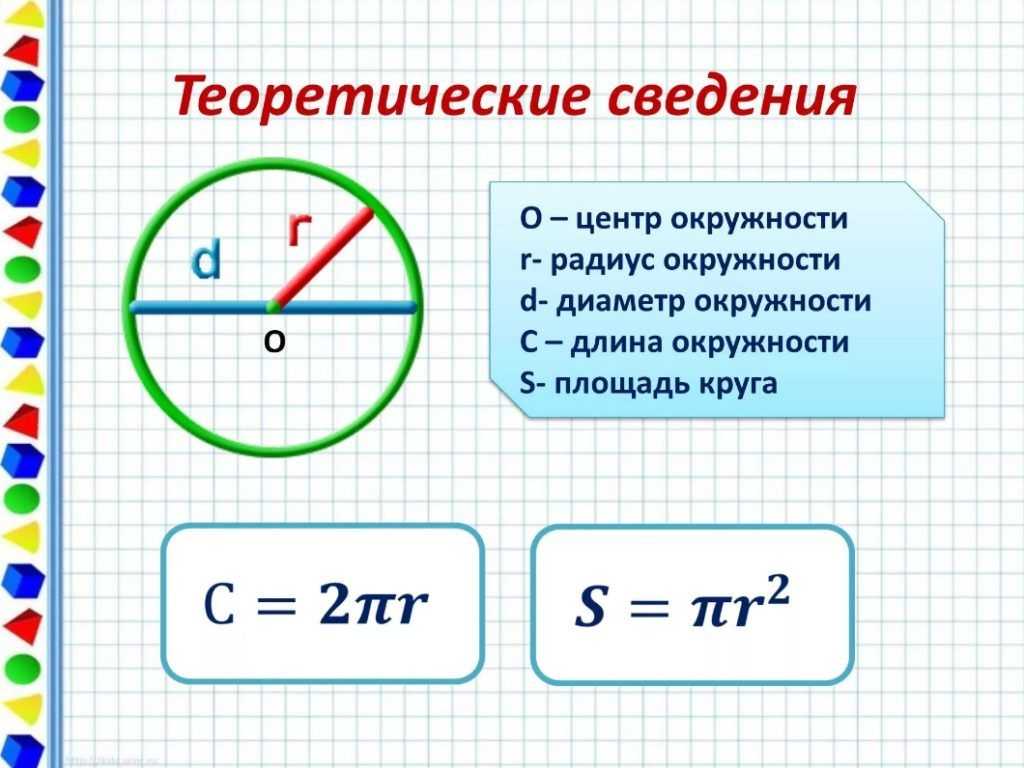 Используйте формулу площади:
Используйте формулу площади:
Сообщить об ошибке
Точка A является центром круга выше.
Фигура ABCD представляет собой квадрат.
Отрезки AB и AD являются радиусами окружности.
Радиус круга единиц.
Найдите площадь фигуры красного цвета.
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку известно, что A — центр окружности, а ABCD — квадрат, угол BAD — прямой угол, который составляет ровно одну четвертую окружности (90 o — это одна четвертая часть 360 o ) . Это также можно увидеть через пропорцию.
Поскольку угол, содержащий красную область, составляет одну четвертую часть круга, нахождение площади всего круга, а затем одной четверти этого числа дает ответ. Используйте уравнение , чтобы найти площадь круга, где это площадь, а это радиус.
Сообщить об ошибке
Найдите площадь катка, образованного прямоугольником и полукругами с указанными размерами.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти площадь всего катка, найдите площадь прямоугольника в середине катка и прибавьте ее к площади круга, который будет образован двумя полукружьями по краям этого прямоугольника. .
Площадь прямоугольника находится путем умножения его ширины на длину.
Чтобы найти площадь круга, на который приходится два полукруга, используйте формулу , где – радиус круга.
Радиус круга равен половине его диаметра. Диаметр круга такой же, как ширина прямоугольника в случае с этим катком, и составляет половину от этого.
Добавление этой площади к площади прямоугольника дает площадь всего катка.
Сообщить об ошибке
Если у круга есть длина окружности, какова его площадь?
Возможные ответы:
Правильный ответ:
Объяснение:
Если длина окружности равна , то, поскольку мы знаем . Далее мы знаем, что , поэтому
Сообщить об ошибке
Если уравнение окружности (x – 7) 2 + (y + 1) 2 = 81, какова площадь круга?
Возможные ответы:
6561π
49π
2π
18π
81π
Правильный ответ:
81π
Объяснение:
Уравнение уже представляет собой уравнение окружности, и правая часть уравнения обозначает r 2 → r 2 = 81 и r = 9
Площадь круга равна πr 2 , поэтому площадь этого круга равна 81π.
Сообщить об ошибке
Предположим, что π = 3,14
Мужчина хотел бы поставить круговой водоворот на своем заднем дворе. Он хотел бы, чтобы водоворот был шириной шесть футов. Его задний двор имеет длину 8 футов и ширину 7 футов. По государственному постановлению, чтобы поставить гидромассажную ванну на заднем дворе, площадь должна быть в 1,5 раза больше, чем бассейн. Может ли мужчина законно установить водоворот?
Возможные ответы:
Нет, потому что площадь заднего двора меньше площади водоворота.
Да, потому что площадь водоворота составляет 28,26 квадратных футов и в 1,5 раза меньше площади заднего двора.
Нет, потому что площадь заднего двора составляет 30 квадратных футов, и поэтому водоворот слишком велик, чтобы соответствовать требованиям закона.
Нет, потому что площадь водоворота 42,39 кв. фута и его площадь в 1,5 раза больше, чем площадь заднего двора.
Да, потому что площадь водоворота составляет 18,84 квадратных фута и в 1,5 раза его площадь будет меньше площади заднего двора.
Правильный ответ:
Да, потому что площадь водоворота составляет 28,26 кв. фута, и его площадь в 1,5 раза меньше площади заднего двора.
Объяснение:
Если вы ответили, что площадь водоворота составляет 18,84 фута и, следовательно, подходит, вы ошиблись, потому что 18,84 — это длина окружности водоворота, а не площадь.
Если вы ответили, что площадь водоворота составляет 56,52 фута, вы умножили площадь водоворота на 1,5 и предположили, что это правильная площадь, а не законный предел.
Если вы ответили, что площадь заднего двора меньше площади водоворота, значит, вы неправильно рассчитали площадь.
И если вы думали, что площадь заднего двора составляет 30 футов, вы нашли периметр заднего двора, а не площадь.
Правильный ответ состоит в том, что площадь водоворота составляет 28,26 фута, а при умножении на 1,5 = 42,39 это меньше площади заднего двора, которая составляет 56 квадратных футов.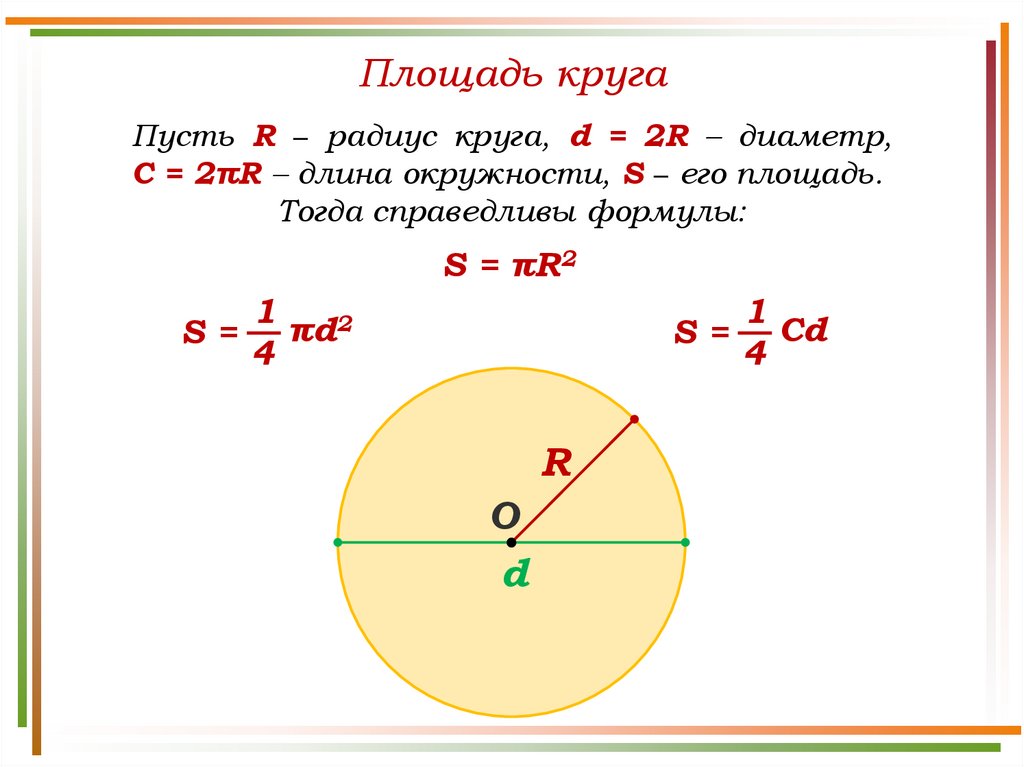
Сообщить об ошибке
На плоскости есть две одинаковые окружности, которые перекрываются. Радиус обоих кругов равен 1. Область, в которой они перекрываются, имеет площадь № .
Какова общая площадь двух перекрывающихся кругов?
Возможные ответы:
π
0
2 π
1
2
Правильный ответ:
π
6666666666666666666666666666666666666666666666666666666666666666666666666666666н. Объяснение:
Общая площадь обоих кругов равна π + π = 2 π
Поскольку область перекрывается, мы не можем сосчитать ее дважды, поэтому ее нужно вычесть.
получаем 2 π – π = π
Сообщить об ошибке
Квадрат со стороной 4 дюйма вписан в окружность, как показано ниже. Какова площадь незаштрихованной области внутри круга в квадратных дюймах?
Какова площадь незаштрихованной области внутри круга в квадратных дюймах?
Возможные ответы:
8π-4
8π-8
4π-4
8π-16
2π-4
Правильный Ответ:
8 8
.0016 Пояснение:
Используя теорему Пифагора, можно найти, что диаметр круга (а также диагональ квадрата) равен 4√2. Таким образом, радиус круга равен половине диаметра, или 2√2. Тогда площадь круга равна π(2√2) 2 , что равно 8π. Затем из всего круга нужно вычесть площадь квадрата, что даст площадь 8π-16 квадратных дюймов.
Сообщить об ошибке
← Предыдущий 1 2 3 4 5 6 7 8 9 … 15 16 Следующий →
Уведомление об авторских правах
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
Площадь круга – объяснение и примеры
Напомним, площадь – это область, занимающая фигуру в двухмерной плоскости. В этой статье вы узнаете площадь круга и формулы для расчета площади круга.
В этой статье вы узнаете площадь круга и формулы для расчета площади круга.
Какова площадь круга?
Площадь круга – это мера пространства или области, заключенной внутри круга. Проще говоря, площадь круга — это общее количество квадратных единиц внутри этого круга.
Например, , если вы начертите квадраты размером 1 см на 1 см внутри круга. Тогда общее количество полных квадратов, расположенных внутри круга, представляет собой площадь круга. Мы можем измерить площадь круга в м 2 , км 2 , в 2 , мм 2, и т.д.
Формула площади круга
Площадь круга можно рассчитать с помощью трех формул . Эти формулы применяются в зависимости от предоставленной вам информации.
Давайте обсудим эти формулы для нахождения площади круга.
Площадь круга с использованием радиуса
Учитывая радиус круга, формула для расчета площади круга гласит:
Площадь круга = πr 2 квадратные единицы
A = πr 2 квадратные единицы
Где A = площадь круга.
пи (π) = 22/7 или 3,14, а r = радиус окружности.
Давайте лучше поймем эту формулу, решив несколько примеров задач.
Пример 1
Найдите площадь круга, радиус которого равен 15 мм.
Раствор
A = πr 2 Квадратные единицы
по замене,
a = 3,14 x 15 2
= (3,14 x 15 x 15) мм 2
= 706,5 мм 2
Итак, область круга 706,5 ММ 2
.
Пример 2
Вычислите площадь круга, показанного ниже.
Раствор
A = πr 2 Квадратные единицы
= (3,14 x 28 2 ) см 2
9092 = 2 931040121 2= 2461,76 см 2
Пример 3
Площадь круга равна 254,34 квадратных ярда. Каков радиус окружности?
Решение
A = πr 2 квадратные единицы
254,34 = 3,14 x r 2
Разделите обе части на 3,14.
r 2 = 254,34/3,14 = 81
Найдите квадратный корень из обеих частей.
√r 2 = √81
r = -9, 9
Так как радиус не может иметь отрицательное значение, мы принимаем положительное 9 как правильный ответ.
Итак, радиус круга равен 9 ярдам.
Пример 4
При вращении газонокосилка разбрызгивает воду на 10 футов в каждом направлении. Какова площадь посыпанного газона?
Решение
Здесь радиус равен 10 футам.
A = πr 2 квадратных единиц
= 3,14 x 10 2
= (3,14 x 10 x 10) кв. футов
= 314 кв. футов
Следовательно, площадь посыпанного газона составляет 314 кв. футов. Когда диаметр круга известен, площадь круга определяется как
Площадь круга = πd 2 /4 квадратных единиц
Где d = диаметр круга.
Пример 5
Найдите площадь круга диаметром 6 дюймов.
Раствор
A = πd 2 / 4 квадратных единицы
= 3,14 x 6 2 / 4 кв. дюймы.
= (3,14 х 6 х 6)/4 кв. дюймов
= 28,26 квадратных дюймов
Итак, площадь круга диаметром 6 дюймов равна 28,26 квадратных дюймов.
Пример 6
Вычислите площадь круга, показанного ниже.
Решение
Учитывая диаметр,
A = πd 2 /4 квадратных единиц
= 3,14 x 50 2 /4
= (3,14 x 50 x 50) /4
= 1962,5 CM 2
Пример
Пример
99000 40004
. площадь обеденной тарелки диаметром 10 см. Решение a = πd 2 /4 квадратных единиц = 3,14 x 10 2 /4 = (3,14 x 10 x 10) /4 = 78,5,5 С. = 78,5,5 C 2 2 2 = 78,5,5 C 2 = 78,5,5 C 2 = 78,5,5 C 2 . Пример 8 Диаметр круглой тарелки 20 см. Найдите размеры квадратной пластины, которая будет иметь ту же площадь, что и круглая пластина. Решение Приравнивайте площадь круга к площади квадратной πd 2 /4 = S 2 3,14 x 20 2 /4 = S 2 9 2 /4 = S 2 9 9000 9000 9000 9000 9000 9000 9000 2 2 /4 = S 2 9 2 /4 = S 2 9000 9000 2 /4 = S 2 9000 9000 2 /4 = S 2 2
2
Найдите квадратный корень из обеих сторон, чтобы получить
s = 17,72
Следовательно, размеры квадратной тарелки будут 17,72 см на 17,72 см.
Пример 9
Найдите диаметр круга площадью 156 м 2 .
Решение
a = πd 2 /4
156 = 3,14d 2 /4
МАЙСКАЯ САМА НА 4.
624 = 3,14D 2 9
624 = 3,14D 2
624 = 3,14D 2
624 = 3,14D 2 9012 2 624 = . 198,726 = d 2 d = 14,1 м Таким образом, диаметр окружности будет 14,1 м. Как мы уже знаем, длина окружности — это расстояние по окружности. Можно вычислить площадь круга, зная его длину окружности. Площадь круга = C 2 /4π A = C 2 /4π Где C = длина окружности. Пример 10 Найдите площадь круга, длина окружности которого равна 25,12 см. Раствор Учитывая окружность, Площадь = C 2 /4π A = 25,12 2 /4π = 50,24 см 2 8 Площадь круга по длине окружности
9000.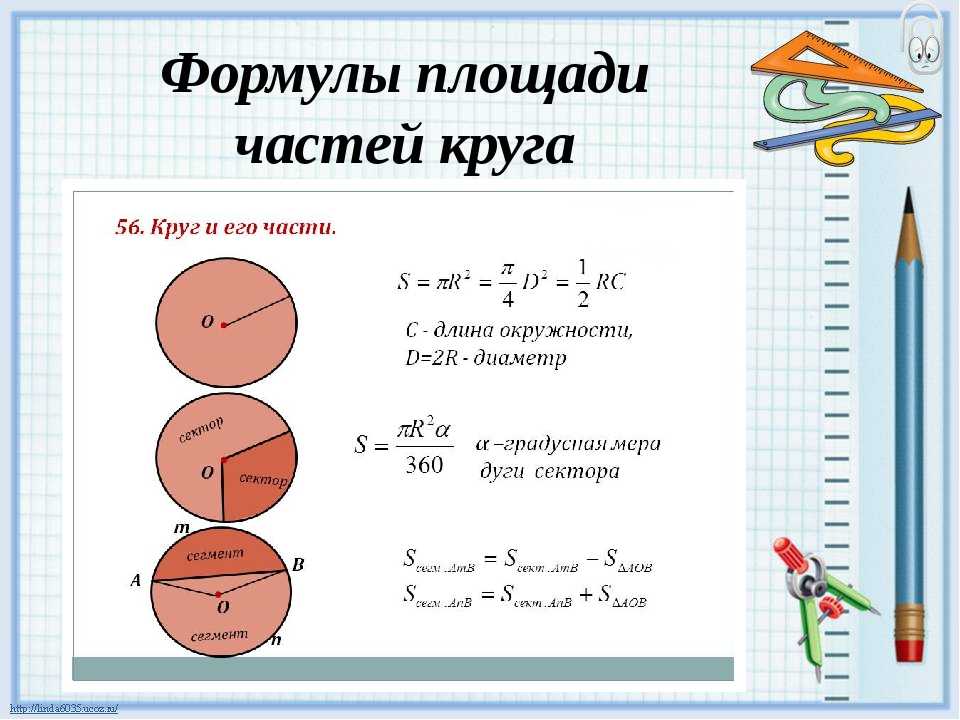 круг площадью 78,5 мм 2 ?
круг площадью 78,5 мм 2 ?
Решение
A = C 2 /4π
78,5 = C 2 /4π
Умножьте обе части на 4π.
C 2 = 985,96
Найдите квадратный корень из обеих частей.
С = 31,4 мм.
Итак, длина окружности равна 31,4 мм.
Площадь круга: формула, определение и примеры
- Автор Асит Баранкар
- Последнее изменение 27-09-2022
- Автор Асит Баранкар
- Последнее изменение 27-09-2022
Площадь круга: Площадь круга — это пространство, занимаемое кругом на двумерной плоскости. Круг — это важная геометрическая фигура, которая присутствует во многих областях, таких как строительство, машиностроение и многие другие. Решение задач, связанных с кругами в геометрии, требует, чтобы мы могли вычислить площадь круга.
Решение задач, связанных с кругами в геометрии, требует, чтобы мы могли вычислить площадь круга.
Формула площади круга: A = πr2, где r — радиус круга. Единицей площади является квадратная единица, например, м2, см2, дюйм2 и т. д. В этой статье мы изучим термины, связанные с кругами, такие как радиус, диаметр, периметр, площадь круга и т. д. Продолжайте читать, чтобы узнать больше. .
Определение Круга : Окружность — это совокупность всех точек на плоскости, расстояние до которых от фиксированной точки всегда одинаково. Неподвижная точка называется центром окружности, а граница окружности называется окружностью окружности.
Радиус круга
Радиус окружности — это отрезок, соединяющий центр и любую точку на окружности.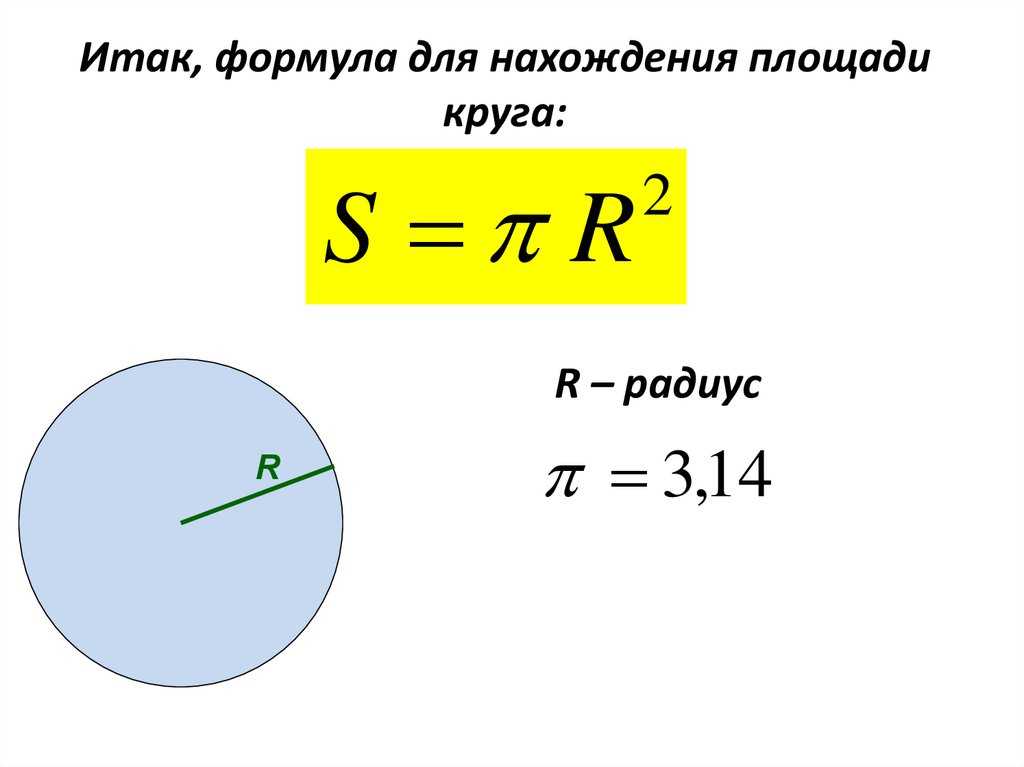
Диаметр круга
Диаметр окружности — это отрезок, начинающийся из любой точки на окружности, проходящий через центр и заканчивающийся в точке на противоположной стороне окружности. Длина диаметра в два раза больше длины радиуса окружности.
Полукруг
Полукруг — это половина круга. Диаметр делит окружность на две полуокружности.
Практические экзаменационные вопросы
Хорда круга
Отрезок, соединяющий любые две точки окружности, называется хордой окружности.
Сегменты кругаЕсли хорда представляет собой длину окружности, она делит площадь на две равные части. Однако, если хорда не является окружностью круга, она делит площадь на две неравные части. Аккорд расположен в центре круга, который является основным сегментом. Аккорд, помещенный в минорную область круга, называется минорным сегментом.
Дуга окружности
Любая часть окружности называется дугой окружности.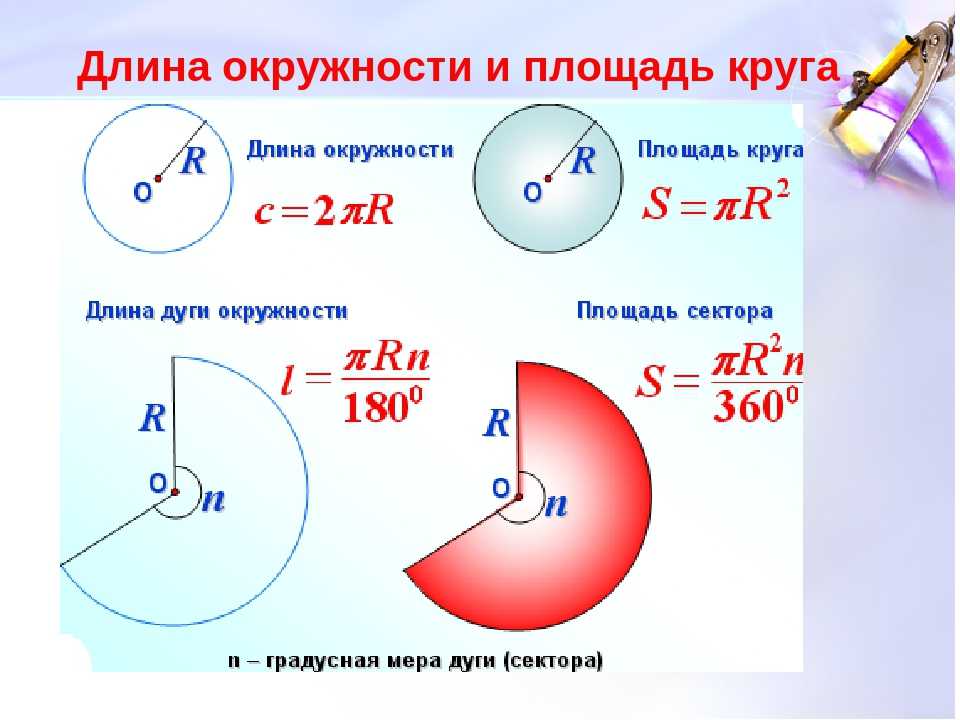 Если длина дуги больше полуокружности, она называется Большой дугой , а если длина дуги меньше полуокружности, она называется Малой дугой . Сумма длин большой дуги и малой дуги всегда дает длину окружности.
Если длина дуги больше полуокружности, она называется Большой дугой , а если длина дуги меньше полуокружности, она называется Малой дугой . Сумма длин большой дуги и малой дуги всегда дает длину окружности.
Сектор круга
Площадь, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром, называется сектором окружности. Когда большая дуга образует сектор, она называется Большим сектором, а когда меньшая дуга образует сектор, она называется Малым сектором.
Концентрические круги
Если два или более круга имеют один и тот же центр, такие круги называются концентрическими кругами.
Какова площадь круга?
Площадь круга определяется пространством или областью, занимаемой кругом на двумерной плоскости.
Значение пи\(\слева( \пи \справа)\)
В формуле площади круга используется постоянный член \(\pi \) (pi). \(\pi \) — постоянный член, также известный как постоянная Архимеда. Один из способов определить \(\pi \) состоит в том, что это отношение длины окружности к ее диаметру. Это иррациональное число, значение которого равно \(3,141592}.\)
Один из способов определить \(\pi \) состоит в том, что это отношение длины окружности к ее диаметру. Это иррациональное число, значение которого равно \(3,141592}.\)
Формула площади круга: вывод
Существует несколько методов вывода формулы площади круга. Среди них наиболее популярными являются следующие методы: (а) использование площади прямоугольника и (б) использование площади треугольника. Исчисление также используется для получения площади круга.
Здесь будет обсуждаться техника использования площадей прямоугольника и треугольника:
Площадь круга с использованием площади прямоугольника
В этом методе круг разделен на множество маленьких секторов, а расположение секторов выполнено в виде параллелограмма, как показано на рисунке ниже. Ясно, что параллелограмм превратится в прямоугольник, если круг разделить на большее количество секторов.
Как видно на рисунке, круг разбит на \(16\) секторов, \(8\) из которых окрашены в синий цвет, а остальные \(8\) — в желтый.
Синие и желтые сектора расположены попеременно, как показано на рисунке выше. 92}.\)
Площадь круга с использованием площади треугольника
В этом методе вся площадь круга считается состоящей из бесконечного числа концентрических окружностей. Если окружность разрезать по радиусу так, как показано на рисунке, и если все эти бесконечно много прямых (окружностей концентрических окружностей) расположить в виде прямоугольного треугольника или в виде равнобедренного треугольника, то прямоугольный получается равнобедренный или равнобедренный треугольник с основанием \(2\,\pi r\) и высотой \(r.\) 92}\)
Другие формулы, относящиеся к площади круга
Мы выведем еще несколько формул, основанных на основной формуле площади круга, выведенной выше, и приведем их ниже, которые широко используются для многих целей, например:
Площадь полукруга
Длина диаметра в два раза больше длины радиуса. Итак, если \(r\) радиус и \(d\) диаметр окружности, то \(d = 2r\) или \(r = \frac{d}{2}\)
Следовательно, площадь полукруга равна \(\frac{1}{2} \times \pi {r^2} = \frac{1}{2} \times \pi \times {(r)^2} = \frac {1} {2} \ раз \ пи \ раз {\ влево ( {\ гидроразрыва {d} {2}} \ справа) ^ 2} = \ гидроразрыва {1} {2} \ раз \ пи \ раз \ гидроразрыва { {{d^2}}}{4} = \frac{{\pi {d^2}}}{8}\) 92}. \)
\)
Интересные факты
- Среди всех фигур, имеющих одинаковую площадь, периметр круга будет наименьшим.
- Площадь круга увеличивается в четыре раза, если его радиус удваивается.
- Площадь круга увеличивается в четыре раза, если его диаметр увеличивается вдвое.
- Площадь круга увеличивается в четыре раза, если его периметр удваивается.
- Если круг диаметром \(1\) единица катится по числовой прямой один раз, начиная с нуля, то он приземляется примерно на \(3.14.\) 92}\)
Q. 5. Окружность круглого экрана радара составляет \(176\,{\rm{cm}}.\) Эффективна только \(90\% \) его площади. Рассчитайте эффективную площадь экрана.
Ans : Пусть \(r\,{\rm{см}}\) — радиус круглого экрана радара. Тогда его длина окружности \( = 2\pi r\,{\rm{см}}\)
Согласно приведенной информации, \(2\pi r = 176\)
\(\Rightarrow 2 \times \frac{{22 }}{7} \times r = 176\) 92}\)Q.
 2}.\) 92}}}\)
2}.\) 92}}}\)Часто задаваемые вопросы о площади круга
Ниже приведены часто задаваемые вопросы о площади круга:
Q.1. Как найти площадь с диаметром?
Ответ : Диаметр в два раза больше радиуса. Итак, разделите диаметр на 22 и получите радиус. Затем используйте этот радиус, чтобы найти нужную площадь по формуле πr2πr2 Или иначе используйте формулу площади =πd24=πd24 непосредственно, где dd – диаметр окружности.Q.2. Что такое площадь круга?
Ответ: Площадь круга – это пространство, занимаемое кругом в двумерной плоскости. Круг — это важная геометрическая фигура, которая присутствует во многих областях, таких как строительство, машиностроение и многие другие. Решение задач, связанных с кругами в геометрии, требует, чтобы мы могли вычислить площадь круга. Формула площади круга: A = πr2, где r — радиус круга. Единицей площади является квадратная единица, например, м2, см2, дюйм2 и т. д.
д.Q.3. Если квадрат вписан в круг, каково будет отношение площади квадрата к площади круга?
Ответ : Пусть радиус круга равен r.r.
Следовательно, площадь круга =πr2=πr2
Длина диагонали квадрата =2r=2r
Значит, длина стороны квадрата =2–√r=2r
Следовательно, площадь квадрата =2r2=2r2
Следовательно , требуемое соотношение 2:πQ.4. Какая формула площади круга? 92}\) и для длины окружности используйте длину окружности \( = 2\pi r,\), где \(r\) — радиус окружности.
Q.6. Если радиус круга дан в метрах, какова будет единица площади круга?
Ответ : \({\rm{sq}}{\rm{.}}\,{\rm{метр}}{\rm{.}}\)Q.7. В чем разница между сектором и сегментом круга?
Ответ : Сектор круга – это часть площади круга, ограниченная двумя радиусами и дугой, заключенной между ними, круга. Сегмент окружности – это площадь окружности, ограниченная хордой и дугой окружности.
Сегмент окружности – это площадь окружности, ограниченная хордой и дугой окружности.В.8. Как изменится площадь круга, если диаметр круга увеличить вдвое?
Ответ : Площадь круга увеличивается в четыре раза, если его диаметр увеличивается вдвое.Q.9. В чем разница между площадью и периметром круга?
Ответ : Площадь круга — это пространство, занимаемое кругом в двумерной плоскости. Периметр – это длина границы окружности.Q.10. В чем разница между большим и малым сегментами окружности?
Ответ : Если сегмент круга меньше полукруга, то он называется малым сегментом, а если он больше полукруга, то он называется большим сегментом. Сумма площадей малого и большого сегментов равна площади круга.УЗНАТЬ ОБ ОКРУЖНОСТИ КРУГА
Мы надеемся, что эта статья о площади круга помогла вам.


 Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.
Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.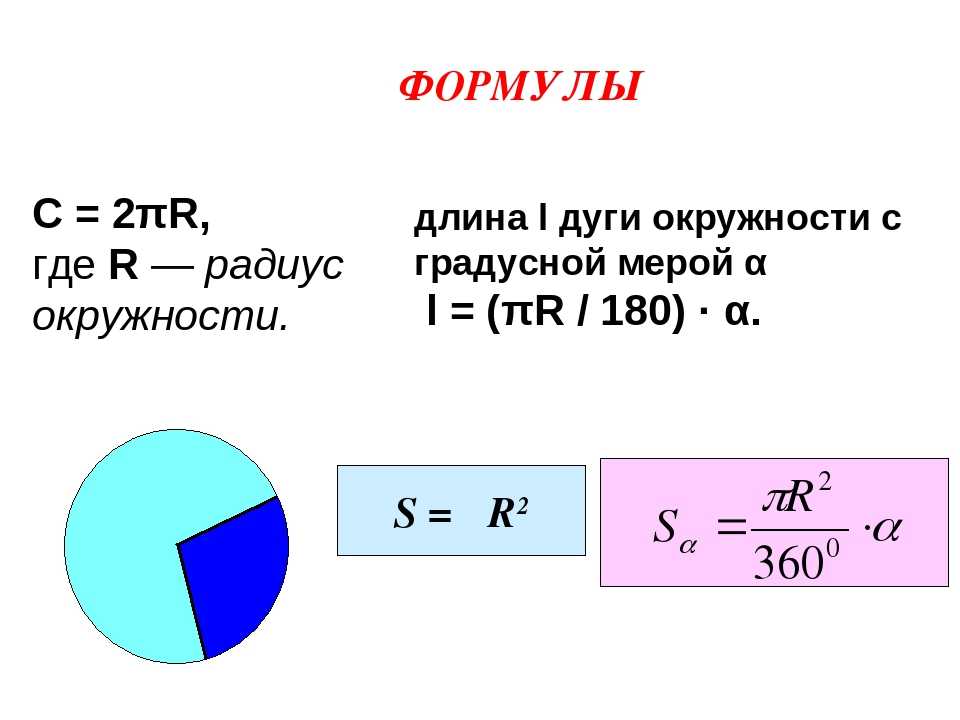
 2}.\) 92}}}\)
2}.\) 92}}}\) д.
д. Сегмент окружности – это площадь окружности, ограниченная хордой и дугой окружности.
Сегмент окружности – это площадь окружности, ограниченная хордой и дугой окружности.