Как из длины вычислить радиус окружности: 1) Найти радиус окружности, если её длина 6,28 см. Число пи округлите до сотых. 2)…

Быстрый ответ: как рассчитать радиус звезды

содержание

Как мы можем вычислить радиус звезды?

Например: звезда в 4 раза ярче Солнца и в 2 раза горячее, поэтому √4/2 в квадрате. Делая деление, получаем радиус в 0.0113 раза меньше. 0.0113 x 700.000 8000 км ≈ радиус XNUMX км :D.

Как рассчитывается радиус?

Радиус круга всегда равен половине длины его диаметра.

1. Например, если диаметр равен 4 см, то радиус будет равен 4 см ÷ 2 = 2 см.
2. В математических формулах радиус обозначается буквой r, а диаметр — буквой d.

Как измерить диаметр звезды?

L = 4, умноженное на «Пи», умноженное на «R», умноженное на «СИГМА», умноженное на «Т», возведенное в четвертую степень.

Как найти радиус круга по площади?

Используйте формулу C/2π. Поскольку длина окружности равна πD, что равно 2πr, деление ее на 2π даст вам радиус. Если у вас есть сфера с окружностью 20 м, найдите радиус, разделив 20/2π, и получите окончательный результат 3,183 м. Используйте ту же формулу для преобразования между радиусом круга и окружностью.

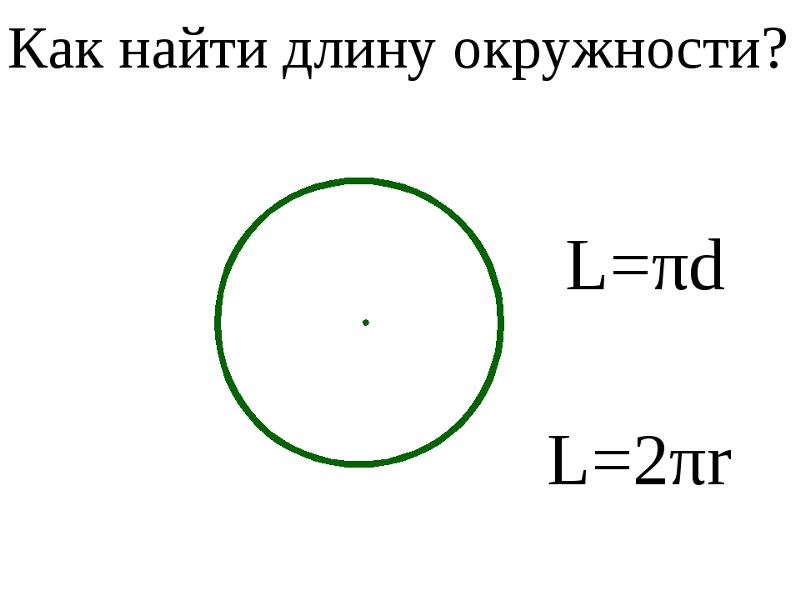
Чтобы вычислить значение длины окружности, мы используем формулу C = 2πr, где r — радиус окружности, а π (читай: пи) — константа, представленная этим символом, потому что это повторяющаяся десятичная дробь.

Что такое диаметр и радиус?

Известные как элементы окружности, мы называем центром или началом точки, которая находится в центре; радиус, отрезок линии, соединяющий центр с окружностью; хорда, любой отрезок, соединяющий два конца окружности; а по диаметру любая хорда, проходящая через центр.

Каково значение числа пи?

Поскольку это иррациональное число, оно является неповторяющимся десятичным числом и имеет бесконечные десятичные разряды, поэтому для решения задач обычно используется приближение значения π. Это число является константой, и его значение приблизительно равно 3,141592653…, но наиболее часто используемое приближение для значения π равно 3,14.

Как измерить радиус планеты?

Эратосфен получил 40.000 40.075 километров периметра, и в настоящее время мы знаем, что это 3,14 6369 километров. Разница была минимальной», — говорит Пауло Хорхе Лоуренсу, добавляя, что впоследствии, чтобы получить радиус, нужно просто разделить периметр на два Пи (XNUMX). Таким образом, Эратосфен получил значение XNUMX километров.

Какова скорость молнии?

При этом внутри облака между его отрицательной и положительной областями образуются небольшие электрические разряды. Затем из облака в сторону земли выходит вообще невидимый электрический разряд, называемый шахматным лидером, скорость которого может достигать 400. 000 XNUMX км/ч!

Каков размер звезды?

Размеры звезд варьируются от массы Юпитера в 70 раз до сверхгигантов, таких как Бетельгейзе в созвездии Ориона, диаметр которой примерно в 650 раз больше диаметра Солнца — около 0,9 миллиарда километров.

Как называется самая большая звезда во Вселенной?

1-й — VY Большого Пса: также известный как VY Cma, этот гипергигант имеет красноватое свечение, его диаметр в 2.100 раз больше, чем у Солнца. Чтобы иметь представление о его величине, внутри него поместилось бы почти три миллиарда планет, равных Земле.

Как далеко звезда?

Свет от других звезд доходит до нас годами, поэтому мы измеряем расстояния между звездами в единицах, называемых световыми годами. Световой год — это расстояние, пройденное светом за 1 год, около 10 триллионов километров. Обратите внимание, что световой год — это единица расстояния, а не времени.

Чему равно 2 пи в квадрате?

На основе этого открытия длина области, ограниченной окружностью, рассчитывается с использованием математического выражения C = 2 * π * r.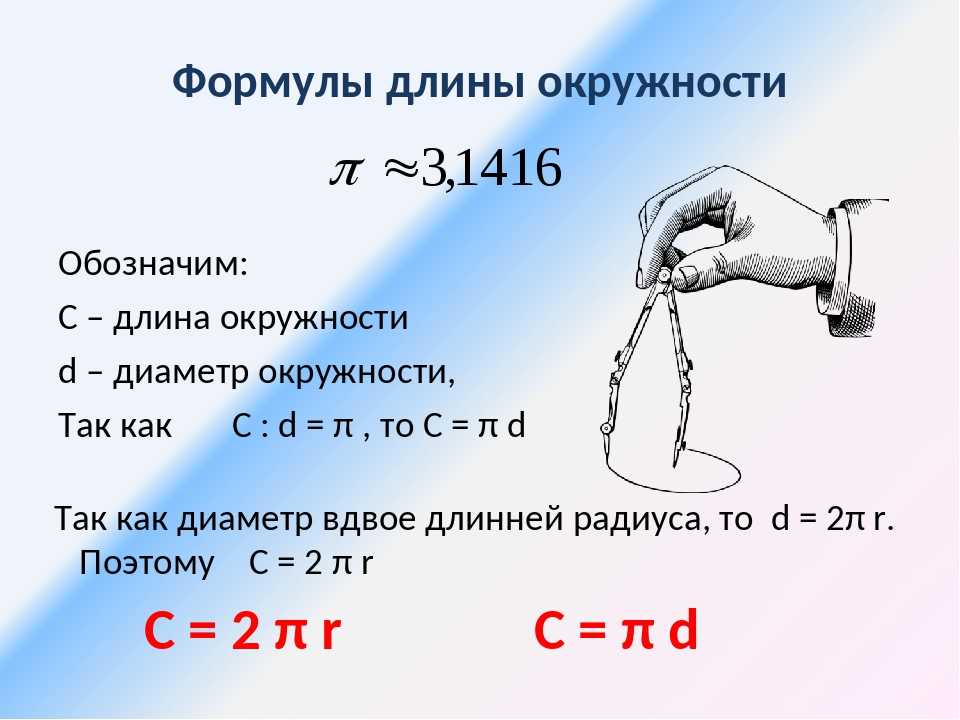

Как рассчитать радиус шара?

Для вычисления радиуса сферы используем формулу, которая вычисляет объем сферы. Если значение объема имеет форму 288π см, просто подставьте значение объема в формулу. Если он числовой, типа V = 904,32, перед заменой объем делим на значение π (pi) = 3,14.

Каков радиус сферы?

Точка O является центром сферы, а отрезок OB называется радиусом сферы. Точки в пространстве, расстояние которых от точки О точно равно радиусу, составляют поверхность или «оболочку» сферы.

Что такое пи радиус?

Длина окружности равна 2, умноженному на π, умноженному на радиус. Таким образом, это будет равно 2, умноженному на π, умноженному на радиус, умноженному на 3 метра, равно 6 метрам, умноженному на π, или 6π метрам.

Как рассчитывается диаметр?

Если вы знаете радиус окружности, умножьте его на 2, чтобы получить диаметр. Радиус — это расстояние от центра круга до края. Например, если радиус круга равен 4 см, то диаметр равен 4 см х 2 = 8 см. Если вы знаете длину окружности, разделите ее на π, чтобы получить диаметр.

Как измерить диаметр?

Вычислить диаметр круга

Диаметр (d) — это отрезок, соединяющий две точки внутри окружности и проходящий через центр. На изображении выше отрезок BC называется диаметром, потому что он соединяет два конца окружности и проходит через центр. Зная диаметр, то можно сказать, что d = 2r.

Как вычислить радиус квадрата?

Таким образом, мы можем сказать, что радиус круга равен r = d/2 или половине длины стороны квадрата.

Сколько радиусов имеет диаметр?

Таким образом, диаметр является наибольшей возможной хордой в окружности, а его мера равна удвоенному радиусу.

Какова история числа Пи?

Число пи: откуда оно взялось? Согласно историческим записям, число пи изучалось с древности. Ученым был любопытен тот факт, что его вычисление привело к триллионам знаков после запятой. Среди вавилонских и египетских вычислений были и такие, которые приближались к числу пи.

Почему пи бесконечно?

Определяемая как отношение длины окружности к ее диаметру, константа Пи является иррациональным числом: она имеет бесконечное количество десятичных разрядов и не может быть выражена в виде доли от двух целых чисел. Поэтому приближение к нему с древних времен пробуждает любопытство общества.

Кем был человек, который изобрел математику?

Греческий философ и математик Пифагор Самосский (ок. 570 г. до н. э. – ок. 496 г. до н. э.) многими считается «отцом математики».

Почему пи равно 180 градусам?

Полный оборот по тригонометрическому кругу соответствует в градусах 360º и в радианах 2π, потому что в случае измерения угла значение π (пи) становится равным 180º.

Как измерить расстояние между двумя звездами?

Параллакс в 1 угловую секунду (1″) соответствует расстоянию, называемому парсеком, равному 3,261 светового года, то есть 206265 астрономических единиц. Методом параллакса можно измерить расстояния до звезд чуть более 1000 световых лет.

Как сделать расчет Кеплера?

Формула третьего закона Кеплера

Куб среднего радиуса орбиты планеты (т.е. R3) прямо пропорционален квадрату периода обращения (т.е. Т2) небесного тела вокруг Солнца. Т1 и Т2 – периоды обращения двух планет. R1 и R2 — средние радиусы орбит этих двух планет.

Как сделать 3-й закон Кеплера?

Третий закон Кеплера гласит, что квадрат периода обращения планеты (T²) прямо пропорционален кубу ее среднего расстояния от Солнца (R³).

3-й закон Кеплера: закон периодов или закон гармонии.

Планета	Меркурий
Средний радиус орбиты (R) в а.е.	0,387
Период в земных годах (T)	0,241
Т²/R³	1,002

Почему бьет молния?

Для возникновения молнии должны быть заряды противоположных знаков между облаками или между облаками и землей, когда это происходит, притяжение между зарядами настолько велико, что вызывает электрический разряд.

Сколько градусов составляет радиус?

В конце концов, такое событие может вызвать температуру около 50 XNUMX градусов по Цельсию, такую ​​же горячую, как поверхность Солнца.

Какая самая быстрая молния в мире?

Всемирная метеорологическая организация (ВМО) объявила, что молния, проехавшая 768 апреля 29 года в США 2020 км, побила рекорд по самому большому расстоянию для такого типа явлений.

Какого цвета Солнце?

Из космоса Солнце предстает в своем истинном цвете: белом.

Какова продолжительность жизни звезды?

Время жизни звезды напрямую связано с ее массой. «Те, у которых масса намного больше, чем у Солнца, примерно в десять раз больше, например, просуществуют десятки миллионов лет, в то время как время жизни солнечной звезды составляет 10 миллиардов лет.

Сколько раз Земля помещается в Солнце?

Солнце — звезда, длина которой 1 392 700 км, то есть оно в 109 тысяч раз больше Земли. Земля составляет 12 742 км, а это значит, что внутри Солнца можно было бы разместить 1,3 миллиона земных планет.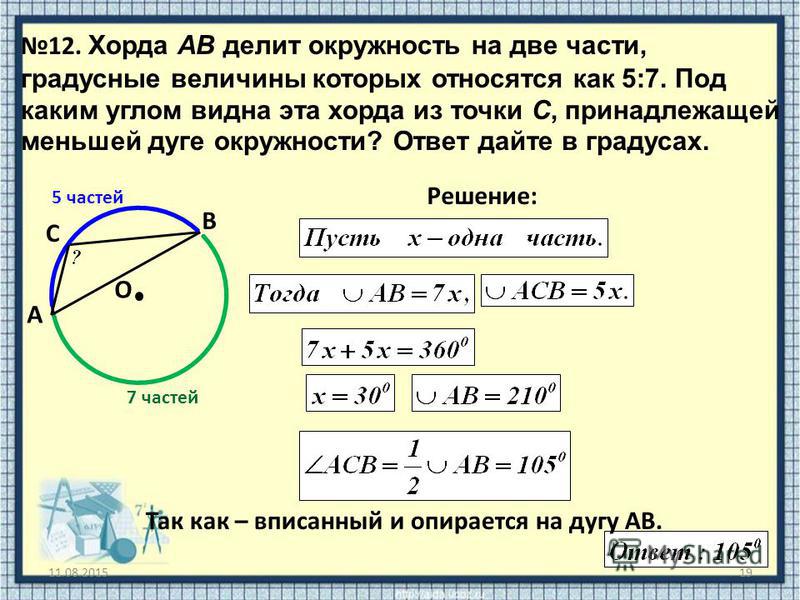

Какова температура Солнца?

Звезды состоят в основном из водорода и гелия. Эти элементы остаются объединенными в большую сферу плазмы благодаря сильному гравитационному полю. Превращая водород в гелий, они создают энергию в виде электромагнитных лучей. Поэтому они генерируют свет и тепло.

Какова длина 1 светового года?

Световой год — это расстояние, которое свет проходит в вакууме за один год. Чтобы рассчитать, сколько стоит расстояние в 1 световой год, необходимо знать скорость света в вакууме, которая равна 299792,458 км/с, и учесть, что время года по григорианскому календарю равно 365,2425, XNUMX дней.

Сколько длится световой год?

Световой год — это единица длины, используемая для выражения астрономических расстояний и эквивалентная примерно 9.46 триллионам километров (9.46 × 10¹² км). Согласно определению Международного астрономического союза (МАС), световой год — это расстояние, которое свет проходит в вакууме за один юлианский год (365. 25 дня).

Какое расстояние между тремя Мариями?

Знаменитые Трес Мариас легко увидеть невооруженным глазом, будь то в северном или южном полушарии. Это голубые звезды мощной яркости, намного крупнее Солнца и находящиеся на расстоянии около 1500 световых лет от Земли.

Сколько стоит 1 пир?

Получение значения числа пи

При делении длины окружности на измерение ее диаметра полученное значение всегда можно округлить до 3,14. Один из методов, который можно использовать для нахождения более точного приближения к значению числа пи, был разработан Архимедом.

Como se Calcula a área?

Как правило, чтобы найти площадь фигуры, просто умножьте основание (b) на высоту (h). Периметр – это сумма отрезков, образующих фигуру, называемых сторонами (l).

Как рассчитать длину окружности радиусом 40 см?

Длина круга определяется по формуле: где π = 3,14, а r = радиус 40 см. Радиус, умноженный на 2, является мерой диаметра, то есть длина окружности определяется диаметром, умноженным на PI.

Как измерить радиус планеты?

Эратосфен получил 40.000 40.075 километров периметра, и в настоящее время мы знаем, что это 3,14 6369 километров. Разница была минимальной», — говорит Пауло Хорхе Лоуренсу, добавляя, что впоследствии, чтобы получить радиус, нужно просто разделить периметр на два Пи (XNUMX). Таким образом, Эратосфен получил значение XNUMX километров.

Как рассчитать радиус шара?

Для вычисления радиуса сферы используем формулу, которая вычисляет объем сферы. Если значение объема имеет форму 288π см, просто подставьте значение объема в формулу. Если он числовой, типа V = 904,32, перед заменой объем делим на значение π (pi) = 3,14.

Как рассчитать зенитное расстояние звезды?

Z’ = [360º + (PD-PI)] /2, если вы делаете сопряженные прицеливания, что называется полным прицеливанием. Это значение Z’ = 50º 26′ 51,5” является наблюдаемым зенитным расстоянием.

Как измерить расстояние звезды от Земли?

Поэтому необходимо использовать большие телескопы. Путем измерения параллакса определяется расстояние, так как оно — для того же базиса — обратно пропорционально параллаксу. Параллакс в 1 угловую секунду (1″) соответствует расстоянию, называемому парсеком, равному 3,261 светового года, то есть 206265 астрономических единиц.

через диаметр и радиус. Терминология, основные формулы и характеристика фигуры

Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.

Что такое окружность и где она встречается?

Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.

В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.

В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.

Обозначения величин и формулы

Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:

Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов. Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:

l = π * d.

Как быть, если нужно вычислить периметр круга?

Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.

Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.

Примеры заданий

Задача первая

Условие. Узнать длину окружности, радиус которой равен 5 см.

Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).

Ответ: l = 31,4 см.

Задача вторая

Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.

Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28.

После деления остается число: 200. Это искомая величина.

Ответ: r = 200 мм.

Задача третья

Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.

Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых. В результате такого действия получается число 18. Результат получен.

Ответ: d = 18 см.

Задача четвертая

Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.

Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.

Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.

Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.

Ответ: l 1 = 18,84 см, l 2 = 31,4 см.

Задача пятая

Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?

Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.

Ответ: Белка пробегает 6,28 м.

Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.

Вычислить радиус

Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.

Рассчитать диаметр

Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.

Узнать длину окружности

Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.

Вычислить площадь круга

Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.

Рассчитать площадь шара

Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах.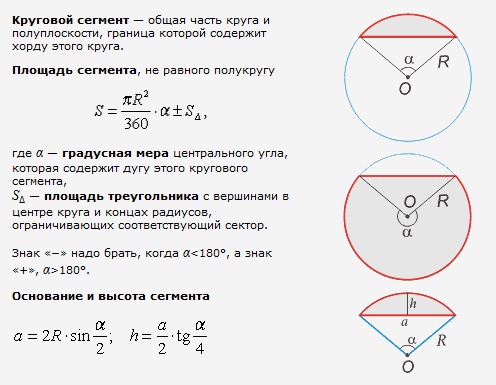 S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.

Вычислить объем шара

Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.

Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие

формулы , понятия и определения требуются для этого.

Вконтакте

Основные понятия и определения

1. Радиус — это линия, соединяющая центр окружности и её произвольную точку . Он обозначается латинской буквой r.
2. Хордой называется линия, соединяющая две произвольные точки лежащие на окружности .
3. Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр . Он обозначается латинской буквой d.
4. — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром. Её длину будем обозначать латинской буквой l.

Площадь круга — это вся территория, заключённая внутри окружности . Она измеряется в квадратных единицах и обозначается латинской буквой s.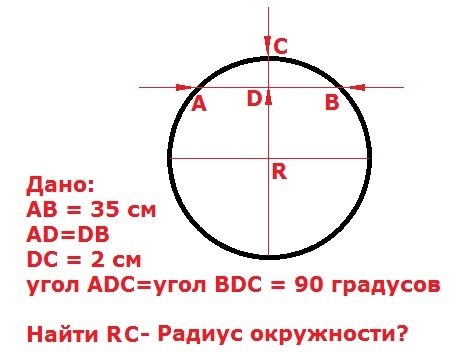

Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.

Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!

Диаметр окружности.

Нахождение длины окружности и её площади

Если нам дан радиус окружности, то диаметр окружности описывает формула d = 2*r . Таким образом, для ответа на вопрос, как найти диаметр круга, зная его радиус, достаточно последний умножить на два .

Формула длины окружности, выраженная через её радиус, имеет вид l = 2*П*r .

Внимание! Латинской буквой П (Пи) обозначается отношение длины окружности к её диаметру, и это есть непериодическая десятичная дробь. В школьной математике она считается заранее известной табличной величиной, равной 3,14!

Теперь перепишем предыдущую формулу, чтобы найти длину окружности через её диаметр, помня, в чём состоит его разница по отношению к радиусу.

2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).

Решение типовых заданий

1. Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
2. Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга. Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см . Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
3. Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр.
   2/(4П) = 2209/12,56 = 175,87 кв. м.

Длина окружности

§ 117. Длина окружности и площадь круга.

1. Длина окружности. Окружностью называется замкнутая плоская кривая линия, все точки которой находятся на равном расстоянии от одной точки (О), называемой центром окружности (рис. 27).

Окружность вычерчивается с помощью циркуля. Для этого острую ножку циркуля ставят в центр, а другую (с карандашом) вращают вокруг первой до тех пор, пока конец карандаша не вычертит полной окружности. Расстояние от центра до любой точки окружности называется её радиусом. Из определения следует, что все радиусы одной окружности равны между собой.

Отрезок прямой линии (АВ), соединяющий две любые точки окружности и проходящий через её центр, называется

диаметром . Все диаметры одной окружности равны между собой; диаметр равен двум радиусам.

Как найти длину окружности? Практически в некоторых случаях длину окружности можно найти путём непосредственного измерения. Это можно сделать, например, при измерении окружности сравнительно небольших предметов (ведро, стакан и т. п.). Для этого можно воспользоваться рулеткой, тесьмой или шнуром.

В математике применяется приём косвенного определения длины окружности. Он состоит в вычислении по готовой формуле, которую мы сейчас выведем.

Если мы возьмём несколько больших и малых круглых предметов (монета, стакан, ведро, бочка и т. д.) и измерим у каждого из них длину окружности и длину диаметра, то получим для каждого предмета два числа (одно, измеряющее длину окружности, и другое — длину диаметра). Естественно, что для малых предметов эти числа будут небольшими, а для крупных — большими.

Однако если мы в каждом из этих случаев возьмём отношение полученных двух чисел (длины окружности и диаметра), то при тщательном выполнении измерения найдём почти одно и то же число. Обозначим длину окружности буквой С , длину диаметра буквой D , тогда отношение их будет иметь вид С: D . Фактические измерения всегда сопровождаются неизбежными неточностями. Но, выполнив указанный опыт и произведя необходимые вычисления, мы получим для отношения С: D примерно следующие числа: 3,13; 3,14; 3,15. Эти числа очень мало отличаются одно от другого.

В математике путём теоретических соображений установлено, что искомое отношение С: D никогда не меняется и оно равно бесконечной непериодической дроби, приближённое значение которой с точностью до десятитысячных долей равно

3,1416 . Это значит, что всякая окружность длиннее своего диаметра в одно и то же число раз. Это число принято обозначать греческой буквой π (пи). Тогда отношение длины окружности к диаметру запишется так: С: D = π . Мы будем ограничивать это число только сотыми долями, т. е. брать π = 3,14.

Напишем формулу для определения длины окружности.

Так как С: D = π , то

C = πD

т. е. длина окружности равна произведению числа π на диаметр.

Задача 1. Найти длину окружности (С ) круглой комнаты, если диаметр её D = 5,5 м.

Принимая во внимание изложенное выше, мы должны для решения этой задачи увеличить диаметр в 3,14 раза:

5,5 3,14 = 17,27 {м).

Задача 2. Найти радиус колеса, у которого длина окружности 125,6 см.

Эта задача обратна предыдущей. Найдём диаметр колеса:

125,6: 3,14 = 40 (см).

Найдём теперь радиус колеса:

40: 2 = 20 (см).

2. Площадь круга. Чтобы определить площадь круга, можно было бы начертить на бумаге круг данного радиуса, покрыть его прозрачной клетчатой бумагой и потом сосчитать клетки, находящиеся внутри окружности (рис. 28).

Но такой способ неудобен по многим причинам. Во-первых, вблизи контура круга получается ряд неполных клеток, о величине которых судить трудно. Во-вторых, нельзя покрыть листом бумаги большой предмет (круглую клумбу, бассейн, фонтан и др.). В-третьих, подсчитав клетки, мы всё-таки не получаем никакого правила, позволяющего нам решать другую подобную задачу. В силу этого поступим иначе. Сравним круг с какой-нибудь знакомой нам фигурой и сделаем это следующим образом: вырежем круг из бумаги, разрежем его сначала по диаметру пополам, затем каждую половину разрежем ещё пополам, каждую четверть — ещё пополам и т. д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).

Затем сложим их так, как показано на рисунке 30, т. е. сначала расположим 16 зубцов в виде пилы, а затем в образовавшиеся отверстия вложим 15 зубцов и, наконец, последний оставшийся зубец разрежем по радиусу пополам и приложим одну часть слева, другую — справа. Тогда получится фигура, напоминающая прямоугольник.

Длина этой фигуры (основание) равна приблизительно длине полуокружности, а высота — приблизительно радиусу. Тогда площадь такой фигуры можно найти путём умножения чисел, выражающих длину полуокружности и длину радиуса. Если обозначим площадь круга буквой S , длину окружности буквой С , радиус буквой r , то можем записать формулу для определения площади круга:

которая читается так: площадь круга равна длине полуокружности, умноженной на радиус.

Задача. Найти площадь круга, радиус которого равен 4 см. Найдём сначала длину окружности, потом длину полуокружности, а затем умножим её на радиус.

1) Длина окружности С = π D = 3,14 8 = 25,12 (см).

2) Длина половины окружности C / 2 = 25,12: 2= 12,56 (см).

3) Площадь круга S = C / 2 r = 12,56 4 = 50,24 (кв. см).

§ 118. Поверхность и объём цилиндра.

Задача 1. Найти полную поверхность цилиндра, у которого диаметр основания 20,6 см и высота 30,5 см.

Форму цилиндра (рис. 31) имеют: ведро, стакан (не гранёный), кастрюля и множество других предметов.

Полная поверхность цилиндра (как и полная поверхность прямоугольного параллелепипеда) состоит из боковой поверхности и площадей двух оснований (рис. 32).

Чтобы наглядно представить себе, о чём идёт речь, необходимо аккуратно сделать модель цилиндра из бумаги. Если мы от этой модели отнимем два основания, т. е. два круга, а боковую поверхность разрежем вдоль и развернём, то будет совершенно ясно, как нужно вычислять полную поверхность цилиндра. Боковая поверхность развернётся в прямоугольник, основание которого равно длине окружности. Поэтому решение задачи будет иметь вид:

1) Длина окружности: 20,6 3,14 = 64,684 (см).

2) Площадь боковой поверхности: 64,684 30,5= 1972,862(кв.см).

3) Площадь одного основания: 32,342 10,3 = 333,1226 (кв.см).

4) Полная поверхность цилиндра:

1972,862 + 333,1226 + 333,1226 = 2639,1072 (кв. см) ≈ 2639 (кв. см).

Задача 2. Найти объём железной бочки, имеющей форму цилиндра с размерами: диаметр основания 60 см и высота 110 см.

Чтобы вычислить объём цилиндра, нужно припомнить, как мы вычисляли объём прямоугольного параллелепипеда (полезно прочитать § 61).

Единицей измерения объёма у нас будет кубический сантиметр. Сначала надо узнать, сколько кубических сантиметров можно расположить на площади основания, а затем найденное число умножить на высоту.

Чтобы узнать, сколько кубических сантиметров можно уложить на площади основания, надо вычислить площадь основания цилиндра. Так как основанием служит круг, то нужно найти площадь круга. Затем для определения объёма умножить её на высоту. Решение задачи имеет вид:

1) Длина окружности: 60 3,14 = 188,4 (см).

2) Площадь круга: 94,2 30 = 2826 (кв. см).

3) Объём цилиндра: 2826 110 = 310 860 (куб. см).

Ответ. Объём бочки 310,86 куб. дм.

Если обозначим объём цилиндра буквой V , площадь основания S , высоту цилиндра H , то можно написать формулу для определения объёма цилиндра:

V = S H

которая читается так: объём цилиндра равен площади основания, умноженной на высоту.

§ 119. Таблицы для вычисления длины окружности по диаметру.

При решении различных производственных задач часто приходится вычислять длину окружности. Представим себе рабочего, который изготовляет круглые детали по указанным ему диаметрам.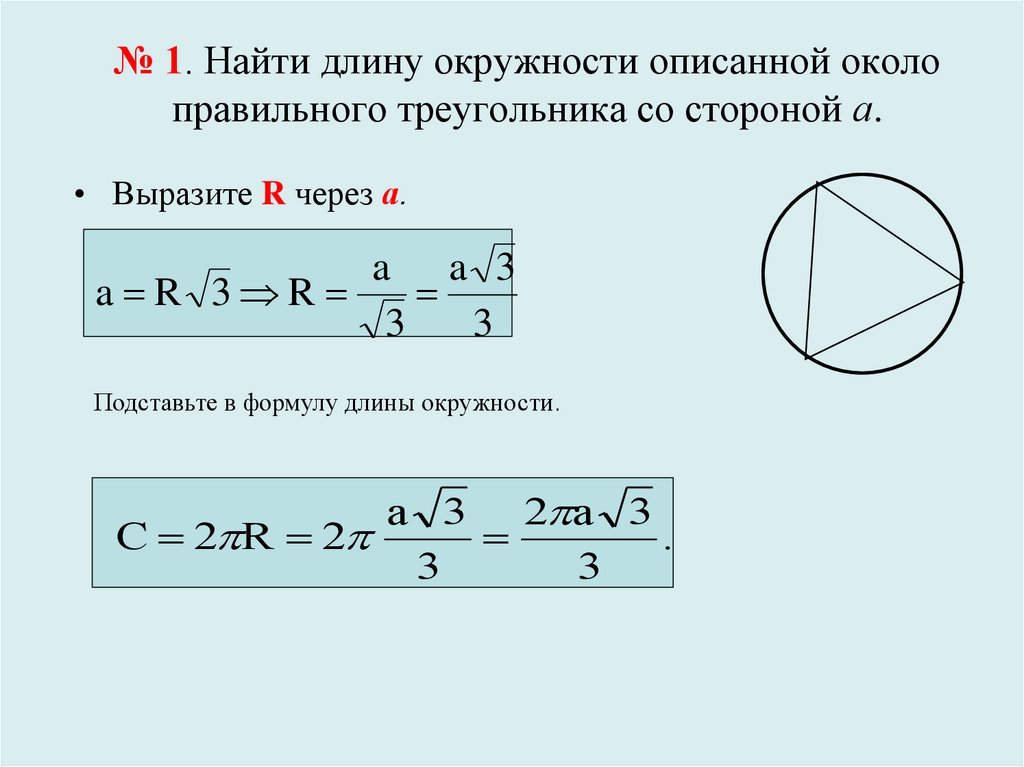 Он должен всякий раз, зная диаметр, вычислить длину окружности. Чтобы сэкономить время и застраховать себя от ошибок, он обращается к готовым таблицам, в которых указаны диаметры и соответствующие им длины окружностей.

Приведём небольшую часть таких таблиц и расскажем, как ими пользоваться.

Пусть известно, что диаметр окружности равен 5 м. Ищем в таблице в вертикальном столбце под буквой D число 5. Это длина диаметра. Рядом с этим числом (вправо, в столбце под названием «Длина окружности») увидим число 15,708 (м). Совершенно так же найдём, что если D = 10 см, то длина окружности равна 31,416 см.

По этим же таблицам можно производить и обратные вычисления. Если известна длина окружности, то можно найти в таблице соответствующий ей диаметр. Пусть длина окружности равна приблизительно 34,56 см. Найдём в таблице число, наиболее близкое к данному. Таковым будет 34,558 (разница 0,002). Соответствующий такой длине окружности диаметр равен приблизительно 11 см.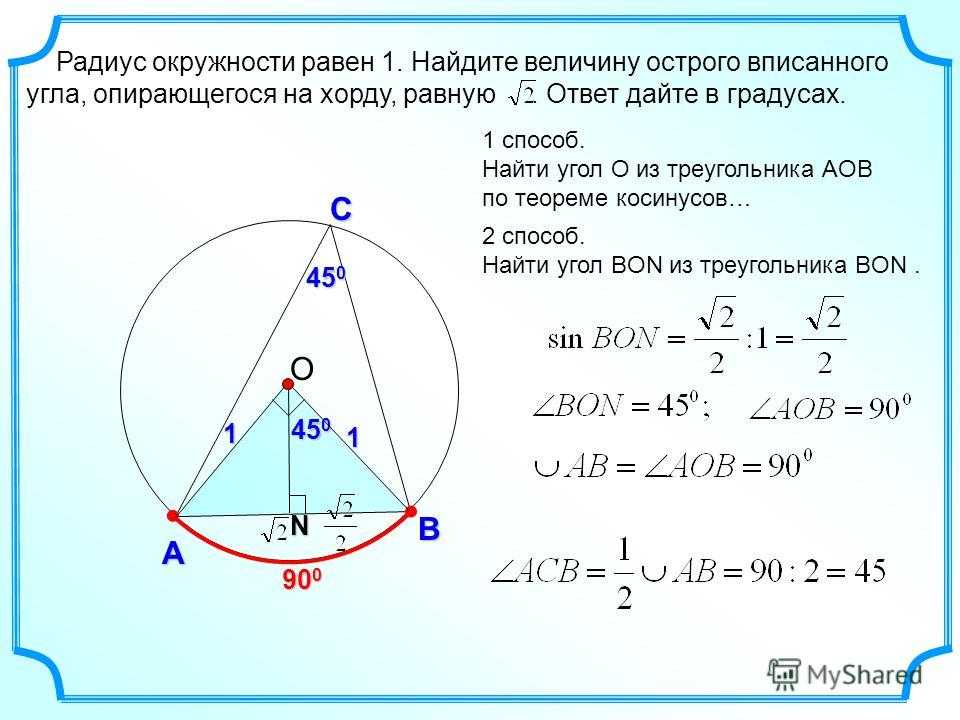

Таблицы, о которых здесь сказано, имеются в различных справочниках. В частности, их можно найти в книжке «Четырёхзначные математические таблицы» В. М. Брадиса. и в задачнике по арифметике С. А. Пономарёва и Н. И. Сырнева.

1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.

Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.

После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.

2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см

Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.

5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!

Онлайн калькулятор длины окружности

Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.

Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.

Как рассчитать и решить угол, радиус и длину дуги окружности | The Calculator Encyclopedia

Изображение выше представляет длину дуги окружности.

Чтобы вычислить длину дуги окружности, необходимы два основных параметра: радиус окружности (r)  и угол окружности (α).

Формула расчета длины дуги окружности:

L = ^απr / ₁₈₀

Где;
L = длина дуги окружности
α = угол окружности
r = радиус окружности

Давайте решим пример:
Найдите длину дуги окружности, когда угол окружности равен 90° а радиус окружности 20 см.

Это означает, что;
α = угол окружности = 90°
r = радиус окружности = 20 см

L = ^απr / _{1800016 / 180
L = ^5655,6 / 180
L = 31,42}

Следовательно, длина дуги окружности равна см 31,4221.

Вычисление угла окружности с использованием радиуса окружности и длины дуги окружности.

α = ^180L / _πr

Где;
L = длина дуги окружности
r = радиус окружности

Давайте решим пример;
Найдите угол окружности, если длина дуги окружности равна 60°, а радиус равен 140 см.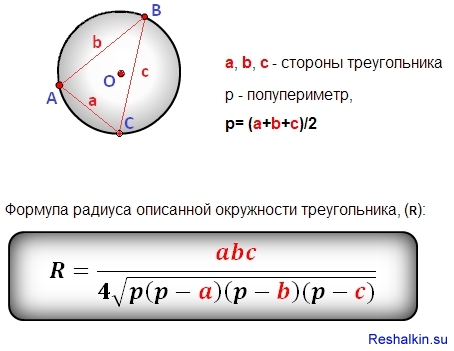

Это означает, что;
L = длина дуги круга = 60 °
R = радиус круга = 140 см

α = ^180L / _πr
α = ^{180 x 6016 / _{3.142 x 140}}

16 / _{3.142 x 140}

116 / _{3.142 x 140}

116 / 3.142 x 14018

116 / 3.142 x 140018

515. = ¹⁰⁸⁰⁰ / _439,88
a = 24,55

Следовательно, угол окружности равен 24,55°.

Вычисление радиуса окружности с использованием длины дуги окружности и угла окружности.

r = ^180L / _πα

Где;
L = длина дуги окружности
α = угол окружности

Давайте решим пример;
Учитывая, что угол окружности равен 100°, а длина дуги окружности 70 см. Найдите радиус окружности?

Это означает, что;
α = угол окружности = 100°
L = длина дуги окружности = 70 см

r = ^180L / _πα
r = ^{180 x 70} / _{3.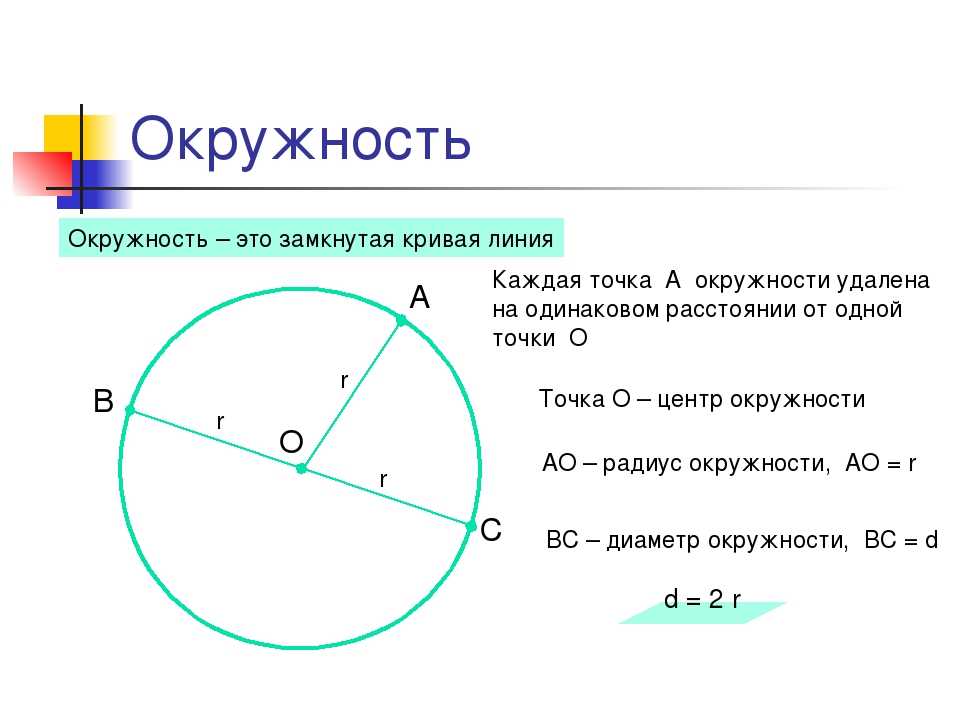 142 x 70}
r = ¹²⁶⁰⁰ / _219.94
r = 57.29

Therefore, the radius of the circle 57,29 см.

Калькулятор Никзома – Энциклопедия калькулятора  способна вычислить длину дуги окружности.

Чтобы получить ответ и вычисления длины дуги окружности с помощью Калькулятор Никзома — Энциклопедия калькуляторов. Во-первых, вам нужно получить приложение.

Вы можете получить это приложение любым из следующих способов:

Web  – https://www.nickzom.org/calculator-plus

Чтобы получить доступ к профессиональной версии через Интернет, вам необходимо  регистрация и подписка на 1500 NGN за год , чтобы иметь полный доступ ко всем функциям.
Вы также можете попробовать демоверсию   9Версия 0008 через https://www.nickzom. org/calculator

Android (платная)  – – https://play.google.com/store/apps/details?id=org.nickzom.nickzomcalculator
Android ( Бесплатно)  – https://play.google.com/store/apps/details?id=com.nickzom.nickzomcalculator
Apple (платно)  – https://itunes.apple.com/us/app/nickzom -calculator/id1331162702?mt=8

После того, как вы получили приложение энциклопедии калькулятора, перейдите к карте калькулятора , , затем нажмите Mensuration в соответствии с Mathematics Раздел

Теперь нажмите на длину дуги круга под Муженно , чтобы получить ответ для длины дуги окружности по соответствующим параметрам, которые являются радиусом окружности (r) и углом окружности (α).

Теперь введите соответствующее значение для параметров, как того требует пример выше, где радиус окружности   20 см и угол окружности равен 90°.

Наконец, нажмите Рассчитать

Как видно из приведенного выше снимка экрана, Nickzom Calculator  – Энциклопедия калькулятора вычисляет рабочую длину дуги окружности и представляет формулу шаги тоже.

Радиус окружности с учетом длины дуги

✖Длина дуги окружности — это длина части кривой, отрезанной от окружности окружности под определенным центральным углом.ⓘ Длина дуги окружности [l Дуга ]		AlnAngstromArpentAstronomical UnitAttometerAU of LengthBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical )EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Миля (Международная)Морская миля (Великобритания)ПарсекОкуньПетаметрПикаПикометрПланк ДлинаТочкаПолюсКварталТростник (Длинный)РодРоман АктусВеревкаРусский АрчинПротяженность (Ткань)Радиус СолнцаТераметрТвипВара КастелланаВара КонукераВара Де ТареаЯрдЙоктометрЙоттаметрЗептометрЗеттаметр	+10% -10%
✖Центральный угол окружности — это угол, вершина (вершина) которого является центром O окружности, а катеты (стороны) являются радиусами, пересекающими окружность в две различные точки. ⓘ Центральный угол окружности [∠ Центральный ]		0241 +10% -10%

✖Радиус окружности – это длина любого отрезка, соединяющего центр и любую точку окружности.ⓘ Радиус окружности при заданной длине дуги [r]

AlnAngstromArpentAstronomical UnitAttometerAU of LengthBarleycornBillion Light YearBohr RadiusCable (International)Cable (UK)Cable (US)CaliberCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)DecameterDecimeterEarth Distance from MoonEarth Distance from SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Cloth)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsecKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMicroinchMicrometerMicronMilMileMile (Roman)Mile (US Survey)MillimeterMillion Light YearNail (Cloth)NanometerNautical League (int)Nautical League UKNautical Mile (International)Nautical Mile (UK)ParsecPerchPetameterPicaPicometerPlanck LengthPointPoleQuarterReedReed (Long)RodRoman ActusRopeRussian ArchinSpan ( Ткань)Sun RadiusTerameterTwipVara CastellanaVara ConuqueraVara De TareaYardYoctometerYottameterZeptometerZettameter

⎘ Копировать

👎

Формула

Перезагрузить

👍

Радиус окружности при заданной длине дуги Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1: Преобразование входных данных в базовые единицы

Длина дуги окружности: 15 метров —> 15 метров Преобразование не требуется
Центральный угол окружности: 170 градусов —> 2.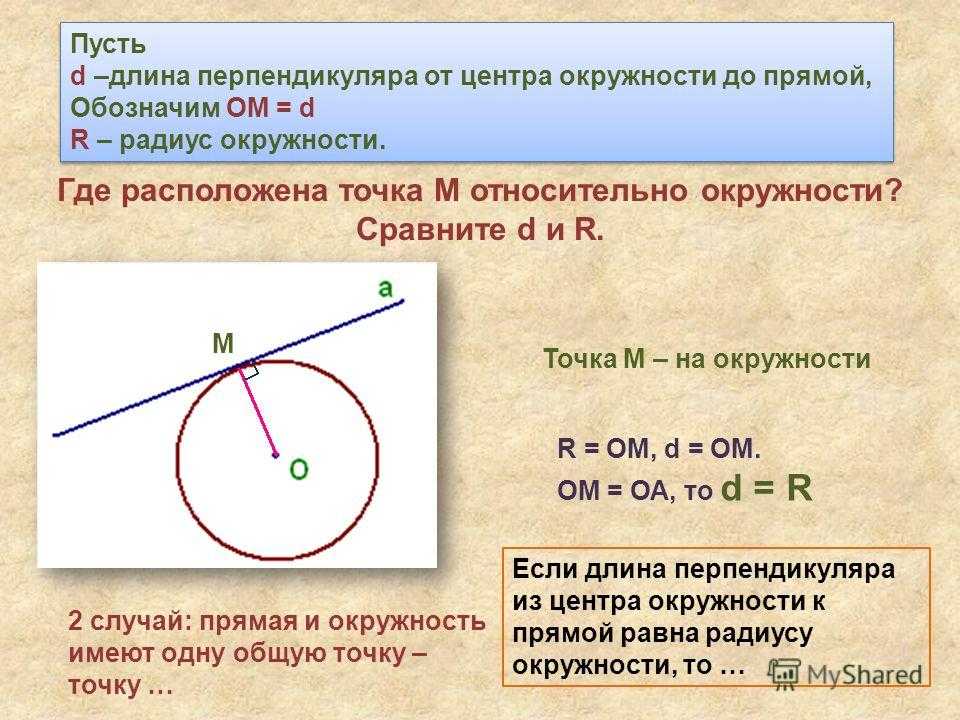 9670597283898 Радиан (Проверьте преобразование здесь)

ШАГ 2: вычисление формулы

ШАГ 3: преобразование результата в единицу измерения

5.05550995703763 метр —> преобразование не требуется

< 5 Калькуляторы радиуса окружности

Радиус окружности по формуле длины дуги

Радиус окружности = длина дуги окружности/центральный угол окружности
r = l _Дуга /∠ _{Центральная}

Что такое Круг?

Окружность — это базовая двухмерная геометрическая фигура, которая определяется как совокупность всех точек на плоскости, находящихся на фиксированном расстоянии от фиксированной точки. Фиксированная точка называется центром круга, а фиксированное расстояние называется радиусом круга. Когда два радиуса становятся коллинеарными, эта общая длина называется диаметром круга.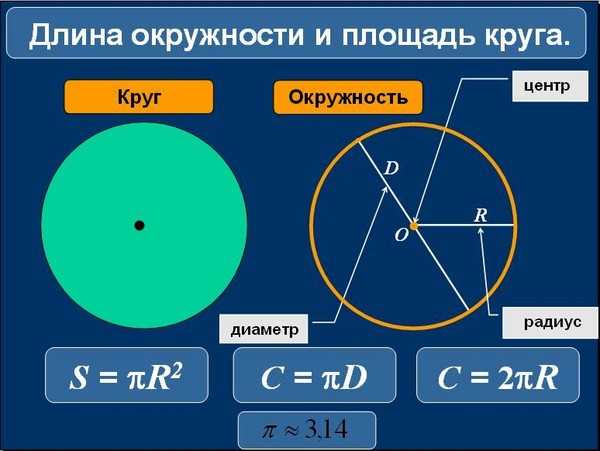 То есть диаметр — это длина отрезка внутри круга, проходящего через центр, и он будет в два раза больше радиуса.

Как рассчитать радиус окружности по длине дуги?

Калькулятор радиуса окружности с учетом длины дуги использует Радиус окружности = длина дуги окружности / центральный угол окружности для расчета радиуса окружности, формула радиуса окружности с учетом длины дуги определяется как длина любой линии от центра до любого точка на окружности и рассчитывается с использованием длины дуги окружности под определенным центральным углом. Радиус окружности обозначается цифрой 9.0341 р символ.

Как рассчитать радиус окружности при заданной длине дуги с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для радиуса окружности с учетом длины дуги, введите длину дуги окружности (l _дуга ) и центральный угол окружности (∠ _{центральный} ) и нажмите кнопку расчета. Вот как можно объяснить расчет радиуса окружности с учетом длины дуги с заданными входными значениями -> 5,05551 = 15/2,9670597283898 .

Часто задаваемые вопросы

Чему равен радиус окружности при заданной длине дуги?

Радиус окружности с заданной формулой длины дуги определяется как длина любой линии от центра до любой точки окружности и рассчитывается с использованием длины дуги окружности под определенным центральным углом и представляется как r = l _Дуга /∠ _{Центральный} или Радиус окружности = Длина дуги окружности/Центральный угол окружности . Длина дуги окружности — это длина части кривой, отрезанной от окружности окружности под определенным центральным углом, а центральный угол окружности — это угол, вершина (вершина) которого является центром O окружности, а стороны (стороны) равны радиусы, пересекающие окружность в двух различных точках.

Как рассчитать радиус окружности по длине дуги?

Радиус окружности с учетом Формула длины дуги определяется как длина любой линии от центра до любой точки на окружности и рассчитывается с использованием длины дуги окружности под определенным центральным углом, вычисляемой по формуле Радиус окружности = длина дуги окружности/центральный угол окружности .

No related posts.