Примеры применения 3D-технологий в различных сферах и областях
Ни для кого не новость, что прежде чем построить здание, сконструировать автомобиль или сделать современный дизайн интерьера в квартире, необходимо создать проект. Во все времена это было трудоёмким и сложным делом. Требовался немалый труд и талант конструкторов, чертежников и художников. Каждый отдельный ракурс, каждая проекция чертились и рисовались отдельно. Общее представление о будущей конструкции складывалось в основном за счет воображения.
В наше время благодаря компьютерному трехмерному моделированию появилась удивительная возможность создавать объемную модель сооружения или 3D-модель. Она наиболее полно описывает проект, позволяет увидеть конструкцию со всех сторон. Презентация на основе 3D-модели производит самое яркое впечатление.
Что же такое 3D графика?
3D-графика (трехмерная графика) – это область конструирования, в которой объемная модель создается при помощи специальных компьютерных программ.
Для работы этих программ необходимо соответствующее оборудование: компьютеры, планшеты и оргтехника.
Моделирование включает в себя несколько этапов: построение геометрической основы, наложение материалов, постановка света и рендеринг – максимально приближенная к реальности визуализация выбранных видов модели. Результатом рендеринга является красивая картинка, почти не отличимая по качеству от фотографии.
На основе 3D-графики можно разработать высокоточную копию существующего объекта или создать нечто совершенно новое. Можно воплотить в жизнь самые смелые творческие мечты.
Применение 3D-графики в современном мире
3D моделирование прочно вошло в нашу повседневную жизнь. Оно применяется в сфере маркетинга, архитектуры, дизайна, в развлекательной индустрии, не говоря уже о промышленности. Благодаря появлению 3D-печати трехмерное моделирование перешло на новый уровень и стало востребовано, как никогда. Однако построение 3D-моделей требует особых знаний и навыков, необходимо специальное обучение.
Появилась новая профессия 3D-дизайнер, интересная, творческая и очень нужная.
Где сегодня используется 3D моделирование? Спектр очень широк:
- Мультипликация. Создание трехмерных персонажей для мультфильмов и компьютерных видеоигр
- 3D визуализация зданий и интерьеров
- Реклама и маркетинг. Часто требуются нестандартные объекты для рекламирования. 3D презентации позволяют произвести более яркое впечатление на заинтересованных лиц и сэкономить на реквизите
- Производство мебели. Производственные мебельные компании используют трехмерную модель для размещения своей продукции в электронных каталогах
- Промышленность. Каждую сложную деталь собирают по готовой и продуманной 3D-модели
- Медицинская сфера
Преимущества трехмерного моделирования
Преимуществ у 3D моделирования перед другими способами визуализации много. Трехмерное моделирование позволяет создать очень точную модель, максимально приближенную к реальности.
Современные графические программы характеризуются высокой детализацией. Отобразить трехмерный объект в двухмерной плоскости не просто. 3D визуализации дает возможность тщательно просчитать и просмотреть все нюансы модели.
Трехмерная модель позволяет вносить изменения и правки, без перерисовки всей конструкции. Предварительный просмотр показывает, как эти изменения влияют на результат.
3D моделирование удобно не только для презентации конечному заказчику, но и дает много преимуществ изготовителю. Из трехмерной модели получают чертежи отдельных деталей или всей конструкции целиком. Несмотря на то, что создание трехмерной модели процесс тщательный и не быстрый, работать с ним в дальнейшем гораздо проще и удобнее, чем с традиционными чертежами.
Вам будет это интересно: курсы компьютерного дизайна для школьников
Обучение трехмерному моделированию сейчас – это инвестиция в будущее вашего ребенка
Подводя итог обзору 3D моделирования и визуализации, можно с уверенность сказать – это впечатляет, это востребовано и нужно.
3D технологии развиваются и усложняются с каждым днем, они все больше внедряются в нашу жизнь. Начать изучение трехмерного моделирования с раннего возраста – это значит дать ребенку старт в профессии. К моменту выпуска из института он будет уже на достаточном профессиональном уровне, чтобы стать востребованным молодым специалистом.
Графики в 3D, лепестковые диаграммы и контурные карты в PyPlot
Помимо классических графиков, таких как столбчатые и круговые, можно представлять данные и другими способами. В интернете и разных источниках можно найти самые разные примеры визуализации данных, некоторые из которых выглядят невероятно. В этом разделе речь пойдет только о графических представлениях, но не о подробных способах их реализации. Можете считать это введением в мир визуализации данных.
Для выполнения кода импортируйте pyplot и numpy
import matplotlib.pyplot as plt import numpy as np
Контурные графики
В научном мире часто встречается тип контурных графиков или контурных карт.
z).Хотя визуально контурный график — довольно сложная структура, ее реализация не так сложна, и все благодаря matplotlib. Во-первых, нужна функция z = f(x, y) для генерации трехмерной поверхности. Затем, имея значения x и y, определяющие площадь карты для вывода, можно вычислять значения z для каждой пары x и y с помощью функции f(x, y), которая и используется для этих целей. Наконец, благодаря функции contour() можно сгенерировать контурную карту на поверхности. Также часто требуется добавить цветную карту. Это площади, ограниченные кривыми уровней, заполненные цветным градиентом. Например, следующее изображения показывает отрицательные значения с помощью темных оттенков синего, а приближение к желтому и красному указывает на более высокие значения.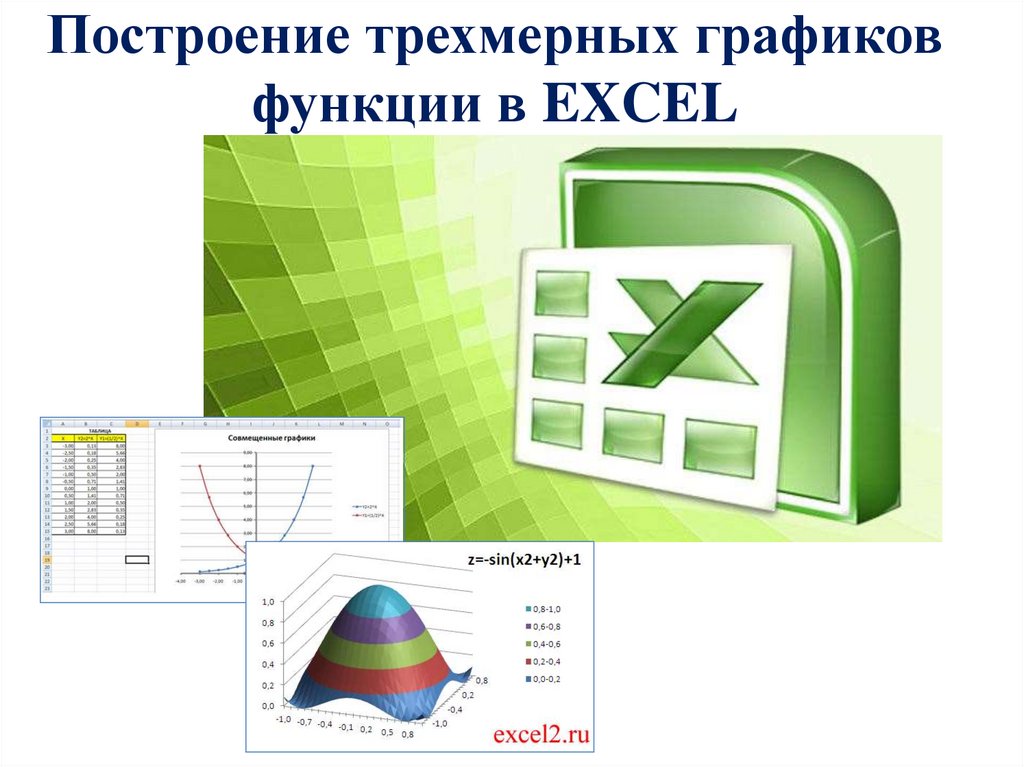
dx = 0.01; dy = 0.01
x = np.arange(-2.0,2.0,dx)
y = np.arange(-2.0,2.0,dy)
X,Y = np.meshgrid(x,y)
def f(x,y):
return (1 - y**5 + x**5)*np.exp(-x**2-y**2)
C = plt.contour(X,Y,f(X,Y),8,colors='black')
plt.contourf(X,Y,f(X,Y),8)
plt.clabel(C, inline=1, fontsize=10)
plt.show()
Это стандартный цветовой градиент. Но с помощью именованного аргумента cmap можно выбрать из большого число цветных карт.
Более того при работе с таким визуальным представлением добавление градации цвета сторонам графа — это прямо необходимость. Для этого есть функция colorbar() в конце кода. В следующем изображении можно увидеть другой пример карты, которая начинается с черного, проходит через красный и затем превращается в желтый и белый на максимальных значениях. Это карта plt.cm.hot.
dx = 0.01; dy = 0.01
x = np.arange(-2.0,2.0,dx)
y = np.arange(-2.0,2.0,dy)
X,Y = np.meshgrid(x,y)
def f(x,y):
return (1 - y**5 + x**5)*np.exp(-x**2-y**2)
C = plt.
contour(X,Y,f(X,Y),8,colors='black')
plt.contourf(X,Y,f(X,Y),8,cmap=plt.cm.hot)
plt.clabel(C, inline=1, fontsize=10)
plt.colorbar()
plt.show()
contour(X,Y,f(X,Y),8,colors='black')
plt.contourf(X,Y,f(X,Y),8,cmap=plt.cm.hot)
plt.clabel(C, inline=1, fontsize=10)
plt.colorbar()
plt.show()
Лепестковые диаграммы
Еще один продвинутый тип диаграмм — лепестковые диаграммы. Он представляет собой набор круговых секторов, каждый из которых занимает определенный угол. Таким образом можно изобразить два значения, присвоив их величинам, обозначающим диаграмму: радиус r и угол θ. На самом деле, это полярные координаты — альтернативный способ представления функций на осях координат. С графической точки зрения такая диаграмма имеет свойства круговой и столбчатой. Как и в круговой диаграмме каждый сектор здесь указывает на значение в процентах по отношению к целому. Как и в столбчатой, расширение по радиусу — это числовое значение категории.
До сих пор в примерах использовался стандартный набор цветов, обозначаемых кодами (например, r — это красный). Однако есть возможность использовать любую последовательность цветов.
Нужно лишь определить список строковых значений, содержащих RGB-коды в формате #rrggbb, которые будут соответствовать нужным цветам.
Странно, но для вывода лепестковой диаграммы нужно использовать функцию bar() и передать ей список углов θ и список радиальных расширений для каждого сектора.
N = 8 theta = np.arange(0.,2 * np.pi, 2 * np.pi / N) radii = np.array([4,7,5,3,1,5,6,7]) plt.axes([0.025, 0.025, 0.95, 0.95], polar=True) colors = np.array(['#4bb2c5','#c5b47f','#EAA228','#579575','#839557','#958c12','#953579','#4b5de4']) bars = plt.bar(theta, radii, width=(2*np.pi/N), bottom=0.0, color=colors) plt.show()
В этом примере определена последовательность цветов в формате #rrggbb, но ничто не мешает использовать строки с реальными названиями цветов.
N = 8 theta = np.arange(0.,2 * np.pi, 2 * np.pi / N) radii = np.array([4,7,5,3,1,5,6,7]) plt.axes([0.025, 0.025, 0.95, 0.95], polar=True) colors = np.array(['lightgreen','darkred','navy','brown','violet','plum','yellow','darkgreen']) bars = plt.
bar(theta, radii, width=(2*np.pi/N), bottom=0.0, color=colors)
plt.show()
Набор инструментов mplot3d
Набор mplot3d включен во все стандартные версии matplotlib и позволят расширить возможности создания трехмерных визуализаций данных. Если объект Figure выводится в отдельном окне, можно вращать оси трехмерного представления с помощью мыши.
Даже с этим пакетом продолжает использоваться объект Figure, но вместо объектов Axes определяется новый тип, Axes3D из этого набора. Поэтому нужно добавить один импорт в код.
from mpl_toolkits.mplot3d import Axes3D
Трехмерные поверхности
В прошлом разделе для представления трехмерных поверхностей использовался контурный график. Но с помощью mplot3D поверхности можно рисовать прямо в 3D. В этом примере используем ту же функцию z = f(x, y), что и в прошлом.
Когда meshgrid вычислена, можно вывести поверхность графика с помощью функции plot_surface().
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = Axes3D(fig)
X = np.arange(-2,2,0.1)
Y = np.arange(-2,2,0.1)
X,Y = np.meshgrid(X,Y)
def f(x,y):
return (1 - y**5 + x**5)*np.exp(-x**2-y**2)
ax.plot_surface(X,Y,f(X,Y), rstride=1, cstride=1)
plt.show()
Трехмерная поверхность выделяется за счет изменения карты с помощью именованного аргумента cmap. Поверхность также можно вращать с помощью функции view_unit(). На самом деле, эта функция подстраивает точку обзора, откуда можно будет рассмотреть поверхность, изменяя аргументы elev и azim. С помощью их комбинирования можно получить поверхность, изображенную с любого угла. Первый аргумент настраивает высоту, а второй — угол поворота поверхности.
Например, можно поменять карту с помощью plt.cm.hot и повернуть угол на elev=30 и azim=125.
from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() ax = Axes3D(fig) X = np.
Диаграмма рассеяния
Самым используемым трехмерным графиком остается 3D график рассеяния. С его помощью можно определить, следуют ли точки определенным трендам и, что самое важное, скапливаются ли они.
В этом случае используется функция scatter() как и при построении обычного двумерного графика, но на объекте Axed3D. Таким образом можно визуализировать разные объекты Series, представленные через вызовы функции scatter() в единой трехмерной форме.
from mpl_toolkits.mplot3d import Axes3D xs = np.random.randint(30,40,100) ys = np.random.randint(20,30,100) zs = np.random.randint(10,20,100) xs2 = np.random.randint(50,60,100) ys2 = np.random.randint(30,40,100) zs2 = np.random.randint(50,70,100) xs3 = np.
Столбчатые диаграммы в 3D
Также в анализе данных используются трехмерные столбчатые диаграммы. Здесь тоже нужно применять функциюbar() к объекту Axes3D. Если же определить несколько Series, то их можно накопить в нескольких вызовах функции bar() для одной 3D-визуализации.from mpl_toolkits.mplot3d import Axes3D
x = np.arange(8)
y = np.random.randint(0,10,8)
y2 = y + np.random.randint(0,3,8)
y3 = y2 + np.random.randint(0,3,8)
y4 = y3 + np.random.randint(0,3,8)
y5 = y4 + np.random.randint(0,3,8)
clr = ['#4bb2c5','#c5b47f','#EAA228','#579575','#839557','#958c12','#953579','#4b5de4']
fig = plt.figure()
ax = Axes3D(fig)
ax.bar(x,y,0,zdir='y',color=clr)
ax.bar(x,y2,10,zdir='y',color=clr)
ax.bar(x,y3,20,zdir='y',color=clr)
ax.bar(x,y4,30,zdir='y',color=clr)
ax.bar(x,y5,40,zdir='y',color=clr)
ax.set_xlabel('X Axis')
ax. set_ylabel('Y Axis')
ax.set_zlabel('Z Axis')
ax.view_init(elev=40)
plt.show()
Многопанельные графики
Были рассмотрены самые разные способы представления данных на графике, в том числе и случаи, когда несколько наборов данных разделены в одном объекте Figure на нескольких подграфиках. В этом разделе речь пойдет о более сложных случаях.
Подграфики внутри графиков
Есть возможность рассматривать графики внутри других ограниченных рамками. Поскольку речь идет о границах — объектах figures(). С ее помощью нужно получить объект Figure, где будут определены два разных объекта Axes с помощью add_axes().
fig = plt.figure() ax = fig.add_axes([0.1,0.1,0.8,0.8]) inner_ax = fig.add_axes([0.6,0.6,0.25,0.25]) plt.show()
Чтобы лучше понять эффект этого режима, лучше заполнить предыдущий объект Axes с помощью реальных данных.
fig = plt.figure() ax = fig.add_axes([0.1,0.1,0.8,0.8]) inner_ax = fig.add_axes([0.6,0.6,0.25,0.25]) x1 = np.arange(10) y1 = np.array([1,2,7,1,5,2,4,2,3,1]) x2 = np.arange(10) y2 = np.array([1,3,4,5,4,5,2,6,4,3]) ax.plot(x1,y1) inner_ax.plot(x2,y2) plt.show()
Сетка подграфиков
Есть другой способ создания подграфиков. С помощью функции subplots() их нужно добавить, разбив таким образом график на секторы. matplotlib позволяет работать даже с более сложными случаями с помощью функции GridSpec(). Это подразделение позволяет разбить область на сетку подграфиков, каждому из которых можно присвоить свой график, так что результатом будет сетка с подграфиками разных размеров с разными направлениями.
gs = plt.GridSpec(3,3) fig = plt.figure(figsize=(6,6)) fig.add_subplot(gs[1,:2]) fig.add_subplot(gs[0,:2]) fig.add_subplot(gs[2,0]) fig.add_subplot(gs[:2,2]) fig.add_subplot(gs[2,1:]) plt.show()
Создать такую сетку несложно. ‘,x2,y2,’yo’)
plt.show()
Все книгиКниги, не связанные с программированием Руководство пользователя Учебники Быстрая справка Справка OriginКниги по программированию X-Function Origin C LabTalk Programming Python Python (внешний) Automation Server LabVIEW VI Приложения Разработка приложений Code Builder Лицензия Orlab 9 gMOCA0012 | |||||||||||||||||||||||||||||||||||||||||||
Трехмерные графики находят широкое применение в науке, технике и финансах. Origin включает в себя широкий спектр типов 3D-графиков, включая 3D Scatter, 3D Bars и 3D Surfaces. Создавать эти графики с Origin быстро и легко: вы можете просто выбрать свои данные и щелкнуть нужную кнопку графика или команду меню, чтобы создать свой график.
Типы трехмерных графиковТипы графиков перечислены ниже вместе с форматами данных, которые можно использовать для создания каждого типа. Определение виртуальной матрицы см. в разделе «Создание трехмерных и контурных графиков из виртуальной матрицы».
Как создавать и настраивать 3D-графики Чтобы создать 3D-график из данных матрицы или рабочего листа, выберите данные и нажмите соответствующую кнопку графика на панели инструментов 3D и контурные графики . В качестве альтернативы вы выбираете график из меню Plot . Чтобы создать график из виртуальной матрицы, вы должны нажать кнопку графика на панели инструментов 3D и Contour Graphs , чтобы открыть диалоговое окно, которое поможет вам указать данные X, Y, Z и создать график. Дополнительные сведения о создании графиков из виртуальных матриц см. Настройка трехмерных графиков в основном выполняется в диалоговых окнах Axis и Plot Details . Вы можете узнать больше о диалоговом окне Axis и узнать, как настроить оси графика в Оси графика . Дополнительные сведения о диалоговом окне Plot Details см. в разделе 9.0019 Настройка графика . | |||||||||||||||||||||||||||||||||||||||||||
Трехмерное построение
Python позволяет строить трехмерные диаграммы благодаря набору инструментов mplot3d библиотеки matplotlib . Однако обратите внимание, что 3D-диаграммы чаще всего являются плохой практикой. В этом разделе основное внимание уделяется 3D-диаграммам рассеяния и поверхностным графикам, которые представляют собой интересные варианты использования.
⏱ Быстрый старт
Набор инструментов mplot3d из 9Здесь используется 0371 matplotlib .
- Параметр проекции функции add_subplot() установлен на
3d - Обычная функция
scatter()теперь может быть вызвана с 3 входными данными для осей X, Y и Z - Положение камеры может быть установлен благодаря функции
view_init()
Базовая 3D-диаграмма рассеяния с Python и Matplotlib.
# библиотеки
из mpl_toolkits.mplot3d импортировать Axes3D
импортировать matplotlib.pyplot как plt
импортировать numpy как np
импортировать панд как pd
# Набор данных
df=pd.DataFrame({'X': диапазон (1101), 'Y': np.random.randn(100)*15+range(1101), 'Z': (np.random.randn(100)* 15+диапазон(1,101))*2 })
# участок
рис = plt.figure()
топор = fig.add_subplot(111, проекция='3d')
ax.scatter(df['X'], df['Y'], df['Z'], c='skyblue', s=60)
ax.view_init (30, 185)
plt.show()
⚠️ Помните о 3d
Трехмерные объекты очень популярны, но негативно влияют на точность и скорость , при которых в большинстве случаев можно интерпретировать графику.
В приведенном ниже примере коричневая часть спереди выглядит намного больше, чем розовая часть сзади, даже несмотря на то, что их реальные значения составляют 30% против 35%. Данные искажены.
Пример плохой трехмерной круговой диаграммы
Примечание : помните, что в большинстве случаев круговых диаграмм следует избегать
Трехмерные диаграммы рассеяния с помощью
Matplotlib Как описано в разделе быстрого запуска выше, трехмерные диаграммы могут быть построены с помощью Python благодаря инструментарию mplot3d из matplotlib . Пример ниже поможет вам использовать его для получения этого рисунка:
Базовая 3D-диаграмма рассеяния с Python и Matplotlib.
Этот метод полезен для визуализации результатов PCA (анализа главных компонентов). В следующем примере объясняется, как запустить PCA с помощью python и проверить его результат с помощью трехмерной диаграммы рассеяния:
Результат PCA показан в виде трехмерной диаграммы рассеяния с помощью python
Поверхностный график с
Matplotlib Поверхностный график рассматривает координаты X и Y как широту и долготу, а Z как высоту.