Как найти обратную функцию онлайн: Калькулятор Обратных Функций

Содержание

Обратная функция — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

2. Обратная функция

Цели обучения:
10.3.1.5 — знать определение обратной функции и уметь находить
функцию, обратную заданной и знать свойство расположения
графиков взаимно обратных функций;
Критерии оценивания:
Учащийся
1. Знает определение обратной функции;
2. Знает особенность расположения графиков
взаимно обратных функций;
3.

Находит функцию, обратную заданной.
ПОВТОРЕНИЕ
1.По рисункам определите монотонность функции
Если функция у = f ( х ), х € Х принимает каждое своё
значение у только при одном значении х из Х, то эту
функцию называют обратимой.
Т.е. разным значениям аргумента соответствуют разные
значения функции
у 2х 2
у х2
1
у 2
х
у х
3
х1 у
х2 у
Теорема. Если функция у=f(x) строго монотонна на
множестве Х., то она обратима
Пусть у = f(x) – обратимая функция. Тогда каждому у из
множества значений функции соответствует одно
определённое число х из области её определения, такое, что
f(x) = y. Это соответствие определяет функцию х от у,
которую обозначим х = g(y). Поменяем местами х и у:
у = g(x).
Функцию у = g(x) называют обратной к функции у = f(x).
Функция у = f(x) обратима на некотором интервале (a; b)
тогда и только тогда, когда она на этом интервале
взаимно однозначна.

Алгоритм нахождения обратной
функции:
1.

Заменяем х на у
2. Выражаем у
3. Получаем функцию у = g(x), обратную функции у = f(x).
Примечание: иногда обратную функцию обозначают:
1
y f ( x)
Пример
1
х 2
Найти функцию, обратную данной, т.е. у = f -1(x).
Решение:
1
x
y 2
Дано: у
хy 2 x 1
хy 2 x 1
Ответ:
1
у 2
х
f 1 ( x) 2
1
x
или g ( x) 2
1
x
ВТОРОЙ СПОСОБ
Алгоритм нахождения обратной
функции:
1. Выражаем х на у
2. Меняем местами у и х
3. Получаем функцию у = g(x), обратную функции у = f(x).
Пример
1
х 2
Найти функцию, обратную данной, т.е. у = f -1(x).
Решение:
Дано: у
1
у 2
х
Ответ:
f 1 ( x) 2
1
x
или g ( x) 2
1
x
1) Область определения. Пусть f и g – взаимно обратные
функции. Область определения функции f совпадает с
областью значений функции g, и наоборот, область
значений функции f совпадает с областью определения
функции g.

2) Монотонность. Если одна из взаимно обратных
функций возрастает, то и другая возрастает. Аналогичное
верно и для убывающих функций.
3) Графики. Графики взаимно обратных функций,
построенные в одной и той же системе координат,
симметричны друг другу относительно прямой y = x.

English Русский Правила

Функция спроса (прямая и обратная) с примерами и графиками движения и сдвига

Содержание

Множественный регрессионный анализ
Обратная функция спроса
Примеры и графики

Функция спроса – это математическое уравнение, которое выражает спрос на продукт или услугу в зависимости от его цены и других факторов, таких как цены на заменители и дополнительные товары, доход и так далее.

Функция спроса создает связь между спросом (требуемым количеством) на продукт (который является зависимой переменной) и факторами, влияющими на спрос, такими как цена продукта, цена замещающих и дополняющих товаров, средний доход и прочие (которые являются независимыми переменными).

Давайте рассмотрим рынок приложений для найма автомобиля с водителем и выясним факторы, которые могут повлиять на ежедневный пробег таксистов, предлагающих данный вид услуги.

Множественный регрессионный анализ

Самым важным фактором является стоимость проезда (цена, взимаемая за километр пути).

Другие потенциальные факторы являются детерминантами спроса, включая цену заменителей, то есть цену общественного транспорта или конкурирующих услуг такси независимо от того, рабочий или выходной день, ясная или дождливая погода и так далее.

Один из методов создания функции спроса заключается в использовании множественного регрессионного анализа для выяснения взаимосвязи между требуемым количеством, ценой продукта и всеми другими факторами.

Множественный регрессионный анализ присваивает различные коэффициенты каждому из факторов, влияющих на спрос. Знак коэффициента – положительный или отрицательный – говорит нам, связаны ли спрос и фактор положительно или отрицательно.

Предположим для упрощения, что вы использовали только две переменные – (1) цену самого продукта и (2) рост цены конкурирующего общественного транспорта – и пришли к следующему уравнению:

Q = 1,200,000 – 150,000 × P + 200,000 × P_PT, где

Q – это потребляемые километры,

P – цена за километр услуги по вызову пассажиров,

P_PT – увеличение цены за поездку в системе общественного транспорта.

Параметр Р имеет отрицательный знак, который показывает, что с каждым долларовым увеличением стоимости проезда за километр требуемое количество будет уменьшаться на 150 000 километров в день.

С другой стороны, параметр P_PTимеет положительный знак, а это означает, что увеличение платы за проезд в общественном транспорте на один доллар приведет к увеличению спроса на 200 000 километров.

Поскольку приведенное выше уравнение создает связь не только между требуемыми километрами и взимаемой ценой, но и с ценой заменителя, оно представляет собой как сдвиг кривой спроса, так и движение вдоль кривой спроса.

До тех пор, пока цены на общественный транспорт не изменятся, мы можем упростить функцию спроса до соотношения между Q и P:

Q = 1,200,000 – 150,000 × P

Мы можем разработать график спроса, используя приведенное выше уравнение, просто подключив различные цены за километр.

Обратная функция спроса

График спроса и предложения обычно строится таким образом, что количество находится на оси X, а цена – на оси Y, но функция спроса, которую мы определили выше, имеет цену (P) как независимую переменную и количество (Q) как независимую переменную.

Функция спроса иногда определяется ценой P как независимой переменной. Такая функция спроса называется обратной функцией спроса.

С помощью всего лишь нескольких математических манипуляций мы можем преобразовать функцию спроса, определенную выше, в обратную функцию спроса:

150,000 × P = 1,200,000 – Q

P = (1,200,000 – Q) / 150,000

P = 8 – Q / 150,000

Обратная функция спроса полезна, когда мы заинтересованы в поиске предельного дохода, дополнительного дохода, полученного от одной проданной дополнительной единицы.

Функция предельного дохода является первой производной от обратной функции спроса. Для обратной функции спроса вида P = a – bQ функция предельного дохода равна MR = a – 2bQ. Функция предельного дохода в данном случае выглядит следующим образом:

P = 8 – 2 × Q / 150,000 = 8 – Q / 75,000

Примеры и графики

Давайте выясним, каков объем перевозок в километрах будет востребован при следующих сценариях: (A) средняя цена за километр (Р) составляет $ 1. 5 и $ 1.75; и (B) средняя цена за километр (Р) составляет $ 1.5, а рост цен на общественный транспорт (Р_РТ) – $ 0.25

Сценарий А

Следующее уравнение показывает требуемое количество, соответствующее каждой цене:

Q_1.50 = 1,200,000 – 150,000 × $ 1.50 = 975,000

Q_1.75 = 1,200,000 – 150,000 × $ 1.75 = 937,500

Сценарий В

В этом случае происходит изменение цены заменителя, поэтому она представляет собой сдвиг кривой:

Q_1.50;0.25 = 1,200,000 – 150,000 × $ 1.50 + 200,000 × $ 0.25 = 1,025,000

В нашем примере Q_1.50;0.25 выше, чем Q_1.50, потому что рост цен на общественный транспорт вызвал внешний сдвиг кривой спроса.

На следующей диаграмме показано движение вдоль начальной кривой спроса в сценарии А и сдвиг в случае сценария B:

Функция спроса и функция предложения могут быть использованы для решения задач рыночного равновесия и рыночной клиринговой цены.

Калькулятор обратной линейной функции

Инструкции: Найдите обратную функцию заданной вами линейной функции. Пожалуйста, введите допустимое линейное уравнение в поле приведенный ниже, чтобы найти его обратный.

9{-1}(f(x)) = x\), для всех $x$ в соответствующем наборе.

Теперь вычисление обратной функции в целом не обязательно является простым алгебраическим упражнением, поскольку оно обычно включает в себя решение для x, начиная с исходной функции \ (y = f (x) \), которая может быть алгебраически трудно или невозможно.

Но когда вы имеете дело с линейной функцией формы $y = ax + b$, тогда становится немного проще решить для x и, наконец, найти обратный.

Как найти обратную линейную функцию?

Сначала вы начинаете с допустимой линейной функции вида $y = ax + b$. Ваша первая задача — найти x:

. \[ах = у-б\] \[\Rightarrow x = \frac{y-b}{a}\]

Теперь вы сделаете острое наблюдение, «что произойдет, если $a = 0$», и вы будете правы в этом. Возникает проблема, когда $a = 0$, в этом случае вы не можете решить для $x$ и нет обратного. 9{-1}(x) = \frac{x-b}{a}\]

Как пользоваться этим калькулятором

Чтобы найти обратную линейную функцию с шагами, просто подставьте правильную линейную функцию вида $y = ax + b$.

Если вы укажете допустимую линейную функцию, калькулятор покажет вам все шаги, необходимые для получения обратной, а также вы получите график исходной функции и ее обратной, если обратная существует.

Обратите внимание, что этот калькулятор работает только для линейных функций. Вычисление обратной функции, которая не является линейной, может быть более сложным, и это не всегда возможно.

Пример

Найдите обратную функцию следующей линейной функции $y = 3x — 2$.

Ответ:

Чтобы найти функцию, обратную заданной линейной функции, необходимо выполнить следующие шаги.

Шаг 1 — Решение для x : Первым шагом в поиске обратного линейного уравнения является решение для $x$:

Мы получили следующее уравнение:

\[\displaystyle у=3x-2\]

Положив $x$ в левую часть, а $y$ и константу в правую, получим

\[\displaystyle 3x = y + 2\]

Теперь, решая $x$, получаем следующее

\[\displaystyle x=\frac{1}{3}y+\frac{2}{3}\]

и упрощая все термины, которые нуждаются в упрощении, окончательно получаем следующее

\[\displaystyle x=\frac{1}{3}y+\frac{2}{3}\]

Таким образом, на основе представленного уравнения мы заключаем, что результатом решения для $x$ из данного уравнения является $\displaystyle x=\frac{1}{3}y+\frac{2}{3 }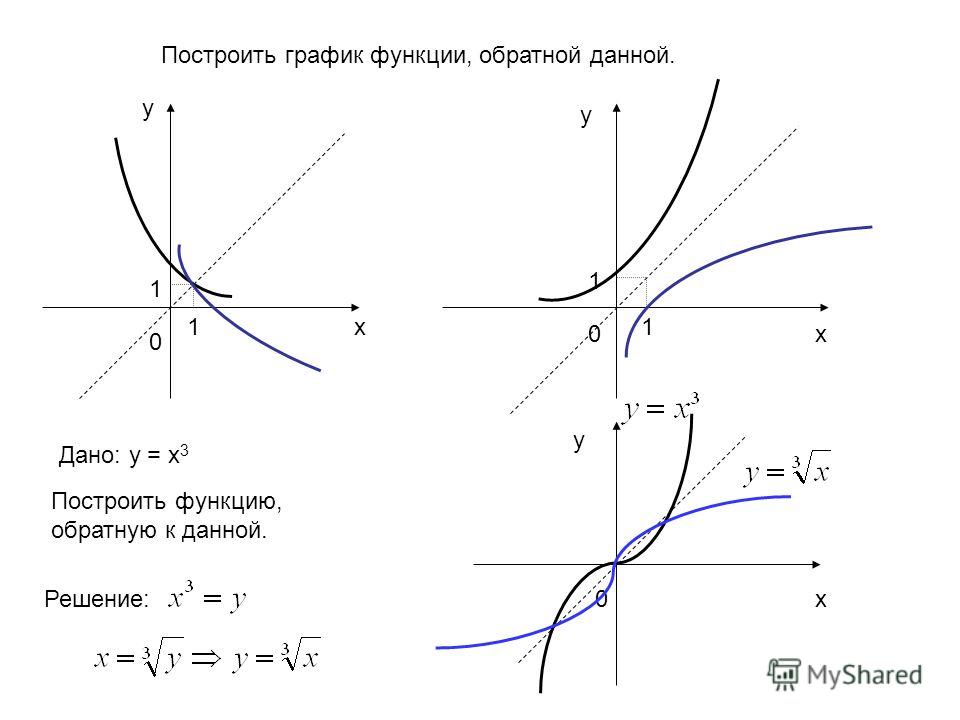$. {-1}(x)\) в предыдущем уравнении, что приводит к: 9{-1}(x)=\frac{1}{3}x+\frac{2}{3}\).

Онлайн-калькулятор: Модульный мультипликативный обратный калькулятор

  Исследование  Математика  Алгебра

Этот обратный калькулятор по модулю вычисляет модульный мультипликативный обратный по модулю m заданного целого числа.

Обратное мультипликативное и модульное обратное мультипликативное предупреждение

Прежде всего, существует мультипликативное обратное или обратное для числа x , обозначаемый 1/x или x⁻¹, и это не то же самое, что модульное мультипликативное обратное. Обратное число х — это число, которое при умножении на исходное х дает 1, называемое мультипликативным тождеством. Вы можете найти взаимное довольно легко. Для дроби a/b мультипликативным обратным является b/a. Чтобы найти мультипликативную обратную величину действительного числа, просто разделите 1 на это число.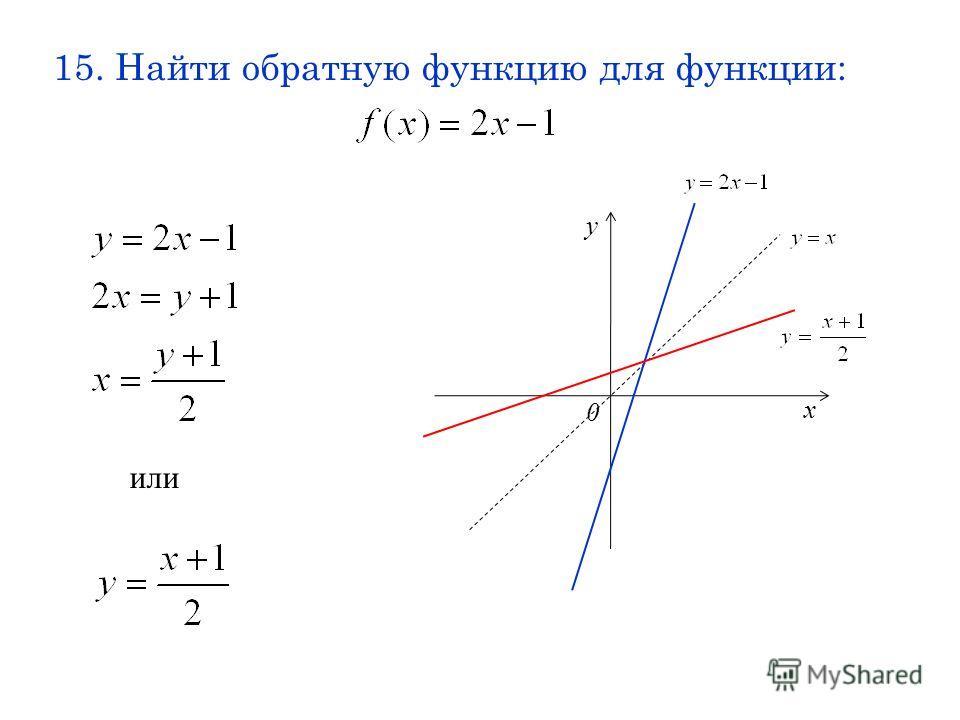 Не думаю, что в каждом из этих случаев нужен какой-то специальный калькулятор. Но модульный мультипликативный обратный — это совсем другое, поэтому вы можете увидеть наш обратный калькулятор по модулю ниже. Теорию можно найти после калькулятора.

Inverse Modulo Calculator

Integer

Modulo

Modular Multiplicative Inverse

Modular multiplicative inverse

The modular multiplicative inverse of an integer a modulo m is an integer b such that
,
Его можно обозначить как , где m-модулярность обращения подразумевается.

Мультипликативная обратная величина по модулю m существует тогда и только тогда, когда a и m взаимно просты (т. е. если

НОД(а, м) = 1 ). Если модульное мультипликативное обратное значение по модулю m существует, операция деления на модуль m может быть определена как умножение на обратное.