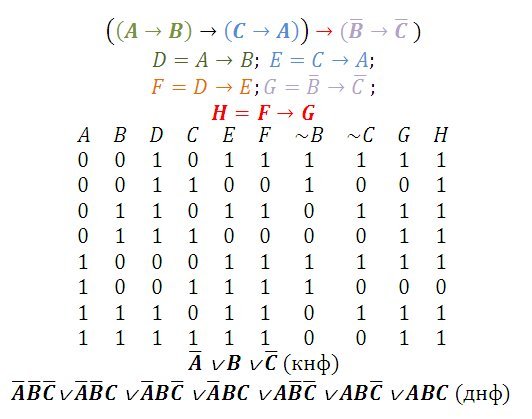2_ ДНФ ,КНФ ДНФ, СКНФ алгоритмы преобразования
Логические функции, СДНФ СКНФ
1.4 Формы представления функций алгебры логики
Функции алгебры логики могут быть заданы различными способами:
— таблицей истинности — в аналитической форме- в числовой форме..
Если функция имеет значения на всех наборах, то она называется полностью определенной.
элементарная дизъюнкция — дизъюнктивный терм или макстерм — это дизъюнктивный терм или макстерм — это дизъюнкция произв числа попарно независимых перем Например,
элементарная конъюнкция — конъюнктивный терм или минтерм — конъюнкция произв числа попарно независимых перем. Напр, Х 1Х 2 Х3 — минтерм 3-его ранг
– это не минтерм, так как перем и зависимы.
Для аналитической записи функций используют две формы:
1) Дизъюнктивную Нормальную Форму — ДНФ
2) Конъюнктивную Нормальную Форму – КНФ
ДНФ это дизъюнкция минтермов разл ранга
КНФ это конъюнкция макстермов различного ранга
Если все термы, входяшие в нормальную форму имеют одинаковый и максимальный ранг,= числу переменных функции — n, то такая форма называется совершенной.
При этом, минтерм называют констинтуентой (составля) 1 (КЕ), а макстерм — конституентой 0 (КН).
— это СДНФ
— это СКНФ
Т е СДНФ есть дизъюнкция конституент 1, а СКНФ — есть конъюнкция конституент 0
Составление совершенных форм по табл истинности
Совершенные формы составляют по табл истинности функции. СДНФ : для каждого набора переменных на которых функция=1, записывают минтерм ранга n , в которых с отрицанием берутся переменные = 0 на данном наборе. Все минтермы объединены дизъюнктивно.
СКНФ =для каждого набора переменных, на которых функция=0, записывают макстерм ранга n, в кот с отрицанием берутся переменные, имеющие значение=1 на данном наборе. Все макстермы объединены конъюнктивно
Для компактной записи функций исп числовую форму, в которой заданы только номера наборов. Числовая форма для СДНФ:
Числовая форма для СКНФ:
Алгоритм преобразованияя в ДНФ
1) Сначала избавляемся от операций импликации, эквивалентности и неравнозначности, выразив их через логические связки ¬, & и ∨ по законам:
2) Доводят знаки отрицания до независимых переменных, используя законы де Моргана:
3) Применяя з-н дистрибутивности
преобразуют формулу к дизъюнкции элементарных конъюнкций
4) 4) Постоянно избавляются от двойных отрицаний:
ДНФ A наз совершенной и обозн СДНФ, если каждая переменная формулы A входит с отрицанием или без отрицания в каждый конъюнкт точно 1 раз.
Алгебраическая форма представления булевых функций используется для минимизации (упрощения формулл) и для построения логических схем. Существукт 2 формы алгебраических функций – дизъюнктивная и конъюнктивн. Дизъюнктивная нормальная форма представляет сумму элементарных произведения аргументов, например
Если кажд слаг содер все арг или их отриц, то получ соверш дизъюнкт норм форму (СДФН), напр
Для перехода от табл истинн к СДНФ учит только те сост, для кот функц= 1. Для каждого такого сост запис элем произв всех ар. Если арг имеет зн «0», то запис его отриц. Для привед примера СДНФ имеет вид (17.4)
Совершенная конъюнктивная нормальная форма (СКНФ) представляет логическое произведение элементарных логических сумм, причем каждая сумма содержит все аргументы или их отрицания, например
ДНФ, но не СДНФ от 3 перем
-ДНФ от 2 перем
-представл импликации в виде ДНФ.
-СДНФ для импликации
-СДНФ для оп эквивалентности
-СДНФ для оп неравнозначности
Прим.
1 Привести к ДНФ формулу
Реш.
2. Привести ту же формулу к СДНФ. Начав преобразования с ДНФ
Нахождение СДНФ по табл истинности функции | Нахождение СКНФ по табл истинности функции |
1)Отметить те строки таблицы истинности, в последнем столбце которых стоят 1. 2)Выписать для каждой отмеченной строки конъюнкцию всех переменных так: если значение некоторой переменной в данной строке — 1, то в конъюнкцию включать саму эту переменную, если равно 1, то ее отрицание. 3)Все полученные конъюнкции связать в дизъюнкцию. | 1)Отметить те строки таблицы истинности, в последнем столбце которых стоят 0. 2)Выписать для каждой отмеченной строки дизъюнкцию всех переменных так: если значение некоторой переменной в данной строке= 1, то в дизъюнкцию включать саму эту переменную, если равно 0, то ее отрицание. 3)Все полученные дизъюнкции связать в конъюнкцию. |
Прим1
Прим 2
построение СДНФ: | построение СКНФ: |
Для перехода от таблицы истинности к СКНФ учитывают только те состояния, для которых функция= «0». Для каждого такого состояния записывается элементарная сумма аргументов. Если аргуент имеет значение «1», то пишут его отрицание. Для примера СКНФ имеет вид
Примеры
1)Привести к КНФ и СКНФ.
Реш. упростим выражение, используя законы де Моргана и правило x y x y → = ∨
Теперь приводим к КНФ
Приведем к СКНФ:
2) С помощью эквивалентных преобразований построить д.н.ф. функции f (x):
Решение. Преобразуем функцию:
3) Используя СКНФ, найти наиболее простую формулу алгебры высказываний от 4 переменных, принимающую значение 0 на следующих наборах значений переменных, и только на них:
Решение.
Запишем СКНФ функции по данным задачи
Получили
ЛИТЕРАТУРА и ССЫЛКИ
1)Курилова М.Н. Информатика-логика, СПБ Лес-техн ун-т им.Кирова
https://studfiles.net/preview/2069515/page:5/
2) http://ptca.narod.ru/lec/lec4_3.html
3) https://www.matburo.ru/ex_dm.php?p1=bfpg
Помогите решить / разобраться (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
Посмотреть правила форума
| ariel777 |
| ||
04/07/19 |
| ||
| |||
| ariel777 |
| ||
04/07/19 |
| ||
| |||
| iifat |
| |||
16/02/13 |
| |||
| ||||
Повзрослев и тщательно изучив психологию (и, наверное, этологию с антропологией и теорией эволюции, а может, и ещё много чего разного), можно найти вполне реальные глубокие смыслы этого действа; однако, дети, не вникая в перечисленные науки, просто лепят куличики, потому что им это нравится.| ariel777 |
| ||
04/07/19 |
| ||
| |||
11.2020, 08:22 | Mihr |
| |||
18/09/14 |
| |||
| ||||
| Mikhail_K |
| |||
26/01/14 |
| |||
| ||||
Когда математики развивали теорию чисел, они не думали, что она пригодится в криптографии. Таких примеров множество.| Sender |
| ||
14/01/11 |
| ||
| |||
11.2020, 11:30 
Во-первых, представление в виде СДНФ (СКНФ) для данной булевой функции единственно, что позволяет его использовать в качестве канонического представления, если угодно, «паспорта» этой функции, по которому её можно однозначно идентифицировать. Во-вторых, одного взгляда на СДНФ (СКНФ) достаточно, чтобы определить множество значений переменных, где она принимает истинные(ложные) значения, т.е. они наиболее наглядно отражают, если можно выразиться, саму суть булевой функции, фактически их можно рассматривать как запись таблицы истинности булевой функции. Но, поскольку СДНФ и СКНФ, как правило, очень громоздки, на практике этими удобствами жертвуют в пользу компактности представления в виде несовершенных форм. Собственно, булевы функции, применяемые на практике в народном хозяйстве, чаще всего записываются и хранятся именно в виде ДНФ и КНФ. КНФ удобна для процедур автоматизированного логического вывода в том смысле, что если удаётся получить дизъюнкцию, являющуюся следствием данной КНФ, её можно без лишних усилий присоединить к этой КНФ, получив новую КНФ, являющуюся логическим следствием исходной.
Поэтому КНФ используется в т.н. решателях — программах, определяющих, принимает ли данная булева функция истинное значение хоть на каком-то наборе переменных(ДНФ тоже используется схожим образом, но реже), проще говоря, умеющих делать логические выводы. Это может применяться в таких сферах, как автоматизированное планирование, проектирование, системы искусственного интеллекта.| Mihr |
| |||
18/09/14 |
| |||
| ||||
Потому как прекрасно помню: когда-то и меня — студента — заставляли учить историю КПСС, политэкономию и т.п. «хотя бы для того, чтобы вы были грамотными» — так нам говорили. Подобную формулу я всегда считал издательством над здравым смыслом. Уверен: если бы я никогда не учил историю КПСС, то отрицательных эмоций в моей жизни было бы поменьше А грамотности, уверен и в этом, не поубавилось бы. Вот я и думаю: возможно, у кого-то математика вызывает те же самые эмоции, что у меня когда-то — марксистская шелуха. Поэтому какой-либо категоричной позиции я здесь не занимаю.
И на такие вопросы я стараюсь отвечать серьёзно. Если могу хоть что-то сказать.| ariel777 |
| ||
04/07/19 |
| ||
| |||
Философия, например, совсем не имеет никакого «практического» (непосредственного) применения в реальной жизни. То есть совсем никакого. При этом я не настолько глуп, чтобы ставить под сомнение ее «нужность» и самоценность для изучающего. В то же время, в философии есть перекличка идей, и похожую перекличку я пытаюсь найти между сабжем, всей дисциплиной логики и другими областями знаний.| bot |
| |||
21/12/05 |
| |||
| ||||
| ariel777 |
| ||
04/07/19 |
| ||
| |||
Поинтересуйтесь у первокуров мехматян. Большинство из них уверены, что философия (да ещё в таком объёме) им вообще не нужна. Да даже не только первокуры в этом уверены.| Sender |
| ||
14/01/11 |
| ||
| |||
2020, 13:36 | george66 |
| |||
31/12/15 |
| |||
| ||||
11.2020, 16:09 
| kernel1983 |
| ||
10/11/15 |
| ||
| |||
Най мой взгляд, это главное назначение совершенных нормальных форм.| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 14 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Конъюнктивной нормальной формой логической функции.
«учебник по дискретной математике днф, сднф, кнф, скнфДля всякой логической формулы с помощью тождественных преобразований можно построить бесконечно много равносильных ей формул. В алгебре логики одной из основных задач является поиск канонических форм (т. е. формул, построенных по единому правилу, канону).
Если логическая функция выражена через дизъюнкцию, конъюнкцию и отрицание переменных, то такая форма представления называется нормальной.
Среди нормальных форм выделяются совершенные нормальные формы (такие формы, в которых функции записываются единственным образом).
Совершенная дизъюнктивная нормальная форма (СДНФ)
Определение. Формулу называют элементарной конъюнкцией, если она образованна конъюнкцией некоторого числа переменных или их отрицаний.
Примеры: y, ¬ y, х 1 ∧ ¬ х 2 ∧ х 3 ∧ х 4
Определение. Формула называтся дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией неповторяющихся элементарных конъюнкций.
ДНФ записывается в следующей форме: F 1 ∨ F 2 ∨ .
.. ∨ F n , где F i — элементарная конъюнкция
Примеры: ¬ х 1 ∧ х 2 ∨ х 1 ∧ ¬ х 2 ∨ х 1 ∧ ¬ х 2 ∧ х 3 , ¬ y 1 ∨ y 1 ∧ y 2 ∨ ¬ y 2
Определение.
Логическая формула от k переменных называется совершенной дизъюнктивной нормальной формой (СДНФ), если:
1) формула является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция k переменных х 1 , х 2 , …, х k , причем на i-м месте этой конъюнкции стоит либо переменная х i , либо ее отрицание;
2) все элементарные конъюнкции в такой ДНФ попарно различны.
Пример: (¬ х 1 ∧ х 2 ∧ х 3) ∨ (х 1 ∧ ¬ х 2 ∧ х 3) ∨ (х 1 ∧ х 2 ∧ ¬ х 3)
Совершенная конъюнктивная нормальная форма (СКНФ)
Определение. Формулу называют элементарной дизъюнкцией, если она образована дизъюнкцией некоторого числа переменных или их отрицаний.
Примеры: ¬ х 3 , х 1 ∨ х 2 , х 1 ∨ х 2 ∨ ¬ х 3
Определение.
Формула называется конъюнктивной нормальной формой (КНФ), если она является конъюнкцией неповторяющихся элементарных дизъюнкций.
КНФ записывается в следующей форме: F 1 ∧ F 2 ∧ … ∧ F n , где F i — элементарная дизъюнкция
Примеры: (х 1 ∨ ¬ х 2) ∧ х 3 , (х 1 ∨ х 2) ∧ (¬ х 1 ∨ х 2 ∨ х 3) ∧ (х 1 ∨ ¬ х 2 ∨ ¬ х 3)
Определение.
Логическая формула от k переменных называется совершенной конъюнктивной нормальной формой (КДНФ), если:
1) формула является КНФ, в которой каждая элементарная дизъюнкция есть дизъюнкция k переменных х 1 , х 2 , …, х k , причем на i-м месте этой дизъюнкции стоит либо переменная х i , либо ее отрицание;
2) все элементарные дизъюнкции в такой КНФ попарно различны.
Пример: (х 1 ∨ х 2 ∨ х 3) ∧ (¬ х 1 ∨ ¬ х 2 ∨ х 3)
Заметим, что любую логическую функцию, не равную тождественно 0 или 1, можно представить в виде СДНФ или СКНФ .
Алгоритм построения СДНФ по таблице истинности
- Выбрать все строки таблицы, в которых значение функции равно единице.
- Для каждой такой строки записать конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание.
- Все полученные конъюнкции связываем операциями дизъюнкции.
Алгоритм построения СКНФ по таблице истинности
- Выбрать все строки таблицы, в которых значение функции равно нулю.
- Для каждой такой строки записать дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 0, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание.
- Все полученные дизъюнкции связываем операциями конъюнкции.
Анализ алгоритмов показывает, что если на большей части строк таблицы истинности значение функции равно 0, то для получения ее логической формулы лучше построить СДНФ, в противном случае — СКНФ.
Пример: Дана таблица истинности логической функции от трех переменных. Построить логическую формулу, реализующую эту функцию.
| x | y | z | F (x, y, z) |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Т.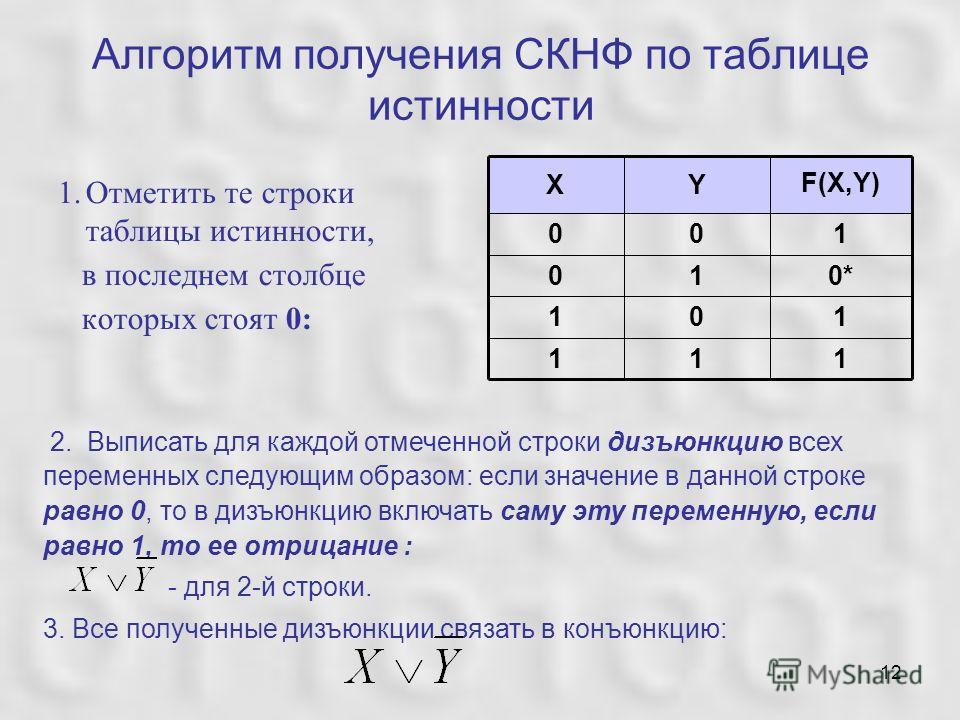
к. на большинстве строк таблицы истинности значение функции равно 1, то построим СКНФ. В результате получим следующую логическую формулу:
F = (¬ x ∨ y ∨ z) ∧ (¬ x ∨ y ∨ ¬ z)
Проверим полученную формулу. Для этого построим таблицу истинности функции.
| x | y | z | ¬ x | ¬ x ∨ y ∨ z | ¬ z | ¬ x ∨ y ∨ ¬ z | F (x, y, z) |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
Сравнив исходную таблицу истинности и построенную для логической формулы, заметим, что столбцы значений функции совпадают.
Значит, логическая функция построена верно.
Нормальная форма логической формулы не содержит знаков импликации, эквивалентности и отрицания неэлементарных формул.
Нормальная форма существует в двух видах:
конъюнктивная нормальная форма (КНФ) — конъюнкция нескольких дизъюнкций, например, $\left(A\vee \overline{B}\vee C\right)\wedge \left(A\vee C\right)$;
дизъюнктивная нормальная форма (ДНФ) — дизъюнкция нескольких конъюнкций, например, $\left(A\wedge \overline{B}\wedge C\right)\vee \left(B\wedge C\right)$.
СКНФ
Совершенная конъюнктивная нормальная форма (СКНФ) — это КНФ, удовлетворяющая трем условиям:
не содержит одинаковых элементарных дизъюнкций;
ни одна из дизъюнкций не содержит одинаковых переменных;
каждая элементарная дизъюнкция содержит каждую переменную из входящих в данную КНФ.
Любая булева формула, которая не является тождественно истинной, может быть представлена в СКНФ.
Правила построения СКНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 0, записывается сумма, причем переменные, которые имеют значение 1, берутся с отрицанием.
СДНФ
Совершенная дизъюнктивная нормальная форма (СДНФ) — это ДНФ, удовлетворяющая трем условиям:
не содержит одинаковых элементарных конъюнкций;
ни одна из конъюнкций не содержит одинаковых переменных;
каждая элементарная конъюнкция содержит каждую переменную из входящих в данную ДНФ, к тому же в одинаковом порядке.
Любая булева формула, которая не является тождественно ложной, может быть представлена в СДНФ, к тому же единственным образом.
Правила построения СДНФ по таблице истинности
Для каждого набора переменных, при котором функция равна 1, записывается произведение, причем переменные, которые имеют значение 0 берут с отрицанием.
Примеры нахождения СКНФ и СДНФ
Пример 1
Записать логическую функцию по ее таблице истинности:
Рисунок 1.
Решение:
Воспользуемся правилом построения СДНФ:
Рисунок 2.
Получим СДНФ:
Воспользуемся правилом построения СКНФ.
Простой конъюнкцией называется конъюнкция одной или нескольких переменных , при этом каждая переменная встречается не более одного раза (либо сама , либо ее отрицание ).
Например, является простой конъюнкцией,
Дизъюнктивной нормальной формой (ДНФ) называется дизъюнкция простых конъюнкций .
Например, выражение является ДНФ.
Совершенной дизъюнктивной нормальной формой (СДНФ) называется такая дизъюнктивная нормальная форма , у которой в каждую конъюнкцию входят все переменные данного списка (либо сами , либо их отрицания ), причем в одном и том же порядке .
Например, выражение является ДНФ, но не СДНФ. Выражение является СДНФ.
Аналогичные определения (с заменой конъюнкции на дизъюнкцию и наоборот) верны для КНФ и СКНФ. Приведем точные формулировки.
Простой дизъюнкцией называется дизъюнкция одной или нескольких переменных , при этом каждая переменная входит не более одного раза (либо сама , либо ее отрицание ).Например, выражение — простая дизъюнкция,
Конъюнктивной нормальной формой (КНФ) называется конъюнкция простых дизъюнкций (например выражение — КНФ).
Совершенной конъюнктивной нормальной формой (СКНФ) называется такая КНФ, у которой в каждую простую дизъюнкцию входят все переменные данного списка (либо сами, либо их отрицания), причем в одинаковом порядке.
Например, выражение является СКНФ.
Приведем алгоритмы переходов от одной формы к другой. Естественно, что в конкретных случаях (при определенном творческом подходе) применение алгоритмов бывает более трудоемким, чем простые преобразования, использующие конкретный вид данной формы:
а) переход от ДНФ к КНФ
Алгоритм этого перехода следующий: ставим над ДНФ два отрицания и с помощью правил де Моргана (не трогая верхнее отрицание) приводим отрицание ДНФ снова к ДНФ. При этом приходится раскрывать скобки с использованием правила поглощения (или правила Блейка). Отрицание (верхнее) полученной ДНФ (снова по правилу де Моргана) сразу дает нам КНФ:
Заметим, что КНФ можно получить и из первоначального выражения, если вынести у за скобки;
б) переход от КНФ к ДНФ
Этот переход осуществляется простым раскрытием скобок (при этом опять-таки используется правило поглощения)
Таким образом, получили ДНФ.
Обратный переход (от СДНФ к ДНФ) связан с проблемой минимизации ДНФ. Подробнее об этом будет рассказано в разд.
5, здесь же мы покажем, как упростить ДНФ (или СДНФ) по правилу Блейка. Такая ДНФ называется сокращенной ДНФ;
в) сокращение ДНФ (или СДНФ) по правилу Блейка
Применение этого правила состоит из двух частей:
Если среди дизъюнктных слагаемых в ДНФ имеются слагаемые , то ко всей дизъюнкции добавляем слагаемое К 1 К 2 . Проделываем эту операцию несколько раз (можно последовательно, можно одновременно) для всех возможных пар слагаемых, а затем, применяем обычное поглощение;
Если добавляемое слагаемое уже содержалось в ДНФ, то его можно отбросить совсем, например,
или
Разумеется, сокращенная ДНФ не определяется единственным образом, но все они содержат одинаковое число букв (например, имеется ДНФ , после применения к ней правила Блейка можно прийти к ДНФ, равносильной данной):
в) переход от ДНФ к СДНФ
Если в какой-то простой конъюнкции недостает переменной, например, z , вставляем в нее выражение ,после чего раскрываем скобки (при этом повторяющиеся дизъюнктные слагаемые не пишем).
Например:
г) переход от КНФ к СКНФ
Этот переход осуществляется способом, аналогичным предыдущему: если в простой дизъюнкции не хватает какой-то переменной (например, z , то добавляем в нее выражение (это не меняет самой дизъюнкции), после чего раскрываем скобки с использованием распределительного закона):
Таким образом, из КНФ получена СКНФ.
Заметим, что минимальную или сокращенную КНФ обычно получают из соответствующей ДНФ.
Введем понятие элементарной дизъюнкции.
Элементарной дизъюнкцией называется выражение вида
Конъюнктивной нормальной формой (КНФ) логической функции называется конъюнкция любого конечного множества попарно различных элементарных дизъюнкций. Например, логические функции
представляют собой конъюнкции элементарных дизъюнкций. Следовательно, они записаны в конъюнктивной нормальной форме.
Произвольная логическая функция, заданная аналитическим выражением, может быть приведена к КНФ путем выполнения следующих операций:
Использования правила инверсии, если операция отрицания применена к логическому выражению;
Использования аксиомы дистрибутивности относительно умножения:
Использования операции поглощения:
Исключения в дизъюнкциях повторяющихся переменных или их отрицаний;
Удаления всех одинаковых элементарных дизъюнкций, кроме одной;
Удаления всех дизъюнкций, в которые одновременно входят переменная и ее отрицание.
Справедливость перечисленных операций вытекает из основных аксиом и тождественных соотношений алгебры логики.
Конъюнктивная нормальная форма называется совершенной, если каждая входящая в нее элементарная дизъюнкция содержит в прямом или инверсном виде все переменные, от которых зависит функция.
Преобразование КНФ к совершенной КНФ осуществляется путем выполнения следующих операций:
Прибавления к каждой элементарной дизъюнкции конъюнкций переменных и их отрицаний, если они не входят в данную элементарную дизъюнкцию;
Использования аксиомы дистрибутивности;
Удаление всех одинаковых элементарных дизъюнкций, кроме одной.
В совершенной КНФ может быть представлена любая логическая функция, кроме
тождественно равной единице (). Отличительным свойством совершенной КНФ является то, что представление в ней логической функции единственно.
Элементарные дизъюнкции, входящие в совершенную КНФ функции, носят название конституент нуля. Каждая конституента нуля, входящая в совершенную КНФ, обращается в нуль на единственном наборе значений переменных, который является нулевым набором функции.
Следовательно, число нулевых наборов логической функции совпадает с числом конституент нуля, входящих в ее совершенную КНФ.
Логическая функция константа нуля в совершенной КНФ представляется конъюнкцией 2nконституент нуля. Сформулируем правило составления СКНФ логической функции по таблице соответствия.
Для каждой строки таблицы соответствия, в которой функция равна нулю, составляется элементарная дизъюнкция всех переменных. При этом в дизъюнкцию входит сама переменная, если ее значение равно нулю, или отрицание, если ее значение равно единице. Полученные элементарные дизъюнкции объединяются знаком конъюнкции.
Пример 3.4. Для логической функции z(x), заданной таблицей соответствия 2.2, определим совершенную конъюнктивную форму.
Для первой строки таблицы, которая соответствует нулевому набору функции 000, находим конституенту нуля . Выполнив аналогичные операции для второй, третьей и пятой строк, определим искомую совершенную КНФ функции:
Необходимо отметить, что для функций, число единичных наборов которых превышает число нулевых наборов, более компактной является их запись в виде СКНФ и наоборот.
Нормальные формы логических функций Представление булевой функции в форме дизъюнкции конъюнктивных термов конституент единицы Ki 2.7 называется дизъюнктивной нормальной формой ДНФ этой функции. содержат в точности по одной все логические переменные взятые с отрицаниями или без них то такая форма представления функции называется совершенной дизъюнктивной нормальной формой СДНФ этой функции. Как видно при составлении СДНФ функции нужно составить дизъюнкцию всех минтермов при которых функция принимает значение 1.
Поделитесь работой в социальных сетях
Если эта работа Вам не подошла внизу страницы есть список похожих работ. Так же Вы можете воспользоваться кнопкой поиск
Лекция 1.хх
Нормальные формы логических функций
Представление булевой функции в форме дизъюнкции конъюнктивных термов (конституент единицы) K i
, (2.7)
называется дизъюнктивной нормальной формой (ДНФ ) этой функции.
Если все конъюнктивные термы в ДНФ являются
минтермами
, т.
е. содержат в точности по одной все логические переменные, взятые с отрицаниями или без них, то такая форма представления функции называется
совершенной дизъюнктивной нормальной формой
(СДНФ
) этой функции. СДНФ называется
совершенной
, потому что каждый терм в дизъюнкции включает все переменные;
дизъюнктивной
, потому что главная операция в формуле дизъюнкция. Понятие “
нормальной формы
” означает однозначный способ записи формулы, реализующей заданную функцию.
С учётом сказанного выше из теоремы 2.1 вытекает следующая теорема.
Теорема 2. Любая булева функция (не равная тождественно 0 ) может быть представлена в СДНФ , .
Пример 3. Пусть имеем таблично заданную функцию f (x 1 , x 2 , x 3 ) (табл. 10).
Таблица 10
f (x 1 , x 2 , x 3 ) | |||
На основании формулы (2.
6) получаем:
Как видно, при составлении СДНФ функции нужно составить дизъюнкцию всех минтермов, при которых функция принимает значение 1.
Представление булевой функции в форме конъюнкции дизъюнктивных термов (конституент нуля) D i
, (2.8)
называется конъюнктивной нормальной формой (КНФ ) этой функции.
Если все дизъюнктивные термы КНФ являются макстермами , т. е. содержат в точности по одной все логические переменные функции, взятые с отрицаниями или без них, то такая КНФ называется совершенной конъюнктивной нормальной формой (СКНФ ) этой функции.
Теорема 3. Любая булева функция (не равная тождественно 1 ) может быть представлена в СКНФ , причём такое представление единственно .
Доказательство теоремы может быть проведено аналогично доказательству теоремы 2.1 на основании следующей леммы Шеннона о конъюнктивном разложении.
Лемма Шеннона . Любая булева функция f (x 1 , x 2 , …, x m ) от m переменных может быть представлена так :
.
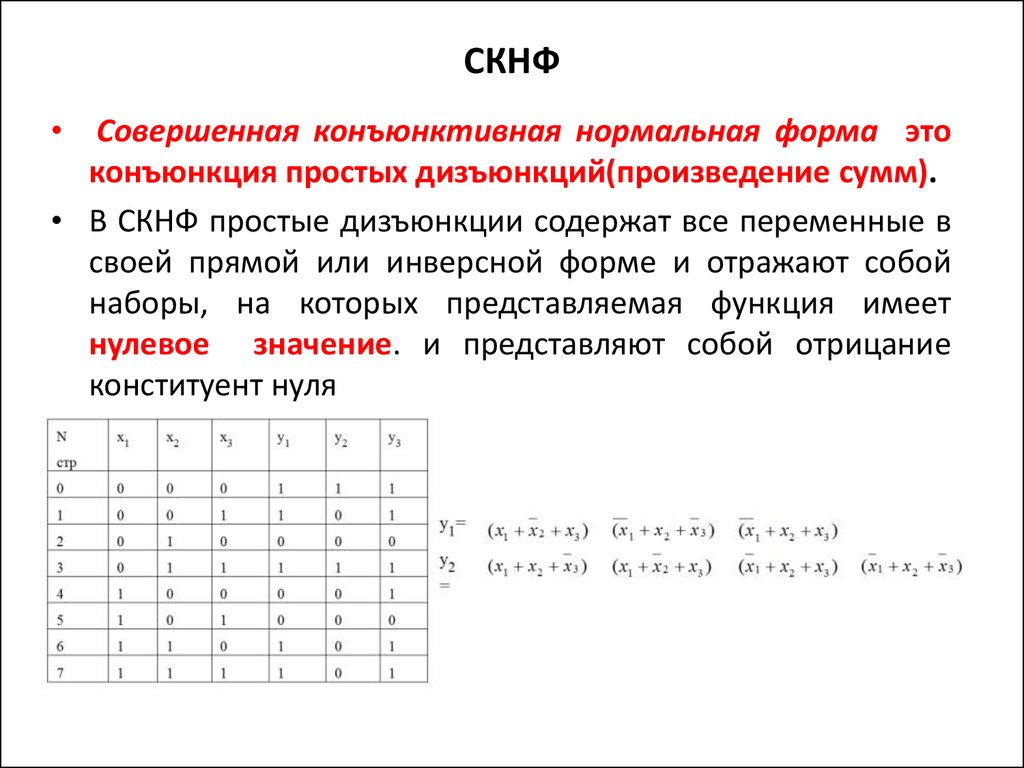(2.9)
Нужно отметить, что обе формы представления логической функции (ДНФ и КНФ) теоретически являются равными по своим возможностям: любую логическую формулу можно представить как в ДНФ (кроме тождественного нуля), так и в КНФ (кроме тождественной единицы). В зависимости от ситуации представление функции в той или иной форме может быть короче.
На практике же чаще всего используется ДНФ , т. к. эта форма является для человека более привычной: с детства ему привычнее складывать произведения, чем умножать суммы (в последнем случае у него интуитивно появляется желание раскрыть скобки и перейти тем самым к ДНФ).
Пример 4. Для функции f (x 1 , x 2 , x 3 ), заданной табл. 10, написать её СКНФ.
В отличие от СДНФ, при составлении СКНФ в таблице истинности логической функции нужно смотреть комбинации переменных, при которых функция принимает значение 0, и составить конъюнкцию соответствующих макстермов, но переменные нужно брать с обратной инверсией :
Нужно отметить, что непосредственно перейти от СДНФ функции к её СКНФ или наоборот невозможно. При попытке таких преобразований получаются функции, обратные по отношению к желаемым. Выражения для СДНФ и СКНФ функции непосредственно можно получить только из её таблицы истинности.
Пример 5. Для функции f (x 1 , x 2 , x 3 ), заданной табл. 10, попробовать перейти от СДНФ к СКНФ.
Используя результат примера 2.3 получим:
Как видно, под общей инверсией получилась СКНФ логической функции, которая является обратной по отношению к функции, полученной в примере 2.4:
т. к. содержит все макстермы, которых нет в выражении для СКНФ рассматриваемой функции.
1. Используя свойства операций (см. табл. 9) тождественность (), сумма по модулю 2 (), импликация (), переходим к операциям И, ИЛИ, НЕ (в базис Буля).
2. Используя свойства отрицания и законы де Моргана (см. табл. 9) добиваемся, чтобы операции отрицания относились только к отдельным переменным, а не к целым выражениям.
3. Используя свойства логических операций И и ИЛИ (см. табл. 9), получаем нормальную форму (ДНФ или КНФ).
4. При необходимости переходим к совершенным формам (СДНФ или СКНФ). Например, для получения СКНФ часто нужно использовать свойство: .
Пример 6. Преобразовать в СКНФ логическую функцию
Выполняя по порядку шаги приведённого выше алгоритма, получим:
Используя свойство поглощения, получим:
Таким образом, мы получили КНФ функции f (x 1 , x 2 , x 3 ). Чтобы получить её СКНФ, нужно каждую дизъюнкцию, в которой не хватает какой-либо переменной, повторить дважды с этой переменной и с её отрицанием:
2.2.6. Минимизация логических функций
Поскольку одну и ту же логическую функцию можно представить ра
з
личными формулами, то нахождение наиболее простой фо
р
мулы, задающей булеву функцию, упрощает логическую схему, реализующую булеву фун
к
цию.
Минимальной формой л
о
гической функции
в некотором базисе можно считать такую, которая содержит минимальное число суперпозиций фун
к
ций базиса, допуская и скобки. Однако трудно построить эффективный а
л
горитм такой минимизации с получением минимальной скобочной фо
р
мы.
Рассмотрим более простую задачу минимизации при синтезе комбинационных схем, при которой ищется не минимальная скобочная форма функции, а её минимальная ДНФ. Для этой задачи существуют простые эффективные алгоритмы.
Метод Квайна
Минимизируемая функция представляется в СДНФ, и к ней применяются все возможные операции неполного склеивания
, (2.10)
а затем поглощения
, (2.11)
и эта пара этапов применяется многократно. Таким образом, удаётся снизить ранг термов. Это процедура повторяется до тех пор, пока не останется ни одного терма, допускающего склеивание с каким-либо другим термом.
Заметим, что левую часть уравнения (2.10) сразу можно было минимизировать более простым и очевидным способом:
Этот способ плох тем, что при такой непосредственной минимизации конъюнктивные термы или исчезают, хотя возможны ещё случаи их использования для склеивания и поглощения с оставшимися термами.
Нужно отметить, что метод Квайна является достаточно трудоёмким, поэтому вероятность допущения ошибок во время преобразований достаточно велик. Но его преимуществом является то, что теоретически его можно использовать для любого числа аргументов и при увеличении количества переменных преобразования усложняются не так сильно.
Метод карт Карно
Метод карт (таблиц) Карно является более наглядным, менее трудоёмким и надёжным способом минимизации логических функций, но его использование практически ограничено функциями 3-4 переменных, максимум 5-6 переменных.
Карта Карно это двумерная табличная форма представления таблицы истинности булевой функции, позволяющая в графической наглядной форме легко отыскать минимальные ДНФ логических функций. Каждой клетке таблицы сопоставляется минтерм СДНФ минимизируемой функции, причём так, что любым осям симметрии таблицы соответствуют зоны, взаимно инверсные по какой-либо переменной. Такое расположение клеток в таблице позволяет легко определить склеивающиеся термы СДНФ (отличающиеся знаком инверсии только одной переменной): они располагаются в таблице симметрично.
Таблицы истинности и карты Карно для функций И и ИЛИ двух пер
е
менных представлены на рис. 8. В каждую клетку карты записывается зн
а
чение функции на соответствующем этой клетке наборе значений аргуме
н
тов.
А ) И б ) ИЛИ
Рис. 8. Пример карт Карно для функций двух переменных
В карте Карно для функции И только одна 1, поэтому её ни с чем невозможно склеить. В выражении для минимальной функции будет только терм, соответствующий этой 1:
f = x y .
В карте Карно для функции ИЛИ уже три 1 и можно составить две склеивающиеся пары, при этом 1, соответствующая терму xy , используется дважды. В выражении для минимальной функции нужно записать термы для склеиваемых пар, оставляя в них все переменные, которые для этой пары не меняются, и убирая переменные, которые меняют своё значение. Для горизонтальной склейки получим x , а для вертикальной y , в итоге получим выражение
f = x + y .
На рис. 9 приведены таблицы истинности двух функций трёх переменных (а
) и их карты Карно (б
и
в
). Функция
f
2
отличается от первой тем, что на трёх наборах переменных она не определена (в таблице это обозначено прочерком).
При определении минимальной ДНФ функции используются следующие правила. Все клетки, содержащие 1, объединяются в замкнутые прямоугольные области, которые называются k -кубами , где k = log 2 K , K количество 1 в прямоугольной области. При этом каждая область должна представлять собой прямоугольник с числом клеток 2 k , где k = 0, 1, 2, 3, … . Для k = 1 прямоугольник называется один-куб и содержит 2 1 = 2 единицы; для k = 2 прямоугольник содержит 2 2 = 4 единицы и называется два-куб ; при k = 3 область из 2 3 = 8 единиц называется три-куб ; и т. д. Единицы, которые невозможно объединить в прямоугольники, можно назвать ноль-кубами , которые содержат только одну единицу (2 0 = 1). Как видно, при чётном k области могут иметь форму квадрата (но не обязательно), а при нечётном k только прямоугольников.
Рис. 9. Пример карт Карно для функций трёх переменных
Эти области могут пересекаться, т. е. одни и те же клетки могут входить в разные области. Затем записывается минимальная ДНФ функции как дизъюнкция всех конъюнктивных термов, соответствующих
k
—
кубам.
Каждая из указанных областей на карте Карно представляется в минимальной ДНФ конъюнкцией, число аргументов в которой на k меньше общего числа аргументов функции m , т. е. это число равно m k . Каждая конъюнкция минимальной ДНФ составляется лишь из тех аргументов, которые для соответствующей области карты имеют значения либо без инверсий, либо только с инверсией, т. е. не меняют своего значения.
Таким образом, при охвате клеток карты замкнутыми областями следует стремиться к тому, чтобы число областей было минимальным, а каждая область содержала возможно большее число клеток, так как при этом будет минимальным число членов в минимальной ДНФ и число аргументов в соответствующей конъюнкции будет минимальным.
Для функции по карте Карно на рис. 9, б находим
поскольку для верхней замкнутой области переменные x 1 и x 2 имеют значения без инверсий, для нижней x 1 имеет значение с инверсией, а x 3 без инверсии.
Неопредёленные значения в карте на рис. 9,
в
можно доопределить, заменив нулём или единицей. Для данной функции видно, что оба неопределённых значения выгоднее заменить 1. При этом образуются две области, являющиеся различными видами 2-кубов. Тогда выражение для минимальной ДНФ функции будет следующим:
При построении замкнутых областей допускается сворачивание карты Карно в цилиндр как по горизонтальной, так и по ве р тикальной осям с объединением противоположных граней ка р ты, т. е. единицы, расположенные по краям карты Карно симметри ч но, также могут быть объединены.
Карты Карно можно рисовать разными способами (рис. 10).
x 2 x 3 | ||||||||||
а б
Рис. 10.
Разные способы изображения карт Карно
для функции 3 переменных
Но самыми удобными вариантами карт Карно для функций 2-4 переменных являются показанные на рис. 11 таблицы, т. к. в них для каждой ячейки показ а ны все переменные в прямом или инверсном виде.
а б
Рис. 11.
Наиболее удобное изображение карт Карно
для функций 3 (а
) и 4 (б
) переменных
Для функций 5 и 6 переменных больше подходит способ, показанный на рис. 10, в .
Рис. 12. Изображение карты Карно для функции 5 переменных
Рис. 13. Изображение карты Карно для функции 6 переменных
Другие похожие работы, которые могут вас заинтересовать.вшм> | |||
| 9020. | ПРИНЦИП ДВОЙСТВЕННОСТИ. РАЗЛОЖЕНИЕ БУЛЕВЫХ ФУНКЦИЙ ПО ПЕРЕМЕННЫМ. СОВЕРШЕННЫЕ ДИЗЪЮНКТИВНАЯ И КОНЪЮНКТИВНАЯ НОРМАЛЬНЫЕ ФОРМЫ | 96.34 KB | |
| Данная теорема носит конструктивный характер, так как она позволяет для каждой функции построить реализующую ее формулу в виде совершенной д. н. ф. Для этого в таблице истинности для каждой для функции отмечаем все строки, в которых | |||
| 6490. | Описание и минимизация логических функций | 187.21 KB | |
| В словесной форме выражается взаимосвязь между аргументами функции и ее значениями. Пример: функция трех аргументов принимает значение когда любые два или более аргументов функции равны. Состоит в построении таблицы истинности содержащей значения функции для всех наборов значений аргументов. В данном примере по таблице истинности получаем такую запись в виде ДНФ… | |||
| 6707. | Проектирование реляционных баз данных. Проблемы проектирования в классическом подходе. Принципы нормализации, нормальные формы | 70.48 KB | |
| Что такое проект реляционной базы данных Это набор взаимосвязанных отношений в которых определены все атрибуты заданы первичные ключи отношений и заданы еще некоторые дополнительные свойства отношений которые относятся к принципам поддержки целостности. Поэтому проект базы данных должен быть очень точен и выверен. Фактически проект базы данных это фундамент будущего программного комплекса который будет использоваться достаточно долго и многими пользователями. | |||
| 4849. | Формы и методы осуществления функций государства | 197.3 KB | |
| Термин «функция» имеет в отечественной и зарубежной научной литературе далеко не одинаковое значение. В философском и общесоциологическом плане, он рассматривается, как «внешнее проявление свойств какого-либо объекта в данной системе отношений»; как совокупность обычных или же специфических действий отдельных лиц или органов | |||
| 17873. | Формирование логических УУД у учащихся 3 класса | 846.71 KB | |
| Психолого-педагогические аспекты проблемы формирования логических универсальных действий у младших школьников Методики оценки сформированности логических УУД. Разработка концепции развития универсальных учебных действий в системе общего образования отвечает новым социальным запросам. Важнейшей задачей современной системы образования является формирование универсальных учебных действий УУД. Сформированность универсальных учебных действий является залогом профилактики школьных трудностей. | |||
| 2638. | Техническая реализация логических связей в системах автоблокировки | 1.04 MB | |
| Техническая реализация логических связей в системах автоблокировки Техническая реализация алгоритмов управления трехзначной и четырехзначной АБ может быть достигнута при помощи релейных контактных и бесконтактных дискретных и интегральных логических элементов… | |||
| 10203. | ПРИМЕНЕНИЕ КОНЦЕПЦИИ РИСК ОРИЕНТИРОВАННОГО ПОДХОДА ДЛЯ ПОСТРОЕНИЯ СТРУКТУРНО-ЛОГИЧЕСКИХ МОДЕЛЕЙ ВОЗНИКНОВЕНИЯ И РАЗВИТИЯ ЧС | 70.8 KB | |
| Общий анализ риска Производственная среда насыщается мощными технологическими системами и технологиями которые делают труд человека производительным и менее тяжелым физически однако более опасным. Для риска характерны неожиданность и внезапность наступления опасной ситуации. Ежедневно мы сталкиваемся с многочисленными рисками но большая часть из них остается потенциальными т. Теория риска предусматривает количественную оценку негативного воздействия на человека а также нанесения ущерба его здоровью и жизни. | |||
| 11576. | Понятие, виды и формы сделок. Последствия несоблюдения требуемой формы сделок | 49.82 KB | |
| Признание сделки недействительной виды недействительной сделки. Прикладная ценность курсовой работы заключается в упрощении понятия сделки то есть публичного его представления в более доступной форме. | |||
| 6213. | Приближение функций | 3.08 MB | |
| Первая состоит в замене некоторой функции заданный аналитически или таблично другой функцией близкой к исходной но более простой и удобной для вычислений. Например замена функции многочленом позволяет получать простые формулы численного интегрирования и дифференцирования; замена таблицы приближающей функцией позволяет получать значения в ее промежуточных точках. Возникает также и вторая задача восстановление функции на некотором отрезке по заданным на этом отрезке значениям функции в дискретном множестве точек. Ответ на такой вопрос… | |||
| 14058. | Эволюция функций государства | 29.99 KB | |
| Российское государство как правовое явление прежде всего должно обеспечивать реализацию назначения государства а также его основных конституционных характеристик как демократического федеративного правового социального светского государства с республиканской формой правления. Главное назначение государства определяется ст. | |||
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного. Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает… Интересное: Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все… Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 3 из 4Следующая ⇒ Нормальные формы формул алгебры высказываний бывают двух типов: дизъюктивные и конъюктивные, в каждом из этих типов выделен класс совершенных форм. Алгоритм построения ДНФ: 1. Перейти к булевым операциям. 2. Перейти к формуле с тесными отрицаниями, т.е. к формуле, в которой отрицания находятся не выше, чем над переменными. 3. Раскрыть скобки. 4. Повторяющейся слагаемые взять по одному разу. 5. Применить законы поглощения и полупоглощения. Пример.Найти ДНФ формулы ► ◄ Конъюнктивная нормальная форма (КНФ) – двойственное для ДНФ понятие, поэтому ее легко построить по схеме: . Пример.Найти КНФ формулы ► ~ ~ .◄ Совершенную дизъюнктивную нормальную форму СДНФ можно строить, используя следующий алгоритм: 1. = 1. алгоритма ДНФ 2. = 2. алгоритма ДНФ 3. = 3. 4. = 4. алгоритма ДНФ 5. Опустить тождественно ложные слагаемые, т. е. слагаемые вида . 6. Пополнить оставшиеся слагаемые недостающими переменными 7. Повторить пункт 4. Пример.Найти СДНФ формулы. ► ~ .◄ Для построения СКНФ можно пользоваться следующей схемой: Пример.Найти СДНФ формулы. ► ~ .◄ Известно (теоремы 2.11, 2.12), что СДНФ и СКНФ определены формулой однозначно и, значит, их можно строить по таблице истинности формулы [1]. ►Схема построения СДНФ и СКНФ по таблице истинности приведена ниже, для формулы ~ :
2.2. Задание. 2.2.1 Ниже приведены логические выражения. Максимально упростите выражения своего варианта, воспользовавшись законами логики Буля. Затем с помощью таблиц истинности сравните ваше упрощенное выражение с исходным.
2.2.2. Выяснить вопрос о равносильности f1 и f 2 путем сведения их к СДНФ (табл. 1). 2.2.3. Найти двойственную функцию для f3 по обобщенному и булевому принципу (табл.1). Сравнить полученные результаты.
2. 2.3.1. Дайте определение высказывания. 2.3.2. Перечислите основные операции над высказыванием. 2.3.3. Что такое таблица истинности? 2.3.4. Составить таблицы истинности для следующих формул: ~ ~ ; ~ ; ~ ~ ~ ; ~ ~ ~ ~ . 2.3.5. Учитывая соглашения о порядке выполнения операций, опустить «лишние» скобки и знак « » в формулах: ; ; ; ; ~ . 2.3.6. Применяя равносильные преобразования, доказать тождественную истинность формул: ; ; ; . 2.3.7.Найти двойственные формулы: ) . 2.3.8. Привести к совершенной ДНФ (СДНФ) форме следующие формулы: ~ 2.3.9. Привести к совершенной КНФ (СКНФ) форме следующие формулы: ~ ~
Лабораторная работа № 3 Тема: «Минимизация булевых функций. Цель: Приобретение практических навыков работы с методами минимизации булевых функций. 3.1. Теоретические сведения [1]. Минимальные формы Как было показано в [1], любая булева функция представима в совершенной нормальной форме (дизъюнктивной или конъюнктивной). Более того, такое представление является первым шагом перехода от табличного задания функции к ее аналитическому выражению. В дальнейшем будем исходить из дизъюнктивной формы, а соответствующие результаты для конъюнктивной формы получается на основе принципа двойственности [1]. Каноническая задача синтеза логических схем в булевом базисе сводится к минимизации булевых функций, т.е. к представлению их в дизъюнктивной нормальной форме, которая содержит наименьшее число букв (переменных и их отрицаний). Такие формы называют минимальными. При каноническом синтезе предполагается, что на входы схемы подаются как сигналы , так и их инверсий . Формула, представленная в дизъюнктивной нормальной форме, упрощается многократными применением операции склеивания и операции поглощения и (дуальные тождества для конъюнктивной нормальной формы имеют вид: и ). Среди тупиковых форм находится и минимальная дизъюнктивная форма, причем она может быть неединственной. Чтобы убедиться в том, что данная тупиковая форма является минимальной, необходимо найти все тупиковые формы и сравнить их по числу входящих в них букв. Пусть, например, функция задана в совершенной нормальной дизъюнктивной форме: . Группируя члены и применяя операцию склеивания, имеем . При другом способе группировки получим: . Обе тупиковые формы не являются минимальными. Чтобы получить минимальную форму, нужно догадаться повторить в исходной формуле один член (это всегда можно сделать, так как ). В первом случае таким членом может быть . Тогда . Добавив член , получим: . Перебрав все возможные варианты, можно убедиться, что две последние формы являются минимальными. Работа с формулами на таком уровне подобна блужданию в потемках. Процесс поиска минимальных форм становится более наглядным и целеустремленным, если использовать некоторые графические и аналитические представления и специально разработанную для этой цели символику. Многомерный куб Каждой вершине -мерного куба можно поставить в соответствие конституенту единицы. Следовательно, подмножество отмеченных вершин является отображением на -мерном кубе булевой функции от переменных в совершенной дизъюнктивной нормальной форме. На рис. 3.1 показано такое отображение для функции из п.3.7.
Рис.3.1 Отображение на трехмерном кубе функции, представленной в СДНФ Для отображения функции от переменных, представленной в любой дизъюнктивной нормальной форме, необходимо установить соответствие между ее минитермами и элементами -мерного куба. Минитерм ( -1)-го ранга можно рассматривать как результат склеивания двух минитермов -го ранга (конституент единицы), т. Элементы -мерного куба, характеризующиеся измерениями, называют -кубами. Так, вершины являются 0-кубами, ребра – 1-кубами, грани – 2-кубами и т.д. Обобщая приведенные рассуждения, можно считать, что минитерм ( )-го ранга в дизъюнктивной нормальной форме для функции переменных отображается -кубом, причем каждый -куб покрывает все те -кубы низшей размерности, которые связаны с его вершинами. В качестве примера на рис. 3.2 дано отображение функции трех переменных. Здесь минитермы и соответствуют 1-кубам ( ), а минитерм отображается 2-кубом ( ).
Рис.3.2 Покрытие функции Итак, любая дизъюнктивная нормальная форма отображается на -мерном кубе совокупностью -кубов, которые покрывают все вершины, соответствующие конституентам единицы (0-кубы). Справедливо и обратное утверждение: если некоторая совокупность -кубов покрывает множество всех вершин, соответствующих единичным значениям функции, то дизъюнкция соответствующих этим -кубам минитермов является выражение данной функции в дизъюнктивной нормальной форме. Говорят, что такая совокупность -кубов (или соответствующих им минитермов) образует покрытие функции. Стремление к минимальной форме интуитивно понимается как поиск такого покрытия, число -кубов которого было бы поменьше, а их размерность — побольше. Покрытие, соответствующее минимальной форме, называют минимальным покрытием. Например, для функции покрытие на рис. 3.3 соответствует минимальным формам и .
Рис. 3.3 Покрытия функции . слева – ; справа – Отображение функции на -мерном кубе наглядно и просто при .
Рис. 3.4 Отображение функции на четырехмерном кубе Карты Карно В другом методе графического отображения булевых функций используются карты Карно, которые представляют собой специально организованные таблицы соответствия. Столбцы и строки таблицы соответствуют всевозможным наборам значений не более двух переменных, причем эти наборы расположены в таком порядке, что каждый последующий отличается от предыдущего значением только одной из переменных. Благодаря этому и соседние клетки таблицы по горизонтали и вертикали отличаются значением только одной переменной. Клетки, расположенные по краям таблицы, также считаются соседними и обладают этим свойством. На рис. 3.5 показаны карты Карно для двух, трех, четырех переменных.
Рис. 3.5 Карты Карно для двух, трех и четырех переменных Как и в обычных таблицах истинности, клетки наборов, на которых функция принимает значение 1, заполняются единицами (нули обычно не вписываются, им соответствуют пустые клетки). Например, на рис. 3.6, а показана карта Карно для функции, отображение которой на четырехмерном кубе дано на рис. 3.4. Для упрощения строки и столбцы, соответствующие значениям 1 для некоторой переменной, выделяются фигурной скобкой с обозначением этой переменной.
а б Рис. 3.6 Отображение на карте Карно функции четырех переменных (а) и ее минимального покрытия (б) Между отображениями функции на n-мерном кубе и на карте Карно имеет место взаимно-однозначное соответствие. На карте Карно s-кубу соответствует совокупность 2 соседних клеток, размещенных в строке, столбце, квадрате или прямоугольнике (с учетом соседства противоположных краев карты). Считывание минитермов с карты Карно осуществляется по простому правилу. Клетки, образующие s-куб, дают минитер (n–s)-го ранга, в который входят те (n–s) переменные, которые сохраняют одинаковые значения на этом s-кубе, причем значении 1 соответствуют сами переменные, а значениям 0 – их отрицания. Переменные, которые не сохраняют свои значения на s-кубе, в минитерме отсутствуют. Различные способы считывания приводят к различным представлениям функции в дизъюнктивной нормальной форме (крайняя правая является минимальной) (рис. 3.7).
Рис. 3.7 Способы считывания с карты Карно дизъюнктивной нормальной формы булевой функции (слева направо: ; ; Пример.
Пример.Получить минимальную форму для функции, заданной на карте.
Использование карт Карно требует более простых построений по сравнению с отображением на n-мерном кубе, особенно в случае четырех переменных. Для отображения функций пяти переменных используется две карты Карно на четыре переменные, а для функции шести переменных – четыре таких карты. При дальнейшем увеличении числа переменных карты Карно становятся практически непригодными. Известные в литературе карты Вейча отличаются только другим порядком следования наборов значений переменных и обладают теми же свойствами, что и карты Карно. Комплекс кубов Несостоятельность графических методов при большом числе переменных компенсируется различными аналитическими методами представления булевых функций. Одним из таких представлений является комплекс кубов, использующий терминологию многомерного логического пространства в сочетании со специально разработанной символикой. Комплекс кубов К(у) функции определяется как объединение множеств Кs(у) всех ее s-кубов (s=0.1,…,n), т. е. , причем некоторые из Кs(у) могут быть пустыми. Для записи s-кубов и минитермов функции от n переменных используются слова длины n, буквы которых соответствуют всем n переменным. Входящие в минитерм переменные называются связанными и представляются значениями, при которых минитерм равен единице (1 для и 0 для ). Не входящие в минитерм переменные являются свободными и обозначаются через . Например, 2-куб функции пяти переменных, соответствующий минитерму запишем как ( ). Множество всех s-кубов записывается как совокупность слов, соответствующих каждому s-кубу. Для удобства будем располагать слова s-кубов в столбцы, а их совокупность заключать в фигурные скобки. Например, комплекс кубов, соответствующий представлению функции на трехмерном кубе (рис. 3,10а), выражается как , где
; ; . Для сравнения на рис. 3.8 изображен комплекс кубов в принятых обозначениях.
Рис. 3.8 Комплекс кубов функции трех переменных (а) и его символическое представление (б) Комплекс кубов образует максимальное покрытие функции. , которое соответствует функции . В данном случае это покрытие является и минимальным. Для двух булевых функций операция дизъюнкции соответствует объединению их комплексов кубов , а операция конъюнкции — пересечению комплексов кубов . Отрицанию функции соответствует дополнение комплекса кубов, т. е. , причем определяется всеми вершинами, на которых функция принимает значение 0. Таким образом, имеет место взаимно-однозначное соответствие (изоморфизм) между алгеброй булевых функций и булевых множеств, представляющих комплексы кубов. Представление функции в виде комплексов кубов менее наглядно, однако его важнейшие достоинства состоят в том, что снимаются ограничения по числу переменных и облегчается кодирование информации при использовании вычислительных машин. Минимизация булевых функций Постановка задачи. Минимизация схемы в булевом базисе сводится к поиску минимальной дизъюнктивной формы, которой соответствует минимальное покрытие. Общее число букв, входящих в нормальную форму, выражается ценой покрытия , где — число — кубов, образующих покрытие данной функции от п переменных. Минимальное покрытие характеризуется наименьшим значением его цены. Обычно задача минимизации решается в два шага. Сначала ищут сокращенное покрытие, которое включает все -кубы максимальной размерности, но не содержит ни одного куба, покрывающегося каким-либо кубом этого покрытия. Соответствующею дизъюнктивную нормальную форму называют сокращенной, а ее минитермы — простыми импликантами. Для данной функции сокращенное покрытие является единственным, но оно может быть избыточным вследствие того, что некоторые из кубов покрываются совокупностями других кубов. На втором шаге осуществляется переход от сокращенной к тупиковым дизъюнктивным нормальным формам, из которых выбираются минимальные формы. Куб сокращенного покрытия, который покрывает вершины данной функции, не покрываемые никакими другими кубами, не может оказаться избыточным и всегда войдет в минимальное покрытие. Такой куб, как и соответствующая ему импликанта, называют экстремалью (существенной импликантой), а покрываемые им вершины — отмененными вершинами. Множество экстремалей образует ядро покрытия, ясно, что при переходе от сокращенного покрытия к минимальному прежде всего следует выделить все экстремали. Если множество экстремалей не образует покрытия, то оно дополняется до покрытия кубами из сокращенного покрытия. Приведенные определения иллюстрируются на рис. 3.9, где сокращенное покрытие (см.
Рис. 3.9 Сокращен ⇐ Предыдущая1234Следующая ⇒ Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… |
1
Первый слайд презентации: БУЛЕВА АЛГЕБРА ДИЗЪЮНКТИВНЫЕ И КОНЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ (ДНФ и КНФ).
СОВЕРШЕННЫЕ ДНФ и КНФ
1 БУЛЕВА АЛГЕБРА ДИЗЪЮНКТИВНЫЕ И КОНЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ (ДНФ и КНФ). СОВЕРШЕННЫЕ ДНФ и КНФ ЛЕКЦИЯ 8 В.И.ХАХАНОВ Факультет компьютерной инженерии и управления, кафедра АПВТ, ХНУРЭ ДИСКРЕТНАЯ МАТЕМАТИКА
Изображение слайда
2
Слайд 2: Цель лекции – изучить способы представления булевых функций в виде дизъюнктивных и конъюнктивных нормальных форм, а также их совершенных форм, определить связь и различие между ними, выявить их назначение
2 Цель лекции – изучить способы представления булевых функций в виде дизъюнктивных и конъюнктивных нормальных форм, а также их совершенных форм, определить связь и различие между ними, выявить их назначение Содержание: ДНФ и КНФ СДНФ и СКНФ Теорема Шеннона Тема: ДНФ и КНФ. СДНФ и СКНФ.
Изображение слайда
3
Слайд 3
3
Горбатов В. А. Основы дискретной математики. М.: Высш. шк., 1986. 32-61с.
Савельев А.Я. Прикладная теория цифровых автоматов. М.: Высш. шк., 1987. 272 с.
Беннеттс Р.Д. Проектирование тестопригодных логических схем: Пер. с англ. М.: Радио и связь. 1990. 176 с.
Бондаренко М.Ф., Кривуля Г.Ф., Рябцев В.Г., Фрадков С.А., Хаханов В.И. Проектирование и диагностика компьютерных систем и сетей. К.: НМЦ ВО. 2000. 306 с.
Богомолов А.М., Сперанский Д.В. Аналитические методы в задачах контроля и анализа дискретных устройств. Саратов: Изд-во Саратовкого ун-та, 1986. 240с.
Хаханов В.И. Техническая диагностика элементов и узлов персональных компьюторов. К.: ИСМО, 1997. 308 с.
Хаханов В. І., Хаханова І.В., Кулак Е.М., Чумаченко С.В. Методичні вказівки до практичних занять з курсу “Дискретна математика”. Харків, ХНУРЕ. 2001. 87с.
Новиков Ф.А. Дискретная математика для программистов. С.-П., 2001.
С. 263-268.
Литература
Изображение слайда
4
Слайд 4
4 Базовые понятия: логические операции логические переменные логические функции Термины Ключевые слова: первичный терм конъюнктивный терм дизъюнктивный терм дизъюнктивная нормальная форма (ДНФ) конъюнктивная нормальная форма (КНФ) совершенная ДНФ совершенная КНФ
Изображение слайда
5
Слайд 5
5 ДНФ и КНФ Термин Обозначение Пример Первичный терм x 1, x 1 Двоичный набор (0,1,1,0,1) Элементарная конъюнкция (ЭК) x 1 x 2 x 3 x 4 ДНФ x 1 x 2 x 3 x 1 x 2 Элементарная дизъюнкция (ЭД) x 1 x 2 x 3 x 4 КНФ (x 1 x 2 x 3 ) ( x 1 x 2 )
Изображение слайда
6
Слайд 6
6
Def: Совершенной ДНФ (СДНФ) называется ДНФ, в которой нет равных элементарных конъюнкций и все элементарные конъюнкции содержат одни и те же переменные, от котор ых зависит функция, причем каждую – только один раз (включая вхождения под знаком отрицания). Def: Совершенная КНФ (СКНФ) определяется как такая КНФ, в которой нет одинаковых сомножителей; все сомножители содержат одни и те же переменные, от которых зависит функция, причем каждую переменную – только один раз.
Совершенные ДНФ и КНФ (СДНФ и СКНФ). 1
Изображение слайда
7
Слайд 7
7 Пример получения СДНФ и СКНФ x 1 x 2 x 3 f(x 1, x 2, x 3 ) x 1 x 2 x 3 f(x 1, x 2, x 3 ) 0 0 0 1 1 0 0 0 0 0 1 0 1 0 1 1 0 1 0 1 1 1 0 0 0 1 1 0 1 1 1 1
Изображение слайда
8
Слайд 8: Теорема Шеннона
8 Теорема Шеннона Любая булева функция f 0 представима в виде разложения Шеннона: Следствие Предельное разложение Шеннона ( k=n ) булевой функции f 0 имеет вид
Изображение слайда
9
Слайд 9: Time-Out
9 Time-Out
Изображение слайда
10
Слайд 10: Эквивалентность форм ДНФ и КНФ
10 Эквивалентность форм ДНФ и КНФ Привести функцию к ДНФ и КНФ: Получение ДНФ: Получение КНФ
Изображение слайда
11
Слайд 11: Сложность формы булевой функции
11
Сложность формы булевой функции
Оценка сложности функции
по Квайну есть
Q=L(f)+k,
где L(f) – число букв, k – число конъюнктивных термов
функции. Уменьшить функцию или ее сложность можно с помощью
законов булевой алгебры.
Изображение слайда
12
Слайд 12: Пример оценки сложности функции
12 Пример оценки сложности функции Уменьшить функцию и оценить ее сложность Оценка сложности по Квайну: Q=L(f)+k=12+4=16 Сложность по Квайну: Q=L(f)+k=7+3=10
Изображение слайда
13
Слайд 13: Пример дизъюнктивного разложения по Шеннону
13 Пример дизъюнктивного разложения по Шеннону Получить дизъюнктивное разложение функции по переменным x, z: Разложение по указанным переменным имеет вид: Вычисление составляющих дает: Искомое разложение:
Изображение слайда
14
Слайд 14: Выводы
14 Выводы Всякая ФАЛ может быть реализована формулой, оперирующей символами , , ¬, скобками и знаком равенства Любая булева функция может быть представлена в виде ДНФ, КНФ, СДНФ, СКНФ ДНФ и КНФ есть сокращенная форма записи СДНФ и СКНФ (таблицы истинности) ДНФ есть наиболее распространенная форма описания цифровых систем, максимально приближенная к аппаратурной реализации ДНФ КНФ СДНФ СКНФ
Изображение слайда
15
Последний слайд презентации: БУЛЕВА АЛГЕБРА ДИЗЪЮНКТИВНЫЕ И КОНЪЮНКТИВНЫЕ НОРМАЛЬНЫЕ ФОРМЫ (ДНФ и КНФ): Тест-задание
15 Тест-задание Определить сложность функции по Квайну
Изображение слайда
Сокращенная и тупиковая ДНФ (КНФ) — Мегаобучалка
В совершенной ДНФ каждая единица ФАЛ представляется соответствующей конституентой единицы, являющейся конъюнкцией всех переменных функции. Количество конституент единицы, входящих в СДНФ, равно числу наборов, на которых ФАЛ равна единице.
В отличие от СДНФ в сокращенную ДНФ включают элементарные конъюнкции, которые получаются в результате проведения операции склеивания конституент единицы, входящих в заданную ФАЛ. Такие элементарные конъюнкции заменяют в заданной ФАЛ несколько конституент единицы.
Функцию j, входящую в заданную функцию f, называют ее импликантой.
Вхождение одной функции в другую можно определить с помощью понятия накрытия.
Пусть на каком-либо наборе переменных функция f равна а1, а функция j на том же наборе равна а2. Тогда говорят, что на данном наборе функция f своим значением а1 накрывает значение а2 функции j.
Функция j входит в функцию f, если все единицы функции j накрываются единицами функции f, а нули функции j могут быть накрыты как нулями, так и единицами функции f. Функцию j, входящую в данную функцию f, называют импликантой функции f.
Простой импликантой функции f называется элементарная конъюнкция, входящая в данную функцию и из которой не может быть получена другая конъюнкция, входящая в эту функцию, исключением из первой какой-либо переменной. Простые импликанты, входящие в заданную ФАЛ, представляют собой элементарные конъюнкции, содержащие наименьшее число переменных, т.е. элементарные конъюнкции наименьшего ранга.
Любая ФАЛ имеет конечное число простых импликант, но не более числа конституент единицы в СДНФ этой функции. Так как простые импликанты – это элементарные конъюнкции, в которые входят все конституенты единицы функции, то дизъюнкция всех простых импликант функции f(хn, …, х2, х1) равна этой функции и называется сокращенной ДНФ.
Любая ФАЛ имеет единственную сокращенную ДНФ. По методу Квайна сокращенную ДНФ (КНФ) можно получить путем преобразования СДНФ (СКНФ) с помощью операций неполного склеивания и поглощения.
Если две элементарные конъюнкции/дизъюнкции( в том числе и конституенты единицы/нуля) одного и того же ранга и одних и тех же переменных отличаются только знаком отрицания одной из переменных , то они склеиваются по этой переменной:
где А — элементарная конъюнкция/дизъюнкция.
Такие элементарные конъюнкции/дизъюнкции называются соседними.
Операции неполного склеивания определяются формулами:
(7)
т.е. в правой части равенств (7), кроме члена А, остаются обе склеивающиеся конъюнкции Ахiи или дизъюнкции и
Согласно теореме Квайна, если в СДНФ (СКНФ) ФАЛ выполнить все операции неполного склеивания и затем все операции поглощения, то получится сокращенная ДНФ (КНФ) этой функции.
Одна и та же конституента единицы может склеиваться не с одной, а с несколькими конституентами единицы, в результате чего получаются различные простые импликанты. Поэтому для нахождения всех простых импликант функции выполняется операция неполного склеивания.
В общем случае сокращенная ДНФ не является минимальной, так как некоторые простые импликанты могут накрываться дизъюнкцией других импликант и эти простые импликанты можно исключить.
Дизъюнкция простых импликант, ни одну из которых нельзя исключить, называется тупиковой ДНФ заданной ФАЛ.
ФАЛ может иметь несколько тупиковых форм. Тупиковые формы, содержащие наименьшее количество букв, называются минимальными. Поэтому для нахождения минимальных форм нужно получить все тупиковые формы ФАЛ и из последних выбрать минимальные. Некоторые ФАЛ могут иметь несколько как тупиковых, так и минимальных форм.
Минимизация функций алгебры логики выполняется по методам Квайна, Квайна – Мак-Класки, по методу Квайна с применением карт Карно, по методу Квайна с применением карт Карно и преобразования Петрика и другими методами. Метод Квайна является основополагающим методом минимизации в классе ДНФ и КНФ ФАЛ. Однако трудоемкими этапами минимизации ФАЛ по методу Квайна являются нахождение простых и существенных (ядровых) импликант функций. Карты Карно позволяют существенно сократить количество сравнений конституент единицы и нуля для выявления склеивающихся конъюнкций. Преобразования Петрика позволяют после нахождения простых импликант, т.е. после нахождения сокращенной ДНФ, и существенных импликант найти аналитически все тупиковые и минимальные ДНФ и КНФ.
Для нахождения минимальных КНФ можно рекомендовать два метода:
1. Метод Квайна, в основу которого берется операция склеивания конституент нуля функции. Конституентам нуля на карте Карно соответствуют пустые клетки (или клетки, содержащие нули). Правила склеивания конституент нуля аналогичны правилам склеивания конституент единицы. Для нахождения простых и существенных дизъюнкций и тупиковых и минимальных КНФ можно использовать карты Карно и преобразование Петрика.
2. Минимизация функции, инверсной заданной, и преобразование полученной минимальной ДНФ функции по законам инверсии и де Моргана.
исчисление высказываний — Найти ДНФ и КНФ выражения
Вопрос
Изменено 1 год, 9 месяцев назад
Просмотрено 100 тысяч раз
$\begingroup$
Я хочу найти DNF и CNF следующего выражения \клин y) \vee (x\клин \neg y)$$
но все запуталось.
Я также нарисовал это в Wolfram Alpha, и, конечно, он показал их, но не шаги, которые нужно сделать, чтобы туда добраться.
Есть идеи, как это можно сделать?
- исчисление высказываний
- булева алгебра
- конъюнктивная нормальная форма
- дизъюнктивная нормальная форма
$\endgroup$
2
$\begingroup$
Просто запишите таблицу истинности, найти которую довольно просто, и вывести свою КНФ и ДНФ.
\begin{массив}{| с | с | с | с |} \hline X&Y&Z&\\\hline Т&Т&Т&Т\\hline T&T&F&F\\hline Т&Ф&Т&Ф\\hline T&F&F&T\\hline F&T&T&F\\hline Ф&Т&Ф&Т\\hline F&F&T&T\\hline F&F&F&F\\hline \end{array}
Если вы хотите найти DNF, вам нужно просмотреть все строки, которые заканчиваются на $T$. Когда вы найдете эти строки, возьмите значения $x, y, $ и $z$ из каждого соответствующего столбца. Таким образом, вы получаете $$(x \клин у \клин z) \vee (x \клин \neg y \клин \neg z) \vee (\neg x \клин y \клин \neg z) \vee (\neg х \клин \neg y \клин z).$$
Точно так же вы можете найти CNF
$$ (\lnot x \lor \lnot y \lor z) \land (\lnot x \lor y \lor \lnot z) \land (x \lor \lnot y \lor \lnot z) \land ( х \лор у \лор г) $$
$\endgroup$
3
$\begingroup$
Ага. В такой более общей настройке вы можете интерпретировать $\oplus$ как сложение по модулю 2 . Например, если у вас есть 5 переменных $a_1, \ldots, a_4 \in \{0, 1\}$. Тогда $a_1 \oplus \cdots \oplus a_4 = (a_1 + \ldots + a_4) \mod 2$. Используя этот факт, вы можете записать свою КНФ. Фактически, этот «метод» неявно использует таблицы истинности.
Например, предположим, что мы хотим найти КНФ $a \oplus b \oplus c \oplus d$. Затем вам нужно перечислить все дизъюнкции $a, b, c, d$ с четным числом отрицаний. В CNF вы найдете $(a \vee b \vee c \vee d)$, $(\neg a \vee \neg b \vee c \vee d)$, $(\neg a \vee b \vee \neg c \vee d)$ и т. д., но не $(\neg a \vee b \vee c \vee d)$.
Обратите внимание, что в общем случае преобразование формул с помощью преобразований эквивалентности в КНФ и ДНФ является NP-трудным.
Надеюсь мысль понятна?
$\endgroup$
3
$\begingroup$
Использование SymPy:
>>> x, y, z = символы ('x y z')
>>> Фи = Xor(x,y,z)
DNF равен
>>> to_dnf(Phi,simplify=true) Или(И(х, у, z), И(х, Не(у), Не(z)), И(у, Не(х), Не(z)), И(z, Не(х), Нет, спасибо)))
В $\LaTeX$,
$$\left(x \клин y \клин z\право) \vee \left(x \клин \neg y \клин \neg z\right) \vee \left(y \клин \neg x \клин \neg z\right) \vee \left(z \wedge \neg x \wedge \neg y\right)$$
CNF равен
>>> to_cnf(Phi,simplify=true) И(Или(х, у, z), Или(х, Не(у), Не(z)), Или(у, Не(х), Не(z)), Или(z, Не(х), Нет, спасибо)))
В $\LaTeX$,
$$\left(x \vee y \vee z\right) \wedge \left(x \vee \neg y \vee \neg z\right) \wedge \left(y \vee \neg x \vee \neg z\right) \wedge \left(z \vee \neg x \vee \neg y\right)$$
$\endgroup$
$\begingroup$
Для DNF:
- посмотрите на каждую строку, где $p = 1$
- закодируйте предложение из атомов $p_i$ для строки $i$ (что дает $p$ равно 1), которое имеет $a_i$, если этот атом равен 1 в таблице истинности, и $\neg a_i$, если он равен 0. Вы используя и , чтобы объединить атомы так, чтобы только этот термин был равен 1, когда вы находитесь в этой строке. Вы можете думать об этом соединении как о продукте.
- возьмем ИЛИ всех таких предложений, соответствующих строкам, равным 1
- , так как это предложение является дизъюнкцией (думайте об этом как о сложении), которое составляет только 1 для уникальных строк, вы получаете, что все это только 1, когда вам нужно, чтобы оно было 1.
Для CNF:
- Посмотрите на строки, где $p=0$
- закодируйте предложение из атомов $p_i$ для строки $i$ (что дает p равно нулю), которое имеет $a_i$, если этот атом равен 1 в таблице истинности, и $\neg a_i$, если он равен 0. Теперь соедините их. Это не та форма, которая вам действительно нужна, поэтому инвертируйте $p_i$, чтобы получить $\neg p_i$. По Деморгансу все дизъюнкции стали союзами.
- Теперь возьмем И всех таких дизъюнктивных предложений.
- Это правильно, потому что всякий раз, когда вы выбираете строку, построенное вами предложение возвращает 1 ЕСЛИ, вас нет в этой строке. Поскольку вы не находитесь в этой строке, все эти строки возвращают 1 одновременно, указывая на то, что вас нет ни в одной из строк, что дает ноль. Таким образом, вы получаете все, что дает 1,
Если вам нужна дополнительная помощь, посмотрите это видео:
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
днф кнф | Tiktok Search
TiktokЗагрузка
для вас
после
Ranboreo
Ranboreo
Это с наушниками >> также DNF в ближайшее время. dteam
2,4 тыс. лайков, 40 комментариев. Видео TikTok от Ranboreo (@ranboreo): «Это в наушниках>> тоже dnf скоро ❤️ не могу дождаться omg #knf #dnf #dteammeetup #dteam». оригинальный звук.
9274 просмотра|
оригинальный звук — Ranboreo
dweamiss
Adele🎗 • inniter
dnf>>>knf || #karljacobs #georgenotfound #edit #knf #dweamiss #dnf #mcyt #dsmp #viral #goviral #fyp
833 Likes, 12 Комментарии. Видео в TikTok от Адель🎗 • inniter (@dweamiss): «dnf>>>knf || #karljacobs#georgenotfound#edit#knf#dweamiss#dnf#mcyt#dsmp#viral#goviral#fyp». оригинальный звук.
3716 просмотров|
оригинальный звук — Adele🎗 • inniter
sanegnf
m !!
dnf, потому что я knf анти #sanegnf #fyp #foryoupage #edit #dream #george
5 90 Likes. Видео в TikTok от m!! (@sanegnf): «dnf, потому что я knf против #sanegnf #fyp #foryoupage #edit #dream #george». оригинальный звук.
374,3 тыс. просмотров|
оригинальный звук — м !!
dnfsglasscloset
𝙷
DNF 😾❤️🫶 I LOVE DNF #DNF #dnf #dreamnotfound #dream #dreamwastaken #george #georgenotfound #gnf #snf #knf #mcyt #dsmp #dreamsmp
8,8 тыс. лайков, 75 комментариев. Видео TikTok от 𝙷 (@dnfsglasscloset): «DNF 😾❤️🫶 Я ЛЮБЛЮ DNF #DNF #dnf #dreamnotfound #dream #dreamwastaken #george #georgenotfound #gnf #snf #knf #mcyt #dsmp #dreamsmp». Метеоритный душ.
29 тыс. просмотров|
Meteor Shower — Cavetown
lorenawastaken
Lol #fyp #dnf #lgtbq🏳️🌈 #pride #dnfsupremacy #knf🤮 #gnf #KarlJacobs #Dream #DSMP #DreamSMP #DreamTeam #DreamWastastaken #FYP #FYP #FYP #FYP #FYP #FYP #FYP #FYP #FYP #FYP #FYP #FYP #FYP #FYP #FYP 0013 #fyp #fyp #fyp #fyp #fyp #fyp #fyp #fyp #fyp #fyp #fyp #fyp # #fyp #fyp #fyp
2,6 тыс. 10,2 тыс. просмотров| гвозди dee en eff ? #knf #dnf #dreamnotfound #karljacobs #georgenotfound #dreamwastaken #georgeflorida #fyp #fy #dsmp #dreamsmp #tommyinnit # fypppp 99,5 тыс. лайков, 1 тыс. комментариев. 380,1 тыс. просмотров| makes me sad to think dream has to watch all his friends have fun without him #dream #mcyt #dreamsmp #dsmp #minecraft #dnf # knf #fyp #fypシ 117,6 тыс. лайков, 1,4 тыс. комментариев. Видео TikTok от пользователя usernamefour0four (@usernamefour0four): «Мне грустно думать, что Дрим должен смотреть, как все его друзья веселятся без него #dream #mcyt #dreamsmp #dsmp #minecraft #dnf #knf #fyp #fypシ». 518,3 тыс. просмотров| буквально убить. они такие милые #slay #dnf #knf #georgenotfound #karljacobs #london #greenscreen 8 90 лайков Видео из ТикТок. (@mommy.m1n3craft): «буквально убей. они такие милые #slay #dnf #knf #georgenotfound #karljacobs #london #greenscreen». бойфренды снова в деле | umm karl подготовлен с цветными ногтями dnf! . идеальная пара. 9 рыцарство мертво, как и dnf. #knf #karljacobs #georgenotfound #dreamwastaken #dnf #dreamnotfound #karlnotfound #rvsq 2. 16,2 тыс. просмотров| Загрузить лайков, 1,6 тыс. лайков. Видео TikTok от оригинальный звук —
dreamluva27
bella !!
Видео TikTok от Беллы !! (@dreamluva27): «dee en effnails ? #knf #dnf #dreamnotfound #karljacobs #georgenotfound #dreamwastaken #georgeflorida #fyp #fy #dsmp #dreamsmp #tommyinnit #fypppp». оригинальный звук оригинальный звук dreamwastakenwastaken — Белла !!
usernamefour0four
usernamefour0four
один. один — имя пользователяfour0four
mommy.m1n3craft
.
reeservsq
wowah
3K Likes, 55 Comments. Видео TikTok от wowah (@reeservsq): «Рыцарство мертво, как и dnf. #knf #karljacobs #georgenotfound #dreamwastaken #dnf #dreamnotfound #karlnotfound #rvsq». оригинальный звук — правки дамп. оригинальный звук — едит дамп — wowah
knf фанфики | Поиск в TikTok
TikTok Для вас
Читать
😔😔
#knf #karlnotfound #fanficition #wattpad #dsmp #mcyt
599 лайков, 18 комментариев. Видео TikTok от Limebed 💚 (@lime.bed): «Ответ @freya._.notfound, это такой милый корабль, почему НИ ОДНОГО!!!! 😔😔 #knf #karlnotfound #fanficition #wattpad #dsmp #mcyt» . мой любимый фанфик по knf 🥹. сом оригинал.
6825 просмотров|
som original — Mary
swaggy_edits16
Qu1lless
I SMELL the fanfics brewing 🤣😭 #knf #karljacobs #georgenotfound
345 Likes, 19 Comments. Видео TikTok от Qu1lless (@swaggy_edits16): «Я ЧУХУ готовящиеся фанфики 🤣😭#knf #karljacobs #georgenotfound». Lobby Music (оригинальный саундтрек).
1358 просмотров|
Музыка в лобби (оригинальный саундтрек) — Kahoot!
астевери
туманность❤️🔥
Я был мертв здесь навсегда 😳 вы можете найти меня @/lavagnf в Твиттере, я пишу там треды!! #karljacobs #georgenotfound #knf #karlnotfound #dnf #dreamwastaken
28,2 тыс. лайков, 68,2 тыс. лайков. Видео в TikTok от Nebula❤️🔥 (@asteveri): «Я был мертв здесь навсегда 😳 вы можете найти меня @/lavagnf в Твиттере, я пишу там треды!! #karljacobs #georgenotfound #knf #karlnotfound #dnf #dreamwastaken» . тааак… кнф?. дурачок.
142,4 тыс. просмотров|
Lovefool — Лучшие песни о любви
st4rmybeloved_
этан ака звезда и/или звезда 😎
Когда я делал фик, я не знал, что они встретятся, так что теперь я злюсь 😡😡😡😡 в любом случае днф происходит в фанфике #dnf #knf #dsmp #mcyt #fyp
видео из TikTok от Итана ака звезда и/или звезда 😎 (@st4rmybeloved_), я не знал, что они были встретимся, так что теперь я злюсь 😡😡😡😡 что бы dnf ни случилось в фике #dnf #knf #dsmp #mcyt #fyp». Я не ненавижу KNF, даже несмотря на то, что KNF есть в моем фике что угодно днф на всю жизнь. ИЛИ ВСЕ.
64 просмотра|
ILY ALL — lois
billzoballs
Grog • sex with dream
MATURING JS REALISING KNF SUCKS ASS #fyp #dnf #dnf #dnf #dnf #dnfsupremacy # dnffanart #dnffanfiction #dnfisreal #dnf #knfsucks #knfsucks #fuckknf #knfisshit #AAAAAAA
895 лайков, 215 комментариев. TikTok видео от Грога • секс с мечтой (@billzoballs): «ВЗРОСЛЕВАЯ JS ПОНИМАЯ KNF СОСТОЯТ В ЖОПЕ #fyp #dnf #dnf #dnf #dnf #dnfsupremacy #dnffanart #dnffanfiction #dnfisreal #dnf#knfsucks #knfsucks #fuckknf #knfisshit #AAAAAAAA «. ДНФ. | если ты knfer убирайся с моей страницы dnf намного лучше я ненавижу knf больше, чем я ненавижу своего папу и проклятый путин, как девочка карл отступи от мечты сука не делай его беспощадным со своей собачьей мордой OFF я говорю НАЗАД OFFFFFF | ВАШЕ МНЕНИЕ НЕДЕЙСТВИТЕЛЬНО, ЕСЛИ ВАМ НРАВИТСЯ KNF, ЭТО ОТСТОЙ | …. оригинальный звук.
4593 просмотра|
оригинальный звук — Шай 🙂
noki_cosplays
NocturnalNoki
Pt. 1 написать фанфик по тому, что мне подскажут колеса! #fyp #foryou #foryoupage #fypシ #fy #mcyt #minecraft #minecraftyoutuber #fanfic #fanfiction #writing #monogamous #карлнотфаунд #knf #reincarnatedlovers #trope
91 лайк, 7 комментариев. Видео TikTok от NocturnalNoki (@noki_cosplays): «Первая часть написания фанфика по тому, что мне говорят колеса! karlnotfound #knf #reincarnatedlovers #троп». Торговый автомат любви.
752 просмотра|
Торговый автомат любви — Ступендиум
angie__202h
Angelina 🙂
Anyways stan dnf and karlnap 🤭 no need for dreamnap or knf 🥱 #dnf #knf #snf #dreAmnap #karlnap #karlnapity #ReTokforNature # PostitAffirmations #dream #george #fyp #dreamteam
686 лайков, 7 комментариев. Видео TikTok от Анджелины 🙂 (@angie__202h): «В любом случае, stan dnf и karlnap 🤭 нет необходимости в dreamnap или knf 🥱 #dnf #knf #snf #dreAmnap #karlnap #karlnapity #ReTokforNature #PostitAffirmations #dream #george #fyp #dreamteam» . Воах воах воах воах что ты читаешь? | Ничего, просто фанфик | Фанфик.. подождите, это фанфик по днф или кнф? | …. оригинальный звук.
2566 просмотров|
оригинальный звук — Оуэн
менас.лойка
менас.лойка
КНФ временно ДНФ навсегда! #gnf #georgenotfound #georgenotfoundedit #georgenotfoundedits #georgenotfoundcosplay #georgenotfoundfanart #georgenotfoundsupremacy #gnfedit #gnfcosplay #gnfedits #dsmp #dsmpfanart #dsmpedit #dsmplore #dsmptiktok #mcyt #mcyttiktok #mcytedit #dnf #dnffanfiction #dreamnotfoundcosplay #dreamnotfoundedit #dnfsupremacy #dnffanart 0014 #KNF #KNFEDIT #Karlojacobs #Karlgeorge #KarlJacobsedit #KarlNotFound #KarlNOTFOUNDEDITFOUNDITDITFOUNDITDIT. Видео TikTok от menas.loyka (@menas.loyka): «KNF временно DNF навсегда! dsmptiktok #mcyt #mcyttiktok #mcytedit #dnf #dnffanfiction #dreamnotfoundcosplay #dreamnotfoundedit #dnfsupremacy #dnffanart #dreamwastakenedit #dreamwastakenfanart #dreamwastakenwastakenedit #dreamwastaken #dreamwastakenwastaken #knf #knfedit #karlojacobs #karlgeorge #karljacobsedit #karlnotfound #karlnotfoundedit». оригинальный сес.
5227 просмотров|
orijinal ses — menas.loyka
teanbiscuiit
meg
ITS SUCH A CUTE FIC #dnf #dreamnotfound #dnffic #dnffanfiction #dream #georgenotfound #karljacobs #sapnap #quackity #teanbiscuiit #knf #fyp #mcyt #ao3
26K лайков, комментариев 4K. Видео TikTok от meg (@teanbiscuiit): «ЭТО ТАКОЙ МИЛЫЙ ФИК #dnf #dreamnotfound #dnffic #dnffanfiction #dream #georgenotfound #karljacobs #sapnap #quackity #teanbiscuiit #knf #fyp #mcyt #ao3». *мечтает хандрить в постели в течение нескольких дней после того, как его годичная подруга изменила ему* | вдохновлен:
Киноко Кац
автор: mimispoppingoff
ваншот на ао3 | *джордж из кошачьего приюта звонит во сне о своем назначении на день святого валентина, чтобы взять кошку* | …. это мой папа.
23,7 тыс. просмотров|
dis my daddy — dsmpantij
dsmpfactszz
Dsmpfactsz
KNF shippers make me mad #dnf #dnffanfiction #fyp #foryoupage #dsmp #no
139 Likes, 23 Комментарии. Видео TikTok от Dsmpfactsz (@dsmpfactszz): «Шипперы KNF меня бесят #dnf #dnffanfiction #fyp #foryoupage #dsmp #no». нет, почему вы все отправляете KNF, как черт, эти MFS меня бесят. И подождите, пока лицо мечты не откроется, и Джордж не будет во Флориде, тогда посмотрим. оригинальный звук.
1270 просмотров|
оригинальный звук — speedupaudios123_😜
Knf Stories — Wattpad
#1
KNF: DRUNK KISSby vain_rae
КОРОТКИЙ ФАНФИК KNF ПГ-16; читать на свой страх и риск. автор: invain_rae
- dsmp
- shipping
- dreammp
+15 more
#2
поздний ночной разговор (knf) от Ноя
«хммм», шарлатан думает на секунду, «я смею тебя… поцеловать Карла!!» «почему я??» карл скулит. шарлатанство просто подмигивает ему. карл закатывает глаза…
- karlnotfound
- knf
- quackity
+8 еще
#3
Свитер Weatherby worm
Карл поцеловал Джорджа, когда он был в Великобритании, но что, если это было нечто большее? Что, если то, что они нам сказали, было лишь верхушкой айсберга?
На самом деле это не то, что я думаю. ..
Завершено
- dsmp
- knf
- dreammp
+2 more
#4
Любовник — Karlnotfoundby L0veXs1ck
У Карла самый банальный момент, когда он встречает в книжном магазине парня, от которого глаза разбегаются, от волнения дает брюнетке свой номер и неожиданно получает м…
Завершено
- мечта
- lgbtqfiction
- майнкрафт
+21 еще
#5
Я люблю тебя, ты любишь его. (DreamNa…by Elton.es•_•guapo
⚠️ВНИМАНИЕ ⚠️ Следующая история не рекомендуется для лиц моложе 18+. ЧИТАЙТЕ НА СВОЙ РИСК!! Я отправляю это, это просто…
Завершено
- днф
- дримнап
- кнф
#6
Просто дружба?.. // !Golden Du…by Poisoned_Illusion
Запущено: 21 июля 2022 г. Закончено: Еще нет. 🙂
Завершено редактирование/исправление орфографических ошибок: Не начато.
Tw: Может быть кровь, ругань, насилие, членовредительство, жестокое обращение…
- dsmp
- angst
- mcyt
+14 еще
#7
Не отказывайтесь от нас (Dreamnotfound… by IsaktheBrave
После TwitchCon Amsterdam и Dream, и Sapnap обеспокоены своими отношениями с Джорджем и Карлом. Джордж клянется, что между ним и Карлом ничего не было, но почему …
Завершено
- georgenotfound
- mcyt
- sapnap
+8 еще
#8
Я ненавижу школу by Heart eyes saqnap
Старшая школа Dreamnap au!
- фанфики
- школа
- сапнап
+10 еще
#9
Mcyt smutshots👍by ivuaxz
Первая книга😃
Если бы вы дали запросы, это было бы очень полезно
Дааа. .-
- днф
- кунцнап
- кнф
+7 еще
#10
GeorgeNotFound Oneshotsby ꒰ 💭 ꒱
Ваншот случайных кораблей GeorgeNotFound. Больше информации в книге , наслаждайтесь !
- ninjanotfound
- georgenotfound
- wnf
+15 еще
#11
Я ненавижу имя Томми… //maskinn…by Tammyinnit69
!!Я не знаю, кто сделал обложку!! Я НЕ ОТПРАВЛЯЮ НИКОМУ, КРОМЕ DREAMNAP И КНФ В ЭТОМ!!!!!!! когда Томми возвращался в Иманбург, он услышал Таббо, Уилбура и Фанди…
- diskduo
- dreamisadad
- villanintommy
+5 еще
#12
Мы принадлежим друг другу🖤 ( кадры) от LOVE JORGE😻
Эти кадры будут о Карлнотфаунде и Уилбернофаунде. Я сделал эти кадры, потому что я шипперю этих людей, и, возможно, некоторые люди сделают это.
Чертежи, которые…
- смп
- пух
- кнф
+6 еще
#13
Ваши следы | dnf fanfic |от honkkyli
⚠️ВНИМАНИЕ⚠️ эта история содержит непристойный/сексуальный контент 14+ Написал: Кайли Исправление грамматики: maart Читать резюме :).
Завершено
- knf
- snf
- smuttyfanfic
+16 more
#14
~~The Incident~~ (Wilbur x Reader… by Dreamstoenails
Привет! Это мой первый фанфик Я почему-то решил сделать его в 12:00, так что наслаждайтесь!
- майнкрафт
- кнф
- днф
+7 еще
#15
Dreamsmp one-shots :)от Orange Skittle
Fluff, Angst, Lemon/Lime. ❤️- лимон/лайм
💙- Ангст
💛- Пух
________________
Джорджбур
Карлнотфаунд
КарлНап
сон
Карлвастакен
сапнотнайден
- wnf
- dreamnap
- георгебур
+1 еще
#16
через железную дорогу строчными буквами ྀ࿐ ˊˎ-
«Есть причина, Лондон ставит барьеры на линии метро» Карл оказывается потерянным после переезда в новую страну, жизнь, кажется, течет мимо, и он…
- команда мечты
- романтика
- карлнап
+13 еще
#17
Подсказки о доставке GNF (Dnf, Snf, knf… by 𝙰𝚙𝚘𝚕𝚕𝚘
У меня есть коллекция из 37 подсказок, которые я собираюсь выбрать наугад, а затем написать их. Я попытаюсь загрузить это как можно быстрее, но я не делаю про…
- пух
- dnf
- snf
+11 еще
#18
Поцелуй, который мальчики держали в секрете (Kin… by Zeph
У группы была сильная связь, но то, что было у Карла и Джорджа, было особенным. KЭта пара всегда испытывала чувства друг к другу, хотя Джордж пожал плечами. прочь (как он обычно д… 9_~
Completed
- knf
- lol
- killer
+9 more
#20
My Jolly Sailor Boldby mooshroomtina
«Нельзя отнять море у моряка, Джордж. Он сойдет с ума или вернется к нему.» «Значит, ему придется оставить меня, потому что он не может оставить это?» Или, Дреа…
Completed
- sad
- quackity
- dnf
+17 еще
ленивый писатель dnf
gnfsdream
встреча dteam в цвете
мечта не найдена днф СКОРОgnfships
«Если бы у меня была одна вещь на свете, что бы это было? Билет на самолет до дома Дрима. И постоянная комната в его доме»
«Ну, мы поцелуемся»
«Ты будет ли держать мою мечту за руку»
«У нас есть кот, куда я переезжаю»
«Когда он приедет, у меня будет маленькая подарочная корзина со всеми этими крутыми вещами, которые я ему подарил, которые он сможет открыть »
«Скоро станет реальностью, когда мы все вместе»
«Чего я жду больше всего? Я думаю, что мы все время существуем втроем»
«Патчи будут любить тебя» «ты не знаешь этого» «Я знаю это»
» Чего вы больше всего ждете от приезда Джорджа в Америку… Гм, ДЖОРДЖ»
«Всякий раз, когда я встречу его , это будет… Он будет здесь… навсегда. Итак.»
мечта не найдена днф кричать плакать бросаться в океанdwter
дрим ведет войну против rpf на стороне rpf
мечта днф почему он такойdreamquackity
мне очень нужно увидеть сравнение мистера зверя и рекомендательных писем мечты, потому что представьте веселье мистера зверя, перечисляющего экономически жизнеспособные причины, почему Джордж поможет Америке процветать, и я мечтаю, как я люблю его всем своим сердцем. сердце… разве этого недостаточно
gnfgothisvisa
Джордж действительно выскочил на этой фотографии, как те плохие сучки, фото на паспорт, обычные суки, которые трясутся в своих сапогах прямо сейчас
georgenetfound ребята это происходит это действительно происходитВентилятор охлаждения | Вентиляторы | Хауден
Вентиляторы охлаждения
Компания Howden уже более 50 лет находится в авангарде технологий охлаждающих вентиляторов и продолжает внедрять инновации. Наши вентиляторы занимают лидирующие позиции в области высокой эффективности и низкого уровня шума.
Наш ассортимент охлаждающих вентиляторов состоит из серий D, E, SX и FPX и используется как часть влажных, сухих и гибридных систем охлаждения. Они обслуживают самые разные отрасли: от энергетики на нефтегазовых объектах и электростанциях до предприятий легкой промышленности, центров обработки данных и коммерческих зданий.
Серия предлагает вентиляторы с низким перепадом давления до 250 Па и высоким расходом воздуха до 3000 м3/с. Вентиляторы могут работать в стандартном диапазоне температур от -20 до 85⁰C и, при необходимости, могут быть специально спроектированы для работы при температурах от -60 до 135⁰C.
Каждая модель вентилятора предлагает уникальные преимущества конечным пользователям и инженерам, которые ищут наилучшую долгосрочную производительность, а также компактные и гибкие конструктивные решения.
Наши вентиляторы подкреплены комплексными возможностями послепродажного обслуживания, чтобы обеспечить максимальную производительность на протяжении всего срока службы каждой операции.
Загрузить брошюру Свяжитесь с нами
Серия D
Серия D была разработана и зарекомендовала себя как лучшее сочетание производительности, надежности и цены для работы в конденсаторах с воздушным охлаждением и градирнях.
Серия E
Серия E предназначена для тяжелых условий эксплуатации в вертикальной или горизонтальной конфигурации для широкого спектра применений.
Серия SX
Серия SX является предпочтительным решением для приложений с жесткими требованиями к уровню шума и способна снизить уровень шума до 20 дБ(А) по сравнению со стандартными охлаждающими вентиляторами.
Серия FPX
В серии FPX используются лопасти с фиксированным шагом, изготовленные как единое рабочее колесо, которое обеспечивает очень простую сборку и минимальное техническое обслуживание в сочетании со сверхнизким уровнем шума.
Послепродажное обслуживание
Оптимизированное охлаждение за счет специализированного обслуживанияВозможности Howden для послепродажного обслуживания варьируются от обслуживания и поставки запасных частей до повышения производительности и модернизации. Более продвинутые услуги могут максимально увеличить срок службы вентиляторов в каждой системе, а также привести их работу в соответствие с последними техническими параметрами.
Программное обеспечение для выбора охлаждающего вентилятора
Узнать большеС конца 80-х годов Howden предлагает рынку инструмент для выбора охлаждающих вентиляторов. Постоянная разработка привела от базового инженерного инструмента к инструменту выбора охлаждающих вентиляторов CF-P20, а теперь и к текущему преемнику Howden Select for Cooling Fans.
Конденсаторы с воздушным охлаждением
Градирни
Вентиляторы Howden используются в градирнях, устанавливаемых на месте, и в блочных градирнях (СТ) – с противотоком, с поперечным потоком и с естественной тягой с вентилятором
Используется в таких отраслях, как электростанции, нефтеперерабатывающие заводы, нефтегазовая, химическая промышленность и системы HVAC-R.
Теплообменники с воздушным охлаждением
Вентиляторы Howden используются в теплообменниках с принудительной и вытяжной тягой с воздушным охлаждением (ACHE)
Используется на нефтеперерабатывающих, нефтехимических, газоперерабатывающих заводах, компрессорных станциях, электростанциях и других объектах
Также используется в качестве охладителя радиатора для газовых двигателей
Вентиляция
Послепродажное обслуживание
Ознакомьтесь с нашим руководством по поиску и устранению неисправностей охлаждающих вентиляторов и узнайте, как мы можем оптимизировать ваше решение по охлаждению. Наши специалисты по сервисному обслуживанию могут максимально продлить срок службы ваших вентиляторов.
Восстановление лопастей
Самый экономичный способ продлить срок службы вентилятора, восстановление лопастей поможет восстановить максимальную производительность ваших вентиляторов.
Производство и испытания
Мы вложили средства в создание современного оборудования, которое позволило нам достичь ранее недостижимого уровня тишины.
Услуги по модернизации
Наши инженеры могут проанализировать и оценить вашу систему охлаждения и предоставить подробные рекомендации по потенциальным улучшениям.
Ознакомьтесь с нашим ассортиментом решений для охлаждающих вентиляторов
Загрузите копию брошюры
Адрес электронной почты
First name
Last name
Company
Country
(Select a country)AfghanistanAlbaniaAlgeriaAmerican SamoaAndorraAngolaAnguillaAntarcticaAntigua and BarbudaArgentinaArmeniaArubaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelarusBelgiumBelizeBeninBermudaBhutanBoliviaBosnia and HerzegovinaBotswanaBouvet IslandBrazilBritish Indian Ocean TerritoryBrunei DarussalamBulgariaBurkina FasoBurundiCambodiaCameroonCanadaCape VerdeCayman IslandsCentral African RepublicChadChileChinaChristmas IslandCocos (Keeling) IslandsColombiaComorosCongoCongo (Dem. Republic) Острова КукаКоста-РикаХорватияКипрЧехияДанияДжибутиДоминикаДоминиканская РеспубликаВосточный ТиморЭквадорЕгипетСальвадорЭкваториальная ГвинеяЭритреяЭстонияЭфиопияФолклендские островаФарерские островаФиджиФинляндияФранцияФранцузская ГвианаФранцузская ПолинезияФранцузские Южные ТерриторииГабонГамбияГрузияГерманияГанаГуалуГибралтарГрецияГуамалуГренадаГренада ineaGuinea-BissauGuyanaHaitiHeard and McDonald IslandsHondurasHong KongHungaryIcelandIndiaIndonesiaIraqIrelandIsland of ManIsraelItalyIvory CoastJamaicaJapanJerseyJordanKazakhstanKenyaKiribatiKorea, SouthKosovoKuwaitKyrgyz RepublicLaosLatviaLebanonLesothoLiberiaLibyaLiechtensteinLithuaniaLuxembourgMacauMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMexicoMicronesiaMoldaviaMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmarNamibiaNauruNepalNetherlandsNetherlands AntillesNew CaledoniaNew ZealandNicaraguaNigerNigeriaNiueNorfolk IslandNorth MacedoniaNorthern Mariana IslandsNorwayOmanPakistanPalauPalestinian TerritoryPanamaPapua New GuineaParaguayPeruPhilippinesPitcairnPolandPortugalPuerto RicoQatarRe unionRomaniaRussiaRwandaSaint BarthelemySaint HelenaSaint Kitts and NevisSaint LuciaSaint MartinSaint Pierre and MiquelonSaint Vincent and the GrenadinesSamoaSan MarinoSao Tome and PrincipeSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneSinga poreSlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Georgia and South Sandwich IslandsSpainSri LankaSurinameSvalbard and Jan Mayen IslandsSwazilandSwedenSwitzerlandTaiwanTajikistanTanzaniaThailandTogoTokelauTongaTrinidad and TobagoTunisiaTurkeyTurkmenistanTurks and Caicos IslandsTuvaluUgandaUkraineUnited Arab EmiratesUnited KingdomUruguayUSAUzbekistanVanuatuVatican CityVietnamVirgin Islands (British)Virgin Islands (U.