|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 3 из 4Следующая ⇒ 1) Диагонали прямоугольника равны. 2) Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник. 21. Ромб. Ромбом называется четырехугольник, все стороны которого равны. Свойства и признаки ромба. 1) Диагонали ромба перпендикулярны. 2) Диагонали ромба делят его углы пополам. 3) Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб. 4) Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб. 22. Квадрат. Квадратом называется прямоугольник, все стороны которого равны. 23. Геометрическое место точек, равноудаленных от данной прямой — две параллельные прямые. 24. Теорема Фалеса. 25. Средняя линия треугольника. Отрезок, соединяющий середины двух сторон треугольника называется средней линией треугольника. Теорема о средней линии треугольника. Средняя линия треугольника параллельна стороне треугольника и равна ее половине. 26. Свойство середин сторон четырехугольника. Середины сторон любого четырехугольника являются вершинами параллелограмма. 27. Теорема о медианах треугольника. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2 : 1, считая от вершины. 28. а) Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный. б) Медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы. 29. Трапеция. Трапецией называется четырехугольник, у которого только две противоположные стороны (основания) параллельны. Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон). Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме. 30. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований. 31. Трапеция называется равнобедренной, если ее боковые стороны равны. Свойства и признаки равнобедренной трапеции. 1) Углы при основании равнобедренной трапеции равны. 2) Диагонали равнобедренной трапеции равны. 3) Если углы при основании трапеции равны, то она равнобедренная. 4) Если диагонали трапеции равны, то она равнобедренная. 5) Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали — полусумме оснований. 32. Окружность. Окружностью называется геометрическое место точек плоскости, удаленных от данной точки, называемой центром окружности, на одно и то же положительное расстояние. Свойства окружности. 1) Диаметр, перпендикулярный хорде, делит ее пополам. 2) Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде. 3) Серединный перпендикуляр к хорде проходит через центр окружности. 4) Равные хорды удалены от центра окружности на равные расстояния. 5) Хорды окружности, удаленные от центра на равные расстояния, равны. 6) Окружность симметрична относительно любого своего диаметра. 7) Дуги окружности, заключенные между параллельными хордами, равны. 8) Из двух хорд больше та, которая менее удалена от центра. 9) Диаметр есть наибольшая хорда окружности. 33. Замечательное свойство окружности. Геометрическое место точек M, из которых отрезок AB виден под прямым углом (∠AMB = 90º), есть окружность с диаметром AB без точек A и B. 34. Свойство серединных перпендикуляров к сторонам треугольника. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника. 35. Линия центров двух пересекающихся окружностей перпендикулярна их общей хорде. 36. Центр окружности, описанной около прямоугольного треугольника — середина гипотенузы. 37. Теорема о высотах треугольника. 38. Касательная к окружности. Прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности. 1) Касательная перпендикулярна радиусу, проведенному в точку касания. 2) Если прямая l, проходящая через точку на окружности, перпендикулярна радиусу, проведенному в эту точку, то прямая l — касательная к окружности. 3) Если прямые, проходящие через точку M, касаются окружности в точках A и B, то MA = MB. 4) Центр окружности, вписанной в угол, лежит на биссектрисе этого угла. 5) Теорема о биссектрисах треугольника. Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник. 39. Радиус окружности, вписанной в прямоугольный треугольник с катетами a, b и гипотенузой c, равен (a+b −c)/2. 40. Если M — точка касания со стороной AC окружности, вписанной в треугольник ABC, то AM = p −BC, где p — полупериметр треугольника. 41. Окружность касается стороны BC треугольника ABC и продолжений сторон AB и AC. Тогда расстояние от вершины A до точки касания окружности с прямой AB равно полупериметру треугольника ABC. 42. Окружность, вписанная в треугольник ABC, касается сторон AB, BC и AC соответственно в точках K, L и M. Если ∠BAC =, то ∠KLM =90º − /2. 43. Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны. 44. Касающиеся окружности. Говорят, что две окружности касаются, если они имеют единственную общую точку (точка касания). 1) Точка касания двух окружностей лежит на их линии центров. 2) Окружности радиусов r и R с центрами O1 и O2 касаются внешним образом тогда и только тогда, когда R + r =O1O2. 3) Окружности радиусов r и R (r < R) с центрами O1 и O2 касаются внутренним образом тогда и только тогда, когда R −r =O1O2. 4) Окружности с центрами O1 и O2 касаются внешним образом в точке K. Некоторая прямая касается этих окружностей в различных точках A и B и пересекается с общей касательной, проходящей через точку K, в точке C. Тогда ∠AKB =90º и ∠O1CO2 =90º. ⇐ Предыдущая1234Следующая ⇒ Читайте также: Где возникла философия и почему? Относительная высота сжатой зоны бетона Тарифы на перевозку пассажиров |
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 126; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
1.Параллелограмм. 4.Теорема Фалеса. 5.Средняя линия треугольника. 6.Трапеция. 7.Теорема о пропорциональных отрезках. 8.Примеры.
|
|||||||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 9 10 11 12 | |||||||||||||||||||||||||||||
1. Параллелограмм Параллелограмм
|
|||||||||||||||||||||||||||||
|
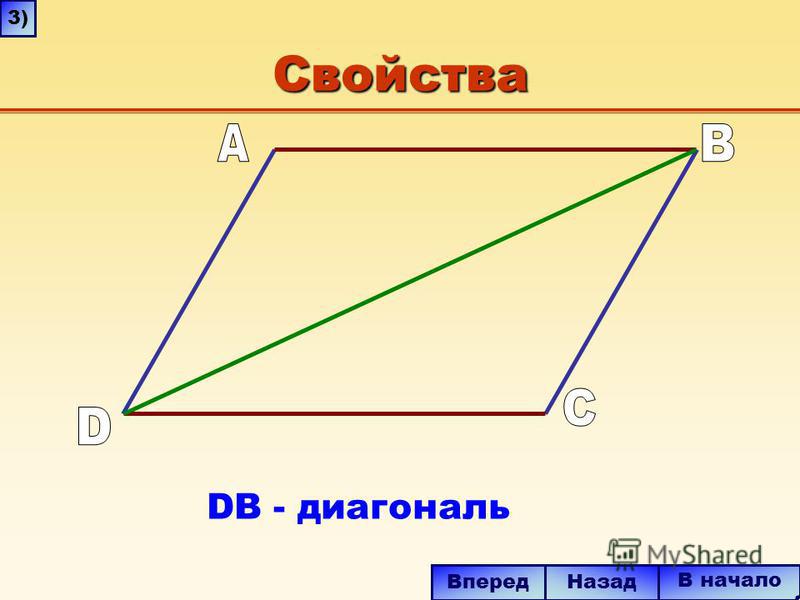
Параллелограмм — это геометрическая фигура, у которой диагонали пересекаются в точке, делящей их пополам, а противолежащие стороны параллельны. Теорема: если диагонали четырехугольника пересекаются и делятся этой точкой пересечения пополам, то такой четырехугольник называется параллелограммом. Доказательство. Пусть АВСD данный четырехугольник. Точка О — точка пересечения его диагоналей (рис.1). Тогда треугольники Δ АОD и Δ ВOC равны по двум сторонам и углу между ними. А следовательно, угол ODA равен углу CBO и угол OAD равен углу BCO. Таким образом, эти углы являются внутренними накрест лежащими для прямых AD и BC и секущей AC. А по признаку параллельности прямых, прямые AD и BC параллельны. |
Рис.1 Теорема. Параллелограмм. |
||||||||||||||||||||||||||||
| 2.Свойство диагоналей параллелограмма | |||||||||||||||||||||||||||||
Теорема. если четырехугольник является параллелограммом, то его диагонали делятся точкой пересечения пополам. Доказательство. Пусть дан параллелограмм АВСD. (Рис. 2) Тогда его стороны AD и BC равны и лежат на параллельных прямых а и b. Если мы проведем секущие с и d так, чтобы прямая с проходила через точку А и С, а прямая d проходила через точку B и D, то угол ОАD будет равен углу ОСВ, а угол ОDА будет равен углу ОВС, как внутренние накрест лежащие. |
Рис.2 Теорема. Свойство диагоналей параллелограмма. |
||||||||||||||||||||||||||||
3.Ромб |
|||||||||||||||||||||||||||||
Ромб — это геометрическая фигура, у которой все стороны равны. Теорема. диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов. Доказательство. |
Рис.3 Теорема. Свойство диагоналей ромба. |
||||||||||||||||||||||||||||
Задача |
|||||||||||||||||||||||||||||
В параллелограмме АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е. Необходимо найти отрезки ВЕ и ЕС, если АВ = 9 см, АD = 14 см (рис.4) Решение. |
Рис.4 Задача. |
||||||||||||||||||||||||||||
4.Теорема Фалеса |
|||||||||||||||||||||||||||||
|
Теорема: параллельные прямые, пересекающие стороны угла и отсекающие на одной его стороне равные отрезки, отсекают равные отрезки и на другой его стороне. Доказательство. Пусть дан угол и пересекающие его параллельные прямые (рис.5). Точки А1А2А3А4 и В1В2В3В4 — точки пересечения. Проведем прямую ОЕ. Тогда А1ЕОА3 — параллелограмм. И ОЕ = А1А3 Треугольники В1В2Е и ОВ2В3 равны по стороне (ОВ2 = ЕВ2) и прилегающим к ней углам. Из равенства треугольников следует, что В1В2 = В2В3. |
Рис.5 Теорема Фалеса. |
||||||||||||||||||||||||||||
5.Средняя линия треугольника |
|||||||||||||||||||||||||||||
Теорема. средняя линия треугольника, которая соединяет середины двух данных сторон, параллельна третьей его стороне и равна ее половине. Доказательство. |
Рис.5 Теорема. Средняя линия треугольника. |
||||||||||||||||||||||||||||
6.Трапеция |
|||||||||||||||||||||||||||||
Трапеция — это геометрическая фигура, у которой только две противолежащие стороны параллельны. Теорема. средняя линия трапеции параллельна двум своим основаниям и равна их полусумме. Доказательство. Пусть АВСD — трапеция.(Рис. 6). Проведем прямую от вершины В через середину стороны СD точку Н к основанию, т.е. достроим треугольник АВО. Тогда треугольники ВСН и DHO равны по сторонам СН и НD и прилегающим к ним углам. Следовательно отрезок АО равен сумме оснований АD и ВС. Рассмотрим треугольник АВО. ЕН это средняя линия треугольника, которая равна половине основания АО, т.е. полусумме оснований трапеции АD и ВС. |
Рис.6 Теорема. Средняя линия трапеции. |
||||||||||||||||||||||||||||
7. Теорема о пропорциональных отрезках Теорема о пропорциональных отрезках |
|||||||||||||||||||||||||||||
Теорема. параллельные прямые, которые пересекают стороны угла, отсекают от его сторон пропорциональные отрезки. Доказательство. Пусть дан угол и пересекающие его параллельные прямые. Разобьем угол ВAС параллельными прямыми на n частей. Тогда АВ = ns, a AB1 = ms. Где s — отрезок некоторой длины. По теореме Фалеса эти прямые разбивают сторону AС также на равные части. Тогда: |
Рис.7 Теорема о пропорциональных отрезках. |
||||||||||||||||||||||||||||
Допустим, что Отложим на луче АС отрезок АС2 Т.е. мы пришли к противоречию, так как изначально мы взяли отрезок АС2 = АС*АВ1/АВ. |
Рис.8 Теорема о пропорциональных отрезках. |
||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
Пример 1 |
|||||||||||||||||||||||||||||
Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что ее отрезок, заключенный между параллельными сторонами, делится этой точкой пополам. |
|||||||||||||||||||||||||||||
Доказательство: Пусть ABCD данный параллелограмм. EF данный отрезок, проходящий через точку О пересечения диагоналей. Рассмотрим треугольники COF и AOE. Сторона АО треугольника АОЕ равна стороне ОС треугольника COF по свойству параллелограмма. Угол при вершине А треугольника АОЕ равен углу при вершине С треугольника COF, как внутренние накрест лежащие углы. Углы при вершине О у обоих треугольников равны как вертикальные. Отсюда можно сделать вывод, что треугольники АОЕ и COF равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам). Следовательно, отрезки OF и ОЕ равны. |
Рис. |
||||||||||||||||||||||||||||
Пример 2 |
|||||||||||||||||||||||||||||
Две стороны параллелограмма относятся как 3:4, а его периметр равен 2,8 м. Найдите стороны параллелограмма. (Рис.10) |
|||||||||||||||||||||||||||||
Решение: Пусть ABCD данный параллелограмм. Обозначим сторону АВ как 3х, а сторону ВС как 4х. Тогда составим следующее соотношение: 2*(3х + 4х) = 2,8 14х = 2,8 Отсюда: х = 0,2 м. Следовательно, АВ = 3х = 0,6 м. ВС = 4х = 0,8 м. |
Рис.10 Задача. Две стороны параллелограмма… |
||||||||||||||||||||||||||||
Пример 3 |
|||||||||||||||||||||||||||||
В параллелограмме ABCD перпендикуляр, опущенный из вершины В на сторону AD, делит ее пополам. Найдите диагональ BD и стороны параллелограмма, если периметр параллелограмма равен 4 м, а периметр треугольника ABD равен 3 м. (Рис.11) |
|||||||||||||||||||||||||||||
Решение: Так как перпендикуляр BE, опущенный на сторону AD, делит ее пополам, то треугольники ABE и BED равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). Обозначим сторону АВ как х, а сторону AD — как 2y. Тогда можно составить следующие соотношения: PABCD = 2*(х + 2y) = 4, PABD = 2x +2y = 3 Следовательно, PABCD = 2х + 4y = 4, а 2х = 4 — 4y. Тогда подставим 4 — 4y во второе уравнение: 4 — 4y + 2y = 3 и,следовательно, y = 0,5, а х = 1 АВ = BD = 1 м. AD = 1 м. |
Рис.11 Задача. В параллелограмме ABCD перпендикуляр… |
||||||||||||||||||||||||||||
Пример 4 |
|||||||||||||||||||||||||||||
В прямоугольный треугольник, каждый катет которого равен 8 см, вписан прямоугольник, имеющий с треугольником общий угол. |
|||||||||||||||||||||||||||||
Решение: Пусть АВС данный треугольник. АВ = АС = 8 см. Тогда углы при вершинах В и С равны 45°. А следовательно, углы при вершине Е в треугольниках FEC и BDE также равны 45°. Если обозначить часть катета АF как х, то FC будет равно 8 — х. Отсюда следует, что FE = AD = 8-х, а BD = х. Теперь можно составить следующее соотношение: РADEF = 2*(х + 8 — х) = 16 см. Периметр прямоугольника ADEF равен 16 см. |
Рис.12 Задача. В прямоугольный треугольник… |
||||||||||||||||||||||||||||
Пример 5 |
|||||||||||||||||||||||||||||
Докажите, что если у параллелограмма диагонали перпендикулярны, то он является ромбом. |
|||||||||||||||||||||||||||||
Доказательство: Пусть АВСD данный параллелограмм. По свойству параллелограмма, у него противоположные стороны параллельны и равны. Следовательно, стороны АВ и CD можно рассматривать как параллельные прямые, а диагональ BD — как секущую. Тогда в треугольниках АВО и DOC углы при вершинах B и D равны как внутренние накрест лежащие. Так же как и углы при вершинах А и С. Отсюда следует, что эти треугольники равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам). Сторона АВ = DC и внутренние накрест лежащие углы при них равны. Следовательно, АО = ОС, а ВО = OD. Теперь рассмотрим треугольники AOD и DOC. Они также равны, но по первому признаку равенства треугольников. Сторона АО = ОС, а сторона OD у них общая. Следовательно, можно сделать вывод, что сторона AD = DC = AB = BC, т.е. данный параллелограмм является ромбом. |
Рис.13 Задача. Докажите, что если у параллелограмма… |
||||||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 9 10 11 12 | |||||||||||||||||||||||||||||
Содержание |
|||||||||||||||||||||||||||||
| Страница 1 | Страница 7 | ||||||||||||||||||||||||||||
1. Основные фигуры планиметрии. Основные фигуры планиметрии.
2.Аксиомы планиметрии. 3.Смежные углы. 4.Вертикальные углы. 5.Перпендикулярные прямые. 6.Признаки равенства треугольников. |
1.Движение и его свойства.
2.Симметрия относительно точки. 3.Симметрия относительно прямой. 4.Параллельный перенос и его свойства. |
||||||||||||||||||||||||||||
| Страница 2 | Страница 8 | ||||||||||||||||||||||||||||
|
1.Параллельность прямых.
2.Признаки параллельности прямых. 3.Свойство углов при пересечении параллельных прямых. 4.Сумма углов треугольника. 5.  Единственность перпендикуляра к прямой. Единственность перпендикуляра к прямой.
6.Высота, биссектриса и медиана треугольника. 7.Свойство медианы равнобедренного треугольника. |
1.Вектор и его абсолютная величина.
2.Сложение векторов. 3.Умножение вектора на число. 4.Разложение вектора по двум неколлинеарным векторам. 5.Скалярное произведение векторов. |
||||||||||||||||||||||||||||
| Страница 3 | Страница 9 | ||||||||||||||||||||||||||||
|
1.Окружность.
2.Окружность описанная около треугольника. 3.Окружность вписанная в треугольник. 4.Геометрическое место точек. |
1. Преобразование подобия и его свойства. Преобразование подобия и его свойства.
2.Подобие фигур. Подобие треугольников по двум углам. 3.Подобие треугольников по двум пропорциональным сторонам и углу между ними. 4.Подобие треугольников по трем пропорциональным сторонам. 5.Подобие прямоугольных треугольников. |
||||||||||||||||||||||||||||
| Страница 4 | Страница 10 | ||||||||||||||||||||||||||||
|
1.Параллелограмм.
2.Свойства диагоналей параллелограмма. 3.Ромб. 4.Теорема Фалеса. 5.Средняя линия треугольника. 6.Трапеция. 7.Теорема о пропорциональных отрезках. |
1.Углы, вписанные в окружность.
2.Пропорциональность хорд и секущих окружности. 3.Теорема косинусов. 4.Теорема синусов. 5.Соотношение между углами и сторонами в треугольнике. |
||||||||||||||||||||||||||||
| Страница 5 | Страница 11 | ||||||||||||||||||||||||||||
|
1.Теорема Пифагора.
2.Египетский треугольник. 3.Соотношение между углами и сторонами в прямоугольном треугольнике. 4.Основные тригонометрические тождества. |
1.Многоугольники. Правильные многоугольники.
2.Радиус вписанной и описанной окружностей правильных многоугольников. 3.Подобие многоугольников. 4.Длина окружности. |
||||||||||||||||||||||||||||
| Страница 6 | Страница 12 | ||||||||||||||||||||||||||||
1. Декартова система координат. Декартова система координат.
2.Расстояние между точками. 3.Уравнение окружности. 4.Уравнение прямой. 5.Координаты точки пересечения. |
1.Площадь прямоугольника.
2.Площадь параллелограмма. 3.Площадь треугольника. 4.Площадь круга. 5.Площадь подобных фигур. 6.Площадь трапеции. |
||||||||||||||||||||||||||||
Доказать теорему если диагонали параллелограмма перпендик… -reshimne.ru
Новые вопросы
Ответы
ПустьABCD – данный параллелограмм, AC и BD – его диагонали и (AC) (BD). Пусть O – точка пересечения диагоналей параллелограмма. Треугольник ABC – равнобедренный с основанием AC. Действительно, так как диагонали параллелограмма в точке пересечения делятся пополам, то AO = OC, и тогда BO – медиана треугольника ABC, проведенная к стороне AC. Но по условию (BO) (AC) и [BO] – высота треугольника ABC. Тогда ABC – равнобедренный треугольник с основанием AC. Отсюда – AB = BC. По свойству равенства противоположных сторон параллелограмма следует, что AB = BC = CD = AD. Таким образом, данный параллелограмм – ромб. Теорема доказана.
Но по условию (BO) (AC) и [BO] – высота треугольника ABC. Тогда ABC – равнобедренный треугольник с основанием AC. Отсюда – AB = BC. По свойству равенства противоположных сторон параллелограмма следует, что AB = BC = CD = AD. Таким образом, данный параллелограмм – ромб. Теорема доказана.
Похожие вопросы
Помогите решить эту работу. Очень срочно пожалуйста…
Один из углов, образовавшихся при пересечение двух прямых на 70 градуса больше другого….
Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB = 34…
Как будет: лучшая подруга.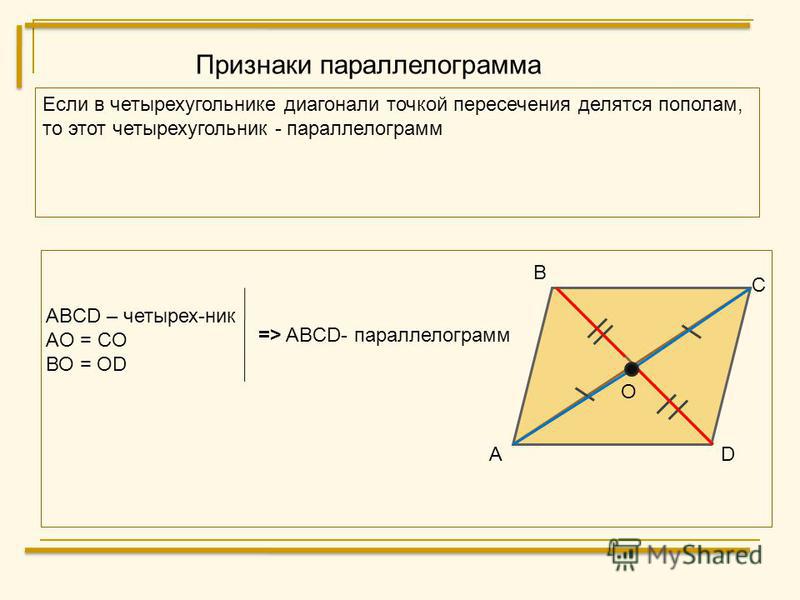 По английскому…
По английскому…
Улитка ползёт 5 см за 10 минут. За сколько минут она с такой скоростью проползёт всю длину вашего стола?…
Найти углы параллелограмма ABCD
Угол А 40 ,Угол С 25…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
| 1 | Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, делит основание на две равные части. | Смотреть видеоразбор >> |
| 2 | Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию. | Смотреть видеоразбор >> |
| 3 | Биссектриса треугольника делит пополам сторону, к которой проведена. | Смотреть видеоразбор >> |
| 4 | Биссектрисы треугольника пересекаются в центре его вписанной окружности. | Смотреть видеоразбор >> |
| 5 | В любой прямоугольник можно вписать окружность. | Смотреть видеоразбор >> |
| 6 | В любой ромб можно вписать окружность. | Смотреть видеоразбор >> |
| 7 | В любой треугольник можно вписать окружность. | Смотреть видеоразбор >> |
| 8 | В любой четырёхугольник можно вписать окружность. | Смотреть видеоразбор >> |
| 9 | В любом параллелограмме диагонали точкой пересечения делятся пополам. | Смотреть видеоразбор >> |
| 10 | В любом прямоугольнике диагонали взаимно перпендикулярны. | Смотреть видеоразбор >> |
| 11 | В любом тупоугольном треугольнике есть острый угол. | Смотреть видеоразбор >> |
| 12 | В остроугольном треугольнике все углы острые. | Смотреть видеоразбор >> |
| 13 | В параллелограмме есть два равных угла. | Смотреть видеоразбор >> |
| 14 | В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности. | Смотреть видеоразбор >> |
| 15 | В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса. | Смотреть видеоразбор >> |
| 16 | В прямоугольном треугольнике гипотенуза равна сумме катетов.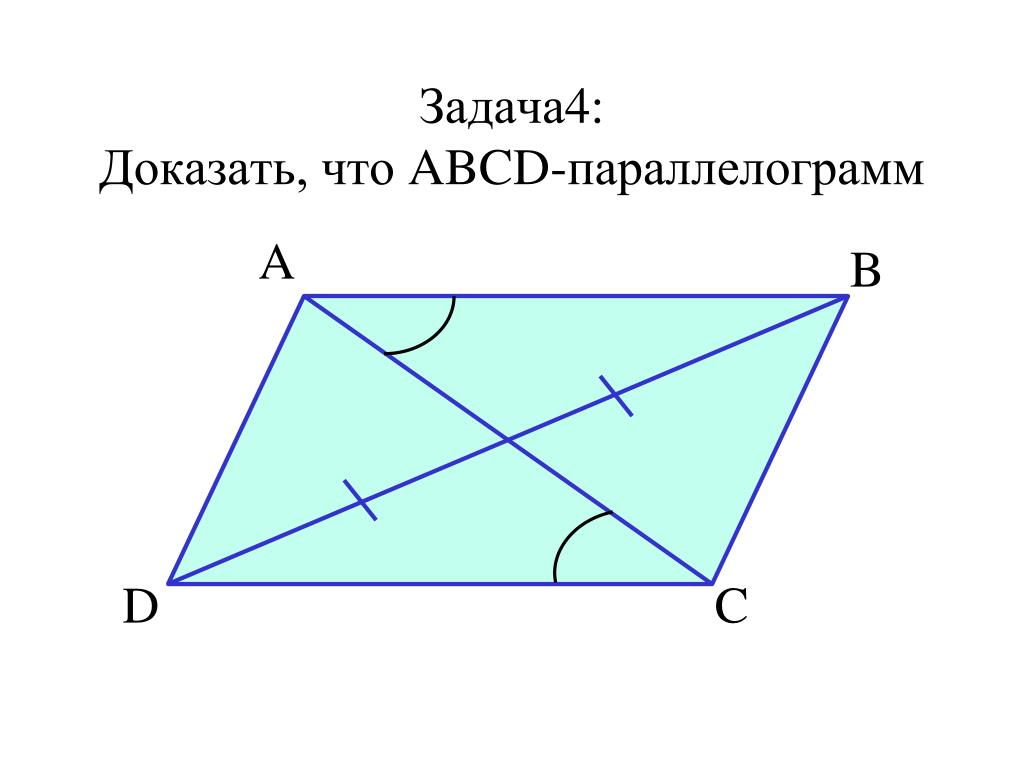 | Смотреть видеоразбор >> |
| 17 | В прямоугольном треугольнике квадрат гипотенузы равен разности квадратов катетов. | Смотреть видеоразбор >> |
| 18 | В треугольнике против большего угла лежит большая сторона. | Смотреть видеоразбор >> |
| 19 | В треугольнике против большей стороны лежит больший угол. | Смотреть видеоразбор >> |
| 20 | В тупоугольном треугольнике все углы тупые. | Смотреть видеоразбор >> |
| 21 | Вертикальные углы равны. | Смотреть видеоразбор >> |
| 22 | Внешний угол треугольника больше не смежного с ним внутреннего угла. | Смотреть видеоразбор >> |
| 23 | Внешний угол треугольника равен сумме его внутренних углов. | Смотреть видеоразбор >> |
| 24 | Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.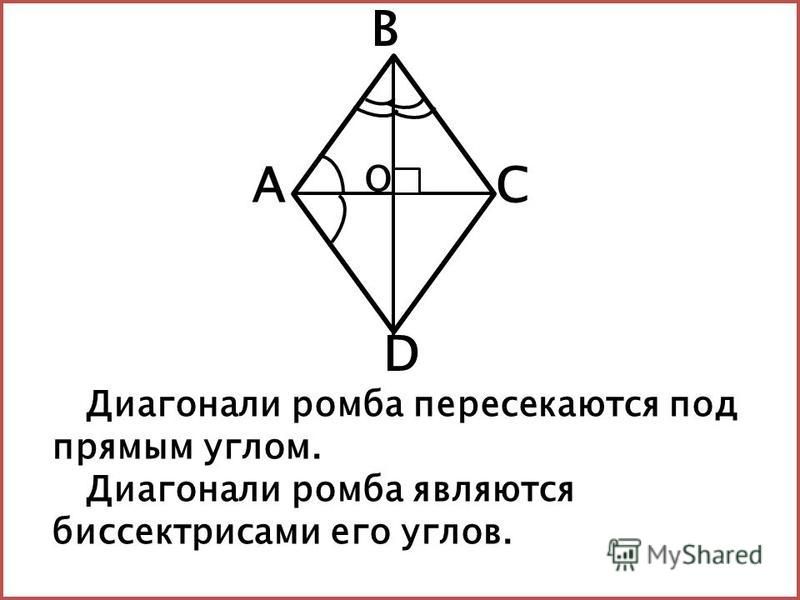 | Смотреть видеоразбор >> |
| 25 | Вокруг любого параллелограмма можно описать окружность. | Смотреть видеоразбор >> |
| 26 | Вокруг любого треугольника можно описать окружность. | Смотреть видеоразбор >> |
| 27 | Вписанный угол, опирающийся на диаметр окружности, прямой. | Смотреть видеоразбор >> |
| 28 | Вписанный угол, опирающийся на диаметр окружности, прямой. | Смотреть видеоразбор >> |
| 29 | Все высоты равностороннего треугольника равны. | Смотреть видеоразбор >> |
| 30 | Все диаметры окружности равны между собой. | Смотреть видеоразбор >> |
| 31 | Все квадраты имеют равные площади. | Смотреть видеоразбор >> |
| 32 | Все прямоугольные треугольники подобны. | Смотреть видеоразбор >> |
| 33 | Все равнобедренные треугольники подобны.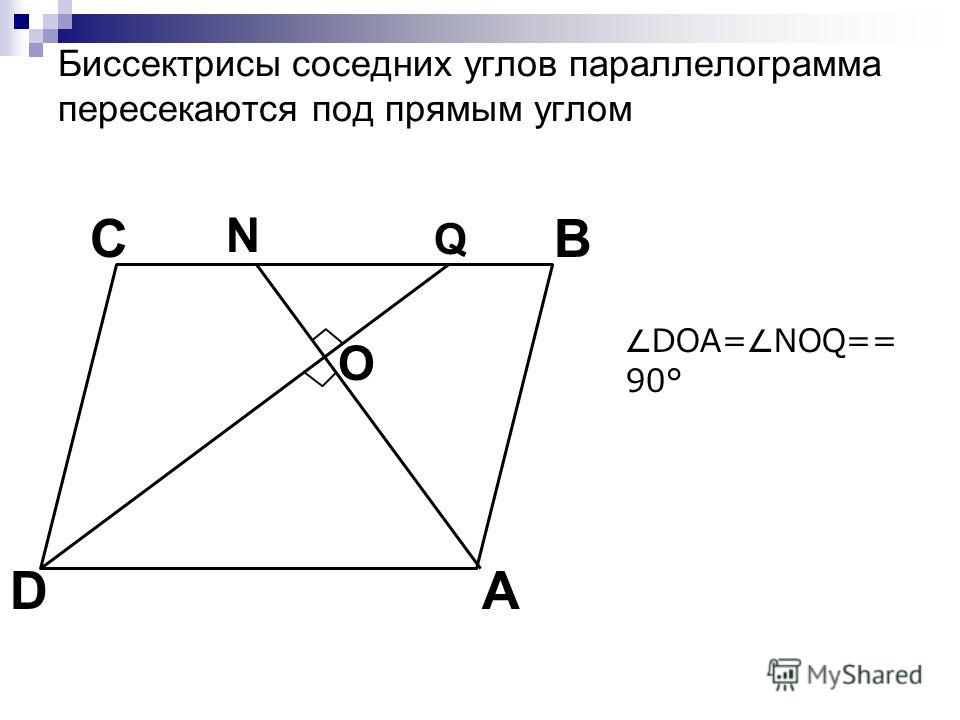 | Смотреть видеоразбор >> |
| 34 | Все равносторонние треугольники подобны. | Смотреть видеоразбор >> |
| 35 | Все углы прямоугольника равны. | Смотреть видеоразбор >> |
| 36 | Все углы ромба равны. | Смотреть видеоразбор >> |
| 37 | Все хорды одной окружности равны между собой. | Смотреть видеоразбор >> |
| 38 | Все хорды одной окружности равны между собой. | Смотреть видеоразбор >> |
| 39 | Всякий равнобедренный треугольник является остроугольным. | Смотреть видеоразбор >> |
| 40 | Всякий равносторонний треугольник является остроугольным. | Смотреть видеоразбор >> |
| 41 | Всякий равносторонний треугольник является равнобедренным. | Смотреть видеоразбор >> |
| 42 | Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.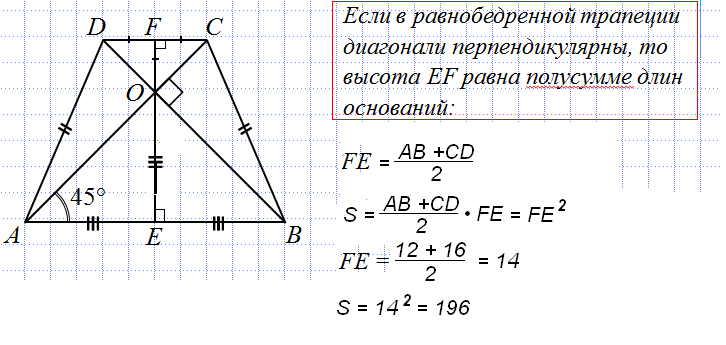 | Смотреть видеоразбор >> |
| 43 | Две прямые, параллельные третьей прямой, перпендикулярны друг другу. | Смотреть видеоразбор >> |
| 44 | Две прямые, перпендикулярные третьей прямой, параллельны друг другу. | Смотреть видеоразбор >> |
| 45 | Две прямые, перпендикулярные третьей прямой, перпендикулярны друг другу. | Смотреть видеоразбор >> |
| 46 | Диагонали квадрата взаимно перпендикулярны. | Смотреть видеоразбор >> |
| 47 | Диагонали квадрата точкой пересечения делятся пополам. | Смотреть видеоразбор >> |
| 48 | Диагонали любого прямоугольника делят его на 4 равных треугольника. | Смотреть видеоразбор >> |
| 49 | Диагонали любого прямоугольника равны. | Смотреть видеоразбор >> |
| 50 | Диагонали параллелограмма равны. | Смотреть видеоразбор >> |
| 51 | Диагонали прямоугольника равны. | Смотреть видеоразбор >> |
| 52 | Диагонали прямоугольной трапеции равны. | Смотреть видеоразбор >> |
| 53 | Диагонали равнобедренной трапеции равны. | Смотреть видеоразбор >> |
| 54 | Диагонали ромба перпендикулярны. | Смотреть видеоразбор >> |
| 55 | Диагонали ромба равны. | Смотреть видеоразбор >> |
| 56 | Диагонали ромба точкой пересечения делятся пополам. | Смотреть видеоразбор >> |
| 57 | Диагонали трапеции пересекаются и делятся точкой пересечения пополам. | Смотреть видеоразбор >> |
| 58 | Диагональ параллелограмма делит его на два равных треугольника. | Смотреть видеоразбор >> |
| 59 | Диагональ равнобедренной трапеции делит её на два равных треугольника. | Смотреть видеоразбор >> |
| 60 | Диагональ трапеции делит её на два равных треугольника. | Смотреть видеоразбор >> |
| 61 | Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса. | Смотреть видеоразбор >> |
| 62 | Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу. | Смотреть видеоразбор >> |
| 63 | Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом. | Смотреть видеоразбор >> |
| 64 | Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом. | Смотреть видеоразбор >> |
| 65 | Если в параллелограмме две соседние стороны равны, то такой параллелограмм является ромбом. | Смотреть видеоразбор >> |
| 66 | Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм – квадрат. | Смотреть видеоразбор >> |
| 67 | Если в ромбе один из углов равен 90°, то такой ромб – квадрат. | Смотреть видеоразбор >> |
| 68 | Если в треугольнике есть один острый угол, то этот треугольник остроугольный. | Смотреть видеоразбор >> |
| 69 | Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник – ромб. | Смотреть видеоразбор >> |
| 70 | Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны. | Смотреть видеоразбор >> |
| 71 | Если два угла треугольника равны, то равны и противолежащие им стороны. | Смотреть видеоразбор >> |
| 72 | Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны. | Смотреть видеоразбор >> |
| 73 | Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны. | Смотреть видеоразбор >> |
| 74 | Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны. | Смотреть видеоразбор >> |
| 75 | Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны. | Смотреть видеоразбор >> |
| 76 | Если две стороны треугольника равны, то равны и противолежащие им углы. | Смотреть видеоразбор >> |
| 77 | Если диагонали выпуклого четырёхугольника равны и перпендикулярны, то это квадрат. | Смотреть видеоразбор >> |
| 78 | Если диагонали параллелограмма перпендикулярны, то это ромб. | Смотреть видеоразбор >> |
| 79 | Если диагонали параллелограмма равны, то он является ромбом. | Смотреть видеоразбор >> |
| 80 | Если диагонали параллелограмма равны, то это квадрат. | Смотреть видеоразбор >> |
| 81 | Если диагонали параллелограмма равны, то это прямоугольник. | Смотреть видеоразбор >> |
| 82 | Если диагонали параллелограмма равны, то это ромб. | Смотреть видеоразбор >> |
| 83 | Если один из углов треугольника прямой, то треугольник прямоугольный. | Смотреть видеоразбор >> |
| 84 | Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны. | Смотреть видеоразбор >> |
| 85 | Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны, то эти прямые параллельны. | Смотреть видеоразбор >> |
| 86 | Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны. | Смотреть видеоразбор >> |
| 87 | Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.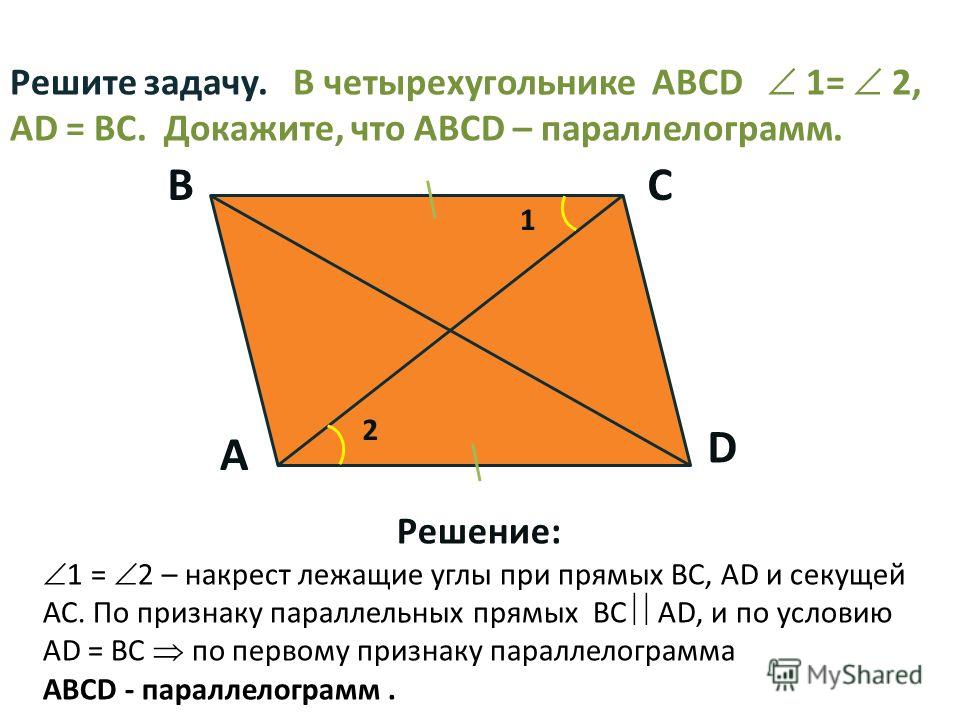 | Смотреть видеоразбор >> |
| 88 | Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла. | Смотреть видеоразбор >> |
| 89 | Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны. | Смотреть видеоразбор >> |
| 90 | Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны. | Смотреть видеоразбор >> |
| 91 | Если три угла одного треугольника равны трём углам другого треугольника, то такие треугольники подобны. | Смотреть видеоразбор >> |
| 92 | Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны. | Смотреть видеоразбор >> |
| 93 | Если угол острый, то смежный с ним угол также является острым. | Смотреть видеоразбор >> |
| 94 | Из двух хорд окружности больше та, середина которой находится дальше от центра окружности. | Смотреть видеоразбор >> |
| 95 | Каждая из биссектрис равнобедренного треугольника является его высотой. | Смотреть видеоразбор >> |
| 96 | Каждая из биссектрис равнобедренного треугольника является его медианой. | Смотреть видеоразбор >> |
| 97 | Касательная к окружности перпендикулярна радиусу, проведённому в точку касания. | Смотреть видеоразбор >> |
| 98 | Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон. | Смотреть видеоразбор >> |
| 99 | Квадрат является прямоугольником. | Смотреть видеоразбор >> |
| 100 | Косинус острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему к этому углу катету. | Смотреть видеоразбор >> |
| 101 | Любая биссектриса равнобедренного треугольника является его медианой. | Смотреть видеоразбор >> |
| 102 | Любая высота равнобедренного треугольника является его биссектрисой. | Смотреть видеоразбор >> |
| 103 | Любая медиана равнобедренного треугольника является его биссектрисой. | Смотреть видеоразбор >> |
| 104 | Любой квадрат можно вписать в окружность. | Смотреть видеоразбор >> |
| 105 | Любой квадрат является прямоугольником. | Смотреть видеоразбор >> |
| 106 | Любой квадрат является ромбом. | Смотреть видеоразбор >> |
| 107 | Любой параллелограмм можно вписать в окружность. | Смотреть видеоразбор >> |
| 108 | Любой прямоугольник можно вписать в окружность. | Смотреть видеоразбор >> |
| 109 | Любые два диаметра окружности пересекаются. | Смотреть видеоразбор >> |
| 110 | Любые два равносторонних треугольника подобны. | Смотреть видеоразбор >> |
| 111 | Медиана равнобедренного треугольника, проведённая из вершины угла, противолежащего основанию, делит этот угол пополам. | Смотреть видеоразбор >> |
| 112 | Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой. | Смотреть видеоразбор >> |
| 113 | Медиана треугольника делит пополам угол, из которого проведена. | Смотреть видеоразбор >> |
| 114 | На плоскости существует единственная точка, равноудалённая от концов отрезка. | Смотреть видеоразбор >> |
| 115 | Не существует прямоугольника, диагонали которого взаимно перпендикулярны. | Смотреть видеоразбор >> |
| 116 | Один из двух смежных углов острый, а другой тупой. | Смотреть видеоразбор >> |
| 117 | Один из углов треугольника всегда не превышает 60°. | Смотреть видеоразбор >> |
| 118 | Основания равнобедренной трапеции равны. | Смотреть видеоразбор >> |
| 119 | Отношение площадей подобных треугольников равно коэффициенту подобия. | Смотреть видеоразбор >> |
| 120 | Площадь квадрата равна произведению двух его смежных сторон. | Смотреть видеоразбор >> |
| 121 | Площадь квадрата равна произведению его диагоналей. | Смотреть видеоразбор >> |
| 122 | Площадь круга меньше квадрата длины его диаметра. | Смотреть видеоразбор >> |
| 123 | Площадь любого параллелограмма равна произведению длин его сторон. | Смотреть видеоразбор >> |
| 124 | Площадь параллелограмма равна половине произведения его диагоналей.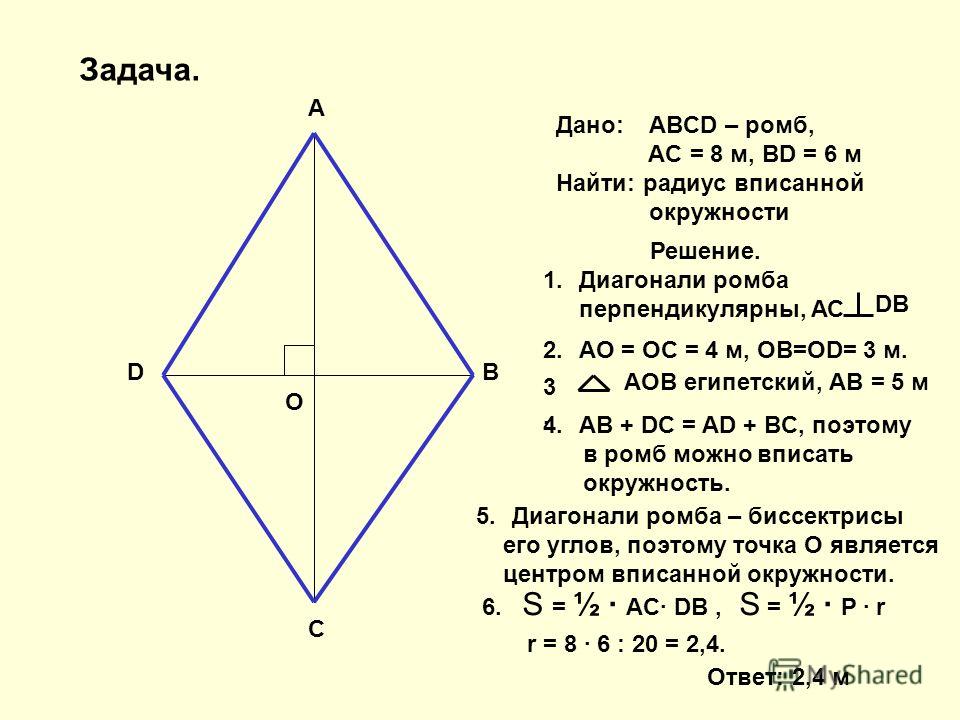 | Смотреть видеоразбор >> |
| 125 | Площадь прямоугольника равна произведению длин всех его сторон. | Смотреть видеоразбор >> |
| 126 | Площадь прямоугольника равна произведению длин его смежных сторон. | Смотреть видеоразбор >> |
| 127 | Площадь прямоугольного треугольника равна произведению длин его катетов. | Смотреть видеоразбор >> |
| 128 | Площадь ромба равна произведению двух его смежных сторон на синус угла между ними. | Смотреть видеоразбор >> |
| 129 | Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне. | Смотреть видеоразбор >> |
| 130 | Площадь трапеции равна произведению основания трапеции на высоту. | Смотреть видеоразбор >> |
| 131 | Площадь трапеции равна произведению средней линии на высоту. | Смотреть видеоразбор >> |
| 132 | Площадь треугольника не превышает произведения двух его сторон. | Смотреть видеоразбор >> |
| 133 | Против большей стороны треугольника лежит больший угол. | Смотреть видеоразбор >> |
| 134 | Против большей стороны треугольника лежит меньший угол. | Смотреть видеоразбор >> |
| 135 | Против равных сторон треугольника лежат равные углы. | Смотреть видеоразбор >> |
| 136 | Ромб не является параллелограммом. | Смотреть видеоразбор >> |
| 137 | Серединные перпендикуляры к сторонам треугольника пересекаются в центре его описанной окружности. | Смотреть видеоразбор >> |
| 138 | Смежные углы равны. | Смотреть видеоразбор >> |
| 139 | Средняя линия трапеции параллельна её основаниям.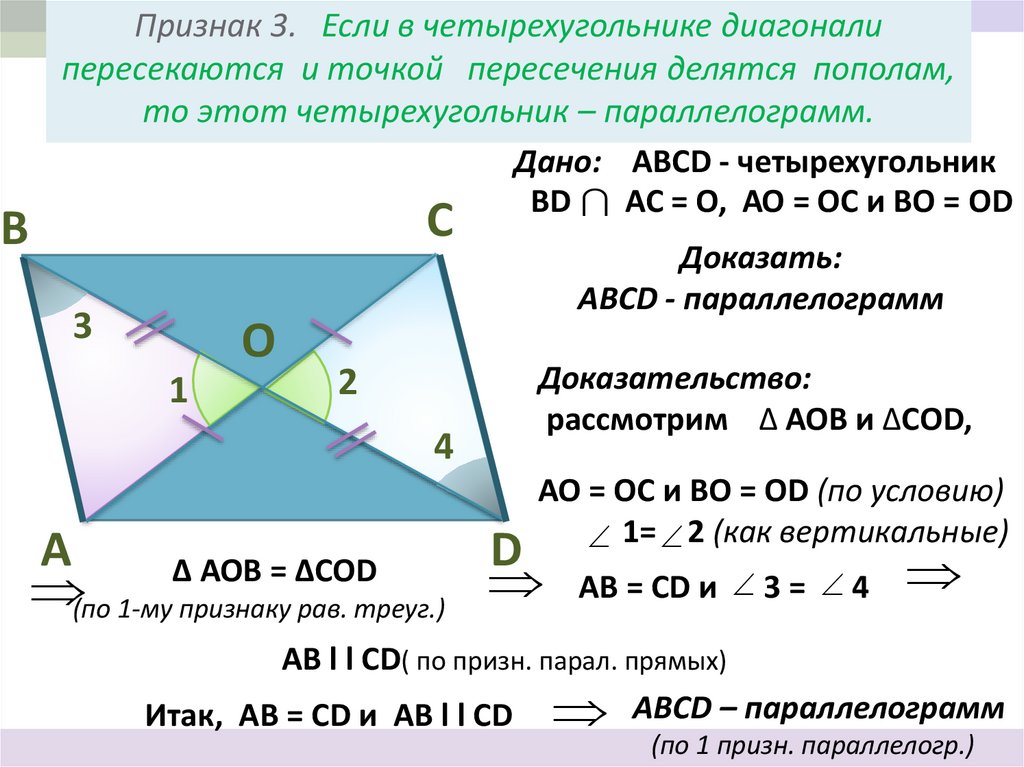 | Смотреть видеоразбор >> |
| 140 | Средняя линия трапеции равна полусумме её оснований. | Смотреть видеоразбор >> |
| 141 | Средняя линия трапеции равна сумме её оснований. | Смотреть видеоразбор >> |
| 142 | Сумма квадратов диагоналей прямоугольника равна сумме квадратов всех его сторон. | Смотреть видеоразбор >> |
| 143 | Сумма острых углов прямоугольного треугольника равна 90°. | Смотреть видеоразбор >> |
| 144 | Сумма смежных углов равна 180°. | Смотреть видеоразбор >> |
| 145 | Сумма углов выпуклого четырёхугольника равна 360°. | Смотреть видеоразбор >> |
| 146 | Сумма углов любого треугольника равна 180°. | Смотреть видеоразбор >> |
| 147 | Сумма углов любого треугольника равна 360°. | Смотреть видеоразбор >> |
| 148 | Сумма углов остроугольного треугольника равна 180°. | Смотреть видеоразбор >> |
| 149 | Сумма углов прямоугольного треугольника равна 90°. | Смотреть видеоразбор >> |
| 150 | Сумма углов равнобедренного треугольника равна 180°. | Смотреть видеоразбор >> |
| 151 | Сумма углов тупоугольного треугольника равна 180°. | Смотреть видеоразбор >> |
| 152 | Существует квадрат, который не является прямоугольником. | Смотреть видеоразбор >> |
| 153 | Существует квадрат, который не является ромбом. | Смотреть видеоразбор >> |
| 154 | Существует параллелограмм, который не является прямоугольником. | Смотреть видеоразбор >> |
| 155 | Существует прямоугольник, диагонали которого взаимно перпендикулярны. | Смотреть видеоразбор >> |
| 156 | Существует прямоугольник, который не является параллелограммом. | Смотреть видеоразбор >> |
| 157 | Существует ромб, который не является квадратом. | Смотреть видеоразбор >> |
| 158 | Существуют три прямые, которые проходят через одну точку. | Смотреть видеоразбор >> |
| 159 | Тангенс любого острого угла меньше единицы. | Смотреть видеоразбор >> |
| 160 | Точка пересечения двух окружностей равноудалена от центров этих окружностей. | Смотреть видеоразбор >> |
| 161 | Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка. | Смотреть видеоразбор >> |
| 162 | Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к этому отрезку. | Смотреть видеоразбор >> |
| 163 | Треугольник с углами 40°, 70°, 70° – равнобедренный. | Смотреть видеоразбор >> |
| 164 | Треугольник со сторонами 1, 2 и 4 существует. | Смотреть видеоразбор >> |
| 165 | Треугольника со сторонами 1, 2 и 4 не существует. | Смотреть видеоразбор >> |
| 166 | У любой прямоугольной трапеции есть два равных угла. | Смотреть видеоразбор >> |
| 167 | У любой трапеции боковые стороны равны. | Смотреть видеоразбор >> |
| 168 | У любой трапеции боковые стороны равны. | Смотреть видеоразбор >> |
| 169 | У любой трапеции основания параллельны. | Смотреть видеоразбор >> |
| 170 | У равнобедренного треугольника есть ось симметрии. | Смотреть видеоразбор >> |
| 171 | У равнобедренного треугольника есть центр симметрии. | Смотреть видеоразбор >> |
| 172 | У равностороннего треугольника есть центр симметрии. | Смотреть видеоразбор >> |
| 173 | У равностороннего треугольника три оси симметрии. | Смотреть видеоразбор >> |
| 174 | Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу. | Смотреть видеоразбор >> |
| 175 | Угол, опирающийся на диаметр окружности, прямой. | Смотреть видеоразбор >> |
| 176 | Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника. | Смотреть видеоразбор >> |
| 177 | Центр описанной около треугольника окружности всегда лежит внутри этого треугольника. | Смотреть видеоразбор >> |
| 178 | Центр описанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника. | Смотреть видеоразбор >> |
| 179 | Центром вписанной в треугольник окружности является точка пересечения его биссектрис. | Смотреть видеоразбор >> |
| 180 | Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника. | Смотреть видеоразбор >> |
| 181 | Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам. | Смотреть видеоразбор >> |
| 182 | Центры вписанной и описанной окружностей равнобедренного треугольника совпадают. | Смотреть видеоразбор >> |
| 183 | Центры вписанной и описанной окружностей равностороннего треугольника совпадают. | Смотреть видеоразбор >> |
| 184 | Через две различные точки на плоскости проходит единственная прямая. | Смотреть видеоразбор >> |
| 185 | Через заданную точку плоскости можно провести единственную прямую. | Смотреть видеоразбор >> |
| 186 | Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой. | Смотреть видеоразбор >> |
| 187 | Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.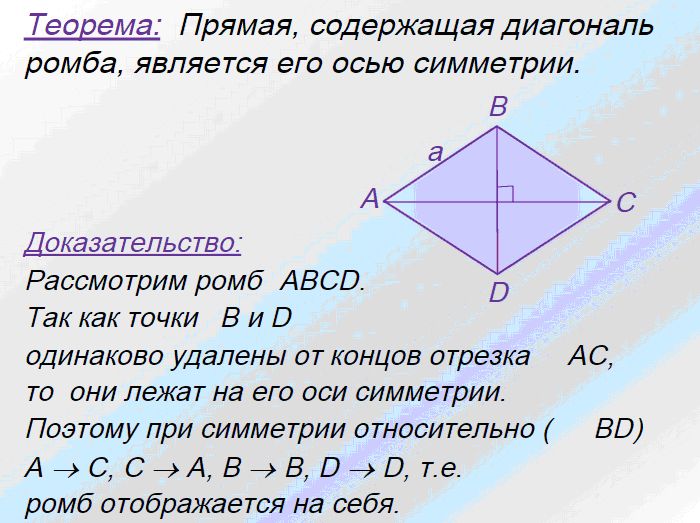 | Смотреть видеоразбор >> |
Математика по полочкам: 26. Четырехугольники
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Параллелограмм
Четырехугольник, противоположные стороны которого попарно параллельны, называется параллелограммом.
Свойства параллелограмма
1. Противоположные стороны параллелограмма равны: AB=CD, AD=BC.
2. Противоположные углы параллелограмма равны: A=C, B=D.
3. Диагонали параллелограмма делятся точкой пересечения пополам AO=OC, BO=OD.
4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон: d12+d22=2(a2+b2).
5. Каждая диагональ параллелограмма делит его на два равных треугольника.
6. Сумма внутренних углов параллелограмма 360°.
7. Сумма углов при двух соседних вершинах равна 180°.
Признаки параллелограмма
1. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
2. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
3. Если у четырехугольника диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Площадь параллелограмма
1. Площадь параллелограмма равна произведению его основания на высоту: S=BH*AD.
2. Площадь параллелограмма равна произведению его смежных сторон на синус угла между ними: S=AB*AD*sin A.
Ромб
Параллелограмм у которого все стороны равны называется ромбом.
Свойства ромба
Так ромб является параллелограммом, то он имеет все свойства параллелограмма.
1. Диагонали ромба взаимно перпендикулярны: АС ┴ ВD.
Диагонали ромба взаимно перпендикулярны: АС ┴ ВD.
2. Диагонали ромба являются биссектрисами его углов.
Признаки ромба
1. Если у параллелограмма диагонали взаимно перпендикулярны, то этот параллелограмм — ромб.
2. Если у параллелограмма одна из диагоналей лежит на биссектрисе, то этот параллелограмм — ромб.
Площадь ромба
1. Площадь ромба равна произведению его основания на высоту: S=СH*AВ.
2. Площадь ромба равна произведению квадрата его стороны на синус угла между сторонами: S=AB2*sin A.
3. Площадь ромба равна половине произведения его диагоналей: S=(d1*d2):2.
Прямоугольник
Параллелограмм, у которого все углы прямые называется прямоугольником.
Свойства прямоугольника
Так прямоугольник является параллелограммом, то он имеет все свойства параллелограмма.
1. Диагонали прямоугольника равны.
Признак прямоугольника
Если у параллелограмма диагонали равны, то этот параллелограмм — прямоугольник.
Площадь прямоугольника
Площадь прямоугольника равна произведению его смежных сторон: S = a*b.
Квадрат
Прямоугольник, у которого все стороны равны называется квадратом.
Свойства квадрата
Квадрату имеет все свойства параллелограмма, ромба и прямоугольника.
Площадь квадрата
Площадь квадрата равна квадрату его стороны: S=а2
Трапеция
Четырехугольник, две стороны которого параллельны, а две другие не параллельны называется трапецией.
Параллельные стороны трапеции называются ее основаниями (AD и ВС), а две другие — боковыми сторонами (АВ и СD).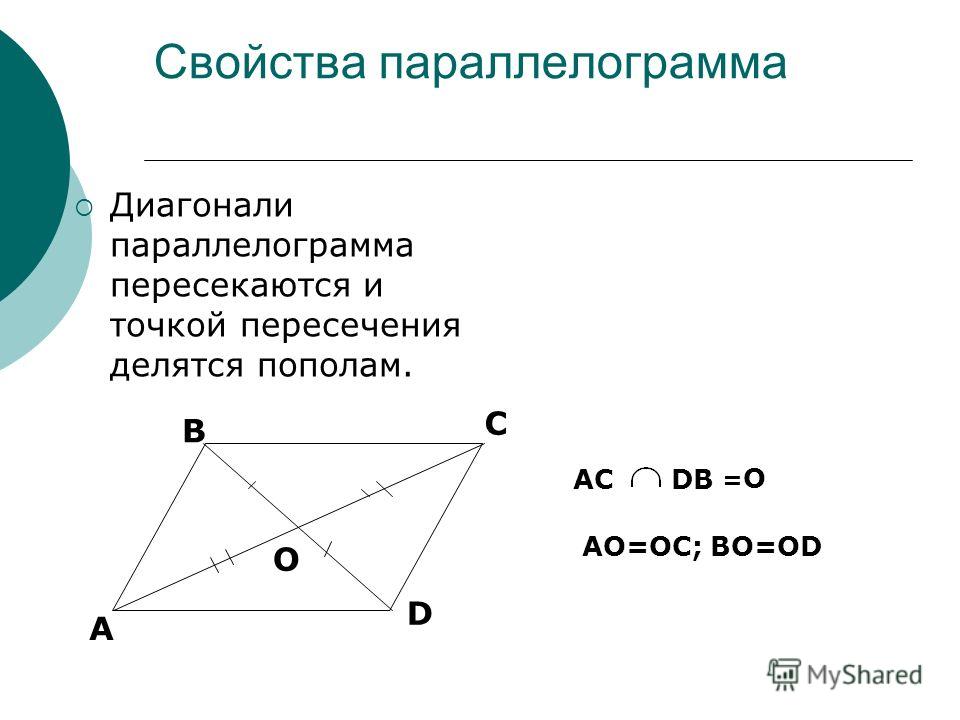
Трапеция, боковые стороны которой равны (АВ=СD), называется равнобедренной.
У равнобедренной трапеции углы при основании равны: A=D, B=C.
Диагонали равнобедренной трапеции равны: АС=BD.
Трапеция, у которой есть прямой угол называется прямоугольной.
Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям трапеции равна их полусумме: MN=(a+b):2.
Средняя линия трапеции делит высоту трапеции на два равных отрезка.
Площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту: S =(a+b):2*h.
УПРАЖНЕНИЯ
1. а) Любой ли параллелограмм является ромбом:
1) Да; 2) Нет; 3) зависит от длин его сторон; 4) зависит от величин его углов.
б) Любой ли параллелограмм является прямоугольником:
1) Да; 2) Нет; 3) зависит от длин его сторон; 4) зависит от величин его углов.
Решение:
а)зависит от длин его сторон.
Ответ: 3.
2. Является ли четырехугольник параллелограммом:
Решение:
а) В параллелограмме диагонали точкой пересечения делятся пополам, т.е. должно быть АО=ОС и ВО=OD, но ВО не равно OD ( 3 не равно 4).
Ответ: не является.
3. Найдите площадь закрашенной голубым цветом фигуры:
Решение:
а) Площадь прямоугольника ABCD равна 12*16=192.
Площадь квадрата KLMN равна 4*4=16.
Площадь фигуры, закрашенной голубым цветом равна 192-16=176.
Ответ: 176 кв.ед.
4. а) Сумма противоположных углов параллелограмма равна 160°. Найдите все углы параллелограмма.
б) Сумма противоположных углов параллелограмма равна 20°. Найдите все углы параллелограмма.
Решение:
а)
∠A+∠C=160°, т.к. противоположные углы параллелограмма равны, то ∠A=∠C=80°.
∠A+∠В =180° — по свойствам параллелограмма, тогда ∠В=180°-80°=100°.
Т.к. противоположные углы параллелограмма равны, то ∠В=∠D=100°.
Ответ: 80°, 100°, 80°, 100°.
5. а) Периметр ромба равен 24 см, а один из углов равен 120°. Найдите большую диагональ ромба.
б) Один из углов ромба равен 60°. Найдите периметр ромба, если его меньшая диагональ равна 4 см.
Решение:
а)
1) У ромба все стороны равны, тогда АВ=Р:4=24:4=6 см.
2) Пусть ∠A=120°, тогда большая диагональ ромба BD.
BD=BO+OD, т.к. диагонали ромба точкой пересечения делятся пополам.
3) ∠ВAО=120°: 2=60°, т.к. диагонали ромба являются биссектрисами его углов.
4) Рассмотри треугольник АВО, он прямоугольный, т.к. диагонали ромба пересекаются под прямым углом.
5) Найдем ВО:
ВО=АВ*sin ∠ВAО;
6. а) Докажите, что биссектрисы углов А и В параллелограмма ABCD взаимно перпендикулярны.
б) Докажите, что биссектрисы углов А и С параллелограмма ABCD параллельны.
Решение:
а)
Доказательство:
1) ∠DAК=∠ВКA как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей АК.
2) ∠ВAК=∠КAD, т.к. АК — биссектриса угла BAD.
3) Следовательно, ∠ВAК=∠ВКA, тогда треугольник АВК — равнобедренный.
4) Биссектриса ВО в равнобедренном треугольнике АВК является и высотой, т.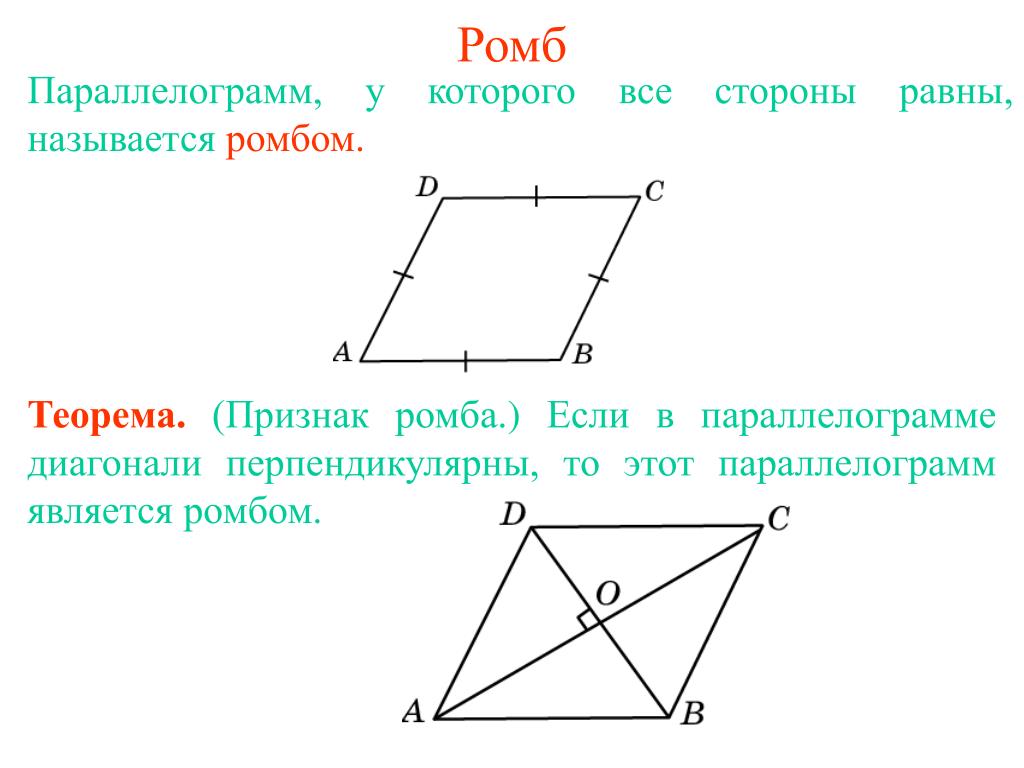 е. ВО перпендикулярно АК, а следовательно ВМ перпендикулярно АК.
е. ВО перпендикулярно АК, а следовательно ВМ перпендикулярно АК.
Что и требовалось доказать.
7. а) Диагональ DB параллелограмма ABCD перпендикулярна стороне АВ. сosA=3/5. Сторона AD=20 см. Найдите площадь параллелограмма.
б) Диагональ АС параллелограмма ABCD перпендикулярна стороне СD. sin CAD=2/3. Сторона AD=15 см. Найдите площадь параллелограмма.
Решение:
а)
Площадь параллелограмма может быть вычислена по формуле S=BD*AB.
1) Найдем АВ:
cos A=AB:AD, AB=AD*cos A=20*3/5=12 см.
2) Найдем BD:
По теореме Пифагора: BD2=AD2-AB2=400-144=256, BD=16 см.
3) Найдем площадь:
S=16*12=192 см2
Ответ: 192 см2
8. а) В равнобедренной трапеции с основаниями 10 см и 6 см диагонали перпендикулярны боковым сторонам. Найдите площадь трапеции.
а) В равнобедренной трапеции с основаниями 10 см и 6 см диагонали перпендикулярны боковым сторонам. Найдите площадь трапеции.
б) Площадь равнобедренной трапеции равна 54 см2. Средняя линия трапеции равна 9 см. Диагонали перпендикулярны боковым сторонам. Найдите основания трапеции.
Решение:
а)
1) Треугольник ACD прямоугольный. Проведем к гипотенузе этого треугольника высоту СН.
HD=(AD-BC):2=(10-6):2=2 см, т.к. ABCD — равнобедренная трапеция.
2)CH2=АН*HD=10*2=20,
2)
9. а) АМ и DM — биссектрисы параллелограмма ABCD. М лежит на стороне ВС параллелограмма. Найти площадь параллелограмма, если АМ=4 см, DM=3 см.
б) BМ и CM — биссектрисы параллелограмма ABCD. М лежит на стороне AD параллелограмма. Найти площадь параллелограмма, если BМ=6 см, CM=4 см.
Найти площадь параллелограмма, если BМ=6 см, CM=4 см.
Решение:
а)
1) Найдем угол AMD:
∠А+∠D=180° как углы при соседних вершинах. ∠МАD+∠ADM=(∠А+∠D):2=90°, т.к. АМ и DM — биссектрисы углов А и D.
Тогда ∠AMD=180-(∠МАD+∠ADM)=180-90=90°.
2) Треугольник AMD — прямоугольный, тогда по теореме Пифагора найдем AD:
AD2=AM2+MD2=16+9=25, AD=5 см.
3) Найдем высоту параллелограмма.
МН — высота в прямоугольном треугольнике, а также и высота параллелограмма.
SAMD = AM*MD:2=4*3:2=6 см.
SAMD = MH*AD:2; 6=MH*5:2; MH=2,4 см
4) Найдем площадь параллелограмма:
S=MH*AD=2,4*5=12 см2.
Ответ: 12 см2.
10. а) В трапеции ABCD проведена прямая, параллельная основаниям, которая пересекает боковые стороны трапеции в точках E и F. Найти площадь трапеции AEFD, если площадь трапеции EBCF равна 20 см2 и ВС=4 см, EF=8 см, AD=16 см.
б) В трапеции ABCD проведена прямая, параллельная основаниям, которая пересекает боковые стороны трапеции в точках M и N. Найти площадь трапеции MBCN, если площадь трапеции AMND равна 48 см2 и ВС=4 см, MN=6 см, AD=9 см.
Решение:
а)
1) Трапеции AEFD и EBCF подобны:
1. ∠1=∠2, ∠3=∠4 как соответственные углы при параллельных прямых EF и AD.
2. ∠5=∠6, ∠7=∠8 как соответственные углы при параллельных прямых EF и ВС.
2) Найдем коэффициент подобия:
k=EF:BC=8:4=2.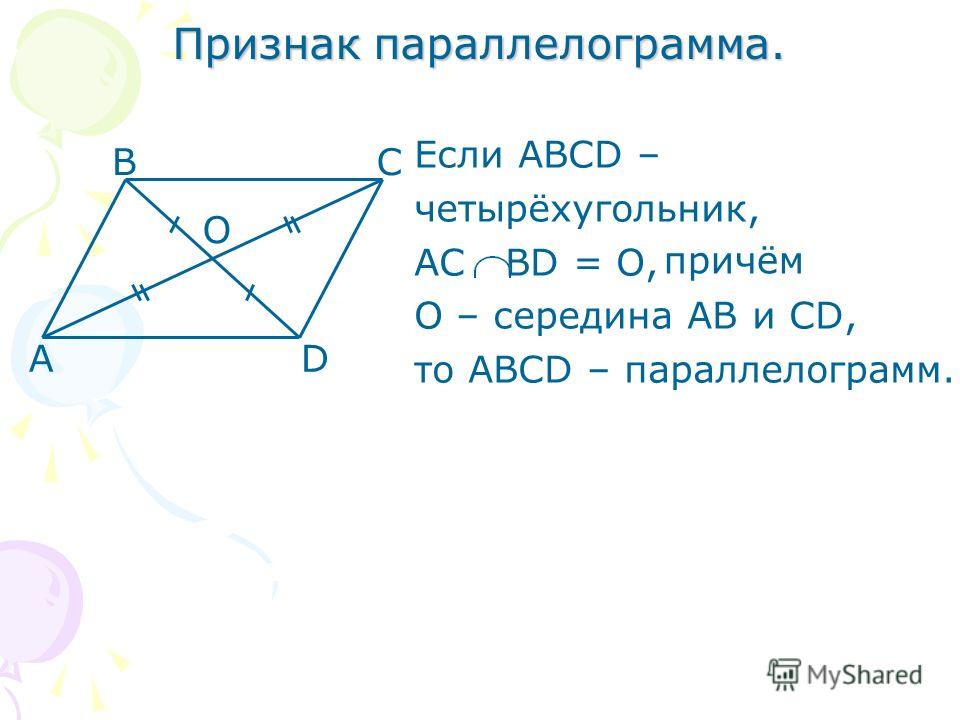
3) Площади подобных фигур относятся как коэффициент подобия в квадрате.
SAEFD = SEDCF *k2= 20*4=80 см2.
Ответ: 80 см2.
11. а) В параллелограмме ABCD отрезок CF пересекает диагональ BD в точке О (F лежит на стороне АD). Найдите площадь параллелограмма, если площади треугольников ODF и CDO раны 12 см2 и 20 см2 соответственно.
б) В параллелограмме ABCD отрезок ВF пересекает диагональ АС в точке О (F лежит на стороне АD). Найдите площадь параллелограмма, если площади треугольников OFA и OBA раны 12 см2 и 8 см2 соответственно.
Решение:
а)
1) Проведем к CF высоту DH.
Рассмотрим площади треугольников FOD и OCD:
SODF = DH*OE:2; 12= DH*OE:2; DH*OF=24. (1)
SCDO = DH*OC:2; 20 = DH*OC:2; DH*OC=40. (2)
Разделим выражение (2) на (1): OC:OF=40:24, OC:OF=5:3.
2) Треугольники BOC и FOD подобны по двум углам:
1. ∠FOD=∠BOC как вертикальные углы;
2. ∠СFD=∠FCB как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей FC.
3) Площади подобных фигур относятся как коэффициент подобия в квадрате.
SBOC = SFOD*k2=12*(5/3)2=100/3 см2.
4) Найдем площадь треугольника BCD:
SBCD= SBCO + SOCD=100/3+20=53 1/3 см2.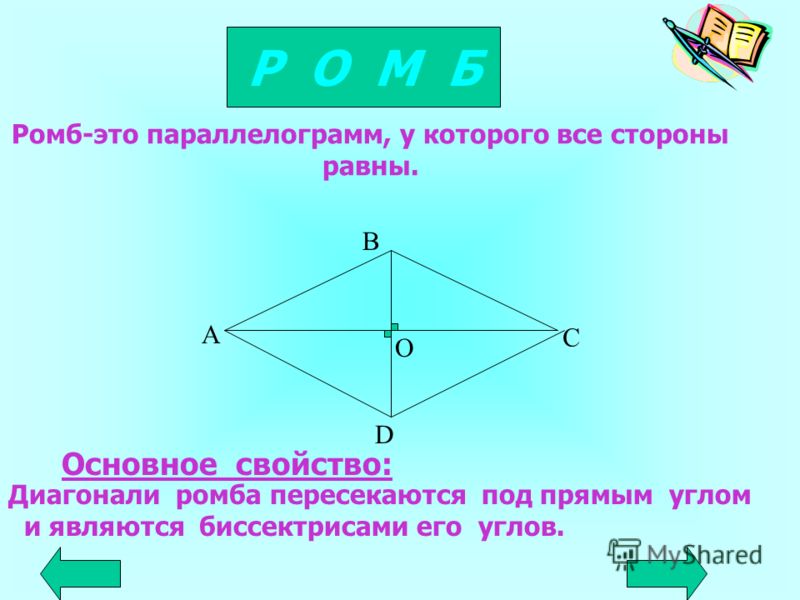
5) Найдем площадь параллелограмма:
SABCD=2*SBCD=106 2/3 см2.
Ответ: 106 2/3 см2.
12. а) Средняя линия трапеции равна 5 см, диагонали трапеции равны 14 см и 8 см. Найдите площадь трапеции.
б) Средняя линия трапеции равна 10 см, диагонали трапеции равны 14 см и 10 см. Найдите площадь трапеции.
Решение:
а)
Дано: ABCD — трапеция;
АС=14 см;
BD=8 см;
MN — средняя линия; MN=5 см.
Найти: S трапеции.
1) AD+BC=2*MN=2*5=10 см.
2) AB+CD=BC+AD=10 cм.
3) Проведем прямую СЕ параллельно прямой BD. E — точка пересечения прямых AD и CE.
DBCE — параллелограмм, т.к. две пары противолежащих сторон параллельны.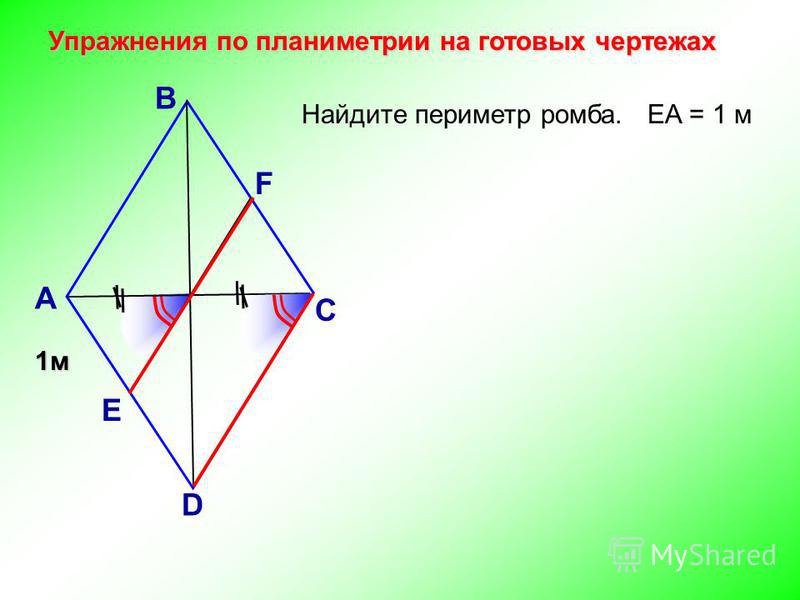
DE=BC и BD=CE=8 см, т.к. противолежащие стороны параллелограмма равны.
АЕ=AD+DE=AD+BC=10 см.
4) Найдем площадь треугольника АСЕ по формуле Герона:
р=(АС+СЕ+АЕ):2=(14+8+10):2=16 см.
5) Найдем площадь трапеции:
Треугольники ABC и CED имеют одинаковую площадь, т.к. их площади равны половине произведения высоты трапеции на равные стороны ВС и DE.
Тогда площадь трапеции равна площади треугольника АСЕ:
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Если в четырехугольнике противоположные стороны попарно равны, то это:
а) квадрат; б) ромб; в) трапеция; г) прямоугольник; д) параллелограмм.
2. Является ли четырехугольник параллелограммом, если одна пара его противоположных сторон равна, а другая параллельна?
3. В равнобедренной трапеции ABCD с основаниями AB и CD сумма углов А, В, С равна 340°.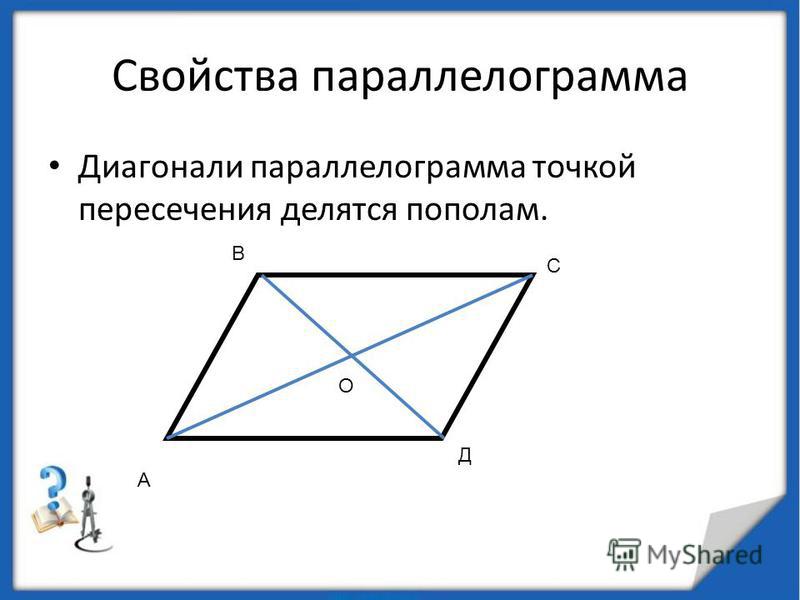 Найдите все углы трапеции.
Найдите все углы трапеции.
4. В параллелограмме ABCD угол А равен 60°, сторона ВС равна 10 см, высота СН проведена из вершины С к стороне AD и АН=14 см. Найдите периметр параллелограмма.
5. Диагонали ромба относятся как 2:5. Найдите площадь ромба, если его периметр равен 10 см.
6. Площадь прямоугольника равна 54 см2. Найдите площадь четырехугольника вершинами которого являются середины сторон данного прямоугольника.
7. В параллелограмме ABCD к сторонам BC и DC проведены высоты из точки А, угол между высотами равен 45° и одна из высот делит сторону DC на отрезки 3 см и 4 см, считая от вершины С. Найдите площадь параллелограмма.
8. Найдите среднюю линию трапеции, если ее диагонали взаимно перпендикулярны и равны 12 см и 16 см.
9. Может ли четырехугольник с противоположными наборами сторон a и b, c и d являться трапецией, если да, то найти ее площадь:
а) a=5 см, b=4 см, c=6 см, d=3 см; б) a= 3 см, b=4 см, c=5 см, d=3 см.
10. Площадь трапеции ABCD равна 100 см2. Из середины стороны АВ к стороне CD проведен перпендикуляр, который равен 16 см. Найдите боковую сторону CD.
Площадь трапеции ABCD равна 100 см2. Из середины стороны АВ к стороне CD проведен перпендикуляр, который равен 16 см. Найдите боковую сторону CD.
ПРОВЕРЬТЕ СЕБЯ
ЕГЭ — математика (база): Трапеция
Четырёхугольник
Параллелограмм.
Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.
Свойства и признаки параллелограмма
1. Диагональ разбивает параллелограмм на два равных треугольника.
2. Противоположные стороны параллелограмма попарно равны.
3. Противоположные углы параллелограмма попарно равны.
4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
5. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.
6. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.
7. Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник — параллелограмм.
Свойство середин сторон четырёхугольника. Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырёхугольника.
Прямоугольник. Прямоугольником называется параллелограмм с прямым углом.
Свойства и признаки прямоугольника
1. Диагонали прямоугольника равны.
2. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник
Квадрат. Квадратом называется прямоугольник, все стороны которого равны.
Формулы площади четырёхугольника
1. Площадь параллелограмма равна произведению основания на высоту
2. Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.
3. Площадь прямоугольника равна произведению двух его соседних сторон.
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
| a, b, c, d — стороны; D1, D2 — диагонали; γ — угол между диагоналями; h2, h3 — длины перпендикуляров, опущенных на диагональ D1; α, β — два противолежащих угла четырёхугольника. | ||
| a, b — стороны; h — расстояние между сторонами b; α — угол параллелограмма; D1, D2 — диагонали; γ — угол между диагоналями |
Площадь четырёхугольника
Площадь прямоугольника равна произведению его смежных сторон:
S = ab.
На рисунке 156 приведены чертежи некоторых прямоугольников, у которых показаны смежные стороны a и b
Ромб
Квадрат. Квадратом называется прямоугольник, все стороны которого равны.
Свойства и признаки ромба
1. Диагонали ромба перпендикулярны.
2. Диагонали ромба делят его углы пополам
3. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.
Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.
4. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
Площадь ромба равна половине произведения его диагоналей
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
| a, b, c, d — стороны; D1, D2 — диагонали; γ — угол между диагоналями; h2, h3 — длины перпендикуляров, опущенных на диагональ D1; α, β — два противолежащих угла четырёхугольника. | ||
| a — сторона; α — угол ромба; D1, D2 — диагонали. |
Трапеция
Трапецией называется четырёхугольник, у которого только две противоположные стороны (основания) параллельны. Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).
1. Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
Замечательное свойство трапеции. Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.
Равнобедренная трапеция. Трапеция называется равнобедренной, если её боковые стороны равны.
Свойства и признаки равнобедренной трапеции
1. Углы при основании равнобедренной трапеции равны.
2. Диагонали равнобедренной трапеции равны
3. Если углы при основании трапеции равны, то она равнобедренная.
4. Если диагонали трапеции равны, то она равнобедренная
5. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали — полусумме оснований.
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.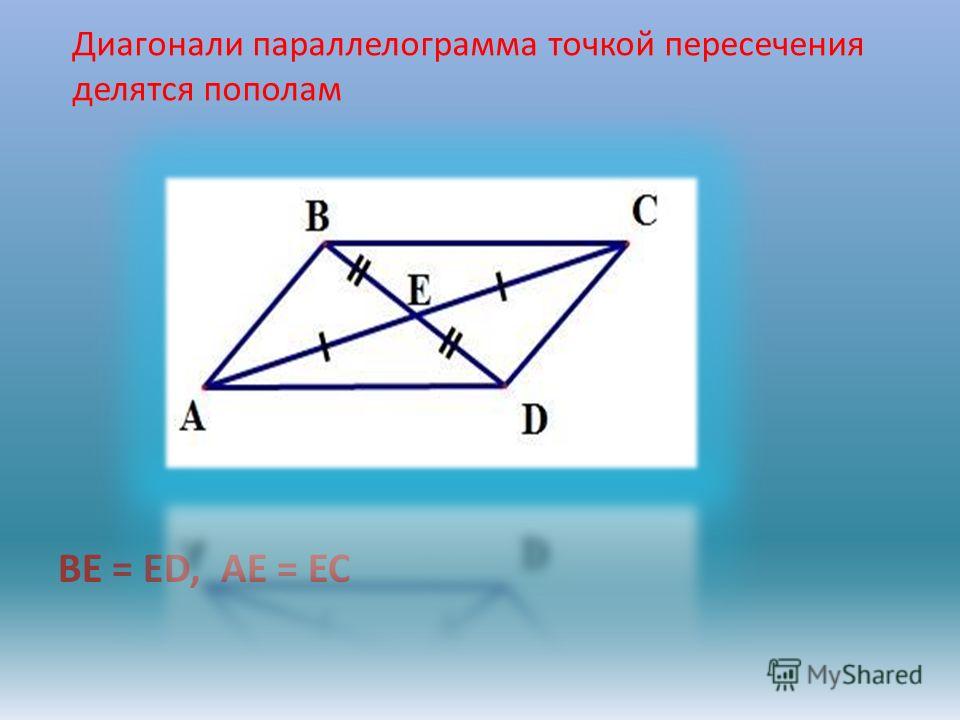
| Чертежи | Обозначения | Формулы |
| a, b, c, d — стороны; D1, D2 — диагонали; γ — угол между диагоналями; h2, h3 — длины перпендикуляров, опущенных на диагональ D1; α, β — два противолежащих угла четырёхугольника. | ||
| a, b — основания; c, d — боковые стороны; D1, D2 — диагонали; α — угол между диагоналями; m — средняя линия; h — высота |
Площадь трапеции равна половине произведения суммы оснований (a + b) на высоту (h):
На рисунке 168 приведены чертежи некоторых трапеций, у каждой из которых показаны основания a и b и высота h.
Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
| a, b, c, d — стороны; D1, D2 — диагонали; γ — угол между диагоналями; h2, h3 — длины перпендикуляров, опущенных на диагональ D1; α, β — два противолежащих угла четырёхугольника.  | ||
| n — число сторон; a — сторона; R — радиус описанной окружности; r — радиус вписанной окружности; α = 180° − 2γ — угол многоугольника |
Когда параллелограмм является ромбом?
Я думаю о параллелограмме, диагонали которого перпендикулярны. Назовите этот параллелограмм.
Если вы догадались, что это квадрат, то вы плохо читали заголовок этого раздела. Это ромб! Хорошая вещь в работе с параллелограммами заключается в том, что диагонали создают множество треугольников, просто умоляющих, чтобы их конгруэнтность была доказана. На рис. 16.6 диагонали параллелограмма ABCD перпендикулярны. Конгруэнтные треугольники пытаются общаться с вами. Слушайте внимательно.
Рисунок 16.6 Параллелограмм ABCD с ¯AC ¯BD.
- Теорема 16.6 : Если диагонали параллелограмма перпендикулярны, то параллелограмм является ромбом.
Давайте сразу перейдем к плану игры. Вы знаете, что ¯AC ¯BD, поэтому mAMB = 90º и mCMB = 90º. Поскольку диагонали параллелограмма делят друг друга пополам, вы знаете, что ¯AM ~= ¯MC. Рефлексивное свойство ~= позволяет писать ¯BM ~= ¯BM. По постулату SAS вы знаете, что AMB ~= CMB. По CPOCTAC вы знаете, что ¯AB ~= ¯BC. Поскольку ¯AB ~= ¯BC и ¯AB ~= ¯BC являются смежными сторонами, у вас есть параллелограмм с конгруэнтными смежными сторонами, он же ромб.
Вы знаете, что ¯AC ¯BD, поэтому mAMB = 90º и mCMB = 90º. Поскольку диагонали параллелограмма делят друг друга пополам, вы знаете, что ¯AM ~= ¯MC. Рефлексивное свойство ~= позволяет писать ¯BM ~= ¯BM. По постулату SAS вы знаете, что AMB ~= CMB. По CPOCTAC вы знаете, что ¯AB ~= ¯BC. Поскольку ¯AB ~= ¯BC и ¯AB ~= ¯BC являются смежными сторонами, у вас есть параллелограмм с конгруэнтными смежными сторонами, он же ромб.
| Statements | Reasons | |||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | Parallelogram ABCD has ¯AC ¯BD | Given | ||||||||||||||||||||||||||||||||||||||||||||
| 2. | AMB and CMB are right | Definition of | ||||||||||||||||||||||||||||||||||||||||||||
| 3 | mAMB = 90° и mCMB = 90° | Определение прямого угла | ||||||||||||||||||||||||||||||||||||||||||||
| 4. | AMB ~= CMB | Определение ~= | 5 0029¯AM ~= ¯MC | Theorem 15.6 | ||||||||||||||||||||||||||||||||||||||||||
| 6. | ¯BM ~= ¯BM | Reflexive property of ~= | ||||||||||||||||||||||||||||||||||||||||||||
7. | AMB ~= CMB | SAS Postulate | ||||||||||||||||||||||||||||||||||||||||||||
| 8. | ¯ab ~ = ¯BC | CPOCTAC | ||||||||||||||||||||||||||||||||||||||||||||
| 9. | Parallelogram ABCD — Rhombus | . Предположим, у вас есть прямоугольник ABCD. Найдите середины каждой стороны прямоугольника и последовательно соедините их, чтобы получился четырехугольник MNOP, как показано на рис. 16.7. Какой четырехугольник получился? Рисунок 16.7 Прямоугольник ABCD, середины каждой стороны которого последовательно соединены вместе, образуя четырехугольник MNOP. Судя по картинке, это похоже на параллелограмм. Вы должны быть осторожны, потому что ooks может быть обманчивым. Также похоже, что диагонали вновь созданного четырехугольника перпендикулярны. Если рисунок точен, у вас может возникнуть соблазн заключить, что четырехугольник является ромбом. Давайте докажем это.
Для этого нужен серьезный план игры. Поскольку M, N, O и P являются серединами ¯AB, ¯BC, ¯CD и ¯AD, вы знаете, что ¯BN ~= ¯NC ~= ¯AP ~= ¯PD и ¯AM ~= ¯MB ~= ¯OD ~= ¯CO. Поскольку вы имеете дело с прямоугольником, вы знаете, что mA = 90°, mB = 90°, mC = 90° и mD = 90°. Итак, согласно постулату SAS, PAM ~= NBM ~= PDO ~= NCO. Применяя принцип CPOCTAC ¯MN ~= ¯MP ~= ¯PO ~= ¯NO. Значит противоположные стороны равны и четырехугольник MNOP является параллелограммом. Кроме того, смежные стороны равны, поэтому параллелограмм MNOP является ромбом.
Выдержки из Полное руководство идиота по геометрии © 2004 Дениз Сечеи, доктор философии. Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете приобрести эту книгу на Amazon.com и в Barnes & Noble.
РомбГорячая математикаА ромб это параллелограмм с четырьмя конгруэнтный стороны. Множественное число слова ромб ромбы . (Я люблю это слово.) Формула для область формула ромба аналогична формуле параллелограмма: А знак равно б час , куда б это длина основания и час это высота. Область
знак равно
5
⋅
4
знак равно
20
см
2
. Диагонали ромбаЕсли параллелограмм является ромбом, то его диагонали перпендикулярны. Например: Если п Вопрос р С является ромбом, то п р ¯ ⊥ Вопрос С ¯ . Если параллелограмм является ромбом, то каждая диагональ делит пополам пару противоположных углов. Например: Если п Вопрос р С является ромбом, то ∠
1
≅
∠
2
,
∠
3
≅
∠
4
,
∠
5
≅
∠
6
,
а также
∠
7
≅
∠
8
. Пример 1: В ромбе А Б С Д , м ∠ А Б С знак равно 2 Икс − 7 а также м ∠ Б С Д знак равно 2 Икс + 3 . Находить м ∠ Д А Б . В ромбе последовательные внутренние углы являются дополнительными. Так, м ∠ А Б С + м ∠ Б С Д знак равно 180 ° . Подставьте меры и решите
Икс
. 2 Икс − 7 + 2 Икс + 3 знак равно 180 ° 4 Икс знак равно 184 Икс знак равно 46 Используйте значение Икс найти м ∠ Д А Б . Каждая пара противоположных углов ромба конгруэнтна. Так, м ∠ Д А Б знак равно м ∠ Б С Д знак равно 2 ( 46 ) + 3 знак равно 95 ° . Пример 2: В ромбе
Икс
Д
Z
Вт
,
м
∠
Вт
Д
Z
знак равно
63
°
. Диагонали ромба перпендикулярны. Так, м ∠ Д В Z знак равно 90 ° а также Δ Д В Z это прямоугольный треугольник . Используйте теорему о сумме углов. м ∠ Д Z В + м ∠ Z В Д + м ∠ В Д Z знак равно 180 ° Подставьте меры и решите. м ∠ Д Z В + 90 ° + 63 ° знак равно 180 ° м ∠ Д Z В + 153 ° знак равно 180 ° м ∠ Д Z В знак равно 27 ° Площадь ромба: диагональ, формула и примеры Если бы вы увидели воздушного змея, летящего по небу в ветреный день, вы, вероятно, сказали бы, что он имеет форму алмаза. Ромб — это четырехугольник, у которого все 4 стороны равны, что делает его равносторонним. Формула площади ромбаУ нас есть специальная формула для нахождения площади ромба. Рассмотрим следующий ромб с диагоналями d 1 и d 2 . Ромб с диагоналями d1 и d2 — Nilabhro Datta, StudySmarter Originals Площадь ромба находится по формуле: Параллелограмм также применим к ромбу и может быть использован для нахождения площади любого ромба. Рассмотрим следующий параллелограмм. Параллелограмм с основанием b и высотой h — Nilabhro Datta, StudySmarter Originals Площадь параллелограмма определяется по формуле: Площадь параллелограмма = b × h где b = основание, h = высота Теперь значение b — это длина стороны AB, которая здесь считается основанием. Условно за основание принимают одну из длинных сторон параллелограмма. Однако, поскольку все стороны ромба равны, любую сторону можно считать основанием. Кроме того, высота или высота будут одинаковыми независимо от того, какая сторона принята за основу. В параллелограмме, показанном выше, мы видим, что не все стороны имеют одинаковую длину, что означает, что этот параллелограмм не является ромбом. Обратите внимание, что для площади мы всегда используем квадратные единицы. Например, если мы используем единицы СИ, единицей длины в СИ будет метр (м), а это означает, что единицей площади в СИ будет квадратный метр (м²). Примеры: Уравнение площади ромба Давайте рассмотрим несколько примеров задач, связанных с площадью ромба. Площадь показанного ниже ромба WXYZ равна 138 в 2 . Найдите длину диагонали XZ в дюймах. РастворМы знаем, что для ромба: Следовательно: Диагонали ромба равны 6 м и 7 м. Чему равна площадь ромба? РешениеРомб площадью 100 квадратных единиц имеет высоту 8 единиц. Какова длина сторон ромба. РешениеПоскольку ромб является параллелограммом, здесь можно применить формулу площади параллелограмма: Площадь = основание × высота Мы знаем, что площадь равна 100 кв. единиц, а высота равна 8 единицам. Итак, 100 = основание × 8 ⇒ основание = 100 ÷ 8 = 12,5 Длина сторон ромба 12,5 единиц. Особый случай ромба: Площадь квадрата Возможно, вы заметили, что квадрат также соответствует определению ромба (четырехугольник с 4 равными сторонами). Квадрат на самом деле является частным случаем ромба, потому что все 4 стороны квадрата равны. Квадрат — частный случай ромба и прямоугольника — Nilabhro Datta, StudySmarter Originals Как и в случае с ромбом, формула площади ромба может быть применена к квадрату. Однако использование формулы площади для параллелограммов также является применимым методом, поскольку квадраты и ромбы также являются параллелограммами. Посмотрите на приведенный выше квадрат и вспомните формулу площади параллелограмма: Площадь = основание × высота Возьмем основание за сторону АВ. Поскольку углы в квадрате прямые, высота считается длиной любой из сторон, AD или BC. Это означает, что сторона основания равна размеру высоты, так как все 4 стороны квадрата равны. Таким образом, в случае квадрата приведенную выше формулу можно сократить до: Площадь = сторона × сторона Площадь квадрата равна 64. Найдите длины сторон и диагоналей квадрата. РешениеПлощадь = сторона × сторона ⇒ 64 = сторона 2 ⇒ сторона = Длина сторон квадрата равна 8. Так как квадрат также является ромбом формула площади ромба к нему. Диагонали квадрата также можно вычислить с помощью теоремы Пифагора, если сторона известна. Например, в приведенном выше примере диагональ можно было бы также вычислить с помощью теоремы Пифагора после того, как мы узнали, что длины сторон равны 8,9.0003 По теореме Пифагора, Поскольку диагонали квадрата равны, это вычисление дает длину обеих диагоналей. Площади ромбов. Ключевые выводы
Свойства параллелограмма — теоремы, доказательства, примеры Свойства параллелограмма помогают нам легко и быстро идентифицировать параллелограмм из заданного набора фигур.
Каковы свойства параллелограмма? Параллелограмм — это тип четырехугольника, в котором противоположные стороны параллельны и равны. В параллелограмме при вершинах четыре угла. Понимание свойств параллелограмма помогает легко связать его углы и стороны. Кроме того, свойства полезны для вычислений в задачах, касающихся сторон и углов параллелограмма. Четыре важных свойства углов и сторон параллелограмма таковы:
Все вышеперечисленные свойства справедливы для всех типов параллелограммов, но теперь давайте также узнаем об индивидуальных свойствах некоторых специальных параллелограммов. Три разных параллелограмма — квадрат, прямоугольник и ромб, которые отличаются друг от друга из-за своих свойств, но все они подпадают под категорию параллелограммов. Свойства квадрата:
Свойства прямоугольника:
Свойства ромба:
Теперь давайте расширим наши знания, изучив свойства диагоналей параллелограммов в следующем разделе. Свойства диагоналей параллелограмма Сначала вспомним значение диагонали. Диагонали – это отрезки, соединяющие противоположные вершины.
Теоремы о свойствах параллелограммаТеоремы о свойствах параллелограмма помогают определить правила решения задач на параллелограммы. Свойства, относящиеся к сторонам и углам параллелограмма, легко понять и применить для решения различных задач. Кроме того, эти теоремы также поддерживают понимание концепций других четырехугольников. Ниже приведены четыре важные теоремы, относящиеся к свойствам параллелограмма:
Теорема 1. Доказательство: Дано: ABCD — параллелограмм. Доказать: Противоположные стороны равны, AB = CD и BC = AD. В параллелограмме ABCD сравните треугольники ABC и CDA. В этих треугольниках:
Следовательно, по критерию ASA оба треугольника конгруэнтны и соответствующие стороны равны. Следовательно, мы имеем AB = CD и BC = AD. Обратное к теореме 1: если в четырехугольнике противоположные стороны равны, то это параллелограмм. Доказательство: Дано: В четырехугольнике ABCD противоположные стороны равны, AB = CD и BC = AD. Доказать: ABCD — параллелограмм. В четырехугольнике ABCD дано, что AB = CD и AD = BC.
Таким образом, по критерию SSS оба треугольника равны и соответствующие углы равны. Отсюда можно сделать вывод, что ∠BAC = ∠DCA, а ∠BCA = ∠DAC. Поэтому AB || CD, Британская Колумбия || AD, ABCD — параллелограмм. Теорема 2. В параллелограмме противоположные углы равны. Проба: Дано: ABCD — параллелограмм, а ∠A, ∠B, ∠C, ∠D — четыре угла. Доказать: ∠A = ∠C и ∠B = ∠D Предположим, что ABCD — параллелограмм. Теперь сравните треугольники ABC и CDA. Здесь у нас есть,
Таким образом, согласно ASA, два треугольника конгруэнтны, а это означает, что ∠B = ∠D. Обратное к теореме 2: Если в четырехугольнике противоположные углы равны, то это параллелограмм. Доказательство: Дано: ∠A = ∠C и ∠B = ∠D в четырехугольнике ABCD. Доказать: ABCD — параллелограмм. Предположим, что ∠A = ∠C и ∠B = ∠D в приведенном выше параллелограмме ABCD. Нам нужно доказать, что ABCD — параллелограмм. Имеем: ∠A + ∠B + ∠C + ∠D = 360º 2(∠A + ∠B) =360º ∠А + ∠В = 180º. Это должно означать, что AD || ДО Н.Э. Аналогично можно показать, что AB || CD. Следовательно, АД || до н.э. и АВ || CD. Следовательно, ABCD — параллелограмм. Теорема 3. Диагонали параллелограмма делят друг друга пополам. Доказательство: Дано: PQTR — параллелограмм. Доказать: Диагонали PT и RQ делят друг друга пополам, т. е. PE = ET и ER = EQ. Сначала предположим, что PQTR — параллелограмм. Сравните треугольники TER и треугольник PEQ. Имеем,
По критерию ASA два треугольника конгруэнтны, что означает по CPCTC, PE = ET и RE = EQ. Таким образом, две диагонали PT и RQ делят друг друга пополам, а PE = ET и ER = EQ. Обратное к теореме 3: Если диагонали в четырехугольнике делят друг друга пополам, то это параллелограмм. В четырехугольнике PQTR, если PE=ET и ER=EQ, то это параллелограмм. Дано: Диагонали PT и QR делят друг друга пополам. Доказать: PQRT — параллелограмм. Доказательство: Предположим, что диагонали PT и QR делят друг друга пополам.
Следовательно, по критерию SAS два треугольника конгруэнтны. Это означает, что ∠QRT = ∠PQR и ∠PRT = ∠QPT. Следовательно, PQ || РТ и РТ || КТ. Таким образом, PQRT является параллелограммом. Теорема 4: Если одна пара противоположных сторон равна и параллельна в четырехугольнике, то это параллелограмм. Доказательство: Дано: Дано, что AB = CD и AB || CD. Доказать: ABCD — параллелограмм. Сравним треугольник AEB и треугольник CED. Имеем,
Таким образом, по критерию ASA два треугольника конгруэнтны. Отсюда можно сделать вывод, что по CPCTC AE = EC, а BE = ED. Важные примечания: Четырехугольник является параллелограммом, если:
Вы знаете?
Также проверьте:
Часто задаваемые вопросы о свойствах параллелограммаКаковы 7 свойств параллелограмма?Семь свойств параллелограмма таковы:
Каковы свойства параллелограмма относительно диагоналей?Диагонали параллелограмма обладают двумя важными свойствами. Диагональ параллелограмма делит параллелограмм на два равных треугольника. А диагонали параллелограмма делят друг друга пополам. Диагонали параллелограмма равны?Диагонали параллелограмма НЕ равны. Противоположные стороны и противоположные углы параллелограмма равны. Диагонали квадрата и прямоугольника равны, что является особым видом параллелограмма. Каковы четыре важных свойства параллелограмма? Параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны.
Можно ли прямоугольник назвать параллелограммом?Противоположные стороны прямоугольника равны и параллельны. Таким образом, прямоугольник удовлетворяет всем свойствам параллелограмма, поэтому его можно назвать параллелограммом. Каковы уникальные свойства параллелограммов?Уникальные свойства параллелограмма, отличающие его от других четырехугольников, приведены ниже:
Каковы различные свойства каждого специального параллелограмма?Существует три особых типа параллелограммов — квадрат, прямоугольник и ромб. Квадрат – это четырехугольник, у которого все стороны и углы равны. У прямоугольника противоположные стороны равны и параллельны. Все углы квадрата и прямоугольника равны и равны 9по 0 градусов каждый. Ромб — это параллелограмм с четырьмя равными сторонами, но его углы не обязательно должны быть прямыми. Как отличить параллелограмм от четырехугольника по свойствам параллелограмма?Каждый параллелограмм можно назвать четырехугольником, но не каждый четырехугольник можно назвать параллелограммом. Трапецию и воздушного змея можно назвать четырехугольниками, но они не полностью удовлетворяют свойствам параллелограмма и, следовательно, не могут быть названы параллелограммом. CA Диагонали параллелограммаCA Диагонали параллелограммаДеятельность в классе и самооценка в классе 16 октября 2000 г. Задача 1 была задана как групповое задание в классе. Время отведено 25 минут. Эта теорема является «если и только если», поэтому решение состоит из двух частей.Задача 2 была быстро продемонстрирована на слайде и не выполнялась в групповом режиме. Задача 1. Диагонали параллелограмма Укажите определение параллелограмма (тот, что в B&B). Докажите, что четырехугольник является параллелограммом тогда и только тогда, когда его диагонали делят друг друга пополам. (Другими словами, диагонали пересекаются в точке M, которая является серединой каждой диагонали.) Определение. Четырехугольник ABCD является параллелограммом, если AB параллелен CD, а BC параллелен DA. Утверждение 1. Если ABCD — параллелограмм, то диагонали ABCD делят друг друга пополам. Доказательство утверждения 1. Пусть O пересечение диагоналей AC и BD. Утверждение можно переформулировать так: О — середина АС, а также середина BD. Поскольку O находится на отрезке AC, O является серединой AC, если AO = CO. Точно так же O является серединой BD, если BO = DO. Это то, что мы докажем, используя конгруэнтные треугольники. Сначала мы покажем, что треугольник ABO подобен треугольнику CDO, используя угол-угол. Так как прямая AC является секущей параллельных прямых AB и CD, то угол OAB = угол CAB = угол ACD = угол OCD. Кроме того, по вертикальным углам угол AOB = угол COD. Таким образом, треугольник ABO подобен треугольнику CDO. Далее мы покажем, что эти два треугольника конгруэнтны, показав, что отношение подобия равно 1. Мы знаем из домашнего задания (*), что противоположные стороны ABCD, AB = CD. Это две соответствующие стороны подобных треугольников, поэтому треугольники ABO и CDO равны. Из сравнения заключаем, что АО = СО и ВО = DO. QED Утверждение 2. Если ABCD — четырехугольник, у которого диагонали AC и BD делят друг друга пополам, то ABCD — параллелограмм. Доказательство утверждения 2. Пусть M — пересечение AC и BD. Нам дано, что M является серединой AC, а также BD, поэтому MA = MC и MB = MD. Мы также знаем, что угол AMB равен углу CMD по вертикальным углам. Таким образом, мы заключаем, что треугольник AMB конгруэнтен треугольнику CMD по SAS. Соответственные углы равны. Таким образом, угол MAB (равный углу CAB) и угол MCD (равный углу ACD) равны. Поскольку AC является секущей прямых AB и CD, из этих равных внутренних углов следует, что прямые AB и CD параллельны. Таким образом, мы видим, что две противоположные стороны ABCD параллельны. Поскольку в этих двух сторонах не было ничего особенного, используя тот же аргумент, мы также можем заключить, что BC и DA параллельны, поэтому по определению ABCD является параллелограммом. Задача 2. Ромб 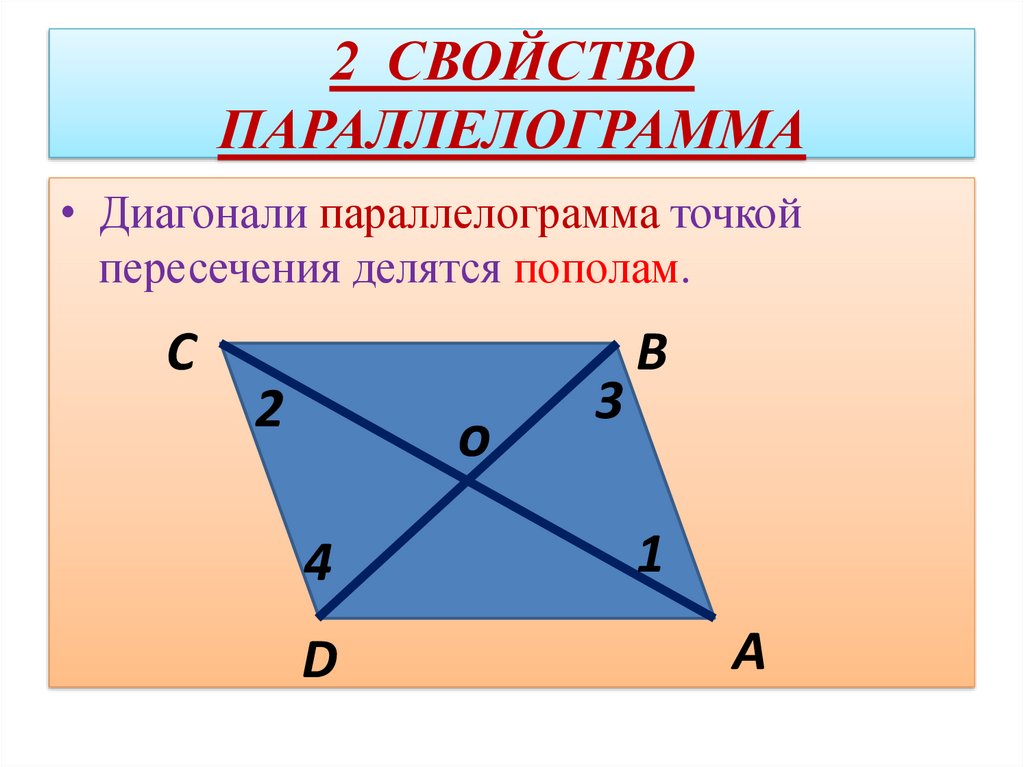 Доказательство: В домашнем задании было доказано, что если четырехугольник ABCD имеет равные противоположные стороны, то это параллелограмм. Это следует из этого результата. (b) Докажите, что параллелограмм с перпендикулярными диагоналями является ромбом. Доказательство. Из задачи 1 мы знаем, что диагонали параллелограмма ABCD делят друг друга пополам. Пусть М — пересечение диагоналей. Отсюда мы знаем, что MA = MC и MB = MD. Если мы также предположим, что AC перпендикулярен BC, то каждый из углов AMB, AMD, CMB и CMD будет прямым. Таким образом, треугольники AMB, AMD, CMB и CMD конгруэнтны по SAS. Отсюда следует, что все гипотенузы конгруэнтны: AB = AD = CB = CD. Это говорит о том, что ABCD по определению является ромбом. QED (*) Доказательство домашней задачи. (Противоположные стороны параллелограмма равны.) Утверждение: если ABCD — параллелограмм, то его противоположные стороны равны. Доказательство. По определению прямая AB параллельна прямой CD, а прямая BC параллельна прямой DA. Мы должны доказать, что AB = CD и BC = DA. Докажем, что треугольник ABC равен треугольнику CDA по ASA. Два треугольника имеют общую сторону АС = СА. Чтобы доказать равенство углов, мы используем секущую. Прямая AC является секущей параллельных прямых AB и CD, поэтому угол CAB равен углу ACD. Также прямая AC является секущей параллельных прямых BC и DA, поэтому угол ACB равен углу CAD. Таким образом, по ASA треугольники ABC и CDA равны. Соответствующие стороны равны, поэтому AB = CD и BC = DA. QED [Дополнительная кредитная возможность. Первый человек, отправивший электронное письмо на адрес электронной почты Math 444-487 и сообщивший, какие слова обозначают инициалы Q.E.D и что они означают, получает дополнительный балл.] Диагонали параллелограмма перпендикулярны?Вопрос задан: Судьей Николаем III Оценка: 4,9/5 (53 голоса) Если четырехугольник ромб, то он параллелограмм. Всегда ли диагонали в параллелограмме перпендикулярны?Диагонали параллелограмма иногда совпадают. диагоналей ромба всегда перпендикулярны . Последовательные углы параллелограмма никогда не дополняют друг друга. Квадрат всегда ромб. Как называется параллелограмм с перпендикулярными диагоналями?‘Если диагонали параллелограмма перпендикулярны, то это ромб . ‘ Содержит ли параллелограмм перпендикуляр?Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны, но смежные стороны не перпендикулярны . Как доказать, что диагонали параллелограмма перпендикулярны?Доказательство того, что диагонали ромба перпендикулярны Соответствующие части равных треугольников равны , поэтому все 4 угла (те, что в середине) равны. Докажите, что диагонали этого параллелограмма перпендикулярныНайдено 27 связанных вопросов Что такое перпендикуляр в параллелограмме? Высотой (или высотой) параллелограмма является перпендикулярное расстояние от основания до противоположной стороны (которую, возможно, придется продлить). … Противоположные стороны конгруэнтны (равны по длине) и параллельны. Изменяя форму параллелограмма в верхней части страницы, обратите внимание на то, что противоположные стороны всегда имеют одинаковую длину. Какой параллелограмм имеет перпендикулярные стороны?Параллелограмм с перпендикулярными диагоналями — это ромб Ромб — особый вид параллелограмма, у которого все стороны равны. Мы видели, что одним из свойств ромба является то, что его диагонали перпендикулярны друг другу. Диагонали квадрата перпендикулярны?Диагонали квадрата делят друг друга пополам и перпендикулярны (показаны красным на рисунке выше). Кроме того, они делят пополам каждую пару противоположных углов (показаны синим цветом). Диагонали какого четырехугольника не перпендикулярны?Прямоугольник — это четырехугольник, диагонали которого равны и делятся пополам, но не перпендикулярны. Делят ли диагонали углы пополам в параллелограмме? Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны. Противоположные углы параллелограмма равны. … Диагонали параллелограмма делят друг друга пополам . Что верно в отношении диагоналей параллелограмма?Диагонали параллелограмма делят друг друга пополам . … В любом параллелограмме диагонали (линии, соединяющие противоположные углы) делят друг друга пополам. То есть каждая диагональ разрезает другую на две равные части. Все ли диагонали параллелограмма равны?Применяются все свойства параллелограмма (здесь важны параллельность сторон, конгруэнтность противоположных сторон и делимость диагоналей пополам). … Диагонали равны . Почему диагонали параллелограмма не равны?Диагонали в параллелограммах Диагонали параллелограмма проводятся от одной противоположной стороны параллелограмма к другой. … Это происходит потому, что противоположные углы параллелограмма равны . Сами диагонали не будут конгруэнтны друг другу, если параллелограмм также не является квадратом или ромбом. Диагонали параллелограмма равны? Диагонали параллелограмма равны? диагоналей параллелограмма НЕ равны . Какие четырехугольники обладают всеми свойствами параллелограмма?Прямоугольник обладает всеми свойствами параллелограмма, а также следующими: Диагонали равны. Что из следующего не верно в отношении параллелограмма?Если провести диагонали, соединив противоположные вершины в параллелограмм, то нельзя сказать, что диагоналей делят пополам противоположные углы . Диагонали делят друг друга пополам, но не делят углы пополам. Следовательно, это утверждение неверно. Диагонали ромба перпендикулярны?Сал доказывает, что диагонали ромба перпендикулярны и пересекаются в их серединах. Как найти диагонали параллелограмма?Часто задаваемые вопросы о формуле диагонали параллелограмма Для любого параллелограмма abcd формула для длин диагоналей имеет вид: p=√x2+y2−2xycosA=√x2+y2+2xycosB p = x 2 + y 2 − 2 x y cos A = x 2 + y 2 + 2 x y cos B и q = √x2 + y2 + 2xycosA = √x2 + y2−2xycosB q = x 2 + y 2 + 2 x y cos A = x 2 + y 2 − 2 х у, потому что У каких из них диагонали перпендикулярны друг другу? Ответ: Ромб ; площадь. Делят ли диагонали противоположные углы пополам?Противоположные углы равны . … Диагонали делят друг друга пополам, и каждая диагональ делит параллелограмм на два конгруэнтных треугольника. Если один из углов параллелограмма прямой, то все остальные углы прямые и параллелограмм становится прямоугольником. Если все углы прямые, то параллелограмм A?Параллелограмм, у которого все углы прямые это прямоугольник ! Диагонали какого из следующих параллелограммов не равны, но перпендикулярны друг другу?Если параллелограмм является ромбом , то его диагонали перпендикулярны. Если параллелограмм является ромбом, то каждая диагональ делит пополам пару противоположных углов. Если диагонали параллелограмма перпендикулярны, то параллелограмм является ромбом. Как узнать, перпендикулярна ли диагональ? Чтобы доказать, что две прямые перпендикулярны, когда все, что у нас есть, это эти две прямые, мы можем использовать Теорему о парных перпендикулярах — Если две прямые пересекаются в точке и образуют линейную пару равных углов , они перпендикулярны . |

 Все правила по сольфеджио
Все правила по сольфеджио
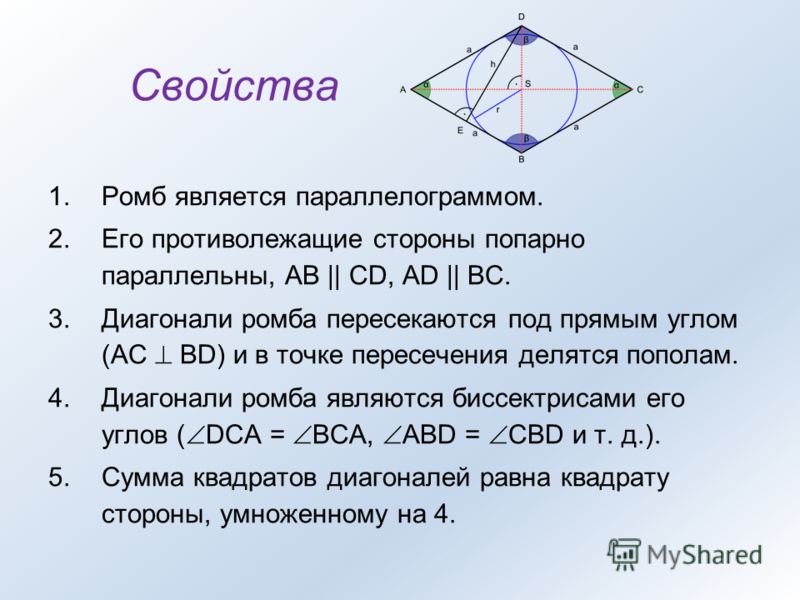 Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие второю сторону угла, то на второй стороне угла отложатся также равные отрезки.
Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие второю сторону угла, то на второй стороне угла отложатся также равные отрезки.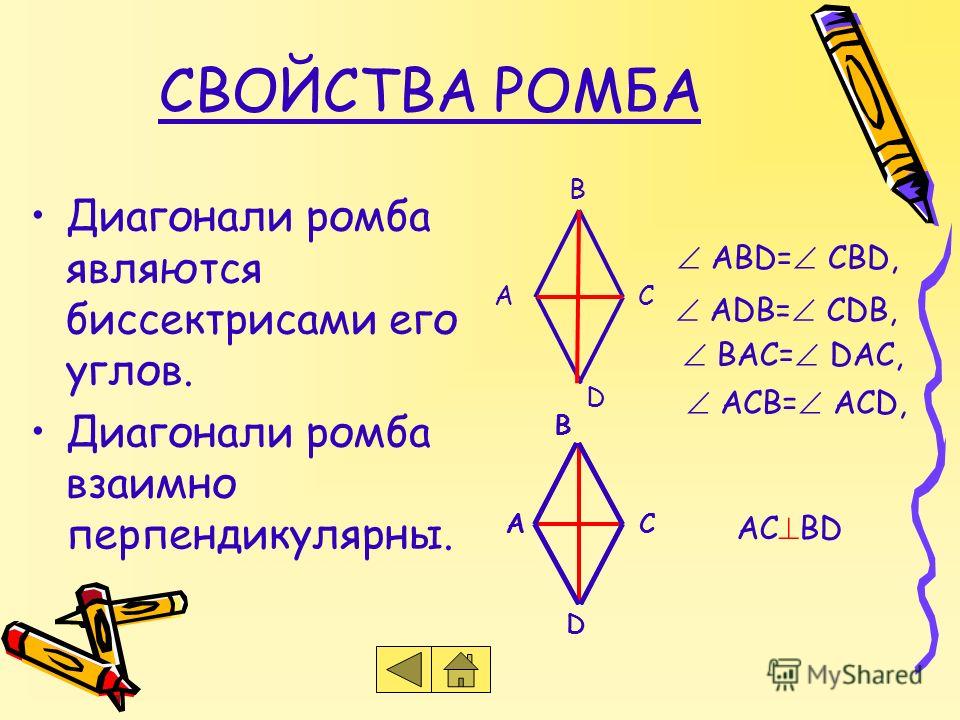

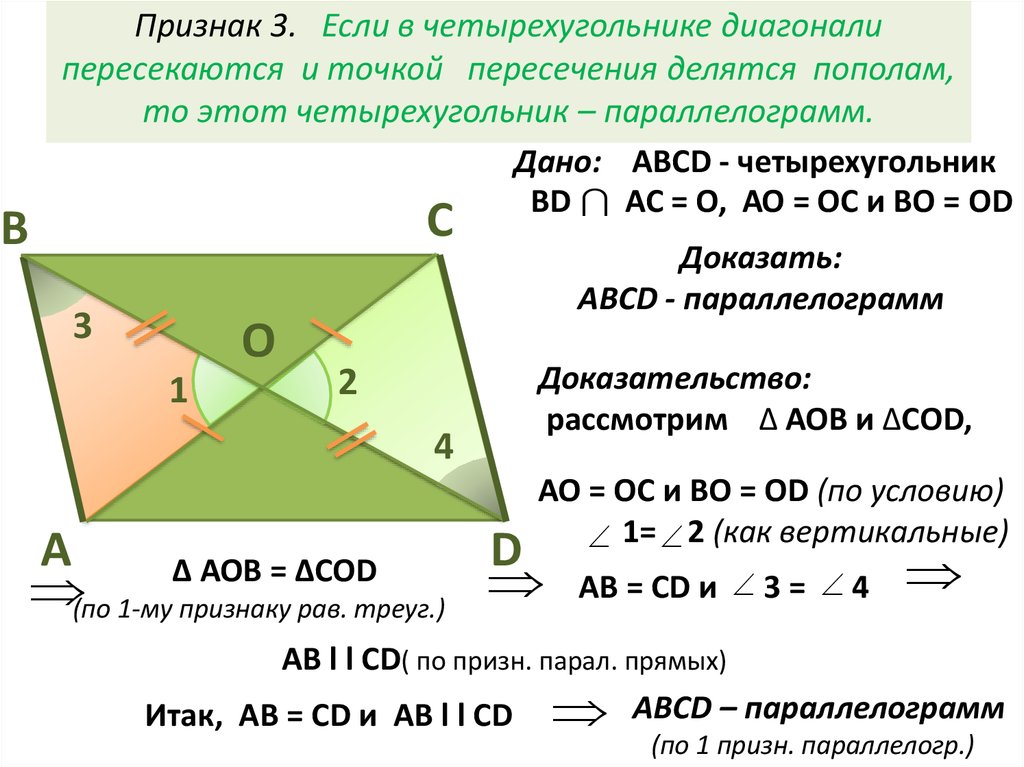


 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.01 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.01 с.)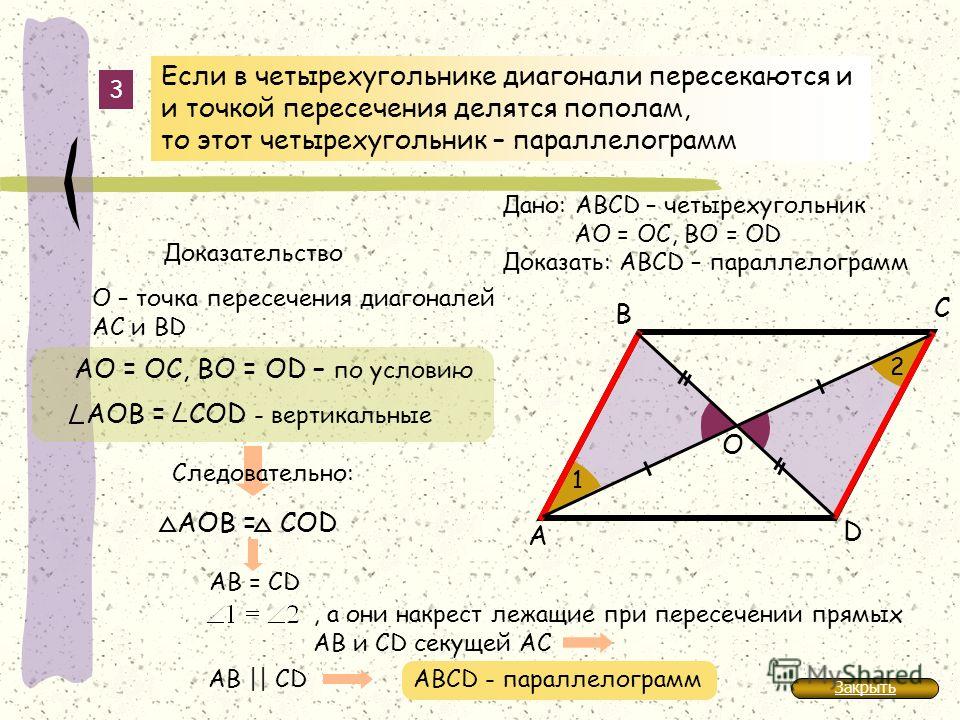 Аналогично можно доказать, что прямая АВ параллельна ВС. Теорема доказана.
Аналогично можно доказать, что прямая АВ параллельна ВС. Теорема доказана. Следовательно, треугольники АОD и ВОС равны по стороне и прилегающим к ней углам. А отсюда следует и равенство сторон этих треугольников. Т.е. АО = ОС, а ВО = ОD. Сумма этих сторон и есть диагонали параллелограмма.
Следовательно, треугольники АОD и ВОС равны по стороне и прилегающим к ней углам. А отсюда следует и равенство сторон этих треугольников. Т.е. АО = ОС, а ВО = ОD. Сумма этих сторон и есть диагонали параллелограмма. Пусть АВСD — ромб.(Рис. 3). Тогда треугольник АВС — равнобедренный. А это значит, что отрезок ВО, который является половиной диагонали, является биссектрисой медианой и высотой. Следовательно диагонали ромба АС и ВD пересекаются под прямым углом.
Пусть АВСD — ромб.(Рис. 3). Тогда треугольник АВС — равнобедренный. А это значит, что отрезок ВО, который является половиной диагонали, является биссектрисой медианой и высотой. Следовательно диагонали ромба АС и ВD пересекаются под прямым углом.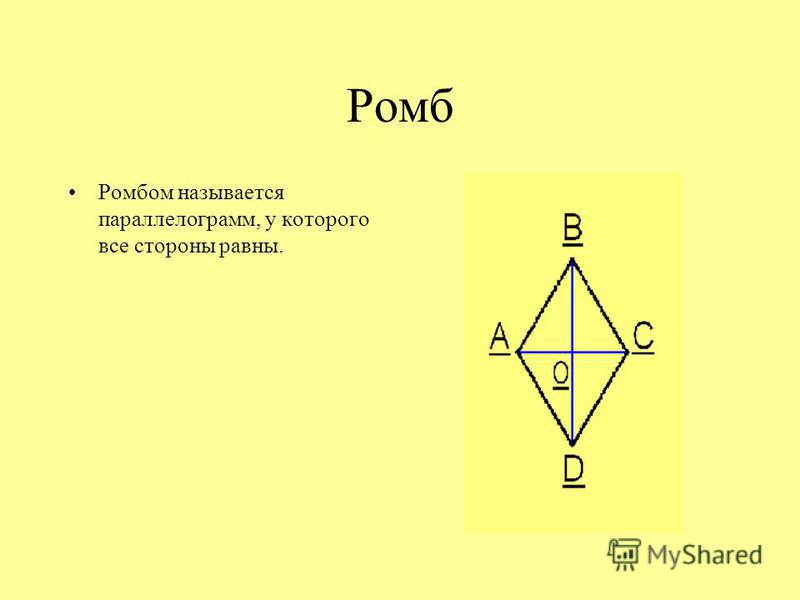 Так как прямая АЕ биссектриса, то это значит, что треугольники АВЕ и АЕР равны. Так как угол ВАЕ равен углу АЕР, а угол ЕАР равен углу ВЕА как внутренние накрест лежащие. Следовательно АВЕР — ромб, так как угол ВАЕ равен углу ЕАР ( по условию). Отсюда следует, что АВ = ВЕ = 9 см, а ЕС = 5 см.
Так как прямая АЕ биссектриса, то это значит, что треугольники АВЕ и АЕР равны. Так как угол ВАЕ равен углу АЕР, а угол ЕАР равен углу ВЕА как внутренние накрест лежащие. Следовательно АВЕР — ромб, так как угол ВАЕ равен углу ЕАР ( по условию). Отсюда следует, что АВ = ВЕ = 9 см, а ЕС = 5 см.
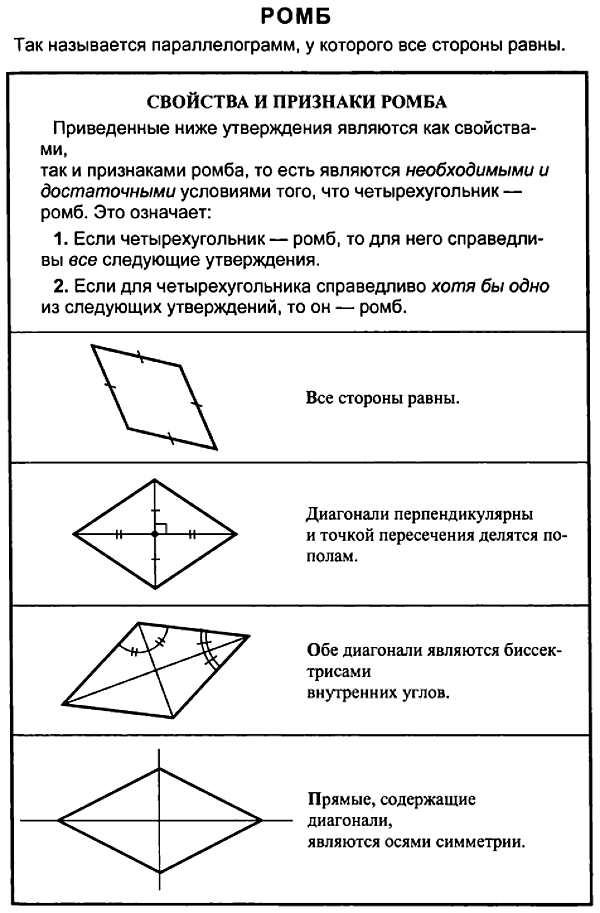 Пусть АВС — треугольник. Отрезок ЕР соединяет середины сторон АВ и ВС (Рис. 5). Тогда по теореме Фалеса отрезок ЕР параллелен основанию АС, так как он делит стороны АВ и ВС на равные части.
Пусть АВС — треугольник. Отрезок ЕР соединяет середины сторон АВ и ВС (Рис. 5). Тогда по теореме Фалеса отрезок ЕР параллелен основанию АС, так как он делит стороны АВ и ВС на равные части.
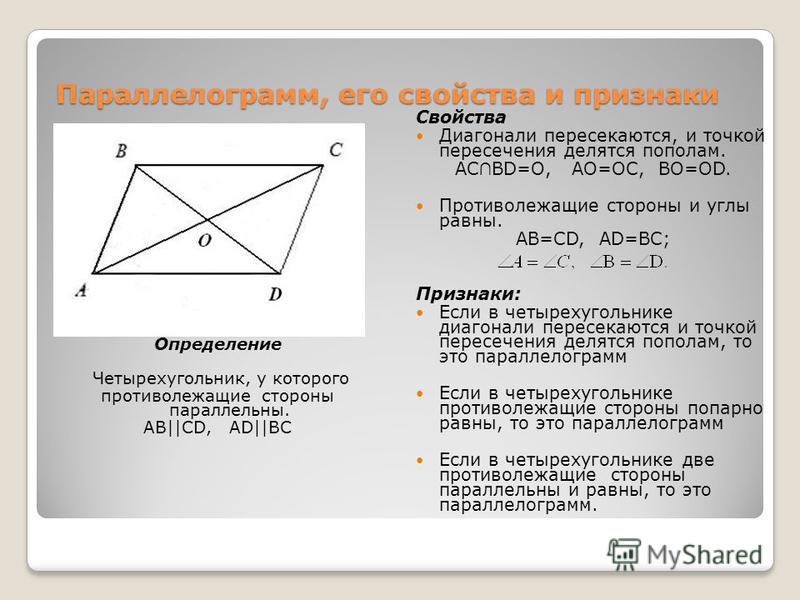


 (Рис.9)
(Рис.9) 9 Задача. Через точку пересечения диагоналей…
9 Задача. Через точку пересечения диагоналей…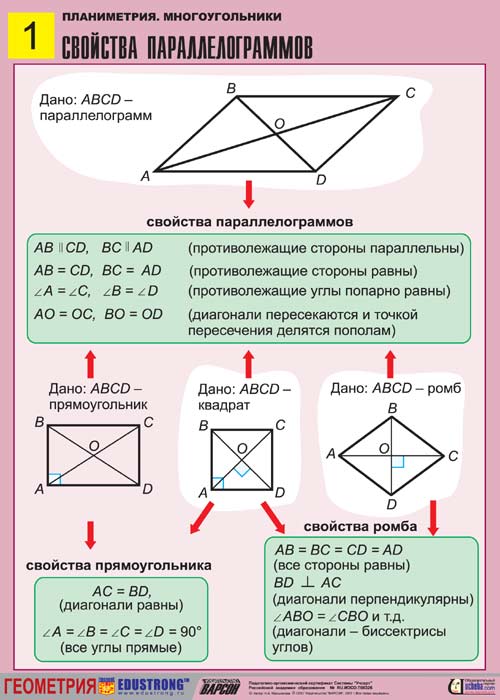
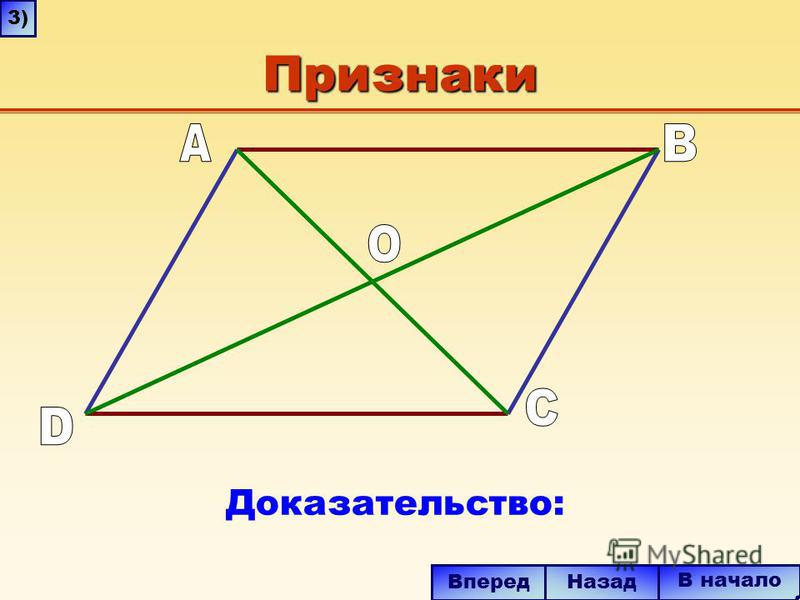 У них сторона АЕ равна стороне ED, сторона BE — общая, а углы при вершине Е равны 90°.Отсюда следует, что диагональ BD равна стороне АВ.
У них сторона АЕ равна стороне ED, сторона BE — общая, а углы при вершине Е равны 90°.Отсюда следует, что диагональ BD равна стороне АВ.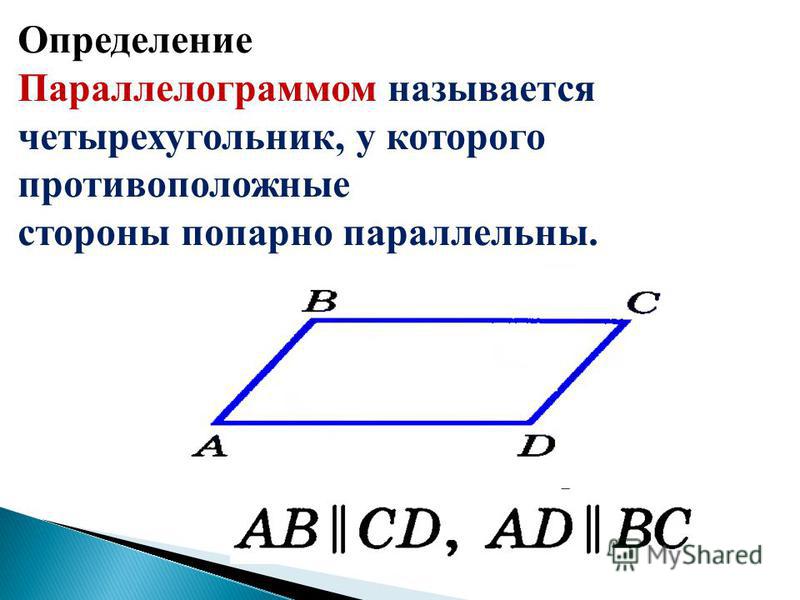 Найдите периметр прямоугольника.(Рис.12)
Найдите периметр прямоугольника.(Рис.12) (Рис.13)
(Рис.13) Углы при вершине О равны 90°. Т.е. по двум сторонам и углу между ними.
Углы при вершине О равны 90°. Т.е. по двум сторонам и углу между ними. Задания 19 ОГЭ по математике
Задания 19 ОГЭ по математике
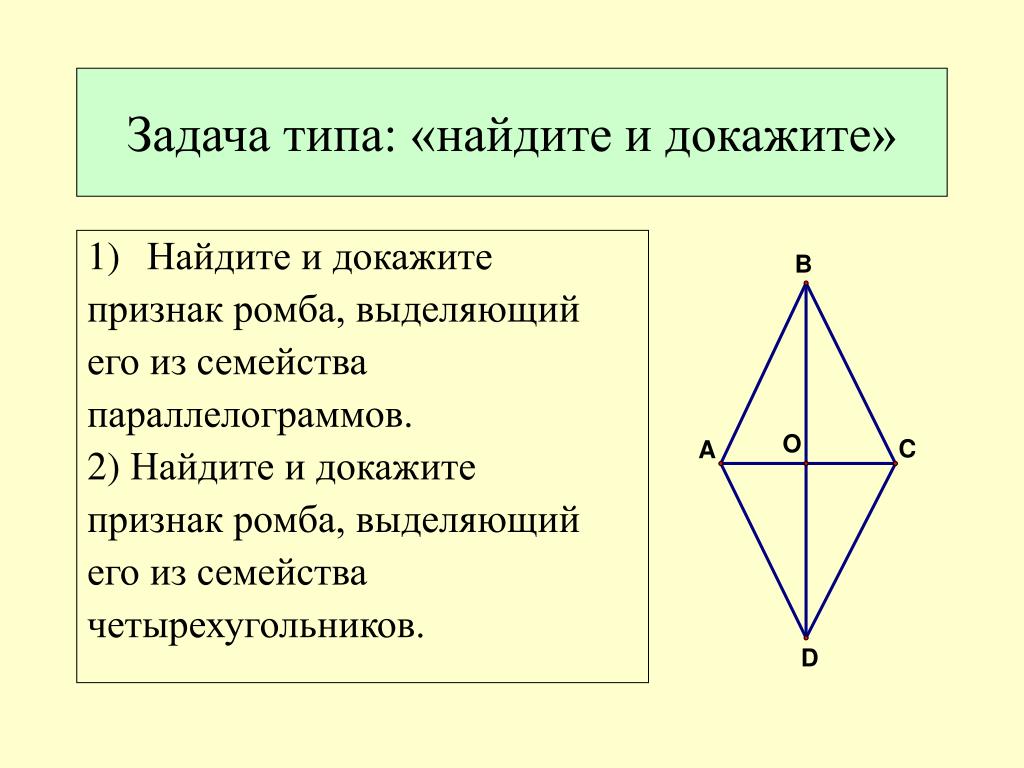 4
4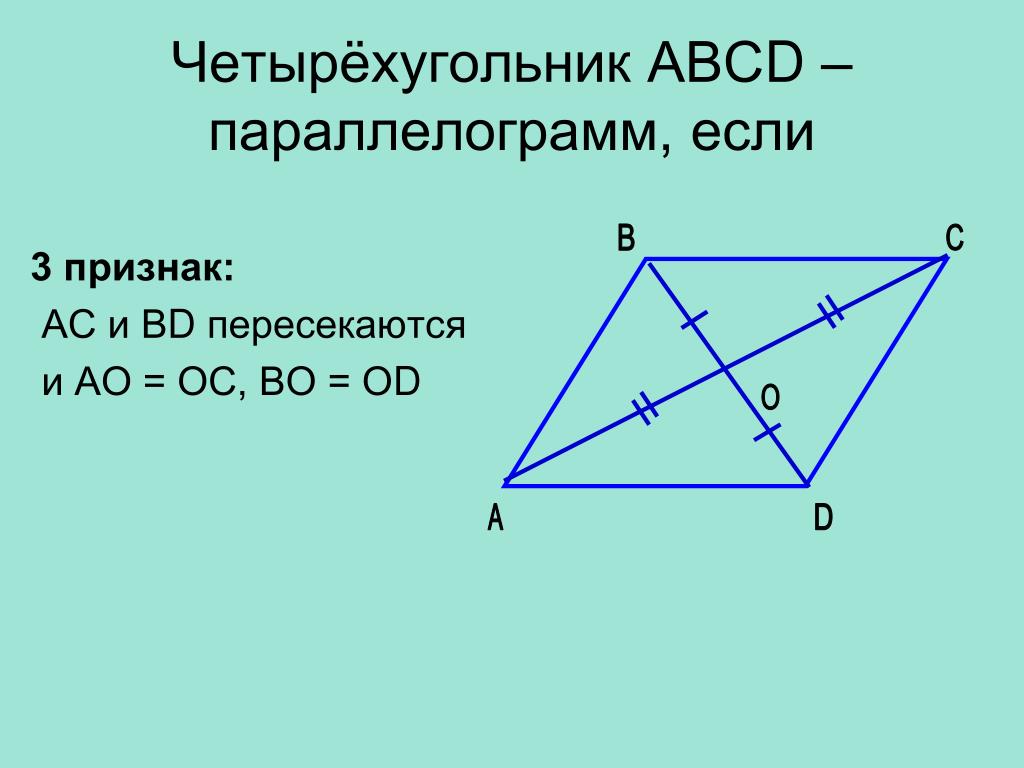 Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
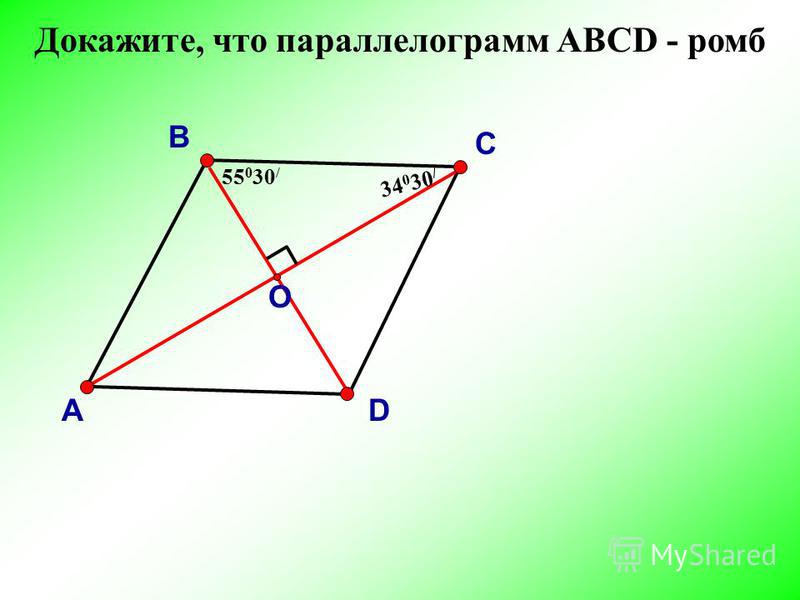

 Находить
м
∠
Д
Z
В
.
Находить
м
∠
Д
Z
В
. В геометрии этот ромб называется ромбом: геометрическая фигура с четырьмя равными сторонами. Ромб является одновременно и параллелограммом, и четырехугольником. В частности, ромб представляет собой четырехстороннюю плоскую фигуру (четырехугольник), противоположные стороны которой параллельны друг другу (параллелограмм). Однако его особая характеристика наличия четырех равных сторон — это то, что отличает ромбы от других четырехугольников.
В геометрии этот ромб называется ромбом: геометрическая фигура с четырьмя равными сторонами. Ромб является одновременно и параллелограммом, и четырехугольником. В частности, ромб представляет собой четырехстороннюю плоскую фигуру (четырехугольник), противоположные стороны которой параллельны друг другу (параллелограмм). Однако его особая характеристика наличия четырех равных сторон — это то, что отличает ромбы от других четырехугольников.

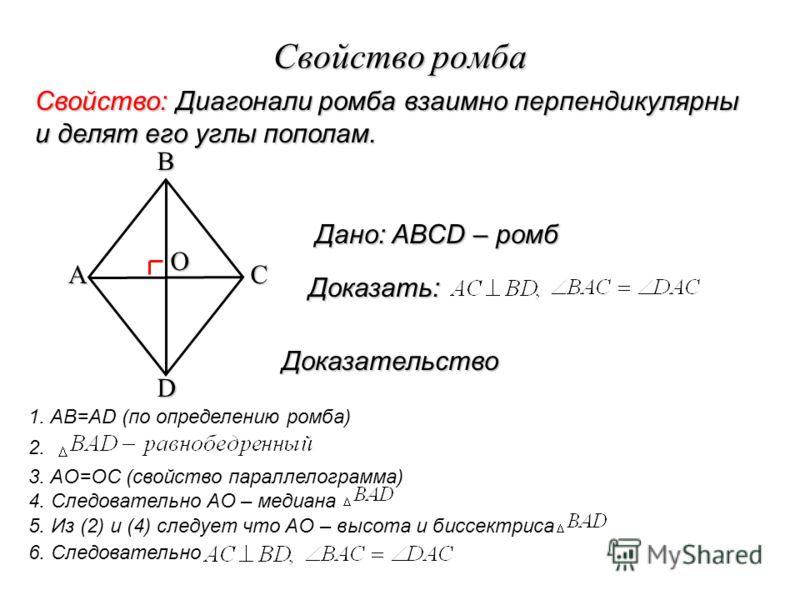 Кроме того, все 4 угла квадрата прямые.
Кроме того, все 4 угла квадрата прямые.
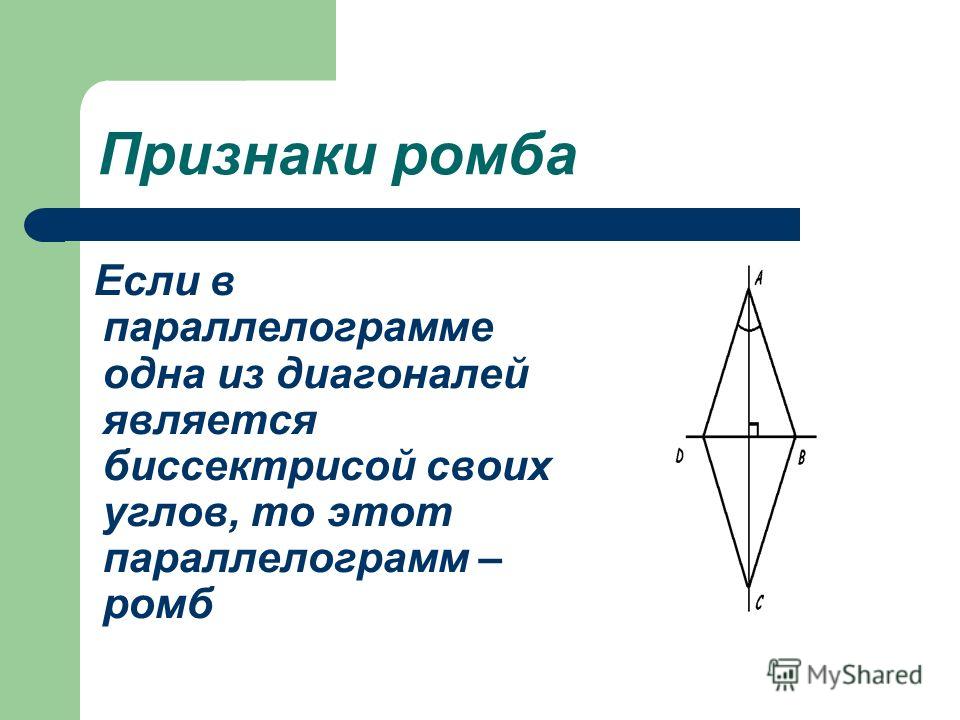 Прежде чем мы узнаем о свойствах, давайте сначала узнаем о параллелограммах. Это четырехсторонняя замкнутая фигура с равными и параллельными противоположными сторонами и равными противоположными углами. Давайте узнаем больше о свойствах параллелограмма подробно в этой статье.
Прежде чем мы узнаем о свойствах, давайте сначала узнаем о параллелограммах. Это четырехсторонняя замкнутая фигура с равными и параллельными противоположными сторонами и равными противоположными углами. Давайте узнаем больше о свойствах параллелограмма подробно в этой статье.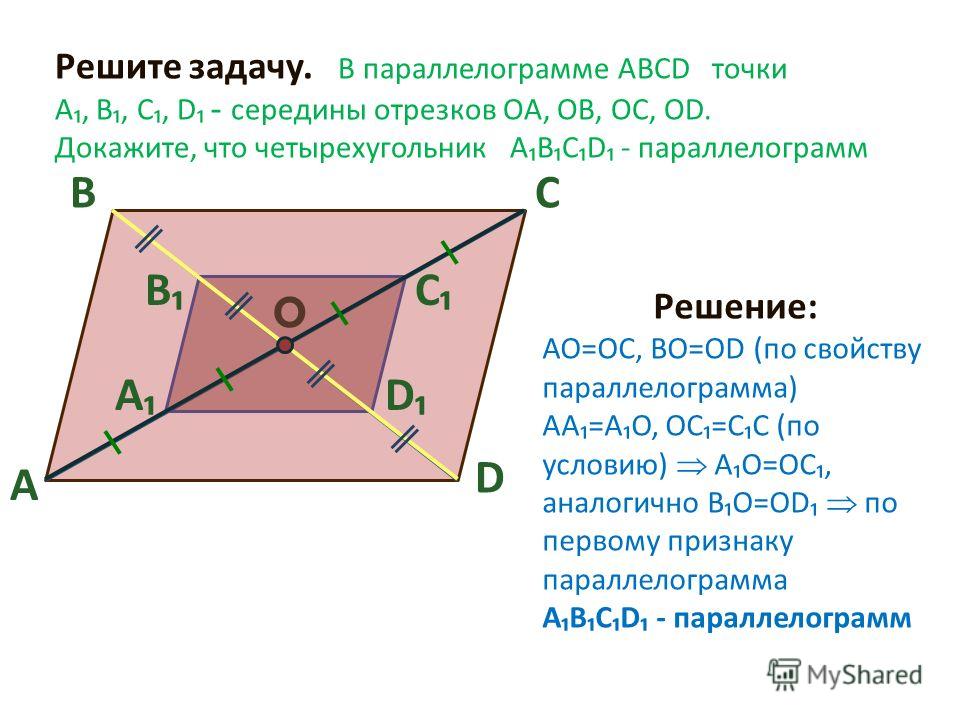

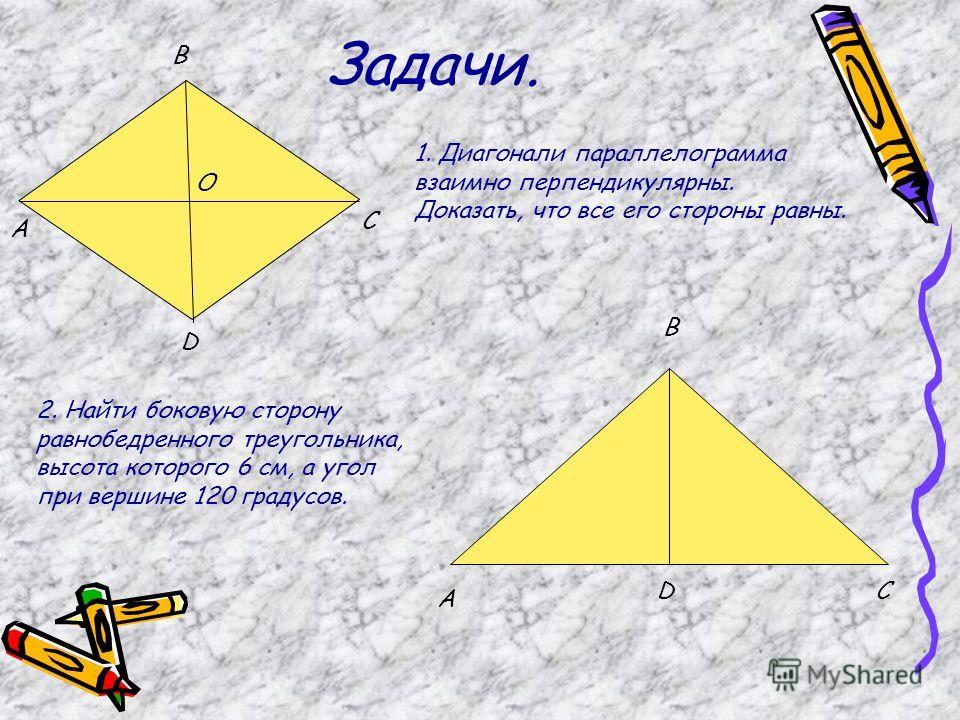 В параллелограмме ABCD (см. рисунок выше) диагонали AC и BD. Предположим, что O — точка пересечения диагоналей AC и BD. Свойства диагоналей параллелограмма следующие:
В параллелограмме ABCD (см. рисунок выше) диагонали AC и BD. Предположим, что O — точка пересечения диагоналей AC и BD. Свойства диагоналей параллелограмма следующие: В параллелограмме противоположные стороны равны.
В параллелограмме противоположные стороны равны. 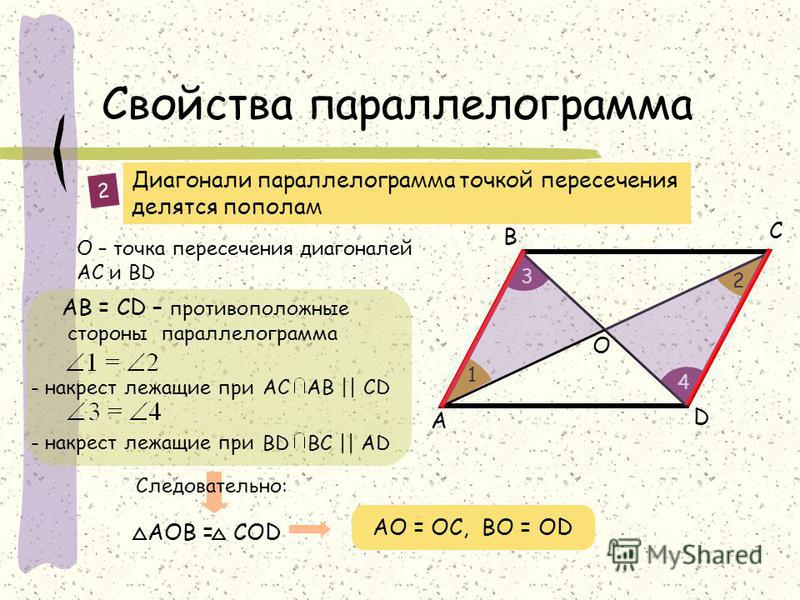 Теперь сравните два треугольника ABC и CDA. Здесь мы имеем
Теперь сравните два треугольника ABC и CDA. Здесь мы имеем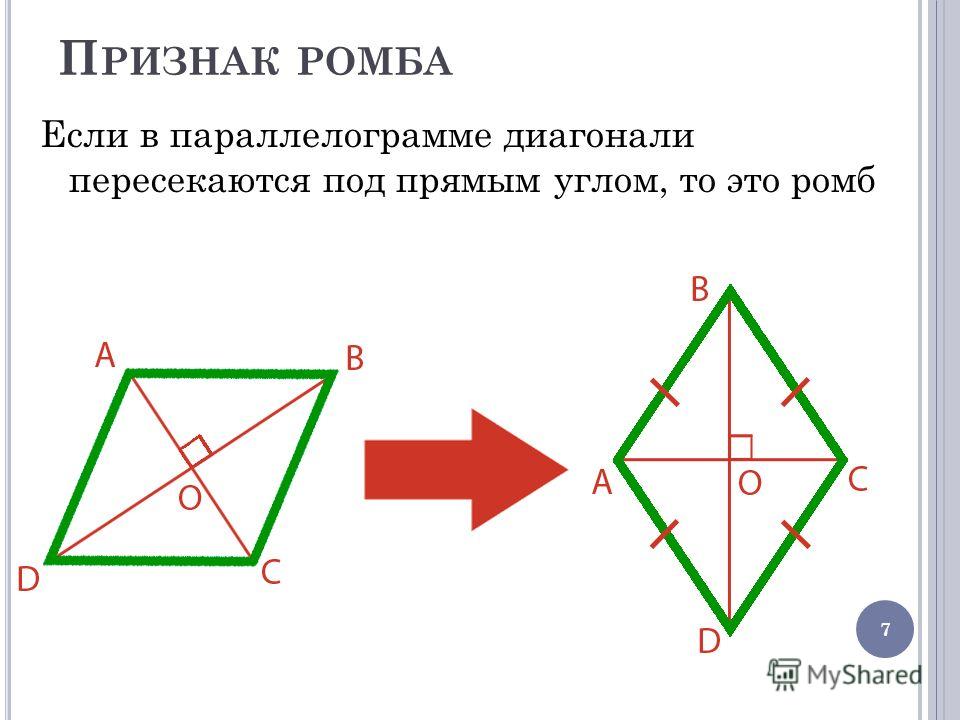 Точно так же мы можем показать, что ∠A = ∠C. Это доказывает, что противоположные углы в любом параллелограмме равны.
Точно так же мы можем показать, что ∠A = ∠C. Это доказывает, что противоположные углы в любом параллелограмме равны. PT и QR — диагонали параллелограмма.
PT и QR — диагонали параллелограмма.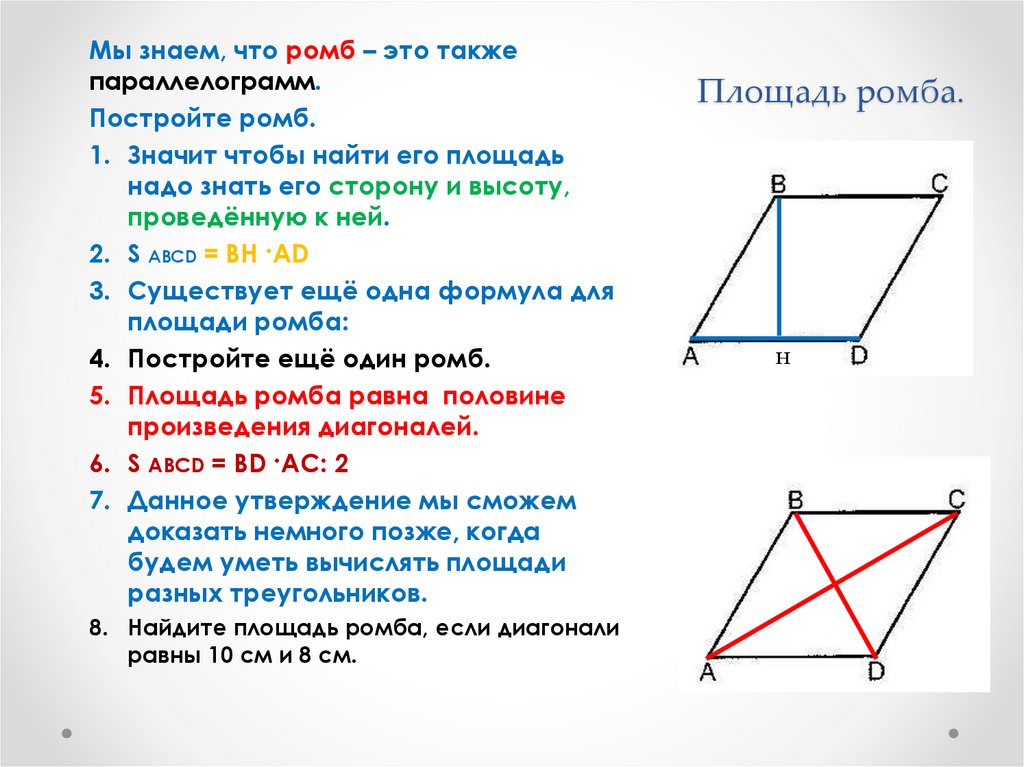 Еще раз сравните треугольник RET и треугольник PEQ. У нас есть:
Еще раз сравните треугольник RET и треугольник PEQ. У нас есть: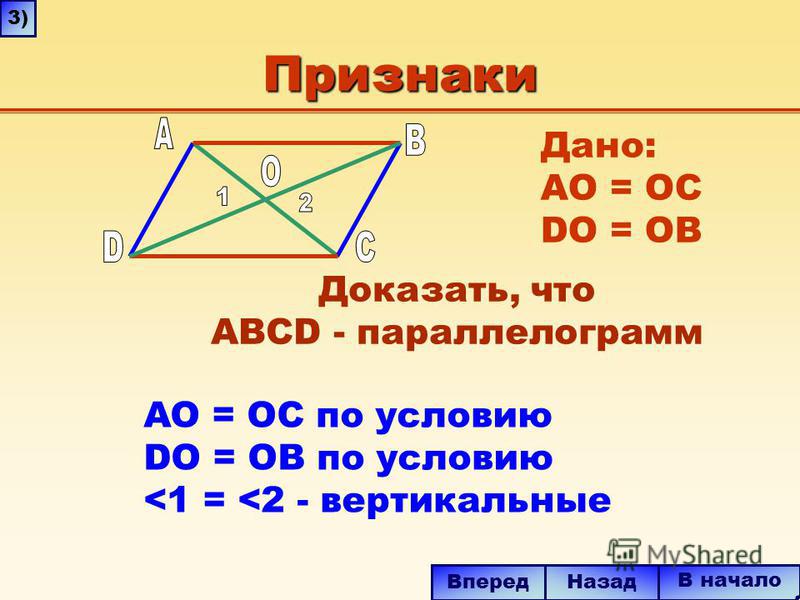 Следовательно, диагонали AC и BD делят друг друга пополам, а это в дальнейшем означает, что ABCD — параллелограмм.
Следовательно, диагонали AC и BD делят друг друга пополам, а это в дальнейшем означает, что ABCD — параллелограмм.
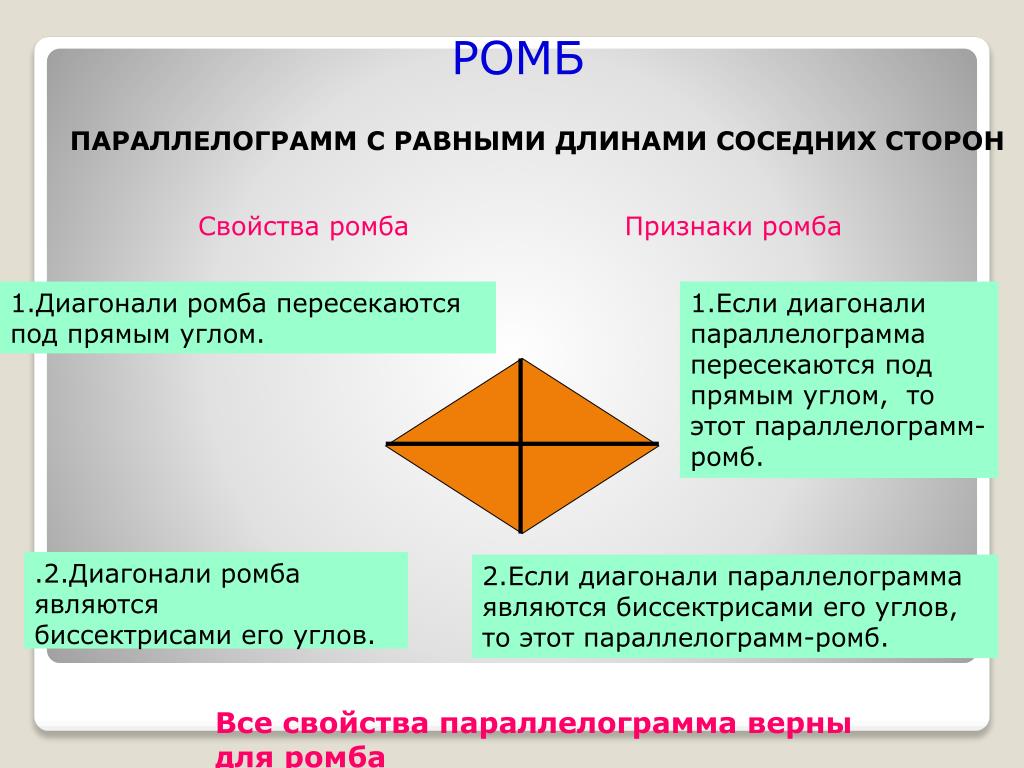 Противоположные углы параллелограмма также равны. Короче говоря, параллелограмм можно рассматривать как скрученный прямоугольник. Это скорее прямоугольник, но углы при вершинах не обязательно должны быть прямыми. Четыре важных свойства параллелограмма таковы:
Противоположные углы параллелограмма также равны. Короче говоря, параллелограмм можно рассматривать как скрученный прямоугольник. Это скорее прямоугольник, но углы при вершинах не обязательно должны быть прямыми. Четыре важных свойства параллелограмма таковы:
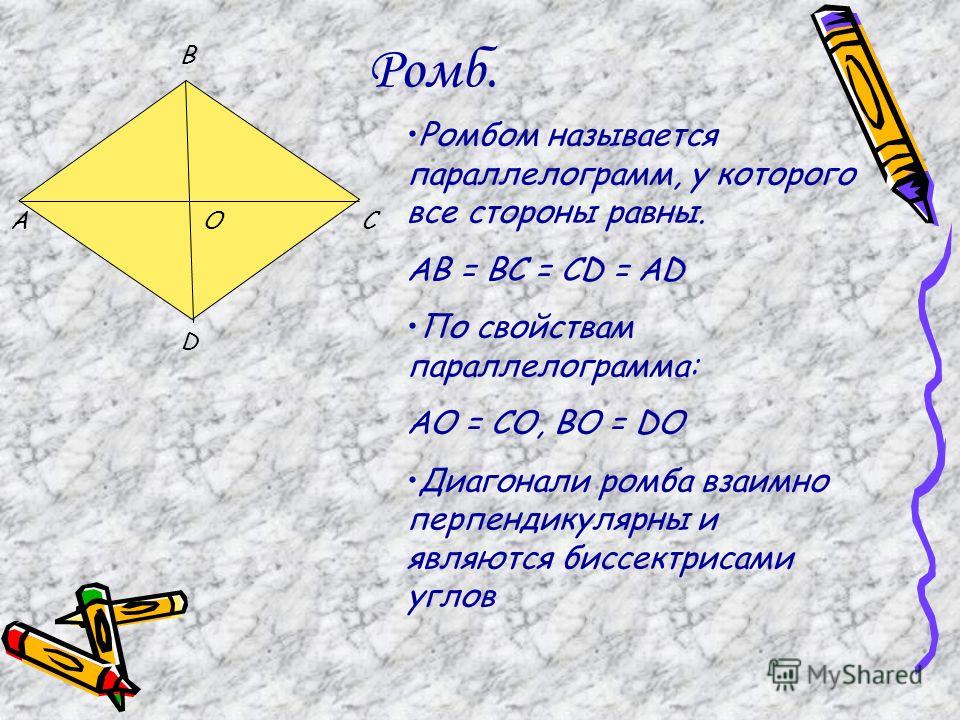


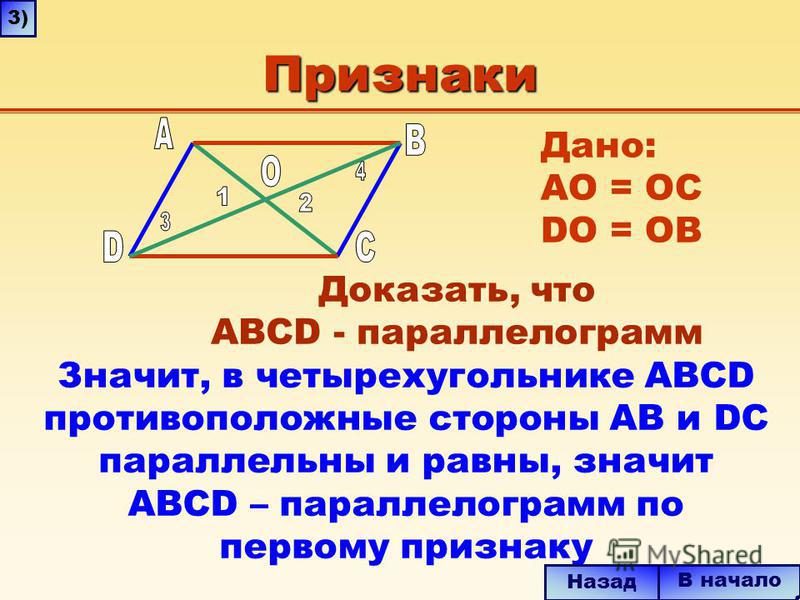
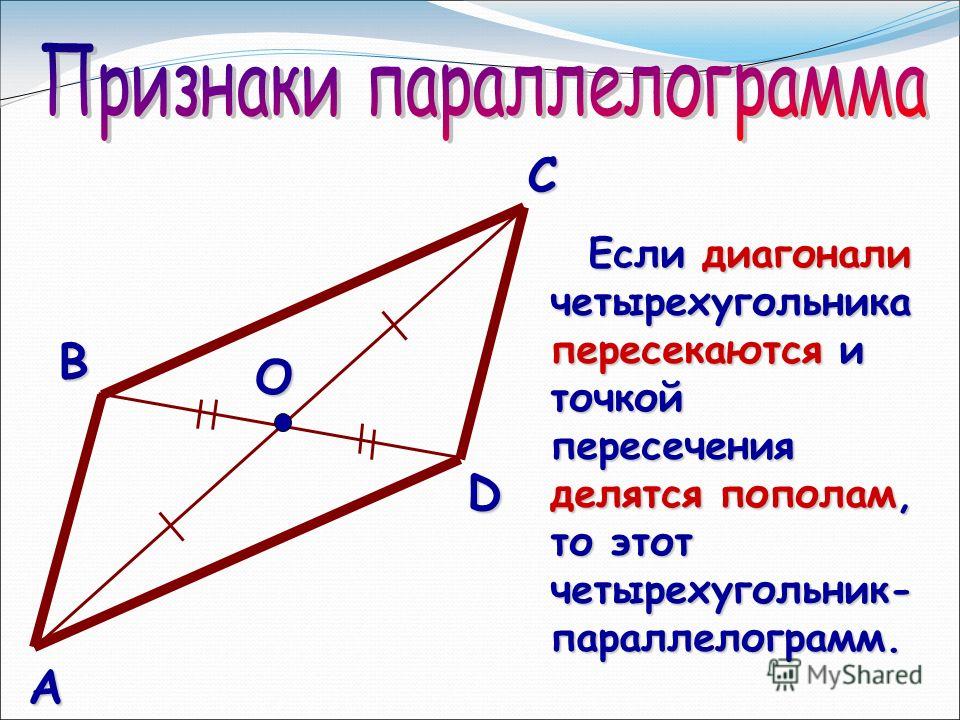 Если параллелограмм является ромбом, то его диагонали перпендикулярны . Если параллелограмм является ромбом, то каждая диагональ делит пополам пару противоположных углов. Если диагонали параллелограмма перпендикулярны, то параллелограмм является ромбом.
Если параллелограмм является ромбом, то его диагонали перпендикулярны . Если параллелограмм является ромбом, то каждая диагональ делит пополам пару противоположных углов. Если диагонали параллелограмма перпендикулярны, то параллелограмм является ромбом. Это приводит к тому, что все они равны 90 градусам, а диагонали перпендикулярны друг другу.
Это приводит к тому, что все они равны 90 градусам, а диагонали перпендикулярны друг другу.
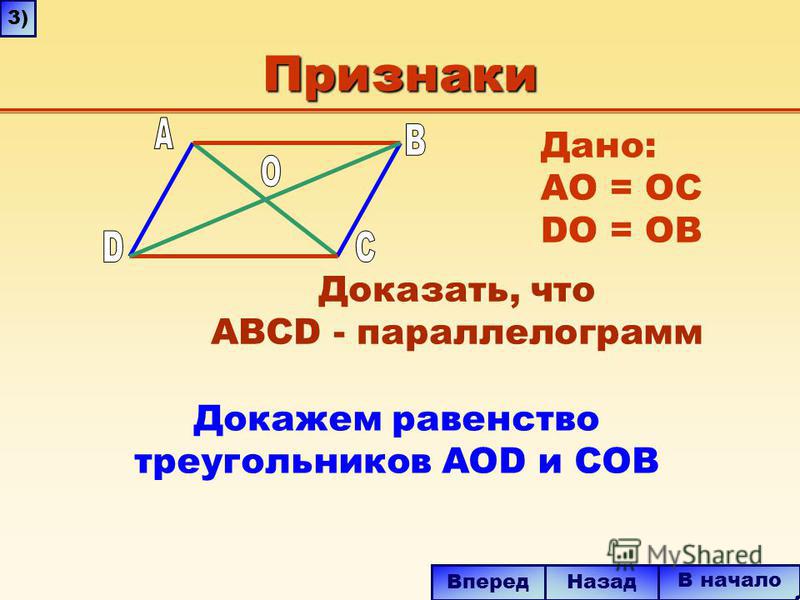
 Противоположные стороны и противоположные углы параллелограмма равны.
Противоположные стороны и противоположные углы параллелограмма равны.
