Примеры на сложение и вычитание трёхзначных чисел
Примеры на сложение и вычитание трёхзначных чиселПримерОнлайн.ru
Генератор примеров по математике 1-3 класс
Онлайн примеры на сложение трёхзначных чисел позволяют вывести большое количество неповторяющихся примеров с трёхзначными числами на сложение и вычитание.
Сочетание примеров позволяет выработать навыки устного счёта, и закрепить их большим количеством решённых примеров.
Примеры можно разделить по степени сложности: лёгкие – это примеры без перехода через десяток, сложные – с обязательным переходом, обычные – слагаемые выбираются случайным образом.
| Настройка генератора примеров |
|---|
|
|
|
Образец примеров
583 + 387
518 + 131
516 + 139
261 + 222
248 — 211
480 + 396
723 — 460
482 + 312
334 + 539
282 + 551
399 + 549
298 + 275
497 + 261
501 + 304
708 — 365
696 — 146
297 + 567
279 + 506
938 — 831
469 + 380
573 — 321
848 — 189
165 + 716
692 — 471
913 — 590
696 — 575
794 — 204
964 — 398
497 + 340
364 + 144
480 + 394
757 — 424
899 — 764
480 — 195
620 — 192
641 — 557
187 + 166
233 + 203
546 — 426
969 — 782
690 — 629
924 — 607
132 + 398
518 + 302
575 + 144
665 + 102
982 — 202
411 + 330
505 — 295
257 + 251
291 + 279
528 — 392
692 — 402
716 — 501
170 + 727
420 + 185
595 — 400
183 + 308
879 — 689
905 — 137
448 + 389
647 + 244
242 + 349
885 — 205
642 — 520
484 — 168
245 + 315
750 — 310
776 — 473
304 + 305
366 + 397
451 — 440
439 + 299
322 — 127
769 — 323
186 + 721
459 — 133
248 — 195
943 — 703
875 — 337
299 + 181
775 — 721
770 — 639
911 — 739
530 — 382
565 + 386
495 + 263
303 + 587
700 + 159
872 — 534
478 — 103
334 + 550
278 — 250
765 — 100
386 + 314
480 + 388
527 + 391
503 — 193
521 + 157
604 — 347
190 + 212
895 — 694
154 + 406
380 + 273
788 — 481
561 — 466
446 — 191
617 — 240
417 — 295
207 + 485
515 — 114
684 + 199
535 — 214
791 — 235
676 — 648
292 — 187
386 + 305
840 — 657
713 — 172
136 + 722
164 + 661
574 + 191366 + 339
351 + 123
476 + 444
738 + 175
570 + 321
296 — 180
163 + 456
143 — 111
320 + 472
968 — 353
247 + 279
351 + 198
208 + 686
878 — 545
420 + 184
239 + 743
828 — 588
705 — 395
503 + 282
511 + 296
321 + 353
503 — 299
423 + 123
909 — 348
526 + 451
785 — 164
362 + 240
316 — 172
256 + 739
277 + 307
619 — 220
781 — 727
699 + 133
310 — 269
355 + 300
309 + 560
389 — 203
890 — 487
621 + 191
379 + 111
400 + 550
860 — 199
181 + 753
707 — 615
906 — 755
723 + 183
273 + 472
881 — 472
529 + 244
861 — 353
212 + 740
187 + 602
299 + 335
819 — 527
168 + 573
752 — 645
889 — 180
285 + 648
639 + 163
945 — 712
711 + 109
219 + 215
193 — 110
686 + 164
734 — 148
193 + 780
456 + 529
864 — 289
337 + 177
769 — 687
958 — 297
853 — 451
402 + 589
882 — 770
875 — 247
220 — 114
499 — 241
716 + 136
403 — 316
622 — 499
332 — 132
334 + 596
963 — 659
554 + 101
915 — 104
834 — 334
316 + 564
172 + 219
270 — 192
137 + 345
798 — 479
630 + 194
784 — 693
486 — 290
688 + 276
352 — 283
942 — 670
390 + 531
318 + 657
149 + 731
118 + 364
178 — 159
539 — 472
711 — 119
979 — 767
860 — 132
501 + 457
902 — 698
324 + 505
850 — 487
635 — 555
849 — 121
743 — 122
315 + 384
655 — 339
391 + 271
322 + 265
115 + 171
987 — 832
780 — 367
776 — 228
171 + 675
797 + 150
286 + 206
149 + 559385 — 340
575 + 178
880 — 263
277 + 332
265 + 127
451 + 275
170 + 642
426 + 138
495 — 378
176 + 460
536 + 143
236 + 707
295 + 575
774 — 568
898 — 800
569 + 386
836 — 566
914 — 885
712 — 488
561 + 235
610 — 578
694 + 289
912 — 664
730 + 195
761 + 224
671 — 213
617 + 244
430 — 313
431 — 109
380 + 521
900 — 861
402 + 356
255 — 133
369 + 363
740 + 176
232 + 517
771 — 657
171 + 569
995 — 418
668 — 387
140 + 126
810 — 465
243 + 426
863 — 298
144 + 471
677 — 549
817 — 215
121 + 603
484 + 390
554 + 426
813 — 466
811 — 206
248 + 195
839 — 615
933 — 310
339 + 593
900 — 443
214 + 664
803 — 595
472 + 167
129 + 456
203 + 526
806 + 149
780 — 617
965 — 607
803 — 390
399 + 139
819 — 162
629 + 322
298 + 489
582 — 317
770 — 655
309 — 259
619 + 206
459 + 135
401 + 347
293 + 483
552 — 458
187 + 645
633 — 207
363 + 496
882 — 247
835 — 648
125 + 475
409 + 106
984 — 892
327 + 154
571 + 349
272 + 232
194 + 237
404 — 117
241 + 388
225 — 111
133 + 450
515 + 128
663 + 226
306 + 226
181 + 302
507 — 354
906 — 443
411 + 147
242 + 417
691 — 488
386 + 423
704 + 242
113 + 786
360 + 505
581 — 463
125 + 340
425 — 325
841 — 275
582 + 215
774 — 170
660 — 515
963 — 299
260 + 232
911 — 469
613 — 198
803 — 220
830 — 427
771 — 489
375 + 218
411 + 269
822 — 415
210 — 147701 + 214
336 + 442
803 + 196
128 + 124
655 + 117
791 — 301
158 + 228
395 — 195
550 — 542
592 + 183
436 — 264
357 — 316
217 + 267
945 — 852
322 + 580
532 + 159
439 + 411
150 + 402
570 + 187
982 — 215
246 + 337
800 — 626
437 + 546
612 — 302
444 + 113
948 — 590
500 + 260
864 — 285
699 + 263
239 + 755
974 — 497
941 — 770
500 — 460
404 + 541
572 — 305
310 — 153
998 — 931
482 + 403
134 + 222
412 — 406
647 — 158
567 — 294
555 + 255
478 — 417
483 + 338
708 — 313
203 + 286
251 + 727
404 + 170
782 — 739
654 — 602
103 + 506
216 + 320
163 + 152
570 — 374
888 — 503
351 + 186
959 — 330
560 — 100
167 + 611
680 — 214
665 — 406
717 — 282
327 — 260
457 + 338
212 + 276
553 — 525
803 — 761
336 + 538
517 — 233
344 — 253
661 + 272
361 + 144
503 — 441
484 + 349
519 + 302
400 + 188
682 — 111
347 + 623
591 + 142
153 + 831
175 + 402
745 + 215
939 — 668
562 — 348
865 — 415
795 + 186
426 — 287
180 + 714
718 — 534
612 — 294
635 + 158
909 — 730
612 — 274
767 + 213
857 — 475
288 + 688
107 + 500
749 + 210
108 — 103
882 — 744
327 + 325
497 + 100
173 + 710
914 — 642
500 + 193
710 — 710
691 — 488
266 + 665
910 — 696
339 + 401
616 — 226
220 + 769
403 + 550
470 + 362
259 + 461
643 — 556
442 + 289
629 — 192
967 — 628
660 — 104
883 — 699
163 + 373
673 — 495
301 + 107404 + 505
Карточки «Сложение и вычитание трехзначных чисел» с ответами | Тренажёр по математике (3 класс) по теме:
Опубликовано 08. 09.2018 — 12:44 — Аммосова Елена Васильевна
09.2018 — 12:44 — Аммосова Елена Васильевна
Карточки предназначены для формирования у учащихся навыков письменного сложения и вычитания трехзначных чисел. Применяются как дополнительный материал.
Скачать:
Предварительный просмотр:
_________________
Реши в столбик:
339 + 119 =
188 + 743 =
139 + 328 =
203 + 765 =
519 + 423 =
351 + 362 =
332 + 296 =
407 + 233 =
371 + 522 =
205 + 116 =
346 + 239 =
259 + 286 =
261 + 538 =
169 + 302 =
192 + 375 =
362 + 414 =
795 + 159 =
253 + 166 =
508 + 477 =
436 + 434 =
473 + 123 =
112 + 429 =
378 + 153 =
118 + 147 =
427 + 394 =
173 + 357 =
296 + 493 =
671 + 277 =
616 + 312 =
326 + 453 =
428 + 418 =
158 + 721 =
_________________
Реши в столбик:
781 — 142 =
558 — 179 =
789 — 186 =
526 — 377 =
485 — 323 =
356 — 318 =
429 — 323 =
671 — 237 =
396 — 199 =
624 — 286 =
476 — 407 =
493 — 331 =
383 — 174 =
601 — 364 =
466 — 202 =
673 — 239 =
472 — 243 =
265 — 135 =
451 — 311 =
574 — 199 =
395 — 292 =
531 — 326 =
493 — 459 =
207 — 108 =
335 — 329 =
456 — 277 =
336 — 319 =
585 — 157 =
471 — 437 =
369 — 122 =
269 — 139 =
538 — 113 =
Предварительный просмотр:
_________________
Реши в столбик:
339 + 119 = 458
188 + 743 = 931
139 + 328 = 467
203 + 765 = 968
519 + 423 = 942
351 + 362 = 713
332 + 296 = 628
407 + 233 = 640
371 + 522 = 893
205 + 116 = 321
346 + 239 = 585
259 + 286 = 545
261 + 538 = 799
169 + 302 = 471
192 + 375 = 567
362 + 414 = 776
795 + 159 = 954
253 + 166 = 419
508 + 477 = 985
436 + 434 = 870
473 + 123 = 596
112 + 429 = 541
378 + 153 = 531
118 + 147 = 265
427 + 394 = 821
173 + 357 = 530
296 + 493 = 789
671 + 277 = 948
616 + 312 = 928
326 + 453 = 779
428 + 418 = 846
158 + 721 = 879
_________________
Реши в столбик:
781 — 142 = 639
558 — 179 = 379
789 — 186 = 603
526 — 377 = 149
485 — 323 = 162
356 — 318 = 38
429 — 323 = 106
671 — 237 = 434
396 — 199 = 197
624 — 286 = 338
476 — 407 = 69
493 — 331 = 162
383 — 174 = 209
601 — 364 = 237
466 — 202 = 264
673 — 239 = 434
472 — 243 = 229
265 — 135 = 130
451 — 311 = 140
574 — 199 = 375
395 — 292 = 103
531 — 326 = 205
493 — 459 = 34
207 — 108 = 99
335 — 329 = 6
456 — 277 = 179
336 — 319 = 17
585 — 157 = 428
471 — 437 = 34
369 — 122 = 247
269 — 139 = 130
538 — 113 = 425
Предварительный просмотр:
_________________
Реши в столбик:
123 + 596 =
146 + 323 =
165 + 388 =
215 + 663 =
147 + 395 =
267 + 402 =
251 + 281 =
317 + 492 =
193 + 334 =
445 + 416 =
458 + 129 =
352 + 282 =
529 + 152 =
568 + 232 =
394 + 558 =
333 + 619 =
717 + 227 =
413 + 107 =
148 + 345 =
499 + 422 =
715 + 102 =
414 + 467 =
512 + 343 =
285 + 212 =
295 + 338 =
163 + 666 =
573 + 353 =
313 + 438 =
109 + 735 =
111 + 393 =
161 + 222 =
469 + 126 =
_________________
Реши в столбик:
261 — 165 =
603 — 171 =
304 — 152 =
278 — 236 =
498 — 379 =
517 — 117 =
484 — 443 =
591 — 145 =
627 — 307 =
409 — 229 =
384 — 206 =
494 — 432 =
511 — 137 =
444 — 238 =
399 — 231 =
633 — 146 =
552 — 165 =
434 — 415 =
413 — 272 =
652 — 214 =
847 — 148 =
382 — 349 =
252 — 136 =
739 — 223 =
614 — 334 =
421 — 253 =
741 — 242 =
497 — 389 =
705 — 133 =
383 — 348 =
485 — 483 =
546 — 441 =
Предварительный просмотр:
_________________
Реши в столбик:
123 + 596 = 719
146 + 323 = 469
165 + 388 = 553
215 + 663 = 878
147 + 395 = 542
267 + 402 = 669
251 + 281 = 532
317 + 492 = 809
193 + 334 = 527
445 + 416 = 861
458 + 129 = 587
352 + 282 = 634
529 + 152 = 681
568 + 232 = 800
394 + 558 = 952
333 + 619 = 952
717 + 227 = 944
413 + 107 = 520
148 + 345 = 493
499 + 422 = 921
715 + 102 = 817
414 + 467 = 881
512 + 343 = 855
285 + 212 = 497
295 + 338 = 633
163 + 666 = 829
573 + 353 = 926
313 + 438 = 751
109 + 735 = 844
111 + 393 = 504
161 + 222 = 383
469 + 126 = 595
_________________
Реши в столбик:
261 — 165 = 96
603 — 171 = 432
304 — 152 = 152
278 — 236 = 42
498 — 379 = 119
517 — 117 = 400
484 — 443 = 41
591 — 145 = 446
627 — 307 = 320
409 — 229 = 180
384 — 206 = 178
494 — 432 = 62
511 — 137 = 374
444 — 238 = 206
399 — 231 = 168
633 — 146 = 487
552 — 165 = 387
434 — 415 = 19
413 — 272 = 141
652 — 214 = 438
847 — 148 = 699
382 — 349 = 33
252 — 136 = 116
739 — 223 = 516
614 — 334 = 280
421 — 253 = 168
741 — 242 = 499
497 — 389 = 108
705 — 133 = 572
383 — 348 = 35
485 — 483 = 2
546 — 441 = 105
По теме: методические разработки, презентации и конспекты
Урок математики во 2 классе «Сложение и вычитание трехзначных чисел»
Урок математики по учебнику Л. Г. Петерсон. Цель: формировать умение выполнять сложение и вычитание трехзначных чисел, выполнять проверку действий….
Г. Петерсон. Цель: формировать умение выполнять сложение и вычитание трехзначных чисел, выполнять проверку действий….
конспект урока «Сложение и вычитание трехзначных чисел »
конспект урока «Сложение и вычитание трехзначных чисел » для урока математики во 3 классе…
Сложение и вычитание трехзначных чисел
Урок математики в 3 классе…
КОНСПЕКТ УРОКА МАТЕМАТИКИ ПО ТЕМЕ: «СЛОЖЕНИЕ И ВЫЧИТАНИЕ ТРЕХЗНАЧНЫХ ЧИСЕЛ. ТРЕТЬЕ РАТНОЕ ПОЛЕ РОССИИ» 3 класс
Урок, как и любой другой урок в системе Л.В. Занкова, прежде всего был нацелен на общее развитие школьников.Его эффективность доказывается разными показателями: реализацией дидактических принцип…
Конспект урока по математике во 2 классе на тему «Сложение и вычитание трехзначных чисел»
Конспект урока может быть использован на уроках математики во 2 классе….
Конспект урока по математике во 2 классе. Сложение и вычитание трехзначных чисел. Даты и числа из истории Москвы.
Специфика экспериментальной деятельности предполагает преобразование всего учебного процесса, его форм, методов, содержания, отношений его субъектов. Внедрение проекта в учебную деятельнос…
Внедрение проекта в учебную деятельнос…
Сложение и вычитание трехзначных чисел
Урок математики в 3 классе в форме «Зимней олимпиады. Класс разделен на 5 команд. У каждой команды есть своя зачетная карточка, куда вписываются результаты работы командыв течение всего урока.. В конц…
Поделиться:
256 + 272, 637 – 273″
Математика, 3 класс
Тема урока: «Сложение и вычитание трехзначных чисел: 256 + 272, 637 – 273»
Тип урока: ОНЗ
Основные цели:
1) сформировать умение строить алгоритмы на примере построения алгоритма сложения и вычитания трёхзначных чисел;
2) сформировать умение складывать и вычитать трёхзначные числа без перехода через разряд;
3) тренировать способность к умению учиться;
4) тренировать умения анализировать и решать задачи.
Планируемые результаты: учащиеся научатся выполнять сложение и вычитание трёхзначных чисел в столбик по эталону (алгоритму), решать задачи изученных видов, выполнять задания творческого и поискового характера, анализировать и делать выводы, работать в группах
Демонстрационный материал: 1) приемы на сложение и вычитание двузначных чисел,
2) опорный сигнал обозначения трехзначных чисел, 3) эталон сложения и вычитания двузначных чисел в столбик, 4) алгоритм сложения и вычитания трехзначных чисел в столбик, 5) эталон сложения и вычитания трехзначных чисел в столбик.
Раздаточный материал: 1) чистые листы А4 по количеству групп, 2) карточки трех цветов (красный, зеленый, желтый) для этапа рефлексии.
Ход урока
1. Мотивация к учебной деятельности.
− Ребята, сегодня вы посетите очень интересную страну, которая называется «Страна сложения и вычитания». Как вы думаете, кто будет жить в этой стране? (Разные способы сложения и вычитания.)
Как вы думаете, кто будет жить в этой стране? (Разные способы сложения и вычитания.)
На экране или доске:
− Вспомните и назовите ее жителей. (Прием сложения и вычитания двузначных чисел; прием сложения двузначных чисел, когда в разряде единиц получается 10; прием вычитания двузначных чисел, когда в уменьшаемом в разряде единиц 0; сложение двузначных чисел с переходом через разряд; вычитание двузначных чисел с переходом через разряд.)
− А почему в волшебной стране появился знак вопроса? (Наверное, здесь живет еще один способ, который мы пока не знаем.)
− Скажите, чему же будет посвящен сегодняшний урок? (Сложению и вычитанию.)
− А с какими числами вы работали на последних уроках? (С трехзначными числами.)
− Значит, вы сегодня будете учиться складывать и вычитать какие числа? (Трехзначные.)
− А как вы узнаете новое на уроке? (Мы сначала повторим то, что нам понадобится, обобщим, выполним пробное задание, у нас может не получиться, мы остановимся, подумаем и сами откроем новый способ. )
)
− Как вы будете работать? (Самостоятельно.)
− Тогда пожелайте друг другу удачи − и в путь.
2. Актуализация знаний и фиксация индивидуального затруднения в пробном действии.
− Чтобы узнать что-то новое, что надо сделать сначала? (Повторить те знания, которые нам понадобятся на уроке.)
На доске даны числа: 123, 456.
− Прочитайте данные числа и назовите, сколько в них сотен, десятков и единиц.
− Какой эталон вам помог выполнить это задание? (Опорный сигнал обозначения трехзначных чисел.)
Учитель вешает его на доску.
С Д Е
− Посмотрите на эти числа, что интересного вы замечаете? (Все цифры, использованные для записи чисел, разные, задействованы все цифры по порядку от 1 до 6.)
− Как можно продолжить этот ряд? (Дописать число 789.)
Учитель на доске дописывает число 789.
− В каком порядке расположены числа? (В порядке возрастания.)
− Посмотрите на числовые выражения:
34 + 25 78 – 16 51 + 36 84 – 61
− Какое задание можно с ними выполнить? (Разделить на группы по виду арифметического действия, найти значения выражений…)
− Какие выражения будут в первой группе, во второй?
34 + 25 78 — 16
51 + 36 84 – 61
− Найдите значения этих числовых выражений, используя запись в столбик.
− Какой эталон вам помог выполнить это задание? (Эталон сложения и вычитания двузначных чисел в столбик.)
− Проговорите эталон.
Одно выражение на сложение и одно на вычитание дети объясняют у доски, два других – комментируют с места.
− Итак, ребята, что же вы сейчас повторили? (Разряды трехзначных чисел, сложение и вычитание двузначных чисел в столбик.)
− Какое задание я вам сейчас предложу? (Задание на пробное действие.)
− Зачем? (Чтобы мы поняли, что нам не известно.)
Учитель открывает на доске выражение: 256 +272.
− Что нового вы увидели в этом задании? (Надо найти сумму трехзначных чисел.)
− Что же вы должны будете сделать дальше? (Попробовать найти значение этого выражения.)
− Найдите значение этого выражения, записав числа в столбик.
− Стоп. Посмотрим результаты.
− Поднимите руки, кто не смог найти сумму? Что показало вам ваше пробное действие? (Я не могу сложить трехзначные числа в столбик.)
− Те, кто решил, можете назвать, каким эталоном воспользовались?
− Что вы не можете сделать? (Я не могу назвать, каким эталоном воспользовался. )
)
− Что надо сделать дальше? (Остановиться и подумать).
3. Выявление места и причины затруднения.
− Какое задание выполняли?
− Как вы рассуждали? На какой эталон вы опирались в своих действиях?
− Подошел ли к вашему заданию известный эталон? (Нет.)
− Где же возникло затруднение? Какой шаг отсутствует в известном алгоритме? (Сложение сотен.)
− Почему же вы не смогли справиться с этим заданием? (Мы не знаем алгоритм сложения трехзначных чисел.)
4. Построение проекта выхода из затруднения.
− Прежде чем продолжить работу дальше, что надо сделать? (Поставить цель.)
− Сформулируйте цель своей деятельности. (Узнать алгоритм сложения трехзначных чисел.)
− Вы будете открывать новый алгоритм или уточнять уже известный? (Уточнять известный алгоритм.)
− Сформулируйте тему урока. (Сложение трехзначных чисел.)
− Вы сегодня на уроке будете составлять алгоритм не только для сложения, но и для вычитания трехзначных чисел, поэтому тема урока будет звучать так: «Сложение и вычитание трехзначных чисел».
− Повторите еще раз, какой алгоритм вы будете уточнять?
− Как звучит первый шаг в алгоритме сложения двузначных чисел? (Пишу единицы под единицами, десятки под десятками.)
− Какой же будет первый шаг в алгоритме сложения трехзначных чисел? (Пишу единицы под единицами, десятки под десятками, сотни под сотнями.)
− Что вы будете делать дальше? (Складывать единицы.)
− А затем? (Десятки.)
− А следующий шаг вы сформулируете самостоятельно.
− Составим план вашей дальнейшей работы.
− Что вы сделаете сначала? (Запишем числа в столбик.)
− Дальше что вы можете сделать? (Вычислить.)
− Дальше вам надо будет сформулировать недостающий шаг. И в конце, − что вы должны сделать? (Составить эталон.)
На доске фиксируется план:
1. Записать выражение в столбик и вычислить.
2. Сформулировать недостающий шаг.
3. Составить опорный сигнал.
5. Реализация построенного проекта.
– Работать вы будете в группах. Но сначала вспомните основные правила работы в группе.
Но сначала вспомните основные правила работы в группе.
На работу в группах отводится 3 минуты.
− Представьте свои результаты. Объясните свои действия.
У доски отвечают по одному представителю от группы.
− Ребята, скажите, а для вычитания трехзначных чисел подойдет составленный вами опорный сигнал? Как его можно изменить, чтобы он подошел и для вычитания? Расскажите, как вы будете вычитать?
Учитель на доске фиксирует эталон
− Решите пример на вычитание трехзначных чисел, опираясь на полученный вами опорный сигнал: 637 – 273
Один ученик работает на доске, другие ребята – в рабочих тетрадях.
− А теперь сформулируйте общий алгоритм сложения и вычитания трехзначных чисел.
Дети называют каждый шаг, учитель фиксирует его на доске.
−Сравните полученный алгоритм со своим эталоном. Вы все сделали правильно?
− Скажите, все ли затруднения вы сняли? (Да.)
− Докажите. (Мы знаем, как правильно выполнить сложение или вычитание трехзначных чисел, можем обосновать свои действия. )
)
− Какие же задания вы теперь сможете выполнять? (Складывать и вычитать трехзначные числа.)
Алгоритмы сложения и вычитания трехзначных чисел стр. 71-72
— Совпадает ли наш эталон с алгоритмами?
Физкультминутка.
− Если я называю трехзначное число, вы подпрыгиваете, а если двузначное – приседаете.
345; 126; 18; 20; 99; 5; 580; 724; 10;15; 640; 2.
6. Первичное закрепление с проговариванием во внешней речи.
– Можно ли сказать, что вы уже все сделали на уроке? (Нет.)
− Какую цель вы поставите на оставшиеся этапы? (Научиться применять построенный алгоритм при сложении и вычитании трехзначных чисел.)
− Что для этого надо сделать? (Потренироваться в использовании нового алгоритма.)
Задание:
Выполни действия. Что ты замечаешь? Сделай вывод.
а)
б)
Решение:
а)
б)
– Прочитайте задание.
– Выполним три примера на сложение и три примера на вычитание.
По одному с места с объяснением:
− Первое слагаемое одинаковое, а второе уменьшается, поэтому сумма уменьшается.
− Вычитаемое одинаковое, а уменьшаемое уменьшается, поэтому и разность уменьшается.
− Вы поработали все вместе, а как надо поработать теперь? (В парах.)
№ 2, стр. 71-72 (по 1 выражению из каждого номера) – первое выражение объясняют ученики первого варианта, второе – ученики второго варианта.
456 +252 306 — 262
Задание выполняется в рабочих тетрадях. Выполнение задания проверяется по образцу:
+
−
306 456
262 252
84 708
Те ребята, которые допустили ошибки, проговаривают решение вслух, находят место ошибки, анализируют ее и исправляют.
7. Самостоятельная работа с самопроверкой по эталону.
− Вы поработали вместе, в парах, а что теперь необходимо сделать? (Поработать самостоятельно. )
)
− С какой целью вы будете работать самостоятельно? (Мы должны для себя выяснить, понятен ли нам новый способ, можем мы им самостоятельно пользоваться.)
– Выполните № 3 (первый и четвертый примеры) на стр. 50.
690 +188 635 — 283
– Какой вид записи выберете? (В столбик.)
– Задание выполняйте в тетрадях.
– Проверьте.
Открыть на доске эталон для самопроверки:
– У кого получился другой ответ – поставьте «?», найдите место, где допущена ошибка, объясните.
– Кто справился с заданием без ошибок? Поставьте себе «+».
8. Включение в систему знаний и повторение.
− При выполнении каких заданий вы сможете использовать умения, приобретенные на уроке? (При решении уравнений, задач…)
− Решите задачу.
«В нашей школе 248 мальчиков и 211 девочек. Сколько всего учеников в нашей школе? На сколько мальчиков больше, чем девочек?»
− Прочитайте условие и первый вопрос задачи. Что известно и что надо узнать?
Что известно и что надо узнать?
− Можете ли вы сразу ответить на вопрос задачи? (Да.)
− Каким действием?
− Выполните решение в тетради.
Один ученик работает у доски, остальные дети – в тетрадях.
− Прочитайте второй вопрос задачи. Можете ли вы сразу на него ответить? (Да.)
− Каким действием?
− Выполните решение в тетради.
Другой ученик у доски, остальные ребята – в рабочих тетрадях.
9. Самостоятельная работа.
Решите задачу.
«В гараже было 305 «Жигулей» и 142 «Москвича». Утром уехало 237машин. Сколько машин осталось в гараже?»
Для слабых учеников используется карточка-помощница.
305 + 142
осталось
уехали
?
237
10. Рефлексия учебной деятельности на уроке.
– Какой же новый способ живет в нашей стране? (Сложение и вычитание трехзначных чисел.)
− Как же складывают и вычитают трехзначные числа?
− Какие цели вы сегодня ставили?
− Достигли вы этих целей? Докажите.
− У кого остались затруднения по новой теме?
− Над чем еще вам надо будет поработать?
− Можно ли сказать, что сегодня вы были настоящими учениками? (Да.)
− Докажите.
− Оцените свою работу на уроке, используя цветные карточки.
Далее учитель предлагает учащимся обсудить домашнее задание. Оно дано на дополнительных карточках.
Домашнее задание:
Учебник № 4 стр. 71; № 4 стр. 72
− Расскажите, а как вы будете выполнять свое домашнее задание? Вспомните алгоритм самостоятельного выполнения домашнего задания.
− Спасибо за урок!
Вычитание трехзначных чисел столбиком. Вычитание столбиком трехзначных чисел.
- Альфашкола
- Статьи org/ListItem»>Вычитание трехзначных чисел в столбик
Вычитание \(3-\)значных чисел в столбик аналогично вычитанию \(2\)-значных чисел в столбик Вычитание в столбик. Записываем сверху большее из двух чисел, снизу меньшее. Если уменьшаемое больше вычитаемого ставим в разности плюс, если наоборот минус (вычитаемое больше уменьшаемого). Десятки располагаются под десятками, сотни под сотнями, тысячные под тысячными и т. д.
Пример 1. Вычислите \(488-187\) в столбик.
Решение:
\(8-7=1\)
\(8-8=0\)
\(4-1=3\)
Ответ: \(301.\)
Пример 2. Вычислите \(578-299\) в столбик.
Решение:
\(18-9=9\)
\(16-9=7\)
\(4-2=2\)
Ответ: \(279.\)
Пример 3.. Вычислите \(456-592\) в столбик.
Решение:
Ответ: \(-136.\)
Пример 4.. Найдите \(756-398\) в столбик.
Решение:
\(16-8=8\)
\(14-9=5\)
\(6-3=3\)
Ответ: \(358.\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Иван Владимирович Чикин
Репетитор по математике
Стаж (лет)
Образование:
Рязанский государственный университет имени С.А. Есенина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Более пяти лет успешно готовлю учеников к сдаче ОГЭ и ЕГЭ, кроме того могу помочь развить разговорные навыки, подтянуть школьную программу. Обучаю в основном по учебникам иностранных издательств, но беру лучшее от классической школы. Ученик это в первую очередь личность со своими интересами и стремлениями, так что всегда нахожу индивидуальный подход.
Обучаю в основном по учебникам иностранных издательств, но беру лучшее от классической школы. Ученик это в первую очередь личность со своими интересами и стремлениями, так что всегда нахожу индивидуальный подход.
Елена Анатольевна Фомина
Репетитор по математике
Стаж (лет)
Образование:
Орловский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов. Мною разработана собственная методика повышения уровня грамотности. Использую только индивидуальный подход к каждому ученику. С радостью буду ждать на занятиях!
Использую только индивидуальный подход к каждому ученику. С радостью буду ждать на занятиях!
Светлана Николаевна Комашко
Репетитор по математике
Стаж (лет)
Образование:
Минский государственный лингвистический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по английскому языку для 1-7 классов.
Помогу освоить грамматику, аудирование, а также разговорную речь.
В том числе разбор школьной программы и выполнение домашних заданий. Занятия проходят с использованием современной методики обучения.
План каждого занятия разрабатывается индивидуально исходя из целей и текущего уровня ученика. В свой работе использую современные издания, видео и аудио материалы.
Жду вас на своих занятиях.
Занятия проходят с использованием современной методики обучения.
План каждого занятия разрабатывается индивидуально исходя из целей и текущего уровня ученика. В свой работе использую современные издания, видео и аудио материалы.
Жду вас на своих занятиях.
Похожие статьи
- Как заинтересовать детей учить математику?
- Сфера
- Как разделить число в отношении
- Финансовый Университет (Прикладная информатика): учебный план, баллы для поступления
- РУДН: факультет Государственного и Муниципального Управления (ГМУ)
- Задачи с прикладным содержанием (вариант 3)
- Как выбрать велосипед для школьника
- Обучение старшеклассников: как найти общий язык с учениками, если разница в возрасте небольшая?
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
176 + 145 / Открытый урок
Основные цели:
1) Сформировать умение складывать трёхзначные числа с переходом через два разряда.
2) Тренировать умения записывать сложение столбиком, соотносить единицы длины с единицами счёта, решать примеры с помощью графических моделей.
3) Сформировать умение решать задачи на одновременное движение навстречу.
Мыслительные операции, необходимые на этапе проектирования: сравнение, анализ, обобщение, аналогия.
Демонстрационный материал:
1) «Книга рекордов Гиннеса»;
2) карточки, на которых:
на обратной стороне каждой карточки написано соответствующее число: 245, 76, 168, 130;
3) фото самого высокого и самого низкого человека (если возможно):
4) опорные сигналы для распознавания примеров на сложение
трёхзначных чисел с переходом через разряд (из урока 2-1-28):
5) опорный сигнал для распознавания примеров нового типа:
6) пособие «Треугольники и точки»;
7) эталоны сложения трехзначных чисел с переходом через один разряд (из урока 2-1-28):
8) эталон сложения трёхзначных чисел с переходом через два разряда:
Раздаточный материал:
1) листы с заданием для пробного действия:
2) листы А–4 по количеству групп с заготовкой для уточнения эталона:
Ход урока:
1. Мотивация к учебной деятельности.
Мотивация к учебной деятельности.
Цель:
1) создать условия для возникновения внутренней потребности включения в учебную деятельность на уроке посредством связи с темами предыдущих уроков;
2) актуализировать требования к ученику со стороны учебной деятельности;
3) установить тематические рамки урока: работа с трёхзначными числами.
Организация учебного процесса на этапе 1:
– С какими числами вы работали на последних уроках математики? (С трёхзначными.)
– Что вы умеете делать с этими числами? (Сравнивать, складывать, вычитать, …)
– Сегодня вы продолжите работу с трёхзначными числами и узнаете новое о сложении трёхзначных чисел. Скажите, а как человек может узнать что-то новое, т.е. научиться чему-то? (Надо попробовать сделать то, чего никогда не делал. Если не получится, надо подумать, почему не получилось, поставить себе цель …)
– Молодцы! С чего предлагаете начать? (С повторения необходимого. )
)
2. Актуализация знаний и фиксация затруднения в пробном учебном действии.
Цель:
1) тренировать умения соотносить единицы длины с единицами счёта, решать примеры на сложение трёхзначных чисел с переходом через разряд в столбик;
2) провести контроль устных вычислительных навыков учащихся;
3) активизировать мыслительные операции: сравнение, анализ, аналогию;
4) мотивировать учащихся к выполнению пробного действия;
5) организовать самостоятельное выполнение учащимися индивидуального задания на применение нового знания, запланированного для изучения на данном уроке;
6) организовать фиксацию учащимися возникшего затруднения в обосновании правильности полученного результата.
Организация учебного процесса на этапе 2:
1) Соотношение единиц измерения длины с единицами счёта.
– На уроках математики мы постоянно работаем с числами. Числа могут рассказать много интересного. Удивительные факты, связанные с числами, собраны в необычной книге – «Книге рекордов Гиннеса».
Числа могут рассказать много интересного. Удивительные факты, связанные с числами, собраны в необычной книге – «Книге рекордов Гиннеса».
Учитель показывает книгу.
– Рекорд – это наибольший или наилучший показатель чего-либо, т.е. «самый-самый»: самый ловкий, самый быстрый и т.д. В этой книге собраны сведения о самых разных рекордах в жизни нашей планеты. В ней можно найти сведения о самых высоких и самых низких людях. Например, самым высоким жителем планеты является китаец Ван Фензель. Его рост 2 м45 см.
Повесить карточку на доску:
– Рост обычного взрослого человека – 1 м68 см.
Повесить карточку на доску: . Рядом с карточкой повесить фото.
– Самый маленький в мире человек – португалец Антонио Феррейро, рост которого в 44 года был
7 дм 6 см.
Повесить карточку на доску:
– Для того чтобы себе это представить, сравните с вашим ростом, который равен примерно 1 м30 см.
Повесить карточку на доску:
– Каждый из вас на 60-70 сантиметров выше этого человека.
– Выразите эти величины в сантиметрах и соотнесите с единицами счёта.
По одному с места устно. (2 м45 см = 245 см, соответствует числу 245. 1 м68 см = 168 см, соответствует числу 168. 7 дм 6 см = 76 см, соответствует числу 76. 1 м30 см = 130 см, соответствует числу 130.)
Учитель со слов детей переворачивает карточки, открывая ответы:
– Расположите эти числа в порядке возрастания. (76, 130, 168, 245.)
Учитель по ходу ответов передвигает карточки.
2) Сложение трёхзначных чисел с переходом через разряд в столбик
– Вы считали устно. А какой письменный приём сложения и вычитания трёхзначных чисел вы знаете? (В столбик.)
– Решите пример, записав его столбиком: 128 + 114.
Открыть запись выражения на доске.
– Каким алгоритмом воспользуетесь? Почему именно этим? (Алгоритмом сложения с переходом через разряд, т.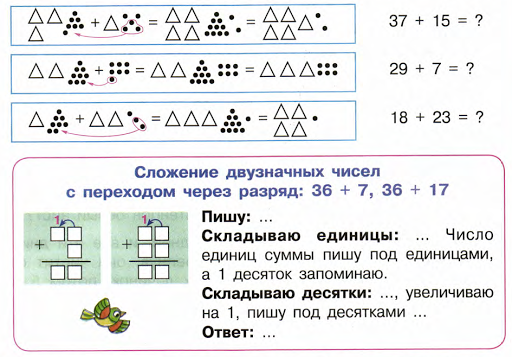 к. при сложении единиц получится число больше 10.)
к. при сложении единиц получится число больше 10.)
Обратить внимание детей на эталон (первый), вывешенный на стенде:
Один у доски с объяснением, остальные – в тетрадях.
(Пишу единицы по единицами,… Складываю единицы: 8 + 4 = 12 единицам, 2 единицы пишу под единицами, 1 десяток запоминаю. Складываю десятки: 2 + 1 + 1 = 4 десяткам, 4 пишу под десятками. Складываю сотни: 1 + 1 = 2 сотням. Ответ: 242.)
По ходу ответа учитель обращает внимание детей на эталон сложения (первый) трёхзначных чисел с переходом через разряд в столбик:
– Отлично! Именно знание способа сложения трёхзначных чисел с переходом через разряд будет вам сегодня необходимо.
– Этап повторения завершён. Что дальше? (Надо выполнить задание для пробного действия.)
– В чём особенность задания для пробного действия? (В нём есть что-то для нас новое.)
3) Задание для пробного действия.
Раздать листы с заданием.
Открыть то же выражение на доске.
– Что нового в этом примере, постарайтесь понять в ходе выполнения. Итак, запишите пример в столбик и решите его.
На выполнение задания » 30–40 секунд.
– Проверим. Назовите ответ примера. (321; 221; 211; …)
После каждого ответа учитель задаёт вопрос: «У кого такой же ответ?» и фиксирует варианты ответов детей на доске.
– Что получилось? (Получили разные ответы.)
– Поднимите руку, кто может доказать, что решил пример 176 + 145 верно.
– Вы не подняли рук, значит, в чём ваше затруднение? (Мы не можем доказать, что верно решили пример 176 + 145.)
– И что делать? (Подумать над причиной затруднения.)
3. Выявление места и причины затруднения.
Цель:
1) создать условия для проведения учащимися анализа своих действий;
2) организовать выявление и фиксацию учащимися места и причины затруднения: нет способа сложения трёхзначных чисел с переходом через два разряда.
Организация учебного процесса на этапе 3:
– Выясним причину трудности. Какое действие, и с какими числами вы выполняли? (Сложение трёхзначных чисел.)
– Ведь вы умеете это делать. Какие виды примеров на сложение трёхзначных чисел вы умеете решать? (Без перехода через разряд. Когда при сложении единиц получается больше 10 или при сложении десятков получается больше 10.)
– А что же в этом примере было для вас новым? (В этом примере при сложении получилось больше 10 и в разряде десятков, и в разряде единиц.)
Повесить на доску опорный сигнал для распознавания нового типа примеров:
– Как в математике называют такое сложение? (Сложение с переходом через разряд.)
– Только в таком типе примеров переход не через один, а через два разряда.
– Расскажите, как вы рассуждали при решении примера на сложение трёхзначных чисел с переходом через два разряда, и было ли место в ходе ваших рассуждений, где вы засомневались.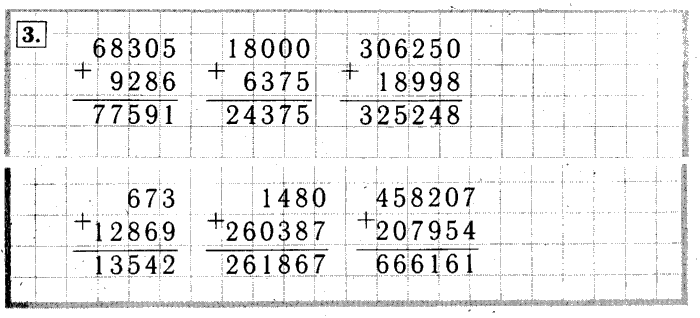 (…)
(…)
– Почему же у вас возникло затруднение в доказательстве правильности решения примера на сложение с переходом через два разряда? (Нам неизвестен способ сложения трёхзначных чисел с переходом через два разряда.)
– Причину затруднения вы зафиксировали. Что надо сделать дальше? (Надо поставить цель и выбрать средства.)
4. Построение проекта выхода из затруднения.
Цель:
1) создать условия для формулирования учащимися конкретной цели будущих учебных действий;
2) согласовать тему урока;
3) организовать выбор учащимися способа и средств для построения нового знания;
4) создать условия для составления учащимися плана дальнейших действий для достижения цели.
Организация учебного процесса на этапе 4:
– Какую цель вы перед собой поставите? (Построить способ решения примеров на сложение трёхзначных чисел с переходом через два разряда. )
)
– А как вы назовёте урок? (Сложение трёхзначных чисел с переходом через два разряда.)
Открыть тему на доске.
– Какие инструменты вам будут необходимы для построения нового способа? (Графические модели, способ записи и решения примеров в столбик.)
– Составьте план вашей дальнейшей работы. (Сначала решим пример с помощью графических моделей.)
Учитель последовательно фиксирует план на доске.
– Зачем вам необходимо воспользоваться графическими моделями? (Чтобы увидеть, как происходит действие.)
– Что сделаете потом? (Запишем и решим этот пример в столбик.)
Зафиксировать следующий пункт плана.
– А затем? (Сделаем вывод, построим эталон, …)
– Вы будете создавать новый эталон или будете уточнять какие-то эталоны? (Надо будет уточнить эталоны сложения трёхзначных чисел с переходом через один разряд – их надо объединить.)
Зафиксировать последний пункт плана: 3. Уточнить эталон.
5. Реализация построенного проекта.
Цель:
1) организовать построение нового способа решения примеров на сложение трёхзначных чисел с переходом через два разряда, используя предметные действия с графическими моделями;
2) организовать построение нового способа на примере, вызвавшем затруднение;
3) организовать фиксацию нового способа действий в речи и знаково путём объединения известных эталонов сложения с переходом через разряд в одном из разрядов;
4) зафиксировать преодоление возникшего ранее затруднения.
Организация учебного процесса на этапе 5:
– С чего начнёте разбираться в решении этого примера? (С составления графической модели примера.)
– Сказано – сделано.
Один ученик работает у доски, остальные – на партах:
– Расскажите, как будете складывать. (Складываем сотни: 1 с + 1 с = 2 с. Складываем десятки:
Складываем десятки:
7 д + 4 д = 11 д. Складываем единицы: 6 е + 5 е = 11 е. Получилось 2 с 11 д 11 е.)
– Что делать с «лишними» десятками и единицами? (Нужно из 10 десятков образовать 1 сотню, из 10 единиц – 1 десяток.)
– Отлично, так и сделаем.
– Сколько в итоге получилось сотен, десятков, единиц? (3 с 2 д 1 е.)
– Прочитайте правильный ответ этого примера. (321.)
– Что дальше по плану? (Надо записать решение этого примера в столбик.)
– Как расположить числа, записывая решение в столбик? Почему? (Единицы под единицами, десятки под десятками, сотни под сотнями, так как удобно складывать разрядные единицы.)
– С какого разряда надо начинать сложение? Почему? (С разряда единиц, так как число десятков и сотен при переходе через разряд может изменяться. )
)
Один учащийся у доски с объяснением, остальные работают в тетрадях. Учитель привлекает всех учащихся к обсуждению нового способа действий при решении примера в столбик.
(Складываю единицы: 6 + 5 = 11 единицам, 1 единицу пишу под единицами, 1 десяток запоминаю. Складываю десятки: 7 + 4 + 1 = 12 десяткам, 2 пишу под десятками, 1 сотню запоминаю. Складываю сотни: 1 + 1 + 1 = 3 сотням. Ответ: 321.)
– Где возможна ошибка при решении таких примеров? (Можно забыть увеличить количество десятков или сотен на 1.)
– Что нужно сделать, чтобы это не забыть? (Надписать число 1 над разрядами десятков и сотен.)
– Что осталось сделать? (Осталось уточнить эталон.)
– Объединитесь в группы и уточните эталон.
Учитель руководит объединением детей в группы и раздаёт заготовки на листах А–4 каждой группе.
– Выберите представителя от группы для отчёта. Посмотрим, что у вас получилось.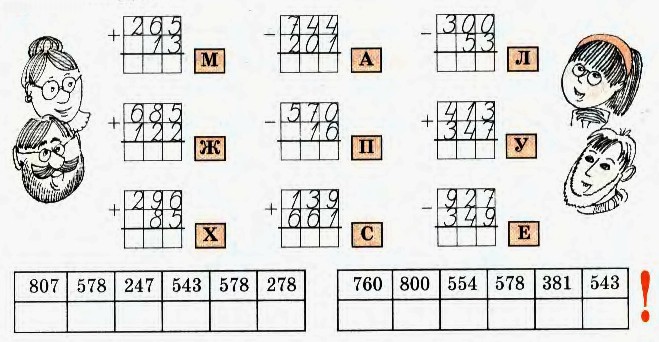
Представитель от каждой группы представляет уточнённый эталон. После согласования и выступления групп лучший вариант остается на доске. В итоге эталон должен принять примерно такой вид:
– Какую цель вы перед собой ставили? (Построить способ сложения трёхзначных чисел с переходом через два разряда.)
– Достигли цели? Докажите. (Мы достигли цели, так как построили способ сложения трёхзначных чисел с переходом через два разряда.)
– Этого достаточно или вам необходимо поставить перед собой ещё одну цель? (Надо научиться применять этот способ для решения примеров.)
– Итак, чем займётесь дальше? (Потренируемся в решении примеров на сложение с переходом через два разряда.)
6. Первичное закрепление с проговариванием во внешней речи.
Цель:
создать условия для выполнения учащимися нескольких типовых заданий на применение изученного способа действий с проговариванием во внешней речи.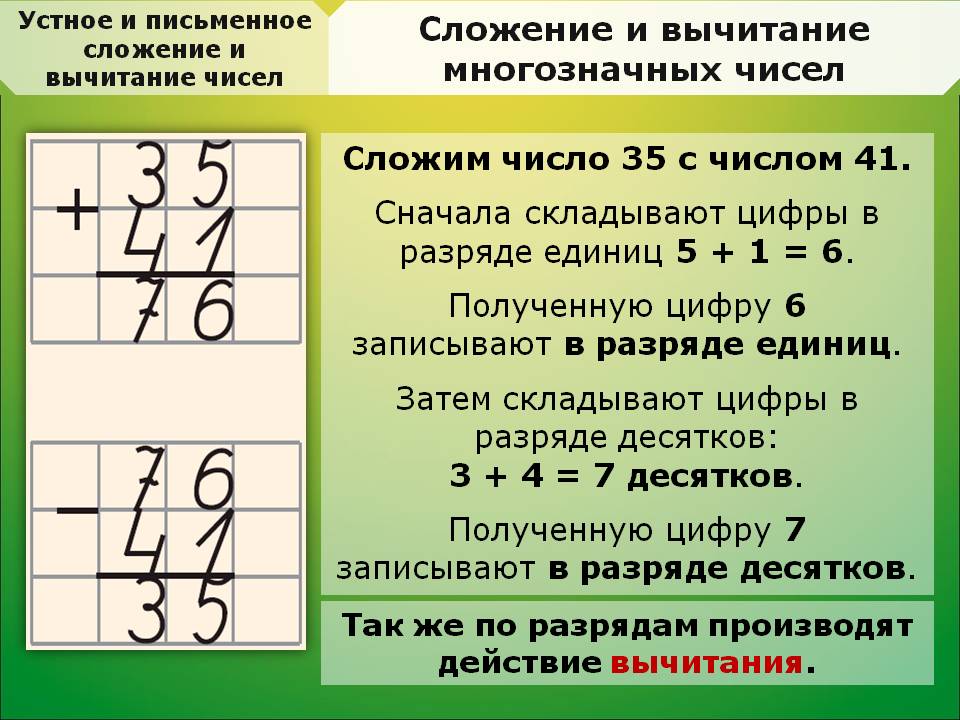
Организация учебного процесса на этапе 6:
– Откройте № 1 (б) на стр. 56.
– Прочитайте задание. В чем особенность этих примеров? (Они на сложение трёхзначных чисел с переходом через два разряда.)
– Докажите, что это именно этот вид примеров. (При сложении единиц и при сложении десятков получается больше 10.)
– Решите три первых примера.
По одному у доски с объяснением, остальные – в тетрадях. (Складываю единицы: 5 + 9 = 14, 4 пишу под единицами, 1 десяток запоминаю. Складываю десятки: 2 + 9 + 1 = 12, 2 пишу под десятками, 1 сотню запоминаю. Складываю сотни: 7 + 1 + 1 = 9. Ответ: 924.)
Далее аналогично.
– Как вы можете проверить, что поняли новый способ? (Надо поработать самостоятельно.)
7. Самостоятельная работа с самопроверкой по эталону.
Цель:
1) организовать самостоятельное выполнение учащимися типовых заданий на новый способ действий;
2) организовать самопроверку учащимися своих работ по эталону для самопроверки;
3) создать (по возможности) ситуацию успеха для каждого ребёнка.
Организация учебного процесса на этапе 7:
Открыть запись на доске: 326 + 152 538 + 273 757 + 54 429 + 532.
1) – Сначала я предлагаю вам выбрать примеры на новое правило и написать карандашом на полях номера этих примеров. Какова цель этого задания? Зачем нужно различать вид примеров? (Чтобы применять соответствующий способ.)
– Что поможет при выполнении этого задания? (Опорный сигнал для выбора типа примера.)
Для выполнения работы даётся » 40 секунд.
– Проверьте себя по эталону.
Открыть на доске эталон:
– Допустили ли ошибки в выборе примеров? В чём причина? (Не сложили (сложили с ошибкой) единицы и десятки, чтобы определить тип примера)
– У кого примеры выбраны верно, поставьте на полях учебника «+».
2) – Какое задание будет следующим? (Решить эти примеры, записав их в столбик. )
)
– Верно. А какова цель этого задания? (Проверить, поняли ли мы способ сложения трёхзначных чисел с переходом через два разряда.)
– Запишите в тетрадь выбранные примеры в столбик и решите их.
– Проверьте.
Открыть на доске эталон:
– Какие трудности возникли при решении примеров? (Неверно записали столбиком второй пример, забыли прибавить 1 десяток и 1 сотню, которую надо было запомнить, …)
– Какие правила вам надо повторить? (При записи примеров столбиком сотни пишем под сотнями, десятки – под десятками, единицы – под единицами. Чтобы не забыть прибавить один к следующему разряду, надо надписать единицу над этим разрядом.)
– У кого оба примера решены верно? Поставьте себе на полях тетради ещё один «+».
– Что интересного заметили? (Ответы обоих примеров одинаковы: 811, 811.)
– Какая здесь есть закономерность? (Закономерности нет – это просто совпадение. )
)
8. Включение в систему знаний и повторение.
Цель:
сформировать умение решать задачи на одновременное движение навстречу.
Организация учебного процесса на этапе 8:
– Где вам может пригодиться умение решать примеры на сложение трёхзначных чисел с переходом через два разряда? (При решении задач, уравнений, …)
– Давайте убедимся в этом, тем более что осталось время для решения задачи.
№ 2, стр. 56.
– Прочитайте условие задачи в учебнике № 2 на стр. 56.
– Как показано на чертеже, что мальчики двигаются навстречу друг другу? (Стрелками.)
– Как отмечено место встречи? (Красным флажком.)
– Выполните анализ задачи. (В задаче известно, что мальчики шли навстречу друг другу. Вадим прошёл до места встречи 342 м, а Костя – 458 м. Нужно узнать, какое расстояние было между ними вначале. Чтобы ответить на вопрос задачи, нужно к расстоянию, которое прошёл Вадим прибавить расстояние, которое прошёл Костя, т.к. ищем целое.)
Чтобы ответить на вопрос задачи, нужно к расстоянию, которое прошёл Вадим прибавить расстояние, которое прошёл Костя, т.к. ищем целое.)
– Запишите решение задачи. Как удобно это сделать? (В столбик.)
Один у доски с объяснением, остальные – в тетрадях.
9. Рефлексия учебной деятельности на уроке.
Цель:
1) организовать фиксацию учащимися степени соответствия поставленной цели и полученного результата учебной деятельности;
2) создать условия для фиксации учащимися в речи нового способа действий, изученного на уроке: сложение трёхзначных чисел с переходом через два разряда;
3) организовать фиксацию затруднений, которые остались, и способов их преодоления;
4) организовать самооценку учениками собственной учебной деятельности на уроке;
5) согласовать домашнее задание.
Организация учебного процесса на этапе 9:
– Какова была цель вашей работы на уроке? (Построить способ сложения трёхзначных чисел с переходом через два разряда. )
)
– Достигли цели? Докажите.
– Какие алгоритмы помогли при построении способа решения примеров нового типа? (Алгоритмы сложения трёхзначных чисел с переходом в разряде единиц и с переходом в разряде десятков)
– Какую ошибку будете стараться не допускать при решении этих примеров? (Будем стараться не забывать увеличивать количество десятков и сотен на один.)
– Когда было трудно? Удалось ли справиться с затруднениями? Как? (…)
– Кому сегодня удалось учиться по-настоящему? Почему вы так считаете? (…)
– Посмотрите ещё раз на карточки, с которых мы начали урок. Из какой книги я взяла эти числа, и что означает каждое из них?
Скачать публикацию
Урок математики «Сложение и вычитание трёхзначных чисел». 3-й класс
Урок математики «Сложение и вычитание трёхзначных чисел». 3-й класс
3-й класс- Солодько Татьяна Владимировна, учитель начальных классов
Разделы: Математика, Начальная школа
Класс: 3
Ключевые слова: математика, трехзначные числа
Цели:
- Закрепить нумерацию трёхзначных чисел, устные вычислительные приёмы сложения и вычитания;
- Способствовать закреплению умения решать примеры на сложение и вычитание «в столбик», с переходом через разряд;
- Развивать мыслительные операции, внимание, память, речь;
- Формировать способность к применению полученных знаний на практике при решении уравнений и задач; способность к анализу собственных ошибок;
- Способствовать воспитанию навыка объективной оценки своей работы на уроке, умению принимать решение и отстаивать его при работе в группе.

Методы: самостоятельной работы, стимулирования и мотивации интереса к учению (по Ю.К.Бабанскому).
Тип урока: практическое применение знаний, умений.
Формы работы: общеклассная дискуссия, индивидуальная самостоятельная работа, работа в группах.
Приёмы работы: средства речевого взаимодействия учителя с обучающимися (вопросы, побуждение, обращение).
Оборудование:
у учителя:
- образцы правильного решения заданий для проверки;
- образец записи трёхзначного числа карточка-алгоритм решения примеров индивидуальные карточки для обучающихся.
у обучающихся:
- тетрадь,
- маркерная доска,
- таблички для фиксации ошибок
Этапы урока | Содержание, деятельность учителя | Деятельность обучающихся | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. | Ошибка — это не пустяк — Как вы думаете, как связан сегодняшний урок с записанным на доске стихотворением?
— Аналогично разбираем другой пример. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. Построение проекта выхода из затруднения | — А сейчас мы применим наш алгоритм при решении уравнений. (Уравнения по уровням: справа на доске для…………. (1 уровня), слева для … . (2 уровень)). | На маркерных досках решают ученик из 1 уровня и ученик из 2 уровня, проверка решения у доски. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Физминутка | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Сейчас вы поработаете в группах, каждой группе будет предложена задача, в решении которой необходимо будет применение наших алгоритмов. | Обсуждение построения схемы, решения задачи. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. Обобщение затруднения во внешней речи | — Какое задание оказалось для вас самым трудным? | Рефлексия | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5. Самостоятельная работа с самопроверкой по эталону | Посмотрите в каком задании, на каком шаге у вас было больше всего ошибок и исходя из этого выберете себе задание, (у учителя карточки с разными видами заданий — примеры на сложение, вычитание, уравнения, задачи) | Дети самостоятельно решают затем самопроверка по образцу | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рефлексия деятельности | — Какие операции мы выполняли с трёхзначными числами? | Самооценка | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3-значное сложение — без перегруппировки
LearnPracticeDownload
3-значное сложение — это сложение чисел, в которых одно или все слагаемые состоят из 3 цифр. Мы знаем, что сложение — это операция, используемая в математике для получения суммы чисел. Если складывать однозначные числа можно в уме, то для сложения трехзначных чисел необходимо следовать некоторым правилам. Сложение 3-значного числа можно выполнить с перегруппировкой или без перегруппировки, используя основные правила сложения. Давайте узнаем больше о 3-значном сложении в этой статье.
| 1. | Что такое 3-значное сложение? |
| 2. | 3-значное сложение без перегруппировки |
| 3. | Трехзначное сложение с перегруппировкой |
| 4. | Часто задаваемые вопросы о 3-значном дополнении |
Что такое 3-значное сложение?
В 3-значном сложении нам нужно поместить заданные числа в столбцы в соответствии с их соответствующими разрядами, например, единицы, десятки, сотни, тысячи и т. д. Сложение 3-значных чисел аналогично 2-значным числам, где числа можно добавлять без перегруппировки (переноса) или с перегруппировкой. Следует отметить, что числа, которые складываются, называются слагаемыми, а ответ, который получается после сложения этих чисел, называется их суммой. Давайте посмотрим основные шаги, которые выполняются при сложении трехзначного числа.
- Шаг 1: Расположите заданные числа (сложения) одно под другим так, чтобы они правильно попадали в столбцы единиц, десятков и сотен.

- Шаг 2: Начните складывать числа справа налево, начиная со столбца единиц, затем столбца десятков, а затем столбца сотен.
- Шаг 3: После сложения всех столбцов мы получаем сумму заданных чисел.
3-значное сложение без перегруппировки
При сложении трехзначных чисел, если сумма любых двух цифр меньше или равна 9, мы записываем сумму под соответствующим столбцом, и после сложения всех столбцов получается ответ. Это называется сложением без перегруппировки. Например, давайте сложим числа 148 и 431, чтобы увидеть 3-значное сложение без перегруппировки.
Давайте разберемся с 3-значным сложением с помощью следующих шагов:
- Шаг 1: Добавьте числа в столбце единиц. 8 + 1 = 9. Запишите сумму (9) в столбце единиц.
- Шаг 2: Добавьте числа в столбце десятков. 4 + 3 = 7. Запишите сумму (7) в столбце десятков.
- Шаг 3: Добавьте числа в столбец сотен. 1 + 4 = 5.
 Запишите сумму (5) в столбце сотен.
Запишите сумму (5) в столбце сотен.
Таким образом, сумма чисел 148 и 431 равна 579.
Трехзначное сложение с перегруппировкой
Перегруппировка — другое название переноса. В операции сложения, когда сумма слагаемых в любом из столбцов больше 9, мы перегруппировываем числа и переносим лишнюю цифру в предыдущий столбец. Давайте разберемся в этом на следующем примере, давайте сложим 582 и 173.
Разберемся с 3-значным сложением с перегруппировкой, используя следующие шаги:
- Шаг 1: Складываем числа под один столбец. 2 + 3 = 5. Напишите 5 в столбце единиц.
- Шаг 2: Добавьте числа в столбце десятков. 8 + 7 = 15. Напишите 5 в столбце десятков и перенесите 1 в столбец сотен. Мы сделали этот шаг, потому что после сложения 8 и 7 мы получаем 15, но мы не можем поместить 15 в столбец десятков, потому что мы можем написать только одну цифру под каждым столбцом. Итак, мы перегруппируем число 15.
 Для этого мы поместим 5 в столбец десятков (соответствующий столбец) и поместим 1 поверх столбца сотен (предыдущий столбец). Другими словами, когда мы получаем двузначные числа в виде суммы, мы помещаем цифру единиц в соответствующий столбец, а цифру десятков переносим в следующий столбец слева. Этот перенос добавляется в тот столбец, где он размещен, и добавление продолжается.
Для этого мы поместим 5 в столбец десятков (соответствующий столбец) и поместим 1 поверх столбца сотен (предыдущий столбец). Другими словами, когда мы получаем двузначные числа в виде суммы, мы помещаем цифру единиц в соответствующий столбец, а цифру десятков переносим в следующий столбец слева. Этот перенос добавляется в тот столбец, где он размещен, и добавление продолжается. - Шаг 3: Добавьте числа в столбце сотен. Это означает, что 5 + 1 + 1 (перенос) = 7. Здесь после того, как перенос помещается в столбец сотен, он добавляется вместе с другими слагаемыми.
Таким образом, сумма чисел 582 и 173 равна 755.
☛ Статьи по теме
- Двузначное сложение
- 2-значное вычитание
- 2-значное умножение
- 3-значное вычитание
- 3-значное умножение
- 4-значное дополнение
- 4-значное вычитание
- Добавление с перегруппировкой
- Сложение и вычитание десятичных дробей
Примеры трехзначного сложения
Пример 1: Складываем трехзначные числа: 623 + 215.

Решение:
Напишем числа одно под другим и сложим их.
- Шаг 1: Добавьте числа в колонку единиц. 3 + 5 = 8. Напишите 8 в столбце единиц.
- Шаг 2: Добавьте числа в столбце десятков. 2 + 1 = 3. Запишите 3 в столбце десятков.
- Шаг 3: Добавьте числа в столбец сотен. 6 + 2 = 8. Запишите 8 в столбце сотен.
Это было 3-значное сложение без перегруппировки, а сумма данных чисел равна 838.
Пример 2: Выполнить трехзначное сложение данных чисел: 537 + 365
Решение:
Поместим числа одно под другим и сложим их.
- Шаг 1: Добавьте числа в столбце единиц. 7 + 5 = 12. Напишите 2 в колонке единиц и перенесите 1 в колонку десятков.
- Шаг 2: Добавьте числа в столбце десятков. 3 + 6 + 1 (перенос) = 10. Напишите 0 в столбце десятков и перенесите 1 в столбец сотен.
- Шаг 3: Добавьте числа в столбец сотен. Это означает, что 5 + 3 + 1 (перенос) = 9.

Это было 3-значное сложение с перегруппировкой, и сумма данных чисел равна 902.
Пример 3: Укажите истинное или ложное значение в отношении сложения трех цифр.
a.) 101 + 202 = 303
b.) 202 + 807 = 909
Решение:
а.) = 1009
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.
Часто задаваемые вопросы о трехзначном дополнении
Что такое 3-значное сложение в математике?
3-значное сложение — это сложение чисел, в которых одно или все слагаемые состоят из 3 цифр. Сложение 3-значного числа можно выполнить с перегруппировкой или без перегруппировки, используя основные правила сложения. Обычно мы используем метод сложения столбцов для сложения трехзначных чисел, где мы помещаем заданные слагаемые одно под другим в соответствии с их разрядными значениями и начинаем складывать их, начиная со столбца единиц, затем переходя к столбцу десятков, а затем столбец сотен.
Обычно мы используем метод сложения столбцов для сложения трехзначных чисел, где мы помещаем заданные слагаемые одно под другим в соответствии с их разрядными значениями и начинаем складывать их, начиная со столбца единиц, затем переходя к столбцу десятков, а затем столбец сотен.
Что такое 3-значное сложение с перегруппировкой?
Перегруппировка — другое название переноса. В операции сложения, когда сумма слагаемых в любом из столбцов больше 9, это называется перегруппировкой или сложением с переносом. Например, давайте добавим 487 и 143 и поймем трехзначное сложение с перегруппировкой, выполнив следующие шаги.
- Шаг 1: Поместите указанные числа одно под другим в соответствии с их разрядностью.
- Шаг 2: Добавьте числа в столбце единиц. 7 + 3 = 10. Теперь мы не можем поместить «10» в столбец единиц, так как мы можем написать только одну цифру под каждым столбцом, поэтому мы перегруппируем число 10. Для этого мы запишем 0 в столбце единиц и перенесем 1 в десятки столбец.
 Эта 1 (перенос) будет добавлена вместе с числами в столбце десятков.
Эта 1 (перенос) будет добавлена вместе с числами в столбце десятков. - Шаг 3: Добавьте числа в столбце десятков. Это означает, что 8 + 4 + 1 (перенос) = 13. Мы снова перегруппируем 13 и напишем 3 в столбце десятков, а 1 перенесем в столбец сотен.
- Шаг 3: Добавьте числа в столбец сотен. Это означает, что 4 + 1 + 1 (перенос) = 6. Таким образом, сумма чисел 487 и 143 равна 630.
Как сложить 3 цифры?
Трехзначное сложение — это сложение чисел, в котором любое слагаемое или все слагаемые имеют 3 цифры. Мы можем складывать трехзначные числа, записывая их в столбцы в соответствии с их разрядностью. Затем мы начинаем складывать числа из столбцов единиц, переходя к столбцу десятков, а затем к столбцу сотен. Например, чтобы добавить 342 + 123, мы добавляем цифры в столбце единиц (2 + 3 = 5). Затем мы добавляем цифры в столбце десятков (4 + 2 = 6). Затем мы добавляем цифры в столбце сотен (3 + 1 = 4). Итак, сумма данных чисел 342 и 123 равна 465.
Что такое 3-значное сложение без переноса?
При сложении трехзначных чисел, если сумма любых двух цифр меньше или равна 9, мы записываем сумму под соответствующим столбцом, и после сложения всех столбцов получается окончательный ответ. Это называется сложением без переноса или перегруппировки. Например, сложим числа 412 и 243 и увидим 3-значное сложение без перегруппировки.
Это называется сложением без переноса или перегруппировки. Например, сложим числа 412 и 243 и увидим 3-значное сложение без перегруппировки.
- Шаг 1: Добавьте числа в столбце единиц. 2 + 3 = 5. Запишите сумму (5) в столбце единиц.
- Шаг 2: Добавьте числа в столбце десятков. 1 + 4 = 5. Запишите сумму (5) в столбце десятков.
- Шаг 3: Добавьте числа в столбец сотен. 4 + 2 = 6. Запишите сумму (6) в столбце сотен.
Таким образом, сумма трехзначных чисел 412 и 243 без переноса равна 655.
Что такое трехзначное сложение и вычитание с перегруппировкой?
В операции сложения перегруппировка также известна как перенос, а в операции вычитания перегруппировка известна как заимствование. Например, при трехзначном сложении иногда сумма двух чисел больше 9.. В этом случае мы перегруппируем сумму, перенеся лишнюю цифру в предыдущий столбец. Например, добавим 148 и 124.
- Шаг 1: Добавьте числа в столбце единиц. 8 + 4 = 12. Теперь мы не можем поместить «12» в столбец единиц, потому что мы можем написать только одну цифру под каждым столбцом, поэтому мы перегруппируем число 12.
 Для этого мы запишем 2 в столбце единиц и перенесем 1 в десятки столбец. Эта 1 (перенос) будет добавлена вместе с числами в столбце десятков.
Для этого мы запишем 2 в столбце единиц и перенесем 1 в десятки столбец. Эта 1 (перенос) будет добавлена вместе с числами в столбце десятков. - Шаг 3: Добавьте числа в столбце десятков. Это означает, что 4 + 2 + 1 (перенос) = 7,9.0046
- Шаг 3: Добавьте числа в столбец сотен. Это означает, что 1 + 1 = 2. Таким образом, сумма чисел 148 и 124 равна 272.
При вычитании трехзначного числа иногда цифра в верхнем ряду меньше, чем цифра в нижнем ряду. В этом случае мы заимствуем число из предыдущего столбца, так что меньшее уменьшаемое становится больше вычитаемого. Это называется перегруппировкой или заимствованием. Например, вычтем из 792 478.
- Шаг 1: Расположите числа в соответствии с их разрядностью. Начните вычитать цифры с разряда единиц. Мы видим, что 2 меньше 8. Итак, мы возьмем 1 из столбца десятков, что сделает его 12. Итак, 12 — 8 = 4. Это известно как перегруппировка или заимствование при вычитании. Теперь мы напишем 4 в столбце единиц.

- Шаг 2: После присвоения 1 столбцу единиц на предыдущем шаге «9» в столбце десятков изменится на 8. Теперь давайте вычтем цифры из разряда десятков и запишем 1 под столбцом десятков (8 — 7 = 1).
- Шаг 3: В столбце сотен мы вычтем 4 из 7 и запишем 3 в столбце. (7 — 4 = 3). Таким образом, вычитая данные числа перегруппировкой, мы получаем разницу в виде 314.
Скачать БЕСПЛАТНЫЕ учебные материалы
Сложение трех цифр
Рабочие листы по математике и
наглядный учебный план
Игры на вычитание для 3-х классов онлайн
Сложение и вычитание как обратные операции
Сложение и вычитание называются обратными математическими операциями напротив’ другого. Следовательно, их следует преподавать параллельно, рядом друг с другом, а не как два отдельных предмета. Очень важно, чтобы дети учились ценить и использовать эту математическую взаимосвязь при разработке и использовании стратегий умственных вычислений. Сравнивая различные концептуальные структуры для сложения и вычитания, изученные до сих пор, мы ясно видим, что каждая модель сложения имеет соответствующую модель вычитания в качестве обратной:
Сравнивая различные концептуальные структуры для сложения и вычитания, изученные до сих пор, мы ясно видим, что каждая модель сложения имеет соответствующую модель вычитания в качестве обратной:
Чтобы решить математические задачи на сложение и вычитание, необходимо хорошо знать не только определение сложения и вычитания, но и терминологию. Вот список терминов, созданных для помощи в решении математических задач, связанных со сложением и вычитанием.
Для сложения: плюс, сложение, сумма, итого, вместе, сложение, увеличение, больше, дополнительно
Для вычитания: минус, вычитание, вычитание, Меньше, разница, уменьшение, отнять, вычесть
Требования к стратегиям умственного сложения и вычитания
Разрядное значение цифр в любом числе
Хорошее понимание аспектов разрядной системы крайне важно для детей, чтобы добиться успеха в умственных задачах на сложение и вычитание. Поэтому важно, чтобы дети могли разбивать числа или разлагать их на составляющие. Это возможно, когда дети могут распознавать значение цифр в числах, таким образом, 53 = 50 + 3; 527 = 500 + 20 + 7, и на более поздних этапах они должны понимать то же самое для десятичных дробей. Например, 9·23 = 9 + 0,2 + 0,03.
Это возможно, когда дети могут распознавать значение цифр в числах, таким образом, 53 = 50 + 3; 527 = 500 + 20 + 7, и на более поздних этапах они должны понимать то же самое для десятичных дробей. Например, 9·23 = 9 + 0,2 + 0,03.
Сравнение чисел
Детям также необходимо знать относительные размеры чисел. Они должны помнить об этом из всех действий по упорядочиванию в системе стоимостных значений
Связь между сложением и вычитанием
Обратная связь между сложением и вычитанием также должна быть понятна детям, поскольку знание стратегий сложения поможет им автоматически разблокировать стратегии вычитания.
Некоторые мыслительные стратегии сложения и вычитания
1. Перестановка чисел
Переставьте числа так, чтобы большее число ставилось первым при сложении по закону перестановки. Например, 6 + 14 легче решить как 14 + 6.
2. Использование повторяющихся операций
Повторное вычитание легче выполнять при вычитании большого числа.
Например, вычитание 300 путем трехкратного вычитания 100.
3. Компенсация или корректировка
Иногда проще рассчитать, немного подкорректировав цифры. Например, считать с 10 проще, чем с 9.. Вычисление 43 + 19 путем вычисления 43 + 20 и последующего вычитания 1 — гораздо более эффективный способ решения задачи.
4. Использование почти двойных или половинных чисел
Когда числа, участвующие в математической задаче, являются последовательными числами.
Например, вычисление 18 + 17 как «удвоить 17 и прибавить 1» или «удвоить 18 и вычесть 1»
Или вычисление 24 − 13 как (24 − 12) – 1
5. Разбиение на части
20 или разделить число иногда более эффективно.
Например, 27 + 34 = (20 + 30) + (7 + 4) = 50 + 11 = 61
или 27 + 34 = (20 + 30) + 7 + 4 = 50 + 7 + 4 = 57 + 4 = 61
6. Переход к следующему кратному 10 или 100
Например, вычисление 238 + 17 путем разбиения 17 на 2 + 15.
Итак, 238 + 17 = (238 + 2) + 15 = 240 + 15 = 255
7. Использование обратных отношений
Мы знаем, что сложение и вычитание связаны обратной зависимостью, поэтому задачи на вычитание можно сделать аддитивными. Например, вычисление 100 − 70, зная, что 70 + 30 = 100 и что сложение и вычитание являются обратными операциями.
8. Округление (для аппроксимации ответов)
Например, чтобы решить 24 + 67, округлить 24 до 20, 67 до 70, а затем добавить 20 + 70 = 90
Этот подход в основном используется при множественном выборе ответы, где также работает знание приблизительного ответа.
9. Использование эквивалентностей
В некоторых случаях может использоваться отношение эквивалентности.
Например, вычисление 101 − 35, заметив, что это эквивалентно вычислению 100 – 34, или вычисление 5 + 8, заметив, что это эквивалентно 5 + 10 – 2 = 15 – 3 = 13
Прогресс в письменных методах вычитания
К этому классу учащиеся уже хорошо разбираются в вычитании двузначных чисел с перегруппировкой и без перегруппировки. В 3 классе дети должны быть вооружены четырехзначным и трехзначным вычитанием с перегруппировкой. Следующие методы могут использоваться для определения вычитания и расширения их знаний о вычитании двух цифр с перегруппировкой для вычитания целых чисел, десятичных дробей, смешанных чисел и дробей. Вычитание времени, векторное вычитание и матричное вычитание также будут выполняться аналогичным образом на более поздних этапах.
В 3 классе дети должны быть вооружены четырехзначным и трехзначным вычитанием с перегруппировкой. Следующие методы могут использоваться для определения вычитания и расширения их знаний о вычитании двух цифр с перегруппировкой для вычитания целых чисел, десятичных дробей, смешанных чисел и дробей. Вычитание времени, векторное вычитание и матричное вычитание также будут выполняться аналогичным образом на более поздних этапах.
Методы вычитания
Подсчет от меньшего к большему
Этот метод сочетает использование дополнительного сложения с использованием числовой прямой.
Компенсация (Отнимите слишком много, прибавьте обратно)
Чтобы решить задачи на вычитание с помощью этого метода, сначала вычтите слишком много, а затем прибавьте обратно то, что было вычтено из уменьшаемого.
Например, 783-356
Расширенная форма стандартного алгоритма
Этот метод используется, когда некоторые цифры в первом числе меньше, чем соответствующие цифры во втором числе. Это делает необходимым использование декомпозиции.
Это делает необходимым использование декомпозиции.
1. разложением десятков на единицы (с помощью обмена 1 десяток = 10 единиц)
2. разложением сотен на десятки (с использованием обмена 1 сотня = 10 десятков)
3 3 разложение из сотен в десятки, а затем десятки в единицы
Этот алгоритм можно смоделировать, используя аппарат Дьенеса с основанием 10, следующим образом:
Рассмотрим пример вычитания 243-179
: 243 = 200 + 40 + 3. Поместите соответствующие блоки Диенеса в соответствующие столбцы.
Шаг 2: Разделите второе число на сотни, десятки и единицы: 179 = 100 + 70 + 9. На этом этапе необходимо принять решение о том, возможно ли вычитание отдельных столбцов сразу или нет. В этом примере столбцов десятков и единиц нет.
Шаг 3: Один из блоков сотен разбивается на 10 десятков, чтобы можно было вычитать цифры десятков.
Однако столбец единиц по-прежнему невозможен, поэтому необходима дальнейшая декомпозиция.
Шаг 4: На этот раз один из десятков разбивается на 10 единиц. Это, наконец, делает возможным вычитание столбца за столбцом.
Шаг 5: Столбец за столбцом блоки, соответствующие значениям цифр во втором числе, удаляются из первого числа.
Шаг 6: Блоки, оставшиеся от первого числа после выполнения вычитания, теперь помещаются в поле ответа, и их значения объединяются для получения ответа: 60 + 4 = 64.
Сокращение расширенного алгоритма к стандартному алгоритму
Этот метод является сокращенной формой описанного выше алгоритма. Ниже приведены несколько примеров вычитания трех цифр с перегруппировкой.
Например,
1. с разложением десятков на единицы (при обмене 1 десяток = 10 единиц)
2. с разложением сотен на десятки (при обмене 1 сотня = 10 десятков)
3. с разложением сотен на десятки, а затем десятки на единицы
Используйте те же алгоритмы для длинного вычитания. Для больших чисел сначала введите расширенные форматы, а затем сократите их до стандартного алгоритма. После того, как вы освоитесь со стандартным алгоритмом, используйте его, чтобы попрактиковаться в листах сложения и вычитания отрицательных чисел, затем перейдите к листу сложения и вычитания целых чисел, затем потренируйтесь в листах сложения и вычитания десятичных дробей и, наконец, попрактикуйтесь в листе сложения и вычитания смешанных чисел.
Для больших чисел сначала введите расширенные форматы, а затем сократите их до стандартного алгоритма. После того, как вы освоитесь со стандартным алгоритмом, используйте его, чтобы попрактиковаться в листах сложения и вычитания отрицательных чисел, затем перейдите к листу сложения и вычитания целых чисел, затем потренируйтесь в листах сложения и вычитания десятичных дробей и, наконец, попрактикуйтесь в листе сложения и вычитания смешанных чисел.
Расширение до отрицательных чисел
Детей следует учить складывать и вычитать целые числа сначала с помощью обучающих игр и занятий, а затем с помощью стандартных алгоритмов. Как вычитать целые числа или как вычитать отрицательные числа легко, если учащиеся знакомы со стандартным алгоритмом вычитания. Однако правила сложения и вычитания отрицательных чисел должны быть установлены для того, чтобы дети могли правильно представлять все математические задачи.
Расширить до десятичных чисел
Дети могут продолжать выравнивать крайние правые цифры каждого числа по вертикали, даже если это не подходит для десятичных чисел. Важно, чтобы детей учили, даже при вычитании целых чисел, выравнивать цифры второго числа под цифрами первого числа в соответствии со значением разряда каждой из цифр, то есть десятки под десятками, единицы под единицами, десятые доли под десятыми и т. д. Как только эта концепция станет ясной, подчеркните правила сложения и вычитания десятичных знаков. Предоставьте детям лист вычитания десятичных дробей, чтобы хорошо отработать стандартный алгоритм.
Важно, чтобы детей учили, даже при вычитании целых чисел, выравнивать цифры второго числа под цифрами первого числа в соответствии со значением разряда каждой из цифр, то есть десятки под десятками, единицы под единицами, десятые доли под десятыми и т. д. Как только эта концепция станет ясной, подчеркните правила сложения и вычитания десятичных знаков. Предоставьте детям лист вычитания десятичных дробей, чтобы хорошо отработать стандартный алгоритм.
Сложение двух- и трехзначных чисел
Урок 2: Сложение двух- и трехзначных чисел
/en/additionsubtraction/introduction-to-addition/content/
Сложение больших чисел
Как мы видели во введении Кроме того, часто можно использовать , считая и , визуалы для решения основных задач сложения. Например, представьте, что 3 человека собираются в путешествие и еще 2 решили присоединиться. Чтобы узнать, сколько всего людей пошло, вы можете представить ситуацию следующим образом:
Чтобы узнать, сколько всего людей пошло, вы можете представить ситуацию следующим образом:
Как только вы посмотрите на проблему визуально, вы можете подсчитать и увидеть, что 5 человек отправляются в путешествие.
Что делать, если вам нужно решить большую проблему? Представьте, что несколько групп людей собираются куда-то вместе. 30 человек едет в одном автобусе, а 21 едет в другом. Мы могли бы записать это как 30 + 21.
Возможно, не стоит решать эту задачу путем подсчета. Прежде всего, независимо от того, как вы решите считать, вероятно, потребуется довольно много времени, чтобы решить проблему. Представьте, что вы рисуете на странице 30 и 21 отметку карандашом или считаете столько же мелких предметов! Во-вторых, фактический подсчет объектов может занять достаточно много времени, и вы можете даже потерять счет.
По этой причине, когда люди решают большую задачу на сложение, они формулируют задачу таким образом, чтобы было легче решать ее шаг за шагом. Давайте посмотрим на проблему, которую мы обсуждали выше, 30 + 21 .
Давайте посмотрим на проблему, которую мы обсуждали выше, 30 + 21 .
На прошлом уроке мы научились писать выражения. Однако, когда мы добавляем больших чисел , это помогает писать выражения по-другому.
Вместо того, чтобы писать числа рядом…
…Мы складываем их друг на друга.
Поместите знак плюс (+) к слева чисел.
Вместо равно знак (=), поставьте строку под меньшим номером.
Когда вы складываете выражение сложения, убедитесь, что числа выстроены правильно. Цифры всегда должны быть выстроены по справа .
Давайте рассмотрим другую задачу, 365 + 1. Видите, как 1 находится под 5?
Независимо от того, насколько велики числа, которые вы добавляете, цифры в справа всегда должны выстраиваться в ряд.

Мы видим, что 30 + 21 означают одно и то же. Они просто пишутся по другому.
Решение задач на сложение с накоплением
Для решения задач на сложение с накоплением вам потребуются только навыки, полученные в разделе «Введение в сложение».
Давайте попробуем решить эту задачу, 24 + 12.
Чтобы решить задачу сложения с накоплением, начните с добавления цифр, расположенных дальше всего от справа .
В данном случае это означает, что мы добавим 4 и 2.
Как и в любой задаче на сложение, мы можем использовать , считая , чтобы помочь нам сложить. Так как наша первая цифра 4, мы начнем с четырех объектов.
Мы прибавляем 4 к 2, поэтому будем использовать еще два объекта.
Мы можем сосчитать, чтобы получить в сумме 6. Мы знаем, что 4 + 2 = 6.
Напишите 6 под чертой. Важно поставить непосредственно под числами, которые мы только что добавили.

Далее мы добавим цифры к слева из тех, что мы только что добавили. Это 2 и 1.
Мы будем использовать два объекта, чтобы показать 2.
Затем мы добавим один объект, чтобы представить 1.
Когда мы посчитаем, мы получим 3.
Мы напишем 3 под чертой, под 2 и 1.
Готово! Всего у нас 36, или тридцать шесть.
Давайте рассмотрим еще одну задачу, просто для практики. На этот раз мы решим 62 + 5.
Начнем со сложения цифр справа, 2 и 5.
2 + 5 равно 7. цифры слева. Верхняя цифра 6, но под ней ничего нет.
6 плюс ничего равно 6, поэтому мы напишем 6 под чертой.
Всего у нас 67, или шестьдесят семь.
Как вы видели, задачи на сложение всегда решаются от справа до слева. Это означает, что вы всегда начинаете с добавления цифр справа .
Попробуйте это!
Решите приведенные ниже задачи на сложение. Затем проверьте свой ответ, введя его в поле.
45 + 34 =
72 + 3 =
13 + 12 =
Сложение очень больших чисел
Сложение с накоплением также можно использовать для сложения больших чисел . Независимо от того, сколько цифр в числах, которые вы добавляете, вы добавляете их одинаково: справа налево.
Попробуем сложить два 3-значных числа . Завершим это выражение: 213 + 406.
Как всегда, начнем с крайних правых цифр . Здесь это означает, что мы решим 3 + 6.
3 + 6 равно 9, поэтому мы напишем 9 непосредственно под 3 и 6.
Затем мы добавим цифры к осталось из тех, что мы только что добавили, 1 и 0.
1 + 0 равно 1, поэтому мы напишем 1 под строкой. Не забудьте поместить непосредственно под цифрами, которые мы только что добавили, к слева из 9.

Наконец, давайте добавим следующий набор цифр, 2 и 4.
2 + 4 равно 6. Запишем 6 под чертой, под 2 и 4.
Задача решена. Итого у нас 619, или шестьсот девятнадцать. 213 + 406 = 619.
Попробуйте!
Добавьте эти большие числа. Затем проверьте свой ответ, введя его в поле.
214 + 262 =
101 + 505 =
787 + 11 =
Использование переноса
На последней странице вы потренировались складывать числа, расположенные вертикально. Некоторые проблемы требуют дополнительного шага. Например, давайте рассмотрим следующую задачу:
Наш первый шаг — добавить цифры справа — 5 и 9 . Однако вы можете заметить, что нет места для записи суммы 14 . Когда сумма двух цифр в математической задаче больше, чем 9 , обычный способ сложения чисел не работает. Вам придется использовать технику под названием , несущую .
Давайте посмотрим, как это работает. Мы попробуем эту задачу, 25 + 39.
Как обычно, мы начнем с добавления цифр на справа . Здесь это 5 и 9.
5 + 9 равно 14, но нет места для записи обеих цифр числа 14 под 5 и 9.
Мы запишем правую цифру 4 под чертой …
Запишем правую цифру 4 под чертой… затем перенесем левую цифру 1 до следующего набора цифр в задаче.
Вы видите, что мы сделали? Наша сумма равнялась 14. Мы поставили 4 под чертой, а 1 перенесли и поместили над следующим набором цифр.
Далее мы добавим левые цифры. Поскольку у нас есть 1, мы добавим и его.
1 + 2 + 3 равно 6, поэтому мы напишем 6 под чертой.
Готово. 25 + 39 = 64.
Давайте потренируемся еще с одной задачей: 178 + 42.
Как всегда, начнем с добавления цифр справа. Здесь 8 + 2.

8 + 2 равно 10, так что, похоже, нам придется нести.
0 остается под 8 и 2.
Перенесите 1 и поместите его над следующим набором цифр слева.
Теперь сдвиньте влево, чтобы добавить следующий набор цифр. Поскольку мы перенесли 1, добавьте и его.
1 + 7 + 4 = 12.
Поместите правильное число, 2, под добавленными цифрами.
Возьмите 1 и поместите ее над следующей колонкой слева.
Чтобы закончить, добавьте этот столбец. Не забудьте включить 1, который мы только что перенесли.
1 + 1 + ничто равно 2, поэтому мы напишем 2 под 1.
Готово. Наш ответ: 220. 178 + 42 = 220.
При переноске следите за различными числами. Если вы записываете проблемы, не забудьте написать пропущенные цифры мелким шрифтом над столбцом цифр слева.
Попробуйте это!
Решите эти проблемы переноской. Затем проверьте свой ответ, введя его в поле.
Затем проверьте свой ответ, введя его в поле.
124 + 36 =
99 + 7 =
165 + 59 =
Практика!
Потренируйтесь добавлять эти задачи. Вам придется использовать переноску, чтобы решить некоторые проблемы. Имеется 4 наборов задач по 3 задач в каждом.
SET 1
25 + 11 =
64 + 32 =
12 + 16 =
Установите 2
19 + 7 =
33 + 29 =
65 + 17 =
SET 3
65 + 17 =
. 66 + 54 =
99 + 4 =
83 + 74 =
Набор 4
323 + 601 =
909 + 19 =
725 + 75 =
ПродолжатьПредыдущий: Введение в дополнение
Далее:Видео: Дополнение
/ru/additionsubtraction/video-addition/content/
Сложение трехзначных чисел
Числа являются наиболее важной частью математики и нашей повседневной жизни, без чисел мы не можем вести счет, как подсчитывать общее число вещей, даты, времени, денег и т. д. В математике числа определяются как арифметические значения, которые используются для представления количества и в дальнейшем используются в расчетах. Числа могут быть четными, нечетными, простыми, составными, десятичными, дробными, рациональными, иррациональными, натуральными, целыми, действительными, сложными и т. д. Используя числа, мы можем выполнять различные типы арифметических операций, такие как сложение, вычитание, умножение, деление и т. д. В этой статье мы научимся складывать трехзначные числа.
д. В математике числа определяются как арифметические значения, которые используются для представления количества и в дальнейшем используются в расчетах. Числа могут быть четными, нечетными, простыми, составными, десятичными, дробными, рациональными, иррациональными, натуральными, целыми, действительными, сложными и т. д. Используя числа, мы можем выполнять различные типы арифметических операций, такие как сложение, вычитание, умножение, деление и т. д. В этой статье мы научимся складывать трехзначные числа.
Сложение трехзначных чисел
Сумма трехзначных чисел так же проста, как сумма двузначных чисел, и требует от вас только изучения суммы однозначных чисел и того, как работать с переносами.
Шаги для добавления 3-значных чисел:
Шаг 1: Поместите данное 3-значное число под другим заданным 3-значным числом и расположите их в столбцах в соответствии с их позициями, такими как единицы, десятки и сотни.
Шаг 2: Теперь начните добавлять столбцы в последовательности, начиная с единиц.
Шаг 3: Когда сумма двух цифр в столбце единиц превышает 9, например 8 + 5 = 13, тогда введите 3 в результат и передайте 1 в качестве переноса в столбец десятков, который будет складываться с числами, присутствующими в ту колонку. Эта концепция переноса одинакова для всех столбцов.
Ниже наглядный пример того, как складывать трехзначные числа.
1. Сложение трехзначных чисел, не приводящее к переносу
Даны трехзначные числа 111 и 111. Теперь мы складываем их в соответствии с описанными выше шагами:
Шаг 1: Поместите заданное трехзначное число 111 под другим трехзначным числом 111, а затем расположите их в столбцы в соответствии с их местами, например, один раз, десятки и сотни.
| H | T | O | |
| + | 1 1 | 1 0002 1 | 1 1 |
Шаг 2: Теперь мы складываем числа по столбцам. Сначала мы добавляем число из столбца единиц (т. е. 1 + 1 = 2), затем столбца десятков (т. е. 1 + 1 = 2), а затем столбца сотен (т. е. 1 + 1 = 2).
Сначала мы добавляем число из столбца единиц (т. е. 1 + 1 = 2), затем столбца десятков (т. е. 1 + 1 = 2), а затем столбца сотен (т. е. 1 + 1 = 2).
| H | T | O | |||
| + | 1 1 | 1 1 | 1 1 | 1 1 | 90030011 1 1 |
| 2 | 2 | 2 |
Таким образом, конечный результат добавления-222.
9.
Даны трехзначные числа 354 и 279. Теперь вычислим их сумму шаг за шагом:
Шаг 1: Расположите числа в соответствии с их местами, например, один раз, десятки и сотни.
| H | T | O | |
| 1 | 1 | 0 | |
+ | 3 2 | 5 7 | 4 9 |
Шаг 2: Теперь мы сначала добавляем номер столбца один раз, который равен 4 + 9 = 13. Здесь сумма больше 9, поэтому мы записываем 3 в результат и повышаем1 как нести за столбец десятков.
Здесь сумма больше 9, поэтому мы записываем 3 в результат и повышаем1 как нести за столбец десятков.
| H | T | O | |
| 1 | 0 | ||
+ | 3 2 | 5 7 | 4 9 |
| 3 |
Шаг 3: Добавить количество колонны TENS, а перенос — 5 + 7 + 1 (перенос) = 13. Точно так же записываем 3 в результат и возводим 1 в качестве переноса для столбцов сотен.
| H | T | O | |
| (carry) | 1 | 1 | 0 |
+ | 3 2 | 5 7 | 4 |
| 3 | 3 |
Шаг 4: Добавьте цифры сотен колонны, а нанесение 3 + 2 + 2 + 2 + 2 + 2+. (перенос) = 6.
(перенос) = 6.
| H | T | O | |
| (carry) | 1 | 1 | 0 |
+ | 3 2 | 5 7 | 4 |
| 6 | 3 | 3 |
Таким образом, окончательный результат добавления — 633.
, поэтому окончательный результат добавления — 633.
9002.0005 3. Сложение трех трехзначных чисел
Даны три трехзначных числа 471, 582 и 693. Теперь вычислим их сумму шаг за шагом:
Шаг 1: Расположите числа в соответствии с их местами как раз, десятки и сотни.
| H | T | O | |
+ | 4 5 6 | 7 8 9 | 1 2 3 |
Шаг 2: Теперь мы сначала добавим номер «Один раз», который составляет 1 + 2 + 3 = 6.
| H |
| H | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| H |
| H |
| . | T | O | |
+ | 4 5 6 | 7 8 9 | 1 2 3 |
| 6 |
Шаг 3: Складываем числа в столбце десятков, то есть 7 + 24 + 9 сотенная колонна.
| H | T | O | |
| (carry) | 2 | 0 | |
+ | 4 5 6 | 7 8 9 | 1 2 3 |
| 4 | 6 |
Step 3: Add the numbers of hundreds’s column that is 4 + 5 + 6 + 2(carry) = 17.
| H | T | O | |
| (carry) | 2 | 0 | |
+ | 4 5 6 | 7 8 9 | 1 2 3 |
| 17 | 4 | 6 |
Таким образом, окончательный результат сложения равен 1746.0003
Given numbers are 713 and 624.
H T O (carry) 0 0
+
7
6
1
2
3
4
13 3 7 Таким образом, результат добавления составляет 1337.
Вопрос 2: Найдите сумму 728, 340 и 521.
Решение:
.
H T O (carry) 1 0
+
7
3
5
2
4
6
8
0
1
16 2 9
So the result of the addition is 1629.
ВОПРОС 3: Найдите сумму 954, 262 и 72.
Решение:
. Числа 954, 262 и 72
H 9
H T O (carry) 1 0
+
9
2
0
5
6
7
4
2
2
12 8 8 Таким образом0003
Question 4: Find the sum of 981, 981, and 981.

Solution:
. 976, and 201.Given numbers are 981, 981, and 981.
H T O (carry) 2 0
9
9
9
8
8
8
1
1
1
29 4 3 , поэтому результат дополнения 943.
Solution:
Given numbers are 981, 976, and 201.
H T O (carry) 1 0
9
9
2
8
7
0
1
6
1
21 5 8 Таким образом, результат сложения равен 2943.
Вычитание — | Основы арифметики
На этой странице рассказывается об основах арифметики, простейшем способе манипулирования числами посредством вычитания (-).
См. другие наши арифметические страницы, где можно найти обсуждение и примеры: сложение (+), умножение ( × ) и деление ( ÷ ).
Вычитание
Вычитание — это термин, используемый для описания того, как мы «вынимаем» одно или несколько чисел из другого.
Вычитание также используется для нахождения разности между двумя числами. Вычитание противоположно сложению. Если вы еще этого не сделали, мы рекомендуем прочитать нашу страницу дополнений.
Знак минус «-» используется для обозначения операции вычитания, например, 4 − 2 = 2. Знак «−» может использоваться несколько раз по мере необходимости: например, 8 − 2 − 2 = 4.
Этот расчет правильный, но его можно упростить, сложив числа, которые мы вычитаем.
В нашем примере 8 — 2 — 2 = 4 можно упростить до 8 — 4 = 4 (две двойки были сложены вместе, чтобы получить 4, которые затем вычитаются из 8).
Предупреждение
Необходимо соблюдать осторожность при использовании знака «-». Числа, имеющие отрицательное значение, записываются с предшествующим «-», поэтому минус два записывается как -2. Это просто означает, что на 2 меньше нуля или на 2 меньше нуля.
Для получения дополнительной информации см. нашу страницу о положительных и отрицательных числах .
Остерегайтесь знаков и порядка при вычитании
Когда мы выполняем вычисление сложения , порядок сложения чисел не имеет значения.
Например,
8 + 3 + 5 совпадает с 3 + 8 + 5 и дает нам тот же ответ, 16.с порядком номеров.
Обычно при вычитании мы сначала пишем число, которое мы вычитаем из , , а затем числа, которые мы отнимаем, в любом порядке.
Например,
8 − 5 = 3
Это НЕ то же самое, что 5 − 8 = −3Мы видим, что у нас тот же числовой ответ (3), но его значение отличается: 3 в первый расчет, но минус 3 (-3) во втором.
Точно так же 8 − 5 − 3 = 0, но 5 − 8 − 3 = −6, что является совершенно другим ответом.
Причина, по которой ответы различаются, не в том, что мы расставили числа в «неправильном» порядке, а в том, что мы не позаботились о том, чтобы отметить, положительные они или отрицательные.
В нашем примере 8 — положительное число, поэтому мы могли бы написать его как «+ 8», и это было бы правильно, но по соглашению нам не нужно писать символ «+». Однако символ «+» очень важен, если мы изменим порядок, как и символы «-», предшествующие 5 и 3.
Вот последний пример, переписанный так, чтобы дать правильный ответ:
8 − 5 − 3 = 0, как и раньше, и − 5 + 8 − 3 = 0, что дает тот же ответ. В этом случае мы записали числа в том же порядке, что и раньше, но приняли во внимание их положительное или отрицательное значение.
Более подробное объяснение и примеры см. в разделе «Вычитание в особых ситуациях: нулевые и отрицательные числа » ниже.
Вычитание
Простое вычитание можно выполнять так же, как и сложение, путем подсчета или использования числовой строки:
Если у Фиби 9 конфет, а у Люка 5 конфет, в чем разница?
Начиная с меньшего числа (5) и считая до большего числа (9).
6 (1), 7 (2), 8 (3), 9 (4).
У Фиби на 4 конфеты больше, чем у Люка, разница в конфетах 4.
Итак: 9 − 5 = 4 .
Для более сложного вычитания, когда использование подсчета нецелесообразно, полезно записывать наши числа в столбцах одно над другим — аналогично вычислению сложения.
Предположим, Майк зарабатывает 755 фунтов стерлингов в неделю и платит 180 фунтов стерлингов в неделю за аренду. Сколько денег осталось у Майка после того, как он заплатил за квартиру?
В этом примере мы собираемся вычесть 180 фунтов стерлингов из 755 фунтов стерлингов.
Сначала мы пишем начальный номер, а под ним номер, который мы убираем, следя за тем, чтобы числа были в правильных столбцах.
Сотни Десятки шт. 7 5 5 1 8 0 Шаг 1: Сначала мы выполняем вычитание чисел в столбце «Единицы» справа, затем записываем ответ внизу в том же столбце. В этом случае 5 − 0 = 5,
Сотни Десятки шт. 7 5 5 1 8 0 Итого 5 Шаг 2: Используя тот же подход, что и при вычислении сложения, мы работаем по столбцам справа налево. Далее нам нужно вычесть числа в столбце десятков. В нашем примере нам нужно вычесть восемь из пяти (5 − 8), но 8 больше 5, поэтому мы не можем этого сделать, так как в итоге получим отрицательное число.
Нам нужно позаимствовать число из столбца сотен. Это может быть сложной концепцией, и мы рассмотрим ее более подробно ниже: у нас есть 7 в столбце сотен, поэтому мы «заимствуем» 1 для столбца десятков, оставляя нам 6 в сотнях. Перечеркните 7 и напишите 6 в колонке сотен, чтобы потом не ошибиться. Переместите 1 в столбец десятков и напишите его перед 5. Мы не добавляем «1» к десяткам, мы кредитуем «1 лот из 10». Итак, вместо 5 десятков у нас теперь 15 десятков.
15 больше восьми, поэтому мы можем выполнить вычитание в столбце десятков. Возьмите 8 из 15 и запишите ответ (7) внизу столбца десятков.
Сотни Десятки шт. 7615 5 1 8 0 Итого 7 5 Шаг 3: Наконец, отнимите 1 от 6 в столбце сотен.
6 − 1 = 5, поэтому поставьте 5 в ответе столбца сотен, чтобы получить окончательный ответ. У Майка осталось 575 фунтов стерлингов после того, как он заплатил арендную плату.
Сотни Десятки шт. 7615 5 1 8 0 Итого 5 7 5 Заимствование при вычитании
Заимствование , как в приведенном выше примере, может привести к путанице при вычислениях с вычитанием. Это похоже на «перенос» в вычислениях сложения, но в обратном порядке, потому что вычитание является обратным (противоположным) сложению.
Повторное заимствование может происходить при вычислении вычитания.
Предположим, у нас есть 10,01 фунта стерлингов, и мы хотим забрать 9,99 фунта стерлингов. Мы можем решить это, не записывая ничего — ответ 0,02 фунта стерлингов или 2 пенса.Однако если мы запишем этот расчет формально, то понятие заимствования станет более ясным.
В этом примере мы проигнорировали десятичную точку и записали числа как 1001 и 999.
1 0 0 1 9 9 9 Начиная со столбца единиц измерения справа, нам нужно отнять 9 от 1. В наших вычислениях с вычитанием правило (как в приведенном выше примере) состоит в том, что мы никогда не отнимаем большее число от меньшего числа, потому что оно даст нам отрицательный ответ.
Для того, чтобы расчет работал, нам нужно ‘ заимствовать ‘ число из следующего столбца слева. В столбце десятков стоит 0, поэтому заимствовать нечего, поэтому нам нужно перейти к следующему столбцу слева. Столбец сотен также имеет 0, поэтому мы также не можем заимствовать из этого столбца, поэтому переходим к следующему столбцу слева. В столбце тысяч есть 1, поэтому мы можем позаимствовать его и переместить в следующий столбец справа, столбец сотен.
Мы перечеркиваем 1 в столбце тысяч, чтобы избежать ошибок позже.
Одна тысяча равна 10 сотням, так что теперь у нас есть 10 в столбце сотен, где раньше был ноль:
Перенесено 0 10 10 0 1 9 9 9 Однако это не помогает с 1 − 9 (в столбце единиц), потому что у нас все еще есть нуль для заимствования в столбце десятков, но это первый шаг в процессе.
Теперь, когда у нас есть 10 сотен, мы можем позаимствовать одну из них для столбца десятков. Сотня — это то же самое, что 10 десятков, поэтому мы переносим 10 в столбец десятков. Мы не должны забывать корректировать столбец сотен, поэтому мы перечеркиваем 10 и вместо этого пишем 9.
Перевозится 9 10 Перевозится 0 1010 0 1 9 9 9 Наконец, мы можем выполнить вычитание в столбце единиц, позаимствовав 1 десяток из столбца десятков.
Это оставляет 9 десятков в столбце десятков и 10 + 1, которые у нас уже были в столбце единиц, что дает нам 11 единиц.
Перевозится 9 10 Перевозится 9 10Перевозится 0 1010 0 1 9 9 9 Теперь мы можем выполнить полный расчет, начиная со столбца единиц, 10 + 1 = 11 − 9.= 2. Тогда в столбце десятков 9 − 9 = 0. То же самое для столбца сотен 9 − 9 = 0. Наконец, в столбце тысяч 0 − 0 = 0.
Перенесено 9 10 Перевозится 9 10Перевозится 0 1010 0 1 9 9 9 Итого 0 0 0 2 Заняв несколько раз, мы пришли к нашему ответу 2.
Когда мы заменяем десятичную точку, мы получаем 0,02 фунта стерлингов.
Вычитание в особых случаях: нули и отрицательные числа
Если бы мы выполняли простое сложение, мы могли бы считать в уме или, возможно, на пальцах. Когда мы выполняем вычитание, особенно если оно включает отрицательные числа, полезно представить, что мы идем по прямой. Каждый шаг — это число в этой строке. Если мы начнем с нуля, каждый шаг вперед будет прибавлять число, а каждый шаг назад отнимать единицу. Самое важное, что нужно помнить, это то, что мы всегда смотрим в позитивном направлении. Возможно, вам будет полезно представить свою линию как восхождение вверх и вниз по лестнице, где каждая ступенька представляет собой число. Или, возможно, вы более знакомы с путешествием вверх и вниз по высотному блоку в лифте, где ноль — это первый этаж, положительные числа — над землей, а отрицательные числа — в подвале.
Если бы мы нарисовали эту линию на листе бумаги, она выглядела бы как линейка.
Мы можем двигать пером вперед и назад по линии так же, как представляем себе свои шаги назад и вперед. Это называется числовой линией и является очень полезным инструментом для сложения и вычитания.
Мы воспользуемся этой аналогией, чтобы понять следующие примеры.
Когда числа одинакового значения вычитаются друг из друга, результат всегда равен нулю: 19−19 = 0,
Используя нашу аналогию, начав с нуля, если мы пройдем 19 шагов вперед по линии, а затем 19 шагов назад, мы вернемся к нулю.
При вычитании нуля из любого числа число остается неизменным: 19−0 = 19.
Используя нашу числовую прямую, мы начинаем с 19 и идем назад 19.
Когда мы вычитаем любое положительное число из нуля, ответ равен отрицательный : 0 – 15 = –15
Помните из наших предыдущих примеров, что положительное число обычно не нужно записывать с положительным знаком. Когда мы видим число «67», математическое соглашение говорит нам, что оно положительное, то есть «+67».
В этом примере из нуля вычитаем +15: 0 – (+15) = –15. Используя нашу аналогию, мы начинаем с нуля и делаем 15 шагов назад.
Когда мы вычитаем любое положительное число из отрицательного числа , ответ становится равным более отрицательное ’ .
Например, если мы начнем с нашего ответа сверху (–15) и вычтем 6, мы получим: –15 – 6 = –21. Помните, что «6» положительно, поэтому мы могли бы записать –15 – (+6) = –21, и это означает то же самое. Используя нашу числовую линию, чтобы помочь нам понять, мы начинаем с -15. Мы делаем шесть шагов назад, по-прежнему глядя в позитивном направлении. Мы заканчиваем на 21 шаге назад от нуля, то есть –21.
Но что произойдет, если нам нужно вычесть отрицательное число из любого другого числа?
Начнем с примера: 15 – (–6) = 15 + 6 = 21
Правило два минуса дают положительное , т.е. вычитание отрицательного числа становится сложением.
Давайте вернемся к нашей числовой прямой, чтобы нам было легче понять: начиная с 15, мы знаем, что нам нужно двигаться назад (в отрицательном направлении), потому что мы делаем вычитание. Но у нас есть отрицательное число, которое нужно вычесть, поэтому, чтобы проиллюстрировать это, мы должны перевернуть . Затем мы перемещаемся назад на 6 позиций, чтобы получить ответ. Поворачиваясь, а затем двигаясь назад (два отрицательных числа), наше общее направление движения находится в положительном направлении, то есть мы выполнили сложение .
Вычитание отрицательного числа — это абстрактная концепция, и вы можете подумать, что в повседневной жизни она не применяется. Ведь мы не можем удержать отрицательное количество яблок или налить отрицательное количество кофе. Однако это очень важно, когда речь идет о таких математических понятиях, как векторов . Вектор имеет направления , а также величины , поэтому, например, важно не только то, как далеко проплыла лодка, но нам также нужно знать направление, в котором она путешествовала.
Дальнейшее чтение из книги «Навыки, которые вам нужны»
Основы счета
Часть руководства «Навыки, которые вам нужны для счета»операции и начать манипулировать числами. Он также включает примеры из реальной жизни, чтобы прояснить, как эти концепции полезны в реальной жизни.
Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.
Модели и стратегии для сложения и вычитания двузначных чисел
Второй класс — очень важный год, когда учащиеся развивают свободное владение двузначным сложением и вычитанием . В этом году мы работаем над множеством стратегий сложения и вычитания, которые учащиеся могут использовать для решения задач. Мы тратим много времени на обсуждение различных стратегий, использование множества различных моделей и расчеты в уме.
Почему? Для развития гибкости учащихся при решении математических задач .
Общий базовый стандарт для двузначного сложения и вычитания:
CCSS.MATH.CONTENT.2.NBT.B.5
Свободно сложение и вычитание в пределах 100 с использованием стратегий на основе разрядного значения, свойств операций и/или отношения между сложением и вычитанием.И стандарт для трехзначного сложения и вычитания, чтобы показать, куда мы движемся:
CCSS.MATH.CONTENT.2.NBT.B.7
Сложение и вычитание в пределах 1000, с использованием конкретных моделей или чертежей и стратегий на основе разрядного значения, свойств операций и/или связи между сложением и вычитанием ; связать стратегию с письменным методом. Поймите, что при сложении или вычитании трехзначных чисел добавляются или вычитаются сотни и сотни, десятки и десятки, единицы и единицы; а иногда надо составить или разложить десятки или сотни.Нигде в этих двух стандартах ничего не говорится о стандартном алгоритме, который мы все выучили в школе (скорее всего, на языке «перенос» и «заимствование»), и стандартный алгоритм не упоминается напрямую в Общем стандарте второго класса.
Основные стандарты. Прочтите до конца, чтобы узнать, как я применяю стандартный алгоритм в нашем классе.
Вас интересует бесплатный образец некоторых из моих продуктов сложения и вычитания двузначных чисел?
Стратегии и модели
Если вы знакомы с моими задачами на сложение и вычитание, вы, возможно, заметили, что я делаю большое различие между стратегиями, используемыми при решении задач, и моделями, которые учащихся используют с этими стратегиями.
Стратегии обычно представляют собой то, как учащиеся подходят к числам и манипулируют ими. Модели — это то, как стратегии организованы на бумаге, чтобы учащиеся могли объяснить или увидеть стратегию.
Глядя на приведенные выше стандарты, я вижу, что стратегии четко указаны в стандарте:
В 2.NBT.B.5 и стратегии:
- разрядное значение
- свойства операций
- отношения между сложением и вычитанием
Стандарт 2.
NBT.B.7 даже отмечает, что модели или чертежи (которые я также называю моделями) отделены от стратегий, которые основаны на:
- разрядном значении
- свойствах операций
- взаимосвязь между сложением и вычитанием
Как видите, стратегии четко изложены в стандартах. Теперь в каждой из вышеперечисленных общих категорий стратегий действительно есть много разных стратегий, которые могут использовать учащиеся, и вы можете обозначить их как хотите в своем классе. Мне нравится маркировать их именами учеников для удобства. Таким образом, мы можем ссылаться на стратегию Саманты при решении проблемы. Или вы можете пометить стратегию действием, которое учащийся предпринимает в задаче (например, «Сначала добавьте десятки»).
Однако я все же различаю стратегию и модель. Почему? Потому что учащиеся могут использовать несколько стратегий с одной моделью. Не существует единственно правильного способа использования модели, пока учащийся может объяснить свое мышление.
Модели (или рисунки) просто дают учащимся инструмент для объяснения своего мышления на бумаге или с помощью манипуляций. Мышление или то, что ученики делают с числами, и есть стратегия. То, что они используют, чтобы показать это вам, является моделью.
Честно говоря, я не всегда последовательно называю что-то стратегией или моделью. Я стараюсь быть таким, но, как и вы, я человек и иногда путаю их, особенно когда я нахожусь в данный момент со студентами. Это процесс обучения, и я постоянно размышляю об этом на протяжении многих лет. Все это говорит о том, что вы можете увидеть несколько вещей, обозначенных одним способом, и усомниться в этом. Идите вперед и спросите об этом, подумайте об этом, обдумайте это и выясните, является ли это точным или нет. Все это еще в новинку для многих из нас.
Вот несколько опорных диаграмм, которые я использовал за последние пару лет и которые иллюстрируют некоторые из приведенных ниже моделей и стратегий.
Модели для сложения двух цифр
Ниже приведены несколько моделей, которые мы используем для сложения или вычитания двух цифр.
Это единственные модели, которые вы можете использовать? Нет, это не исчерпывающий список. Это то, что я нашел полезным в классе для студентов, чтобы практиковать и использовать для построения концептуального понимания и чувства числа.
Числовые строки для двузначного сложения и вычитания
Я обычно начинаю с числовых линий, когда знакомлю учащихся с бумажными/карандашными моделями. Открытая числовая линия очень гибкая. Студенты могут делать прыжки от одного до десяти (или более) и легко манипулировать ими, чтобы показать свое математическое мышление.
Я обычно помогаю учащимся добраться до ближайших 10 или дружественных или эталонных чисел при использовании числовой прямой, потому что легче делать скачки на 10. Это пример разницы между моделью и стратегией. Моделью является числовая линия. Стратегия делает прыжки на 10.
Обучение тому, как использовать числовые ряды при использовании 10 для сложения фактов +9 и +8, укрепляет эту стратегию, когда учащиеся складывают большие двузначные числа.
Помните, что числовая линия является моделью, и ее можно использовать с различными стратегиями. Моделирование и практика использования числовой прямой с более простыми задачами поможет учащимся при использовании числовой прямой с более сложными задачами.
Одно из наших ежедневных занятий с числовыми линиями — это ежедневная математика. Это лист белой доски, который мы просматриваем ежедневно. Числовая линия внизу помогает учащимся укрепить свое понимание того, как использовать числовую линию и как «сделать 100 или сделать 1000».
Вот еще несколько примеров того, как мы используем числовые ряды в классе.
Это с моих математических станций Roll & Spin. В этом упражнении учащиеся тренируются делать прыжки на 10 и 100 вверх по числовой строке.Существуют также версии, в которых учащиеся вычитают 10 и 100 по числовой строке. Одним из навыков, необходимых учащимся для успешного решения числовых рядов, является способность делать прыжки от 10 до 100.
Это пример из одной из наших задач на сложение и вычитание, где учащиеся должны были вычислить 9.1974 отдельный запуск неизвестная проблема . Этот ученик начал с 15 и насчитал 35 прыжков, а в конце убрал один. Это также отличный пример компенсации (см. ниже), потому что ученик добавил единицу к 34, чтобы облегчить прыжки, а затем убрал ее в конце.
Это из моих заданий по математике «Вырезать и вставить» во втором классе. В этом упражнении учащиеся тренируются, как складывать, начиная с наименьшего числа и выясняя, кто доберется до большего числа, перепрыгивая к дружественным числам. Этот студент начал в 19, подскочил до 20, затем сделал прыжки от 10 до 60 и сделал прыжок на 3. Ученик сложил свои прыжки вместе, чтобы получить 44.
Выше приведены несколько примеров из моих математических станций сложения двух цифр. Моим ученикам нужно было больше практиковаться с числовыми линиями и делать прыжки, несмотря на всю нашу групповую практику. Итак, я давал им указания, и студенты следовали за ними по числовым линиям.
Более новый ресурс, который я разработал, чтобы помочь учащимся развить беглость счета, — это ресурс «Сделай 100» и «Сделай 1000». На этом ресурсе есть МНОЖЕСТВО заданий, в которых учащиеся тренируются в счете 100 и 1000. Числовые строки — одно из заданий.
У меня также есть целая запись в блоге о том, как использовать числовую линейку, с еще большим количеством примеров того, как развивать беглость числовой линейки в классе.
Блоки с основанием 10
Блоки с основанием 10 — еще одна модель, которой я обучаю студентов; тем не менее, я обычно учу студентов рисовать кубики с основанием 10. На занятиях мы используем настоящие пеноблоки, но я стараюсь как можно быстрее от них отойти.
Почему? У учеников всегда будет карандаш и бумага для решения задач, но не всегда у них будут манипуляции. Использование блоков с основанием 10 также занимает много времени. Я не против потратить на них время для студентов, которым они нужны, но я также хочу подтолкнуть студентов к более эффективным инструментам.
Вот несколько примеров того, как мы используем блоки с основанием 10:
Вышеприведенные два используют блоки с основанием 10, вытягивая десятки как «палочки», как мы называем их в нашем классе. Этим ученикам было трудно сосчитать более 100 десятками, поэтому я попросил их нарисовать каждое число десятками, затем считать десятками, пока они не дойдут до 100, а затем снова начать считать по десяткам. Это не только помогло им складывать числа после 100, но и увеличило расходы с нашей системой счисления с основанием 10.
Приведенный выше пример снова взят из моих математических станций сложения двухзначных чисел и представляет собой просто базовую задачу — сопоставление ответов с блочными представлениями по основанию 10.
Запись в блоге «Числовая линия» также содержит интересное визуальное задание, помогающее учащимся перейти от блоков с основанием 10 к числовым линиям.
Стратегии сложения двухзначных чисел
Как отмечалось выше, основными тремя стратегиями, указанными в стандартах, являются:
- разрядное значение
- свойства операций
- связь между сложением и вычитанием
Ниже приведены несколько стратегий, которые мы используем для решения задач на сложение двузначных чисел.
Большинство из них основаны на стратегиях позиционной стоимости, поскольку я считаю, что учащимся легче их понять и применить. Опять же, именно так учащиеся манипулируют числами в задаче, чтобы упростить ее решение.
Ни одна стратегия не является «правильной» для каждого учащегося при решении каждой проблемы. Некоторые проблемы поддаются определенным стратегиям из-за чисел. Студенты также могут переключаться между стратегиями в рамках одной и той же задачи, в зависимости от того, как они манипулируют числами. Главное, на что нужно обращать внимание, это то, может ли ученик объяснить свои мысли при решении задачи.
Разбить или разгруппировать (поместить значение)
Эта стратегия требует немного больше умственной математической практики, но она может быть очень мощной. Основная идея заключается в том, что число разбивается на десятки и единицы, а затем, используя числовую линейку, блоки с основанием 10 или просто числа, учащиеся манипулируют частями, чтобы складывать или вычитать числа.
Разбиение или разгруппирование части числа помогает учащимся увидеть значение разряда. Разряд десятков это не просто 4. Его значение 40 или 4 десятка.
Одним из ресурсов, помогающих разработать эту стратегию, является книга Number Talks (партнерская ссылка). В течение года мы проводим беседы о числах, начиная со сложения фактов и переходя к двузначному сложению и вычитанию к концу года. Мне нравится видеть стратегии, которые могут придумать мои ученики! Книга Number Talk – это также отличная книга, которая помогает развить навыки слушания.
Подумай над задачей 64-47. Учащиеся разбивают задачу на 50+14-7-40 и отбирают части по разрядности. Я бы, наверное, начал с 14-7, но студенты могут начать с любого, что для них имеет смысл.
Приведенные выше примеры взяты из моих математических станций сложения двух цифр и иллюстрируют, как учащиеся могут разбивать числа на части и складывать значения каждого разряда. Разделение также называется разгруппированием или декомпозицией, в зависимости от используемой математической программы.
Вы заметили, что в одной из задач выше ученик прибавил 60 +40 и получил 106, но написал правильный ответ на задачу? Как вы думаете, что происходило с этим студентом? У вас тогда он не смог сложить 60+40, сделал глупую ошибку, или есть другая причина, по которой он написал 106? Увидев, как учащиеся взаимодействуют с этими типами стратегий, вы сможете начать разговор с ними об их математическом мышлении.
Еще один пример из некоторых карточек с дополнительными заданиями, где учащиеся только разбивают второе число, а затем делают прыжки на 10 и 1, используя таблицы 100 и 1000. Несмотря на то, что в первом классе мы много практикуемся, используя таблицу со сотнями, я обнаружил, что учащиеся не обязательно переносят свое обучение на более крупные числа во втором классе.
Прибавление десятков к десяткам и единиц к единицам (разрядное значение)
Это очень похоже на стратегии разбиения на части, за исключением того, что числа не разбиваются на части. Учащиеся могут мысленно складывать части числа (десятки или единицы), потому что они знают факты сложения.
В основном мы используем v-модель для рисования линий, соединяющих десятки, и сложения или вычитания этих частей.
Вот один пример того, как мы использовали это в классе:
Вычитание десятков, вычитание единиц (разрядное значение)
Подобно сложению десятков к десяткам и единиц к единицам, учащиеся вычитают каждое разрядное значение отдельно, а затем вычитают те из десятков (или добавить его). Есть два основных способа использования этой стратегии. Студенты могут разложить десять или студенты могут использовать отрицательные числа.
Я использую эту стратегию со студентами с отрицательными числами. Я знаю, что мы не учим отрицательные числа во втором классе, но для некоторых учеников это действительно способ, которым они понимают и могут придерживаться большего, чем другие стратегии. Вы можете увидеть примеры этого на второй и третьей якорных диаграммах выше.
Подумайте о 64-47. Если я вычту 4-7, я получу -3. Я говорю учащимся, что перед большим числом стоит знак «минус», поэтому у него есть еще что-то, что нужно убрать.
Затем ученики вычитают 60-40, получают 20 и вычитают еще, чтобы получить 17. эта стратегия касается отношений между сложением и вычитанием или позиционным значением. Стратегия «думай-сложение» похожа (если не совпадает) на стратегию «Подсчитай» или «Сложи». Эта стратегия также очень похожа на стратегию «Разделить на части» в том смысле, что учащимся необходимо разбить хотя бы одно из чисел, чтобы произносить звук вверх или вниз по частям числа.
Хотя учащиеся умеют считать единицами, я настоятельно рекомендую вам помочь им перейти к более эффективным стратегиям и считать сначала десятками, а затем единицами. Использование диаграммы сотен позволяет учащимся практиковаться в перемещении на 10 секунд вверх и вниз по диаграмме. Диаграмма сотен похожа на сжатую числовую линию. См. фото выше с графиками 100 и 1000.
Вот несколько примеров подсчета:
Приведенные выше два примера — это всего лишь те, которые мы выполнили на доске, и я попросил учеников записать их в своих тетрадях.
Это страница из моей тетради с двузначным вычитанием. Эти книги с клапанами проходят через несколько различных моделей и стратегий и дают учащимся возможность попрактиковаться в словарном запасе и объяснении своего мышления.
Что мне НРАВИТСЯ в этих тетрадях, так это то, что учащиеся могут глубоко погрузиться в один из аспектов вычитания двузначных чисел и прикрепить язык к числам и процессам, которые они используют.
Использовать компенсацию (свойства операций)
Последняя стратегия не похожа ни на одну из предыдущих. По сути, вы должны убедиться, что числа сбалансированы в рамках проблемы и что вы учитываете все части. Это предшественник алгебры и отличная стратегия для ментальной арифметики.
Существует несколько различных способов использования компенсации, но основная идея заключается в том, что вы добавляете или вычитаете часть одного числа и прибавляете его к другому числу, чтобы получить понятное число. Вы должны следить за тем, что было добавлено или убрано, и как-то учитывать это в задаче.
Компенсация особенно полезна для чисел, близких к дружественным числам, хотя ее можно использовать для любого числа. Например, 68 — 39 можно преобразовать в 69 — 40. Я добавил к каждому числу единицу. Значение +1 и -1 равно 0, поэтому я вообще не изменил задачу.
Вот еще один пример: 53 + 38. Я мог бы добавить 53 + 40 и получить 93, но поскольку я добавил два к 38, чтобы получить 40, мне нужно вычесть два из 93, чтобы получить 91.
Базовый Идея с компенсацией заключается в том, что вы превращаете одну часть числа в понятное число, чтобы упростить сложение или вычитание. Однако, когда вы корректируете одно число, вы должны отслеживать то, что вы корректировали, и компенсировать это.
Что нужно знать учащимся, прежде чем использовать эти стратегии?
Вышеупомянутые стратегии очень эффективны, если учащиеся могут добавить их в свой набор инструментов при приближении к двузначному сложению и вычитанию. Тем не менее, чтобы эффективно использовать вышеуказанные стратегии, учащимся необходимо иметь несколько вещей.
Факты сложения и вычитания – Учащиеся должны довольно бегло владеть фактами сложения и вычитания. Нужно ли запоминать их все быстро? Нет. Однако, если учащиеся тратят слишком много времени, пытаясь понять факт сложения, и это мешает им сосредоточиться на стратегии, потому что они забывают, что они делали, тогда им нужно более бегло обращаться со своими фактами сложения и вычитания. Мои оценки автоматизма помогают учащимся практиковать свои факты с помощью стратегии.
Способность находить дружественные числа — В начале года мы долго развиваем беглость речи, используя 10 в качестве эталонного числа. Хотя мы делаем это в начале года, чтобы улучшить беглость математических фактов, это также полезно, когда учащиеся начинают свое путешествие со сложения и вычитания двузначных чисел. Учащиеся должны знать, как перейти к следующему дружественному числу, которое, по сути, является их фактами о десятках, но применяя их к двузначным числам, чтобы найти следующие десять.
Прибавление 10 к числу — Мы начнем наш модуль сложения двух цифр с большой практики прибавления и вычитания десяти из числа. Это базовый навык как в моих двузначных продуктах сложения, так и в моих двухзначных продуктах вычитания. Учащиеся должны увидеть схему прибавления 10 к числу.
Разрядное значение — Чтобы складывать двузначные числа, учащиеся должны хорошо знать понятия единиц и десятков и понимать, что значит разбивать число на единицы и десятки. С первого дня в школе мы делаем ежедневные математические упражнения, которые развивают беглость со значением разряда, а также пропускают счет на 10 с любого числа.
Обучу ли я традиционному алгоритму?
Да и нет. Да, я преподаю концепцию перегруппировки и да, я учу студентов двигаться к эффективности при сложении и вычитании. Это может включать традиционный алгоритм , если они смогут понять его значение.
Ученикам не нужно использовать стандартный алгоритм до четвертого класса (в соответствии с Common Core Standards).
Могут ли они сделать это раньше? Может быть.
Я показываю им это во втором классе как модель, которую они могут использовать; однако мы не уделяем этому много времени, потому что я хочу, чтобы студенты вырабатывали стратегии решения задач, а не были привязаны к одной модели.
Когда мы работаем с традиционным алгоритмом, мы придаем ему много слов и значений, как правило, связывая его с работой, которую мы уже сделали, например, с нашей работой с блоками с основанием 10. Вот несколько примеров того, как я обучаю студентов традиционному алгоритму, связывая его с моделями, которые мы уже использовали, и давая студентам точный язык для объяснения их мышления.
Вот несколько примеров того, как я даю учащимся опыт работы с традиционным алгоритмом.
Вы заметили, что должно быть 7 десятков и 11 единиц? Ученик не обратил внимания на блоки с основанием 10!
Они взяты из моего пакета «Разложи десять», который уравновешивает работу традиционного алгоритма с моделями с основанием 10 и дает учащимся язык разложения чисел.
Ух ты, столько информации нужно переварить! Существует множество различных моделей и стратегий, которые учащиеся могут использовать для решения задач на сложение и вычитание двузначных чисел. То, что я обрисовал в общих чертах выше, является некоторыми, которые я нашел особенно полезными для студентов. Они помогают учащимся разработать прочную основу для сложения и вычитания двузначных чисел, создать мост к сложению и вычитанию трехзначных чисел, а также подчеркнуть идею использования стратегий и моделей для решения проблем, а не просто следования шагам в процессе.
Если вы преподаете во втором классе, вам могут понравиться несколько страниц из некоторых моих продуктов для сложения и вычитания двузначных чисел. Я собрал этот PDF-файл ресурсов в качестве образца из нескольких различных продуктов, которые действительно подчеркивают всю работу, которую мы делаем в нашем классе, для углубленной разработки этих стратегий.
Различные компоненты сэмплера могут использоваться всей группой или небольшой группой и идеально подходят для того, чтобы помочь вашим ученикам мыслить нестандартно, когда дело доходит до решения многозначного сложения и вычитания.


 Этап самоопределения к деятельности
Этап самоопределения к деятельности
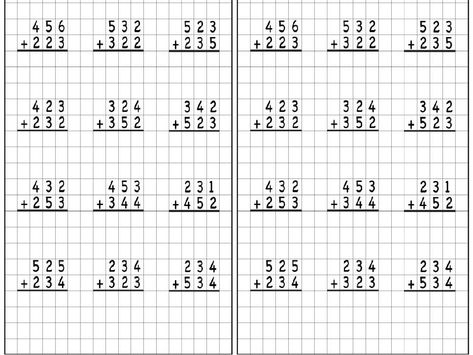 На маркерной доске чертите схему, обсуждаете решение, затем каждый решает сам, сверяете ответ и зажигаете звёздочку, затем я даю образец решения, вы проверяете и фиксируете в табличках свои успехи.
На маркерной доске чертите схему, обсуждаете решение, затем каждый решает сам, сверяете ответ и зажигаете звёздочку, затем я даю образец решения, вы проверяете и фиксируете в табличках свои успехи.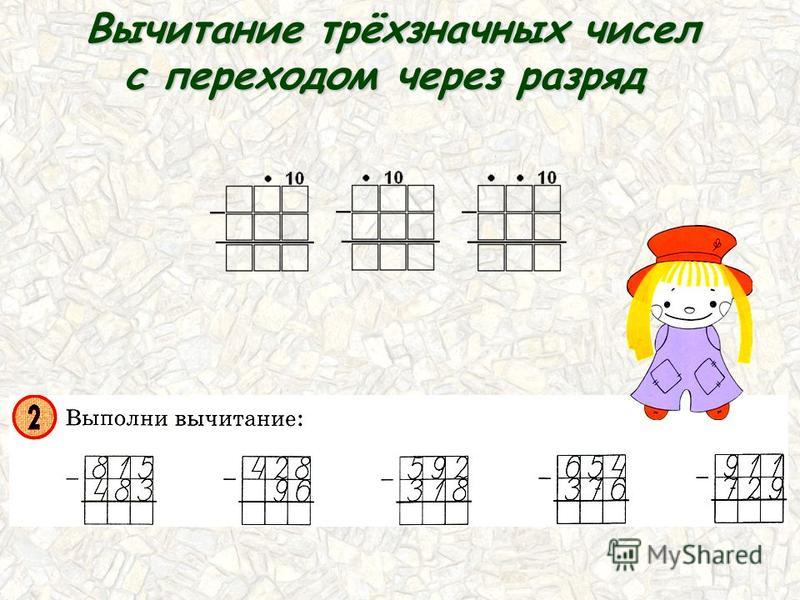

 Запишите сумму (5) в столбце сотен.
Запишите сумму (5) в столбце сотен. Для этого мы поместим 5 в столбец десятков (соответствующий столбец) и поместим 1 поверх столбца сотен (предыдущий столбец). Другими словами, когда мы получаем двузначные числа в виде суммы, мы помещаем цифру единиц в соответствующий столбец, а цифру десятков переносим в следующий столбец слева. Этот перенос добавляется в тот столбец, где он размещен, и добавление продолжается.
Для этого мы поместим 5 в столбец десятков (соответствующий столбец) и поместим 1 поверх столбца сотен (предыдущий столбец). Другими словами, когда мы получаем двузначные числа в виде суммы, мы помещаем цифру единиц в соответствующий столбец, а цифру десятков переносим в следующий столбец слева. Этот перенос добавляется в тот столбец, где он размещен, и добавление продолжается.
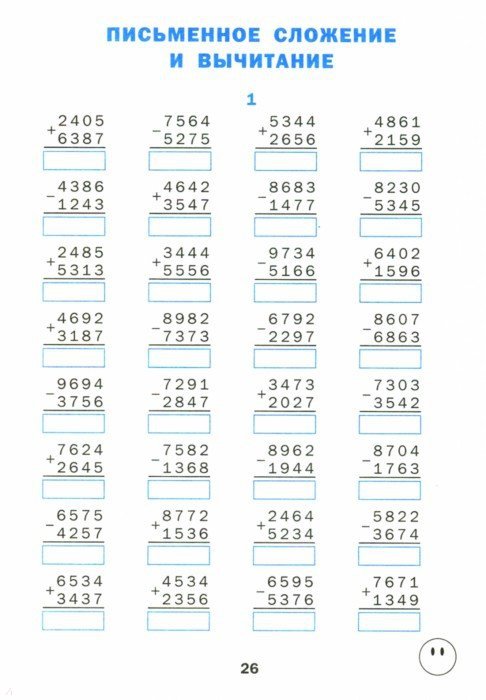
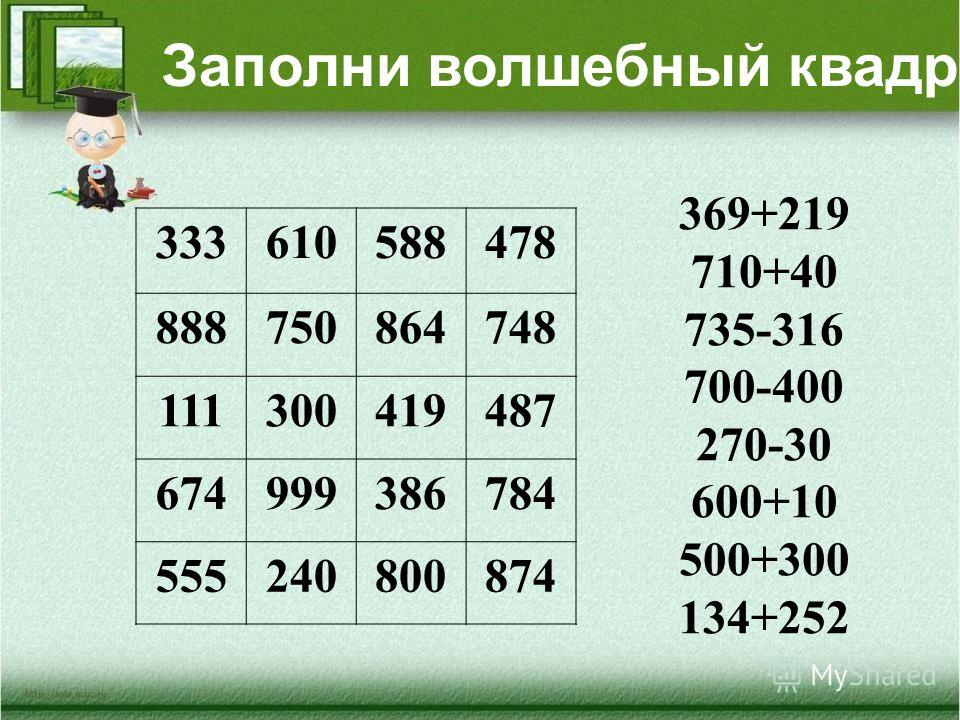 Эта 1 (перенос) будет добавлена вместе с числами в столбце десятков.
Эта 1 (перенос) будет добавлена вместе с числами в столбце десятков. Для этого мы запишем 2 в столбце единиц и перенесем 1 в десятки столбец. Эта 1 (перенос) будет добавлена вместе с числами в столбце десятков.
Для этого мы запишем 2 в столбце единиц и перенесем 1 в десятки столбец. Эта 1 (перенос) будет добавлена вместе с числами в столбце десятков.